Abstract
In this chapter the author adds an infection feature to an actuarial multiple state model to give a simple model for an infection such as COVID-19. The model is simple enough to be replicated in an Excel worksheet, with one row per day of calculations. The whole population is treated as homogenous, with no distinction by age, sex or anything else; to that extent it is unrealistic, but to include these features would complicate it considerably. To fit it to observed data requires successive optimisation by programme, and this is described. Different variations of the model allow it to fit better and take account of, for example, immunisation by vaccine. It is shown to fit the past events in the United Kingdom (U.K.) quite well, and it has also been fitted to other countries, but this is not shown in this chapter. It is also observed that this, or any other model, is of less use for forecasting the future, because it cannot predict the behaviours of governments or of populations. But various assumptions can be made about the future, as at the latest date of calculation (1 March 2021), and interesting consequences are shown.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
3.1 Introduction
Actuarial multiple state models have great similarities with epidemiological models for infection. In this Chapter the author combines the two to give a simple model for an infection such as COVID-19. In Sect. 3.2 multiple state actuarial models are described. In Sect. 3.3 the elements of the simple model are explained, and comparisons with SIR models are made in Sect. 3.4. The necessary initial assumptions for the model are stated in Sect. 3.5. How the variable daily parameters are estimated is explained in Sect. 3.6.
An alternative, Model 2, is introduced in Sect. 3.7, and results for the U.K. (up to the latest date of calculation) for the two models are shown in Figs. 3.1, 3.2, 3.3, 3.4 with comments in Sect. 3.8. Two new Models, 3 and 4, are introduced in Sect. 3.9, with results shown in Figs. 3.5, 3.6, 3.7, 3.8 and further comments on the results in Sect. 3.10.
Some hypothetical projections from the latest date of calculation are described in Sect. 3.11 and their consequences are shown.
Some remaining problems are discussed in Sect. 3.12, reference is made in Sect. 3.13 to other countries, and Sect. 3.14 concludes.
3.2 Multiple State Actuarial Models
Actuaries are familiar with several multiple state models. The simplest is the life table. A person can be in one of two states, Living or Dead and can move from one to the other, but in this case only in one direction. We assume that at age, or time, x there are L(x) persons in state Living, and D(x) persons in state Dead. The total \(T = L(x) + D(x)\) is necessarily constant.
To describe the rate of transfer between states we can use either a continuous or a discrete model. The continuous model uses the derivate:
where \(\mu (x)\) is the “force of mortality” or “continuous transition intensity” from living to dead. The discrete model uses a unit time step, often, but not necessarily, a year:
where q(x) is the one-year probability of death of a life aged x.
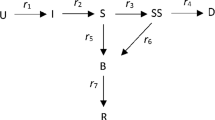
A more complicated actuarial model is that for income protection (IP) insurance for sickness, where the states are: Healthy, Sick and Dead, with exit from Sick either by recovery back to Healthy or by death to Dead, and these rates depend both on age at start of sickness, x, and duration in the Sick state, z, see Continuous Mortality Investigation (1991). For this a continuous model is best, with the numbers in different states as: H(x), D(x) and for sickness a continuum with density S(x, z). Transfers are then:
-
new Sicknesses from Healthy at rate \(\sigma (x)\cdot H(x)\)
-
new Deaths from Healthy at rate \(v(x)\cdot H(x)\)
-
recoveries back to Healthy from Sick(x, z) at rate \(\rho (x, z)\cdot S(x, z)\)
-
new Deaths from Sick(x, z) at rate \(\mu (x, z)\cdot S(x, z)\).
A discrete model is harder to define in this case, because of the possible circular movements from Healthy to Sick and back, and the multiple reasons for exit from Sick. In practice a daily step has to be assumed in the data for the estimation of the (assumed) continuous rates.
3.3 A Simple Daily Model for Infection
An infection model is similar to the IP model for sickness, with a fundamental difference in one respect. Whereas in the IP model the transitions from Healthy to Sick depend only on the numbers in the Healthy state, in an infection model they depend also on the numbers in the Sick (or Infected) state. In the simple model we ignore age and replace x by time t, measured now in days. Initially we also ignore duration of infection, z, and denote those Infected at time t as I(t). We then assume that an infected person can potentially pass the infection to others at a rate of r(t) per day, but that only those who are not infected already can move to the Infected state.
A continuous model would thus give us:
We omit D(t) from the denominator, because we assume that they cannot become infected at all. This is essentially the SIR infection model described in Chap. 2 of this book, with different names for the states.
For simplicity in practice I have used a discrete model, with daily steps, and with the Infected at time t subdivided by days infected, d, giving us I(t, d). For this model I ignore deaths and sicknesses other than from the relevant infection, and I ignore age, sex and any other variability in the population.
Time is measured in discrete days, t, and changes happen at the end of each day. On day 0 there are H(0) in the population, none of whom are infected. On each day t, there are HI(t) new infections (I explain below how these are calculated) moving from Healthy to Infected; thus on day \(t+1\) there are \(I(t+1, 1)\) infected. On each day these may die, with mortality rate m(d), so:
and new deaths on day t are
The total number Infected on day t are
and the total Living on day t are
The proportion healthy among the living is
The total number of deaths by day \(t+1\) is
and the grand total of the population on day t is
This is constant, but it is useful to calculate it to check that the calculations are accurate.
On day t there is a basic infection rate r(t), which can vary by t. Those infected with duration d have a relative infection rate of pr(d) so their infection rate is pr(d).r(t). The number of new infections generated by those infected on day t with duration d is
The total number of new infections on day t is
as noted above.
To start the epidemic we need one or more initial infections. We put these in as so many at the end of day \(t_0\), so that
or such other number as we wish.
Once infected, persons remain in the count of infected, but their relative infectiousness pr(d) may reduce to zero by some duration, say M, so that all of those infected on or after duration M can be added together in I(t, M), with zero infectiousness. We think of them as recovered, but do not, as in the SIR model remove them altogether. They cannot become infected again, so are correctly in the denominator but not the numerator of g(t). All this is true for many infectious diseases and I assume that it is true for COVID-19, but it may not be. For other diseases it may also not be true, and once infected, always infectious. This can be represented in this model by keeping pr(M) non zero.
3.4 Comparisons with the SIR Model
In the simplest SIR model there is no allowance for duration of infection, so no variation in infectiousness by duration. Nor is there any explicit mortality, since those in the R state are recovered. But this simple model has many variations that can include some of these features.
A value in the SIR model that is often publicly quoted is denoted \(R_0\) or just “the R number”. This is the number of infections caused by the (hypothetical) first patient. If \(R = 3\), then one infected passes the disease on to three others, each of them to three more, etc. It is given as an absolute number, but it needs also a time scale: infecting three in a day is very different from three in a month. It seems that the publicly quoted number in the U.K. is about “per week”.
In the simple model described above, a value of \(R_0\) can be calculated, along with a time scale. A new infected is able to infect others depending on his/her duration of infectiousness. The number of new infections on day d depends on the proportion who survive to day d, and their rate of infectiousness. So we first calculate the proportion of survivors, allowing for mortality, by putting
and then
for as far as we need, and assuming that those of duration M and greater are no longer infectious.
We then calculate
and our estimate of \(R_0\) on day t is
The average time till infection is given by first calculating
and then the average time
In this simplest model the values of, S, T and U do not vary with time t.
However, the effectiveness of infection at time t is diminished by the factor g(t), the proportion of the population available to infect. Initially this is close to unity, but as the disease progresses, more of the population may have become infected, and cannot be reinfected, so that a level of population immunity may be reached (“herd” immunity is a term appropriate for cattle). The effective R value at time t is therefore
This damping by g(t) increases with time t.
3.5 Enhancements for COVID-19 and Initial Assumptions
The model so far described suits situation where all infections are known about as soon as they occur, as with a small closed population and a disease that is immediately apparent. However, this is not the case far COVID-19 and we describe the features as they became apparent in the U.K. In other countries it may not be quite the same.
In the first few days an infected person may show no symptoms, so the fact of infection and infectiousness is not known. Then when symptoms do appear, the infected may not be tested and counted as infected unless the symptoms are bad enough for him/her to go to hospital. We represent this by postulating that, of all the new infections on day t, I(t, 1), the symptoms do not appear until duration day K, and then only a fraction, f(t), are recorded as having COVID-19. Then we assume that deaths only occur among those whose infection is bad enough to have been recorded.
In the simplest model effected so far for the U.K., I have assumed that day K is day 6, that day M is 36, that \(f(t) = 0.1\) for all t, i.e. only one tenth of all cases are reported (but this changed later). I then assume that \(pr(d) = 1\) for \(d = 1\)–5, \(= 0.5\) for \(d = 6\)–15, and \(= 0\) thereafter. This implies that in the first few days before symptoms have appeared, the infected is wholly infectious, but that when symptoms appear he/she stays isolated to some extent, so the relative level of infectiousness is halved. I then assume that \(m(d) = 0\) for \(d = 1\)–5, equals some constant level m for days 6–15, and is zero thereafter.
All these assumptions are rather arbitrary. If one had access to full hospital data, one could estimate the values of the mortality rates, m(d), by day of infection, but if these have been calculated by anyone, they do not seem to have been made public yet. With more testing of individuals, the value of f(t) may well increase with time, but it is always difficult to estimate what faction of any large population is not in some category without large sampling, or careful random sampling.
With this model one can insert arbitrary parameters and see what effect different assumptions make. For example, if the infected continue to be infectious beyond day M, then ultimately the whole population becomes infected, but with anything short of this, there may be some value of r(t) that is low enough to leave an uninfected residual. If the mortality of the infected is very high, then with a low enough level of infectiousness the epidemic dies out, perhaps quite quickly, but with a higher level then ultimately everyone dies. These are all extreme cases, but it helps to understand what can produce them, although COVID-19 does not seem to be so extreme.
3.6 Estimating Parameters Model 1
In order to compare this model with the available facts we need to use some available data. I have used the data collected by the European Centre for Disease Prevention and Control (2021), ECDC, which gives data, for a very large number of countries, of the number of New Cases and New Deaths for each day up to 14 December 2020. After that date ECDC gives the numbers in each week, from the start of 2020, but not for individual days. To get continuing daily data one has to look for the records of each country separately, which is much less convenient.
There are many ways in which one could choose parameters that would in some way match the actual numbers of cases and of deaths with those expected by the model. I follow an idea of Wüthrich (2020) and I have chosen one way to do it, but many others might be as good or better. After an initial starting period, as described below, I allow the rate of infection per day, r(t), to vary for each time day t, and I estimate it for each t. I assume that the rates of morality, m(d) are equal for day of infection from day 6 to day 15, and zero outside those days, but that at each estimation step they are the same for all times, t.
To estimate the rates for time t, I choose a 14-day period, with day t as day 7, so from day \(t-6\) to day \(t+7\). For days up to \(t-7\), I assume the values of r(t) which have been estimated already, but the value of the mortality rates, for this estimation, is constant for all t and d and equals m(t). I then choose the values of r(t) and m(t) by equating the expected (E) and actual (A) cumulative number of Cases (C) and the cumulative number of Deaths (D) as at day \(t+7\), the end of the 14-day period. This can be done by minimising the function F(r, m) calculated as:
and at the optimum values of r and m, we get
To start the estimation I choose a day when the numbers of cases and deaths are non-zero for most days, and estimate single rates, r(t) and m(t) up to that day. In the very early stages the numbers of new cases are very erratic, and the numbers of new deaths are often zero for a week or two after the numbers of new cases cease to be zero, and a comparison of actual and expected is poor.
Apart from the initial period, this process produces quite good values for r(t) for the whole period, and the expected numbers of cases for each individual day are fairly close to the actual number. In the initial period of the epidemic, during the “first wave” this method also gave quite good comparisons for deaths, but as time went by the comparison of deaths became poor, so I developed Model 2 described below. Results for Model 1 are shown later along with those for Model 2.
3.7 Estimating Parameters Model 2
Since my Model 1 did not give a good correspondence between actual and expected daily deaths, I changed the model a little. Instead of keeping the mortality varying by duration, but not by time, I allow the rates to vary by time, so that each day, t, has a basic mortality rate, m(t), and there are fixed ratios that vary by duration, d, denoted pm(d) so that the mortality rate at duration d at time t is \(m(t, d) = m(t).pm(d)\). This is a very similar pattern to the rate of infection, with daily rate r(t), and intensity on day d of pr(d).
I fix the values of pm(d), to be zero except for days 6–15 inclusive, when they have value 1.0. This is the same pattern as described for Model 1. This can be accommodated in an Excel spreadsheet, with more columns, to show the values of m(t, d), and of p(d), the surviving infected, which now also vary with time t, as do T, U and S.
I then use almost the same estimation procedure for fitting the values of r(t) and m(t), except that instead of making m the same for all past days in one calculation, it varies like m(t). I show the results in Figs. 3.1, 3.2, 3.3, 3.4, using the ECDC data for the U.K. data up to 14 December 2020, and adding data from Office of National Statistics (2021) up to 28 February 2021.
The inception rates for Models 1 and 2 are almost identical, so only one set is shown.
3.8 Comments on Results of Models 1 and 2
We can see from Fig. 3.1 that the numbers of actual new cases reported each day are very erratic, nothing like consistent with the expected numbers with a binomial, Poisson or normal probability model. From Fig. 3.2 we see that the numbers of reported deaths are even more erratic. We have assumed uniformity in our population, and the true position is very far from this, so some variation would be expected as with any actuarial model. However, the gross irregularities shown are more likely because of great irregularities in reporting.
Both models show almost the same quite smooth curve for expected cases reported and fit the centre of the irregular actual events quite well. We see the smaller first wave of March and April 2020, reduced by the first lockdown. After a comparatively mild summer the second and third waves appear in late 2020 and early 2021, with far more reported cases than in the first wave, and more deaths, but with a smaller proportionate increase. We continue the model to mid-May 2021 and we comment on these results below.
In Fig. 3.2 we see that the actual numbers of deaths reported each day and the numbers expected by both models are fairly different from each other. The reported numbers are also very irregular, but the expected numbers with Model 2 are reasonably good, whereas Model 1 fits rather badly.
In Fig. 3.3 we see the estimated values of the infection rates, both the “gross” \(R_0(t)\) described earlier, and the “net” Rg(t). In the early stages of the epidemic, these are quite close because very few of those that are not currently infectious have been infected already. But as more of the population becomes infected, the more those who are infectious are in contact with those who have already been infected, and population immunity grows.
I explained above that I had initially assumed, on the basis of casual press comments, that only 10% of those infected were sufficiently ill to report their infection, and so have their infection recorded. I assume that \(f(t) = 0.1\) for all t. By the middle of January 2021 some 3.4 million people had been reported as infected, which would imply that some 34 million people in the U.K. had been infected, or about half the population. So my estimate of g(t) is about 0.5, and the net infection rate is about halved, going down from a gross rate of about 1.8 to about 0.9 and progressively lower as the rest of the population becomes infected. At these levels the epidemic quite rapidly dies out, and my “projections” of the numbers of new cases and deaths reduce rapidly, as implied in Figs. 3.1 and 3.2.
This is a typical result for any infection that continues with a constant value of r(t) such that \(R_0(t)\) is greater than 1. The curves of expected cases and of deaths rises exponentially initially, curve over at peak, and fall symmetrically on the way down. On a vertical logarithmic scale the curve closely resembles a hyperbola, but is not exactly equal to one. The maximum is when \(g(t) = 0.5\), and the number of cases so far is at half its total number, as are the numbers of deaths with perhaps some time-lag. Figures 3.1 and 3.2 show that the peaks of new cases and new deaths were reached during January 2021, and by mid-April would be quite small. It assumes that the present level of lockdown continues indefinitely so that the value of r(t) is held constant. This seems at the time of writing a very optimistic scenario. My assumption of half the population being infected seems wrong.
The increase in testing suggests that far more than 10% of cases of COVID-19 are being reported, but I see no indications of how many this would be. Indeed, if many people experience the infection, but show no symptoms at all, it seems difficult for anyone to estimate their numbers without either very extensive testing of a population, or testing of a very carefully selected sample. I see no way of estimating a variable f(t) from the published data, but it would be possible, by extending the model, to insert an arbitrarily changing value of f(t), going up from say 10% at the start to some much higher value, perhaps 70% at some later date.
Figure 3.4 shows my estimates of the aggregate mortality rate m(t) on the two models. It seems to have been quite high, about 2% in the first wave, but much lower, below 1/2% by the end of the period. It is reported that treatment has greatly improved, so this is not implausible. But the estimates are greatly affected by the estimate of the proportion reported. If the observed deaths (all of which are included in the reported cases) come from only 10% of those actually sick, then the population “case fatality rate” is only one tenth of that observed among the reported cases, but if the reported cases are half the total actual cases, then the observed deaths come from a smaller total number of cases and the cases and the rates should just be halved. It is possible that my observed reductions in mortality are in fact caused by the increase in testing, and consequent changes in f(t).
3.9 Further Extensions: Models 3 and 4
Taking account of these various considerations I add two more models. In Model 3 I vary f(t), starting as before at 10%, then increasing by 1/2% per day from 16 July 2020 to reach 70% by 12 November 2020 and leaving it at 70% thereafter. This is rather arbitrary, but it does produce the result that by 31 December 2020, when the number of reported cases exceeded 2.4 million, my estimate of the number of actual cases is about 6.9 million or just over 10% of the total population of the U.K. (I assume that this is 67.8 million). This accords with press reports of other estimates made at that time.
In early 2021 vaccination on a large scale started in the U.K., and elsewhere. This can easily be inserted into the model. One has an extra status, Vaccinated, with V(t) persons in it. People are transferred from Healthy at so many per day depending on available and estimated figures. They come into the denominator of g(t), but are excluded from the numerator; it is assumed that the infectious can meet the vaccinated, but not infect them. So with more vaccinations the value of g(t) is reduced, and consequently the net infection rate reduces and the epidemic diminishes. This can be fitted into my simple model.
In Model 4 I introduce vaccination. I simplify this greatly by assuming that only one vaccination is necessary to give full immunity, with no delays. I use the published figures for first vaccinations given, with a little estimation initially, starting on 26 December 2020 with about 140,000 vaccinations per day, increasing to about 350,000 per day during February 2021, and I then assume 350,000 per day thereafter, until all Healthy are vaccinated by about the middle of June. This is unrealistic in that I assume that the first vaccination is wholly effective, and that all persons of all ages, except for those who have been infected with COVID, are vaccinated, including “antivaxers” and infants and children.
The results are shown in Figs. 3.5, 3.6, 3.7, 3.8 along with those for Model 2 (I now discard Model 1).
3.10 Comments on Results of Models 3 and 4
We can see from Fig. 3.5, as in Fig. 3.1 that the numbers of actual daily new cases have dropped during the latter part of January 2021. Presumably this is the result of the most recent lockdown at that time. My estimated \(R_0(t)\) drops to just below 1 for Model 3, but is higher for Model 4. But the net rate, Rg(t), for Model 3 is below 1, at about 0.8, and for Model 4 is much lower. All three curves of expected new cases in Fig. 3.5 show them declining quite rapidly, with the too optimistic Model 2 being lowest, Model 3, with variable f(t), the highest and Model 4, with vaccines, intermediate. By September, the latest date shown here, the expected number of cases in Model 3 is about 100 per day, with a handful of deaths. This Model assumes that the latest estimated value of r(t) continues indefinitely, which is unlikely to be the case if lockdown measures are relaxed as the cases reduce.
Fig. 3.6 shows the same patterns of results for expected deaths.
It is interesting, however, that with the assumptions of Model 3 the epidemic dies out long before everyone has been infected. Continuing the model projections gives ultimately about 10 million infections, of which about half, or 5 million, are reported, and there are about 140,000 deaths in total. On these assumptions, population immunity is not achieved, nor required. But perhaps a permanent lockdown is required for this model to be valid, which would have other severe consequences, social and economic, which I do not go into here.
With Model 4 the estimated r(t) rate when vaccinations start rises above that estimated with Model 3. As many become vaccinated, one needs a higher transmission rate to get the same number of expected cases, to match the actual numbers. But the net rate Rg(t) falls well below that for Model 3 because of the vaccinations. On my assumptions the entire uninfected population is vaccinated by later in June 2021, and a few weeks before that the expected numbers of reported new cases and of deaths have dropped to a handful. Within my homogeneous population I do not separate out children, but very young children might well not be vaccinated at all; and also there will be some people that decline to be vaccinated or have some medical reason for not being vaccinated. I also assume no further imports of infection, so Model 4 is likely to prove too optimistic.
3.11 Projection Models
Using my estimation results as at the end of February 2021 it is possible to make experimental projections of the numbers, on different, but arbitrary, assumptions. I make four of these, called 5A, 5B, 5C and 5D and the projected numbers of new reported cases and of deaths are shown in Figs. 3.9 and 3.10.
In Model 5A I continue Model 3, assuming that no vaccinations have happened (or alternatively that vaccinations have no effect whatever), and then that on 8 March 2021 most lockdown measures are relaxed, and the r(t) rate goes up immediately to 0.155, about the same as my highest estimated rate in the middle of December 2020, but still well below my highest estimated rate in March 2020 of almost 0.23. The result of this would be a rapid increase in both cases and deaths, with reported cases in June and July exceeding 200,000 a day, and deaths exceeding 8,000 a day, both far higher than in previous waves. These are a long way off the scale of the charts.
By the end of July this projection has g(t) falling to below 0.5, so half the population would have been infected. The numbers of new cases and new deaths would decline to a low level by the end of 2021, by which time total deaths would have reached about 850,000 (compared with about 116,000 at the end of February 2021), but g(t) would still be about 0.45, so not much more than half the population would have been infected. I do not suggest this as a likely projection, but as a warning “what if” one.
In Model 5B I continue Model 4, allowing for the vaccinations that have taken place, but assuming that they stop entirely on 8 March 2021, at the same time as the r(t) rate goes up to 0.155, as in Model 5A. The effect is quite different from that of Model 5A. There is a small jump up in the expected numbers of cases with a continuing fall thereafter, and a continuing fall in deaths. The number of vaccinations is already enough to reduce Rg(t) to well below unity.
In Model 5C I modify Model 5B by assuming that vaccinations continue as in my Model 4, until the whole population is vaccinated by later in June, but with the same relaxation in lockdown as in Models 5A and 5B, rising to 0.155 on 8 March 2021. The projected numbers of aces and of deaths is a bit lower than in Model 5B. and they fall to zero once the whole population is vaccinated.
In Model 5D I follow the dates of what has already been announced by the U.K. government (actually only in respect of England, but I make no distinction in my model between the different nations in the U.K., and England accounts for much the largest part of it). I assume roughly equal steps in increasing r(t), from an estimated 0.137 at the end of February to 0.140 on 8 March 2021, to 0.144 on 29 March, to 0.148 on 12 April, to 0.151 on 17 May and finally to 0.155 on 21 June. These dates have been announced as the earliest dates of steps for unlocking, but I assume that they are in fact realised. The results show projected new cases and deaths even lower than in either of the two previous models.
These experiments suggest that vaccination is likely to do the required job, and to allow certain amount of relaxation of lockdown. But my assumptions that the first vaccine is 100% effective, that the whole population is vaccinated, that there are no imported cases, and no nasty new variants of the virus, are all on the optimistic side.
3.12 Problems and Unknowns
I have mentioned above some of the difficulties with this simple model. I make many assumptions, and I do not know whether these are correct. I assume that those infected show symptoms on day 6; this should perhaps be a distribution of different days. I assume initially that only 10% of cases show bad enough symptoms to go to hospital or even be tested, with this the proportion increasing with Models 3 and 4, but even those assumptions may be wrong.
I assume that those infected are fully infections for five days, but only half as infectious for the next ten days, and not at all thereafter. But many cases are reported of people being sick for much longer than this, and perhaps for much less, so their infectiousness may also vary. I assume equal mortality rates for days 6–15, but this is arbitrary, and cases are reported of much longer periods before death has occurred.
I assume that after some days (15 so far), those infected cannot pass on the disease and cannot themselves get it again. This latter seems in a few cases to have been incorrect, and we cannot know how long any immunity might last, until a longer period has passed. Nor for certain do we know what immunity vaccines will provide.
I assume a single homogenous population, but it is well known that mortality rates vary greatly by the age of the individual and to a lesser extent the sex, and also to some extent the ethnic status. The extent to which different individuals are able to isolate themselves may vary very much by age, and perhaps by other factors. The fit elderly may find it easy to be very isolated at home, and so run very little risk of infection. The seriously ill elderly may be in a care home, and at high risk. So the population available for infection may vary with time quite a lot, depending on what people do and can do; go to work or work from home; live alone or with an extended family; have children at school or not at school. In different stages of lockdown these may have had very varying influence.
Elaborations that would be needed, or at least desirable, in a more comprehensive model would be variation by age and sex, perhaps stratification into a smallish number of discrete classes. This would require the attribution of a different mortality rate to each class, perhaps calculated as an overall m(t) multiplied by a class-specific ratio, to give a value for each class. One might be able to get such relative values from published data. Then one would wish to have a square table of contacts between members of each class with each other class, to vary the relative level of infectiousness across classes; it might be very difficult to get estimates for this.
A further elaboration would be to model region or localities separately. It has been clear that the disease has affected different areas differentially, some having high rates and others low at the same time, but then perhaps then reversing; some having increasing rates and others decreasing rates. Further, different levels of lockdown have been imposed in the different parts of the U.K., both in the separate countries and in separate areas within those countries. Allowing all the variability described above for age classes, and the further complications of contacts between areas might well magnify the model out of the realm of practicability.
I have also assumed that, apart from a single imported infection at some starting date, there has been no contact with other countries. This is manifestly untrue. Almost certainly there were several early imports from different places, and these have probably continued. It would also be the case that other countries have had imports from the U.K. and elsewhere. To identify these cases would be very difficult, and it is not obvious how one would model this feature, except by arbitrarily introducing a new imported infection every so often.
3.13 Other Countries
It is possible to fit these models to the daily data from other countries, but it is difficult to interpret any results without local knowledge of the conditions in those countries. The data may be collected by different regions within another country, and may be defined differently; the reliability of reporting may differ; the social and economic conditions of countries differ, and the various lockdown measures taken or not taken by the relevant authorities may also differ very much. I do not show any results for other countries here.
3.14 Conclusions
Experimenting with models such as I have described may give some insight into features of an epidemic, and they can be made to fit past data tolerably well. But they seem to be of less use in prediction. They can give “what if?” results, showing what would happen if certain assumptions about a stationary, or a changing, future were to occur, but less use in knowing what will actually happen. That depends very much on the actions of governments, the responses of individuals to governments and to the disease, on medical improvements in treating those affected, on whether vaccines will be available and on their possible efficacy, and also on what the virus itself does, with possible new mutations with different characteristics.
However, I hope that the experiments I have done shed some light on infection models for those not previously familiar with them, and also show how experimental projections might allow a better understanding of the effects of different government actions. But I hope that the models used by those who advise governments are considerably better than this very simple one.Footnote 1
Notes
- 1.
The author has placed specimen Excel worksheets, programmes, results, updates and other material on his website at: https://davidwilkieworks.wordpress.com/.
References
Continuous Mortality Investigation The Analysis of Permanent Health Insurance Data. CMI Reports 12, 1–263 (1991). https://www.actuaries.org.uk/system/files/documents/pdf/cmir12all.pdf
European Centre for Disease Prevention and Control (2021). https://www.ecdc.europa.eu/en/publications-data
Office of National Statistics (2021). https://coronavirus.data.gov.uk/details/download
M.V. Wüthrich, Corona COVID-19 analysis: Switzerland and Europe, 18 April 2020. SSRN: https://ssrn.com/abstract=3565765
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2022 The Author(s)
About this chapter
Cite this chapter
Wilkie, A.D. (2022). Some Investigations with a Simple Actuarial Model for Infections Such as COVID-19. In: Boado-Penas, M.d.C., Eisenberg, J., Şahin, Ş. (eds) Pandemics: Insurance and Social Protection. Springer Actuarial. Springer, Cham. https://doi.org/10.1007/978-3-030-78334-1_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-78334-1_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-78333-4
Online ISBN: 978-3-030-78334-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)