Epidemic Compartmental Models and Their Insurance Applications

Abstract

Our society’s efforts to fight pandemics rely heavily on our ability to understand, model and predict the transmission dynamics of infectious diseases. Compartmental models are among the most commonly used mathematical tools to explain reported infections and deaths. This chapter offers a brief overview of basic compartmental models as well as several actuarial applications, ranging from product design and reserving of epidemic insurance, to the projection of healthcare demand and the allocation of scarce resources. The intent is to bridge classical epidemiological models with actuarial and financial applications that provide healthcare coverage and utilise limited healthcare resources during pandemics.

2.1 Introduction

The COVID-19 pandemic has affected the insurance industry in many ways. Some notable impacts include a surge in insurance digitisation, volatile capital markets, and disruption in supply chain. These issues have prompted researchers to think beyond the standard actuarial framework to find ways to tackle them. While there has been extensive research on the transmission dynamics in the epidemiology and medical literature, traditional actuarial work has largely focused on mortality and morbidity rates using classical frequency and severity analysis. Actuarial life tables and mortality models lack flexibility and robustness to describe the rapidly changing environment during a pandemic. To that end, we explore the epidemiology literature and combine some of the commonly used models with actuarial methodologies.

In the past decade, some developments in the actuarial literature have intended to fill the gap between these two fields. A recent survey article by Feng et al. (2020) offers an overview of several approaches for infectious disease modelling such as compartmental, network, or agent–based models, and discusses their applications to epidemic and cyber insurance coverages. These novel applications represent efforts to integrate medical modelling with actuarial techniques.

This chapter focuses on compartmental models commonly used in the medical literature and their applications in the context of epidemic insurance and pandemic risk management. The organisation of this chapter is as follows. Section 2.2 introduces some important compartmental models, such as the celebrated SIR and SEIRD models. These are characterised by a system of differential equations, in the case of deterministic models, or transition probabilities for stochastic models. Section 2.3 presents an overview of some designs of epidemic insurance plans using compartmental models from the preceding section. Common actuarial concepts including annuities, benefits, and insurer’s reserve levels are explored. The section concludes with case studies using the actual COVID-19 data set. Section 2.4 illustrates another application of compartmental models in the subject of allocation of resources during a pandemic. In particular, we project the demand for critical medical resources and use actuarial concepts of capital allocation to optimally stockpile resources prior to a pandemic and to ration limited existing resources during the pandemic.

2.2 Compartmental Models in Epidemiology

The modelling of epidemics has a rich history and dates back at least to Aristotle’s work; see Brauer and Castillo-Chavez (2012) for a historical account. A popular framework is the so-called compartmental modelling, where the entire population is segregated into multiple compartments which correspond to different stages of a disease. Then the dynamics in the system is studied via a system of differential equations.

2.2.1 SIR Model

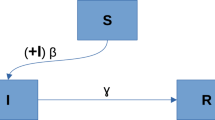
Consider a population of size N(t) which is indexed by time t. Based on the seminal work of Kermack and McKendrick (1927), the SIR model considers the following three compartments: Susceptible, Infected, and Removed. There are many variations of the SIR model; in what follows we lay out the assumptions for the most basic SIR model. First, there are no births or immigration, i.e. no one is added to the susceptible compartment, and the population mixes homogeneously. Second, the transmission dynamic is driven by the law of mass action, which means that the rate of secondary infection depends on both the size of the susceptible class and that of the infected class. The rate $\beta$ represents the number of contacts per individual per time unit to transmit the disease. Hence $\beta I(t)$ can be interpreted as the rate of contagious contacts. Since the disease is only transmittable in a contact between infected and susceptible individuals, then $\beta I(t) S(t)/N$ is the actual rate of transmission. Third, the size of the infected class is subject to exponential decay. The rate $\alpha$ represents the proportion of the infected class being removed and hence $\alpha I(t)$ is the rate of decrease in the infected class. Lastly, this simple model does not distinguish causes of removal, which may include recovery, immunity, or death. Once in the removed class, the R(t) individuals can no longer return to the susceptible or the infected classes. The following figure summarises some of the assumptions in the model:

Based on the assumptions, the population size is fixed, that is $N(t) = N$. Moreover, the assumptions lead to the following system of differential equations

$$\begin{aligned} S'(t)&=-\beta I(t) \frac{S(t)}{N}, \end{aligned}$$

(2.1)

$$\begin{aligned} I'(t)&=\beta I(t) \frac{S(t)}{N}-\alpha I(t), \end{aligned}$$

(2.2)

where S(t) and I(t) are the number of susceptible and infected individuals, respectively. The number of removed individuals is thus $N-S(t)-I(t)$.

A main concern in epidemiology modelling is whether a disease will spread upon its introduction. Observe from (2.2) that the disease spreads (i.e. $I'(t)$ is positive) if $\beta S(t)/N-\alpha >0$, and if $\beta S(t)/N-\alpha <0$ the disease dies out. This explains the relevance of a key quantity called the effective (or general) reproductive number,

$$\displaystyle R_t=\frac{\beta }{\alpha }\frac{S(t)}{N},$$

which represents the average number of secondary infections due to a single infectious individual at a given time t. It is also worth noting that $1/\beta$ is the average time between contagious contacts and $1/\alpha$ is the average time until removal. Then it is easy to see that $\beta /\alpha$ is the average number of contacts by an infected person with others before removal. When $t=0$, $R_0$ is known as the basic reproduction number, a common measure used to determine if a disease will spread out during the early phase of the outbreak. If $R_0>1$, the disease will start to spread, but not if $R_0<1$. Zhao et al. (2020) gives a preliminary estimate of $R_0$ for the coronavirus pandemic in China (from Jan. 10 to Jan. 24, 2020) to be between 2.24 and 3.58.

2.2.2 Other Compartmental Models

Here is a brief description of additional epidemic models that are commonly used in disease modelling. Since mortality analysis is based on ratios instead of absolute counts, consider the deterministic functions $s(t)$, $i(t)$ and $r(t)$ that denote, respectively, the fraction of the population in each of class $S$, $I$ and $R$. Dividing equations (2.1)–(2.2) by the constant total population size $N$ yields

$$\begin{aligned} s'(t)= & {} -\beta \,i(t)\,s(t)\,, \qquad t\ge 0 \,, \nonumber \\ i'(t)= & {} \beta \,i(t)\,s(t) - \alpha \,i(t)\,, \qquad t\ge 0 \,,\\ r(t)= & {} 1 - s(t) - i(t)\,, \qquad t\ge 0\,, \nonumber \end{aligned}$$

(2.3)

where $s(0)+i(0)=1$.

These ratio functions can be interpreted as the probability of an individual being susceptible, infected or removed from infected class, respectively, at time $t$. Note that movements between compartments depend on their relative sizes. Hence these probabilities correspond to mutually dependent risks in the SIR model, as opposed to the usual independent multiple decrements in life insurance models (see, for example, Chap. 8 of Dickson et al. (2013)).

To simplify the notation, the time variable will be dropped whenever it is not strictly necessary. Also, we will use the convention that uppercase letters like S, I and R denote the number of individuals in the compartments whereas lowercase letters like s, i and r refer to the proportion of the population in these compartments.

2.2.2.1 SIS Model

In the SIR model, compartment R represents removal, either by achieving full immunity or by death. Some diseases, such as AIDS, have no cure, and subsequently the infected individuals who have recovered are susceptible to the disease again. This phenomenon motivates a simpler class of models, called SIS, with only two compartments: S and I.

In the most basic SIS model, due to Kermack and McKendrick (1932), no births or immigration can occur, so that the total population $N=S(t)+I(t)$ remains constant. Denoting the infection rate by $\beta$ and the recovery rate by $\alpha$, as above, the corresponding differential equations are given by

$$\begin{aligned} \begin{aligned} s'&=-\beta si+\alpha i,\\ i'&=\beta si-\alpha i. \end{aligned} \end{aligned}$$

(2.4)

Since $s+i=1$, this yields a logistic differential equation

$$\begin{aligned} i'=(\beta (1-i)-\alpha ) i, \end{aligned}$$

(2.5)

hence, unlike the SIR model, the SIS admits explicit analytical solutions to the system of equations in (2.4):

$$\begin{aligned} \begin{aligned} s(t)&\;=\frac{\left( \frac{1-\frac{\alpha }{\beta }}{{i(0)}}-1\right) e^{-\left( \beta -\alpha \right) t}+\frac{\alpha }{\beta }}{1+\left( \frac{1-\frac{\alpha }{\beta }}{{i(0)}}-1\right) e^{-\left( \beta -\alpha \right) t}},\\ i(t)&\;=\frac{1-\frac{\alpha }{\beta }}{{1+\left( \frac{1-\frac{\alpha }{\beta }}{{i(0)}}-1\right) e^{-\left( \beta -\alpha \right) t}}}. \end{aligned} \end{aligned}$$

(2.6)

2.2.2.2 SEIRD Model

To predict the evolution of critical cases, Hill (2020) develops an app based on a variation of the SIR model, called SEIRD. It includes seven mutually exclusive compartments, namely, the susceptible (S), exposed (E), mildly infected ($I_1$), those infected with hospitalisation ($I_2$), infected with intensive care ($I_3$), recovered (R), and the deceased (D). This SEIRD model is characterised by a set of ordinary differential equations that describe population flows among all aforementioned compartments:

$$\begin{aligned} \begin{aligned} S'\;&=-(\beta _1 I_1+\beta _2 I_2+\beta _3 I_3) S,\\ E'\;&= (\beta _1 I_1+\beta _2 I_2+\beta _3 I_3)S-\gamma E,\\ I_1'\;&=\gamma E-(\delta _1+p_1) I_1,\\ I_2'\;&=p_1I_1-(\delta _2+p_2) I_2,\\ I_3'\;&=p_2I_2-(\delta _3+\mu )I_3,\\ R'\;&=\delta _1I_1+\delta _2I_2+\delta _3I_3,\\ D'\;&=\mu I_3. \end{aligned} \end{aligned}$$

(2.7)

All the parameters in this system of equations admit a clinical interpretation; $\beta _i$, $i=1,2,3$, is the transmission rate to the infected class $I_i$; $1/\gamma$ is the average latency period; $1/\delta _i$, $i=1,2,3$, is the average duration of infection in class $I_i$, before recovery to the class R; then $p_i$, $i=1,2,3$, represents the rate at which conditions worsen and individuals require healthcare at the next level of severity; $\mu$ is the transition rate from the most severe cases in class $I_3$ to the deceased class D.

The system of ordinary differential equations above represents a decomposition of the instantaneous change in the population into those in each compartment. For example, the first equation shows that the instantaneous rate of reduction in the number of susceptible, $-S'$ matches the sum of the rates of infection due to contacts with the infected in all classes, $\beta _1 I_1 S+\beta _2 I_2 S+\beta _3 I_3S$. The products are due to the law of mass action in biology. For example, the rate of secondary infection by the mildly infected, $(\beta _1 N) I_1 (S/N)$ can be interpreted as the number of “adequate” contact each infected individual makes to transmit the disease $\beta _1 N$, multiplied by the number of infectives $I_1$, multiplied by the percentage of contacts with a susceptible, S/N. All other equations can be explained in a similar way.

2.2.2.3 Stochastic SIR Model

Stochastic compartmental models form another popular framework in epidemiology modelling. These are natural extensions of the deterministic models presented above. Here we assume a continuous time Markov chain framework. Another approach is to add a Brownian perturbation to each compartment (see e.g. Sect. 4 of Allen (2017)), but it is not discussed here.

For an arbitrary time interval $[t,t+dt]$, the probability of an infection and the probability of recovery are given by:

$$\begin{aligned} \begin{aligned} P((S(t+dt), I(t+dt))- (S(t), I(t))=(-1,1))&= \frac{\beta }{N}S(t) I(t)\, dt +o(dt), \\ P((S(t+dt), I(t+dt))- (S(t), I(t))=(0,-1))&=\alpha I(t) \, dt +o(dt) \end{aligned} \end{aligned}$$

(2.8)

Figure 2.1 shows the dynamics in compartments S and I, respectively, comparing the deterministic and stochastic SIR models.

Fig. 2.1

Ten sample paths of the stochastic SIR model (orange) in (2.8), the deterministic SIR model (black) in (2.1) and (2.2) for $\beta =3$ and $\alpha =1.5$

Another random variable of interest is the duration of the epidemic, defined as:

$$\begin{aligned} T=\inf \{t>0:I(t)=0\}. \end{aligned}$$

(2.9)

In other words, this is the first instant when there are no more infectives in the population (or the time of the disease–free state). Other related random variables are the final size of the susceptible population (S(T)) and the area under the trajectory of the stochastic processes $\int _0^T S(u)\,du \text { and } \int _0^T I(u)\,du$. For a thorough discussion of stochastic epidemic models and methods for their statistical analysis, see e.g. Andersson and Britton (2012).

2.2.2.4 More Compartmental Models

Several other compartmental models have appeared in the epidemiology literature, but are not covered in this chapter. For example, the multi–group model separates the population into different groups, allowing for varying infection and recovery rates along groups. It can be applied to bordering counties, states or countries. Another model pertinent for COVID-19 applications is the quarantine–isolation model; it describes the effect of isolating susceptible individuals from the infected individuals. When no vaccine is available, this is perhaps the only measure available to governments to contain the contagion. Interested readers can refer to Hethcote (1978) and Brauer and Castillo-Chavez (2012) for a plethora of sophisticated epidemic models.

2.3 Epidemic Insurance

The idea of designing an insurance coverage against the financial impact due to infectious diseases is similar to what motivates coverage against other contingencies, such as accidental death or destruction of properties. Where it differs significantly from property and casualty insurance, at least from an actuarial point of view, is in the time–varying reference groups, such as the number of policyholders bearing the premiums and the number of policyholders eligible for compensation, which evolve quickly over time through an epidemic.

To illustrate these differences, this section first reviews some of the insurance policies and models proposed in Feng and Garrido (2011), using the basic SIR model, and subsequently quantifies infection risk by combining epidemiological and actuarial methodologies. The reserve level of an epidemic insurer is also studied, and using historical COVID-19 data, several case studies are presented.

2.3.1 Annuities and Insurance Benefits

Assume that an infectious disease insurance plan collects premiums continuously from susceptibles, as long as they remain healthy and susceptible. In the meantime, medical expenses are paid continuously to infected policyholders during the whole period of treatment, or until death.

Using the Equivalence Principle to determine level net premiums, that is

$$\begin{aligned} \mathbb {E}[\text{ present } \text{ value } \text{ of } \text{ benefits}] =\mathbb {E}[\text{ present } \text{ value } \text{ of } \text{ benefit } \text{ premiums}] \end{aligned}$$

(2.10)

and defining the actuarial present value (APV) of a t-year annuity of benefit payments , and the APV of a t-year annuity of premium payments , the level net premium for a unit annuity claim payment plan is given by . Here, $\delta$ represents the force of interest. As in life insurance, identities linking these APVs can be derived; see Feng and Garrido (2011). For instance, in the SIR model over an infinite term, we have

The intuitive interpretation is that, if each insured in the whole insured population is provided with a unit perpetual annuity, the APV of payments to class and the APV of payments to class $I$ is given by .

From this relation the net level premium for a policy of an infinite term with both premium and claim annuity is given by:

If instead, the infectious disease insurance pays a lump sum compensation when an insured person is diagnosed infected, and immediately hospitalised, then medical expenses are to be paid immediately in a lump sum, terminating the insurance plan’s obligation. The APV of benefit payments, denoted , is thus given by

(2.11)

since the probability of being newly infected at time $t$ is $\beta \,s(t)\,i(t)$. In the SIR model, this leads to additional useful identities:

(2.12)

and

(2.13)

Then net level premium for an infinite term insurance plan with lump sum compensation and annuity premium payments is given by the Equivalence Principle:

(2.14)

Finally, if the coverage includes also a death benefit, say of one monetary unit, paid immediately at the moment of death, then its APV, denoted by , is given by

Therefore, the net level premium for an infinite term plan with both, a unit lump sum death benefit and health–care claim benefits, is:

Similarly, the net level premium for a plan with both coverages, a lump sum benefit for hospitalisation costs and a lump sum death benefit is given by:

The above net premiums are expressed in terms of , which is a Laplace transform of $i(t)$. Although an implicit integral solution is known in the SIR model, no general explicit solution is available for $s(t)$ and $i(t)$. Different numerical methods and approximations which have been proposed provide satisfactory solutions for insurance applications, even for finite term policies; see Feng and Garrido (2011).

2.3.2 Reserves

Reserves are made of assets set aside by an insurer in anticipation of claim payments in the future. It can be determined prospectively at any time t, as the accumulated value of future premiums less that of future benefits. Alternatively, reserve can also be defined in a retrospective manner (see, for example, Chap. 7 of Dickson et al. (2013)). Reserves are a critical tool for insurers to measure their liabilities towards policyholders. When the reserve is adequately set, the insurer should have sufficient funds to cover claims as they become due. In classical life insurance, reserves build up from the beginning of the policy term, as the insurer accumulates premiums, to ultimately run out at the end of the policy term, when all benefits have been paid out to the policyholders. In other words, the reserve as a function of time, typically exhibits a bell shape. However, for epidemic insurance, the reserve function may exhibit quite different patterns, due to the dynamics of an epidemic. This section presents different shapes of reserve functions, and the conditions under which they arise in an epidemic insurance using the SIR and SIS models.

2.3.2.1 SIR Model

Here assume that susceptible individuals pay premiums at a constant rate $\pi$, and once infected, the insurer pays hospitalisation benefits, say at a constant rate of 1. For this particular policy, the insurer’s reserve level is given by:

$$\begin{aligned} V(\pi ,t)=\pi \int _{0}^{t}s(x)dx-\int _{0}^{t}i(x)dx, \end{aligned}$$

(2.15)

where, for simplicity, we take $\delta =0$. Feng and Garrido (2011) shows that there are four possible shapes of $V(\pi ,t)$, as a function of time. It turns out that the shape is dictated by the effective reproduction number, $R_t$, as summarised in Table 2.1.

Table 2.1 Possible shapes of the reserve function

In Table 2.1, the time $t_m$ is defined as to satisfy the equation $s(t_m)=\text {exp}\left( {1-\frac{\beta }{\alpha }c}\right)$, where $c=1-\frac{\alpha }{\beta }\ln s(0)$. For further details, readers can consult Appendix 5 of Feng and Garrido (2011). It is worth noting that a related quantity from the table, namely $1-\frac{1}{R_0}$, is called the herd immunity threshold; see Fine et al. (2011).

2.3.2.2 SIS Model

Now consider the insurer’s reserve function (2.15) for a SIS model. The following results concern its first and second derivatives.

Proposition 2.1

Assume that the infection rate exceeds the recovery rate, $\beta >\alpha$. Then,

• (1) $V(\pi ,t)$ is non-decreasing on $\pi \in [\frac{1}{{s(\infty )}}-1, \infty )$ and non-increasing on $\pi \in (-\infty , \frac{1}{{s(\infty )}}-1)$ if ${s(0)}>\frac{\alpha }{\beta }$.

• (2) $V(\pi ,t)$ is non-decreasing on $\pi \in [\frac{1}{{s(0)}}-1, \infty )$ and non-increasing on $\pi \in (-\infty , \frac{1}{{s(0)}}-1)$ if ${s(0)}\le \frac{\alpha }{\beta }$.

Convexity results for $V(\pi ,t)$ are straightforward since:

$$\begin{aligned} V''(\pi ,t)=\pi s'(t)-i'(t)=(\pi +1)i(t)\left( \alpha -\beta s(t)\right) . \end{aligned}$$

Proposition 2.2

If the infection rate exceeds the recovery rate, $\beta >\alpha$, then

• (1) $V(\pi ,t)$ is concave on $\pi \in [-1, \infty )$ and convex on $\pi \in (-\infty , -1)$ if ${s(0)}>\frac{\alpha }{\beta }$.

• (2) $V(\pi ,t)$ is convex on $\pi \in [-1, \infty )$ and concave on $\pi \in (-\infty , -1)$ if ${s(0)}\le \frac{\alpha }{\beta }$.

2.3.3 Further Extensions

Feng and Garrido (2011) has motivated additional work on deterministic insurance models. Perera (2017) considers control strategies in the simple SIR model as well as the variation of premiums with respect to the model parameters. Then Nkeki and Ekhaguere (2020) constructs the SIDRS model and studies its insurance applications. Billard and Dayananda (2014a) and Billard and Dayananda (2014b) develop a multi–stage HIV/AIDS model, where a waiting time distribution models the time one individual holds in one state. Premiums are defined for different insurance functions, and health–care cost adjustments are also included. Shemendyuk et al. (2019) investigates the deterministic and stochastic SIR models with multiple centres and migration fluxes. The optimal health–care premium is determined by considering different vaccine allocation strategies. Basic ideas in optimal resource allocation and contingency planning are explored in greater detail in Sect. 2.4.

Building on the work of Lefèvre et al. (2017), that explores the interplay between stochastic epidemiology and actuarial modelling, Lefèvre and Picard (2018a) generalised the SIR model to a controlled epidemic model, where the infectious are quarantined to ease the severity of the disease, and studies the epidemic outcomes and path integrals in terms of pseudo–polynomials. Then Lefèvre and Simon (2018) considers cross–infection between two linked populations. A general approach to study the Laplace transform of these integral functionals was developed by Lefèvre and Picard (2018b). More recently, Lefèvre and Simon (2019) proposes a general block–structured Markov processes for epidemic modelling.

2.3.4 Case Studies: COVID-19

This subsection illustrates a practical application of Sect. 2.3.2. Applying historical data, we use three epidemic models (SIR, SEIRD, and stochastic SIR) to describe the outbreak of COVID-19 and investigate their possible insurance applications. The data comes from Worldometer (2020), where as of Oct. 3, 2020, the U.S. population stood at $N=$ 328,300,000 people, and COVID-19 had resulted in $I_1(0)=$ 2,623,708 infected individuals, $E(0)=$ 335,272 exposed individuals, $D(0)=$ 214,637 deceased individuals and $R(0)=$ 4,827,450 recovered individuals.

2.3.4.1 SIR Model

In the case of COVID-19, the Removed compartment in the SIR model can be further divided into two sub–compartments, namely Recovered ($\tilde{R}$) and Death (D). According to Bastos and Cajueiro (2020), the underlying differential equations are:

$$\begin{aligned} \begin{aligned} S'&\;=-\beta S\frac{I}{N},\\ I'&\;=\beta S\frac{I}{N}-\frac{\tilde{\alpha }}{1-d}I,\\ \tilde{R}'&\;=\tilde{\alpha } I,\\ D'&\;=\frac{d}{1-d}\tilde{\alpha }I, \end{aligned} \end{aligned}$$

(2.16)

where $\beta$ is the infection rate, $\alpha$ is the recovery rate and d is the death rate due to COVID-19. From (2.16), one can easily reduce the model to the baseline SIR model by aggregating the $\tilde{R}$ and D compartments into a single compartment R, resulting in the system of differential equations in (2.1) and (2.2) with $\alpha =\tilde{\alpha }/(1-d)$.

For parameter estimation, Bastos and Cajueiro (2020) solve the following minimisation problem:

$$\begin{aligned} \min _{\beta ,\alpha ,d}\sum _{t=1}^{T_0}\left[ \left[ I(t)-\hat{I}(t)\right] ^2+\left[ R(t)-\hat{R}(t)\right] ^2\right] , \end{aligned}$$

where $T_0$ is the end of estimation period.

Using COVID-19 data for the U.S., from Worldometer (2020), the estimated parameters are $\beta =0.03014$ and $\alpha =0.01635$, where we consider $T_0=92$ days from Oct. 3, 2020 to Jan. 2, 2021; interested readers can refer to the data analysis section in Bastos and Cajueiro (2020). Assuming that the initial conditions are $N=$ 328,200,000, $I(0)=$ 2,623,708 and $R(0)=$ 4,827,450, Fig. 2.2 shows the dynamics of the population in compartment S and I for the next 700 days.

Fig. 2.2

Percentage of population in compartments S and I

Similar to the setup in Feng and Garrido (2011), assume that the whole population is enrolled in an insurance plan at the beginning of the COVID-19 outbreak. Susceptible individuals pay a premium of $\pi$ per day to the fund, and in return, infected individuals receive $\$$1,000 per day, until removal from the infectious state, to cover medical costs.

Now, to determine the daily premium rate $\pi$ of a 700-day insurance policy, it should be set so that the reserve function is non–negative over the entire policy term. That is, we set $V(\pi ,t)\ge 0$ in Eq. (2.15), which gives

$$\begin{aligned} \pi \ge \max _t\frac{\int _{0}^{t}i(x)dx}{\int _{0}^{t}s(x)dx}. \end{aligned}$$

Numerically, the premium level can be solved to be $\pi ^{*}=111.80$ and the cash value of the insurance fund at the end of 700 d is $V(111.80, 700)=910.98$. In other words, with a daily premium payment of $\pi ^{*}$, $\$910.98$ is paid to the survivors at the end of the policy period. Figure 2.3 shows the change in reserves with respect to time during the pandemic, where the reserve function is displayed in thousands.

Fig. 2.3

Reserve of the epidemic insurance plan

We see that a daily premium paid by the susceptible class of about 10% of the daily benefit paid to the infected class, leaving a positive final cash value left of the order of one day of benefit.

2.3.4.2 SEIRD Model

The baseline SIR model cannot capture some important features of the COVID-19 outbreak. For example, although it is a highly contagious disease, it takes some time for infected individuals to show symptoms and spread the virus. This time is often referred to as the incubation period. Therefore, infected but not infectious individuals should be classified as exposed. It is only after the incubation period that these exposed individuals become infectious. Furthermore, infected individuals should be divided into different stages according to their clinical record: infected with mild symptoms, severe symptoms, or critical symptoms. Infected individuals with critical symptoms need to seek professional medical treatment.

Fig. 2.4

Population flow of SEIRD model

To that end, consider a 7–compartment SEIRD model, as presented in Sect. 2.2.2.2. A flow chart of the model is presented in Fig. 2.4.

Table 2.2 SEIRD parameters, U.S. data

The interpretation and estimation of the parameters are summarised in Table 2.2. All parameters come from clinical research findings; interested readers can refer to Table 1 in Hill (2020). For instance, Linton et al. (2020) shows that the average incubation period is $\frac{1}{\gamma }=5$ days, and so the rate of transmission from compartments E to $I_1$ is $\gamma =0.2$.

The evolution of COVID-19 in the U.S. can now be simulated for the SEIRD model using the parameters in Table 2.2. Given the initial values for each compartment, $E(0)=$ 335,272, $I_1(0)=$ 2,098,966.4, $I_2(0)=$ 393,556.2, $I_3(0)=$ 131,185.4 $R(0)=$ 4,827,450, $D(0)=$ 214,637 and $N=$ 328,300,000, the evolution of the epidemic is shown in Fig. 2.5. Since the parameters are not estimated by the same optimisation problem as in the SIR model, a different time horizon of $t=100$ days, instead of 700 days, is used here for the SEIRD model.

Fig. 2.5

Evolution in each compartment w.r.t. time t

In terms of actuarial modelling, assume again that U.S. residents are enrolled in one of the insurance plans proposed in Feng and Garrido (2011); the Annuity for Hospitalisation (AH) Plan or the other the Lump–Sum for Hospitalisation (SH) Plan. The insurance company provides $1,000 per day to the individuals in compartments $I_1$ and $I_2$, to cover medical, examination and consultation fees. There is also compensation for individuals in compartment $I_3$ to cover treatment fees. Hospitalised individuals benefit payments of $1,000 per day from the AH plan, while those enrolled in the SH plan, receive a lump–sum payment of $10,000 at the time of hospitalisation. The discounted total benefit payments, and the fair premium level for both plans are summarised in Table 2.3.

Table 2.3 Premium rating for the AH and SH insurance plans

Recall that the parameters in SIR model are estimated by the minimisation problem, while the parameters in SEIRD model come from clinical research findings. Consequently, the evaluation periods are different (100 days in SEIRD versus 700 days in SIR) and the daily premium rates are seen to be about 40% of daily benefit rates in SEIRD, compared to about 10% in the SIR model.

2.3.4.3 Stochastic SIR Model

Lefèvre et al. (2017) considers an epidemic insurance model based on the stochastic SIR model, in Sect. 2.2.2.3. It is assumed that the policyholders pay premiums at a constant rate $\pi$ per unit time, while they remain in the susceptible class. The expected value of all premiums received is

$$\begin{aligned} \mathbb {E}\left[ \int _0^T \pi S(u)\,du\right] . \end{aligned}$$

(2.17)

The insurer reimburses the medical expenses of infected policyholders, continuously, at a rate of $c_1$ per unit time. Furthermore, immediately upon removal, policyholders receive a lump sum of amount $c_2$. So the insurer’s expected liability is

$$\begin{aligned} \mathbb {E}\left[ \int _0^T c_1 I(u) \,du+c_2 R(T)\right] \end{aligned}$$

(2.18)

By the Equivalence Principle (2.10) and the fact that $I(T)=0$, the premium level is

$$\begin{aligned} \pi =\frac{c_1 \mathbb {E}\left( \int _0^T I(u)\,du\right) +c_2[N-\mathbb {E} (S(T))]}{\mathbb {E} \left( \int _0^T S(u)\,du\right) }. \end{aligned}$$

(2.19)

Fig. 2.6

Key quantities of the stochastic epidemic insurance model

The three expectations above are calculated using martingale arguments and recursive methods. Interested readers are referred to Lefèvre et al. (2017) for the detailed recursive formulas and proofs.

What follows is a numerical illustration of the stochastic SIR model. For simplicity, assume constant removal and infection rates, where the infection rate is $\beta =1.5$ and the recovery rate is $\alpha =1$. At time 0, the population counts in the three compartments are assumed to be ${S(0)}=30$, ${I(0)}=3$ and ${R(0)}=0$. Figure 2.6(a) shows the probability mass function of S(T); it suggests a relatively large final number of susceptibles at the end of the pandemic, with a high probability. Figure 2.6(b) shows the expectation of S(T), as a function of different infection rates; if $\beta$ is small (resp. large), more (resp. less) individuals remain uninfected at the end of the pandemic and hence, leading to larger (resp. smaller) expectations of S(T). Finally, Fig. 2.6(c) illustrates the fact that the expected benefit (the numerator in (2.19)) is an increasing function of the infection rate $\beta$; as the epidemic worsens, more payments are made to policyholders in compensation of their medical expenses. Applying the recursive formulas outlined in Lefèvre et al. (2017) and assuming that $c_1=1$, $c_2=2$, gives a fair premium level of $\pi =0.576$. In other words, for the insurer to break even on average, the susceptible policyholders need to pay premiums continuously of 0.576 per unit time for each unit $c_1=1$ of continuous benefits and $c_2=2$ of lump sum units.

Understanding the policy value at time t of an insurance plan is important to ensure solvency of the company. To this end, define the reserve process of the insurer as

$$\begin{aligned} V(t)=\pi \int _0^t S(u)\,du-c_1 \int _0^t I(u)\,du-c_2[N- S(t)-I(t)]. \end{aligned}$$

Figure 2.7 graphs the reserve function V(t) of the stochastic SIR model for $t\in [0,10]$. One hundred simulated scenarios of the stochastic reserve function are shown. Some produce a positive reserve, when most individuals remain in compartment S and fewer benefit payments go to policyholders. Other scenarios show many infected and recovered cases, producing very negative reserves when benefit payments out–pace collected premiums. However, from (2.19), we conclude that the average reserve function at time T should be zero, given the fair level of premium $\pi$ and a sufficiently large number of scenarios.

Fig. 2.7

Simulations of the reserve function V(t), for $t\in [0,10]$, 100 scenarios

2.4 Resource Management

This section discusses another actuarial application of epidemic models. Specifically, we propose a resource management framework for contingency planning and resource allocation, to help prevent and respond to public health crises such as the COVID-19 pandemic.

The outbreak of an infectious disease usually leads to a surge in the demand for medical care and resources, such as ventilators and personal protective equipment. Healthcare systems can experience a shortage of medical supplies that can have devastating effects, such as the loss of lives or the inability to control the spread of disease. A contingent plan in resource management is a critical tool for governments, healthcare systems, and essential businesses to mitigate these inevitable pandemic risks. Stocking resources is one possible mitigation strategy to help meet the demand surge during a pandemic.

Resource management involves demand predictions, ex–ante planning prior to a pandemic and allocation of limited resources during the pandemic. Here, we introduce an overarching framework for an alliance of different regions to optimise stockpiling and resources allocation at different pandemic stages in order to best utilise limited resources. This framework was originally proposed in Chen et al. (2020). Here we use inter–state resources pooling, as an illustrative example, but applications can also include international collaboration for the production, procurement, distribution and pooling of critical medical resources, such as ventilators, pharmaceuticals or vaccines.

This resource management framework can be summarised in three pillars:

• Pillar I: Regional and Aggregate Resources Supply and Demand Forecast. Any pre–pandemic preparation plan should consist of supply and demand assessment and forecast. The supply side should include inventory assessments of critical resources and supplies, the maximum capacity of services, the capability of emergency acquisition and production. The demand side requires an understanding of the dynamics of a potential pandemic across regions and across borders. Historical data and predictive models can be used to project the evolution of a pandemic and the resulting surge demand on the healthcare system.

• Pillar II: Centralised Stockpiling and Distribution. A central authority coordinates the efforts to develop a national preparedness strategy and to set up reserves of critical resources including preventive, diagnostic and therapeutic resources. A response plan is also necessary to understand how the central authority can deliver resources to different regions quickly to meet surge demands and to balance competing interests and priorities.

• Pillar III: Central-Regional Resources Allocation. A pandemic response plan is critical for a central authority to contain and control the spread of a pandemic in all regions under its jurisdiction. As demand may exceed any best–effort pre–pandemic projections, the authority needs to devise optimal strategies that best utilise limited existing resources and minimise the economic cost of supply–demand imbalances. A coordination strategy needs to be in place to ensure smooth communications with regional authorities. The allocation strategy should be based on scientifically sound methods taking into account spatio–temporal differences across regions to ensure fairness and impartiality.

Figure 2.8 illustrates this framework and its underlying workflow. The rest of this section takes a closer look at each pillar and uses numerical examples to illustrate how this global framework can be implemented in practice.

Fig. 2.8

Three-pillar pandemic risk management framework

2.4.1 Pillar I: Regional and Aggregate Resources Demand Forecast

Compartmental epidemiological models can be well integrated in this framework, where the estimation and prediction of different medical resources are derived directly from the evolution of the compartments. To demonstrate how contingency planning and allocation can be optimised for scarce resources we use ventilators as an example. Ventilators are typically durable resources that can perform their required functions for a long period of time without significant expenditures of maintenance or repair. Chen et al. (2020) provides a detailed account of single–use/disposable resources such as personal protective equipment, using similar arguments.

To assess the needs for those resources, which is a key component in Pillar I, consider the number of resources needed as a function of different compartments. Ventilators are not necessarily needed unless patients are in critical conditions and require additional respiratory aid for survival. So, naturally the demand for ventilators can be seen as a function of the number of patients who require intensive care. To predict the evolution of critical cases, we adopt the SEIRD model as presented in Sect. 2.2.2.2. An important feature of this model is that it distinguishes between patients that do not need intensive care and those who need it, which enables us to make estimations and predictions on ventilator demand more accurately.

After the SEIRD model outputs the evolution of the number of cases requiring intensive care, then predictions on ventilator demand can be made. Based on the findings in the medical literature (c.f. Yang et al. (2020), Grasselli et al. (2020)), there exist estimates of the percentage $\alpha$ of the infectives with intensive care that require the use of mechanical ventilators. Regional differences can be addressed in separate regional compartment models. These estimates can be used to project the ventilator demand as $X_j^{\text {VEN}\left( i\right) }=\alpha I_{3,j}^{\left( i\right) }$, where i indicates the ith region in the alliance and j indicates the jth day of the pandemic.

To illustrate how this can be done in practice, consider a hypothetical three–state alliance that includes New York (NY), Florida (FL) and California (CA) as participating states, regardless of any barriers that might prevent them from a full collaboration in practice. Further assume that 90% of ICU cases require ventilators. Once the parameters in the SEIRD model are estimated using real data from those states, we can create projections of the demand for ventilators as shown in Fig. 2.9, where Fig. 2.9(a) represents regional ventilators demand predictions and Fig. 2.9(b) represents the aggregate demand prediction in all three states.

Fig. 2.9

Ventilator regional and aggregate demand prediction in NY, FL, and CA

In summary, the first pillar of resource management can be set–up with the help of compartmental models to obtain predictions on the demand for various resources over time.

Next, shift focus on how contingency planning and resources allocation can be carried out to minimise the impact of epidemics and pandemics on the economy, given these demand projections.

2.4.2 Pillar II: Centralised Stockpiling and Distribution

As the pandemic unfolds, many hospitals and healthcare facilities can run out of pharmaceuticals and other essential resources, before emergency production ramps up and additional supplies become available. A centralised stockpiling strategy is intended to provide a stop–gap measure to meet the surge in resources demand at the early stage of the pandemic.

One should keep in mind that a practical stockpiling strategy is often an act of balance between adequate supply and economic cost. On the one hand, under–stocking is a common choice as resources and their storage can pose a heavy cost, while the actual demand during the pandemic outbreak could deviate from its projections. On the other hand, excessive stockpiling for a long term can lead to unnecessary waste.

In the second pillar of this proposed framework, using the estimated aggregate resources demand, the central authority could develop stockpiling and distribution strategies in normal periods, before any pandemic. In the case of ventilators, the central authority would have to determine an optimal initial stockpile size $K_0$ of resources to maintain in some centralised location. In addition, to meet surges in demand, the authority may need to reach contractual agreements with suppliers for emergency orders, which may be limited by the maximum production rate, say of a units per day during a pandemic. Since ventilators are durable, the stock of ventilators does not decrease over time due to usage. Assume that they can be deployed to different regions at negligible cost. Therefore, the total number of available ventilators in the entire alliance is given by $K_j=K_0+aj$, on the j-th day after the onset of the pandemic. Hence, the only decision variable of the central authority in the case of ventilators is the initial stockpile size $K_0$.

Consider the following optimisation model for an initial stockpiling size.

$$\begin{aligned} \min _{K_0\ge 0}\sum _{j=1}^{m}\omega _j\biggl (&\frac{\theta ^{+} _j}{2}\left( X_j-\left( K_0+aj\right) \right) _{+}^2+ \nonumber \\&\frac{\theta ^{-} _j}{2}\left( X_j-\left( K_0+aj\right) \right) _{-}^2+c_j\left( K_0+aj\right) \biggr )+c_0K_0, \end{aligned}$$

(2.20)

where m is the number of days of the pandemic, $\omega _j$ is a weight for significance of precision for the costs on the j-th day of the pandemic, $\theta _j^{+}$ is an economic cost per square unit of shortage, $\theta _j^{-}$ is an opportunity cost per square unit of oversupply, $c_j$ is the aggregate cost of possession per unit of ventilators per day, $c_0$ is the initial stockpile cost, which may include both the acquisition cost and the expected cost of possession (storage, maintenance, inventory logistics, opportunity cost). The quadratic form above can be interpreted as follows. While one copy of the quantity $X_j-\left( K_0+aj\right)$ represents the amount of resource imbalance (shortage or surplus), the other copy $(\theta ^\pm _j/2) [X_j-\left( K_0+aj\right) ]_{\pm }$ can be viewed as the (linear) variable cost of the imbalance. The quadratic form is the product of cost per unit and the unit of imbalance, which yields the overall economic cost of imbalance. The weight $w_j$ can be used for different purposes. For example, it may be reasonable to make the weight proportional to the daily demand $X_j$ as the demand–supply imbalance can have a greater impact on population dense areas than otherwise, which is the weighting scheme adopted here for numerical examples.

To find the solution to this problem, first calculate the projected shortage without any initial stockpile, $Y_j:=X_j- aj$, for $j=1, \cdots , m,$ which is the accumulated demand less the accumulated supply apart from the initial stockpile. Then, sort them in ascending order and denote the sorted sequence by $\{Y_{[j]}, j=1, \cdots , m\},$ where $Y_{[j]}$ represents the j-th smallest projected shortage. The purpose of sorting the sequence is to find a $J \in \{1, 2, \cdots , m\}$, such that the following inequality holds,

$$\begin{aligned} Y_{[J-1]}\le \frac{\sum _{j=1}^{J-1}\omega _{[j]}{\theta _{[j]}^-}\left( Y_{[j]}-\frac{c_{[j]}}{\theta _{[j]}^-}\right) +\sum _{j=J}^{m}\omega _{[j]}{\theta _{[j]}^+}\left( Y_{[j]}-\frac{c_{[j]}}{\theta _{[j]}^+}\right) -c_0}{\sum _{j=1}^{J-1}\omega _{[j]}{\theta _{[j]}^-}+\sum _{j=J}^{m}\omega _{[j]}{\theta _{[j]}^+}} \le Y_{[J]}. \end{aligned}$$

Once J is identified, the optimal stockpile $K_0^*$ is given by

$$\begin{aligned} K_0^* = \max \left\{ \frac{\sum _{j=1}^{J-1}\omega _{[j]}{\theta _{[j]}^-}\left( Y_{[j]}-\frac{c_{[j]}}{\theta _{[j]}^-}\right) +\sum _{j=J}^{m}\omega _{[j]}{\theta _{[j]}^+}\left( Y_{[j]}-\frac{c_{[j]}}{\theta _{[j]}^+}\right) -c_0}{\sum _{j=1}^{J-1}\omega _{[j]}{\theta _{[j]}^-}+\sum _{j=J}^{m}\omega _{[j]}{\theta _{[j]}^+}},\; 0\right\} . \end{aligned}$$

The proof can be found in Chen et al. (2020). This result shows that the optimal initial stockpile $K_0$ is the weighted average of all projected shortages, discounted by the cost of possession, relative to the economic cost of shortage, $Y_{[j]} - c_{[j]}/\theta ^{\pm }_{[j]}$. The adjustment term $c_{[j]}/\theta ^{\pm }_{[j]}$ indicates that, the higher the cost of possession relative to the economic cost of imbalance, the fewer ventilators should be acquired.

Fig. 2.10

Optimal initial stockpile size $K_0$ under different weights of economic cost

Figure 2.10 depicts optimal initial stockpile size in the case study. When the resource shortage costs are the same or less than the resource surplus, Fig. 2.10a shows that the strategy requires less initial stockpile due to the excessive amount of supply after the pandemic dies out. By contrast, if the shortage costs weigh more than those of a surplus, the strategy is to reduce shortage in the early stages at the expense of increasing oversupply in the late stages; see Fig. 2.10b.

2.4.3 Pillar III: Centralised Resources Allocation

At the time of severe resource shortages, a coordinated effort becomes necessary to obtain additional supplies and to ration limited existing resources. There are two common types of resources allocation problems in the course of a pandemic, both of which can be cast in Pillar III of the proposed framework.

• 1. Macro level resources pooling. A central authority acts in the best interest of a union of many regions to increase supply, as well as to coordinate the distribution of existing and additional resources among different regional healthcare providers.

• 2. Micro level rationing. Facing an imbalance of demands and supplies in medical equipment and resources, hospitals often have to make difficult but necessary decisions to ration limited existing resources, as well as new supplies.

While in both cases the aim of the allocation exercise is to deliver limited resources where they are most needed, the macro level pooling addresses spatio–temporal differences and the micro level rationing focuses on healthcare effectiveness and fairness. The third pillar of the proposed pandemic risk management framework is about the allocation of limited resources to different regions, based on the proposed optimal centralised stockpiling and distribution strategies.

Figure 2.11 puts the regional resources demand and optimal aggregate supply together for the ease of exposition.

Fig. 2.11

Optimal ventilator allocations in NY, FL, and CA

Following the previously mentioned principles, consider the allocation of existing resources in a healthcare system with n regions during a pandemic that lasts for m days. We always use the superscript (i) to indicate quantities for the i-th region. Bear in mind that there could still be aggregate shortage of supply for ventilators in all the alliance regions. The central authority would have to take a holistic view of competing interests among participating regions. On each day, during the pandemic, when the aggregate demand exceeds the aggregate supply, the central authority should choose to allocate resources taking into account spatial differences in demand and supply. This motivates the following optimisation model for ventilator allocations:

$$\begin{aligned} \underset{j=1,2,\dots ,m}{\min _{K_j^{(i)}\ge 0;i=1,2,\dots ,n;}}\;\;&\sum _{j=1}^{m}\sum _{i=1}^{n}\omega _j^{(i)}\left( \frac{\theta _j^{+(i)}}{2}\left( X_j^{(i)}-K_j^{(i)}\right) _+^2+\frac{\theta _j^{-(i)}}{2}\left( X_j^{(i)}-K_j^{(i)}\right) _-^2\right) \\\text {such that }&\sum _{i=1}^{n}K_j^{(i)}=K_j,\quad \text {for }j=1,2,\dots ,m, \end{aligned}$$

where $\omega _j^{\left( i\right) }$ is a weight assigned the j-th day of the pandemic in the i-th allied region, $\theta _j^{+(i)}$ is an economic cost per squared unit of shortage, $\theta _j^{-(i)}$ is an opportunity cost per square unit of oversupply. The quadratic terms $\frac{\theta _j^{\pm (i)}}{2}\left( X_j^{(i)}-K_j^{(i)}\right) ^2$ represent the economic cost for demand–supply imbalance. Note that $\frac{\theta _j^{\pm (i)}}{2}$ measures the rate of increase in cost per unit, and hence $\frac{\theta _j^{\pm (i)}}{2}\left( X_j^{(i)}-K_j^{(i)}\right)$ represents the linear variable cost per unit. The variable cost in principle reflects the law of demand, under which the price increases with the quantity demanded. Therefore, the total cost is the product of the variable cost per unit $\frac{\theta _j^{\pm (i)}}{2}\left( X_j^{(i)}-K_j^{(i)}\right)$ and the total unit of imbalance $\left( X_j^{(i)}-K_j^{(i)}\right)$. The economic cost is used to account for both potential loss of lives due to the lack of resources and the opportunity cost of idle medical resources due to oversupply. This structure of economic cost is used not only for its mathematical tractability, but also to penalise large imbalances between demand and supply. The weight $\omega _j^{(i)}$ can be used to measure the relative importance of the resource allocation for region i at time $t_j$ to other regions and time points.

The constraint $\sum ^n_{i=1} K^{(i)} _j=K_j$ indicates that resources allocated to different regions must add up to the total amount of supply available to the central authority. The evolution of supply $\{K_j, j=1,2,\dots , m\}$ is based on the centralised stockpiling strategy discussed in previous sections. The evolution of demand $\{X^{(i)} _j, i=1,\dots , n, j=1,2,\cdots ,m\}$ can be based on forecasts from epidemiological models fitted to most recent local data.

The analytical solution to this allocation problem is summarised as a holistic allocation algorithm and explained in full detail in Chong et al. (2021). Here we only explain one particular case of the solution. As the allocation is carried out from period to period, we shall suppress the subscript j for brevity, and use $X^{(i)}$ for ventilator demand in region i and $K^{(i)}$ for the quantity of allocated resources in the same region.

If there is an overall surplus in the healthcare system at time j, i.e. $K>\sum \limits _{r=1}^nX^{(r)}=X$, then only the economic cost for oversupply $\theta ^{-(i)}$ applies and the optimal allocation of existing supply to the i-th region is given, for all $i=1,2,\ldots ,n$, by

$$\begin{aligned}&K^{(i)}=\left( 1-\frac{\frac{1}{\omega ^{(i)}\theta ^{-(i)}}}{\sum \limits _{r=1}^{n}\frac{1}{\omega ^{(r)}\theta ^{-(r)}}}\right) X^{(i)}+\frac{\frac{1}{\omega ^{(i)}\theta ^{-(i)}}}{\sum \limits _{r=1}^{n}\frac{1}{\omega ^{(r)}\theta ^{-(r)}}}\left( K-\sum \limits _{r\ne i}X^{(r)}\right) . \end{aligned}$$

(2.21)

The economic interpretation of the allocation formula (2.21) is that the optimal supply for region i results from a balance of two competing optimal solutions.

• Self–concerned optimal supply: $X^{(i)}$

  If region i can ask for as much as it needs, then this amount shows the ideal supply in the best interest of the region alone. The demand and supply for all other regions are ignored in its consideration.

• Altruistic optimal supply: $K-\sum _{r=1;r\ne i}^{n}X^{(r)}$

  If the region i places the interests of all other regions above its own, then the medical supply goes to other regions and region i ends up with the leftover amount.

The central authority has the responsibility to mediate among regions competing for resources. Formula (2.21) indicates that optimality for region i, in consideration of the entire system, is reached by a weighted average of two extremes, namely the self–concerned optimal and the altruistic optimal supplies. The average of two optimal supplies is determined by the harmonic weighting $\frac{1}{\omega ^{(i)}\theta ^{-(i)}}\Big /\sum \limits _{r=1}^{n}\frac{1}{\omega ^{(r)}\theta ^{-(r)}}$ as opposed to arithmetic weight $\omega ^{(i)}\theta ^{-(i)}\Big /\sum \limits _{r=1}^{n} \omega ^{(r)}\theta ^{-(r)}$. It is shown in Chong et al. (2021) that in multi–objective Pareto optimality the harmonic weighting is always used for balancing competing interests of participants whereas the arithmetic weighting serves the purpose of balancing competing objectives of the same participant.

2.5 Conclusion

In summary, this chapter explores several well–known compartmental models in epidemiology (Sect. 2.2) and studies their actuarial applications, in two different compartmental models. Key actuarial quantities are studied for an epidemic insurance plan in Sect. 2.3, such as annuities and benefits. In connection to the COVID-19 pandemic, three case studies are presented in Sect. 2.3.4, modelling the reserve level of an epidemic insurance provider. A second actuarial application of compartmental models in resource management is presented in Sect. 2.4 and contingency planning during a pandemic. To optimise stockpiling and medical resource allocation, we propose an overarching framework that includes supply and demand forecasts, centralised distribution, and regional allocations.

The first results obtained for the COVID-19 case study are that, as expected, premium levels for possible epidemic insurance coverages vary greatly, depending on the compartmental model calibrated to the available epidemic data. It highlights the importance of developing compartmental models as well suited as possible to the particular characteristics of the epidemic under study. Section 2.3 also shows that it is possible to set viable reserves, for epidemic insurance coverages, for different compartmental models, not just for the SIR. Similarly, the results in Sect. 2.4 illustrate possible ways to quantify resources and manage them optimally during a pandemic.

As both actuaries and epidemiologists specialise in quantifying risks, each in their own ways, we hope that this chapter motivates future research in bridging the two fields, to gain further insight into how to quantify the impact of pandemics.