Rotational Cryptanalysis from a Differential-Linear Perspective

Abstract

The differential-linear attack, combining the power of the two most effective techniques for symmetric-key cryptanalysis, was proposed by Langford and Hellman at CRYPTO 1994. From the exact formula for evaluating the bias of a differential-linear distinguisher (JoC 2017), to the differential-linear connectivity table (DLCT) technique for dealing with the dependencies in the switch between the differential and linear parts (EUROCRYPT 2019), and to the improvements in the context of cryptanalysis of ARX primitives (CRYPTO 2020), we have seen significant development of the differential-linear attack during the last four years. In this work, we further extend this framework by replacing the differential part of the attack by rotational-xor differentials. Along the way, we establish the theoretical link between the rotational-xor differential and linear approximations, revealing that it is nontrivial to directly apply the closed formula for the bias of ordinary differential-linear attack to rotational differential-linear cryptanalysis. We then revisit the rotational cryptanalysis from the perspective of differential-linear cryptanalysis and generalize Morawiecki et al.’s technique for analyzing Keccak, which leads to a practical method for estimating the bias of a (rotational) differential-linear distinguisher in the special case where the output linear mask is a unit vector. Finally, we apply the rotational differential-linear technique to the permutations involved in FRIET, Xoodoo, Alzette, and SipHash. This gives significant improvements over existing cryptanalytic results, or offers explanations for previous experimental distinguishers without a theoretical foundation. To confirm the validity of our analysis, all distinguishers with practical complexities are verified experimentally.

1 Introduction

The practical security of a symmetric-key primitive is determined by evaluating its resistance against an almost exhaustive list of known cryptanalytic techniques. Therefore, it is of essential importance to generalize existing cryptanalytic methods or develop new techniques. Sometimes the boundary between the two can be quite blurred. For example, the development of the invariant attacks [23, 24, 35], ploytopic cryptanalysis [33], division properties [34, 36], rotational cryptanalysis [1, 17], etc. in recent years belongs to these two approaches.

Another approach is to employ known techniques in combination to enhance the effectiveness of the individual attacks. The boomerang [37] and differential-linear cryptanalysis are the best examples. In particular, during the past four years, we have seen significant advancements in the development of the differential-linear cryptanalysis introduced by Langford and Hellman at CRYPTO 1994 [22], which combines the power of the two most important techniques (differential and linear attacks) for symmetric-key cryptanalysis. Our work starts with an attempt to further extend the differential-linear framework by replacing the differential part of this cryptanalytic technique with rotational-xor differentials.

Rotational and Rotational-xor Cryptanalysis. Rotational cryptanalysis was first formally introduced in [17] by Khovratovich and Nikolic, where the evolution of the so-called rotational pair $(x, x \lll t)$ through a target cipher was analyzed. The rotational properties of the building blocks of ARX primitives were then applied to the rotational rebound attack on the hash function Skein [19], and later were refined to consider a chain of modular additions [18]. Recently, cryptanalytic results of ARX-based permutations Chaskey and Chacha with respect to rotational cryptanalysis were reported [5, 21]. Apart from the ARX constructions, permutations built with logical operations without modular additions, also known as AND-RX or LRX [3] primitives, are particularly interesting with respect to rotational attacks. In 2010, Morawiecki et al. applied this technique to distinguish the round-reduced Keccak-f[1600] permutation by feeding in rotational pairs and observing the bias of the XOR of the $(i+t)$-th and i-th bits of the corresponding outputs, where t is the rotation offset and the addition should be taken modulo the size of the rotated word [31]. We will come back to Morawiecki et al.’s technique and show that it has an intimate relationship with the so-called rotational differential-linear cryptanalysis we proposed in Sect. 3. To thwart rotational attacks, constants which are not rotation-invariant can be injected into the data path. Still, in certain cases, it is possible to overcome this countermeasure with some ad-hoc techniques.

Later, Ashur and Liu [1] generalized the concept of rotational pair by considering the propagation of a data pair $(x, x')$ that is related by the so-called rotational-xor (RX) difference $(x \lll t) \oplus x' = \delta$. The cryptanalytic technique based on RX-difference was named as rotational-xor cryptanalysis. Note that when the RX-difference of the pair $(x, x')$ is zero, it degenerates to a rotational pair. RX cryptanalysis integrates the effect of constants into the analysis and it has been successfully applied to many ARX or AND-RX designs [26, 28]. Hereafter, we refer both rotational and rotational-xor cryptanalysis as rotational cryptanalysis, or in a general sense, rotational cryptanalysis contains all the statistical attacks requiring chosen data (e.g., plaintexts) with certain rotational relationships.

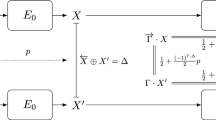
Differential-linear Cryptanalysis. Given an encryption function E, we divide it into two consecutive subparts $E_0$ and $E_1$. Let $\delta \rightarrow \varDelta$ be a differential for $E_0$ with probability p, and $\varGamma \rightarrow \gamma$ be a linear approximation for $E_1$ with bias $\epsilon _{\varGamma , \gamma } = \Pr [ \varGamma \cdot y \oplus \gamma \cdot E_1(y) = 0 ] - \frac{1}{2}$. Then, the overall bias $\mathcal {E}_{\delta , \gamma }$ of the differential-linear distinguisher can be estimated with the piling-up lemma [30] as

$$\begin{aligned} \mathcal {E}_{\delta , \gamma } = \Pr [ \gamma \cdot ( E(x) \oplus E(x \oplus \delta ) ) = 0 ] - \frac{1}{2} = (-1)^{\varGamma \cdot \varDelta } \cdot 2 p \epsilon _{\varGamma , \gamma }^2, \end{aligned}$$

(1)

since $\gamma \cdot ( E(x) \oplus E(x \oplus \delta ) )$ can be decomposed into the XOR sum of the following three terms

$$\begin{aligned} {\left\{ \begin{array}{ll} \varGamma \cdot ( E_0(x) \oplus E_0(x \oplus \delta ) ),\\ \varGamma \cdot E_0(x \oplus \delta ) \oplus \gamma \cdot E(x \oplus \delta ),\\ \varGamma \cdot E_0(x) \oplus \gamma \cdot E(x). \end{array}\right. } \end{aligned}$$

The derivation of Eq. (1) not only relies on the independence of $E_0$ and $E_1$, but also the assumption

$$\begin{aligned} \Pr [ \varGamma \cdot ( E_0(x) \oplus E_0(x \oplus \delta )) = 0 ~|~ E_0(x) \oplus E_0(x \oplus \delta ) \ne \varDelta ] = \frac{1}{2}, \end{aligned}$$

(2)

under which we have $\Pr [ \varGamma \cdot ( E_0(x) \oplus E_0(x \oplus \delta ) ) = 0 ] = \frac{1}{2} + \frac{(-1)^{\varGamma \cdot \varDelta }}{2}p$.

However, it has long been observed that Eq. (2) may fail in many cases and multiple linear approximations have to be taken into account to make the estimates more accurate [22, 27, 29]. In [9], Blondeau, Leander, and Nyberg presented a closed formula for the overall bias $\mathcal {E}_{\delta , \gamma }$ based on the link between differential and linear attacks [12] under the sole assumption that $E_0$ and $E_1$ are independent. However, this closed formula is generally not applicable in practice even if $E_0$ and $E_1$ are independent, since it requires the computation of the exact bias $\epsilon _{\delta , v} = \Pr [ v \cdot ( E_0(x) \oplus E_0(x \oplus \delta ) ) = 0 ] - \frac{1}{2}$ for all v.¹ Moreover, in some cases the dependency between $E_0$ and $E_1$ can be significant. Inspired by the boomerang-connectivity table (BCT) and its successful applications in the context of boomerang attacks [13], Bar-On, Dunkelman, Keller, and Weizman introduced the differential-linear connectivity table (DLCT) [4], where the target cipher is decomposed as $E = E_1\circ E_m \circ E_0$ and the actual differential-linear probability of the middle part $E_m$ is determined by experiments, fully addressing the issue of dependency in the switch between $E_0$ and $E_1$ (The effect of multiple characteristics and approximations still has to be handled by the framework of Blondeau et al. [9]). Most recently, Beierle, Leander, and Todo presented several improvements to the framework of differential-linear attacks with a special focus on ARX ciphers at CRYPTO 2020 [7].

Our Contribution. We start from the natural idea to extend the framework of differential-linear attacks by replacing the differential part with rotational-xor differentials. Specifically, given a pair of data with RX-difference $\delta = (x \lll t)\oplus x'$ and a linear mask $\gamma$, a rotational differential-linear distinguisher of a cipher E exploits the bias of $\gamma \cdot (\mathtt{{rot}}(E(x))\oplus E(\mathtt{{rot}}(x) \oplus \delta ))$, where $\mathtt{{rot}}(\cdot )$ is some rotation-like operation.

We then present an informal formula similar to Eq. (1) to estimate the bias of a rotational differential-linear distinguisher by the probability of the rotational-xor differential covering $E_0$ and the biases of the linear approximation and its rotated version covering $E_1$, where $E = E_1 \circ E_0$. This formula, as in the case of ordinary differential-linear cryptanalysis, requires certain assumptions that may not hold in practice.

Consequently, we try to derive a closed formula for computing the bias of a rotational differential-linear distinguisher, which we expect to be analogous to Blondeau et al.’s result [9]. Although we failed to achieve this goal, we manage to establish a general link between the rotational-xor cryptanalysis and linear cryptanalysis as a by-product of this failed endeavour. From a practical point of view, we do not lose much due to the absence of a closed formula, since this kind of formula will inevitably involve the correlations of exponentially many trails which are hard to evaluate in most situations.

Then, we focus our attention on the special case of rotational differential-linear cryptanalysis where the output linear mask $\gamma$ is a unit vector. In this case, the bias $\Pr [ e_i \cdot (\mathtt{{rot}}(f(x))\oplus f(\mathtt{{rot}}(x)\oplus \delta )) = 0 ] - \frac{1}{2}$ is

$$\begin{aligned} \Pr [ (E(x))_j \oplus (E(x'))_i = 0 ] - \frac{1}{2}= \frac{1}{2} - \Pr [ (E(x))_j \ne (E(x'))_i ], \end{aligned}$$

(3)

for some i and j, where $x' = \mathtt{{rot}}(x)\oplus \delta$. With this formulation, we immediately realize that Morawiecki et al.’s approach [31] gives rise to an efficient method for evaluating the biases of rotational differential-linear distinguishers, as well as ordinary differential-linear distinguishers whose output linear masks are unit vectors. We generalize some results from Morawiecki et al.’s work and arrive at formulas which are able to predict $\Pr [ (f(x))_j \ne f(x')_i ]$ based on the information $\Pr [ x_j \ne x_i]$ for many common operations f appearing in ARX designs. In particular, we give the explicit formula for computing the differential-linear and rotational differential-linear probability for an n-bit modular addition with O(n) operations, while a direct application of Bar-On et al.’s approach [4] based on the Fast Fourier Transformation (FFT) by treating the modular addition as an $2n \times n$ S-box would require a complexity of $\mathcal {O}(2^{2n})$. The probability evaluation can be iteratively applied for an ARX or AND-RX construction. Nevertheless, we note that the accuracy of the probability evaluation is affected by the dependency among the neighbour bits.

Finally, we apply the technique of rotational differential-linear cryptanalysis to the cryptographic permutations involved in FRIET, Xoodoo and Alzette. For FRIET, we find a 6-round rotational differential-linear distinguisher with a correlation $2^{-5.81}$, and it can be extended to a practical 8-round rotational differential-linear distinguisher with a correlation of $2^{-17.81}$. As a comparison, the correlation of the best known 8-round linear trail of FRIET is $2^{-40}$. Moreover, our 6-round distinguisher for FRIET can be further extended to a 13-round one. For Xoodoo, we identify a 4-round rotational differential-linear distinguisher with a correlation 1, while previous best result for Xoodoo is a 3-round differential with a probability $2^{-36}$. For Alzette, the 64-bit ARX-box, we find a 4-round differential-linear distinguisher with a correlation $2^{-0.27}$ and a 4-round rotational differential-linear distinguisher with a correlation $2^{-11.37}$. A summary of the results is shown in Table 1, where all distinguishers with practical complexities are experimentally verified.

Table 1. A summary of the results. R-DL = rotational differential-linear, DL = differential-linear, LC = linear characteristic, DC = differential characteristic. We show differentials with probabilities and LC/DL/R-DL with correlations.

Outline. Section 2 introduces the notations and preliminaries for rotational-xor and linear cryptanalysis. We propose the rotational differential-linear cryptanalysis and establish the theoretical link between the rotational-xor cryptanalysis and linear cryptanalysis in Sect. 3. This is followed by Sect. 4 where we explore the methods for evaluating the biases of rotational differential-linear distinguishers. In Sect. 5 and Sect. 6, we apply the techniques developed in previous sections to AND-RX and ARX primitives. Section 7 concludes the paper with some open problems.

2 Notations and Preliminaries

Let $\mathbb {F}_2 = \{0, 1\}$ be the field with two elements. We denote by $x_i$ the i-th bit of a bit string $x \in \mathbb {F}_2^n$. For a vectorial Boolean function $F: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ with $y = F(x) \in \mathbb {F}_2^m$, its i-th output bit $y_i$ is denoted by $(F(x))_i$. For an n-bit string x, we use the indexing scheme $x = (x_{n-1}, \cdots ,x_1, x_0)$. In addition, concrete values in $\mathbb {F}_2^n$ are specified in hexadecimal notations. For example, we use 1111 to denote the binary string $(\mathtt {0001~0001~0001~0001})_2$.

The XOR-difference and rotational-xor difference with offset t of two bit strings x and $x'$ in $\mathbb {F}_2^n$ are defined as $x \oplus x'$ and $(x \lll t) \oplus x'$, respectively. For the rotational-xor difference $\delta = (x \lll t) \oplus x'$, we may omit the rotation offset and write $\delta = \overleftarrow{x} \oplus x'$ or $\delta = \mathtt{{rot}}(x) \oplus x'$ to make the notation more compact when it is clear from the context. Moreover, by abusing the notation, $\overleftarrow{x}$ and $\mathtt{{rot}}(x)$ may rotate the entire string x or rotate the substrings of x to the left separately with a common offset, depending on the context. For instance, in the analysis of Keccak-f, we rotate each lane of the state by certain amount [31]. Correspondingly, $\overrightarrow{x}$ and $\mathtt{{rot}}^{-1}(x)$ rotate x or its substrings to the right. Similar to differential cryptanalysis with XOR-difference, we can define the probability of an RX-differential as follows.

Definition 1 (RX-differential probability)

Let $f: \mathbb {F}_{2}^n\rightarrow \mathbb {F}_{2}^n$ be a vectorial boolean function. Let $\alpha$ and $\beta$ be n-bit words. Then, the RX-differential probability of the RX-differential $\alpha \rightarrow \beta$ for f is defined as

$$\begin{aligned} \Pr [\alpha \rightarrow \beta ] = 2^{-n}\#\{x \in \mathbb {F}_2^n : \mathtt{{rot}}(f(x))\oplus f(\mathtt{{rot}}(x)\oplus \alpha ) = \beta \} \end{aligned}$$

Finally, the definitions of correlation, bias, and some lemmas concerning Boolean functions together with the piling-up lemma are needed.

Definition 2

([10, 11]). The correlation of a Boolean function $f: \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ is defined as $\mathrm {cor}(f) =2^{-n} (\# \{ x \in \mathbb {F}_2^n: f(x) = 0 \} - \# \{ x \in \mathbb {F}_2^n: f(x) = 1 \})$.

Definition 3

([10, 11]).] The bias $\epsilon (f)$ of a Boolean function $f: \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ is defined as $2^{-n} \# \{ x \in \mathbb {F}_2^n: f(x) = 0 \} - \frac{1}{2}$.

From Definition 2 and Definition 3 we can see that $\mathrm {cor}(f) = 2\epsilon (f)$.

Definition 4

Let $f : \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ be a Boolean function. The Walsh-Hadamard transformation takes in f and produces a real-valued function $\hat{f} : \mathbb {F}_2^n \rightarrow \mathbb {R}$ such that

$$\begin{aligned} \forall w \in \mathbb {F}_2^n,~~ \hat{f}(w) = \sum _{x \in \mathbb {F}_2^n} f(x) (-1)^{x \cdot w}. \end{aligned}$$

Definition 5

Let $f : \mathbb {F}_2^n \rightarrow \mathbb {F}_2$ and $g :\mathbb {F}_2^n \rightarrow \mathbb {F}_2$ be two Boolean functions. The convolutional product of f and g is a Boolean function defined as

$$\begin{aligned} \forall y \in \mathbb {F}_2^n,~~(f \star g)(y) = \sum _{x \in \mathbb {F}_2^n} g(x) f(x \oplus y). \end{aligned}$$

Lemma 1

([11], Corollary 2 ). Let $\hat{f}$ be the Walsh-Hadamard transformation of f. Then the Walsh-Hadamard transformation of $\hat{f}$ is $2^nf$.

Lemma 2

[11], Proposition 6 ). ${\widehat{(f \star g)}} (z) = \hat{f}(z) \hat{g}(z)$ and thus ${\widehat{(f \star f)}} = (\hat{f})^2$.

Lemma 3

(Piling-up Lemma [30]). Let $Z_0$, $\cdots$, $Z_{m-1}$ be m independent binary random variables with $\Pr [Z_i = 0] = p_i$. Then we have that

$$\begin{aligned} \Pr [ Z_0 \oplus \cdots \oplus Z_{m-1} = 0 ] = \frac{1}{2} + 2^{m-1} \prod _{i=0}^{m-1}(p_i - \frac{1}{2}), \end{aligned}$$

or alternatively, $2 \Pr [Z_0 \oplus \cdots \oplus Z_{m-1} = 0] - 1 = \prod _{i=0}^{m-1}(2p_i - 1).$

3 Rotational Differential-Linear Cryptanalysis

A natural extension of the differential-linear cryptanalysis is to replace the differential part of the attack by rotational-xor (RX) differentials. Let $E = E_1 \circ E_0$ be an encryption function. Assume that we have an RX-differential $\delta \rightarrow \varDelta$ covering $E_0$ with $\Pr [ \mathtt{{rot}}(E_0(x)) \oplus E_0 (\mathtt{{rot}}(x) \oplus \delta ) = \varDelta ] = p$ and a linear approximation $\varGamma \rightarrow \gamma$ of $E_1$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{\varGamma , \gamma } = \Pr [ \varGamma \cdot y \oplus \gamma \cdot E_1(y) = 0 ] - \frac{1}{2},\\ \epsilon _{\mathtt{{rot}}^{-1}(\varGamma ), \mathtt{{rot}}^{-1}(\gamma )} = \Pr [ \mathtt{{rot}}^{-1}(\varGamma ) \cdot y \oplus \mathtt{{rot}}^{-1}(\gamma ) \cdot E_1(y) = 0 ] - \frac{1}{2}.\\ \end{array}\right. } \end{aligned}$$

Let $x' = \mathtt{{rot}}(x) \oplus \delta$. If the assumption

$$\begin{aligned} \Pr [ \varGamma \cdot ( \mathtt{{rot}}(E_0(x)) \oplus E_0 (x') ) = 0 ~|~ \mathtt{{rot}}(E_0(x)) \oplus E_0 (x') \ne \varDelta ] = \frac{1}{2} \end{aligned}$$

(4)

holds. We have

$$\begin{aligned} \Pr [ \varGamma \cdot ( \mathtt{{rot}}(E_0(x)) \oplus E_0 (x') ) = 0 ] = \frac{1}{2} + \frac{(-1)^{\varGamma \cdot \varDelta }}{2}p. \end{aligned}$$

Since

$$\begin{aligned} \begin{aligned} \gamma \cdot (\mathtt{{rot}}(E(x))\oplus E(x'))&= \gamma \cdot \mathtt{{rot}}(E(x)) \oplus \varGamma \cdot \mathtt{{rot}}(E_0(x))\\&\oplus \varGamma \cdot (\mathtt{{rot}}(E_0(x))\oplus E_0(x'))\\&\oplus \varGamma \cdot E_0(x')\oplus \gamma \cdot E(x')\\&= \mathtt{{rot}}(\mathtt{{rot}}^{-1}(\gamma )\cdot E(x) \oplus \mathtt{{rot}}^{-1}(\varGamma )\cdot E_0(x))\\&\oplus \varGamma \cdot (\mathtt{{rot}}(E_0(x))\oplus E_0(x'))\\&\oplus \varGamma \cdot E_0(x')\oplus \gamma \cdot E(x'), \end{aligned} \end{aligned}$$

the bias of the rotational differential-linear distinguisher can be estimated by piling-up lemma as

$$\begin{aligned} \mathcal {E}_{\delta ,\gamma }^{\text {R-DL}} = \Pr [ \gamma \cdot ( \overleftarrow{E}(x)\oplus E(x') ) = 0 ] - \frac{1}{2} = (-1)^{\varGamma \cdot \varDelta } \cdot 2 p \epsilon _{\varGamma , \gamma } \epsilon _{\mathtt{{rot}}^{-1}(\varGamma ), \mathtt{{rot}}^{-1}(\gamma )}, \end{aligned}$$

(5)

and the corresponding correlation of the distinguisher is

$$\begin{aligned} \mathcal {C}_{\delta ,\gamma }^{\text {R-DL}} = 2\mathcal {E}_{\delta ,\gamma }^{\text {R-DL}} = (-1)^{\varGamma \cdot \varDelta } \cdot 4 p \epsilon _{\varGamma , \gamma } \epsilon _{\mathtt{{rot}}^{-1}(\varGamma ), \mathtt{{rot}}^{-1}(\gamma )}. \end{aligned}$$

(6)

We can distinguish E from random permutations if the absolute value of $\mathcal {E}_{\delta ,\gamma }^{\mathrm {R-DL}}$ or $\mathcal {C}_{\delta ,\gamma }^{\text {R-DL}}$ is sufficiently high. Note that if we set the rotation offset to zero, the rotational differential-linear attack is exactly the ordinary differential-linear cryptanalysis. Therefore, the rotational differential-linear attack is a strict generalization of the ordinary differential-linear cryptanalysis.

A rotational differential-linear distinguisher can be extended by appending linear approximations at the end. Given a rotational differential-linear distinguisher of a function f with a bias

$$\begin{aligned} \epsilon _{\delta ,\gamma } = \Pr [\gamma \cdot (\mathtt{{rot}}(f(x)) \oplus f(\mathtt{{rot}}(x)\oplus \delta )) = 0] - \frac{1}{2} , \end{aligned}$$

and a linear approximation $(\gamma ,\mu )$ over a function g with

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{\gamma ,\mu } = \Pr [\gamma \cdot x \oplus \mu \cdot g(x) = 0] - \frac{1}{2},\\ \epsilon _{\mathtt{{rot}}^{-1}(\gamma ), \mathtt{{rot}}^{-1}(\mu )} = \Pr [ \mathtt{{rot}}^{-1}(\gamma ) \cdot x \oplus \mathtt{{rot}}^{-1}(\mu ) \cdot g(x) = 0 ] - \frac{1}{2},\\ \end{array}\right. } \end{aligned}$$

we can compute the bias of the rotational differential-linear distinguisher of $h = g\circ f$ with input RX-difference $\delta$ and output linear mask $\mu$ by the piling-up lemma. Since

$$\begin{aligned} \begin{aligned} \mu \cdot (\mathtt{{rot}}(h(x)) \oplus h(\mathtt{{rot}}(x)\oplus \delta ))&= \gamma \cdot (\mathtt{{rot}}(f(x)) \oplus f(\mathtt{{rot}}(x)\oplus \delta )) \\&\oplus \gamma \cdot \mathtt{{rot}}(f(x)) \oplus \mu \cdot \mathtt{{rot}}(h(x)) \\&\oplus \gamma \cdot f(\mathtt{{rot}}(x)\oplus \delta ) \oplus \mu \cdot h(\mathtt{{rot}}(x)\oplus \delta ) \end{aligned}, \end{aligned}$$

the bias of the rotational differential-linear distinguisher can be estimated as

$$\begin{aligned} \Pr [\mu \cdot (\mathtt{{rot}}(h(x)) \oplus h(\mathtt{{rot}}(x)\oplus \delta )) = 0 ] - \frac{1}{2} = 4\epsilon _{\delta ,\gamma }\epsilon _{\gamma ,\mu }\epsilon _{\mathtt{{rot}}^{-1}(\gamma ),\mathtt{{rot}}^{-1}(\mu )}. \end{aligned}$$

(7)

However, as in ordinary differential-linear attacks, the assumption described by Eq. (4) may not hold in practice, and we prefer a closed formula for the bias $\mathcal {E}_{\delta ,\gamma }^{\text {R-DL}}$ without this assumption for much the same reasons leading to Blondeau et al.’s work [9]. Also, we would like to emphasize that if Eq. (5) and (7) are used to estimate the bias, we should verify the results experimentally whenever possible.

3.1 Towards a Closed Formula for the Bias of the Rotational Differential-Linear Distinguisher

In [9], Blondeau et al. proved the following theorem based on the general link between differential and linear cryptanalysis [12].

Theorem 1

([9]). If $E_0$ and $E_1$ are independent, the bias of a differential-linear distinguisher with input difference $\delta$ and output linear mask $\gamma$ can be computed as

$$\begin{aligned} \mathcal {E}_{\delta , \gamma } = \sum _{v \in \mathbb {F}_2^n} \epsilon _{\delta , v} c_{v, \gamma }^2, \end{aligned}$$

(8)

for all $\delta \ne 0$ and $\gamma \ne 0$, where

$$\begin{aligned} {\left\{ \begin{array}{ll} \epsilon _{\delta , v} = \Pr [ v \cdot ( E_0(x) \oplus E_0(x \oplus \delta ) ) = 0 ] - \frac{1}{2}\\ c_{v, \gamma } = \mathrm {cor}( v \cdot y \oplus \gamma \cdot E_1(y) ) \end{array}\right. }. \end{aligned}$$

To replay Blondeau et al.’s technique in an attempt to derive the rotational differential-linear counterpart of Eq. (8), we have to first establish the relationship between rotational differential-linear cryptanalysis and linear cryptanalysis.

Link Between RX-cryptanalysis and Linear Cryptanalysis. Let $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a vectorial Boolean function. The cardinality of the set

$$\begin{aligned} \{ x \in \mathbb {F}_2^n : \overleftarrow{F}(x) \oplus F(\overleftarrow{x} \oplus a) = b \} \end{aligned}$$

is denoted by $\xi _F(a, b)$, and the correlation of $u \cdot x \oplus v \cdot F(x)$ is $\mathrm {cor}(u \cdot x \oplus v \cdot F(x)).$ Let $\underrightarrow{\overleftarrow{F}}: \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be the vectorial Boolean function mapping x to $\overleftarrow{F}(\overrightarrow{x})$. It is easy to show that

$$\begin{aligned} \mathrm {cor}(u \cdot x \oplus v \cdot \underrightarrow{\overleftarrow{F}}(x)) = \mathrm {cor}(\overrightarrow{u} \cdot x \oplus \overrightarrow{v} \cdot F(x)). \end{aligned}$$

In what follows, we are going to establish the relationship between

$$\begin{aligned} \xi _F(a, b), ~~\mathrm {cor}(u \cdot x \oplus v \cdot F(x)),~~\mathrm {and}~~ \mathrm {cor}(\overrightarrow{u} \cdot x \oplus \overrightarrow{v} \cdot F(x)). \end{aligned}$$

Definition 6

Given a vectorial Boolean function $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$, the Boolean function $\theta _F: \mathbb {F}_2^{2n} \rightarrow \mathbb {F}_2$ is defined as

$$\begin{aligned} \theta _F(x, y) = {\left\{ \begin{array}{ll} 1~~\mathrm {if}~~y = F(x),\\ 0~~\mathrm {otherwise}. \end{array}\right. } \end{aligned}$$

(9)

Lemma 4

Let $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a vectorial Boolean function. Then for any $(a, b) \in \mathbb {F}_2^{2n}$, we have $\xi _F(a, b) = ( \theta _{\underrightarrow{\overleftarrow{F}}} \star \theta _F )(a, b)$.

Proof

According to Definition 5, we have

$$\begin{aligned} \begin{aligned} ( \theta _{\underrightarrow{\overleftarrow{F}}} \star \theta _F )(a, b)&= \sum _{x||y \in \mathbb {F}_2^{2n}} \theta _{\underrightarrow{\overleftarrow{F}}} (x, y) \theta _F(a \oplus x, b \oplus y)\\&= \sum _{x \in \mathbb {F}_2^n } \sum _{y \in \mathbb {F}_2^n} \theta _{\underrightarrow{\overleftarrow{F}}} (x, y) \theta _F(a \oplus x, b \oplus y)\\&= \sum _{x \in \mathbb {F}_2^n } \theta _{\underrightarrow{\overleftarrow{F}}} (x, \underrightarrow{\overleftarrow{F}}(x)) \theta _F(a \oplus x, b \oplus \underrightarrow{\overleftarrow{F}}(x)) \\&= \sum _{x \in \mathbb {F}_2^n } \theta _F(a \oplus x, b \oplus \underrightarrow{\overleftarrow{F}}(x)) \\&= \# \{ x \in \mathbb {F}_2^n: b \oplus \underrightarrow{\overleftarrow{F}}(x) = F( a \oplus x) \}\\&= \xi _F(a, b). \end{aligned} \end{aligned}$$

   $\square$

Lemma 5

Let $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^n$ be a vectorial Boolean function. Then for any $(a, b) \in \mathbb {F}_2^{2n}$, we have $\mathrm {cor}(a \cdot x \oplus b \cdot F(x)) = {2^{-n}} \hat{\theta }_{F}(a, b).$

Proof

According to Definition 4, we have

$$\begin{aligned} \begin{aligned} \hat{\theta }_F(a, b)&= \sum _{x||y \in \mathbb {F}_2^{2n}} \theta _F(x, y) (-1)^{(x||y) \cdot (a||b)}\\&= \sum _{x \in \mathbb {F}_2^n}\sum _{y \in \mathbb {F}_2^n} \theta _F(x, y) (-1)^{ a \cdot x \oplus b \cdot y } \\&= \sum _{x \in \mathbb {F}_2^n} (-1)^{ a \cdot x \oplus b \cdot F(x) } \\&= 2^n \mathrm {cor}(a \cdot x \oplus b \cdot F(x)). \end{aligned} \end{aligned}$$

   $\square$

In addition, applying Lemma 5 to $\underrightarrow{\overleftarrow{F}}$ gives $\mathrm {cor}(a \cdot x \oplus b \cdot \underrightarrow{\overleftarrow{F}}(x)) = \frac{1}{2^n} \hat{\theta }_{\underrightarrow{\overleftarrow{F}}}(a, b)$.

Theorem 2

The link between RX-differentials and linear approximations can be summarized as

$$\begin{aligned} \xi _F(a, b) = \sum _{u \in \mathbb {F}_2^n}\sum _{v \in \mathbb {F}_2^n} (-1)^{u \cdot a \oplus v \cdot b} \mathrm {cor}( \overrightarrow{u} \cdot x \oplus \overrightarrow{v} \cdot F(x) ) \mathrm {cor}( u \cdot x \oplus v \cdot F(x) ). \end{aligned}$$

(10)

Proof

According to Lemma 4 and Lemma 2, we have

$$\begin{aligned} 2^{2n} \xi _F(a, b) = \widehat{\widehat{( \theta _{\underrightarrow{\overleftarrow{F}}} \star \theta _F )}}(a, b) = \widehat{ \hat{\theta }_{\underrightarrow{\overleftarrow{F}}} \hat{\theta }_F }(a, b). \end{aligned}$$

Since $\hat{\theta }_{\underrightarrow{\overleftarrow{F}}} \hat{\theta }_F = {2^{2n}} \mathrm {cor}(u \cdot x \oplus v \cdot \underrightarrow{\overleftarrow{F}}(x)) \mathrm {cor}(u \cdot x \oplus v \cdot F(x))$ due to Lemma 5,

$$\begin{aligned} \begin{aligned} \widehat{ \hat{\theta }_{\underrightarrow{\overleftarrow{F}}} \hat{\theta }_F }(a, b)&= 2^{2n}\sum _{u||v \in \mathbb {F}_2^{2n}} (-1)^{(u||v) \cdot (a || b)} \mathrm {cor}(u \cdot x \oplus v \cdot \underrightarrow{\overleftarrow{F}}(x)) \mathrm {cor}(u \cdot x \oplus v \cdot F(x))\\&= 2^{2n}\sum _{u, v\in \mathbb {F}_2^{n}} (-1)^{u \cdot a \oplus v \cdot b } \mathrm {cor}(u \cdot x \oplus v \cdot \underrightarrow{\overleftarrow{F}}(x)) \mathrm {cor}(u \cdot x \oplus v \cdot F(x))\\&= 2^{2n}\sum _{u, v\in \mathbb {F}_2^{n}} (-1)^{u \cdot a \oplus v \cdot b } \mathrm {cor}(\overrightarrow{u} \cdot x \oplus \overrightarrow{v} \cdot F(x)) \mathrm {cor}(u \cdot x \oplus v \cdot F(x)) \end{aligned} \end{aligned}$$

   $\square$

If the function F is rotation invariant, i.e., $\overleftarrow{F(x)} = F(\overleftarrow{x})$, then we have $\mathrm {cor}( \overrightarrow{u} \cdot x \oplus \overrightarrow{v} \cdot F(x) ) =\mathrm {cor}( u \cdot x \oplus v \cdot F(x) )$. As a result, the theoretical link between rotational-xor and linear cryptanalysis degenerates to the link between ordinary differential cryptanalysis and linear cryptanalysis. Moreover, based on the link between differential and linear cryptanalysis, Blondeau et al. derive a closed formula for the bias of an ordinary differential-linear distinguisher as shown in Eq. (8). We try to mimic Blondeau et al.’s approach to obtain a closed formula for the biases of rotational differential-linear distinguishers. However, we failed in this attempt due to a fundamental difference between rotational-xor differentials and ordinary differentials: the output RX-difference is not necessarily zero when the input RX-difference $\mathtt{{rot}}(x) \oplus x'$ is zero. We leave it as an open problem to derive a closed formula for the bias of a rotational differential-linear distinguisher. From a practical point of view, we do not lose much due to the absence of a closed formula since this kind of formula will inevitably involve the correlations of exponentially many trails which are hard to evaluate in most situations.

3.2 Morawiecki et al.’s Technique Revisited

In [31], Morawiecki et al. performed a rotational cryptanalysis on the Keccak-f permutation E. In this attack, the probability of

$$\begin{aligned} \Pr [ (E(x))_{i-t} \ne (E(x\lll t))_{i} ] \end{aligned}$$

was exploited to distinguish the target. In what follows, we show that Morawiecki et al.’s technique can be regarded as a special case of the rotational differential-linear framework.

Eventually, what we exploit in a rotational differential-linear attack associated with an input RX-difference $\delta \in \mathbb {F}_2^n$ and an output linear mask $\gamma \in \mathbb {F}_2^n$ is the abnormally high absolute bias or correlation of the Boolean function

$$\begin{aligned} \gamma \cdot ( \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) ). \end{aligned}$$

Following the notation of [9], let $\mathrm {sp}(\gamma ) \subseteq \mathbb {F}_2^n$ be the linear space spanned by $\gamma$, and $\mathrm {sp}(\gamma )^{\perp } = \{ u \in \mathbb {F}_2^n: \forall v \in \mathrm {sp}(\gamma ), u \cdot v = 0 \}$ be the orthogonal space of $\mathrm {sp}(\gamma )$.

We then define two sets $\mathbb {D}_0$ and $\mathbb {D}_1$ which form a partition of $\mathbb {F}_2^n$:

$$\begin{aligned} \left\{ \begin{array}{l} \mathbb {D}_0 = \{ x \in \mathbb {F}_2^n : \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) \in \mathrm {sp}(\gamma )^{\perp } \}\\ \mathbb {D}_1 = \{ x \in \mathbb {F}_2^n : \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) \in \mathbb {F}_2^n - \mathrm {sp}(\gamma )^{\perp } \} \end{array}\right. . \end{aligned}$$

Under the above notations, for any $x \in \mathbb {D}_0$, $\gamma \cdot ( \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) ) = 0$ and for any $x \in \mathbb {D}_1$, $\gamma \cdot ( \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) ) = 1$.

Thus, the higher the absolute value of

$$\begin{aligned} \# \mathbb {D}_0 - \# \mathbb {D}_1 = 2^n \mathrm {cor}( \gamma \cdot ( \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta ) ) ), \end{aligned}$$

the more effective the attack is.

If $\gamma = e_i$ is the i-th unit vector, we have $\mathrm {sp}(\gamma ) = \{ 0, e_i \}$ and $\mathrm {sp}(\gamma )^{\perp }$ contains all vectors whose i-th bit is 0. In this case,

$$\begin{aligned} \# \mathbb {D}_0 - \# \mathbb {D}_1&= 2^n - 2 \# \mathbb {D}_1 \\&= 2^n-2^{n+1} \left( \mathrm {Pr}[ e_i \cdot ( \mathtt{{rot}}(E(x)) \oplus E( \mathtt{{rot}}(x) \oplus \delta )) = 1 ] \right) \\&= 2^n-2^{n+1} \left( \mathrm {Pr}[ (E(x))_{j} \ne (E(\mathtt{{rot}}(x) \oplus \delta ))_i ] \right) \\&= 2^n-2^{n+1} \left( \mathrm {Pr}[ (E(x))_{j} \ne (E(x')_i ] \right) . \end{aligned}$$

Therefore, the effectiveness of the rotational differential-linear attack can be completely characterized by $\mathrm {Pr}[ (E(x))_{i-t} \ne (E(x'))_i].$ In the next section, we show how to compute this type of probabilities for the target cipher.

4 Evaluate the Bias of Rotational Differential-Linear Distinguishers

According to the previous section, for a rotational differential-linear distinguisher with an input RX-difference $\delta$ and output linear mask $e_i$, the bias of the distinguisher can be completely determined by

$$\begin{aligned} \mathrm {Pr}[ (E(x))_{i-t} \ne (E(x'))_i],~\mathrm {where}~x' = x\lll t \oplus \delta , \end{aligned}$$

and we call it the rotational differential-linear probability or R-DL probability. Note that for a random pair $(x, x' = x\lll t \oplus \delta )$ with rotational-xor difference $\delta \in \mathbb {F}_2^n$, we have

$$\begin{aligned} \Pr [ x_{i-t} \ne x'_i ] = \frac{1 + (-1)^{1 - \delta _i}}{2}, \end{aligned}$$

for $0 \le i < n$. Therefore, what we need is a method to evaluate the probability

$$\begin{aligned} \Pr [ (F(x))_{i-t} \ne (F(x'))_i ] \end{aligned}$$

for $0 \le i < m-1$, where $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ is a vectorial Boolean function that represents a component of E. Then, with certain independence assumptions, we can iteratively determine the probability $\mathrm {Pr}[ (E(x))_{i-t} \ne (E(x'))_i]$.

Observation 1

Let $F : \mathbb {F}_2^n \rightarrow \mathbb {F}_2^m$ be a vectorial Boolean function. Assume that the input pair $(x,x')$ satisfies $\Pr [ x_{i-t} \ne x'_i ] = p_i$ for $0 \le i < n$, where $x, x' \in \mathbb {F}_2^n$. For $u \in \mathbb {F}_2^n$, we define the set $\mathcal {S}_{u} = \{(x,x') \in \mathbb {F}_2^n \times \mathbb {F}_2^n : (x\lll t)\oplus x' = u\}$ with $\# \mathcal {S}_u = 2^n$. Let $y_i$ and $y'_i$ be the i-th bit of F(x) and $F(x')$ respectively for $0 \le i < m$. Then we have

$$\begin{aligned} \Pr [ y_{i-t} \ne y_i ]&= \sum _{u\in \mathbb {F}_2^n}\Pr [ y_{i-t} \ne y_i |(x,x')\in \mathcal {S}_u]\Pr [(x,x')\in \mathcal {S}_u]\\&=\sum _{u\in \mathbb {F}_2^n}\Pr [ y_{i-t} \ne y_i |(x,x')\in \mathcal {S}_u]\prod _{i=0}^{n-1}((1-u_i)-(-1)^{u_i}p_i)\\&= \frac{1}{2^n} \sum _{u\in \mathbb {F}_2^n} \# \{(x,x')\in \mathcal {S}_u : y_{i-t} \ne y_i \} \prod _{i=0}^{n-1}((1-u_i)-(-1)^{u_i}p_i). \end{aligned}$$

The observation is inspired by Morawiecki et al.’s work on rotational cryptanalysis [31] where, given a rotational pair, the bias of the output pair being unequal at certain bit is calculated for one-bit AND, NOT and XOR. In the following, we reformulate and generalize their propagation rules in terms of rotational differential-linear probability. Note that all these rules can be derived from Observation 1.

Proposition 1 (AND-rule)

Let a, b, $a'$, and $b'$ be n-bit strings with $\Pr [a_{i-t} \ne a_i'] = p_i$ and $\Pr [ b_{i-t} \ne b_i' ] = q_i$. Then

$$\begin{aligned} \Pr [ (a \wedge b)_{i-t} \ne (a' \wedge b')_i ] = \frac{1}{2}(p_i + q_i - p_iq_i). \end{aligned}$$

Proposition 2 (XOR-rule)

Let a, b, $a'$, and $b'$ be n-bit strings with $\Pr [a_{i-t} \ne a_i'] = p_i$ and $\Pr [ b_{i-t} \ne b_i' ] = q_i$. Then

$$\begin{aligned} \Pr [ (a \oplus b)_{i-t} \ne (a' \oplus b')_i ] = p_i + q_i - 2p_iq_i. \end{aligned}$$

Proposition 3 (NOT-rule)

Let a and b be n-bit strings with $\Pr [a_{i-t} \ne b_i] = p_i$. Then $\Pr [ \bar{a}_{i-t} \ne \bar{b}_i] = p_i$.

Next, we consider constant additions. Let $(x,x') \in \mathbb {F}_2^{2n}$ be a data pair with $\Pr [x_{i-t}\ne x'_i] = p_i$ for some integer t and $c \in \mathbb {F}_2^n$ be a constant. Then $\Pr [(x\oplus c)_{i-t}\ne (x'\oplus c)_i] = \Pr [x_{i-t} \oplus x'_i \ne c_{i-t} \oplus c_i]$. In [31], only the cases where $c_{i-t} \oplus c_i = 1$ or $c_{i-t} = c_i = 0$ are considered. We generalize the rule for constant addition from [31] to the following proposition with all possibilities taken into account.

Proposition 4 (Adjusted C-rule)

Let a and $a'$ be n-bit strings with $\Pr [ a_{i-t} \ne a'_i ] = p_i$ and $c \in \mathbb {F}_2^n$ be a constant. Then we have

$$\begin{aligned} \Pr [(a \oplus c)_{i-t} \ne (a' \oplus c)_i] = {\left\{ \begin{array}{ll} 1-p_i, ~~~~c_{i-t} \oplus c_i = 1\\ p_i, ~~~~~~~~~c_{i-t} \oplus c_i = 0 \end{array}\right. } \end{aligned}$$

4.1 Propagation of R-DL Probabilities in Arithmetic Operations

For functions with AND-RX or LRX construction, such as the permutation Keccak-f, the propagation of the R-DL probability can be evaluated by the propositions previously shown, under the independency assumptions on the neighbouring bits. However, when dependency takes over, even if a function can be expressed as a boolean circuit, a direct applications of the AND, XOR, NOT and adjusted C-rule may lead to errors that accumulated during the iterated evaluation. One such example is the modular addition. In the following, we will derive the propagation rules of the differential-linear (DL) probability and R-DL probability for an n-bit modular addition.

Lemma 6 (carry-rule)

Let $\varsigma : \mathbb {F}_{2}^3\rightarrow \mathbb {F}_2$ be the carry function

$$\begin{aligned} \varsigma (x_0,x_1,x_2) = x_0x_1\oplus x_1x_2\oplus x_0x_2. \end{aligned}$$

Let a, b, c, $a'$, $b'$, and $c'$ be binary random variables with

$$\begin{aligned} p_0 = \Pr [a\ne a'], p_1 = \Pr [b\ne b'], p_2 = \Pr [c\ne c']. \end{aligned}$$

Then, we have that

$$\begin{aligned} \Pr [\varsigma (a,b,c)\ne \varsigma (a',b',c')]= p_0p_1p_2 - \frac{p_0p_1+p_0p_2+p_1p_2}{2}+ \frac{p_0+p_1+p_2}{2}. \end{aligned}$$

Proof

We prove the carry-rule with Observation 1 by enumerating $u \in \mathbb {F}_2^3$. For $u = (0,0,0)$, $\Pr [\varsigma (a,b,c)\ne \varsigma (a',b',c')|a=a',b=b',c=c'] = 0$. For $u = (0,0,1)$, $\Pr [\varsigma (a,b,c)\ne \varsigma (a',b',c')|a=a',b=b',c \ne c'] = \Pr [a \oplus b = 1] = 1/2$ and $\prod _{i=0}^{2}((1-u_i)+(-1)^{1-u_i}p_i) = (1-p_a)(1-p_b)p_c$.

Similarly, one can derive the expression for all $u\in \mathbb {F}_{2^3}$, and we omit the details.The overall probability of the event $ab\oplus ac\oplus bc \ne a'b'\oplus a'c'\oplus b'c'$ is $p_ap_bp_c - (p_ap_b+p_ap_c+p_bp_c)/2+(p_a+p_b+p_c)/2$.   $\square$

Based on the carry-rule, we can immediately prove the following two theorems on the DL and R-DL probabilities for n-bit modulo additions.

Theorem 3

($\boxplus$-rule for DL). Let x, y and $x',y'$ be n-bit string, such that $\Pr [x_i\ne x'_i] = p_i$ and $\Pr [y_i\ne y'_i] = q_i$. Then, the differential-linear probability for modular addition can be computed as

$$\begin{aligned} \Pr [(x\boxplus y)_i \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i \end{aligned}$$

where $s_0 = 0$ and

$$\begin{aligned} \begin{aligned} s_{i+1} = p_{i}q_{i}s_{i} - \frac{p_{i}q_{i}+p_{i}s_{i}+q_{i}s_{i}}{2} + \frac{p_{i}+q_{i}+s_{i}}{2}, i\le n-1 \\ \end{aligned} \end{aligned}$$

Proof

For inputs x and y, denote the carry by

$$\begin{aligned} c = (x\boxplus y)\oplus x\oplus y= (c_{n-1},\cdots ,c_1,c_0), \end{aligned}$$

where $c_0=0, c_{i+1} = x_{i}y_{i}\oplus x_{i}c_{i}\oplus y_{i}c_{i}$. Similarly, for $x'$ and $y'$, denote the carry by $c'= (c'_{n-1},\cdots ,c'_1,c'_0)$. Let $s_i$ denote the probability $\Pr [c_i\ne c'_i]$. Then, $s_0 = 0$ and for $i \ge 1$, the event $c_i\ne c'_i$ is equivalent to

$$\begin{aligned} x_{i-1}y_{i-1}\oplus x_{i-1}c_{i-1}\oplus y_{i-1}c_{i-1} \ne x'_{i-1}y'_{i-1}\oplus x'_{i-1}c'_{i-1}\oplus y'_{i-1}c'_{i-1}. \end{aligned}$$

Therefore, $s_i$ can be computed as

$$\begin{aligned} p_{i-1}q_{i-1}s_{i-1} - (p_{i-1}q_{i-1}+p_{i-1}q_{i-1}+q_{i-1}s_{i-1})/2+(p_{i-1}+q_{i-1}+s_{i-1})/2 \end{aligned}$$

according to Lemma 6. Since $x\boxplus y = x \oplus y \oplus c$, and $x'\boxplus y' = x' \oplus y' \oplus c'$, with the XOR-rule, we have

$$\begin{aligned} \Pr [(x\boxplus y)_i \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i. \end{aligned}$$

   $\square$

Example 1

Consider an 8-bit modular addition with input difference being $a = \texttt {7}$ and $b = \texttt {7}$. Then, we have for $0\le i \le 7$,

$$\begin{aligned} p_i = \frac{1+(-1)^{1-a_i}}{2}, q_i = \frac{1+(-1)^{1-b_i}}{2}, \end{aligned}$$

so

$$\begin{aligned} p_0 = p_1 = p_2 = 1, p_3 = p_4 = p_5 = p_6 = p_7 = 0,\\ q_0 = q_1 = q_2 = 1, q_3 = q_4 = q_5 = q_6 = q_7 = 0. \end{aligned}$$

The $\boxplus$-rule gives the output DL-probabilities in Table 2. The probabilities predicted in the table are verified by running through the 16-bit input space. In addition, we verified the $\boxplus$-rule in DL with all input differences on an 8-bit modular addition. Under the precision level given in Table 2, the experiments match the theoretical prediction perfectly.

Table 2. The DL-probabilities of an 8-bit modular addition with input differences $a=b = 7$ by theoretical evaluation, which are confirmed by experiments.

As for the rotational differential-linear cryptanalysis of an n-bit modular addition, a left rotation by t bits is applied to the operands. Firstly, we present the $\boxplus$-rule for RX-difference with a rotation offset $t= 1$.

Theorem 4

($\boxplus$-rule for RL, $t=1$ ). Given random n-bit strings x, y and $x',y'$ such that $x' = (x\lll 1) \oplus a, y' = (y\lll 1) \oplus b$, where $\Pr [x_{i-1}\ne x'_i] = p_i, \Pr [y_{i-1}\ne y'_i] = q_i$. Then, the rotational differential-linear probability of the modular addition can be computed as

$$\begin{aligned} \Pr [(x\boxplus y)_{i-1} \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i, \end{aligned}$$

where $s_0 \approx 1/2, s_1 = 1/4,$

$$ s_{i+1} = p_{i}q_{i}s_{i} - \frac{p_{i}q_{i}+p_{i}s_{i}+q_{i}s_{i}}{2} + \frac{p_{i}+q_{i}+s_{i}}{2}, 2 \le i \le n-1. $$

Proof

Denote $x = (x_{n-1},\cdots ,x_1,x_0)$, $y = (y_{n-1},\cdots ,y_1,y_0)$. Then

$$\begin{aligned} x' = ((x'_{n-1},\cdots ,x'_1,x'_0) = (x_{n-2}\oplus a_{n-1},\cdots ,x_0\oplus a_1,x_{n-1}\oplus a_0) \end{aligned}$$

$$\begin{aligned} y' = ((y'_{n-1},\cdots ,y'_1,y'_0) = (y_{n-2}\oplus b_{n-1},\cdots ,y_0\oplus b_1,y_{n-1}\oplus b_0) \end{aligned}$$

Let $c = (c_{n-1},\cdots ,c_0) = (x\boxplus y)\oplus x\oplus y$ and $c' = (c'_{n-1},\cdots ,c'_0) = (x'\boxplus y')\oplus x'\oplus y'$ be the two carries.

Let $s_i$ denote the probability $\Pr [c_{i-1}\ne c'_i]$. When $i=0$, $s_0 = \Pr [c_{n-1}\ne c'_0] = \Pr [x_{n-2}y_{n-2}\oplus x_{n-2}c_{n-2}\oplus y_{n-2}c_{n-2}=0] \approx 1/2$, because the LHS term is balanced for independent random variables x and y. For $i=1$, $s_1= \Pr [c_0\ne c'_1] = \Pr [x'_0y'_0\ne 0] = 1/4$. For $i>1$, $s_{i}$ is equal to

$$\begin{aligned} \begin{aligned} \Pr [c_{i-1}\ne c'_i]&= \Pr [x_{i-2}y_{i-2}\oplus x_{i-2}c_{i-2}\oplus y_{i-2}c_{i-2} \ne x'_{i-1}y'_{i-1}\oplus x'_{i-1}c'_{i-1}\oplus y'_{i-1}c'_{i-1}]\\&= p_{i-1}q_{i-1}s_{i-1} - \frac{p_{i-1}q_{i-1}+p_{i-1}s_{i-1}+q_{i-1}s_{i-1}}{2} + \frac{p_{i-1}+q_{i-1}+s_{i-1}}{2} \end{aligned} \end{aligned}$$

For $x\boxplus y$ and $x'\boxplus y'$, applying the XOR-rule on the inputs and the carry vector gives

$$\begin{aligned} \Pr [(x\boxplus y)_{i-1} \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i \end{aligned}$$

   $\square$

Example 2

Consider an 8-bit modular addition with input RX-difference (left rotate by 1-bit) being $a = \texttt {7}$ and $b = \texttt {7}$, which implies that

$$\begin{aligned} p_0 = p_1 = p_2 = 1, p_3 = p_4 = p_5 = p_6 = p_7 = 0,\\ q_0 = q_1 = q_2 = 1, q_3 = q_4 = q_5 = q_6 = q_7 = 0. \end{aligned}$$

The R-DL probability of the i-th output bit, $0\le i < 8$ is given in Table 3. The probabilities predicted for $i\ge 2$ are verified by running through the 16-bit input space, and the probability for $i=0$ is $2^{-1.01132}$ by experiment.

Table 3. The RL-probabilities of an 8-bit modular addition with input differences $a, b = 7$. $\mathtt{{rot}}(x) = x\lll 1$. The index i represents the position of the output bit.

The experiments on an 8-bit modular addition show that the theoretical estimation of the DL and R-DL probabilities match the experiments well, except that the approximation in R-DL probability for the least significant bit has a marginal error in precision.

With a similar deduction, we give the following theorem for computing the R-DL probability through a modular addition under the condition that $\mathtt{{rot}}(x) = x\lll t$, for an integer $2\le t \le n-1$.

Theorem 5

($\boxplus$-rule for RL for arbitrary $t>1$ ). Given random n-bit strings x, y and $x',y'$ such that $x' = x\lll t \oplus a, y' = y\lll t \oplus b$, where $\Pr [x_{i-1}\ne x'_i] = p_i, \Pr [y_{i-1}\ne y'_i] = q_i$. Then, the rotational differential-linear probability of the modular addition for $i\ge 0$ can be computed as

$$\begin{aligned} \Pr [(x\boxplus y)_{i-1} \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i, \end{aligned}$$

where $s_0 \approx 1/2, s_t = 1/2,$

$$ s_{i+1} = p_{i}q_{i}s_{i} - \frac{p_{i}q_{i}+p_{i}s_{i}+q_{i}s_{i}}{2} + \frac{p_{i}+q_{i}+s_{i}}{2}, 1 \le i \le n-1, i\ne t $$

Proof

Denote $x = (x_{n-1},\cdots ,x_1,x_0)$, $y = (y_{n-1},\cdots ,y_1,y_0)$, then

$$\begin{aligned} x' = ((x'_{n-1},\cdots ,x'_1,x'_0) = (x_{n-1-t}\oplus a_{n-1},\cdots ,x_{n-t+1}\oplus a_1,x_{n-t}\oplus a_0) \end{aligned}$$

$$\begin{aligned} y' = ((y'_{n-1},\cdots ,y'_1,y'_0) = (y_{n-1-t}\oplus b_{n-1},\cdots ,y_0\oplus b_1,y_{n-1}\oplus b_0). \end{aligned}$$

Let $c = (c_{n-1},\cdots , c_1,c_0)$ and $c'=(c'_{n-1},\cdots , c'_1,c'_0)$ be the carries. Let $s_i$ denote the probability $\Pr [c_{i-t}\ne c'_i]$. When $i = 0$,

$$\begin{aligned} s_0 = \Pr [c_{n-t}\ne c'_0] = \Pr [x_{n-t-1}y_{n-t-1}\oplus x_{n-t-1}c_{n-t-1}\oplus y_{n-t-1}c_{n-t-1} \ne 0] \approx 1/2 \end{aligned}$$

When $i=t$, $s_t = \Pr [c_0 \ne c'_t] = \Pr [x'_{t-1}y'_{t-1}\oplus x'_{t-1}c'_{t-1}\oplus y'_{t-1}c'_{t-1} \ne 0] \approx 1/2$ For all i, $i\ne 0,t$,

$$\begin{aligned} \begin{aligned} s_i&= \Pr [c_{i-t}\ne c'_i]\\&= \Pr [x'_{i-1}y'_{i-1}\oplus x'_{i-1}c'_{i-1}\oplus y'_{i-1}c'_{i-1} \\&\quad \quad \quad \quad \quad \ne x_{n-t+i-1}y_{n-t+i-1}\oplus x_{n-t+i-1}c_{n-t+i-1} \oplus c_{n-t+i-1}y_{n-t+i-1}] \\&= p_{i-1}q_{i-1}s_{i-1} - \frac{p_{i-1}q_{i-1}+p_{i-1}s_{i-1}+q_{i-1}s_{i-1}}{2} + \frac{p_{i-1}+q_{i-1}+s_{i-1}}{2}. \end{aligned} \end{aligned}$$

Then, we have

$$\begin{aligned} \Pr [(x\boxplus y)_{i-t} \ne (x'\boxplus y')_i] = p_i + q_i - 2p_iq_i - 2p_is_i - 2q_is_i + 4p_iq_is_i. \end{aligned}$$

   $\square$

The $\boxplus$-rules for DL and R-DL allows us to compute the partial DLCT of an n-bit modular addition accurately and efficiently. A naive application of Bar-On et al.’s approach [4] based on the Fast Fourier Transformation (FFT) by treating the modular addition as an $2n \times n$ S-box would require a complexity of $\mathcal {O}(2^{2n})$, where it requires a complexity of $O(n 2^{2n})$ to obtain the n rows of the DLCT whose output masks are the unit vectors. In contrast, with the $\boxplus$-rule for DL, given the input difference, the DL-probability for all output masks that are unit vectors can be evaluated in $\mathcal {O}(n)$ operations, which achieves an exponential speed-up.

4.2 Finding Input Differences for Local Optimization

According to Proposition 1 and Proposition 2, for x and y in $\mathbb {F}_2$, if $\Pr [x\ne x'] = p_1, \Pr [y\ne y'] = p_2$, we have

$$\begin{aligned} \Pr [xy\ne x'y'] = \frac{1}{2}(p_1+p_2-p_1p_2),\quad \Pr [x\oplus y \ne x'\oplus y'] = p_1+p_2-2p_1p_2. \end{aligned}$$

Obviously, $\Pr [xy\ne x'y']$ is in the interval [0, 0.5] and $\Pr [x\oplus y \ne x'\oplus y']$ is in the interval [0, 1]. Moreover, a behaviour of $\Pr [x\oplus y \ne x'\oplus y']$ is that it collapses to $\frac{1}{2}$ (e.g., correlation zero) whenever one of $p_1$ and $p_2$ is $\frac{1}{2}$. This observation suggests that the input probabilities should be biased from $\frac{1}{2}$ as much as possible. Otherwise, the probabilities will rapidly collapse to $\frac{1}{2}$ for all one-bit output masks after a few iterative evaluations of the round function.

In order to find distinguishers that cover as many rounds of a function F as possible, our strategy is to look for an input RX-difference $\delta$, such that the DL or R-DL probability after one or a few propagations still has a relatively large imbalance for all the output masks whose Hamming weights are one. Therefore, we can define the objective function to maximize the summation of the absolute biases:

$$\begin{aligned} \sum _{i}(|\Pr [e_i\cdot (\mathtt{{rot}}(f(x))\oplus f(\mathtt{{rot}}(x)\oplus \delta )) = 0] - 1/2|). \end{aligned}$$

(11)

For 8-bit modular additions, we observed that the absolute DL and R-DL bias are relatively large when the input RX-differences are either with a large Hamming weight or a small weight. For instance, with RX-difference $(x\lll 1)\oplus x'$, when the input differences are $a = \texttt {0}$ and $b = \texttt {1}$, the RL-probabilities are given as follows for $e_i, i=0,1,\dots ,7.$

$$\begin{aligned} 2^{-1}, 2^{-2}, 2^{-3}, 2^{-4}, 2^{-5}, 2^{-6}, 2^{-7}, 2^{-8}. \end{aligned}$$

Whereas for $a = \texttt {ff}$ and $b = \texttt {ff}$, the RL-probabilities are given as follows for $e_i, i=0,1,\dots ,7.$

$$\begin{aligned} 2^{-1}, 2^{-2}, 2^{-0.678072}, 2^{-0.29956}, 2^{-0.142019}, 2^{-0.0692627}, 2^{-0.0342157}, 2^{-0.0170064}. \end{aligned}$$

When the size of the operands are large (e.g., $n = 32$), it is difficult to find the optimal input difference manually. Next, we show the optimal input RX-difference with respect to the objective function given by Eq. (11) in a 32-bit modular addition. See the full version of this paper [25] for the search of such differences.

Example 3

Consider the R-DL probability for a 32-bit modular addition with $\mathtt{{rot}}(x) = x\lll 1$. With input RX-differences

$$\begin{aligned} a = \texttt {7ffffffc}, b = \texttt {7ffffffe}, \end{aligned}$$

the objective function in Eq. 11 is maximized, and the R-DL probabilities $\Pr [e_i\cdot (\mathtt{{rot}}(x\boxplus y) \oplus ((\mathtt{{rot}}(x)\oplus a)\boxplus (\mathtt{{rot}}(y)\oplus b)))=1]$ for $0\le i \le 31$ are shown as follows.

i	0	1	2	3	4	5	6	7
$p_i$	0.5	0.75	0.5	0.75	0.875	0.9375	0.96875	0.984375
i	8	9	10	11	12	13	14	15
$p_i$	0.992188	0.996094	0.998047	0.999023	0.999512	0.999756	0.999878	0.999939
i	16	17	18	19	20 – 31
$~~p_i~~$	0.999969	0.999985	0.999992	0.999996	1

5 Applications to AND-RX Primitives

In this section, we apply the rotational differential-linear technique to the AND-RX permutations involved in FRIET and Xoodoo, and significant improvements are obtained. To confirm the validity of the results, all distinguishers with practical complexities are experimentally verified, and the source code is available².

5.1 Distinguishers for Round-Reduced FRIET

FRIET is an authenticated encryption scheme with built-in fault detection mechanisms proposed by Simon et al. at EUROCRYPT 2020 [32]. Its fault detection ability comes from its underlying permutation, which is designed based on the so-called code embedding approach.

The core permutation FRIET-P employed in FRIET operates on a $4 \times 128 = 512$-bit state arranged into a rectangular with 4 rows (called limbs) and 128 columns (called slices) as shown in Fig. 1. The permutation FRIET-P is an iterative design with its round function $g_{rc_i}$ visualized in Fig. 2, where a, b, and $c \in \mathbb {F}_2^{128}$ are the four limbs (see Fig. 1) of the input state and $rc_i$ is the round constant for the i-th round.

Fig. 1.

The view of the state

By design, the round function $g_{rc_i}$ is slice-wise code-abiding for the parity code $[4, 3, 2]_{\mathbb {F}_2}$, meaning that every slice of the output state is a code word if every slice of the input state is a code word. Mathematically, it means that $a + b + c = d$ implies $a'+b'+c' = d'$. This slice-wise code-abiding property is inherited by the permutation FRIET-P $= g_{rc_{t-1}} \circ \cdots \circ g_{rc_1} \circ g_{rc_0}$. Consequently, faults will be detected if some output slice is not a code word when all of the slices of the input state are code words. Note that the behavior of the permutation FRIET-PC is identical to FRIET-P by design if we ignore the limb d.

Fig. 2.

The round functions of Friet-PC and Friet-P

Practical Distinguishers for FRIET-PC. Since a distinguisher for the permutation FRIET-PC directly translates to a distinguisher for FRIET-P, we focus on the permutation FRIET-PC. Let (a, b, c) and $(a',b',c')$ in $\mathbb {F}_2^{128 \times 3}$ be the input pair of the permutation with RX-differences

$$\begin{aligned} \varDelta _a= (a\lll t) \oplus a', ~~\varDelta _b = (b\lll t) \oplus b' ,~~\varDelta _c = (c\lll t) \oplus c' . \end{aligned}$$

In our analysis, we only consider input RX-differences such that $wt(\varDelta _a)+wt(\varDelta _b)+wt(\varDelta _c) \le 1$.

According to the adjusted C-rule (see Proposition 4), the constant addition injects an RX-difference $c\oplus (c\lll t)$ to the state, and alters the R-DL-probabilities when the corresponding bits in $c\oplus (c\lll t)$ is nonzero. A rule-of-thumb for choosing the rotational amount is to minimize the weight of the RX-difference introduced by the round constants, so that the effect of the constants on destroying the rotational propagation is presumably decreased. The first 6 round constants of FRIET-PC are (in Hexadecimal)

$$\begin{aligned}{} \texttt {1111}, \texttt {11100000},\texttt {1101},\texttt {10100000},\texttt {101},\texttt {10110000}. \end{aligned}$$

To minimize the Hamming weight of the RX-differences from the round constants, one of the best rotational operations is to left rotate by 4 bits, such that the consecutive nonzero nibbles cancel themselves as many as possible. Then, the injected RX-differences due to the round constants are

$$\begin{aligned}{} \texttt {10001}, \texttt {100100000},\texttt {10111},\texttt {111100000},\texttt {1111},\texttt {111010000}.\end{aligned}$$

With the AND-rule, XOR-rule and adjusted C-rule, the R-DL probability can be evaluated given the input RX-differences with $w_h(\varDelta _a)+w_h(\varDelta _b)+w_h(\varDelta _c) \le 1$ and the output linear mask $e_i$. Table 4 shows the rotational differential-linear distinguishers with the largest absolute correlation we found in reduced-round FRIET-PC, where $\varDelta _a,\varDelta _b,\varDelta _c$ are the input RX-differences, and $\gamma _a,\gamma _b,\gamma _c$ are the output masks for the limbs a, b, c, respectively.

Table 4. Distinguishers for reduced-round FRIET-PC with rotation offset $t = 4$.

For FRIET-PC reduced to 4-round, an R-DL distinguisher with correlation 1 is detected, with input RX-differences (0, 0, 0) and output masks (0, 1, 0). For 5, 6-round FRIET-PC, we found practical rotational differential-linear distinguishers with correlation $2^{-0.96}$ and $2^{-5.81}$, respectively. All the distinguishers shown in Table 4 are verified experimentally with $2^{24}$ random plaintexts.

Extending the Practical Distinguishers. According to the discussion of Sect. 3, we can extend a rotational differential-linear distinguisher by appending a linear approximation $\gamma \rightarrow \mu$, and the bias of the extended distinguisher can be computed with Eq. (7). Consequently, this extension is optimal when $\epsilon _{\gamma ,\mu }$ and $\epsilon _{\mathtt{{rot}}^{-1}(\gamma ),\mathtt{{rot}}^{-1}(\mu )}$ reach their largest possible absolute values simultaneously. For FRIET-PC, we always have $\epsilon _{\gamma ,\mu } = \epsilon _{\mathtt{{rot}}^{-1}(\gamma ),\mathtt{{rot}}^{-1}(\mu )}$, and thus we can focus on finding an optimal linear approximation $\gamma \rightarrow \mu$.

Here we take the 6-round R-DL distinguisher presented in Table 4 and append optimal linear approximations to extend it. The output linear mask of the 6-round distinguisher is $(\mathtt {0},\mathtt {0},\mathtt {40000})$. In Table 5, we list the correlations of the optimal linear approximations for round-reduced FRIET-PC whose input masks are $(\mathtt {0},\mathtt {0},\mathtt {40000})$, which are found with the SMT-based approach [20].

Table 5. The correlation of optimal linear trails found in round-reduced FRIET-PC with the input masks $(\mathtt {0},\mathtt {0},\mathtt {40000})$

The optimal 1-round linear trail we found has output masks

$$\begin{aligned}\begin{aligned}&\mu _a = \mathtt {00000000000000020000000000040000}\\&\mu _b = \mathtt {00004000000000020000000000040000}\\&\mu _c = \mathtt {00000000000080020000000000060000}. \end{aligned}\end{aligned}$$

Thus a 7-round distinguisher can be built by concatenating the 6-round distinguisher with a 1-round linear approximation, and the estimated correlation is $2^{-5.81} \times 2^{-2\times 2} = 2^{-9.81}$. With $2^{24}$ pairs of inputs satisfying the input RX-difference, the output difference under the specified mask are biased with a correlation approximately $2^{-9.12}$. Similarly, by appending a 2-round linear trail with output masks

$$\begin{aligned}\begin{aligned}&\mu _a = \mathtt {00000000000000030000000000060000}\\&\mu _b = \mathtt {00006000000000010000000030020000}\\&\mu _c = \mathtt {600000000000c0010000000000030000}. \end{aligned}\end{aligned}$$

at the end of the 6-round rotational differential-linear distinguisher, we get a 8-round RL-distinguisher with a correlation $2^{-17.81}$. And with $2^{40}$ pairs of inputs satisfying the input RX-difference, we find the experimental correlation of the 8-round distinguisher is $2^{-17.2}$. As a comparison, the 7-,8-round linear trails presented in the specification of FRIET-PC have correlation $2^{-29}$ and $2^{-40}$, respectively. With the linear trails shown in Table 5, the concatenated distinguisher can reach up to 13 rounds, with an estimated correlation $2^{-117.81}$.

5.2 Distinguishers for Round-Reduced Xoodoo

Xoodoo  [14] is a 384-bit lightweight cryptographic permutation whose primary target application is in the Farfalle construction [8]. The state of Xoodoo is arranged into a $4\times 3\times 32$ cuboid and the bit at a specific position is accessed as a[x][y][z]. One round of Xoodoo consists of the following operations.

$$\begin{aligned}\begin{aligned}&a[x][y][z] = a[x][y][z] \oplus \sum _y a[x-1][y][z-5] \oplus \sum _y a[x-1][y][z-14]\\&a[x][1][z] = a[x-1][1][z], a[x][2][z] = a[x][2][z-11]\\&a[0][0] = a[0][0] \oplus RC_i\\&a[x][y][z] = a[x][y][z] \oplus ((a[x][y+1][z]+1)*(a[x][y+2][z]))\\&a[x][1][z] = a[x][1][z-1], a[x][2][z] = a[x-1][2][z-8] \end{aligned}\end{aligned}$$

The total number of rounds in Xoodoo is 12, and in some modes (Farfalle [8] for instance), the core permutation calls a 6-round Xoodoo permutation. The round constants of Xoodoo are shown in the following, and for Xoodoo reduced to r rounds, the round constants are $c_{-(r-1)}, \cdots , c_0$.

$$\begin{aligned} \begin{aligned} c_{-11}&= \texttt {00000058} ,\quad c_{-8} = \texttt {000000D0} ,\quad c_{-5} = \texttt {00000060} ,\quad c_{-2} =\texttt {000000F0} \\ c_{-10}&=\texttt {00000038} ,\quad c_{-7} =\texttt {00000120} ,\quad c_{-4} =\texttt {0000002C} ,\quad c_{-1} =\texttt {000001A0}\\ c_{-9}&=\texttt {000003C0} ,\quad c_{-6} =\texttt {00000014} ,\quad c_{-3} =\texttt {00000380} ,~~\quad c_{0} =\texttt {00000012} \end{aligned} \end{aligned}$$

Given input difference being all-zero, i.e., the input pair is exactly a rotational pair, let the rotation amount be left-rotate by 1-bit. We find that after 3 rounds of Xoodoo, there are still many output bits that are highly biased, with the largest correlation being 1 and the one-bit mask at position (1, 0, 16). This suggests a nonzero mask $\texttt {10000}$ at the lane (1, 0). However, extending one extra round, we no longer see any significant correlation.

Noticing that the round constant is XORed into the state right after the first two linear operations, one can control the input RX-difference such that the difference is cancelled by the injection of the first-round constant. As a result, it gains one round free at the beginning, and we are able to construct a 4-round distinguishers for Xoodoo. When the left-rotational amount is set to 1-bit, the RX-difference of the first constant $c_{-3}$ is $\mathtt {00000480}$. This suggests that if we take input RX-differences

$$\begin{aligned}\begin{aligned} a[0][0] = \mathtt {484ccc80}; a[0][1] = \mathtt {484cc800}; a[0][2] = \mathtt {484cc800};\\ a[1][0] = \mathtt {3ab9821a}; a[1][1] = \mathtt {3ab9821a}; a[1][2] = \mathtt {3ab9821a};\\ a[2][0] = \mathtt {37b6cde9}; a[2][1] = \mathtt {37b6cde9}; a[2][2] = \mathtt {37b6cde9};\\ a[3][0] = \mathtt {45a3f0cb}; a[3][1] = \mathtt {45a3f0cb}; a[3][2] = \mathtt {45a3f0cb}. \end{aligned}\end{aligned}$$

The RX-difference after the first round of Xoodoo will be all zero. Hence, we are able to find a 4-round distinguishers with significant correlations. We find a rotational differential-linear distinguishers with correlation 1 with the output mask being 10000 at lane (1, 0) and zero for the rest lanes. Another two distinguishers with the same correlation are found with output mask 20000 at lane (1, 1) and 1000000 at lane (3, 2).

6 Applications to ARX Primitives

In this section, we apply the rotational differential-linear technique to the ARX permutations involved in Alzette and SipHash, and the source code for experimental verifications is available³.

6.1 Application in the 64-Bit ARX-box Alzette

At CRYPTO 2020, Beierle et al. presented a 64-bit ARX-box Alzette [6] that is efficient for software implementation. The design is along the same research line with a previous design called SPARX [15] with a 32-bit ARX-box where a long trail argument was proposed for deriving a security bound in ARX ciphers. Figure 3 shows an instance of Alzette with an input $(x,y)\in \mathbb {F}_2^{32}\times \mathbb {F}_2^{32}$.

Fig. 3.

The Alzette instance.

The differential and linear properties of Alzette is comparable to the 8-bit S-box of AES. The optimal differential characteristic in Alzette has a probability of $2^{-6}$. In addition, because of the modular additions in Alzette and the diffusion, the designers showed by division property that the Alzette may have full degree in all its coordinates.

In the following, we present the rotational differential-linear and differential-linear distinguishers of Alzette found with the techniques in Sect. 4. The constant $c = \texttt {B7E15162}$ (the first constant in SPARX-based design Sparkle-128) is considered for illustration.

Rotational Differential-Linear Distinguisher. In Sect. 4.2, $(\texttt {7ffffffc},\texttt {7fffffffe})$ is found to be optimal in 32-bit modular addition under the objective function considered in Example 3. Here, the difference can be used as the input difference of the first modular addition in Alzette. Because of the right rotation by 31 bits before the modular addition, the input RX-difference to Alzette is $(\texttt {7ffffffc},\texttt {3ffffffff})$. With an iterative evaluation on the steps in Alzette, we found that the second least significant bit is biased. Specifically, with an output mask $(\texttt {2},\texttt {0})$, the RL-probability is 0.500189, that is a correlation $2^{-11.37}$. By taking $2^{28}$ pairs of random plaintexts, the experimental correlation of the distinguisher is $2^{-7.35}$. In addition, we checked all input RX-differences (a, b) with Hamming weight $wt(a) + wt(b) = 1$, but no rotational differential-linear distinguisher is found.

Differential-linear distinguisher. For all input differences with Hamming weight 1, we compute the differential-linear probability of Alzette with the technique in Sect. 4. The best found distinguisher has an input difference $(\texttt {80000000},\texttt {0})$ and output mask $(\texttt {80000000},\texttt {0})$, with a probability of 0.086, equivalently, a correlation of $2^{-0.27}$. By experiment verification with $2^{28}$ pairs of random plaintexts, the correlation is $2^{-0.1}$.

The following Fig. 4 shows a comparison of the probability for an input difference $(\texttt {80000000},\texttt {0})$ and output masks $(\texttt {1}\lll t,\texttt {0})$ (for all integer $t\in [0,31]$), by our evaluation technique and the experiment with $2^{24}$ pairs of random plaintexts. The theoretical evaluation matches the experiment within a tolerable fluctuation.

Fig. 4.

A comparison between the differential-linear probability in Alzette by theoretical computation and by experiment. The index shows the index of the nonzero bit in the unit-vector output mask. For instance, when the index is 0, the output mask is (0,1), and when the index is 63, it is (80000000,0).

Comparing with RL-distinguishers and DL-distinguisher found in Alzette, the latter is significantly stronger. Also, it is interesting to notice that input differences with low Hamming weight often lead to good differential-linear distinguishers in Alzette, whereas we didn’t find any rotational differential-linear distinguisher with low-weight RX-differences when the rotational offset is greater than zero. The influence of the constants in RL-distinguishers may be the main cause.

6.2 Experimental Distinguishers for SipHash Explained

SipHash [2], designed by Aumasson and Bernstein, is a family of ARX-based pseudorandom functions optimized for short inputs. Instances of SipHash are widely deployed in practice. For example, SipHash-2-4 is used in the dnscache instances of all OpenDNS resolvers and employed as hash() in Python for all major platforms (https://131002.net/siphash/#us).

In [16], from a perspective of differential cryptanalysis, a bias of the difference distribution of one particular output bit for 3-round SipHash is observed when the Hamming weight of the input difference is one. For instance, with input difference $a = 1$, He and Yu showed that the output difference is biased at the 27-th bit with a correlation $2^{-6}$ by experiments. This observation was obtained through extensive experiments and the theoretical reason behind these distinguishers is unclear as stated by He and Yu:

“... we are not concerned about why it shows a rotation property or why it reaches such a bias level. However, a great number of experiments can support those observations. (see [16, Section 4.2, Page 11])”

According to the discussion of Sect. 3.2, the bias of $E(x) \oplus E(x \oplus \delta )$ observed in [16] is equivalent to the bias of

$$\begin{aligned}e_i\cdot (E(x) \oplus E(x \oplus \delta )).\end{aligned}$$

It can be interpreted in the differential-linear framework and analyzed with the theoretical approach presented in Sect. 4. Here, we apply the rules for modular addition and XOR, and compute the DL-probability of the 3-round distinguisher found in SipHash. With our technique, we confirm that the 3-round differential-linear distinguisher with the aforementioned difference and mask, the predicted correlation is $2^{-6.6}$ which is close to He and Yu’s experiments.

In addition, we can explain the observation on the rotation property with the $\boxplus$-rule in differential-linear. We will adopt the notations that are used in Theorem 3.

Because the input difference in their experiment has only one nonzero bit, we consider the DL-probability of an n-bit modular addition where the input difference is $(e_k, 0)$, for an integer k.

Then, for a pair of inputs (x, y) and $(x',y')$, the probability $p_k = \Pr [x_k\ne x'_k] = 1$. And for the remaining bits, $p_i = \Pr [x_i\ne x'_i], i\ne k$ and $q_i = \Pr [y_i,y'_i]$ are equal to zero.

Let $s_i = \Pr [\varsigma (x,y)_i \ne \varsigma (x',y')].$ We have $s_0,\cdots ,s_{k} = 0, s_{k+t} = 2^{-t}, 1\le t \le n-1-k$. As a result, the DL-probabilities through the modular addition at the i-th bit is given by $P_i = \Pr [(x\boxplus y)_i \ne (x'\boxplus y')_i], 0\le i \le n-1$, where

$$\begin{aligned} \Pr [(x\boxplus y)_i \ne (x'\boxplus y')_i] = {\left\{ \begin{array}{ll} 0, \quad \quad \ i\le k\\ 2^{-i+k}, \ \hbox {otherwise} \end{array}\right. } \end{aligned}$$

(12)

By rotating the input difference $(\texttt {1}\lll k, 0)$ to the left by one bit, the differential-linear probability for the i-th bit of the output $\overleftarrow{P_i}$ is equal to $2^{-i+k+1}$ for $k+1 < i \le n-1$, and to zero for $i\le k+1$.

It is obvious that the by rotating the differential-linear probability in Eq. (12), we obtain the probabilities $\overleftarrow{P_i}$ for all but the least significant bit, where $\overleftarrow{P_0} = 0$ and $P_{n-1} = 2^{-n-1+k}$. Nevertheless, the error is negligible if $n-k$ is large, and it holds for large modular additions such as the 64-bit one adopted in SipHash.

For input differences with Hamming weight more than 1, a similar rotational property can be observed for the $\boxplus$-rule in differential-linear. And it gives a straightforward intuition on the rotational property observed in the differential-linear distinguishers of SipHash.

7 Conclusion and Open Problems

We extend the differential-linear framework by using rotational-xor differentials in the differential part of the framework and we name the resulting cryptanalytic technique as rotational differential-linear cryptanalysis. We give an informal formula to estimate the bias of rotational differential-linear distinguisher under certain assumptions. In particular, we show Morawiecki et al.’s technique can be generalized to estimate the bias of a rotational differential-linear distinguisher whose output linear mask is a unit vector. We apply our method to the permutations involved in FRIET, Xoodoo, Alzette, and SipHash, which leads to significant improvements over existing cryptanalytic results or explanations for previous experimental distinguishers without a theoretical foundation. Finally, we would like to mention that we failed to derive a closed formula for the bias of a rotational differential-linear distinguisher under the sole assumption of the independence between the rotational-xor differential part and linear part. This is left open and the link between rotational-xor differential and linear cryptanalysis we presented in this work can be seen as a first step towards solving this problem.

A natural extension of rotational differential-linear cryptanalysis is to the SPN-type primitives, where one aims at finding a rotational relation that is preserved with a significant probability through the nonlinear Sbox layer. Especially, it is feasible to check all the rotational differences for their transition probabilities in a small-scale Sbox. Comparing to binary and arithmetic operations, our observation is that rotational relations are less likely to preserve in Sboxes, so it is challenging to find good distinguishers in Sbox-based designs. We leave it as an interesting future work.