Abstract
In this paper we give an exposition of supersingular isogeny graphs, quaternion ideal graphs and Bruhat–Tits trees, and of their connections. Bruhat–Tits trees are combinatorial objects whose vertices and edges have a very simple representation as two-by-two matrices, which, as we show, is useful for understanding certain aspects of the corresponding elliptic curves and isogenies. Moreover, Bruhat–Tits trees can be given an orientation and a notion of depth that we translate into the setting of supersingular isogeny graphs. We give some suggestions towards using Bruhat–Tits trees as a tool for cryptanalysis of certain cryptosystems based on supersingular isogeny graphs.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
See e.g. [40, Theorem 4.1].
- 2.
Pizer [35] used this description of supersingular isogeny graphs to prove the Ramanujan property when p ≡ 1 (mod 12).
- 3.
- 4.
We are using the prime ℓ to be consistent with the isogeny graphs to which we want to connect this theory. In the Shimura curves literature, p is widely used as the chosen prime, so p-adic upper half-plane is more standard.
- 5.
Although we will focus at first on the SIKE parameters, it could be that the most interesting case occurs for a different parameter set within the SIDH family of protocols.
References
Amorós, L., Milione, P.: Mumford curves covering p-adic Shimura curves and their fundamental domains. Trans. Amer. Math. Soc. 371(2), 1119–1149 (2019)
Arpin, S., Camacho-Navarro, C., Lauter, K., Lim, J., Nelson, K., Scholl, T., Sotáková, J.: Adventures in Supersingularland. Preprint at https://eprint.iacr.org/2019/1056 (2019)
Azarderakhsh, R., Koziel, B., Campagna, M., LaMacchia, B., Costello, C., Longa, P., De Feo, L., Naehrig, M., Hess, B., Renes, J., Jalali, A., Soukharev, V., Jao, D., Urbanik, D.: Supersingular Isogeny Key Encapsulation. Available at http://sike.org (2017)
Beullens, W., Kleinjung, T., Vercauteren, F.: CSI-FiSh: Efficient Isogeny Based Signatures Through Class Group Computations. In: Galbraith, S. D., Moriai, S. (eds.) Advances in Cryptology – ASIACRYPT 2019, Lecture Notes in Comp. Sci, vol. 11921, pp. 227–247. Springer (2019)
Boutot, J.-F., Carayol, H.: Uniformisation p-adique des courbes de Shimura: les théorèmes de Čerednik et de Drinfeld. Astérisque 196–197, 45–158 (1991)
Brandt, H.: Zur Zahlentheorie der Quaternionen. Jahresbericht der Deutschen Mathematiker-Vereinigung 53, 23–57 (1943)
Castryck, W., Decru, T.: CSIDH on the Surface. In: Ding, J., Tillich, J.-P. (eds.) Post-Quantum Cryptography, Security and Cryptology, vol. 12100, pp. 111–129. Springer (2020)
Castryck, W., Lange, T., Martindale, C., Panny, L., Renes, J.: CSIDH: An Efficient Post-Quantum Commutative Group Action. In: Peyrin, P., Galbraith, S. (eds.) Advances in Cryptology – ASIACRYPT 2018, Lecture Notes in Comp. Sci, vol. 11274, pp. 395–427. Springer (2018)
Čerednik, I.V.: Uniformization of algebraic curves by discrete arithmetic subgroups of PGL2(k w) with compact quotients. Math. USSR Sbornik 29(1), 55–78 (1976)
Charles, D.X., Goren, E.Z., Lauter, K.E.: Cryptographic hash functions from expander graphs. Preprint available at https://eprint.iacr.org/2006/021 (2006)
Charles, D.X., Goren, E.Z., Lauter, K.E.: Cryptographic hash functions from expander graphs. Journal of Cryptology 22(1), 93–113 (2009)
Charles, D.X., Goren, E.Z., Lauter, K.E.: Families of Ramanujan graphs and quaternion algebras. In: Harnad, J., Winternitz, P. (eds.) Groups and symmetries. CRM Proc. Lecture Notes, vol. 47, pp. 53–80. Amer. Math. Soc. (2009)
Costache, A., Feigon, B., Lauter, K., Massierer, M., Puskas, A.: Ramanujan Graphs in Cryptography. In: Balakrishnan, J., Folsom, A., Lalín, M., Manes, M. (eds) Research Directions in Number Theory, Association for Women in Mathematics Series, vol 19, pp. 1–40. Springer (2018)
Couveignes, J.-M.: Hard Homogeneous Spaces. Preprint at https://ia.cr/2006/291 (2006)
De Feo, L.: Exploring Isogeny Graphs. Habilitation Thesis (2018)
De Feo, L., Kieffer, J., Smith, B.: Towards Practical Key Exchange from Ordinary Isogeny Graphs. In: Peyrin, T., Galbraith, S. (eds.) Advances in Cryptology – ASIACRYPT 2018. Lecture Notes in Comp. Sci., vol 11274, pp. 365–394. Springer (2018)
Deuring, M.: Die Typen der Multiplikatorenringe elliptischer Funktionenkörper. Abh. Math. Sem. Hansischen Univ 14, 197–272 (1941)
Drinfel’d, V.G.: Coverings of p-adic symmetric regions. Functional Analysis and Its Applications 10(2), 107–115 (1976)
Eisentraeger, K., Hallgren, S., Lauter, K., Morrison, T., Petit, C.: Supersingular isogeny graphs and endomorphism rings: reductions and solutions. In: Nielsen, J., Rijmen, V. (eds.) Advances in Cryptology – EUROCRYPT 2018. Lecture Notes in Comp. Sci., vol 10822, pp. 329–368. Springer (2018)
Franc, C., Masdeu, M.: Computing fundamental domains for the Bruhat–Tits tree for \(\mathrm {GL}_2(\mathbb {Q}_p)\), p-adic automorphic forms, and the canonical embedding of Shimura curves. LMS Journal of Computation and Mathematics 17(1), 1–23 (2014)
Franc, C., Masdeu, M.: BTQuotient package. Available at https://github.com/mmasdeu/btquotients
Franc, C., Masdeu, M.: BTQuotient Module. Available at https://doc.sagemath.org/html/en/reference/modsym/sage/modular/btquotients/btquotient.html
Jao, D., De Feo, L.: Towards quantum-resistant cryptosystems from supersingular elliptic curve isogenies. In: Yang, B. Y.(eds.) Post-Quantum Cryptography. PQCrypto 2011. Lecture Notes in Comp. Sci., vol 707, pp. 19–34. Springer (2011)
Jordan, B.W., Livné, R.: Local diophantine properties of Shimura curves. Math. Ann. 270(2), 235–248 (1984)
Kohel, D.: Endomorphism rings of elliptic curves over finite fields. PhD Thesis of the University of California at Berkely (1996)
Kohel, D., Lauter, K., Petit, C., Tignol, J.-P.: On the quaternion ℓ-isogeny path problem. LMS Journal of Computation and Mathematics 17, 418–432 (2014)
Kurihara, A.: On some examples of equations defining Shimura curves and the Mumford uniformization. J. Fac. Sci. Univ. Tokyo, Sect. IA Math 25(3), 277–300 (1979)
Kutas, P., Martindale, C., Panny, L., Petit, C., Stange, K.E.: Weak instances of SIDH variants under improved torsion-point attacks. Preprint at https://eprint.iacr.org/2020/633 (2020)
Milione, P.: Shimura curves and their p-adic uniformizations. PhD Thesis of the Universitat de Barcelona (2015)
Morita, Y.: Reduction mod
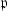 of Shimura curves. Hokkaido Math. J 10(2), 209–238 (1981)
of Shimura curves. Hokkaido Math. J 10(2), 209–238 (1981)National Institute of Standards and Technology. Post-quantum cryptography standardization (December 2016)
Onuki, H., Aikawa, Y., Takagi, T.: The Existence of Cycles in the Supersingular Isogeny Graphs Used in SIKE. In: Proceedings of 2020 International Symposium on Information Theory and its Applications, ISITA 2020, pp. 358–362, 9366119 (2020)
Petit, C.: Faster Algorithms for Isogeny Problems Using Torsion Point Images. In: Takagi, T., Peyrin, T. (eds.) Advances in Cryptology ASIACRYPT 2017. Lecture Notes in Comp. Sci., vol 10625, pp. 330–353. Springer (2017)
Pizer, A.: An Algorithm for Computing Modular Forms on Γ0(N). Journal of Algebra 64(2), 340–390 (1980)
Pizer, A.: Ramanujan graphs and Hecke operators. Bull. Amer. Math. Soc. (N.S.) 23(1), 127–137 (1990)
Ribet, K.A.: On modular representations of \(\mathrm {Gal}(\overline {\mathbb {Q}}/\mathbb {Q})\) arising from modular forms. Invent. Math 100(2), 431–476 (1990)
Rostovtsev, A., Stolbunov, A.: Public-key cryptosystem based on isogenies. Preprint at https://ia.cr/2006/145 (2006)
Serre, J.-P.: Arbres, amalgames, SL2. Société Mathèmatique de France (1977)
Shimura, G.: Construction of Class Fields and Zeta Functions of Algebraic Curves. Ann. of Math. 85(1), 58–159 (1967)
Silverman, J.H.: The Arithmetic of Elliptic Curves, 2nd Edition. Springer (2009)
Vélu, J.: Isogénies entre courbes elliptiques. Comptes Rendus de l’Académie des Sciences de Paris 273, 238–241 (1971)
Vignéras, M.-F.: Arithmátique des algèbres de quaternions. Springer (1980)
Voight, J.: Quaternion Algebras, v.0.9.22. Available at https://math.dartmouth.edu/~jvoight/quat.html (2020)
Acknowledgements
We want to thank the organisers of the Women in Numbers Europe 3 conference for giving us the opportunity to work on this project. We also wish to thank the anonymous reviewers for their helpful comments.
Jana Sotáková, as well as a follow up visit of Laia Amorós, Annamaria Iezzi and Chloe Martindale at the CWI in Amsterdam, were supported by the Dutch Research Council (NWO) through Gravitation-grant Quantum Software Consortium—024.003.037. Laia Amorós was supported by Academy of Finland grant #282938 and by Helsinki Institute for Information Technology HIIT. Chloe Martindale was partially supported by CHIST-ERA USEIT (NWO project 651.002.004).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Amorós, L., Iezzi, A., Lauter, K., Martindale, C., Sotáková, J. (2021). Explicit Connections Between Supersingular Isogeny Graphs and Bruhat–Tits Trees. In: Cojocaru, A.C., Ionica, S., García, E.L. (eds) Women in Numbers Europe III. Association for Women in Mathematics Series, vol 24. Springer, Cham. https://doi.org/10.1007/978-3-030-77700-5_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-77700-5_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-77699-2
Online ISBN: 978-3-030-77700-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


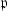 of Shimura curves. Hokkaido Math. J 10(2), 209–238 (1981)
of Shimura curves. Hokkaido Math. J 10(2), 209–238 (1981)