Abstract
Urban water distribution systems (WDS) ensure the demand-driven supply of a city at multiple ends. Well-being of the population as well as multiple economic sectors depend on its viability and thereby classify it as a critical infrastructure. Therefore, its behavior when exposed to changes is of interest to water suppliers as well as local decision-makers. It can be determined by resilience metrics, assessing the capability to meet and recover its functioning when exposed to disturbances. These disturbances can occur in form of changes in the water availability, the WDS topology, or the water demand pattern. Since networks as WDS are studied by graph theory, also different graph-theoretical resilience metrics were derived. In this work a well-established topology-based resilience metric is adapted and deployed to assess the present resilience of the urban main-line WDS of the German city of Darmstadt as well as of a suburb in the Rhine-Main region. Thereby, the intercomparability of the resilience for the different urban structures were of interest. Based on this analysis the comparability of different urban main-line WDS regarding their resilience is facilitated. Additionally, the conducted approach to allow for the comparability of absolute resilience values of urban structures of varying size can be applied to different resilience metrics as well as technical systems.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
An integral part of urban structures are their infrastructures – forming its design and furthermore significantly influencing its livability. One of the main infrastructures is the water distribution system (WDS) meeting multiple needs, starting at the well-being of the population and reaching into the economic prosperity of an urban region. Its layout greatly depends on the present urban structure, especially the urban transportation infrastructure as these two infrastructures are highly in parallel [1].
Urban structures themselves form by different means, studied in the field of urban morphology. Naturally they form when a rural area grows into a metropole or several close rural areas grow into a single urban structure, as it is the case for Dublin and on smaller scale as well the city of Darmstadt [2]. Additionally, there exist planned urban areas. These were often characterized by geometric and homogeneous areal urban design planned and rolled out in a short period of time, even though this approach is challenged today [3]. Both methods of developing urban structures do not have a well-functioning WDS as main objective in mind. Form follows function, a guiding principle defining product design as well as architecture doesn’t seem to apply for urban design considering the WDS. While on small scale this principle is followed by when designing components as pipes, valves, and pumps of the WDS, the overall layout of the WDS then follows the already existing or planned form of the urban structure. This can as well be interpreted as its function, yet it is an interesting question to pose, whether the urban structure shouldn’t be planned or reconstructed to allow for the best WDS design.
To answer this question, one needs to define the function of the WDS as well as a criterion to measure its fulfillment. In this case not only the fulfillment of the water demand itself should be considered but also the ever changing environment it is embedded in. Therefore, it is of interest what changes apply to urban structures and its WDS. On the one hand, there is a trend of constant urbanization [4], which leads to changing water demands. On the other hand, WDS are subject to hazards leading to different disturbances in the availability of water, the WDS’s components as well as changes of the demand pattern. The functioning (to a minimum degree) under changing conditions and furthermore the recovery or adaptation of a system to fully function again is a given for resilient systems [5]. This aim is also often shared in asset management [6]. Therefore, different resilience metrics for infrastructures were defined, also specifically for WDS.
These metrics are often applied, for example in asset management, to improve one system’s resilience. This led to the finding that the present urban structure determines a saturation like maximum resilience for an optimized WDS [7]. Yet, the comparison of different systems towards their resilience, especially for WDSs, is, to the best of the authors’ knowledge, dealt with solely to compare different system adaptations. Therefore, the resilience metric’s informative value to compare different systems not achieving the same goal, as feeding a given urban structure with water, is not given within these metrics. This issue is also addressed in present urban design research [8, 9]. Relative comparison of WDSs’ resilience depends not solely on the present urban design but, depending on the resilience metric considered, furthermore on its size, overall demand resulting from its size as well as demand density, and redundancy as well as robustness. As a result, these additional aspects influencing the resilience have to be considered non-dimensioned within a resilience metric, to compare the possible maximum resilience of different urban designs.
In this research an existing resilience metric is adapted to allow for a relative comparison of urban structures. The derived non-dimensioned resilience metric is tested for the comparison of the main line WDSs of two different real-world cities varying in their urban structure, area size and demand density.
2 Related Work
The resilience of infrastructures, especially of WDSs is subject to present research [10]. There have been established different approaches to measure the resilience of WDSs, most based on graph theory to describe the underlying infrastructure network and its functioning. Therefore, the WDS is represented by a planar graph \( G = \left( {N, E} \right) \) in which the pipes are represented by its edges \( E \) and the sources, tanks, junction and consumer nodes by nodes \( N \). There are different approaches of analyzing the resilience of WDSs, which can be categorized into three types.
First, there are resilience metrics which assess the WDS’s resilience based on its topology. While there are simple graph-theoretical metrics as spectral and statistical metrics which can already count as resilience metrics [11], there are also metrics on a higher scale of sophistication. Analyzing the simpler metrics in context of resilience, resilient networks can be characterized as, at the same time, redundant and robust networks [11, 12]. An established metric to assess the resilience of single consumer nodes considering both of these aspects is the resilience metric first introduced by Herrera et al. [13]. Its physical derivation and its application to optimize the resilience of WDSs has been studied by Lorenz et al. [7, 14]. The topological resilience assessment has the advantage that it is independent of a disruption scenario.
Second and in turn, there are resilience metrics assessing the demand satisfaction considering specific disruptive events. For these metrics special attention has to be given whether they assess robustness instead of resilience. The latter allows for a minimum functionality independent of the disruption scenario. This is considered and realized by the resilience index derived by Todini, applicable independent of the disruption scenario [15] and extended variously [10]. Studying on the one hand increased demand and on the other hand reduced water availability, Amarasinghe et al. [16] introduced a further disruption scenario independent resilience metric considering the demand satisfaction.
Last, the whole dynamic process following a disruptive event and, in the case of a resilient system, recovery is studied by different resilience metrics. Again, attention is to be paid to distinguish resilience and robustness assessment depending on the definition of the disruptive event. A well-known resilience metric for the assessment of the recovery process is the resilience triangle introduced by Bruneau et al. [17]. This metric quantifies the integral time span during which the functionality of a system is impaired after a disruptive event. Apart from that, Meng et al. apply and compare multiple criteria to assess the recovery process following a disruptive event [18].
These metrics have in common that applied to different networks, their absolute values do not allow for a clear distinction of the better network, as the network size and demand are not considered non-dimensioned. Yet, this is of interest when comparing infrastructure layouts towards their resilience against disruptive events.
The infrastructure layout and adaptations are highly dependent on the existing urban structure as infrastructures as the WDS, the power grid and information and communication technology lay highly in parallel to the urban transportation infrastructure, forming the visual structure of a city [19]. Three main types of urban structures can be distinguished. While linear and concentric cities form generically, homogeneous areal cities often are planned [20]. These predefined structures as well as their hybrid forms limit the infrastructure layout significantly. Therefore, Lynch proposed to define performance dimensions of cities to compare cities qualitatively and quantitatively [8]. In present work, the urban structure’s influence on the resilience, which can be understood as a performance dimension, is studied. Fischer et al. [9] analyze the resilience of different urban structures based on the development. Buildings are distinguished based on their construction type as well as their use type. A further topological study conducted by Giudicianni et al. considers the WDS’s functioning depending on the underlying urban structure by analyzing multiple spectral and statistical graph metrics [21]. It was found that the random structure has better values for most graph metrics compared to a homogenous areal urban structure.
Derived from the presented work, the interest emerged to define a resilience metric which allows for a comparison of different urban structures instead of the increased resilience within a system. This resilience metric then allows for infrastructure comparison independent of the present scales.
3 Materials and Methods
This work considers a topology based resilience metric to study the influence of urban structures on the maximum possible resilience of the realizable WDS. Therefore, the topological resilience metric on which this work is based is introduced. The dimensional dependencies and the subsequent non-dimensioning of the resilience metric is studied. Finally, the derived relative resilience metric is tested for two sample real-world WDSs of differing urban structures as well as area and overall demand.
3.1 Resilience Assessment
The graph theoretical resilience metric, first introduced by Herrera et al. [13], considers robustness and redundancy by taking into account, on the one hand, the hydraulic resistance of the feeding path \( r_{s,c} \) between source node \( s \) and consumer node \( c \) and, on the other hand, the alternative \( k \)-shortest feeding paths from any source \( s \) of the WDS. The latter is indexed by \( k \) in the three-dimensional matrix of the hydraulic resistance of feeding paths \( r_{s,c,k} \). Furthermore, as introduced by Lorenz and Pelz [7], to assess the resilience of the overall WDS given in Eq. (1), the resilience of each consumer node \( c \) is weighted with its relative demand \( q_{c} /Q \) to find an overall resilience measure for the present WDS. In this \( q_{c} \) is the demand at the consumer node \( c \) while \( Q \) is the overall demand in the WDS given as \( Q = \sum\nolimits_{c \in C} q_{c} \). Thereby, the resilience of single consumer nodes is prioritized by their relative demand.
The hydraulic resistance of each feeding path results as the sum of the hydraulic resistance of the pipes making up the feeding path. The hydraulic resistance of a pipe is a non-dimensioned measure of the pressure losses along the considered pipe. In the case of WDSs, it can be derived that the pipes can be considered to be hydraulic rough in which turbulent flow takes place. The physical derivation of the hydraulic resistance is given by Lorenz et al. [14].
The number of alternative paths to consider for the resilience assessment is given by \( K_{ \hbox{max} } \), which allows for a significant computational facilitation compared to considering all possible paths. At the same time, alternative feeding paths with a much higher resistance than the shorter feeding paths do not increase the overall resilience significantly. The sum of the hydraulic conductance of single feeding paths, i.e. the inverse of its resistance, is either limited by the number of alternative paths to be considered or if there do not exist as many alternative feeding paths by the number of existing alternative feeding paths for the specific pair of consumer node \( c \) and source \( s \), given in the two-dimensional matrix \( K_{s,c} \).
3.2 Comparability of Resilience
The previously introduced resilience index allows for the assessment of a relative resilience change within one network when adapted. At the same time the absolute value does not allow for a clear comparison of two different WDSs serving two different urban structures. Therefore, the presented resilience index is analyzed towards its non-dimensional characteristics and further is adapted to allow for a relative comparability of WDS within the adapted metric.
As stated before besides topological differences, WDSs can differ in areal size and overall demand or demand density. To assess which topological structure, dictated by the underlying urban structure, allows for the highest resilient WDS, these factors have to be considered in a non-dimensional form. The introduced definition of the WDS’s resilience takes into account the non-dimensioned demand by the weighted sum of each consumer node as well as a non-dimensioned length through the consideration of the hydraulic resistance, which includes the length of the pipes making up a feeding path.
However, the introduced definition of the resilience for a WDS does not differentiate between one node having multiple feeding paths of a certain resistance and single nodes having solely one feeding path of the same resistance as to all nodes having the same number of feeding paths as well as the same total number of feeding paths compared to the first scenario. If consumer nodes are considered as equally important, the second scenario should yield a higher resilience than the first scenario. Therefore, the influence of second, third and kth feeding path on the overall resilience has to be weighted so that a homogenous supply by alternative paths is evaluated superior. This can be realized by adding the hydraulic resistance of the shorter paths to the considered alternative path (\( \sum\nolimits_{i = 1, \ldots ,k} r_{s,c,i} \)). Therefore, the resilience automatically increases less for the \( k + 1 \)-shortest path than it does for the \( k \)-shortest path. This also allows for the drop of the division by the maximum number of alternative paths considered, \( K_{ \hbox{max} } \), compared to Eq. (1). As some consumer nodes have higher demand than others, the importance of high demand consumer nodes is still factored by the weighted sum of the resilience of single consumer nodes. This is mathematically formulated by Eq. (2).
3.3 Real-World Sample WDSs
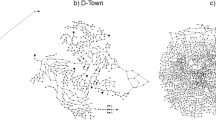
The present work studies the application of the former derived resilience metric for two different real-world main WDSs. The studied main WDSs differ in areal size, demand density as well as in their urban structure. While the first main WDS provides for the German city of Darmstadt, the second feeds a suburban area in the Rhine-Main region. To obtain the main WDS, pipes with diameters smaller than 100 mm are neglected while their demand is added to the nearest node still considered. The remaining connected graph including the source is considered as the main WDS.
The considered urban forms differ greatly in their urban structure. While the city of Darmstadt can be classified as a concentric city, the suburb is mostly of homogeneous areal structure. Additionally, the development in both urban forms leads to a high discrepancy in the demand density. In the city of Darmstadt the demand density is at least 2.5 times larger than in the suburb. Moreover, for the city of Darmstadt there exist two supply lines functioning as sources. In turn, the suburb is solely fed by one source.
To exploit the full potential of the respective urban structures, each existing main WDS is enhanced to the maximum possible main WDS. This is done by adding pipes with the minimum diameter of 100 mm to represent the characteristics of the urban transportation infrastructure. The respective existing and maximum main WDS for each urban structure are presented in Fig. 1. Thereby, the existing main WDS is represented by the blue lines and the additional pipes in the maximum main WDS by the green lines. The grey lines represent the urban transportation system, which is highly parallel to the WDS and therefore, the lines of the WDS often hide the lines representing the urban transportation system.
Each main WDS is represented by a mathematical graph made up of nodes and edges. Edges represent the pipes connecting the different nodes. The nodes can be distinguished into source nodes with unlimited water availability, junction nodes, consumer nodes with a specific water demand and tanks which can store a defined amount of water. The studied WDSs differ greatly in their number of nodes, specifically consumer nodes, for which the resilience index is determined, and their number of edges. Therefore, the computational expenses when assessing the resilience of both WDSs differ.
4 Results
The present data of the WDSs was altered as described in Sect. 3.3 in python using the python package WNTR [22] to receive the main WDSs. To further reduce the complexity of the resulting main WDSs, consumer nodes with lower than the median demand are clustered into the closest consumer node of demand larger than the median demand. In a next step, all nodes which neither have a demand nor serve as significant junction nodes, connecting three or more pipes, are removed while the two pipes connected are replaced by a single pipe of the respectively summed length. Thereby, the forthcoming computational expenses to assess the main WDS’s resilience can be reduced significantly while the possible paths remain unchanged.
As discussed earlier, the existing main WDS is enhanced by adding pipes to better represent the underlying urban structure and leading to a maximum main WDS. This is done with the help of the tool QGIS as well as the openstreetmap data for the existing urban transportation infrastructure [23, 24]. Thereby, solely new pipes and junction nodes are added while the consumer nodes stay the same. This allows for an increased number of alternative paths and at the same time lower resistance paths. The main WDS for the city of Darmstadt consists of 180 consumer nodes while the suburb in the Rhine-Main region has 53 consumer nodes.
The resilience assessment is implemented and conducted in python making use of the packages WNTR as well as NetworkX [25]. In this study both resilience metrics are considered. On the one hand, the alternative paths are considered as parallel hydraulic resistance paths for which their conductance adds up, see Eq. (1). On the other hand, the alternative feeding paths are prioritized so that WDSs with homogeneously multiple feeding paths have a higher resilience value than those with single consumer nodes fed by a large number of feeding paths, see Eq. (2). These resilience definitions are applied to both, the existing and the maximum main WDSs of each urban structure. The absolute values for each resilience metric as well as both WDSs and each urban structure are listed in Table 1.
The comparison of the two real-world main line WDSs of different urban structure, area size, demand density, as well as number of sources shows that for both resilience metrics the concentric urban structure is superior to the homogeneous city. As there are several differences between the two WDSs for both urban structures, a definite claim is not possible. The influence of a second source allows for a resilience increase in the same order of magnitude as the resilience of the same WDS considering solely one source. This impact given by the factor of 2 between the resilience of the two urban structures is solely exceeded when considering the existing main WDSs assessed with the prioritized alternative path resilience index.
5 Discussion
In this work the question of intercomparability of urban structures towards their WDS’s resilience is addressed. Therefore, the non-dimensional form of the resilience metric is of importance, which was derived and tested for two real-world WDSs within this work.
The herein proposed resilience metric takes up an interesting point, whether alternative paths are of higher value when they are spread within the considered WDS. This idea results from the redundancy and robustness aspect of resilient infrastructures. Thereby, the resilience increases when both, redundancy and robustness increase. Prioritizing alternative paths which have less \( k \) shorter preceding paths allows to consider the redundant aspect of alternative paths and at the same time sets a focus on the overall network robustness.
This resilience metric is studied for the existing as well as maximum WDSs of each urban structure. By considering the latter, the full potential of an urban structure can be studied. As the difference in the number of sources has a high impact on the WDS’s resilience, there is no definite claim possible towards which urban structure allows for higher resilience. The resilience assessment suggests that a concentric urban structure allows for a higher resilient main WDS compared with a homogeneous areal urban structure. This hypothesis seems to be in line with previous research conducted by Giudicianni et al. [21], yet has to be validated by further studies of different main WDSs for the considered urban structures to apply as a guiding principal for future urban design.
The introduced resilience metric considers a resistance of paths, which can also be found for different transportation infrastructures, such as the gas network, the electrical network or even the urban transportation system. Therefore, the adapted resilience metric can assess the resilience of different urban infrastructures and allow for a comparison of the suitability of the underlying urban structures for the studied infrastructure.
References
Mair, M., Zischg, J., Rauch, W., Sitzenfrei, R.: Where to find water pipes and sewers?—On the correlation of infrastructure networks in the urban environment. Water 9(2), 146 (2017)
Berry, B.J.L.: Urbanization. In: Marzluff, J.M., Shulenberger, E., Endlicher, W., Alberti, M., Bradley, G., Ryan, C., ZumBrunnen, C., Simon, U. (eds.) Urban Ecology - An International Perspective on the Interaction Between Humans and Nature, pp. 103–119. Springer, US (2008)
Watson, V.: ‘The planned city sweeps the poor away…’: Urban planning and 21st century urbanisation. Prog. Plann. 72(3), 151–193 (2009)
United Nations: World Urbanization Prospects: The 2018 Revision - Key Facts (2018)
Altherr, L.C., et al.: Resilience in mechanical engineering - a concept for controlling uncertainty during design, production and usage phase of load-carrying structures. Appl. Mech. Mater. 885, 187–198 (2018)
Ugarelli, R., Venkatesh, G., Brattebø, H., Di Federico, V., Sægrov, S.: Asset management for urban wastewater pipeline networks. J. Infrastruct. Syst. 16(2), 112–121 (2010)
Lorenz, I.-S., Pelz, P.: Optimal resilience enhancement of water distribution systems. Water 12(9), 2602 (2020)
Lynch, K.A.: What is the form of a city, and how is it made? In: Marzluff, J.M., Shulenberger, E., Endlicher, W., Alberti, M., Bradley, G., Ryan, C., ZumBrunnen, C., Simon, U. (eds.) Urban Ecology. Springer, Boston, pp. 677–690 (2008)
Fischer, K., Hiermaier, S., Riedel, W., Häring, I.: Morphology dependent assessment of resilience for urban areas. Sustainability 10(6), 1800 (2018)
Shin, S., et al.: A systematic review of quantitative resilience measures for water infrastructure systems. Water 10(2), 164 (2018)
Yazdani, A., Otoo, R.A., Jeffrey, P.: Resilience enhancing expansion strategies for water distribution systems: a network theory approach. Environ. Model Softw. 26(12), 1574–1582 (2011)
Yazdani, A., Jeffrey, P.: Complex network analysis of water distribution systems. Chaos Interdiscip. J. Nonlinear Sci. 21(1), (2011)
Herrera, M., Abraham, E., Stoianov, I.: A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour. Manag. 30(5), 1685–1699 (2016)
Lorenz, I.-S., Altherr, L.C., Pelz, P.F.: Resilience enhancement of critical infrastructure – graph-theoretical resilience analysis of the water distribution system in the German City of Darmstadt. In: 14th WCEAM Proceedings Book (2019)
Todini, E.: Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2(2), 115–122 (2000)
Amarasinghe, P.: Resilience of Water Supply Systems in Meeting the Challenges Posed by Climate Change and Population Growth. Queensland University of Technology, Brisbane (2014)
Bruneau, M., et al.: A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 19(4), 733–752 (2003)
Meng, F., Fu, G., Farmani, R., Sweetapple, C., Butler, D.: Topological attributes of network resilience: a study in water distribution systems. Water Res. 143, 376–386 (2018)
DIN-Normausschuss Bauwesen: DIN 1998 - Placement of service conduits in public circulation areas – Guideline for planning, p. ICS 93.025 (2018)
Reicher, C.: Städtebauliches Entwerfen. Springer Fachmedien Wiesbaden, Wiesbaden (2017)
Giudicianni, C., Di Nardo, A., Di Natale, M., Greco, R., Santonastaso, G.F., Scala, A.: Topological taxonomy of water distribution networks. Water (Switzerland) 10(4), 1–19 (2018)
Klise, K.A., Murray, R., Haxton, T., Luther King, M.: An overview of the water network tool for resilience (WNTR). In: 1st International WDSA/CCWI 2018 Joint Conference (2018)
QGIS Development Team: QGIS Geographic Information System. Open Source Geospatial Foundation Project (2020)
OpenStreetMap contributors: “Planet dump” (2015)
Hagberg, A.A., Schult, D.A., Swart, P.J.: Exploring network structure, dynamics, and function using NetworkX. In: Proceedings of the 7th Python in Science Conference (SciPy), vol. 836, pp. 11–15 (2008)
Acknowledgements
The authors thank the KSB Stiftung Stuttgart, Germany for funding this research within the project “Antizipation von Wasserbedarfsszenarien für die Städte der Zukunft”. Moreover, we thank the LOEWE center of Hesse State Ministry for Higher Education, Research and the Arts for partly funding this work within the project emergenCITY.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Lorenz, IS., Pouls, K., Pelz, P.F. (2021). Comparability of Water Infrastructure Resilience of Different Urban Structures. In: Pelz, P.F., Groche, P. (eds) Uncertainty in Mechanical Engineering. ICUME 2021. Lecture Notes in Mechanical Engineering. Springer, Cham. https://doi.org/10.1007/978-3-030-77256-7_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-77256-7_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-77255-0
Online ISBN: 978-3-030-77256-7
eBook Packages: EngineeringEngineering (R0)