Validation of an Optimized Resilient Water Supply System

Abstract

Component failures within water supply systems can lead to significant performance losses. One way to address these losses is the explicit anticipation of failures within the design process. We consider a water supply system for high-rise buildings, where pump failures are the most likely failure scenarios. We explicitly consider these failures within an early design stage which leads to a more resilient system, i.e., a system which is able to operate under a predefined number of arbitrary pump failures. We use a mathematical optimization approach to compute such a resilient design. This is based on a multi-stage model for topology optimization, which can be described by a system of nonlinear inequalities and integrality constraints. Such a model has to be both computationally tractable and to represent the real-world system accurately. We therefore validate the algorithmic solutions using experiments on a scaled test rig for high-rise buildings. The test rig allows for an arbitrary connection of pumps to reproduce scaled versions of booster station designs for high-rise buildings. We experimentally verify the applicability of the presented optimization model and that the proposed resilience properties are also fulfilled in real systems.

1 Introduction

The design and usage of technical systems is subject to uncertainty, which can even lead to a failure of a part or of the complete system. One way to anticipate this uncertainty is to explicitly consider resilience within the design process. A technical system is resilient if it is able to fulfill a predefined functional level even if failures occur. One particular approach to measure resilience with respect to failures is given by the so-called buffering capacity. A technical system has a buffering capacity k, if up to k arbitrary components can fail or be manually deactivated for maintenance and the disturbed system still reaches a predefined level of functionality, see [2]. Using mathematical optimization, the buffering capacity and thus resilience can be ensured in the design process. This leads to a multi-level problem, e.g., a min-max-min problem, since the system may react to failures.

Such multi-level problems are notoriously hard to solve. It is therefore crucial to choose a model of the system that is both computationally tractable and adequately represents the considered system. This trade-off introduces another source of uncertainty, namely that of the model. Thus, a validation of the model is needed. However, how to do this is not obvious, since the model could be valid for a reference solution that can be tested experimentally, but might be inaccurate if failures occur.

In this paper, we consider this issue for the particular example of water supply of high-rise buildings. In such systems, booster stations consisting of one or more pumps are necessary to increase the water pressure to supply all floors of the building. Overall, multiple system layouts are possible. In [3] and [9] it was shown that a decentralized arrangement of pumps allows to achieve significant energy savings due to a reduction of throttling losses. The design and control of such sustainable systems, however, is highly complex and requires the usage of algorithmic approaches. Following [3], we use a Mixed-Integer Nonlinear Programming (MINLP) approach. As an objective, we use a linear-combination of the pump investment cost and the operational cost, which approximates the true life-cycle costs of the system.

The integration of resilience considerations via the buffering capacity yields complex models. In principle, each possible failure scenario resulting from the combination of failures of single pumps must be considered within the constraints of the optimization program, leading to very large models. In order to reduce complexity, usually problem-specific approaches are used. For example, [8] takes one arbitrary component failure in the optimization of an energy system design into account. Considering resilience in layout optimization is also prominent in electric grid planning and commonly known as the N-K property – out of N components K may fail, see e.g., [1, 4, 11, 12]. For water distribution systems in high-rise buildings a method to optimize the buffering capacity with regard to pump failures is presented in [3]. In this paper, we apply a more general algorithm, described in [10], which produces according to the model correct results in acceptable time for small systems.

As mentioned above, it is also important to use mathematical models that represent the considered technical system accurately. For models which describe complex physical phenomena, experiments are the ultimate tool for validation in addition to simulation. Validation is a common step in Operations Research, as mentioned for instance by S. I. Gass in 1983 in [6] and as part of standard references in Operations Research, cf. [5] and [7].

The main contribution of this paper is the experimental validation of resilience properties for topologies generated by the above mentioned algorithmic approach. For this, we use a modular test rig which was presented in [9] to validate the correctness of the underlying MINLP to model the physics of a high-rise water distribution system. The main point is that the computed optimal solution is not only valid for standard situations, but also if failures occurs.

Fig. 1.

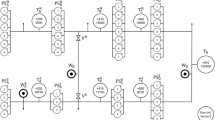
(a) Sketch of the test rig to validate the solutions of the optimization program model. (b) Graph of the possible configurations which are considered in the optimization program. The black connections represent the configuration shown in Fig. 1a.

The paper is organized as follows. Section 2 contains the description of the test rig and Sect. 3 the corresponding optimization model. The experimental validation is presented in Sect. 4. Afterwards, we give a short summary and address future research directions.

2 Test Rig

The test rig presented in [9], and shown schematically in Fig. 1a, represents a downscaled high rise building with five pressure zones on different height levels. Its purpose is to supply each zone with a predefined volume flow and minimum pressure approximating the behavior a building with the same number of pressure zones. In [9] cost and energy optimal solutions have been computed based on different modeling and solution approaches, and the obtained results were validated on the test rig. These experiments do not consider resilience as it is done in this contribution.

In each pressure zone of the test rig, the volume flow is measured and the required demand is set by a control valve. The water is pumped from a reservoir under ambient pressure via various (decentralized) pumps into the pressure zones. In addition to the central pumps, which connect the reservoir and the pressure zones directly, further decentralized pumps may be used. The configuration (pump types, placement, rotational speed of the pumps) can be adjusted according to the optimization results. The possible pipe topologies considered within the optimization model and realizable in validation are shown in Fig. 1b. In total there are 13 pumps available, cf. [9]. Besides the volume flow and valve-position, the power consumption can be measured at the test rig which enables a validation of the obtained optimized results.

We use five different demand scenarios, which differ in their probabilities of occurrence, volume flow demands (up to $q^{\text {nom}}=4.28\ \mathrm {m^3h^{-1}}$) and pressure losses in accordance to [9]. The demand of the different pressure zones is assumed to be equal for the same scenario. Note that the pressure loss is a function of the geodetic height, the volume flow as well as the friction in the system. Due to the various influences, the pressure loss is subject to considerable uncertainty.

As described in the introduction, a failure or deactivation of up to k pumps should be tolerated in the derived system topology and a minimum fulfillment of a predefined function performance has to be guaranteed, cf. [2]. We define that in each failure scenario, at least $\tilde{q}^{\text {fail}}= q^{\text {fail}}/ q^{\text {nom}}=70\mathrm {\%}$ of the maximum required volume flow $q^{\text {nom}}$ has to be supplied.

3 Mathematical Optimization Model

In this section we present a Mixed-Integer Nonlinear Program (MINLP) to find a cost optimal test rig design. Afterwards, we describe the consideration of failures.

A general water network design problem is specified by a directed graph (V, A), for which the vertices V denote in-/outputs of the network and transition points between components. The arcs $A=A^p \cup A^a$ are divided in passive and active arcs and represent possibilities to place pipes and pumps, respectively. Further, the set of demand scenarios S specifies, for each node $v\in V$ and each scenario $s\in S$, lower/upper bounds $\smash {\underline{q}_{v,s}}$/$\smash {\overline{q}_{v,s}}$ on the volume flow demand (negative if v is a sink) and $\smash {\underline{p}_{v,s}}$/$\smash {\overline{p}_{v,s}}$ on the pressure-head. Each arc $a\in A$ also has lower/upper bounds $\underline{q}_a$/$\overline{q}_a$ on the volume flow. For passive arcs, pressure along the pipe does not change, i.e., we assume friction does not depend on the flow and is included in the pressure bounds. An active arc $a \in A^a$ can increase the pressure by an amount $\varDelta p_a$, which is bounded above and below by a quadratic polynomial in the flow $q_a$ over the arc:

$$ \underline{\alpha }_a q_a^2 +\underline{\beta }_a q_a +\underline{\gamma }_a \le \varDelta p_a \le \overline{\alpha }_a q_a^2 +\overline{\beta }_a q_a +\overline{\gamma }_a. $$

This, however, consumes an energy $e_a$ according to a cubic polynomial in $q_a$ and $\varDelta p_a$

$$ e_a = \sum _{0 \le i+j\le 3} \alpha _{a}^{i,j}\,q_a^i\, \varDelta p_a^j. $$

Note that this differs from the pump model used in [9], where we obtain the power consumption and pressure increase in two approximations depending on the volume flow and the pump operating speed.

Altogether, we obtain the following optimization problem, which searches for a network specified by binary variables $x_a$ and its operation such that the arc costs given by $C_a$ and the total energy cost under the demands of each scenario $s \in S$, weighted by $C_s$, are minimized. Here, the usage of the active arcs is represented by binary variables $y_{a,s}$. For each scenario the model furthermore contains volume flow variables q on each arc, pressure variables p for each node and lastly variables $\varDelta p$ for the pressure differential on active arcs. The notation $\delta ^{-}(v)$ and $\delta ^{+}(v)$ is used for the incoming respectively outgoing arcs of node v. We refer to [3] for an in-depth explanation of the constraints.

(1)

The possible test rig layouts are modeled by the following graph (V, A). There exists a node in V for the basement. For each of the five pressure zones two nodes $v_i^{\text {in}}$ and $v_i^{\text {out}}$ are introduced. The input nodes have a flow demand of zero and no restrictions on the pressure. The output nodes have a flow demand and pressure requirements according to the scenarios in S. The set of arcs contains, for each pump and each pressure zone, an active arc from $v_i^{\text {in}}$ to $v_i^{\text {out}}$ and another active arc, which models a bypass without costs or friction (all coefficients in the pump approximations set to zero). Furthermore, there are arcs from the basement to each input node $v_i^{\text {in}}$ and from each output node $v_i^{\text {out}}$ to the input nodes above $v_j^{\text {in}}$, $i < j$. To model the test rig accurately, cardinality constraints are added to Problem (1), which restrict the number of possible arcs corresponding to a given pump to be at most one. Furthermore, for each $v_i^{\text {in}}$ there may be at most one incoming arc.

A solution topology x most likely does not have a buffering capacity k. Thus, there exists a failure scenario of the active arcs such that there exists no operation of the remaining pumps to supply the network, even with the reduced demand $q^{\text {fail}}$ and the corresponding node bounds like $\underline{q}^{\text {fail}}$ and $\underline{p}^{\text {fail}}$. The solution topology x would be resilient, if for each failure scenario, encoded in a binary vector $z\in \{0, 1\}^{A^{a}}$ with $\sum _{a \in A^{a}} z_a\le k$, there exists an operation for the remaining pumps. This can be ensured, if for each z the following system in variables y, q, p and $\varDelta p$ has a solution:

(2)

One theoretical possibility to obtain optimal resilient solutions is to integrate System (2) for each considered failure scenario z into Problem 1 and solve this enlarged MINLP. However, due to the problem size of our instances, this is unsolvable in a tolerable amount of time. To circumvent this, we use the algorithm proposed in [10]. Here, the restriction to be resilient is integrated into the branch and cut algorithm used to solve Problem 1. For solution candidates an auxiliary optimization problem is solved to check whether there exists a violated failure scenario. If this is the case, a linear inequality is derived to cut off this infeasible solution. The approach presented in [3] is not applicable, since it utilizes the structure of the auxiliary problem and requires that only pumps of the same type can be build in parallel.

4 Results and Validation

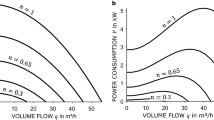
Using the above model, we computed three optimal solutions, which have a guaranteed buffering capacity of $k \in \{0, 1, 2\}$ for a minimal relative volume flow of $\tilde{q}^{\text {fail}}=70\mathrm {\%}$, respectively. This means that – according to the model – for a solution with a specified buffering capacity of k, at least k pumps may fail and the system will still achieve a minimum volume flow of $\tilde{q}^{\text {fail}}$. Together with a reference solution, which consists of only parallel pumps of the same type, these solutions are shown in Fig. 2. Note that the reference solution has a buffering capacity of $k=1$.

All of the optimized solutions contain one or several parallel central pumps and a smaller decentralized pump for the highest pressure zones. The predicted power consumption of the optimized solutions is roughly equal and saves about $22\mathrm {\%}$ compared to the reference solution, cf. Fig. 2. The required resilience is ensured by an increased number of central pumps, leading to higher investment and thus higher total cost. However, not just redundant pumps are used, but different pumps are combined.

Fig. 2.

Solution of optimization and illustration of the set-up on the test rig. The letters S, M, L and XL indicate the pump type and refer to their maximum hydraulic power.

In our experiment we validated all four solutions by setting up the topologies shown in Fig. 2. For the reference system, we solve the optimization problem with fixed topology variables. The input for the test rig in each demand scenario is the pump operation (rotational speeds of the pumps) according to the optimization results. The valves are set such that the volume flow coincides for each zone. The output of the experiment is the measured total power consumption of the pumps and the measured total volume flow for each demand scenario.

Figure 3 compares the theoretical results of the optimization (squares) with the results of the measurements (circles). Associated points of a demand scenario are connected by a line. The measurement errors are rather small ($\varDelta q \le 0.024\,\mathrm {m^3/h}$; $\varDelta p \le 2.61\,\mathrm {W}$). Thus, the error bars of the experimental results would vanish behind the markers and are therefore not shown in the figure.

Fig. 3.

Comparison of the optimization results (circles) and measured (squares) power consumption and volume flow of the solutions for different load scenarios without failures. Associated points of a demand scenario are connected by a line.

When comparing optimization and experiment, it is noticeable that there are deviations due to inaccuracies in the used model: Due to uncertainty in the pressure loss of the test rig and in the characteristic curves of the pumps, the predicted volume flow and power consumption at a given pump rotational speed differ from the measured values. Note that in real systems, such volume flow deviations could be compensated by using a volume flow control rather than a speed control, as assumed here for modeling reasons to validate the computed optimization results. The magnitudes of the deviations depend on the pumps installed and the optimized system topology, as this influences the pressure loss of the system. Overall, the decisive trend between power consumption and volume flow is well correlated, which is crucial for the expected energy consumption. Thus, the experiment confirms the reduced energy consumption for the optimized and decentralized systems and thus the benefit of the optimization. This is consistent with the results of [9].

To validate the buffering capacity of the design, the experimental setup is as follows: For each solution, we configure the remaining system for every possible combination of one up to three failing pumps and measure the maximal achievable volume flow. Thus, we also check the cases in which there are more or less failures than anticipated in the optimization, leading to a total of 28 experimental setups. To simulate a pump failure, the respective pump is replaced by a pipe, which corresponds to a bypass around the pump. In the failure scenario, the remaining pumps are operated at maximum speed. Again, the valves are used to balance the volume flow on different zones. If one zone can not be supplied, the measured total volume flow is set to zero.

These measurements are shown in Fig. 4, in which each marker represents the measured volume flow for a configuration. One can see, that the required minimum functionality $q^{\text {fail}}$ is always achieved. This means that for a specified buffering capacity of k in the optimization and less than k arbitrary pump failures in the experiment, the minimum volume flow of $q^{\text {fail}}$ is fulfilled for all cases. The worst-case failure of all possible failure combinations, shown as a filled marker, is decisive here, as all failure scenarios must be covered. This worst-case volume flow coincides with the minimum functional level ($q^{\text {fail}}$) for the optimized resilient solutions and thus, there is no buffer in the case of failures. This is characteristic for optimization algorithms, which tend to produce solutions close to the border of the feasible solution space.

Fig. 4.

Measured maximal volume flow for the configurations derivable from the combination of the solutions and the failure scenarios with 0 up to 3 failures. Note that some markers overlap and cover each other. The worst-case failure for the anticipated number of failures is indicated by filled markers.

If more pumps than expected fail, the functional level can not be satisfied. A special case is if all central pumps are affected since the lower pressure zones are not supplied anymore. The results show that a higher volume flow can be achieved if there are less failures than expected. For example, if $k=2$ is specified and only one of the pumps fails, a volume flow of $\tilde{q}^{\text {fail}}\ge 92.26\mathrm {\%} > 70\mathrm {\%}$ can be achieved for any failure combination (Fig. 4d).

Also, if no pump fails, a higher volume flow than required can be achieved, which increases with higher k, $\overline{q}^{\text {max}}_{k=2} \ge \overline{q}^{\text {max}}_{k=1} \ge \overline{q}^{\text {max}}_{k=0} \ge 100\mathrm {\%}$, cf. Fig. 4. Since the pressure losses in the system increase quadratically with the volume flow, a significantly higher pressure than originally planned can be achieved as well. These two facts show a desirable feature of the system and confirm the concept of resilience: the system is able to react even to unforeseen events. This can be, for example, a higher volume flow demand than expected, but also covers deviations in the pressure loss of the system (e.g. due to uncertainty during the design phase or due to wear of the components).

5 Conclusion

In this paper we have validated the resilience of solutions given by an optimization method to design resilient water distribution systems. This was done by examining the system for each possible combination of missing pumps. Even for the relatively small system sizes this leads to a high number of costly measurements. Future research could address this by consideration of only those failure scenarios, which are predicted to be critical given some further measure. In our case, these could be all failures for which the maximal volume flow is below 80% of $q^{\text {nom}}$, i.e., the minimum required performance plus an additional safety offset of 10%, assuming the model error is smaller. For the validation of the $k=2$ solution this could have reduced the number of measurements from 15 to 4, which would significantly reduce the effort of validation. To efficiently compute all critical failure scenarios, the adaptive algorithms given in [10] and [3] could be used.