Abstract
Oblivious Pseudorandom Function (OPRF) is a protocol between a client holding input x and a server holding key k for a PRF F. At the end, the client learns \(F_k(x)\) and nothing else while the server learns nothing. OPRF’s have found diverse applications as components of larger protocols, and the currently most efficient instantiation, with security proven in the UC model, is \(F_k(x)=H_2(x,(H_1(x))^k)\) computed using so-called exponential blinding, i.e. the client sends \(a=(H_1(x))^r\) for random r, the server responds \(b=a^k\), which the client unblinds as \(v=b^{1/r}\) to compute \(F_k(x)=H_2(x,v)\).
However, this protocol requires two variable-base exponentiations on the client, while a more efficient multiplicative blinding scheme replaces one or both client exponentiations with fixed-base exponentiation, leading to the decrease of the client’s computational cost by a factor between two to six, depending on pre-computation.
We analyze the security of the above OPRF with multiplicative blinding, showing surprising weaknesses that offer attack avenues which are not present using exponential blinding. We characterize the security of this OPRF implementation as a “Correlated OPRF” functionality, a relaxation of UC OPRF functionality used in prior work.
On the positive side, we show that the Correlated OPRF suffices for the security of OPAQUE, the asymmetric PAKE protocol, hence allowing OPAQUE the computational advantages of multiplicative blinding. Unfortunately, we also show examples of other OPRF applications which become insecure when using such blinding. The conclusion is that usage of multiplicative blinding for \(F_k(x)\) defined as above, in settings where correct value \(g^k\) (needed for multiplicative blinding) is not authenticated, and OPRF inputs are of low entropy, must be carefully analyzed, or avoided all together. We complete the picture by showing a simple and safe alternative definition of function \(F_k(x)\) which offers (full) UC OPRF security using either form of blinding.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
An Oblivious Pseudorandom Function (OPRF) scheme consists of a Pseudorandom Function (PRF) F for which there exists a two-party protocol between a server \(\mathsf {S}\) holding a PRF key k and a client \(\mathsf {C}\) holding an input x through which \(\mathsf {C}\) learns \(F_k(x)\) and \(\mathsf {S}\) learns nothing (in particular, nothing about the input x or the output \(F_k(x)\)). More generally, the security properties of the PRF, namely indistinguishability from a random function under polynomially many queries, must be preserved by the protocol. The OPRF notion was introduced explicitly in [8] but constructions, particularly those based on blinded DH, were studied earlier (e.g., [5, 7, 23]). OPRF has been formally defined under different models [8, 10, 11, 18] with the last two works framing them in the Universally Composable (UC) framework [4]. The OPRF notion has found many applications, and recently such applications have been proposed for actual deployment in practice, including the Privacy Pass protocol [6] and the OPAQUE password-authenticated key exchange protocol [17]. This gave rise to standardization proposals for OPRFs [25] and the OPAQUE protocol [21, 22, 26], which further motivates understanding the costs and benefits of possible OPRF implementations.
Exponential vs. Multiplicative Blinding in Hashed Diffie-Hellman PRF.Footnote 1 In several of the above mentioned applications, the underlying PRF is instantiated with a (Double) Hashed Diffie-Hellman construction (2HashDH) [11], namely:
where hash functions \(H_1,H_2\) are defined respectively as \(H_1:\{0,1\}^*\rightarrow \mathbb {G}{\setminus }\{1\}\) and \(H_2:\{0,1\}^*\times \mathbb {G}\rightarrow \{0,1\}^\tau \) for a multiplicative group \(\mathbb {G}\) of prime order \(q\), and the PRF key k is a random element in \(\mathbb {Z}_q\), while \(\tau \) is a security parameter. The protocol for the oblivious computation of 2HashDH used e.g. in [2, 7, 10, 11] employs the so-called exponential blinding method, i.e. protocol Exp-2HashDH shown in Fig. 1: Client \(\mathsf {C}\) sends to server \(\mathsf {S}\) its input x blinded as \(a=(H_1(x))^r\), for \(r\leftarrow _{\tiny \hbox {R}}\mathbb {Z}_q\), and then unblinds the server’s response \(b=a^k\) as \(v=b^{1/r}~[=(a^k)^{1/r}=(((H_1(x))^r)^k)^{1/r}=(H_1(x))^k]\) and outputs \(H_2(x,v)\). It is easy to see that the client’s input is perfectly hidden from the server because if \(H_1(x)\ne 1\) then a is a random element in \(\mathbb {G}\) independent from x.
Exp-2HashDH: Oblivious PRF using Exponential Blinding [11]
An alternative multiplicative blinding technique, denoted Mult-2HashDH, is shown in Fig. 2. The protocol is an equivalent of Chaum’s technique for blinding RSA signatures: Given generator g of group \(\mathbb {G}\), the client blinds its input as \(a=H_1(x)\cdot g^r\), and using the server’s public key \(z=g^k\) corresponding to the PRF key k, the client unblinds the server’s response \(b=a^k\) as \(v=b\cdot z^{-r}~[=a^k\cdot (g^k)^{-r}=(H_1(x)\cdot g^r)^k\cdot g^{-kr}=(H_1(x))^k]\). It is easy to see that this blinding hides x with perfect security, as in the case of Exp-2HashDH.
Comparing the computational cost of the two techniques, we see that both require a single variable-base exponentiation for the server. However, for the client, Exp-2HashDH requires two variable-base exponentiations (for blinding and unblinding) while Mult-2HashDH involves a single fixed-base exponentiation for blinding and a variable-base exponentiation (to the base z) for unblinding.
In applications where the client stores z,Footnote 2 the latter exponentiation can use fixed-base optimization, reducing the client’s total computation to two-fixed base exponentiations. Given that exponentiation with a fixed base is about 6–7 times faster than with a variable base (cf. [3, 13]), Mult-2HashDH becomes at least 1.7 faster than Exp-2HashDH and 6x faster if z is stored at the client and treated as a fixed base. On the other hand, in cases where the client does not hold z, Mult-2HashDH requires the server to store z and send it with each execution of the OPRF protocol. This cost may not be significant in some cases but in constrained environments where bandwidth and/or storage is a costly resource (e.g., mobile and IoT scenarios) [9], Exp-2HashDH may be preferred. Fortunately, 2HashDH allows an application to choose the blinding mechanism that best fits its needs, possibly choosing one technique or the other depending on the network setting and client configuration.
These are good news for performance and implementation flexibility, but regarding security, things are not as straightforward, as we explain next.
Is Multiplicative Blinding Secure? On the face of it, it would seem that exponential and multiplicative blindings are equivalent, functionally and security-wise, thus allowing for performance optimization and flexibility as discussed above. However, determining the security of Mult-2HashDH turns out to be non-trivial, showing unexpected attack avenues which are not present in Exp-2HashDH. In particular, while Exp-2HashDH has been proven to satisfy the UC OPRF notion from [11], protocol Mult-2HashDH is not secure under this same definition. The problem is, broadly speaking, that the dependency of the protocol on z implies that multiplicative blinding does not ensure full independence between OPRF instances indexed by different public keys.Footnote 3
Let us elaborate. In protocol Exp-2HashDH, server’s response b to the client’s message \(a\ne 1\) defines a unique key \(k={\mathsf {DL}}(a,b)\) for which \(\mathsf {C}\) computes \(y=F_k(x)\). (Since client’s output is \(y=H_2(x,v)\) for \(v=b^{1/r}\) and \(a=(H_1(x))^r\), it follows that \(v=a^{k/r}=(H_1(x))^k\) and therefore \(y=F_k(x)\) for \(k={\mathsf {DL}}(a,b)\).) In other words, server’s response b commits the server to a single value k, hence to a unique function \(F_k(x)\). This commitment to a unique function is central to the OPRF UC modeling from [11]. The same, however, does not hold for Mult-2HashDH where the server’s response (b, z) to the client’s message a gives the attacker an additional degree of freedom in manipulating \(\mathsf {C}\)’s output \(y=H(x,b\cdot z^{-r})\). Specifically, response (b, z) given a determines pair \((\delta ,z)\) where \(\delta =b/a^k\) for \(k={\mathsf {DL}}(g,z)\), thus leading to the following function:
which an honest \(\mathsf {C}\) computes on its input x given \(\mathsf {S}\)’s response (b, z) in the Mult-2HashDH protocol. Indeed, if \(a=h_x\cdot g^r\), \(z=g^k\) and \(\delta =b/a^k\) then
The important point is that value \(\delta =b/a^k\) for \(k={\mathsf {DL}}(g,z)\) introduces a multiplicative shift in the value v computed by \(\mathsf {C}\). Moreover, an adversarial \(\mathsf {S}\) can exploit this shift to create correlated responses that leak information on the client’s input. In particular, for any choice of client input \(\bar{x}\), an attacker \(\mathsf {S}\) can find values \(\delta _1,\delta _2,k_1,k_2\) such that
Using these values the attacker can respond to the first client’s query \(a_1\) with \((b_1,z_1)=(\delta _1 {a_1}^{k_1},g^{k_1})\), and to a second query \(a_2\) with \((\delta _2 {a_2}^{k_2},g^{k_2})\), leading \(\mathsf {C}\) to compute values \(v_1,v_2\) that coincide if \(\mathsf {C}\)’s input is \(x=\bar{x}\) and do not coincide if \(x\ne \bar{x}\). In other words, \(F_{(\delta _1,z_1)}(\bar{x})=F_{(\delta _2,z_2)}(\bar{x})\), showing that in contrast to the family \(\{F_k\}\) defined by Eq. (1), the function family \(\{F_{(\delta ,z)}\}\) defined by Eq. (2) is not a family of independent random functions in ROM.Footnote 4
Potential Vulnerabilities. The core advantage a corrupt server may gain by exploiting the above correlations is the ability to test whether a given value of x has been input by the client in a previous interaction with the server. Our analysis of Mult-2HashDH shows that the server can test at most one such input per interaction. For OPAQUE, this property suffices to prove the security of the protocol with Mult-2HashDH. The intuitive reason is that in OPAQUE, a malicious server already has the ability to test guesses for the client’s inputs (a password in the case of OPAQUE) with each interaction with the client, thus the above attack based on correlation does not add to the attacker’s power. In contrast, in Sect. 7 we show examples of applications where the correlated nature of Mult-2HashDH opens attack avenues not available with exponential blinding. This demonstrates that the two OPRF implementations, Exp-2HashDH and Mult-2HashDH, are not equivalent vis-à-vis security, and replacing one with another within some application needs to be analyzed on a per-case basis, as we do here for OPAQUE.
Modeling Mult-2HashDH as Correlated OPRF. To analyze the security of applications that use Mult-2HashDH, we show that there are limits on the correlations which an adversary can create among the functions effectively evaluated in the Mult-2HashDH protocol. Specifically, each pair of functions can be correlated only as in Eq. (3) and only on one argument x. We prove this formally by introducing a relaxation of the UC OPRF functionality of [11] which we call Correlated OPRF. The purpose of this relaxation is to model the exact nature of function correlations which multiplicative blinding gives to a malicious server. We show that Mult-2HashDH realizes the Correlated OPRF functionality under the Gap\(^+\)-OMDH assumption in ROM, a mild strengthening of the Gap-OMDH assumption which sufficed for Exp-2HashDH to satisfy the UC OPRF functionality [11].
Security of OPAQUE under both Blindings. Based on the UC modeling of Mult-2HashDH as a Correlated OPRF, we prove the OPAQUE strong asymmetric PAKE protocol [17] secure using 2HashDH with multiplicative blinding. (Strong asymmetric PAKE is secure against pre-computation of password hashes before server compromise.) Specifically, we show that OPAQUE remains secure if the OPRF building block it uses is relaxed from the UC OPRF notion of [11] to the Correlated OPRF defined here. This means that the asymmetric PAKE standard being defined by the IETF on the basis of OPAQUE [21, 22, 26] can use the 2HashDH function and leave the choice of exponential or multiplicative blinding to individual implementations.
We believe that the same holds for another construction from [17], which shows that a composition of UC OPRF and any asymmetric PAKE results in a strong asymmetric PAKE. This transformation was proven secure using UC OPRF, implemented by Exp-2HashDH and we believe that this result can also be “upgraded” to the case of UC Correlated OPRF, i.e. using Mult-2HashDH, but we leave the formal verification of that claim to future work.
When is it Safe to Use Mult-2HashDH? In cases where the client has access to the value \(g^k\) in some authenticated/certified form, such as in applications requiring a Verifiable OPRF [10], e.g., Privacy Pass [6], one can use (1) with either blinding. For multiplicative blinding, one just uses the authenticated z in the unblinding. However, when z is received from the server in unauthenticated way, much care is needed, and security under multiplicative blinding needs to be proven on a per-application basis. Even then, small changes in applications and implementations may turn this mechanism insecure as evidenced by the case of using OPAQUE with a threshold OPRF which we show in Sect. 7 to be insecure if used with  . As a rule of thumb, it seems prudent to advise not to use Mult-2HashDH in setting with unauthenticated \(g^k\) and where the input to the OPRF is taken from a low-entropy space.
. As a rule of thumb, it seems prudent to advise not to use Mult-2HashDH in setting with unauthenticated \(g^k\) and where the input to the OPRF is taken from a low-entropy space.
An Alternative OPRF Specification. Another fix is to replace function 2HashDH defined in Eq. (1) with the following simple modification, where \(z=g^k\) is included under the hash, which is secure using either blinding:
It can be shown that this scheme avoids the correlation attacksFootnote 5, and therefore can be proven secure with either blinding method as a realization of the UC OPRF functionality from [11]. The security holds even when the value z input into the hash by the client is the (unauthenticated) z received from the server.
However, while this scheme allows an implementation to choose (even at execution time) the blinding mechanism it prefers, it forces the transmission of z from server to client even in the case of exponential blinding, a drawback in constrained settings discussed above, e.g. [9]. In the case of OPAQUE, one can still use the simpler \(\text{2HashDH }\) without transmitting z but with the subtleties and warnings surrounding security as demonstrated in this paper.Footnote 6
2 Preliminaries
The Gap One-More Diffie-Hellman Assumptions. The security of protocol Mult-2HashDH as UC Correlated OPRF relies on the interactive Gap\(^{+}\)One-More Diffie-Hellman (Gap\(^+\)-OMDH) assumption, a mild strengthening of the Gap-OMDH assumption used to realize UC OPRF [11] or verifiable UC OPRF [10]. Let \(\mathbb {G}\) be a group of prime order \(q\), and let g be an arbitrary generator of \(\mathbb {G}\). Let \((\cdot )^k\) for \(k\in \mathbb {Z}_q\) denote an oracle which returns \(y=x^k\) on input \(x\in \mathbb {G}\). Let \({\mathsf {CDH}}_g\) denote a CDH oracle which returns \(g^{xy}\) on input \((g^x,g^y)\). Let \({\mathsf {DDH}}_g\) denote a DDH oracle which returns 1 on input (A, B, C) s.t. \(C={\mathsf {CDH}}_g(A,B)\), and 0 otherwise. Let \({\mathsf {DDH}}^+_g\) denote an oracle which returns 1 on input \((A,B,A',B',C)\) s.t. \(C={\mathsf {CDH}}_g(A,B)\cdot {\mathsf {CDH}}_g(A',B')\), and 0 otherwise. The (N, Q)-Gap\(^+\)-OMDH assumption on group \(\mathbb {G}\) states that for any polynomial-time algorithm \(\mathcal {A}\),
is negligible, where \(J=(j_1,\ldots ,j_{Q{+}1})\), \(S=((h_{j_1})^k,\ldots ,(h_{j_{Q{+}1}})^k)\), Q is the number of \(\mathcal {A}\)’s \((\cdot )^k\) queries, and \(j_1,\ldots ,j_{Q+1}\) are distinct elements in \(\{1,\ldots ,N\}\).
In other words, Gap\(^+\)-OMDH models the following experiment: Let \(\mathcal {A}\) have access to a \({\mathsf {DDH}}^+\) oracle and an “exponentiation to k-th power” oracle for random k in \(\mathbb {Z}_q\), and the number of queries to the latter is limited by Q. \(\mathcal {A}\) is given N random elements in \(\mathbb {G}\) as the challenge values, and since \(\mathcal {A}\) is allowed to query the exponentiation oracle Q times, it is able to compute the k-th power of any Q of the N elements, but the assumption postulates that it is infeasible that \(\mathcal {A}\) computes the k-th power of any \(Q\,{+}\,1\) of the N group elements, i.e. that it computes the k-th power of “one more” element.
The Gap-OMDH assumption is defined in the exact same way as Gap\(^+\)-OMDH, except \(\mathcal {A}\) has access to oracle \({\mathsf {DDH}}_g\) instead of \({\mathsf {DDH}}^+_g\). We believe that Gap\(^+\)-OMDH is a mild strengthening of Gap-OMDH because assuming OMDH in a group with a bilinear map implies both assumptions: Given an efficiently computable map \(e:\mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_T\) s.t. \(e(g^a,g^b)=e(g,g)^{ab}\), one can implement \({\mathsf {DDH}}_g\) oracle, by checking if \(e(A,B)=e(g,C)\), as well as \({\mathsf {DDH}}^+_g\) oracle, by checking if \(e(A,B)\cdot e(A',B')=e(g,C)\). In the full version [15] we show that the Gap\(^+\)-OMDH assumption holds in the generic group model, which extends similar argument given for Gap-OMDH in [12].
3 The Correlated OPRF Functionality \(\mathcal {F}_{\mathsf {corOPRF}}\)
As we explain in Sect. 1, we will model the type of PRF-correlations which protocol Mult-2HashDH allows with a correlated OPRF functionality, and here we define it as functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) shown in Fig. 3. In Sect. 4 we will argue that protocol  , i.e. the multiplicative blinding protocol together with the PRF defined in Eq. (1), realizes functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) under Gap-OMDH assumption in ROM.
, i.e. the multiplicative blinding protocol together with the PRF defined in Eq. (1), realizes functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) under Gap-OMDH assumption in ROM.
Functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) is a relaxation of the OPRF functionality \(\mathcal {F}_{\mathsf {OPRF}}\) of [17], which is an adaptive extension of the UC OPRF defined in [11]. To make this relation easier to see we mark in Fig. 3 all the code fragments which are novel with respect to functionality \(\mathcal {F}_{\mathsf {OPRF}}\) of [17]. Below we will first explain the basic properties which \(\mathcal {F}_{\mathsf {corOPRF}}\) shares with \(\mathcal {F}_{\mathsf {OPRF}}\), and then we explain the crucial differences which make \(\mathcal {F}_{\mathsf {corOPRF}}\) a relaxation of \(\mathcal {F}_{\mathsf {OPRF}}\).
The Correlated OPRF functionality \(\mathcal {F}_{\mathsf {corOPRF}}\). The (adaptive) OPRF functionality \(\mathcal {F}_{\mathsf {OPRF}}\) of [16] is formed by omitting
 .
.
Correlated OPRF Model: Basic Logic. Functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) models OPRF in a similar way as \(\mathcal {F}_{\mathsf {OPRF}}\) of [11, 17]. First, when an honest server \(\mathsf {S}\) initializes a PRF by picking a random key, this is modeled in the ideal world via call \(\textsc {Init}\) from \(\mathsf {S}\), which initializes a random function \(F_\mathsf {S}:\{0,1\}^*\rightarrow \{0,1\}^\ell \). Second, the real-world \(\mathsf {S}\) can evaluate \(F_\mathsf {S}\) off-line on any argument, which is modeled in the ideal world by call \((\textsc {OfflineEval},\textsf {sid},i,x,L)\) from \(\mathsf {S}\) with \(i=\mathsf {S}\) and \(L=\perp \), which gives \(F_\mathsf {S}(x)\) to \(\mathsf {S}\). (The role of list L, which a malicious server can make non-empty, is discussed further below.) Third, in addition to the off-line evaluation, any client \(\mathsf {C}\) can start an on-line OPRF protocol instance with \(\mathsf {S}\) on local input x, which is modeled by call \((\textsc {Eval},\textsf {sid},\textsf {ssid},\mathsf {S}',x)\) from \(\mathsf {P}=\mathsf {C}\) with \(\mathsf {S}'=\mathsf {S}\), where \(\textsf {ssid}\) stands for sub-session ID, a fresh identifier of this OPRF instance. If \(\mathsf {S}\) honestly engages in this protocol, which is modeled by call \((\textsc {SndrComplete},\textsf {sid},\textsf {ssid})\) from \(\mathsf {S}\), functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) increments the server-specific ticket-counter \(\mathsf {tx}\), initially set to 0. If the real-world adversary allows an uninterrupted interaction between \(\mathsf {C}\) and \(\mathsf {S}\), which is modeled by a call \((\textsc {RcvComplete},\textsf {sid},\textsf {ssid},\mathsf {C},i,L)\) with \(i=\mathsf {S}\) and \(L=\perp \) from the ideal-world adversary \(\mathcal {A^*}\), then \(\mathcal {F}_{\mathsf {corOPRF}}\) decrements counter \(\mathsf {tx}\) and sends \(F_\mathsf {S}(x)\) to \(\mathsf {C}\).Footnote 7
The man-in-the-middle adversary (our OPRF model does not rely on authenticated links) who interacts with client \(\mathsf {C}\), can make \(\mathsf {C}\) output \(F_i(x)\) for a different function \(F_i\,{\ne }\,F_\mathsf {S}\), using a call \((\textsc {RcvComplete},\textsf {ssid},\mathsf {C},i,L)\) for \(i\,{\ne }\,\mathsf {S}\), which models a real-world adversary acting like the server but on a wrong key \(k_i\,{\ne }\,k\) in this interaction. To model a real-world adversary choosing different PRF keys in either offline or online evaluations, functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) keeps a list of indexes \(\mathcal {N}\) of independent random functions, and effectively associates each real-world key with a distinct index in \(\mathcal {N}\), whereas the key of the honest server \(\mathsf {S}\) is associated with a special symbol \(\mathsf {S}\).
Practical Implications. Note that \(\textsc {RcvComplete}\) computes function \(F_\mathsf {S}\) on \(\mathsf {P}\)’s input x only if \(\mathsf {tx}\,{>}\,0\), i.e. if the number of instances completed by \(\mathsf {S}\) is greater than the number of instances completed by any client. This implies that if \(\mathsf {S}\) engages in n OPRF instances this allows function \(F_\mathsf {S}\) to be computed, by all other parties combined, on at most n arguments. However, the functionality does not establish strict binding between these server and client instances. Indeed, this ticket-based enforcement allows an OPRF functionality to be realized using homomorphic blinding without zero-knowledge proofs. Note that in protocol Exp-2HashDH of Fig. 1 the interaction between \(\mathsf {C}\) and \(\mathsf {S}\) can be “double blinded” by the network adversary, who can modify \(\mathsf {P}\)’s original message a as \(a'=a^s\), and then modify \(\mathsf {S}\)’s response \(b=a^k\) as \(b'=b^{1/s}\). Such interaction produces the correct output on the client, but \(a'\) which \(\mathsf {S}\) sees is a random group element, independent of a sent by \(\mathsf {C}\), which makes it impossible to identify the pair of \(\mathsf {C}\) and \(\mathsf {S}\) instances which the network adversary effectively pairs up.
Another feature which enables efficient \(\mathcal {F}_{\mathsf {corOPRF}}\) realization is that the argument x of client \(\mathsf {C}\) engaging in an OPRF instance can be defined only after server \(\mathsf {S}\) completes this instance. Note that in the ideal world \(\mathsf {C}\) outputs \(F_\mathsf {S}(x)\) even if \(\mathsf {S}\) completes an OPRF instance first, by sending message \((\textsc {SvrComplete},\textsf {sid},\textsf {ssid})\), and \(\mathsf {C}\) only afterwards sends \((\textsc {Eval},\textsf {sid},\textsf {ssid},\mathsf {S},x)\), followed by \(\textsc {RcvComplete}\) from \(\mathcal {A^*}\). Indeed, this “delayed input extraction” feature of \(\mathcal {F}_{\mathsf {corOPRF}}\) enables protocol Exp-2HashDH to realize it in ROM, where the ideal-world adversary can extract argument x from the local computation of the real-world client, namely from \(H_2\) query (x, v) for \(v=(H_1(x))^k\), but that computation (and input-extraction) happens after \(\mathsf {S}\) completes the protocol.
In some applications, notably OPAQUE [17], see Sect. 5, it is useful for OPRF to output a transcript, or its prefix, as a handle on OPRF instance in a higher-level protocol. Functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) allows each party to output a transcript prefix \(\mathsf {prfx}\), and if \(\mathsf {prfx}\) output by \(\mathsf {S}\) and \(\mathsf {C}\) match then \(\mathcal {F}_{\mathsf {corOPRF}}\) allows \(\mathsf {C}\) session to compute the PRF output without using the \(\mathsf {tx}\) counter. This does not affect the logic of \(\mathsf {tx}\)-checking: Each run of \(\textsc {SndrComplete}\) either increments \(\mathsf {tx}\) or ok’s some particular client OPRF instance, so either way the number of on-line OPRF evaluations is limited by the number of \(\textsc {SndrComplete}\) instances.
Relaxation of the UC OPRF Model. The crucial difference between the Correlated OPRF functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) and the OPRF functionality \(\mathcal {F}_{\mathsf {OPRF}}\) of [11] is that when any party evaluates function \(F_i\) for a new index \(i\not \in \mathcal {N}\), which corresponds to a real-world adversary evaluating the (O)PRF either offline or online on a new key, the adversary can supply a list L of correlations which the new function \(F_i\) will have with previously initialized functions \(F_j\), \(j\in \mathcal {N}\), potentially including the honest server function \(F_\mathsf {S}\). Such correlations were not allowed in \(\mathcal {F}_{\mathsf {OPRF}}\), and indeed \(\mathcal {F}_{\mathsf {corOPRF}}\) reduces to \(\mathcal {F}_{\mathsf {OPRF}}\) if \(\mathcal {A^*}\) sets L as an empty list in \(\textsc {OfflineEval}\) and \(\textsc {RcvComplete}\) messages. Argument L can specify a sequence of pairs (j, x) where \(j\in \mathcal {N}\) is an index of a previously initialized function \(F_j\), and the correlation consists of setting the value of the new function \(F_i\) on x as \(F_j(x)\). After setting \(F_i(x)\leftarrow F_j(x)\) for all \((j,x)\in L\), the values of \(F_i\) on all other arguments are set at random by \(\mathcal {F}_{\mathsf {corOPRF}}\). Functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) keeps track of these correlations in a graph \(\mathcal {G}=(\mathcal {N},\mathcal {E})\), where \((i,j,x)\in \mathcal {E}\) if \(F_i(x)\) is set to \(F_j(x)\) in the above manner, i.e., an edge between i and j, labeled x, represents a correlation between functions \(F_i\) and \(F_j\) on argument x.
A crucial constraint on the correlation list L is that for each \(j\in \mathcal {N}\) list L can contain only one entry of the form \((j,\cdot )\), i.e. two functions \(F_i,F_j\) can be correlated on at most one argument. Note that if the adversary correlates \(F_i\) with the honest server function \(F_\mathsf {S}\) on argument x, and then evaluates \(F_i(x)\) via the online OPRF instance, i.e. \(\textsc {Eval}\) and \(\textsc {RcvComplete}\) where \(\mathsf {P}=\mathcal {A^*}\), functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) treats this as an evaluation of \(F_\mathsf {S}\) and decrements the ticket-counter \(\mathsf {tx}\). This restriction is necessary because otherwise the adversary could effectively compute \(F_\mathsf {S}\) on more than n arguments even if an honest server \(\mathsf {S}\) engages in only n OPRF instances: It could first correlate \(n'>n\) adversarial functions \(F_1,...,F_{n'}\) with \(F_\mathsf {S}\), each function \(F_i\) on a different argument \(x_i\), and each evaluation of \(F_i(x_i)\) would reveal the value of \(F_\mathsf {S}\) on all these arguments as well. However, our \(\mathcal {F}_{\mathsf {corOPRF}}\) model allows \(\mathcal {A^*}\) to let any honest party \(\mathsf {P}\) compute \(F_i(x)\) for \(F_i\) correlated with \(F_\mathsf {S}\) without decrementing the ticket-counter \(\mathsf {tx}\). This is a weakness, e.g. if the higher-level application reveals these OPRF outputs to the attacker. A stronger version of \(\mathcal {F}_{\mathsf {corOPRF}}\) would decrement \(\mathsf {tx}\) even if \(F_i(x)=F_\mathsf {S}(x)\) is computed by honest parties, but we used a weaker version for two reasons: First, it suffices for OPAQUE security. Second, we can show that Mult-2HashDH realizes this weaker version under Gap\(^+\)-OMDH, and it is an open problem whether the same can shown for the stronger version of the functionality.
Necessity of the Relaxation. As noted in Sect. 1, Exp-2HashDH satisfies the UC OPRF notion of [11] because \(\mathsf {S}\)’s response b to \(\mathsf {C}\)’s message a defines key \(k={\mathsf {DL}}(a,b)\) s.t. \(\mathsf {C}\) outputs \(y=F_k(x)\) for function \(F_k\) defined in Eq. (1). However, in Mult-2HashDH, \(\mathsf {S}\)’s response (b, z) defines the function which \(\mathsf {C}\) effectively computes as \(F_{(\delta ,z)}\) defined in Eq. (2). Moreover, different choices of \((\delta ,z)\) do not define independent random functions. Indeed, an efficient attacker can easily pick \((\delta _1,z_1)\) and \((\delta _2,z_2)\) which satisfy Eq. (3) for any x, which implies that the two functions will be correlated by constraint \(F_{(\delta _1,z_1)}(x)=F_{(\delta _2,z_2)}(x)\).
The consequences of such correlations can be illustrated by the following example. Assume that the higher-level application allows a malicious server to detect whether in two OPRF instances the client outputs the same two values or not. Let \(x_1\) and \(x_2\) be two client input candidates. If the server picks two indexes \((\delta _1,z_1)\) and \((\delta _2,z_2)\) s.t. \(F_{(\delta _1,z_1)}(x_1)\,{=}\,F_{(\delta _2,z_2)}(x_1)\) and \(F_{(\delta _1,z_1)}(x_2)\,{\ne }\,F_{(\delta _2,z_2)}(x_2)\) and inputs \((\delta _1,z_1)\) into the first OPRF instance and \((\delta _2,z_2)\) into the second one, then the client’s outputs in these two executions will be the same if its input is \(x_1\) and different if its input is \(x_2\), and by the assumption on the application context the server will learn which one is the case. (In Sect. 7 we show examples of applications where this knowledge creates an attack avenue.)
The UC OPRF notion of [11] does not allow for this attack avenue because in that model each choice of a function index which server \(\mathsf {S}\) can input into an OPRF instance defines an independent (pseudo)random function. However, no choice of two functions \(F_i,F_j\) for these two instances allows \(\mathsf {S}\) to distinguish between \(\mathsf {C}\)’s input \(x_1\) and \(x_2\): If \(F_i=F_j\) then \(\mathsf {C}\)’s output in the two instances will be the same for any x, and if \(F_i\ne F_j\) then \(\mathsf {C}\)’s output in the two instances will be different, also for any x, except for a negligible probability that \(\mathsf {S}\) finds two functions \(F_i,F_j\) among the polynomially-many random functions it can query offline s.t. \(F_i(x)=F_j(x)\) for \(x\in \{x_1,x_2\}\).
4 Security Analysis of Multiplicative DH-OPRF
Figure 2 in Sect. 1 shows the OPRF protocol Mult-2HashDH, which uses multiplicative blinding for oblivious evaluation of the (Double) Hashed Diffie-Hellman function defined in Eq. (1), i.e. \(F_k(x)=H_2(x,(H_1(x))^k)\). Here, in Fig. 4, we render the same protocol as a realization of the Correlated OPRF functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) defined in Fig. 3. As we explain in Sect. 3, functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) reflects the correlations which a real-world adversary can introduce in the PRF functions the honest users compute in this protocol. Indeed, as we show in Theorem 1 below, under the Gap One-More Diffie-Hellman assumption protocol Mult-2HashDH securely realizes this functionality in ROM.
Protocol Mult-2HashDH of Fig. 2 as a realization of \(\mathcal {F}_{\mathsf {corOPRF}}\).
Theorem 1
Protocol Mult-2HashDH realizes correlated OPRF functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) in the \(\mathcal {F}_{\mathsf {RO}}\)-hybrid world under the Gap-OMDH assumption.
Proof: We show that for any efficient environment \(\mathcal {Z}\) and the real-world adversary \(\mathcal {A}\) (more precisely, for \(\mathcal {A}\) in the \(\mathcal {F}_{\mathsf {RO}}\)-hybrid world, i.e. the real world amended by random oracle hash functions), there exists an efficient simulator \(\mathsf {SIM}\), a.k.a. an “ideal-world adversary”, s.t. the environment’s view in the real world, where the honest parties implement the Mult-2HashDH protocol interacting with adversary \(\mathcal {A}\), is indistinguishable from its view in the ideal world, where the honest parties are “dummy” entities which pass their inputs to (and outputs from) the ideal functionality \(\mathcal {F}_{\mathsf {corOPRF}}\), and where the real-world adversary \(\mathcal {A}\) is replaced by the simulator \(\mathsf {SIM}\) (who locally interacts with \(\mathcal {A}\)). The construction of \(\mathsf {SIM}\) is shown in Fig. 5. While the real-world adversary \(\mathcal {A}\) works in a hybrid world with the random oracle modeled by functionality \(\mathcal {F}_{\mathsf {RO}}\), for notation simplicity in Fig. 5 we short-circuit the \(\mathcal {F}_{\mathsf {RO}}\) syntax and we assume that \(\mathsf {SIM}\) implements oracles \(H_1\), \(H_2\). Without loss of generality, we assume that \(\mathcal {A}\) is a “dummy” adversary who merely passes all messages between \(\mathcal {Z}\) and \(\mathsf {SIM}\), hence we will treat \(\mathcal {A}\) as just an interface of \(\mathcal {Z}\). For brevity we also denote \(\mathcal {F}_{\mathsf {corOPRF}}\) as \(\mathcal {F}\), and we omit the (fixed) session identifier \(\textsf {sid}\) from all messages. Also, the simulator assumes that a unique party \(\mathsf {S}\) for which this \(\mathcal {F}\) instance is initialized is honest, and that its identity “\(\mathsf {S}\)” encoded as a bitstring is different from any pair \((\delta ,z)\in \mathbb {G}^2\).
For a fixed environment \(\mathcal {Z}\), let \(q_\mathrm {H_1},q_\mathrm {H_2}\) be the number of \(\mathcal {A}\)’s queries to resp. \(H_1\) and \(H_2\) hash functions, and let \(q_{\mathsf {C}},q_{\mathsf {S}}\) be the number of \(\mathcal {Z}\)’s invocations of resp. client and server OPRF instances, via resp. queries \(\textsc {Eval}\) sent to some \(\mathsf {C}\) and query \(\textsc {SndrComplete}\) sent to \(\mathsf {S}\).
The Simulator. The simulator \(\mathsf {SIM}\), shown in Fig. 5, follows a similar simulation strategy to the one used to show that exponential blinding protocol realizes UC OPRF notions of [10, 11, 17]. At initialization, the simulator picks a random key k on behalf of server \(\mathsf {S}\). If \(\mathsf {SIM}\) receives \(\textsc {SndrComplete}\) from \(\mathcal {F}\), i.e. server \(\mathsf {S}\) wants to complete an OPRF instance, and \(\mathsf {SIM}\) receives message a with matching \(\textsf {ssid}\) from adversary \(\mathcal {A}\) playing a client, \(\mathsf {SIM}\) replies as the real-world \(\mathsf {S}\) would, i.e. with \((b,z)=(a^k,g^k)\). Responding to \(\mathcal {A}\) playing a server is more complex. The simulator prepares for this by embeding discrete-logarithm trapdoors in \(H_1\) outputs and in messages a formed on behalf of honest clients. Namely, for each x, \(\mathsf {SIM}\) defines \(H_1(x)\) as \(h_x=g^u\) for random u, and it forms each message a on behalf of some honest client as \(a=g^w\) for random w. The discrete-logarithm trapdoor \(u={\mathsf {DL}}(g,a)\) enables \(\mathsf {SIM}\) to compute, given response (b, z) sent by \(\mathcal {A}\) on behalf of some server, the function index \(i=(\delta ,z)\) for which a real-life honest client would effectively compute its output as \(y=F_{(\delta ,z)}(x)\) for \(F_{(\delta ,z)}\) defined as in Eq. (2). This is done by setting \(\delta =b/z^w\) because then \(\delta =b/a^k\) for \(k={\mathsf {DL}}(g,z)\). (See Is multiplicative blinding secure? in Sect. 1 for why the client effectively evaluates \(F_{(\delta ,z)}\) for \(\delta =b/a^k\).) If \(\mathcal {A}\) responds as the honest server \(\mathsf {S}\) (or forwards \(\mathsf {S}\)’s response), \(\mathsf {SIM}\) detects it because then \(\delta =1\), in which case \(\mathsf {SIM}\) sets the function index to the “honest \(\mathsf {S}\) function”, \(i\leftarrow \mathsf {S}\).
Finally, \(\mathsf {SIM}\) checks if \(i=(\delta ,z)\) is in \(\mathcal {N}_{\mathsf {SIM}}\), a sequence of function indices which \(\mathsf {SIM}\) has previously identified, and if \(i\not \in \mathcal {N}_{\mathsf {SIM}}\), i.e. if it is a new function, \(\mathsf {SIM}\) uses the trapdoors it embedded in \(H_1\) outputs to detect if \(F_i(x)=F_j(x)\) for any x queried to \(H_1\) (without such query \(\mathcal {A}\) cannot establish a correlation on x except for negligible probability) and any previously seen function index \(j\in \mathcal {N}_{\mathsf {SIM}}\) or \(j=\mathsf {S}\). The first condition holds if \(\delta '\cdot (h_x)^{{\mathsf {DL}}(g,z')}=\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}\) for \(i=(\delta ,z)\) and \(j=(\delta ',z')\) while the second one holds if \((h_x)^k=\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}\). The simulator cannot compute \({\mathsf {DL}}(g,z)\) for an adversarial public key z, but the trapdoor in the hash function output \(H_1(x)=h_x=g^u\) allows for computing \((h_x)^{{\mathsf {DL}}(g,z)}\) as \(z^u\).
There is a further complication in the simulator’s code, in responding to \(\mathcal {A}\)’s local \(H_2\) queries (x, v). Such calls can represent either (I) an offline PRF evaluation on argument x of function \(F_{(\delta ,z)}\) s.t. \(v=\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}\), where \((\delta ,z)\in \mathcal {N}_{\mathsf {SIM}}\), or, if \(\mathsf {S}\) is compromised (or corrupted), for \((\delta ,z)=(1,g^k)\); or (II) in case \(v=(h_x)^k\) and \(\mathsf {S}\) is not compromised, they can represent a finalization of the computation of \(F_\mathsf {S}(x)\) by a malicious client in the online OPRF instance. Case (I) is treated similarly as the detection of the correlations explained above: \(\mathsf {SIM}\) searches for index \(i=(\delta ,z)\) in \(\mathcal {N}_{\mathsf {SIM}}\) s.t. \(v=\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}=\delta \cdot z^u\) where \(H_1(x)=h_x=g^u\), in which case this is interpreted as evaluation of \(F_i\) and \(\mathsf {SIM}\) sets \(H_2(x,v)\) to the value of \(F_i(x)\) which the functionality defines in response to the offline evaluation call \((\textsc {OfflineEval},i,x,\cdot )\). If \(\mathsf {S}\) is compromised then the simulator does this also for \(i=\mathsf {S}\) if \(v=(h_x)^k\). However, in Case (II), i.e. if \(v=(h_x)^k\) but \(\mathsf {S}\) is not compromised, such query could come from \(\mathcal {A}\)’s post-processing of an online OPRF evaluation, hence \(\mathsf {SIM}\) in this case sends \((\textsc {Eval},\textsf {ssid},\mathsf {S},x)\) and \((\textsc {RcvComplete},\textsf {ssid},\mathsf {SIM},\mathsf {S},\bot )\) to \(\mathcal {F}\). If \(\mathcal {F}\) allows this call to evaluate successfully, i.e. if \(\mathsf {tx}\,{>}\,0\), then \(\mathcal {F}\) return \(y=F_\mathsf {S}(x)\) and \(\mathsf {SIM}\) defines \(H_2(x,v)\leftarrow y\). Otherwise \(\mathcal {F}\) will ignore this \(\textsc {RcvComplete}\) call, in which case \(\mathsf {SIM}\) outputs \(\textsc {halt}\) and aborts, which the environment will detect as a simulation failure. Indeed, this case corresponds to \(\mathcal {A}\) evaluating function \(F_\mathsf {S}\) on more arguments than the number of OPRF instances performed by \(\mathsf {S}\), i.e. the number of \(\textsc {SndrComplete}\) calls from an ideal-world \(\mathsf {S}\) to \(\mathcal {F}\).
Finally, \(\mathsf {SIM}\) must carefully handle \(H_2(x,v)\) queries which are not recognized as evaluations of \(F_i(x)\) for any \(i\in \mathcal {N}_{\mathsf {SIM}}\cup \{\mathsf {S}\}\), because they can correspond to evaluating \(F_{(\delta ,z)}(x)\) for index \((\delta ,z)\) which \(\mathcal {A}\) will reveal in the future. \(\mathsf {SIM}\) picks the simplest pair \((\delta ,z)\) s.t. \(\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}=v\), namely \((\delta ,z)=(v,1)\). If any future index \((\delta ,z)\ne (v,1)\) defined in a subsequent OPRF evaluation satisfies \(\delta \cdot (h_x)^{{\mathsf {DL}}(g,z)}=v\), this will be detected by \(\mathsf {SIM}\) as a correlation between \(F_{(\delta ,z)}\) and \(F_{(v,1)}\). Note that \(\mathsf {SIM}\) must process \(H_2(x,v)\) query as evaluation of \(F_{(v,1)}(x)\) even if \(H_1(x)\) is undefined, because regardless of the value of \(h_x=H_1(x)\) it will hold that \(F_{(v,1)}(x)=H_2(x,v)\), because \(v\cdot (h_x)^{{\mathsf {DL}}(g,1)}=v\cdot (h_x)^0=v\). Indeed, an adversary can first query \(H_2(x,v)\) for some (x, v), then compute \(h_x=H_1(x)\), and then input \((\delta ,z)\) into an OPRF instance for \(\delta =v/(h_x)^{{\mathsf {DL}}(g,z)}\), which corresponds to oblivious evaluation of \(F_{(\delta ,z)}\), which is correlated with \(F_{(v,1)}\) on argument x.
Sequence of Games. Our proof uses the standard sequence of games method, starting from the interaction of \(\mathcal {Z}\) (and “dummy” adversary \(\mathcal {A}\)) with the real-world protocol, and ending with the ideal world, in which \(\mathcal {Z}\) instead interacts with the simulator \(\mathsf {SIM}\) and functionality \(\mathcal {F}\). We fix an arbitrary efficient environment \(\mathcal {Z}\) which without loss of generality outputs a single bit, we use \(\mathbf {G_{i}}\) to denote the event that \(\mathcal {Z}\) outputs 1 when interacting with Game i, and for each two adjacent games, Game i and Game \(i\,{+}\,1\), we argue that these games are indistinguishable to \(\mathcal {Z}\), i.e. that there is a negligible difference between the probabilities of events \(\mathbf {G_{i}}\) and \(\mathbf {G_{i+1}}\), which implies that \(\mathcal {Z}\)’s advantage in distinguishing between the real world and the ideal world is also negligible. Let \(q_\mathrm {H_1},q_\mathrm {H_2}\) be the total number of resp. \(H_1,H_2\) queries made in the security game with \(\mathcal {A}\) and \(\mathcal {Z}\). Let \(q_{\mathsf {C}}\) and \(q_{\mathsf {S}}\) and \(q_{\mathsf {S}}'\) be the number of resp. \(\mathsf {C}\) and \(\mathsf {S}\) sessions and \(\mathsf {S}\) offline PRF evaluations started by \(\mathcal {Z}\) via resp. the \(\textsc {Eval}\), \(\textsc {SndrComplete}\), and \((\textsc {OfflineEval},\mathsf {S},\cdot ,\cdot )\) commands. Let \(\epsilon _{\mathrm {OMDH}}(\mathbb {G},N,Q)\) be the maximum advantage of any algorithm with computational resources comparable to \(\mathcal {Z}\) against the (N, Q)-Gap\(^+\)-OMDH problem in \(\mathbb {G}\).
Game 1: (Real world, except for discrete-logarithm trapdoors in \(H_1\) outputs) This is the real-world interaction, shown in Fig. 6, i.e. the interaction of environment \(\mathcal {Z}\) and its subroutine \(\mathcal {A}\) with honest entities \(\mathsf {C}\) and \(\mathsf {S}\) executing protocol Mult-2HashDH of Fig. 4. We assume that the interaction starts with server initialization, triggered by \(\textsc {Init}\) command from \(\mathcal {Z}\) to \(\mathsf {S}\). We denote the public key of server \(\mathsf {S}\) as \(z^*=g^k\). For visual clarity we omit the fixed \(\textsf {sid}\) tag and the variable \(\textsf {ssid}\) tags from all messages in Fig. 6. We assume that when functions \(H_1,H_2\) are executed by C1, C2, and S2, these hash function calls are serviced as described in the lower-half of Fig. 6. Queries \(H_2(x,v)\) are implemented as in the real world except that the game records tuples \((x,v,H_2(x,v))\) in table \(T_{H_2}\). However, queries \(H_1(x)\) are implemented with trapdoors embedded in values \(h_x=H_1(x)\) by setting \(h_x=g^{u_x}\) for random \(u_x\leftarrow _{\tiny \hbox {R}}\mathbb {Z}_q\) and recording \((x,u_x,h_x)\) in table \(T_{H_1}\).
Game 2: (Abort on hash \(H_1\) collisions) Abort if the security game ever encounters a collision in \(H_1\), i.e. if for some argument x queried either by \(\mathcal {A}\) or by the security game in oracles C1 and S2 (see Fig. 6), oracle \(H_1\) picks u s.t. tuple \((x',u,g^u)\) for some \(x'\ne x\) is already in \(T_{H_1}\). Clearly
Game 1: Interaction of \(\mathcal {Z}/\mathcal {A}\) with Mult-2HashDH protocol.
Game 3: (Making \(\mathsf {C}\)’s message input-oblivious) We change how oracle C1 generates message a so that it is generated obliviously of input x. Namely, instead of computing \(a=H_1(x)\cdot g^r=g^{u_x+r}\) for \(r\leftarrow _{\tiny \hbox {R}}\mathbb {Z}_q\), oracle C1 will now generate \(a=g^w\) for \(w\leftarrow _{\tiny \hbox {R}}\mathbb {Z}_q\). The input x for this session \(\textsf {ssid}\) will be then passed to oracle C2, which (1) queries \(H_1\) on x to retrieve (or create) tuple \((x,u_x,g^{u_x})\) from \(T_{H_1}\), and (2) outputs \(y=H_2(x,v)\) for \(v=b\cdot z^{u_x-w}\). Note that for every x, and hence every \(u_x\), value \(w=(u_x+r)\bmod q\) is random in \(\mathbb {Z}_q\) if r random in \(\mathbb {Z}_q\), hence this modification does not change the distribution of values a output by C1. Moreover, if \(w=(u_x+r)\bmod q\) then \(z^{-r}=z^{u_x-w}\), thus C2’s output is the same as in Game 2, hence Game 3 and Game 2 are externally identical.
Game 4: (Defining adversarial functions) We make a notational change in oracle C2, so that it outputs \(y=H_2(x,v)\) for \(v=\delta \cdot z^{u_x}\) where \(\delta =b/z^w\). Since this is a merely notational difference, Game 4 and Game 3 are identical.
Note that this change makes oracles C1/C2 implement the following process: C1’s message \(a=g^w\) together with \(\mathcal {A}\)’s response (b, z) define \((\delta ,z)\) s.t. \(\delta =b/z^w\), which defines a function which C2 evaluates on \(\mathcal {Z}\)’s input x as \(F_{(\delta ,z)}\) for
Note that Eq. (5) is equivalent to Eq. (2) where \(F_{(\delta ,z)}(x)=H_2(x,\delta \cdot (H_1(x))^k)\) for k s.t. \(z=g^k\). For notational convenience we define also a “helper” function family \(f_i:\{0,1\}^*\rightarrow \mathbb {G}\) for \(i\in \mathbb {G}^2\) s.t.
Note that \(F_{(\delta ,z)}(x)=H_2(x,f_{(\delta ,z)}(x))\).
We will argue that pairs \((\delta ,z)\) encountered in the security game can be thought of as indexes of random functions, including pair \((\delta ,z)=(1,z^*)\) for \(z^*=g^k\) which defines the “honest” random function of \(\mathsf {S}\), except that the adversary can “program” a limited number of correlations in these functions, by setting \(i=(\delta ,g^k)\) and \(j=(\delta ',g^{k'})\) s.t. \(\delta '/\delta =(h_x)^{k-k'}\), which implies that \(F_i(x)=F_j(x)\). In the next few game changes we will show that these correlations are constrained as prescribed by functionality \(\mathcal {F}_{\mathsf {corOPRF}}\), i.e. that (1) each two functions can be “programmed” to have equal output only for a single argument, (2) that if an adversarial function \(F_i\) is correlated on some x with function \(F_\mathsf {S}\) of the honest server \(\mathsf {S}\) then evaluating \(F_i(x)\) is treated the same as \(F_\mathsf {S}(x)\), and in particular requires that \(\mathsf {tx}\,{>}\,0\), and (3) that otherwise all adversarial functions are indistinguishable from independent random functions.
Game 5: (Building correlation graph) The security game will build a graph of correlations between functions \(F_{(\delta ,z)}\) occurring in the game. In particular the game will maintain sequence \(\mathcal {N}_{\mathsf {SIM}}\) and sets \(X_{H_1},\mathcal {E}\), all initially empty:
-
1.
Set \(X_{H_1}\) contains all inputs x queried to \(H_1\), by either \(\mathcal {A}\), C2, or S2.
-
2.
Set \(\mathcal {N}_{\mathsf {SIM}}\) contains all \((\delta ,z)\) function indexes, including (1) the honest server function index \((1,z^*)\), (2) each \((\delta ,z)\) defined by \(\mathcal {A}\)’s interaction with oracles C1/C2, as described in Game 4, and (3) \((\delta ,z)=(v,1)\) for every direct query (x, v) of \(\mathcal {A}\) to \(H_2\).
-
3.
Set \(\mathcal {E}\) contains labeled edges between indexes in \(\mathcal {N}_{\mathsf {SIM}}\), maintained as follows:
(1) When function index \(i=(\beta ,z)\not \in \mathcal {N}_{\mathsf {SIM}}\) is specified in C1/C2 then for each \(j=(\delta ',z')\) in \(\mathcal {N}_{\mathsf {SIM}}\) and \(x'\in X_{H_1}\), test if \(f_j(x')=f_i(x')\), and if so then add \((i,j,x')\), i.e. an edge (i, j) with label \(x'\), to \(\mathcal {E}\).
(2) If \(H_2\) is queried on new (x, v) by \(\mathcal {A}\) or by oracles C2 or S2 for \((v,1)\not \in \mathcal {N}_{\mathsf {SIM}}\) then do step (1) above for \(i=(v,1)\). (Note that \(f_{(v,1)}(x')=v\) for all \(x'\).)
Since these are only notational changes Game 5 and Game 4 are identical.
Game 6: (Discarding double links) We add an abort if there are two distinct values \(x,x'\) in \(X_{H_1}\) and two distinct function indexes \(i=(\delta ,z)\) and \(j=(\delta ',z')\) in \(\mathcal {N}_{\mathsf {SIM}}\) s.t. \(f_i(x)=f_j(x)\) and \(f_i(x')=f_j(x')\). These conditions imply respectively that \(\delta '/\delta =(z/z')^{u_x}\) and \(\delta '/\delta =(z/z')^{u_{x'}}\). Since \(H_1\) collisions are discarded beginning in Game 2, it follows that \(u_{x'}\ne u_x\), which implies that \((\delta ,z)=(\delta ',z')\), i.e. this abort cannot happen. Consequently, Game 6 and Game 5 are identical.
Game 7: (Discarding future correlations) We add an abort in \(H_1\) processing if new query \(x\not \in X_{H_1}\) samples \(h_x=H_1(x)\) s.t. there exists two distinct function indexes \(i,j\in \mathcal {N}_{\mathsf {SIM}}\) s.t. \(f_i(x)=f_j(x)\). Note that in this case there would be no edge (i, j, x) in \(\mathcal {E}\), and that this is the only case in which \(f_i(x)=f_j(x)\) but \((i,j,x)\not \in \mathcal {E}\). However if query x to \(H_1\) is made after defining i, j then \(h_x=H_1(x)\) is independent of i, j, in which case \(\Pr [f_i(x)=f_j(x)]=1/q\), because this equation holds only for a single value \(h_x\) s.t. \(u_x={\mathsf {DL}}(g,h_x)={\mathsf {DL}}((z_i/z_j),(\delta _j/\delta _i))\). If there are \(q_{\mathsf {C}}\) instances of C2 and \(q_\mathrm {H_2}\) queries to \(H_2\) then there can be at most \(q_{\mathsf {C}}\) indexes \((\delta ,z)\) in \(\mathcal {N}_{\mathsf {SIM}}\) s.t. \(z\ne 1\) and at most \(q_\mathrm {H_2}\) indexes \((\delta ,z)\) s.t. \(z=1\). Since condition \(f_i(x)=f_j(x)\) cannot be met if \(i=(v,1)\) and \(j=(v',1)\) for \(v\,{\ne }\,v'\), each new query x to \(H_1\) causes an abort only if \(u_x\) falls in the solution set of at most \(q_{\mathsf {C}}\cdot (q_\mathrm {H_2}+q_{\mathsf {C}})\) equations, which implies that
Interaction defined by Game 9.
Game 8: (Implementing \(H_2\) using correlated random functions) We replace hash function \(H_2\) using an oracle \(\mathcal {R}\) that maintains a random function family, in which the adversary can “program” correlations as follows:
-
When \(\mathcal {R}\) starts it initializes a random function \(R:\{0,1\}^*\times \{0,1\}^*\rightarrow \{0,1\}^\ell \) and an index sequence \(\mathcal {I}\leftarrow [(1,z^*)]\);
-
On query \(\textsc {Correlate}(i,L)\), \(\mathcal {R}\) rejects if \(i\not \in \mathcal {I}\) or list L contains (j, x) and \((j',x')\) s.t. \(j=j'\) and \(x\,{\ne }\,x'\). Otherwise it appends i to \(\mathcal {I}\), and for each \((j,x)\in L\) it re-defines \(R(i,x)\leftarrow R(j,x)\);
-
On query \(\textsc {Eval}(i,x)\), \(\mathcal {R}\) replies R(i, x) if \(i\in \mathcal {I}\), else ignores this query.
We use oracle \(\mathcal {R}\) to change the implementation of \(H_2\) function called by oracles S2, C2, or the direct calls to \(H_2\):
-
1.
When \(\mathcal {A}\) calls S2 on x: Assign \(H_2(x,f_i(x))\leftarrow \mathcal {R}.\textsc {Eval}(i,x)\) for \(i=(1,z^*)\).
-
2.
When oracle C2 calls \(H_2\) on \((x,f_i(x))\) for some \(i\,{=}\,(\delta ,z)\):
-
(a)
if \(i\not \in \mathcal {N}_{\mathsf {SIM}}\) then send \(\textsc {Correlate}(i,L)\) to \(\mathcal {R}\) where L consists of all tuples \((j,x')\) s.t. \(f_i(x')=f_j(x')\) for some \(j\in \mathcal {N}_{\mathsf {SIM}}\) and \(x'\in X_{H_1}\);
-
(b)
set \(H_2(x,f_i(x))\leftarrow \mathcal {R}.\textsc {Eval}(i,x)\).
-
(a)
-
3.
When \(\mathcal {A}\) calls \(H_2\) on (x, v): Service it as in Step 2 but use \(i=(v,1)\).
To see the correspondence between Game 8 and Game 7, observe that starting from Game 5 function \(H_2\) is evaluated only on pairs of the form \((x,f_i(x))\) for some \(i\in \mathcal {N}_{\mathsf {SIM}}\). Define \(\mathcal {R}(i,x)\) as \(H_2(x,f_i(x))\). Function \(\mathcal {R}\) is not random even if \(H_2\) is, because we have that \(\mathcal {R}(i,x)=\mathcal {R}(j,x)\) for any i, j, x s.t. \(f_i(x)=f_j(x)\). However, from Game 7 this equation can hold, for any i, x s.t. \(H_2\) is queried on \((x,f_i(x))\), only if i is a new index, \(i=(\delta ,z)\) or \(i=(v,1)\), appended to \(\mathcal {N}_{\mathsf {SIM}}\) in a query to oracles resp. C1/C2 and \(H_2\), for values j, x s.t. \(j\in \mathcal {N}_{\mathsf {SIM}}\) and \(x\in X_{H_1}\) at the time this query is made. Note that list L sent for a new function \(f_i\) to \(\mathcal {R}\) in Game 8 by oracles C1/C2 and \(H_2\) consists exactly of all such pairs (j, x), hence it follows that Game 8 and Game 7 are identical.
Game 9: (Walking back aborts in \(H_1\)) We remove the aborts in \(H_1\) introduced in Game 2 and Game 7, i.e. we no longer abort if (1) the same \(u_X\) was chosen before on some previous query to \(H_1\), or (2) if there are two function indices \(i=(z,\delta )\) and \(j=(z',\delta ')\) in \(\mathcal {N}_{\mathsf {SIM}}\) s.t. \(f_i(x)=f_j(x)\), i.e. \(\delta \cdot z^{u_x}=\delta '\cdot (z')^{u_x}\). By the same arguments used above where these games are introduced, these two changes can be observed with probability at most \((q_\mathrm {H_1}^2)/q\) and \((q_\mathrm {H_1}\cdot q_{\mathsf {C}}\cdot (q_\mathrm {H_2}+q_{\mathsf {C}}))/q\), respectively, which implies that
Security Game Review. In Fig. 7 we put together all the changes made so far and review how the game oracles operate in Game 9.
Game 10: (Identifying existing functions in \(H_2\) processing) In Game 9 a fresh query (x, v) to \(H_2\) is answered as R(i, x) for \(i=(v,1)\), and if \((v,1)\not \in \mathcal {N}_{\mathsf {SIM}}\) then function \(R((v,1),\cdot )\) is created and correlated with all previous functions \(\{R(i,\cdot )\}_{i\in \mathcal {N}_{\mathsf {SIM}}}\) by the rule that \(R((v,1),x')\leftarrow R(i,x')\) for each \(x'\in X_{H_1}\) and \(i\in \mathcal {N}_{\mathsf {SIM}}\) s.t. \(f_i(x')=v\). In Game 10 we modify the code of oracle \(H_2\) so that when it gets a fresh query (x, v) s.t. \(x\in X_{H_1}\) it first checks if
(Note that if \(x\in X_{H_1}\) the game can evaluate \(f_{(\delta ,z)}(x)=\delta \cdot z^{u_x}\) for any \(\delta ,z\).) If \(v=f_i(x)\) for some \(i\in \mathcal {N}_{\mathsf {SIM}}\) then Game 10 takes the first index i in \(\mathcal {N}_{\mathsf {SIM}}\) s.t. \(v=f_i(x)\) holds, replies R(i, x), and does not create a new function \(R((v,1),\cdot )\) even if \((v,1)\not \in \mathcal {N}_{\mathsf {SIM}}\). (Note that this condition can hold for several indexes i in \(\mathcal {N}_{\mathsf {SIM}}\), and indeed it will hold for all indexes of functions which are correlated on argument x. Note also that the index \(i=(1,z^*)\) of the “honest server function” occurs as the first in \(\mathcal {N}_{\mathsf {SIM}}\).) If \(x\not \in X_{H_1}\) or for all \(i\in \mathcal {N}_{\mathsf {SIM}}\) \(v\ne f_i(x)\) then the processing is as before, i.e. the game processes this query as a call to R((v, 1), x). We show the modification done by Game 10 in Fig. 8.
Note that this modification doesn’t change the value returned by \(H_2(x,v)\): If condition (7) holds then either way \(H_2(x,v)=R(i,x)\). The only other change this modification causes is that if (7) holds then function \(R((v,1),\cdot )\) is not created. However, this does not affect any future interactions with the random function R. Let \(X_{H_1}\) and \(\mathcal {N}_{\mathsf {SIM}}\) are the values of these variables at the time \(R((v,1),\cdot )\) is created in Game 9. Consider that at some subsequent step an evaluation call, either C2 or \(H_2\), creates a new function \(R(i,\cdot )\) s.t. \(f_i(x)=f_{(v,1)}(x)\) for some \(x\in X_{H_1}'\) where \(X_{H_1}'\) and \(\mathcal {N}_{\mathsf {SIM}}'\) denote the new values of these variables. Assume also that until this point there was no other opportunity to create \(\mathcal {R}((v,1),\cdot )\) in Game 10, i.e. \(i=(v,1)\) was not used in oracle C2, and \(H_2(x',v)\) was not queried on any \(x'\) s.t. \(f_i(x')\ne v\) for some \(i\in \mathcal {N}_{\mathsf {SIM}}'\). (This is the case when the modification of Game 10 can affect the security experiment.) There are two cases to consider: (1) If \(x\in X_{H_1}\) and \(f_{(v,1)}(x)=f_j(x)\) for some \(j\in \mathcal {N}_{\mathsf {SIM}}\), then whether or not \(R((v,1),\cdot )\) is created in both games it holds that \(R(i,x)=R(j,c)\); (2) If \(x\not \in X_{H_1}\), or \(x\in X_{H_1}\) but \(f_{(v,1)}(x)\ne f_j(x)\) for any \(j\in \mathcal {N}_{\mathsf {SIM}}\), then R((v, 1), x) is uncorrelated with previous functions, but since R((v, 1), x) is not used before, it does not matter if R(i, x) is chosen at random or assigned as \(R(i,x)\leftarrow R((v,1),x)\). It follows that Game 10 and Game 9 are identical.
Game 11: (Ideal-world interaction) In Fig. 9 we show the ideal-world game, denoted Game 11, defined by the interaction of simulator \(\mathsf {SIM}\) of Fig. 5 and functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) of Fig. 3. We use the same notation used for Game 9 for the correlated random functions, i.e. we define \(F_\mathsf {S}(x)=R((1,z^*),x)\) and for all \(i\ne \mathsf {S}\) we define \(F_i(x)=R(i,x)\). Also, we rename oracles which the game implements as in Game 9: S1 implements \(\mathcal {Z}\)’s query \(\textsc {SndrComplete}\) to \(\mathsf {S}\), S2 implements \(\mathcal {Z}\)’s query \(\textsc {OfflineEval}\) to \(\mathsf {S}\), C1 implements \(\mathcal {Z}\)’s query \(\textsc {Eval}\) to \(\mathsf {C}\), and C2 responds to \(\mathcal {A}\)’s message (b, z) to \(\mathsf {C}\).
Game 11: Interaction of \(\mathcal {Z}/\mathcal {A}\) with the ideal-world execution
Figure 9 simplifies the ideal-world game by not accounting for function correlations using edge set \(\mathcal {E}\), as done by \(\mathcal {F}_{\mathsf {corOPRF}}\), and ignoring some of the conditional clauses in the code of simulator \(\mathsf {SIM}\). However, we argue that these overlooked clauses are never triggered. Assume that whenever sub-procedure \(\textsc {Process}(i)\) programs a correlation \(R(i,x)\leftarrow R(j,x)\) the game adds set (i, j, x) to \(\mathcal {E}\). The conditional clauses missing from Game 11 figure are in clauses (2) and (3) in \(H_2\) processing. In clause (2), \(\mathsf {SIM}\) ignores this call, and the game does not send R(i, x) to \(\mathcal {A}\), if \(\mathsf {S}\) was not compromised and either \(i=(1,g^k)\) or \((i,(1,g^k),x)\in \mathcal {E}\). However, condition \(i=(1,g^k)\) implies that \(v=(g^k)^{u_x}\), which is excluded by case (2). Likewise, condition \((i,(1,g^k),x)\in \mathcal {E}\) implies that \(f_i(x)=f_{(1,g^k)}(x)=(g^k)^{u_x}\), which would trigger case (1) and is excluded in case (2). In clause (3) \(\mathsf {SIM}\) would ignore this call and not send R(i, x) to \(\mathcal {A}\) under the same conditions, i.e. if \(\mathsf {S}\) was not compromised and either \(i=(1,g^k)\) or \((i,(1,g^k),x)\in \mathcal {E}\). Case \(i=(v,1)=(1,g^k)\) implies \(k=0\), which is excluded by sampling k in \(\mathbb {Z}_q^*=\mathbb {Z}_q\setminus \{0\}\), and case \((i,(1,g^k),x)\in \mathcal {E}\) implies that \(x\in X_{H_1}\) and \(f_i(x)=f_{(1,g^k)}(x)\), which would trigger clause (1).
Finally, in Fig. 9 in two clauses when \(\mathsf {tx}=0\), in C2 and \(H_2\) case (1), we wrote that the game aborts. In the actual ideal-world game, the first case corresponds to functionality \(\mathcal {F}_{\mathsf {corOPRF}}\) dropping the \((\textsc {RcvComplete},...,\mathsf {C},...)\) call from \(\mathsf {SIM}\), and not sending R(i, x) to \(\mathsf {C}\), and thus to \(\mathcal {Z}\). The second case corresponds to \(\mathcal {F}_{\mathsf {corOPRF}}\) not responding with R(i, x) to \(\mathsf {SIM}\)’s call \((\textsc {RcvComplete},...,\mathsf {SIM},...)\), in which case \(\mathsf {SIM}\) aborts. The difference is in the first case, but it is a syntactical difference because we can equate \(\mathcal {Z}\)’s not receiving any output from \(\mathsf {C}\) in response to \((\textsc {RcvComplete},...,\mathsf {C},...)\), or any output from \(H_2\) call, with the game returning an abort symbol.
The differences between Game 10 and Game 11, apart of the trivial difference of constraining key k s.t. \(k\ne 0\) in Game 11, consist of the following:
-
1.
S1 either increments \(\mathsf {tx}\) or changes \(\mathsf {ok?}\) in some C1-record from 0 to 1.
-
2.
C2 decrements \(\mathsf {tx}\) if \(\mathsf {S}\) not compromised, \(\mathsf {ok?}=0\), \(i=(1,g^k)\), and \(\mathsf {tx}>0\).
-
3.
C2 aborts the game if \(\mathsf {S}\) not compromised, \(\mathsf {ok?}=0\), \(i=(1,g^k)\), and \(\mathsf {tx}=0\).
-
4.
\(H_2\), clause 1, decrements \(\mathsf {tx}\) if \(\mathsf {S}\) not compromised, \(i=(1,g^k)\), and \(\mathsf {tx}>0\)
-
5.
\(H_2\), clause 1, aborts the game if \(\mathsf {S}\) not compromised, \(i=(1,g^k)\), and \(\mathsf {tx}=0\).
Let E be the event that game aborts either in C2 or \(H_2\), denoted resp. \(E_{C2}\) and \(E_{H_2}\). Note that unless event E happens Game 10 and Game 11 are identical (except for \(1/q\) probability that \(k=0\) in Game 10), and that event E can happen only if \(\mathsf {S}\) is not compromised, thus the two games diverge only before \(\mathsf {S}\) compromise. Note that \(E_{C2}\) requires that \(i=(1,g^k)\), i.e. that \(\mathcal {A}\) sends (b, z) to C2 s.t. \(z=g^k\) and \(b=z^w=g^{kw}=a^k\). Call such C2 query k-computed. Note that \(E_{H_2}\) requires that \(i=(1,g^k)\), i.e. that \(\mathcal {A}\) queries \(H_2\) on (x, v) for \(v=(h_x)^k\). Call such \(H_2\) query k-computed as well. Since counter \(\mathsf {tx}\) is decremented, or \(\mathsf {C}\)-record (x, w, a, 1) is “processed” only on such k-computed C2 and \(H_2\) queries, and \(\mathsf {tx}\) is incremented or record (x, w, a, 1) is created with each query to S1, hence E happens only if \(\mathcal {A}\) triggers more k-computed C2/\(H_2\) queries than S1 queries.
Correlations Monitored only at Evaluation. Before we show that event E can happen with at most negligible probability, we need to change the way Game 10 and Game 11 build correlations in function R. Instead of setting them at the time a new function is added, in the modified games the correlations are checked only when a function is evaluated, i.e. the game keeps track of each referenced value of function R, i.e. each triple \((\delta ',z',x')\) s.t. \(R((\delta ',z'),x')\) was queried eiter in S2, C2, or \(H_2\). When the game queries a new point, R(i, x) for \(i=(\delta ,z)\), the game looks for the first record \((\delta ,z',x')\) on the list of queries s.t. \(x'=x\) and \(f_{(\delta ',z')}(x)=f_{(\delta ,z)}(x)\), i.e. \(\delta '(z')^{u_x}=\delta (z)^{u_x}\). If so, the game first assigns \(R(i,x)\leftarrow R(i',x)\) for \(i=(\delta ,z)\) and \(i'=(\delta ',z')\) and only then replies R(i, x). It is easy to see that this is an equivalent process of keeping correlations because indeed the only information about these functions \(R(i,\cdot )\) which the game reveals is through evaluated points, so it makes no difference if we postpone correlating values of R(i, x) with \(R(i',x)\) until R(i, x) is actually queried.
We show a reduction to the Gap\(^+\)-OMDH assumption in the case E happens in Game 10. Reduction \({\mathcal {R}}\) takes the Gap\(^+\)-OMDH challenge \((g,z^*,h_1,\ldots ,h_N)\) where \(N=(q_\mathrm {H_1}+q_{\mathsf {C}})\), and responds to \(\mathcal {A}\)’s queries as follows:
-
1.
Initialize \(\mathcal {N}_{\mathsf {SIM}}\leftarrow [(1,z^*)]\) and \(\mathcal {S}\leftarrow []\).
-
2.
Embed OMDH challenges into \(H_1\) and C1 outputs, i.e. assign each \(H_1(x)\) output, and each value a sent by C1, to a unique OMDH challenge \(h_i\).
-
3.
On message a to S1, use oracle \((\cdot )^k\) to send back \(b=a^k\) and \(z=z^*\).
-
4.
On query x to S2, set \((a,b,z)\leftarrow (1,1,z^*)\), run \(\textsc {Correlate}((a,b,z),x)\), and output R((a, b, z), x)
-
5.
On message (b, z) to C2, recovers C1 input x and output a, run \(\textsc {Correlate}((a,b,z),x)\), and output R((a, b, z), x).
-
6.
On query (x, v) to \(H_2\), set \((a,b,z)\leftarrow (1,v,1)\), run \(\textsc {Correlate}((a,b,z),x)\), and output R((a, b, z), x).
-
7.
If \(\mathcal {A}\) queries \(\mathsf {S}\)-Compromise, \({\mathcal {R}}\) aborts.
-
8.
\(\textsc {Correlate}((a,b,z),x)\): Return if \((a,b,z,x)\in \mathcal {S}\). Otherwise, set \(h_x\leftarrow H_1(x)\), and if \(\exists \) \((a',b',z',x)\) in \(\mathcal {S}\) s.t.
$$\begin{aligned} b\cdot {\mathsf {CDH}}_g(z,h_x/a)=b'\cdot {\mathsf {CDH}}_g(z',h_x/a') \end{aligned}$$(8)then set \(R((a,b,z),x)\leftarrow R((a',b',z'),x)\). Otherwise add (a, b, z, x) to \(\mathcal {S}\).
Observe that \({\mathcal {R}}\) can verify Eq. (8) using oracle \({\mathsf {DDH}}^+_g\). Secondly, observe that \(b\cdot {\mathsf {CDH}}_g(z,h_x/a)\) correctly evaluates \(f_i(x)\) for the corresponding index i: In S2 we set \((a,b,z)=(1,1,z^*)\), so \(b\cdot {\mathsf {CDH}}_g(z,h_x/a)={\mathsf {CDH}}_g(z^*,h_x)=(h_x)^k\) where \(z^*=g^k\), as in Game 10; In C2, in Game 10 we compute \(f_i(x)=f_{(\delta ,z)}(x)=\delta \cdot (z)^{u_x}=\delta \cdot {\mathsf {CDH}}(z,h_x)\), but since \(\delta =b/z^w=b\cdot {\mathsf {CDH}}(z,a^{-1})\) this implies that \(f_i(x)=\delta \cdot {\mathsf {CDH}}(z,h_x/a)\); In \(H_2\) we set \((a,b,z)=(1,v,1)\), so \(b\cdot {\mathsf {CDH}}_g(z,h_x/a)=v\cdot {\mathsf {CDH}}_g(1,h_x)=v\), also as in Game 10.
Therefore \({\mathcal {R}}\) presents a view which is ideantical to Game 10 as long as \(\mathsf {S}\)-Compromise is not queried. Therefore event E occurs in the interaction with \({\mathcal {R}}\) with the same probability as in Game 10. Let \(Q=q_{\mathsf {S}}\) be the number of S1 queries, hence the number of \((\cdot )^k\) oracle accesses by \({\mathcal {R}}\). Event E implies that the number of k-computed C2 queries and k-computed \(H_2\) queries is larger than Q, i.e. at least \(Q+1\). Note that a k-computed \(H_2\) query is a pair (x, v) s.t. \(v=(h_x)^k\), so each such query computes \((h_i)^k={\mathsf {CDH}}(h_i,z^*)\) on a unique OMDH challenge \(h_i\). Likewise, a k-computed C2 query is a response \((b,z)=(a^k,g^k)\) to C1’s message a, and since \({\mathcal {R}}\) embeds a unique OMDH challenge \(h_i\) into each a, such query also computes \(a^k={\mathsf {CDH}}(h_i,z^*)\) on a unique OMDH challenge \(h_i\). Since \({\mathcal {R}}\) can use \({\mathsf {DDH}}^+_g\) oracle to implement \({\mathsf {DDH}}\), and test whether any \(H_2\) or C2 query is k-computed, \({\mathcal {R}}\) will solve \(Q+1\) OMDH challenges if event E happens, which implies
Summing up we conclude that the real-world and the ideal-world interactions are indistinguishable under the Gap-OMDH assumption.
5 Strong aPAKE Protocol Based on \(\mathcal {F}_{\mathsf {corOPRF}}\)
We show that the OPAQUE protocol of [17] remains secure as UC Strong aPAKE even if it is instantiated with the UC Correlated OPRF of Sect. 3 instead of UC OPRF of [11]. This implies that one can safely modify the OPAQUE protocol by replacing the exponential blinding in the Hashed Diffie-Hellman OPRF with the multiplicative blinding (as done in [22]), thus shaving off either 1 variable-base exponentiation from the client, or 2 such exponentiations if the protocol is routinely performed with the same server.
Technically, we show that the OPAQUE compiler construction of [17], which shows that OPRF + AKE \(\rightarrow \) saPAKE, can be used to construct UC saPAKE from any UC Correlated OPRF and any UC AKE which is adaptively secure and resilient to Key-Compromise Impersonation attack (AKE-KCI). We call this compiler OPAQUE+ and show it in Fig. 10. It is exactly the same as the OPAQUE compiler except that the OPRF functionality \(\mathcal {F}_{\mathsf {OPRF}}\) used in [16] is replaced with the Correlated OPRF functionality \(\mathcal {F}_{\mathsf {corOPRF}}\). We show that protocol OPAQUE+ realizes the UC saPAKE functionality.
The saPAKE and AKE-KCI Functionalities. Protocol OPAQUE+ and its analysis build on two functionalities from of [16]: The (strong) aPAKE functionality \(\mathcal {F}_{\mathsf {saPAKE}}\) and the adaptively-secure UC AKE-KCI functionality \(\mathcal {F}_{\mathsf {AKE-KCI}}\). We refer to that paper for their detailed description and rationale. We note that AKE-KCI protocol can be instantiated, for example, by the 3-message version of the HMQV protocol, called HMQV-C in [20], or the 3-message SIGMA protocol [19] underlying the design of TLS 1.3.
Security of OPAQUE+. We now state the security of OPAQUE+ in Theorem 2. As in [17], we assume that the adversary \(\mathcal {A}\) always sends \((\textsc {Compromise},\textsf {sid})\) aimed at \(\mathcal {F}_{\mathsf {corOPRF}}\) and \((\textsc {StealPwdFile},\textsf {sid})\) aimed at \(\mathsf {S}\) simultaneously, since in the real world when the attacker compromises the server, the corresponding OPRF session is always compromised simultaneously.
Theorem 2
If protocol \(\varPi \) realizes functionality \(\mathcal {F}_{\mathsf {AKE-KCI}}\), then protocol OPAQUE+ in Fig. 10 realizes the strong aPAKE functionality \(\mathcal {F}_{\mathsf {saPAKE}}\) in the \((\mathcal {F}_{\mathsf {corOPRF}},\mathcal {F}_{\mathsf {RO}})\)-hybrid model.
The security argument is very similar to that of OPAQUE in [17]; we briefly explain the differences. First of all, note that when the adversary acts as the client in Correlated OPRF, its power is exactly the same as the client in OPRF, hence for that case the security argument is the same in OPAQUE+ as in OPAQUE.
Secondly, an additional power which Correlated OPRF gives to the adversary is to make correlations between OPRF functions while acting as the server. Yet, this does not change the fact that for every function index i (no matter if \(i=\mathsf {S}\) or i is an index created by the adversary) and every value \(y\in \{0,1\}^\ell \), with overwhelming probability there is at most one argument x s.t. \(y=F_i(x)\). In Correlated OPRF the adversary can find \(F_i\) with two arguments that form a collision in \(F_i\) if it finds \((i_1,x_1)\) and \((i_2,x_2)\) s.t. \(F_{i_1}(x_1)=F_{i_2}(x_2)\) and then sets \(F_i\) to be correlated with \(F_{i_1}\) on \(x_1\) and with \(F_{i_2}\) on \(x_2\). In OPRF the adversary must look for such collisions within each function separately, but in either case the probability of a collision is upper-bounded by \(q^2/2^\ell \) where q is the number of F evaluations on all indices. Hence the ciphertext \(c^*\) sent from the adversary to an honest client together with index \(i^*\) of the random function \(F_{i^*}\) which the adversary makes that honest client compute on its password, together commit to a unique password guess \(\mathsf {pw}^*\) such that \(\mathsf {AuthDec}_{\mathsf {rw}^*}(c^*)\ne \perp \) for \(\mathsf {rw}^*=F_{i^*}(\mathsf {pw}^*)\).
Lastly, in the Correlated OPRF an adversarial function \(F_{i^*}\) is not guaranteed to be completely independent from the honest server’s function \(F_k\) for every \(i^*\ne \mathsf {S}\). Instead, the adversary can correlate \(F_{i^*}\) with \(F_k\), although on only a single point x. This allows the adversary a potentially damaging behavior in which it forwards ciphertext \(c^*=c\) from the honest server to the honest client and lets the honest client evaluate \(F_{i^*}\) on its password. In case both parties’ passwords are equal to x the client will compute \(F_{i^*}(x)=F_k(x)\), and thus the two parties will establish a key if their shared passwords are equal to x, and fail to establish a key otherwise. This “conditional password test” could not be done in protocol OPAQUE, and yet it is not an attack on saPAKE, because it requires the adversary to guess the password; therefore, the simulator can (1) use a \(\textsc {TestAbort}\) command to check if the client and server’s passwords match, and if so, it can then (2) use a \(\textsc {TestPwd}\) command to check if the adversary’s password guess is correct. If both checks pass, the simulator can compromise both client’s and server’s sessions, and make these two sessions connect with the same session key; if either check fails, the simulator can force the client to abort.
We present the full proof of Theorem 2 in the full version of this paper [15].
6 Concrete OPAQUE+ Instantiation Using HMQV
Figure 11 shows a concrete instantiation of protocol OPAQUE+ of Fig. 10, where the UC Correlated OPRF is instantiated with protocol Mult-2HashDH, and UC AKE is instantiated with HMQV [20]. Note that the protocol takes 3 flows (\(\tau _s\) can be piggybacked with \(\mathsf {S}\)’s earlier message), and 2 fixed-base (fb) and 2 variable-base (vb) (multi-base) exp’s for \(\mathsf {C}\) and resp. 1fb and 2vb exp’s for \(\mathsf {S}\).
7 Insecure Applications of Multiplicative Blinding
As we noted in the introduction, the correlations allowed by Mult-2HashDH can be exploited in some applications for the benefit of a corrupt server. We illustrate this ability with several examples.
Consider a setting where a client \(\mathsf {C}\) with input x interacts using Mult-2HashDH with a server \(\mathsf {S}\) with key k to compute \(y=F_k(x)=H_2(x,(h_x)^k)\) where \(h_x\) denotes \(H_1(x)\). \(\mathsf {C}\) then uses y for some task; for concreteness, think of x as a password and y as a key that allows \(\mathsf {C}\) to authenticate to some application. At some point \(\mathsf {S}\) becomes corrupted and wants to check whether a given value \(x'\) equals the user’s input x. Using correlations as described in the introduction, e.g., Eq. (3), \(\mathsf {S}\) mounts the following attack: When \(\mathsf {C}\) sends its blinded value \(a=h_x g^r\), \(\mathsf {S}\) chooses random \(k'\), sets \(z=g^{k'}\) and \(b=(h_{x'})^{k-k'}a^{k'}\), and sends (b, z) to \(\mathsf {C}\), who computes the unblinded value \(v=b(z)^{-r}\) and outputs \(y'=H_2(x,v)\). It can be checked that \(v=(h_x)^k\) if and only if \(x'=x\).Footnote 8 If \(\mathsf {S}\) can observe whether \(\mathsf {C}\) recovered the correct value \(y'=y\), e.g. whether it successfully authenticated using the recoverd \(y'\), then \(\mathsf {S}\) learns whether \(\mathsf {C}\)’s secret x equals \(\mathsf {S}\)’s guess \(x'\).
Protocol OPAQUE+ (Fig. 10) with Mult-2HashDH and HMQV
The Correlated OPRF functionality, which Mult-2HashDH realizes, assures that server \(\mathsf {S}\) cannot test more than one guess \(x'\) per interaction, and while in some applications, like the PAKE protocol OPAQUE, this ability doesn’t affect the application, e.g. because the application itself allows the attacker such on-line guess-and-test avenue, in other cases this suffices to break the application. Below we show a few application examples which are all secure with Exp-2HashDH, but not with Mult-2HashDH. In all examples the application doesn’t expose the client to on-line attacks, and using Exp-2HashDH ensures that the implementation does not either, but using Mult-2HashDH adds this exposure and breaks the application.
OPAQUE with Outsourced Envelope. Recall that OPAQUE [17] combines an OPRF with an authenticated key-exchange (AKE) protocol as follows: At registration, the server and the user choose private-public AKE key pairs. The user then runs an OPRF with the server where the user’s input is a password \(\mathsf {pw}\) and the server’s input is an OPRF key k. The output of the OPRF, learned only by the user, is a random key \(\mathsf {rw}=F_k(\mathsf {pw})\), and the user uses \(\mathsf {rw}\) to authenticate-encrypt her AKE private key and the server’s public key. The ciphertext c that results from this encryption is stored by the server, together with the OPRF key k, the user’s public AKE key, and the server’s AKE key pair. At login, the user runs the OPRF with the server on input \(\mathsf {pw}\), learns \(\mathsf {rw}\), uses \(\mathsf {rw}\) to decrypt its own private key and the server’s public key encrypted in c, and uses these keys to run the AKE with the server. Only a user in possession of the registered password can successfully run the AKE.
However, consider a modification where the user stores ciphertext c at some other location than server \(\mathsf {S}\), e.g. a laptop or another server. In this case a malicious \(\mathsf {S}\), who holds only OPRF key k and the AKE keys, cannot stage either online or offline attacks on the user’s password: Without ciphertext c, \(\mathsf {S}\) cannot test candidate values \(\mathsf {rw}=F_k(\mathsf {pw})\). However, this property is not ensured if OPRF is implemented with Mult-2HashDH. Indeed, using the strategy described above, a malicious \(\mathsf {S}\) can test whether the user’s password is equal to a chosen \(\mathsf {pw}^*\), by running login using function \(F_{k^*}\) which is correlated on argument \(\mathsf {pw}^*\) with function \(F_k\) used in registration. If the user recovers its credentials and authenticates in that login, \(\mathsf {S}\) learns that \(\mathsf {pw}=\mathsf {pw}^*\). Crucially, this online attack opportunity for server \(\mathsf {S}\) is not available using Exp-2HashDH.
Device-Enhanced PAKE. [14, 24] presents a password protocol that uses an auxiliary device (typically a smartphone but can also be an online server) in the role of a password manager. When the user wishes to password-authenticate to a server S, it communicates with the device who holds key k for \(\text{2HashDH }\) OPRF. The user’s input to the OPRF is her password, and the OPRF result \(\mathsf {rw}=F_k(\mathsf {pw})\) is used as the “randomized” password with service S. Using Exp-2HashDH, a corrupt device learns nothing about the user’s password, but it can test a guess for the user’s password at the cost of one online interaction with S per guess. However, using Mult-2HashDH, the corrupt device can validate a guess without interacting with S, by watching if the user’s interaction with S succeeded, thus resulting in weaker security guarantees.
Threshold OPRF (Including Threshold OPAQUE). A multi-server threshold implementation of  is presented in [12]. It ensures the security of the OPRF as long as no more than a threshold of servers are compromised. Such threshold OPRF can be used e.g. to construct Password-Protected Secret Sharing (PPSS) [1, 11], which in turn can implement Threshold PAKE. It is straightforward to see that the above correlation attacks apply to these constructions if
is presented in [12]. It ensures the security of the OPRF as long as no more than a threshold of servers are compromised. Such threshold OPRF can be used e.g. to construct Password-Protected Secret Sharing (PPSS) [1, 11], which in turn can implement Threshold PAKE. It is straightforward to see that the above correlation attacks apply to these constructions if  is replaced with
is replaced with  . They allow a single corrupted server to choose correlated values with which it can verify guesses for the client’s inputs. As an illustration, consider a 2-out-of-2 Threshold OPRF that computes \(h_x^{k}\) as \(h_x^{k_1+k_2}\) using two servers \(S_1,S_2\) with respective keys \(k_1,k_2\). Such a scheme should ensure that nothing can be learned about the input x without compromising both servers. However, a corrupted \(S_2\) can check whether C’s input x equals any guess \(x'\) by mounting the above attack using ony key \(k_2\). If C reconstructs the correct y, then \(x=x'\). This attack also applies to OPAQUE with a multi-server threshold implementation of Mult-2HashDH.
. They allow a single corrupted server to choose correlated values with which it can verify guesses for the client’s inputs. As an illustration, consider a 2-out-of-2 Threshold OPRF that computes \(h_x^{k}\) as \(h_x^{k_1+k_2}\) using two servers \(S_1,S_2\) with respective keys \(k_1,k_2\). Such a scheme should ensure that nothing can be learned about the input x without compromising both servers. However, a corrupted \(S_2\) can check whether C’s input x equals any guess \(x'\) by mounting the above attack using ony key \(k_2\). If C reconstructs the correct y, then \(x=x'\). This attack also applies to OPAQUE with a multi-server threshold implementation of Mult-2HashDH.
All these examples show that in order to use Mult-2HashDH in an application where an authenticated \(g^k\) is not available to the client, a dedicated proof of security (as the one we develop here for OPAQUE) is essential. Even in that case, one can consider this as “fragile evidence”, as eventual changes to the application may void the security proof. Thus a safer alternative is to use the scheme (4) presented in the introduction, which implements UC OPRF using both forms of blinding, and would be secure in all the above applications.
Notes
- 1.
In the context of additive groups, “multiplicative” would be replaced with “additive” and “exponential” with “scalar-multiplicative”. A less confusing terminology could refer to these as fixed-base and var-base blindings, respectively.
- 2.
For example, in a password protocol such as OPAQUE [17], a user can cache values z corresponding to servers it accesses frequently, e.g., Google, Facebook, etc.
- 3.
The potential insecurity of multiplicative blinding as UC OPRF was pointed out in [17], which left its security analysis as an open question.
- 4.
Note that an honest server’s response \((b,z)=(a^k,g^k)\) corresponds to \(\delta =1\) and the evaluated function \(F_{(1,z)}\) is identical to the intended function \(F_k\).
- 5.
The correlation between functions \(F_{(\delta _1,z_1)}\) and \(F_{(\delta _2,z_2)}\) would now require that \(z_1 = z_2\), hence \(k_1 = k_2\), in which case Eq. (3) holds only if \(\delta _1 = \delta _2\), hence \((\delta _1,z_1)=(\delta _2,z_2)\).
- 6.
Another way for \(\text{2HashDH }\) to realize UC OPRF with multiplicative blinding, is to add to
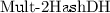 a zero-knowledge proof that (g, z, a, b) is a DDH tuple, but this would void the performance benefit of
a zero-knowledge proof that (g, z, a, b) is a DDH tuple, but this would void the performance benefit of  .
. - 7.
As in the adaptive version of UC OPRF \(\mathcal {F}_{\mathsf {OPRF}}\) [17], we allow server \(\mathsf {S}\) to be adaptively compromised, via call \(\textsc {Compromise}\) from \(\mathcal {A^*}\), which models a leakage of the private state of \(\mathsf {S}\), including its PRF key and all its authentication tokens. One consequence of server compromise is that \(\textsc {RcvComplete}\) will no longer check that \(\mathsf {tx}>0\).
- 8.
Observe that \(v=bz^{-r}=(h_{x'})^{k-k'}(h_x g^r)^{k'}(g^{k'})^{-r}=h_{x'}^k(h_{x'}/h_x)^{k'}\), hence \(v=(h_x)^k\) iff \(h_x=h_{x'}\). Using the terminology of Eq. (2), \(\mathsf {C}\) computes \(y'=F_{(\delta ,z)}(x)\) for \(F_{(\delta ,z)}\) which is correlated with \(F_k\) on \(x'\), hence \(y'=F_k(x)\) iff \(x=x'\).
References
Bagherzandi, A., Jarecki, S., Saxena, N., Lu, Y.: Password-protected secret sharing. In: ACM Conference on Computer and Communications Security — CCS 2011. ACM (2011)
Boyen, X.: HPAKE: password authentication secure against cross-site user impersonation. In: Garay, J.A., Miyaji, A., Otsuka, A. (eds.) CANS 2009. LNCS, vol. 5888, pp. 279–298. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10433-6_19
Brickell, E.F., Gordon, D.M., McCurley, K.S., Wilson, D.B.: Fast exponentiation with precomputation. In: Rueppel, R.A. (ed.) EUROCRYPT 1992. LNCS, vol. 658, pp. 200–207. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-47555-9_18
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: IEEE Symposium on Foundations of Computer Science - FOCS 2001, pp. 136–145. IEEE (2001)
Chaum, D., Pedersen, T.P.: Wallet databases with observers. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 89–105. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_7
Davidson, A., Goldberg, I., Sullivan, N., Tankersley, G., Valsorda, F.: Privacy pass: bypassing internet challenges anonymously. In: Privacy Enhancing Technologies Symposium - PETS 2018, pp. 164–180. Sciendo (2019)
Ford, W., Kaliski, B.S.: Server-assisted generation of a strong secret from a password. In: IEEE 9th International Workshops on Enabling Technologies: Infrastructure for Collaborative Enterprises - WET ICE 2000, pp. 176–180. IEEE (2000)
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_17
Haase, B., Labrique, B.: AuCPace: efficient verifier-based PAKE protocol tailored for the IIoT. In: CHES (2019)
Jarecki, S., Kiayias, A., Krawczyk, H.: Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 233–253. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45608-8_13
Jarecki, S., Kiayias, A., Krawczyk, H., Xu, J.: Highly-efficient and composable password-protected secret sharing (Or: how to protect your bitcoin wallet online). In: IEEE European Symposium on Security and Privacy - EuroS&P 2016, pp. 276–291. IEEE (2016)
Jarecki, S., Kiayias, A., Krawczyk, H., Xu, J.: TOPPSS: cost-minimal password-protected secret sharing based on threshold OPRF. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds.) ACNS 2017. LNCS, vol. 10355, pp. 39–58. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-61204-1_3
Jarecki, S., Krawczyk, H., Resch, J.: Updatable oblivious key management for storage systems. In: ACM Conference on Computer and Communications Security — CCS 2019. ACM (2019)
Jarecki, S., Krawczyk, H., Shirvanian, M., Saxena, N.: Device-enhanced password protocols with optimal online-offline protection. In: Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security, pp. 177–188. ACM (2016)
Jarecki, S., Krawczyk, H., Xu, J.: On the (In)Security of the Diffie-Hellman oblivious PRF with multiplicative blinding. IACR Cryptology ePrint Archive 2021:273
Jarecki, S., Krawczyk, H., Xu. J.: OPAQUE: an asymmetric PAKE protocol secure against pre-computation attacks. IACR Cryptology ePrint Archive 2018:163
Jarecki, S., Krawczyk, H., Xu, J.: OPAQUE: an asymmetric PAKE protocol secure against pre-computation attacks. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10822, pp. 456–486. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_15
Jarecki, S., Liu, X.: Fast secure computation of set intersection. In: Garay, J.A., De Prisco, R. (eds.) SCN 2010. LNCS, vol. 6280, pp. 418–435. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15317-4_26
Krawczyk, H.: SIGMA: The ‘SIGn-and-MAc’ approach to authenticated Diffie-Hellman and its use in the IKE protocols. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 400–425. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_24
Krawczyk, H.: HMQV: a high-performance secure Diffie-Hellman protocol. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 546–566. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_33
Krawczyk, H., The OPAQUE asymmetric PAKE protocol, May 2020. https://tools.ietf.org/html/draft-krawczyk-cfrg-opaque
Krawczyk, H., Lewi, K., Wood, C.A.: The OPAQUE asymmetric PAKE protocol, November 2020. https://tools.ietf.org/html/draft-irtf-cfrg-opaque
Naor, M., Pinkas, B., Reingold, O.: Distributed pseudo-random functions and KDCs. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 327–346. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_23
Shirvanian, M., Saxena, N., Jarecki, S., Krawczyk, H.: Building and studying a password store that perfectly hides passwords from itself. IEEE Trans. Dependable Secure Comput. 16, 5 (2019)
Sullivan, N.: Exported authenticators in TLS, May 2020. https://tools.ietf.org/html/draft-ietf-tls-exported-authenticator
Sullivan, N., Krawczyk, H., Friel, O., Barnes, R.: Usage of OPAQUE with TLS 1.3, March 2019. https://tools.ietf.org/html/draft-sullivan-tls-opaque
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Jarecki, S., Krawczyk, H., Xu, J. (2021). On the (In)Security of the Diffie-Hellman Oblivious PRF with Multiplicative Blinding. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)

















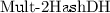 a zero-knowledge proof that (g, z, a, b) is a DDH tuple, but this would void the performance benefit of
a zero-knowledge proof that (g, z, a, b) is a DDH tuple, but this would void the performance benefit of  .
.