Abstract
Verifiable Oblivious Pseudorandom Functions (VOPRFs) are protocols that allow a client to learn verifiable pseudorandom function (PRF) evaluations on inputs of their choice. The PRF evaluations are computed by a server using their own secret key. The security of the protocol prevents both the server from learning anything about the client’s input, and likewise the client from learning anything about the server’s key. VOPRFs have many applications including password-based authentication, secret-sharing, anonymous authentication and efficient private set intersection. In this work, we construct the first round-optimal (online) VOPRF protocol that retains security from well-known subexponential lattice hardness assumptions. Our protocol requires constructions of non-interactive zero-knowledge arguments of knowledge (NIZKAoK). Using recent developments in the area of post-quantum zero-knowledge arguments of knowledge, we show that our VOPRF may be securely instantiated in the quantum random oracle model. We construct such arguments as extensions of prior work in the area of lattice-based zero-knowledge proof systems.
The full version of this work is available as [1].
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
A verifiable oblivious pseudorandom function (VOPRF) is an interactive protocol between two parties; a client and a server. Intuitively, this protocol allows a server to provide a client with an evaluation of a pseudorandom function (PRF) on an input x chosen by the client using the server’s key k. Informally, the security of a VOPRF, from the server’s perspective, guarantees that the client learns nothing more than the PRF evaluated at \(x\) using \(k\) as the key where the server has committed to k in advance. Informally, security from the perspective of the client guarantees the conditions below:
-
1.
the server learns nothing about the input \(x\);
-
2.
the client’s output in the protocol is indeed the evaluation on input \(x\) and key \(k\);
The fact that the client is ensured that its output corresponds to the key committed to by the server makes the protocol a verifiable oblivious PRF. If we were to remove this requirement, the protocol would be an oblivious pseudorandom function (OPRF). From a multi-party computation perspective, an OPRF can be seen as a protocol that securely achieves the functionality \( g(x,k) = (F_k(x), \bot ) \) where \(F_k\) is a PRF using key k and \(\bot \) indicates that the server receives no output. Applications of (V)OPRFs include secure keyword search [24], private set intersection [32], secure data de-duplication [33], password-protected secret sharing [29, 30], password-authenticated key exchange (PAKE) [31] and privacy-preserving lightweight authentication mechanisms [18].
A number of these applications have had recent and considerable real-world impact. The work of Jarecki et al. [31] constructs a PAKE protocol, known as OPAQUE, using an OPRF as a core primitive. The OPAQUE protocol is intended for integration with TLS 1.3 to enable password-based authentication, and it is currently in the process of being standardised [34] by the Crypto Forum Research Group (CFRG)Footnote 1 as part of the PAKE selection process [17]. In addition, the work of Davidson et al. [18] constructs a privacy-preserving authorisation mechanism (known as Privacy Pass) for anonymously bypassing Internet reverse Turing tests based entirely on the security of a VOPRF. The Privacy Pass protocol is currently used at scale by the web performance company Cloudflare [46], and there have also been recent efforts to standardise the protocol design [19]. Both Privacy Pass and OPAQUE use discrete-log (DL) based (V)OPRF constructions to produce notably performant protocols. Finally, there is a separate and ongoing effort being carried forward by the CFRG [20] focusing directly on standardising performant DL-based VOPRF constructions.
Unfortunately, and in spite of the practical value of VOPRFs, all of the available constructions in the literature to date (at the time of writing) are based on classical assumptions, such as decisional Diffie-Hellman (DDH) and RSA. As such, all current VOPRFs would be insecure when confronted with an adversary that can run quantum computations. Therefore, the design of a post-quantum secure VOPRF is required to ensure that the applications above remain secure in these future adversarial conditions.Footnote 2 In fact, for full post-quantum security, both the PRF and the VOPRF protocol itself must be secure in the quantum adversarial model. While PRF constructions with claimed post-quantum security are standard, it remains an open problem to translate these into secure VOPRF protocols.
Constructions of PRFs arising from lattice-based cryptography originated from the work of Banerjee, Peikert and Rosen [6]. These constructions are post-quantum secure assuming the hardness of the learning with errors (LWE) problem against quantum adversaries [45]. To get around the fact that the LWE problem involves the addition of random small errors, carefully chosen rounding is used to obtain deterministic outputs for PRFs based on the LWE assumption [5, 6, 11]. These earlier works on LWE-based PRFs were followed by constructions of more advanced variants of PRFs [14, 16, 44]. Despite this, there is yet to be an OPRF protocol for any LWE-based PRF. The same is true for variants of these constructions based on the ring LWE (RLWE) problem [5].
Contributions. In this work, we instantiate a round-optimalFootnote 3 VOPRF whose security relies on subexponential hardness assumptions over lattices. Our construction assumes certain non-interactive zero-knowledge arguments of knowledge (NIZKAoKs). We use the protocol of Yang et al. [47] as an example instantiation of the required NIZKAoKs, to argue knowledge of inputs to the input-dependent part of PRF evaluations from the Banerjee and Peikert design [5] (henceforth BP14) in the ring setting. Alternatively, one can use Stern-like methods such as those in [36] and the recent protocol of Beullens [7]. These choices come with the advantage that results stating the validity of the Fiat-Shamir transform in the quantum random oracle model (QROM) [22, 37] will apply.
We stress that our results show the feasibility of round-optimal VOPRF protocols based on lattice assumptions, rather than practicality. The performance of the VOPRF is negatively impacted by the required size of parameters (see Sect. 5.3). These parameters are necessary for instantiating our construction using reasonable underlying lattice assumptions – a consequence of using the BP14 PRF construction with our proof technique. Moreover, we require heavy zero-knowledge proof computations to ensure that neither participant deviates from the protocol. Some of these proofs may be removed by considering certain optimisations of our main protocol (see Sect. 3.2). Additionally, removing all zero-knowledge proofs and considering an honest-but-curious setting may result in a relatively efficient protocol (see Sect. 5.3).
Technical Overview. We design a VOPRF for a particular instantiation of the BP14 PRF in the ring setting. Specifically, for a particular function \(\varvec{a}^F: {\{0,1\}}^L \rightarrow R_q^{1\times \ell }\) where \(R_q := \mathbb {Z}_q[X]/\langle X^n+1 \rangle \), we set out to design a VOPRF for the PRF
where the key \( k \in R_q \) has small coefficients when represented in \(\{-q/2, \dots , q/2\}\), and \( \left\lfloor {\cdot } \right\rceil _{} \) represents rounding a rational to the nearest natural number. Our VOPRF protocol can be easily modified to handle other choices of \( \varvec{a}^F(x) \) (up to a change in parameter requirements). The security of this BP14 PRF construction can be reduced to the hardness of RLWE. Consider the PRF for 2-bit inputs: then \(\varvec{a}^F(x) = \varvec{a}_1 \cdot G^{-1}\left( \varvec{a}_2\right) \) where \(\varvec{a}_1, \varvec{a}_2 \in R_q^{1\times \ell }\) are uniform and public, \( G = (1,2,\dots , 2^{\ell -1}) \) and \(G^{-1}\left( \varvec{a}_2 \right) \in R_2^{\ell \times \ell }\) is binary. Very informally, for small \( \varvec{e}, \varvec{e}'' \in R_q^{1 \times \ell } \), uniform \( \varvec{e}' \in R_q^{1 \times \ell } / (R_q \cdot G) \) and q much larger than p, we can write
where \( \varvec{u}, \varvec{u}'', \widetilde{\varvec{u}} \) are uniform in \( R_q^{1 \times \ell } \) and \( u' \) is uniform in \( R_q \). The proof of pseudorandomness builds on these ideas.
To provide intuition for our VOPRF design, we describe the rough form of our protocol (without zero-knowledge proofs). Given a public uniform \( \varvec{a} \in R_q^{1 \times \ell } \), the high level overview is as follows:
-
1.
The server publishes some commitment \( \varvec{c} := \varvec{a} \cdot k + \varvec{e} \) to a small key \( k \in R_q \).
-
2.
On input x, the client picks small \( s \in R_q \), small \( \varvec{e}_1 \in R_q^{1\times \ell } \) and sends \( \varvec{c}_x = \varvec{a} \cdot s + \varvec{e}_1 + \varvec{a}^F(x) \).
-
3.
On input small \( k \in R_q \), the server sends \( \varvec{d}_x = \varvec{c}_x \cdot k + \varvec{e}' \) for small \( \varvec{e}' \in R_q^{1\times \ell } \).
-
4.
The client outputs \( \varvec{y} = \left\lfloor \frac{p}{q} \cdot \left( \varvec{d}_x - \varvec{c} \cdot s\right) \right\rceil \).
For server security, note that \(\varvec{d}_x = \varvec{a} \cdot s \cdot k + \varvec{a}^F(x) \cdot k + \varvec{e}_1 \cdot k + \varvec{e}'\). Suppose that we choose \( \varvec{e}' \) from a distribution that hides addition of terms \(\varvec{e}_1 \cdot k, \varvec{e} \cdot s\) and \( \varvec{e}_x \) (where \( \varvec{e}_x \) is from some other narrow distribution). Then, from the perspective of the client, the server might as well have sent \( \varvec{d}_x = (\varvec{a} \cdot k + \varvec{e}) \cdot s + \varvec{e}' + (\varvec{a}^F(x) \cdot k + \varvec{e}_x) = \varvec{c} \cdot s + (\varvec{a}^F(x) \cdot k + \varvec{e}_x) + \varvec{e}' \). Picking \(\varvec{e}_x\) from an appropriate distribution [5] makes the term in brackets i.e. \( \varvec{a}^F(x) \cdot k + \varvec{e}_x \) computationally indistinguishable from uniform random under a RLWE assumption, even given the value of \( \varvec{c} \) which is also indistinguishable from random by a RLWE assumption. This implies that the message \( \varvec{d}_x \) leaks nothing about the server’s key k.
For client security, we pick s from a valid RLWE secret distribution and a Gaussian \( \varvec{e} \). This implies that \( \varvec{c}_x = \varvec{a} \cdot s + \varvec{e} + \varvec{a}^F(x) \) is indistinguishable from uniform by RLWE. Finally, we must show that the client does indeed recover \( F_k(x) \) as its output \( \varvec{y} \). For correctness, we would like to say that
Thus, we guarantee correctness if all coefficients of \( \frac{p}{q}\cdot \varvec{a}^F(x)\cdot k \) are at least \( \left| \frac{p}{q} \left( \varvec{e}_1\cdot k - \varvec{e} \cdot s + \varvec{e}'\right) \right| _{\infty } \) away from \( \mathbb {Z}+\frac{1}{2}\). It turns out that this condition is satisfied with extremely high probability due to the 1-dimensional short integer solution (1D-SIS) assumption [15] regardless of the way an efficient server chooses its key. The form of \(\varvec{a}^F(x)\) is crucial to the connection with the 1D-SIS problem. In particular, we rely on the fact that we can decompose \( \varvec{a}^F(x) \) as \(\varvec{a}'_1 \cdot \varvec{a}'_2\) where \(\varvec{a}'_1 \in R_q^{1 \times \ell }\) is uniform random and \(\varvec{a}'_2 \in R_q^{\ell \times \ell }\) has entries that are polynomials with binary coefficients.
Ultimately, the security of our VOPRF construction (with particular choices of NIZKAoK instantiations) holds in the QROM and relies on the hardness of sub-exponential RLWE and 1D-SIS which are both at least as hard as certain lattice problems. We discuss parameters in Sect. 5.3.
Related Work and Discussion. Subsequent to this work, Boneh et al. [10] constructed a post-quantum (V)OPRF with comparatively good efficiency from isogenies. Their construction also uses the random oracle model, but is also proven secure in the universal composability (UC) model unlike the construction in this work. A related primitive to a VOPRF is a verifiable random function (VRF). A VRF is a keyed pseudorandom function allowing an entity with the key to create publicly verifiable proofs of correct evaluation. Recently, Yang et al. [47] showed a lattice-based construction of a VRF using the definition of [42]. In fact, the proof systems of Yang et al. serve as a crucial foundation for one way of instantiating the proof systems used in our VOPRF. However, it should be noted that the Yang et al. construction (like ours) is not in the standard model due to the use of the Fiat-Shamir [23] transform.
While our work provides a first construction for a post-quantum VOPRF, it does not resolve this question completely. The reason VOPRFs enjoy popularity is their efficiency in the discrete logarithm setting. In contrast, our construction – while practically instantiable – is far less efficient. This relative inefficiency is partly due to our choice of relying on lattice-based constructions for our zero-knowledge proof systems, along with the super-polynomial factors required for the RLWE-based PRF and noise drowning. Improving these areas thus suggests ways to achieve concretely more efficient schemes. In fact, we do discuss attempts to optimise our main protocol with a view to reducing the impact of the zero-knowledge proofs. In particular, one can amortise the costs of the client zero-knowledge proof by sending queries in batches and sending one proof of a more complex statement. This saves a small additive term in the overall cost compared to sending the queries one at a time. Additionally, we discuss the use of a cut-and-choose approach to removing the server’s zero-knowledge proof at the effective cost of extra repetitions of the protocol. Ultimately, this does not improve overall efficiency, but it does dramatically reduce the burden on the server. For more details, see Sect. 3.2. An alternative approach is to accept, for now, that VOPRFs are less appealing building blocks in a post-quantum world, and to revisit their applications to provide post-quantum alternatives on a per application basis.
One could alternatively instantiate VOPRFs using generic techniques for establishing Multi-Party Computation (MPC) protocols by treating a single execution of the VOPRF protocol, for a PRF like AES, as a single invocation of a classical two-party actively secure MPC protocol. But this does not give the round-optimality that we are after. See the full version of this work for a discussion about this.
Road Map. We begin with preliminaries in Sect. 2. Note that Definition 1 deviates from the usual MPC definition. In particular, we argue security against malicious clients when \(k\) is sampled from a key distribution for which the PRF is pseudorandom, rather than arguing security for arbitrary fixed k. Next is the VOPRF construction and discussion of optimisations (Sect. 3) followed by a high-level description of the zero-knowledge proof instantiations (Sect. 4). Finally, we give the security proof for our VOPRF protocol in Sect. 5.
2 Preliminaries
All algorithms will be considered to be randomised algorithms unless explicitly stated otherwise. A PPT algorithm is a randomised (i.e. probabilistic) algorithm with polynomial running time in the security parameter \( \kappa \). We consider the probability distribution of outputs of algorithms as being over all possible choices of the internal coins of the algorithm. For a distribution \( \mathcal {D} \), we denote the sampling of x according to distribution \( \mathcal {D} \) by \( x \leftarrow \mathcal {D} \). We write \(x \leftarrow S\) for a finite set \(S\) to indicate sampling uniformly at random from \(S\). We use the notation \( \mathcal {D}_1 \approx _c \mathcal {D}_2 \) to mean the distributions \( \mathcal {D}_1 \) and \( \mathcal {D}_2 \) are computationally indistinguishable and \( \approx _s \) to denote statistical indistinguishability. We use the standard asymptotic notations. We let  denote a negligible function (i.e. a function that is \( \kappa ^{-\omega (1)} \)) and write \( r_1 \gg r_2 \) as short-hand for \( r_1 \ge \kappa ^{\omega (1)} \cdot r_2 \). We say a distribution \( \mathcal {D} \) is \( (B,\delta ) \)-bounded if
denote a negligible function (i.e. a function that is \( \kappa ^{-\omega (1)} \)) and write \( r_1 \gg r_2 \) as short-hand for \( r_1 \ge \kappa ^{\omega (1)} \cdot r_2 \). We say a distribution \( \mathcal {D} \) is \( (B,\delta ) \)-bounded if
 . If a distribution is \( (B,\delta ) \)-bounded for a negligible \( \delta \), then we say that distribution is simply B-bounded.
. If a distribution is \( (B,\delta ) \)-bounded for a negligible \( \delta \), then we say that distribution is simply B-bounded.
In this work we will use power of two cyclotomic rings. In particular, for some integer \(q\), we will be considering polynomials in the power-of-two cyclotomic ring \( R = \mathbb {Z}[X]/\langle X^n+1\rangle \) and \( R_q := R/qR\) where \(n\) is a power-of-two. \( R_{\le c} \) is the set of elements of R where all coefficients have an absolute value at most c. We also use a rounding operation from \( \mathbb {Z}_q \) to \( \mathbb {Z}_{q'} \) where \( q' < q \). For \(x \in \mathbb {Z}_q\), this rounding operation is defined as
where \( \lfloor \cdot \rceil \) denotes rounding to the nearest integer (rounding down in the case of a tie). If \(q'\) divides \(q\), we can lift rounded integers back up to \(\mathbb {Z}_q\) by simply multiplying by \(q/q'\). Note that lifting the result of a rounding takes an \( x \in \mathbb {Z}_q \) to the nearest multiple of \(q/q'\). Therefore, the difference between \(x\) and the result of this rounding then lifting is at most \( q/(2 \cdot q') \). Polynomials and vectors are rounded component-wise. We write \(\Vert \cdot \Vert \) for the Euclidean norm and \(\Vert \cdot \Vert _{\infty }\) for the infinity norm. We define the norms of ring elements by considering the norms of their coefficient vectors. Vectors whose entries are ring elements will be denoted using bold characters and integer vectors will be indicated by an over-arrow e.g. \( \varvec{v} \) has ring entries and  has integer entries. Suppose \( \varvec{v} = (v_1, \dots , v_n) \). A norm of \( \varvec{v} \) is the norm of the vector obtained by concatenating the coefficient vectors of \( v_1, \dots , v_n \).
has integer entries. Suppose \( \varvec{v} = (v_1, \dots , v_n) \). A norm of \( \varvec{v} \) is the norm of the vector obtained by concatenating the coefficient vectors of \( v_1, \dots , v_n \).
Gaussian distributions. For any \(\sigma > 0\), define the Gaussian function on \(\mathbb {R}^n\) centred at \(\varvec{c} \in \mathbb {R}^n\) with parameter \(\sigma \) to be:
Define \( \rho _\sigma (\mathbb {Z}) := \sum _{i\in \mathbb {Z}} \rho _\sigma (i) \). The discrete Gaussian distribution over \( \mathbb {Z}\), denoted \( \chi _\sigma \) assigns probability \( \rho _\sigma (i)/\rho _\sigma (\mathbb {Z}) \) to each \( i \in \mathbb {Z}\) and probability 0 to each non-integer point. The discrete Gaussian distribution over R, denoted as \( R(\chi _\sigma ) \), is the distribution over R where each coefficient is distributed according to \( \chi _\sigma \). Using the results of [13, 25], \( \chi _\sigma \) can be sampled in polynomial time. Moreover the Euclidean norm of a sample from \( R(\chi _\sigma ) \) can be bounded using an instantiation of Lemma 1.5 of [4]. We state this lemma next.
Lemma 1
Let \( \sigma >0 \) and  . Then
. Then

In addition, following the same reasoning as in [21] we have the following “drowning/smudging” lemma.
Lemma 2
Let \(\sigma > 0\) and \(y \in \mathbb {Z}\). The statistical distance between \( \chi _{\sigma } \) and \( \chi _\sigma + y \) is at most \( |y| / \sigma \).
2.1 Verifiable Oblivious Pseudorandom Functions
Recall that the main goal of our work is to build a verifiable oblivious pseudorandom function (VOPRF). A VOPRF is a protocol between two parties: a server \( \mathbb {S} \) and a client \( \mathbb {C}\), securely realising the ideal functionality in Fig. 1. The functionality consists of two phases, the initialisation phase and the query phase. The initialisation phase is divided into two steps: one run once by the server, and one run once by any client who wishes to utilise the VOPRF provided by the server. In the event that the functionality \(\mathcal {F}_\mathsf {VOPRF}\) receives a valid input \(k\) from \(\mathbb {S} \) during the initialisation phase, it stores the key for use during the query phase. This models a server (\(\mathbb {S} \)) in a real protocol committing to a PRF key \(k\).
Next comes the query phase, where a client \(\mathbb {C}\) sends some value \(x\) to \(\mathcal {F}_\mathsf {VOPRF}\). Once this value \(x\) has been received, the server \(\mathbb {S} \) either sends the functionality an instruction to abort or to deliver the value \( y = F_k(x) \) to \(\mathbb {C}\). Finally, the functionality carries out this instruction. Importantly, (assuming that no abort is triggered) the client has the guarantee that its output is indeed \( F_k(x) \) i.e. the output of the client is verifiably correct when interacting with \( \mathcal {F}_\mathsf {VOPRF}\).
The Ideal Functionality \(\mathcal {F}_\mathsf {VOPRF}\). \(^{\dagger }\)The notion of a valid key refers to whether the key conforms to a pre-determined distribution. See Definition 1 for more details on this requirement.
We now describe the distributions that arise in the security requirement. We consider malicious adversaries throughout that behave arbitrarily and begin with the distributions of interest when a server has been corrupted. First, we consider a “real” world protocol \( \varPi \) between \( \mathbb {C}(x) \) and \( \mathbb {S} (k) \) along with an adversary \( \mathcal {A}\). We denote \( \mathsf {real}_{\varPi ,\mathcal {A}, \mathbb {S}}(x,k,1^{\kappa }) \) to be the joint output distribution of \( \mathcal {A}(k) \) (when corrupting \( \mathbb {S} (k) \)) and \( \mathbb {C}(x) \) where \( \mathbb {C}(x) \) behaves as specified by \( \varPi \). In this setting, \( \mathcal {A}\) interacts directly with \( \mathbb {C}\). Now we introduce a simulator denoted \( \mathsf {Sim}\) that lives in the “ideal” world. Specifically, still assuming \( \mathcal {A}\) corrupts a server, \( \mathsf {Sim}\) interacts with \( \mathcal {A}\) on one hand and with \( \mathbb {C}(x) \) via \( \mathcal {F}_\mathsf {VOPRF}\) on the other. In this setting, for any client/server input pair (x, k) , we define \( \mathsf {ideal}_{\mathcal {F}_\mathsf {VOPRF}, \mathsf {Sim},\mathcal {A}, \mathbb {S}}(x,k,1^{\kappa }) \) to be the joint output distribution of \( \mathcal {A}(k) \) and the honest client \( \mathbb {C}(x) \) when \( \mathcal {A}(k) \) interacts via \( \mathsf {Sim}\). Informally, one may interpret \( \mathsf {Sim}\) as an attacker-in-the-middle between \( \mathcal {A}\) and the outside world where \( \mathsf {Sim}\) interacts with \( \mathcal {F}_\mathsf {VOPRF}\) external to the view of \( \mathcal {A}\). Security argues that whatever \( \mathcal {A}\) can learn/affect in the real protocol can be emulated via \( \mathsf {Sim}\) in the ideal setting.
Next, we describe the distributions of interest when a client has been corrupted by an adversary \( \mathcal {A}\). We let \( \mathcal {K} \) denote the key distribution under which PRF security of F holds. First, consider a “real” world case where \( \mathcal {A}\) corrupts \( \mathbb {C}(x) \) and directly interacts with honest \( \mathbb {S} (k) \) which follows the specification of protocol \( \varPi \). In this case, we use \( \mathsf {real}_{\varPi ,\mathcal {A}, \mathbb {C}}(x,\mathcal {K},1^{\kappa }) \) to denote the joint output distribution of \( \mathcal {A}(x) \) and \( \mathbb {S} (k) \)Footnote 4 where
 . Now consider an alternative “ideal” world case where we introduce a simulator \( \mathsf {Sim}\) interacting with \( \mathcal {A}\) on one hand and with \( \mathbb {S} (x) \) via \( \mathcal {F}_\mathsf {VOPRF}\) on the other hand. Once again, one may wish to interpret the simulator as an attacker-in-the-middle interacting with \( \mathcal {F}_\mathsf {VOPRF}\) external to the view of \( \mathcal {A}\). In this alternative case, we denote the joint output distribution of \( \mathcal {A}(x) \) and \( \mathbb {S} (k) \) where \( \mathcal {A}\) interacts via \( \mathsf {Sim}\) and
. Now consider an alternative “ideal” world case where we introduce a simulator \( \mathsf {Sim}\) interacting with \( \mathcal {A}\) on one hand and with \( \mathbb {S} (x) \) via \( \mathcal {F}_\mathsf {VOPRF}\) on the other hand. Once again, one may wish to interpret the simulator as an attacker-in-the-middle interacting with \( \mathcal {F}_\mathsf {VOPRF}\) external to the view of \( \mathcal {A}\). In this alternative case, we denote the joint output distribution of \( \mathcal {A}(x) \) and \( \mathbb {S} (k) \) where \( \mathcal {A}\) interacts via \( \mathsf {Sim}\) and
 as \( \mathsf {ideal}_{\mathcal {F}_\mathsf {VOPRF}, \mathsf {Sim}, \mathcal {A}, \mathbb {C}}(x,\mathcal {K},1^{\kappa }) \).
as \( \mathsf {ideal}_{\mathcal {F}_\mathsf {VOPRF}, \mathsf {Sim}, \mathcal {A}, \mathbb {C}}(x,\mathcal {K},1^{\kappa }) \).
Finally, for protocol \( \varPi \), let \( \mathsf {output}(\varPi ,x,k) \) denote the output distribution of a client with input x running protocol \( \varPi \) with a server whose input key is k. Using the notation established above, we can present our definition of a VOPRF.
Definition 1
A protocol \( \varPi \) is a verifiable oblivious pseudorandom function if all of the following hold:
-
1.
Correctness: For every pair of inputs (x, k) ,

-
2.
Malicious server security: For any PPT adversary \( \mathcal {A}\) corrupting a server, there exists a PPT simulator \( \mathsf {Sim}\) such that for every pair of inputs (x, k) :
$$ \mathsf {ideal}_{\mathcal {F}_\mathsf {VOPRF}, \mathsf {Sim}, \mathcal {A}, \mathbb {S}}(x,k,1^{\kappa }) \approx _c \mathsf {real}_{\varPi ,\mathcal {A}, \mathbb {S}}(x,k,1^{\kappa }). $$ -
3.
Average case malicious client security: For any PPT adversary \( \mathcal {A}\) corrupting a client, there exists a PPT simulator \( \mathsf {Sim}\) such that for all client inputs x:
-
\( \mathsf {ideal}_{\mathcal {F}_\mathsf {VOPRF}, \mathsf {Sim}, \mathcal {A}, \mathbb {C}}(x,\mathcal {K},1^{\kappa }) \approx _c \mathsf {real}_{\varPi ,\mathcal {A}, \mathbb {C}}(x,\mathcal {K},1^{\kappa }). \)
-
If \( \mathcal {A}\) correctly outputs \( F_k(x) \) with all but negligible probability over the choice
 when interacting directly with \( \mathbb {S} (k) \) using protocol \( \varPi \), then \( \mathcal {A}\) also outputs \( F_k(x) \) with all but negligible probability when interacting via \( \mathsf {Sim}\).
when interacting directly with \( \mathbb {S} (k) \) using protocol \( \varPi \), then \( \mathcal {A}\) also outputs \( F_k(x) \) with all but negligible probability when interacting via \( \mathsf {Sim}\).
-
We now discuss this definition. Note that the correctness and malicious server security requirements are the standard ones used in MPC. Therefore, we restrict this discussion to the condition that we call average case malicious client security. The motivation for this non-standard property is that an honest server will always sample a key from distribution \( \mathcal {K} \) as it wishes to provide pseudorandom function evaluations. In particular, PRF security holds with respect to this key distribution \( \mathcal {K} \). Therefore, it makes sense to ask what a malicious client may learn/affect only in the case where
 which leads to the first point of our average case malicious client security requirement. The second point of the requirement captures the fact that adversaries may have access to an oracle that checks whether the PRF was evaluated correctly or not. Suppose that we give the adversary \(\mathcal {A}\) access to an oracle which can check an input/output pair to the PRF is valid or not. Then \(\mathcal {A}\) should not be able to distinguish whether it is interacting with a real server \(\mathbb {S} \) or a simulation \(\mathsf {Sim}\). Note that our proof structure relies heavily on our alternative malicious client security definition. In particular, the definition above allows us to argue over the entropy of secret keys when making indistinguishability claims.
which leads to the first point of our average case malicious client security requirement. The second point of the requirement captures the fact that adversaries may have access to an oracle that checks whether the PRF was evaluated correctly or not. Suppose that we give the adversary \(\mathcal {A}\) access to an oracle which can check an input/output pair to the PRF is valid or not. Then \(\mathcal {A}\) should not be able to distinguish whether it is interacting with a real server \(\mathbb {S} \) or a simulation \(\mathsf {Sim}\). Note that our proof structure relies heavily on our alternative malicious client security definition. In particular, the definition above allows us to argue over the entropy of secret keys when making indistinguishability claims.
Alternative Definitions. Note that alternative security definitions exist for (V)OPRFs. In the UC security models that are favoured by Jarecki et al. [29, 30] the output of the PRF is wrapped in the output of a programmable random oracle evaluation. This is a fact that is utilised by the OPAQUE PAKE protocol [31] that allows arguing that the pseudorandom function evaluations are pseudorandom even to the server (the key-holder). Unfortunately, using a similar technique here is difficult as constructing programmable random oracles in the quantum random oracle model (QROM) is known to be difficult [9].
2.2 Computational Assumptions
Here we present the presumed quantum hard computational problems that will be used in our security proofs. Evidence that these problems are indeed quantum hard follows via reductions from standard lattice problems (see the full version of this work). These reductions from lattice problems will be used to asymptotically analyse secure parameter settings for our VOPRF. The first is the standard decisional RLWE problem [40].
Definition 2
(RLWE problem) Let \(q,m,n,\sigma > 0\) depend on \(\kappa \) (\(q,m,n\) are integers). The decision-RLWE problem ( \(\mathsf {dRLWE}_{q,n,m,\sigma }\) ) is to distinguish between:
for
 ;
;
 .
.
We sometimes write \(\mathsf {dRLWE}_{q,n,\sigma } \), leaving the parameter \(m\) (representing the number of samples) implicit. The second problem is slightly less standard. It is the short integer solution problem in dimension 1 (1D-SIS). The following formulation of the problem was used in [15] in conjunction with a lemma attesting to its hardness. See the full version of this work for more details.
Definition 3
(1D-SIS, [15, Definition 3.4]) Let q, m, t depend on \( \kappa \). The one-dimensional SIS problem, denoted \( \mathsf {1D\text {-}SIS}_{q,m,t} \), is the following: Given a uniform
 , find non-zero \(\varvec{z} \in \mathbb {Z}^m\) such that \( ||\varvec{z}||_\infty \le t \) and \( \langle \varvec{v}, \varvec{z} \rangle \in [-t,t] + q \mathbb {Z}\).
, find non-zero \(\varvec{z} \in \mathbb {Z}^m\) such that \( ||\varvec{z}||_\infty \le t \) and \( \langle \varvec{v}, \varvec{z} \rangle \in [-t,t] + q \mathbb {Z}\).
2.3 Non-interactive Zero-Knowledge Arguments of Knowledge
The foundations of zero-knowledge (ZK) proof systems were established in a number of works [8, 23, 27, 28]. At a high level, a ZK proof system for language \( \mathcal {L} \) allows a prover \( \mathbb {P} \) to convince a verifier \(\mathbb {V} \) that some instance x is in \( \mathcal {L} \), without revealing anything beyond this statement. Further, a ZK argument of knowledge (ZKAoK) system allows \( \mathbb {P} \) to convince \( \mathbb {V} \) that they hold a witness w attesting to the fact that x is in \( \mathcal {L} \) (where the \( \mathcal {L} \) is defined by a relation predicate \(\mathsf {P}_{\mathcal {L}}(x,w) \)).
Definition 4
(NIZKAoK) Let \(\mathbb {P} \) be a prover, let \(\mathbb {V} \) be a verifier, let \(\mathcal {L} \) be a language with accompanying relation predicate \(\mathsf {P}_{\mathcal {L}}(\cdot ,\cdot ) \). Let \(\mathcal {W} _{\mathcal {L}}(x)\) be a generic set of witnesses attesting to the fact that \(x \in \mathcal {L} \), i.e. \( \forall x \in \mathcal {L}, \) and \( w \in \mathcal {W} _{\mathcal {L}}(x) \) we have \(\mathsf {P}_{\mathcal {L}}(x,w) =1\). Let \(\mathsf {nizk} = (\mathsf {Setup} {},\mathbb {P},\mathbb {V})\) be a tuple of algorithms defined as follows:
-
\(\mathsf {crs} \leftarrow \mathsf {nizk}.\mathsf {Setup}(1^{\kappa }) \): outputs a common random string \(\mathsf {crs} \).
-
\(\pi \leftarrow \mathsf {nizk}.\mathbb {P} (\mathsf {crs},x,w)\): on input \(\mathsf {crs} \), a word \(x \in \mathcal {L} \) and a witness \(w \in \mathcal {W} _{\mathcal {L}}(x)\); outputs a proof
 .
. -
\(b \leftarrow \mathsf {nizk}.\mathbb {V} (\mathsf {crs},x,\pi )\): on input \(\mathsf {crs} \), a word \(x \in \mathcal {L} \) and a proof
 ; outputs
; outputs
 .
.
Definition 5
(NIZKAoK Security) We say that \(\mathsf {nizk} \) is a non-interactive zero-knowledge argument of knowledge (NIZKAoK) for \(\mathcal {L} \) if the following holds.
-
1.
(Completeness): Consider \(x \in \mathcal {L} \) and \(w \in \mathcal {W} _{\mathcal {L}}(x)\), where \(\mathsf {P}_{\mathcal {L}}(x,w) = 1\). Then:

-
2.
(Computational knowledge extraction): The proof system satisfies computational knowledge extraction with knowledge error \(\bar{\kappa }\) if, for any PPT prover \( \mathbb {P} ^* \) with auxiliary information \( \mathsf {aux} \), the following holds. There exists a PPT algorithm \(\mathsf {nizk}.\mathsf {Extract}\) and a polynomial \(p\) such that, for any input \(x\), then:

is satisfied, where \(\nu \) is the probability that \(\mathsf {nizk}.\mathbb {V} (\mathsf {crs},x,\mathbb {P} ^*(\mathsf {crs},x, \mathsf {aux}))\) outputs 1.
-
3.
(Computational zero-knowledge): There exists a simulated setup algorithm \(\mathsf {nizk}.\mathsf {Sim}\mathsf {Setup}(1^{\kappa }) \) outputting \(\mathsf {crs} _{\mathsf {Sim}}\) and a trapdoor \(\mathcal {T} \) along with a PPT algorithm \(\mathsf {nizk}.\mathsf {Sim}(\mathsf {crs} _{\mathsf {Sim}},\mathcal {T},x)\) satisfying

\( \forall x \in \mathcal {L} \) and \( w \in \mathcal {W} _{\mathcal {L}}(x) \).
Interactive Proof Systems. An interactive proof system is one where the proving algorithm (\(\mathbb {P} \)) requires interaction with the verifier. Such an interaction could be an arbitrary protocol, with many message exchanges, but a typical (in the honest verifier case) scenario is a three-move protocol consisting of a commitment (from the prover), a uniformly chosen challenge (from the verifier) and then a response (from the prover). Such protocols are referred to as \( \varSigma \)-protocols. Fiat and Shamir [23] established a mechanism of switching a (constant-round) honest verifier zero-knowledge interactive proof of knowledge into a non-interactive zero-knowledge proof of knowledge in the random oracle model (ROM). In particular, the random challenge provided by the verifier is replaced with the output of a random oracle evaluation taking as input the statement x and the provers initial commitment. It was recently shown that the standard Fiat-Shamir transform is also secure in the quantum ROM (QROM) [22, 37] assuming the underlying \( \varSigma \)-protocol satisfies certain properties.
2.4 Lattice PRF
We will use an instantiation of the lattice PRF from [5]. Below, we present relevant definitions/results, all of which are particular cases of definitions/results from [5]. We set \( \ell =\lceil \log _2 q \rceil \) throughout. The construction from [5] makes use of gadget matrices that can be found in many previous works [5, 15, 26, 43].
Gadgets \( G, G^{-1}. \) Define \(G : R_q^{\ell \times \ell } \rightarrow R_q^{1\times \ell }\) to be the linear operation corresponding to left multiplication by \( (1,2, \dots , 2^{\ell -1}) \). Further, define \( G^{-1} : R_q^{1 \times \ell } \rightarrow R_q^{\ell \times \ell } \) to be the bit decomposition operation that essentially inverts \(G\) i.e. the \(i^{th}\) column of \(G^{-1}(\varvec{a})\) is the bit decomposition of \(a_i \in R_q\) into binary polynomials.
The instantiation of [5] that we will present our VOPRF with respect to is defined as \(F_k(x) = \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \) for \(\varvec{a}_{x} \in R_q^{1 \times \ell }\) given below.
Definition 6
Fix some \(\varvec{a}_0, \varvec{a}_1 \leftarrow R_q^{1\times \ell } \). For any \(x = (x_1,\dots , x_{L}) \in {\{ 0,1\}}^{L}\). We define \( \varvec{a}_x \in R_q^{1 \times \ell } \) as
The pseudorandomness of this construction follows from the ring learning with errors (RLWE) assumption (with normal form secrets).
Theorem 1
([5]). Sample \( k \leftarrow R(\chi _{\sigma }) \). If \( q \gg p \cdot \sigma \cdot \sqrt{L} \cdot n \cdot \ell \), then the function \(F_k(x) = \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \) is a PRF under the \( \mathsf {dRLWE}_{q,n,\sigma } \) assumption.
When we eventually prove security of our VOPRF, it will be useful to define a special error distribution such that \( \varvec{a}_x \cdot k + \varvec{e} \) remains indistinguishable from uniform (under RLWE) when \( \varvec{e} \) is sampled from this special error distribution. To this end, we introduce the distributions \( \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x, \sigma } \) followed by a lemma that is implicit in the pseudorandomness proof of the PRF from [5].
Definition 7
For \( \varvec{a}_0, \varvec{a}_1 \in R_q^{1 \times \ell } \), define
Furthermore, let \( \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x, \sigma } \) be the distribution that is sampled by choosing
 for \( i=1,\dots , L \) and outputting
for \( i=1,\dots , L \) and outputting
Lemma 3
(Implicit in [5]). If \( \varvec{a}_0,\varvec{a}_1 \leftarrow R_q^{1\times \ell }, \varvec{e} \leftarrow \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x,\sigma } \) and \( s \leftarrow R(\chi _{\sigma }) \), then for any fixed \( x \in {\{0,1\}}^L \),
is indistinguishable from uniform random by the \( \mathsf {dRLWE}_{q,n,\sigma } \) assumption.
In addition to introducing \( \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x, \sigma } \), it will be useful to write down an upper bound on the infinity norm on errors drawn from this distribution. The following lemma follows from the fact that for
 , \( \Vert y\Vert _{\infty } \le \sigma \sqrt{n}\) with all but negligible probability by Lemma 1. In fact, we could use the result that \( \Vert y\Vert _{\infty } \le \sigma n^{c'}\) with probability at least \( 1- c \cdot \exp (-\pi n^{2c'}) \) for any constant \( c'>0 \) and some universal constant c to reduce the upper bound, but we choose not to for simplicity.
, \( \Vert y\Vert _{\infty } \le \sigma \sqrt{n}\) with all but negligible probability by Lemma 1. In fact, we could use the result that \( \Vert y\Vert _{\infty } \le \sigma n^{c'}\) with probability at least \( 1- c \cdot \exp (-\pi n^{2c'}) \) for any constant \( c'>0 \) and some universal constant c to reduce the upper bound, but we choose not to for simplicity.
Lemma 4
(Bound on Errors). Let
 , \( \ell =\lceil \log _2 q \rceil \) and
, \( \ell =\lceil \log _2 q \rceil \) and
 . Samples from \( \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x,\sigma } \) have infinity norm at most \( L \cdot \ell \cdot \sigma \cdot n^{3/2} \) with all but negligible probability.
. Samples from \( \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x,\sigma } \) have infinity norm at most \( L \cdot \ell \cdot \sigma \cdot n^{3/2} \) with all but negligible probability.
3 A VOPRF Construction from Lattices
In this section, we provide a construction emulating the DH blinding construction \({H(x)}^{k} = {\left( H(x)\cdot g^{r}\right) }^{k}/{(g^{k})}^{r}\). In what follows, we will initially ignore the zero-knowledge proofs establishing that all computations are performed honestly. A detailed description of the protocol is in Fig. 2 but the main high-level idea follows.
Recall that we are working with power-of-two cyclotomic rings. Informally, suppose a client wants to obtain \(a' \cdot k + e'\in R_q\) (where \( e' \) is relatively small) from a server holding a short \(k\) without revealing \(a' \in R_q\). Further, suppose that the server has published an LWE instance \( (a,c:=a\cdot k + e) \) for truly uniformly a and small Gaussian e. One way to achieve our goal is to have the client compute \( c_x:=a \cdot s + e_1 + a' \) for Gaussian \( (s,e_1) \). Next the server responds by computing \( d_x:=c_x \cdot k + e'' \) for relatively small \( e'' \) and the client finally outputs
The above gives the intuition behind our actual protocol. Roughly, the idea is to replace \( a' \) with \( \varvec{a}_x \) from a BP14 evaluation. As mentioned above, a more detailed formulation of our construction is given in Fig. 2. In the protocol description, \(\mathbb {P} _i\) and \(\mathbb {V} _i\) denote prover and verifier algorithms for three different zero-knowledge argument systems indexed by \(i \in \{0,1,2\}\).
3.1 Zero-Knowledge Argument of Knowledge Statements
The arguments of \( \mathbb {P} _i \) algorithms fall into two groups separated by a colon. Arguments before a colon are intended as “secret” information pertaining to a witness for a statement. Arguments after a colon should be interpreted as “public” information specifying the statement that is being proved.
Client Proof. The client proof denoted \( \mathbb {P} _1(x, s, \varvec{e}_1: \mathsf {crs} _1, \varvec{c}_x, \varvec{a}, \varvec{a}_0, \varvec{a}_1) \) should prove knowledge of
-

-
\( s \in R \) where \( \Vert s\Vert _{\infty } \le \sigma \cdot \sqrt{n}\)
-
\(\varvec{e}_1 \in R^{1\times \ell } \) where \(\Vert \varvec{e}_1\Vert _{\infty } \le \sigma \sqrt{n}\)
such that \( \varvec{c}_x = \varvec{a} \cdot s + \varvec{e}_1 + \varvec{a}_x \bmod q.\)
Server Proofs. The server proof in the initialisation phase denoted \( \mathbb {P} _0(k,\varvec{e} : \mathsf {crs} _0, \varvec{c}) \) has the purpose of proving knowledge of \( k \in R, \varvec{e} \in R^{1 \times \ell } \) where \(\Vert k\Vert _{\infty }\), \(\Vert \varvec{e}\Vert _{\infty } \le \sigma \cdot \sqrt{n}\) such that \(\varvec{c} = \varvec{a} \cdot k + \varvec{e} \bmod q \) where \( \mathsf {crs} _0 \) contains \( \varvec{a} \).
The server proof in the query phase denoted by \( \mathbb {P} _2(k, \varvec{e}', \varvec{e} : \mathsf {crs} _2, \varvec{c}, \varvec{d}_x, \varvec{c}_x, \varvec{a}) \) has the purpose of proving that there is some
-
\( k \in R \) where \( \Vert k\Vert _{\infty } \le \sigma \cdot \sqrt{n} \)
-
\( \varvec{e} \in R^{1 \times \ell } \) where \( \Vert \varvec{e}\Vert _{\infty } \le \sigma \cdot \sqrt{n} \)
-
\( \varvec{e}' \in R^{1 \times \ell } \) where \( \Vert \varvec{e}'\Vert _{\infty } \le \sigma ' \cdot \sqrt{n} \)
such that
It is important to note that both \( \varvec{c} \) and \( \varvec{d}_x \) each consist of \( \ell \) ring elements. Therefore, the above system consists of a total of \( 2\ell \) noisy products of public ring elements and k. Note that the well-definedness of normal form RLWE (where the secret is drawn from the error distribution) implies that the witnesses used by the prover in \( \pi _0 \) and \( \pi _2 \) share the same value k.
3.2 Optimisations
Removing \( \mathbb {P} _{\mathbf {0}}\) using Trapdoors. The main purpose of proof system 0 is to allow the security proof to extract k and forward it on to the functionality. On removing this proof, if the server does not commit to its key properly, it cannot carry out the zero-knowledge proof in the Query phase, leading to a protocol where no evaluations are given to clients. An alternative to the server’s NIZKAoK in the Init-S phase, the proof could extract k via trapdoors. Using the methods of Micciancio and Peikert [41], one can sample a trapdoored \( \varvec{a} \in R_q^{m} \) for \( m = \mathcal {O}( \ell ) \) that is indistinguishable from uniform where the trapdoor permits efficient inversion of the function \( g_{\varvec{a}}(k,\varvec{e}) = \varvec{a}\cdot k + \varvec{e} \) for small \( \varvec{e} \). Therefore, the malicious server security proof could extract k in the Init-S phase by using a trapdoored \( \varvec{a} \) along with the inversion algorithm. For clarity and simplicity, we do not incorporate these ideas directly into our protocol.
Truncating the PRF. Although the protocol in Fig. 2 is concerned with the evaluation of the full BP14 PRF, we may consider a truncated version of the PRF to improve efficiency. In particular, the BP14 PRF is evaluated as \( F_k(x):= \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \in R_p^{1 \times \ell } \) but we could easily truncate particular quantities in our protocol to consider the PRF \( F'_k(x) := \left\lfloor {a_x \cdot k} \right\rceil _{p} \) where \( a_x \) is the ring element appearing in the first entry of \( \varvec{a}_x \). The relevant values that are truncated from \( \ell \) ring elements to a single ring element from our protocol are \( \varvec{c}, \varvec{a}_x, \varvec{c}_x, \varvec{d}_x, \varvec{y}_x \). Ignoring the zero-knowledge elements of the protocol, this saves us a factor of \( \ell \). However, computation of the full \( \varvec{a}_x \) must still be performed by the client in order to calculate the truncated value. Additionally, the computation of \( \varvec{a}_x \) will still need to be considered by the client’s zero-knowledge proof. As we will see in Sect. 4, the computation of \( \varvec{a}_x \) is the main source of inefficiency in the zero-knowledge proofs and our overall protocol. Therefore, we do not trivially save a factor of \( \ell \) in computation time and zero-knowledge proof size by using a truncated BP14 PRF.
Batching Queries. We can save on the cost of zero-knowledge proof of the server in the Query phase by batching VOPRF queries. When the client sends a single value \( \varvec{c}_{x} \), the server proves that \( \varvec{c} \) and \( \varvec{c}_{x} \) are computed with respect to the same k. If the client sends N individual queries, the server proves that \( \varvec{c} \) and \( \varvec{c}_{x_1} \) are with respect to the same k and then independently proves that \( \varvec{c} \) and \( \varvec{c}_{x_2} \) are with respect to the same k and so on. Instead, the server could simply prove that \( \varvec{c}, \varvec{c}_{x_1}, \dots , \varvec{c}_{x_{N}} \) are all with respect to the same k in one shot, saving an additive term of \( \mathcal {O}(N\cdot \ell ) \) in communication over N different VOPRF evaluations (although the overall complexity of the communication does not change asymptotically).
Cut-and-Choose. Another way in which we can improve efficiency (from the server’s perspective) is to remove some of the zero-knowledge proofs using a cut-and-choose methodology. In particular, we can remove the need for the zero-knowledge proof from the server in the Query phase as follows. Firstly, in the Init-S phase, we make the server publish (for small k) the value \( \varvec{y} := \left\lfloor {\varvec{a}_{x'} \cdot k} \right\rceil _{p} \) for some fixed \(x'\) in addition to the value \( \varvec{a} \cdot k + \varvec{e} \) as well as a zero-knowledge proof attesting to the correct computation of these values for small k. The next change comes in the client message in the Query phase. Instead of sending a single pair \( (\varvec{c}_{x}, \pi _1) \), the client chooses a uniform subset X of \( \{1,\dots ,N\} \) of size K. The client then sends N values \( (\varvec{c}_{x_1}, \dots , \varvec{c}_{x_N}) \) where for all \( j \in X \), \( x_j= x' \) and for all \( j' \notin X \), \( x_{j'}=x \) for some x chosen by the client and a NIZKAoK attesting to this computation. The server then computes \( \varvec{d}_{x_1}, \dots , \varvec{d}_{x_N} \) as it does in Fig. 2 using \( \varvec{c}_{x_1}, \dots ,\varvec{c}_{x_N} \) respectively. Next, the client processes each \( \varvec{d}_{x_i} \) individually to compute the values \( \varvec{y}_{x_1} \dots \varvec{y}_{x_N} \) as in the plain protocol. Finally, the client aborts if any of the following hold:
-
there exists a \( j^* \in X \) such that \( \varvec{y}_{x_{j^*}} \ne \varvec{y} \)
-
\( \varvec{y}_{x_{j'}} \) are not all equal for \( j' \notin X \)
-
\( \varvec{y}_{x_{j'}}=\varvec{y} \) for all \( j' \notin X \) (see explanation below)
Otherwise, the client accepts \( \varvec{y}_x = \varvec{y}_{x_{j'}} \) for any \( j' \notin X \) as the evaluation at x. The client now must create N proofs for the most complex statements. On the other hand, the server does not need to create any proofs whatsoever in the online phase. The only way for the server to cheat now is to somehow guess the \( N-K \) transcripts containing input x which can be done with probability at most
 . Thus, the computational burden is mostly shifted to the client, which might be desirable in some settings.
. Thus, the computational burden is mostly shifted to the client, which might be desirable in some settings.
On close inspection, there is a slight problem with the cut-and-choose optimisation described above. The issue is that a client might ask for an evaluation on input x such that \(\left\lfloor {\varvec{a}_{x} \cdot k} \right\rceil _{p} = \left\lfloor {\varvec{a}_{x'} \cdot k} \right\rceil _{p} \) in which case the third condition causes an abort, even though the client obtained the correct evaluation. One way to get around this is to redefine the PRF slightly so that such collisions only occur with negligible probability. For example, for \( L-1 \) bit inputs \( x \in \{0,1\}^{L-1} \), suppose we use the alternative PRF \( F'_k(x):= \left\lfloor {\varvec{a}_{0\Vert x} \cdot k} \right\rceil _{p} \). Since we can rewrite \( \varvec{a}_{0\Vert x} \cdot k = \varvec{a}_0 \cdot \varvec{Z}_{x,k} \) where \( \varvec{Z}_{x,k} \) has small entries as long as k is short. Then a collision in this PRF must lead to an equation \( \varvec{a}_0 \cdot (\varvec{Z}_{x,k}-\varvec{Z}_{x',k}) = \varvec{u} \bmod q \) where \( \Vert \varvec{u}\Vert _{\infty } \le q/p \). Rearranging, this equation becomes \( [1 | \varvec{a}_0] \cdot \begin{bmatrix} \varvec{u} \\ (\varvec{Z}_{x,k}-\varvec{Z}_{x',k}) \end{bmatrix} = \varvec{0} \bmod q \) which means that such a collision would imply a solution to a ring-SIS problem with respect to \( [1| \varvec{a}] \) (in Hermite normal form). Therefore, for fixed x and any short k, it is unlikely that a collision in this alternative PRF will occur under some SIS assumption.
3.3 Correctness
Before proving correctness, we present a lemma that we will apply below. The proof of this lemma is in the full version of this work.
Lemma 5
Fix any \(x \in \{ 0,1 \}^{L}\). Suppose there exists a PPT algorithm \(\mathcal {D}_x(\varvec{a}_0, \varvec{a}_1)\) that outputs \( r \in R \) such that \( \Vert r\Vert _{\infty } \le B \) and at least one coefficient of \( \varvec{a}_x \cdot r \) is in the set \( (q/p) \cdot \mathbb {Z}+ [-T, T] \) with non-negligible probability (over a uniform choice of
 and its random coins). Then there exists an efficient algorithm solving \( \mathsf {1D\text {-}SIS}_{q/p,n \ell ,\max \{n \ell B, T\}} \) with non-negligible probability.
and its random coins). Then there exists an efficient algorithm solving \( \mathsf {1D\text {-}SIS}_{q/p,n \ell ,\max \{n \ell B, T\}} \) with non-negligible probability.
Lemma 6
(Correctness). Adopt the notation of Fig. 2, assuming an honest client and server. Define \( T := 2\,\sigma ^2\, n^2 + \sigma '\sqrt{n} \). For any \( x \in \{0,1\}^L, k \in R_q \) such that \( \Vert k\Vert _{\infty } \le \sigma \cdot \sqrt{n} \), we have that

over the choice of PRF parameters
 assuming the hardness of \( \mathsf {1D\text {-}SIS}_{q/p,n \ell ,T} \).
assuming the hardness of \( \mathsf {1D\text {-}SIS}_{q/p,n \ell ,T} \).
Proof
Fix an arbitrary x. Assume there exists a \( k' \) such that \( \Vert k'\Vert \le \sigma \cdot \sqrt{n} \) where \( \Pr [\varvec{y}_x \ne F_{k'}(x)] \) is non-negligible over the choice of
 . Expanding \( \varvec{c} \) and \( \varvec{d}_x \) from the protocol, we have that
. Expanding \( \varvec{c} \) and \( \varvec{d}_x \) from the protocol, we have that
Note that \( \varvec{e}'' := \varvec{e}_1 \cdot k' - \varvec{e} \cdot s + \varvec{e}' \) has infinity norm less than T as defined in the lemma statement with all but negligible probability. It follows that there must be at least one coefficient of \( \varvec{a}_x \cdot k' \) in the set \( (q/p) \cdot \mathbb {Z}+ [T,T] \) with non-negligible probability, otherwise \( \varvec{y}_x = \left\lfloor {\varvec{a}_x \cdot k'} \right\rceil _{p}=:F_{k'}(x) \). Applying Lemma 5 to the algorithm \( \mathcal {D}_x(\varvec{a}_0,\varvec{a}_1) \) that ignores \( \varvec{a}_0, \varvec{a}_1 \) and simply outputs \( k' \) implies an efficient algorithm solving \( \mathsf {1D\text {-}SIS}_{q/p,n \ell ,\max \{n^{3/2} \ell \sigma ,T\}} \). \(\square \)
The remainder of the security proof can be found in Sect. 5.
4 Lattice-Based NIZKAoK Instantiations
We now describe various instantiations of our zero-knowledge arguments of knowledge. Note that we use the Fiat-Shamir transform (on parallel repetitions) to obtain non-interactive proofs. We recall that the Fiat-Shamir transform has recently been shown to be secure in the QROM [22, 37] in certain settings. We place most of our attention on discussing how to instantiate Proof System 1, as the other proof systems may be derived straight-forwardly using a subset of the techniques arising in Proof System 1. For more precise details on how to instantiate Proof System 1 using the protocol of Yang et al. [47], see the full version of this work. Alternatively, one could use the same techniques as in [36] to represent the statement of interest in Proof System 1 as a permuted kernel problem and use the recent protocol of Beullens [7]. The advantage of doing so would be that the protocol of Beullens has been shown to be compatible with the aforementioned security results of the Fiat-Shamir transform in the QROM.
Note that the argument system of Yang et al. requires the modulus q to be a prime power. In contrast, 1D-SIS is known to be at least as hard as standard lattice problems when q has many large coprime factors [15]. In order to justify the use of a prime power modulus along with the use of the 1D-SIS assumption, we apply two minor lemmas given in the full version of this work. Alternatively, if one wished to use a highly composite modulus, then a Stern-based protocol such as in [35, 36] or the more efficient recent protocol of Beullens [7] may still be used. Nonetheless, all of the aforementioned argument systems involve rewriting PRF evaluations as a large system of linear equations. In our context, applying the argument system of Yang is slightly simpler. Additionally, a single execution of the protocol of Yang et al. achieves a soundness error of \( 2/(2\bar{p}+1) \) for some polynomial \( \bar{p} \) much less than q. This is similar to the soundness error encountered in the Beullens protocol, but significantly improves on the soundness of Stern-based protocols. Therefore, roughly \( \kappa /\log \bar{p} \) repetitions are required to reach a \( 2^{-\kappa } \) soundness error when using either of the protocol of Yang et al. or Beullens protocols.
Proof System 0: Small Secret RLWE Sample. Let \( A \in \mathbb {Z}_q^{n\ell \times n} \) be the vertical concatenation of the negacyclic matrices associated to multiplication by the ring elements of \( \varvec{a} \in R_q^{1 \times \ell } \) respectively. Further, let  be the vertical concatenation of coefficient vectors of ring elements in \( \varvec{c} \in R_q^{1 \times \ell } \) respectively. The first proof aims to prove in zero knowledge, knowledge of a short solution
be the vertical concatenation of coefficient vectors of ring elements in \( \varvec{c} \in R_q^{1 \times \ell } \) respectively. The first proof aims to prove in zero knowledge, knowledge of a short solution  , where
, where  to the system
to the system

This is an inhomogeneous SIS problem, so the zero-knowledge proof may be instantiated using either the protocol of Yang et al. or Beullens. Additionally, for this proof system, we may also use the protocol from [12]. All of these options avoid the so-called soundness gap seen in many lattice-based proof systems (e.g. [38, 39]) although the efficient protocol in [39] has been shown to be secure in the QROM when the Fiat-Shamir transform is applied [37]. Therefore, for simplicity and neatness we prefer to consider these systems when writing the security proof for our VOPRF although one may use the more efficient protocol of [39] in practice.
Proof System 1: Proofs of Masked Partial PRF Computation. This proof system aims to prove that for a known \( \varvec{a} \) and \( \varvec{c} \), the prover knows short s and \( \varvec{e} \) along with a bit-string x such that \( \varvec{c} = \varvec{a} \cdot s + \varvec{e} + \varvec{a}_x \) where \( \varvec{a}_x \) is part of the BP14 PRF evaluation. At a high level, we will run the protocol of Yang et al. [47] \(\mathcal {O}(\kappa /\log \bar{p})\) times (for some
 ) in parallel and apply the Fiat-Shamir heuristic. We focus on this instantiation for simplicity. We do not actually concretely present any ZKAoK protocol in this work, but we do highlight the reduction in the full version of this work showing that we may use the protocol of Yang et al. Similar methods (e.g. the decomposition-extension framework used by[36]) can be used to prove compatibility with the protocol of Beullens. Let \( P_n \) represent the power set of \( \{1,\dots ,n\}^3 \). The protocol of Yang et al. is a ZKAoK for the instance-witness set given by
) in parallel and apply the Fiat-Shamir heuristic. We focus on this instantiation for simplicity. We do not actually concretely present any ZKAoK protocol in this work, but we do highlight the reduction in the full version of this work showing that we may use the protocol of Yang et al. Similar methods (e.g. the decomposition-extension framework used by[36]) can be used to prove compatibility with the protocol of Beullens. Let \( P_n \) represent the power set of \( \{1,\dots ,n\}^3 \). The protocol of Yang et al. is a ZKAoK for the instance-witness set given by

Therefore, in order to show that we may use the protocol, we simply reduce our statement of interest to an instance  . Then, the protocol of Yang et al. allows to argue knowledge of a witness
. Then, the protocol of Yang et al. allows to argue knowledge of a witness  such that
such that  . Details on reducing statements of the relevant form to instances in \( \mathcal {R}^* \) are given in the full version of this work, but a high level overview follows.
. Details on reducing statements of the relevant form to instances in \( \mathcal {R}^* \) are given in the full version of this work, but a high level overview follows.
First note that we can compute \( \varvec{a}_x \) recursively (similarly to [36]) by setting variables \( B_i \in R_q^{\ell \times \ell } \) for \( i= L-1, \dots , 0 \) via \( B_{L-1} = G^{-1}(\varvec{a}_{x_{L-1}}) \), and \( B_i = G^{-1}(\varvec{a}_{x_{i}} \cdot B_{i+1}) \) for \( i =L-2, \dots , 0 \). Using this, we have \( \varvec{a}_x = G \cdot B_0 \). We can therefore use the system \( G \cdot B_i =\varvec{a}_{x_{i}} \cdot B_{i-1} \) to facilitate computation of \( \varvec{a}_x \) along with the linear equation \( \varvec{c} = \varvec{a} \cdot s +\varvec{e}_1 + G \cdot B_0 \) to completely describe the statement being proved. However, the resulting system is over ring elements and is not linear in unknowns. To solve these issues, we simply replace ring multiplication by integer matrix-vector products and then linearise the resulting system (which places quadratic constraints amongst the entries of the solution). We also make use of binary decompositions to bound the infinity norms of valid solutions and ensure that necessary entries are in \( \{0,1\} \) via quadratic constraintsFootnote 5.
Proof System 2: Proofs of Secret Equivalence. Recall that we wish to prove existence of a solution to Eq. (1). Note that \( \varvec{d}_x \) from the protocol in Sect. 3 are vectors holding \( \ell \) ring elements. Therefore, Eq. (1) can be expressed as a system
where \( {\Vert {e_i}\Vert }_\infty , {\Vert {k}\Vert }_\infty \le \sigma \cdot \sqrt{n} \), \( {\Vert {e_i'}\Vert }_\infty \le \sigma '\cdot \sqrt{n} \). We can conceptualise the above as a large linear system  where
where  is the concatenation of coefficient vectors of \( k,e_1, \dots , e_{\ell }, e'_1, \dots ,e'_\ell \) and
is the concatenation of coefficient vectors of \( k,e_1, \dots , e_{\ell }, e'_1, \dots ,e'_\ell \) and  is the concatenation of the coefficient vectors of \( c_1, \dots , c_{\ell }, (d_x)_1, \dots ,(d_x)_{\ell } \). Using this interpretation, we may instantiate this proof system using the same methods as in Proof System 0.
is the concatenation of the coefficient vectors of \( c_1, \dots , c_{\ell }, (d_x)_1, \dots ,(d_x)_{\ell } \). Using this interpretation, we may instantiate this proof system using the same methods as in Proof System 0.
5 Security Proof
In this section, we show that the protocol in Fig. 2 is a VOPRF achieving security against malicious adversaries. In particular, corrupted clients and servers that attempt to subvert the protocol learn/affect only as much as in an ideal world, where they interact via the functionality \(\mathcal {F}_\mathsf {VOPRF}\).
Theorem 2
(Security) Assume p|q. The protocol in Fig. 2 is a secure VOPRF protocol (according to Definition 1) if the following conditions hold:
-
\( \forall i \in \{0,1,2\}, (\mathbb {P} _i,\mathbb {V} _i) \) is a NIZKAoK
-
\( \mathsf {dRLWE}_{q,n,\sigma } \) is hard,
-
\( \frac{q}{2p} \gg \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2 n^2 \} \),
-
\( \mathsf {1D\text {-}SIS}_{q/(2p),n \cdot \ell ,\max \{ \ell \cdot \sigma n^{3/2}, 2 \sigma ^2 n^2 + \sigma '\sqrt{n} \}} \) is hard.
Note that correctness of our protocol with respect to honest clients and servers is shown in Sect. 3.3. Therefore, what remains is to show average malicious client security and malicious server security.
Correctness of Non-aborting Malicious Protocol Runs. During the malicious client proof, it will be useful to call on the fact that a non-aborting protocol transcript enables computation of \( F_k(x) \) with overwhelming probability:
Lemma 7
Assume that \( \mathsf {dRLWE}_{q,n,\sigma } \) is hard, \( \sigma \) and n are
 , and \( \frac{q}{2p} \gg \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2n^2\} \). For any \( x \in \{0,1\}^L \), consider a non-aborting run of the protocol in Fig. 2 between a (potentially malicious) efficient client \( \mathbb {C}^* \) and honest server \( \mathbb {S} \). Further, let s be the value that is extractable from the client’s proof in the query phase. Then, the value of \( \left\lfloor {\varvec{d}_x - \varvec{c} \cdot s} \right\rceil _{p} \) is equal to \( \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \) with all but negligible probability.
, and \( \frac{q}{2p} \gg \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2n^2\} \). For any \( x \in \{0,1\}^L \), consider a non-aborting run of the protocol in Fig. 2 between a (potentially malicious) efficient client \( \mathbb {C}^* \) and honest server \( \mathbb {S} \). Further, let s be the value that is extractable from the client’s proof in the query phase. Then, the value of \( \left\lfloor {\varvec{d}_x - \varvec{c} \cdot s} \right\rceil _{p} \) is equal to \( \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \) with all but negligible probability.
Proof
We use the notation from Fig. 2. First note that for a non-aborting protocol run, any efficient client \( \mathbb {C}^* \) must have produced \( \varvec{c}_x \) correctly using some \( x \in \{0,1\}^L, s, \varvec{e}_1 \) where \( \Vert s\Vert _{\infty }, \Vert \varvec{e}_1\Vert _{\infty } \le \sigma \cdot \sqrt{n} \). Suppose that
 . We now use the fact that if \( \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2n^2\} \), then
. We now use the fact that if \( \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2n^2\} \), then
 and \( (\varvec{e}_x-\varvec{e}_1 \cdot k-\varvec{e} \cdot s)+ \varvec{e}' \) are statistically close which follows from Lemmas 4 and 2. Therefore, replacing \( \varvec{e}' \) by \( (\varvec{e}_x-\varvec{e}_1 \cdot k-\varvec{e} \cdot s)+ \varvec{e}' \) and noting that \( \varvec{c}_x \) must be well-formed due to the NIZKAoK, the client output equation in Fig. 2 can be written as
and \( (\varvec{e}_x-\varvec{e}_1 \cdot k-\varvec{e} \cdot s)+ \varvec{e}' \) are statistically close which follows from Lemmas 4 and 2. Therefore, replacing \( \varvec{e}' \) by \( (\varvec{e}_x-\varvec{e}_1 \cdot k-\varvec{e} \cdot s)+ \varvec{e}' \) and noting that \( \varvec{c}_x \) must be well-formed due to the NIZKAoK, the client output equation in Fig. 2 can be written as
To complete the proof, we will use the fact that \( \frac{p}{q}(\varvec{a}_x \cdot k + \varvec{e}_x) \) is computationally indistinguishable from uniform random over \( \frac{p}{q}R_q^{1 \times \ell } \) when \( \varvec{e}_x \leftarrow \mathcal {E}_{a_0,a_1,x, \sigma } \) assuming the hardness of \(\mathsf {dRLWE}_{q,n,\sigma }\) (Lemma 3). This implies that every coefficient in \( \frac{p}{q}(\varvec{a}_x k + \varvec{e}_x) \) is at least T away from \( \mathbb {Z}+1/2 \) with all but negligible probability for any \( T \ll 1 \). Setting \( T = \frac{p}{q}\left( \sigma ' \cdot \sqrt{n} + L \cdot \ell \cdot \sigma n^{3/2} \right) \ll 1 \) ensures that \( T \le \frac{p}{q} \cdot \Vert \varvec{e}_x + \varvec{e}'\Vert _{\infty } \) with all but negligible probability. It then follows that
as required. \(\square \)
5.1 Malicious Client Proof
Lemma 8
(Average-case malicious client security). Assume that \( \sigma \) and n are
 , and p|q, and let conditions (i) and (ii) be as follows:
, and p|q, and let conditions (i) and (ii) be as follows:
-
(i)
\( \mathsf {dRLWE}_{q,n,\sigma } \) is hard,
-
(ii)
\( \frac{q}{2p} \gg \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2 n^2 \} \).
If the above conditions hold and \( (\mathbb {P} _1,\mathbb {V} _1) \) is a NIZKAoK, then the protocol in Fig. 2 has average-case security against malicious clients according to Definition 1.
Proof
We describe a simulation \(\mathcal {S}\) that communicates with the functionality \( \mathcal {F}_\mathsf {VOPRF}\) (environment) on one hand, and the malicious client \( \mathbb {C}^* \) on the other. \( \mathcal {S}\) carries out the following steps:
-
1.
During CRS SetUp, publish honest \( \varvec{a}, \varvec{a}_0, \varvec{a}_1,\mathsf {crs} _1\) and (dishonest) simulated versions of \( \mathsf {crs} _0 \) and \(\mathsf {crs} _2 \). Denote the simulated CRS elements \( \mathsf {crs} _0' \) and \( \mathsf {crs} '_{2} \).
-
2.
Pass the \( \mathsf {init}\) message onto \( \mathcal {F}_\mathsf {VOPRF}\), then send \( \mathbb {C}^* \) a uniform
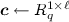 with a simulated proof \( \pi _{0,\mathsf {Sim}} \). Initialise an empty list \( \mathsf {received}\).
with a simulated proof \( \pi _{0,\mathsf {Sim}} \). Initialise an empty list \( \mathsf {received}\). -
3.
During the Query stage, for each message \( (\varvec{c}_x, \pi _1) \) from \( \mathbb {C}^* \), do:
-
(a)
\(b \leftarrow \mathbb {V} _1(\mathsf {crs} _1, \varvec{c}_x, \varvec{a}, \varvec{a}_0, \varvec{a}_1, \pi _1)\). If \(b=0\) send \(\mathsf {abort}\) to the functionality and abort the protocol with the malicious client. If \(b=1\) continue.
-
(b)
Extract the values \(x,s,\varvec{e}_1\) from \(\pi _1\) using the ZKAoK extractor and send \((\mathsf {query}, x)\) to the functionality.
-
(c)
-
If \( \mathcal {F}_\mathsf {VOPRF}\) aborts:
\( \mathcal {S}\) aborts.
-
If \( \mathcal {F}_\mathsf {VOPRF}\) returns \( \varvec{y} \in R_{p}^{1 \times \ell } \mathbf{and} \forall \varvec{y}^*, (x,\varvec{y}^*) \notin \mathsf {received} \):
(i.e. if this is the first time x is queried) uniformly sample

and do \( \mathsf {received.add}(x,\varvec{y}_q).\)
-
If \( \mathcal {F}_\mathsf {VOPRF}\) returns \( \varvec{y} \in R_{p}^{\ell } \mathbf{and} \exists \varvec{y}^* \text {s.t.} (x,\varvec{y}^*) \in \mathsf {received} \): (i.e. x was previously queried) Then set \( \varvec{y}_q = \varvec{y}^* \).
-
-
(d)
Next pick \( \bar{\varvec{e}}' \leftarrow \chi _{\sigma '} \) and set
$$\begin{aligned} \bar{\varvec{d}}_x = \varvec{c} \cdot s + \bar{\varvec{e}}' + \varvec{y}_q \bmod q. \end{aligned}$$Finally, produce a simulated proof \(\pi _{2,\mathsf {Sim}}\) using \( \mathsf {crs} '_2 \) and send \((\bar{\varvec{d}}_x\), \(\pi _{2,\mathsf {Sim}})\) to \( \mathbb {C}^* \).
-
(a)
We now argue that \( \mathbb {C}^* \) cannot decide whether it is interacting with \(\mathcal {S}\) or with a genuine server. Firstly, recognise that \( (\mathsf {crs} _0', \mathsf {crs} '_2) \) is indistinguishable from honestly created \( (\mathsf {crs} _0, \mathsf {crs} _2) \). Secondly, the malicious client cannot distinguish the simulator’s uniform \(\varvec{c}\) sent during the Init phase from the real protocol by the \(\mathsf {dRLWE}_{q,n,\sigma }\) assumption (condition (i)). This implies that both the CRS SetUp and Init phases that \( \mathcal {S}\) performs are indistinguishable from the real protocol.
The most challenging step is arguing that the simulator’s behaviour in the Query phase is indistinguishable from the real protocol from the malicious client’s point of view. We will analyse the behaviour of the simulator assuming that no abort is triggered. We begin by arguing that the server message \( \varvec{d}_x \) in the real protocol with respect to any triple \((x,s,\varvec{e}_1)\) can be replaced by a related message \( \varvec{c}\cdot s + \varvec{a}_x \cdot k + \varvec{e}_{x} + \varvec{e}'''\) where \( \varvec{e}_{x} \leftarrow \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x,\sigma } \) and \( \varvec{e}''' \leftarrow R(\chi _{\sigma '})^{1 \times \ell } \) without detection by the following statistical argument. We have that the server response in the real protocol has \(\varvec{d}_x\) of the form
where \( \varvec{e}' \leftarrow R(\chi _{\sigma '})^{1 \times \ell } \). By Lemma 2, the message distribution in Eq. (2) is statistically indistinguishable from
where \( \varvec{e}'' \leftarrow R(\chi _{\sigma '})^{1 \times \ell } \) due to the fact that \( \sigma ' \gg \sigma ^2 n^2 \). By a similar argument along with Lemma 4, the quantity given in Equation (3) is statistically close in distribution to
where \( \varvec{e}_{x} \leftarrow \mathcal {E}_{\varvec{a}_0,\varvec{a}_1,x,\sigma } \) and \( \varvec{e}''' \leftarrow R(\chi _{\sigma '})^{1 \times \ell } \). Next, using Lemma 3 and condition (i), we have that the bracketed term in Equation (4) is indistinguishable from random over \( R_q^{1 \times \ell } \) by the hardness of \(\mathsf {dRLWE}_{q,n,\sigma } \) (Lemma 3). In particular, from an efficient \( \mathbb {C}^* \)’s point of view, \( \varvec{d}_x \) cannot be distinguished from
Note that on repeated queries, the errors sampled from \( R(\chi _{\sigma '})^{1 \times \ell } \) are fresh. The fact that \( \mathcal {S}\) samples \( \varvec{y}_q \) as a uniformly chosen element of a uniformly chosen interval implies the indistinguishability part of average-case malicious client security.
Next, we show that if the malicious client does indeed compute the correct value from the messages it receives from the honest server (in the real protocol), then it can do the same with the messages that it receives from the simulator. In Lemma 7, we show that a malicious client which does not cause an abort can compute \( \left\lfloor {\varvec{a}_x \cdot k} \right\rceil _{p} \) from the messages it receives from the honest server with all but negligible probability. We now show that this is also the case with the messages it receives from \( \mathcal {S}\). Consider \( \varvec{y}_q \) sampled by \( \mathcal {S}\) and also the corresponding value \( \bar{\varvec{d}}_x \). In addition, define \( \varvec{e}_{\left\lfloor {} \right\rceil _{}}:= \varvec{y}_q - (q/p) \cdot \varvec{y} \in R_{\le \frac{q}{2p}}^{1 \times \ell } \) so that \( \varvec{e}_{\left\lfloor {} \right\rceil _{}} \) follows the uniform distribution over \(R_{\le \frac{q}{2p}}^{1 \times \ell } \). We have that
We also know that with all but negligible probability, \( \Vert \bar{\varvec{e}}'\Vert _{\infty } \le \sigma ' \sqrt{n} \), and that \( \Vert \varvec{e}_{\left\lfloor {} \right\rceil _{}}\Vert _{\infty } \) is less than \( q/(2p)- T \) with all but negligible probability as long as \( T \ll (q/2p) \). Taking \( T = \sigma '\sqrt{n} \), we get that with all but negligible probability,
implying that the quantity in Equation (5) rounds correctly to \( \varvec{y} \) with all but negligible probability. Therefore, both the real protocol and simulator enable correct evaluation of the PRF. \(\square \)
5.2 Malicious Server Proof
Lemma 9
Let conditions (i) and (ii) be as follows:
-
(i)
\( \mathsf {dRLWE}_{q,n,\sigma } \) is hard,
-
(ii)
\( \mathsf {1D\text {-}SIS}_{q/(2p),n \cdot \ell ,\max \{ \ell \cdot \sigma n^{3/2}, 2 \sigma ^2 n^2 + \sigma '\sqrt{n} \}} \) is hard.
If the above conditions hold and \( (\mathbb {P} _0, \mathbb {V} _0) \) and \( (\mathbb {P} _2,\mathbb {V} _2) \) are both NIZKAoKs, then the protocol in Fig. 2 is secure in the presence of malicious servers.
Proof
We construct a simulator \(\mathcal {S}\) interacting with the malicious server \(\mathbb {S} ^*\) on one hand and with the functionality \(\mathcal {F}_\mathsf {VOPRF}\) on the other. The simulator \(\mathcal {S}\) behaves as follows:
-
1.
During the CRS.SetUp phase, publish honest \( \varvec{a}, \varvec{a}_0, \varvec{a}_1, \mathsf {crs} _0, \mathsf {crs} _2 \) and (dishonest) simulated \( \mathsf {crs} '_{1} \) to use with the proof systems.
-
2.
During the Init-C phase, if \(\mathbb {S} ^*\) sends \(\varvec{c}\in R_q^{1 \times \ell }\) and an accepting proof \( \pi _0 \), then use the zero knowledge extractor to obtain a key \( k' \) from \( \pi _0 \) and forward this on to the functionality. If the message is not of the correct format, or the proof does not verify, then abort.
-
3.
During the Query phase, select a uniform random value \(\varvec{u} \leftarrow R^{1 \times \ell }_q\), and using the ZK simulator, produce a simulated proof \( \pi _{1,\mathsf {Sim}} \) using \( \mathsf {crs} '_1 \). Send the message \( (\varvec{u}, \pi _{1,\mathsf {Sim}}) \). Wait for a response of the form \( (\widetilde{\varvec{d}}_x, \widetilde{\pi }_2)\) from \(\mathbb {S} ^*\). If the proof \(\widetilde{\pi }_2\) verifies, forward on \(\mathsf {deliver}\) to \(\mathcal {F}_\mathsf {VOPRF}\). Otherwise, forward \(\mathsf {abort}\) to \(\mathcal {F}_\mathsf {VOPRF}\).
We will show that the joint output of an honest client \( \mathbb {C}\) and \( \mathbb {S} ^* \) in the real world (where they interact directly) and the ideal world (where they interact via \(\mathcal {F}_\mathsf {VOPRF}\) and \( \mathcal {S}\)) are computationally indistinguishable. We begin by arguing that the malicious server \(\mathbb {S} ^*\) cannot distinguish whether it is interacting with a real client or \(\mathcal {S}\), as described above. Firstly, replacing \(\mathsf {crs} _1\) by \( \mathsf {crs} '_1\) is indistinguishable from the point of view of \(\mathbb {S} ^*\) by definition of a simulated CRS. Importantly, if \( \mathbb {S} ^* \) can produce valid proofs in the Init phase, the key \( k' \) obtained by the simulator is the unique ring element consistent with c (see the full version of this work for more details).
All that is left to consider is the Query phase. Note that in the real protocol, the client produces \(\varvec{c}_x\) which takes the form of a RLWE sample offset by some independent value. This implies that the value \( \varvec{c}_x \) is pseudorandom under the hardness of \(\mathsf {dRLWE}_{q,n,\sigma } \). Therefore, the malicious server \(\mathbb {S} ^*\) cannot distinguish a real \(\varvec{c}_x\) from the pair \(\varvec{u}\) that \(\mathcal {S}\) uses. By the properties of a ZK simulator, it follows that a real client message \( (\varvec{c}_x, \pi _1) \) and \( \mathsf {crs} _1 \) is indistinguishable from \((\varvec{u}, \pi _{1,\mathsf {Sim}})\) and \( \mathsf {crs} _1' \). Next, if the response from \(\mathbb {S} ^*\) has a valid proof, then \(\mathcal {S}\) forwards on \(\mathsf {deliver}\). This means that the ideal functionality passes a PRF evaluation to the client using the server key \(k'\). We now argue that this emulates the output on the client side when running the real protocol with malicious server \( \mathbb {S} ^* \).
The case where the proof verification fails is trivial since the client aborts in the real and ideal worlds. As a result, we focus on the case where the zero knowledge proof produced by \( \mathbb {S} ^* \) verifies correctly. Let \({s} \leftarrow R(\chi _{\sigma })\) and \( \varvec{e}_1 \leftarrow R(\chi _{\sigma })^{1\times \ell } \) be sampled by the honest client. For this honest client interacting with malicious \( \mathbb {S} ^* \) in the real protocol, observe that
for \( k', \varvec{e}' \) chosen by \( \mathbb {S} ^* \) where \( \Vert k'\Vert _{\infty } \le \sigma \cdot \sqrt{n} \) and \( \Vert \varvec{e}'\Vert _{\infty }\le \sigma ' \cdot \sqrt{n} \). Therefore, rounding the quantity in Eq. (6) is guaranteed to result in the correct value if every coefficient of \( \frac{p}{q} \cdot \varvec{a}_x \cdot k' \) is further than
away from \( \mathbb {Z}+ 1/2 \). In other words if \( \mathbb {S} ^* \) can force incorrect evaluation, it has found \( k' \le \sigma \cdot \sqrt{n} \) such that a coefficient of \( \varvec{a}_x \cdot k' \) is within a distance
of \( \frac{q}{p} \mathbb {Z}+ \frac{q}{2p} \subset \frac{q}{2p} \mathbb {Z}\). We now apply Lemma 5 with \( 2\cdot p\), \(T=2 \sigma ^2 n^2 + \sigma '\sqrt{n} \) to show that \( \mathbb {S} ^* \) forcing incorrect evaluation with non-negligible probability violates the assumption that \( \mathsf {1D\text {-}SIS}_{q/2p,n \cdot \ell ,\max \{ \ell \cdot \sigma n^{3/2}, 2 \sigma ^2 n^2 + \sigma '\sqrt{n} \}} \) is hard. Therefore, condition (ii) enforces correct evaluation. \(\square \)
5.3 Setting Parameters
Let \( \kappa \) be the security parameter. Ignoring the NIZKAoK requirements for simplicity, Theorem 2 requires the following conditions:
-
\( \mathsf {dRLWE}_{q,n,\sigma } \) is hard,
-
\( \frac{q}{2p} \gg \sigma ' \gg \max \{L \cdot \ell \cdot \sigma n^{3/2}, \sigma ^2 n^2 \} \),
-
\( \mathsf {1D\text {-}SIS}_{q/(2p),n \cdot \ell ,\max \{ \ell \cdot \sigma n^{3/2}, 2 \sigma ^2\, n^2 + \sigma '\sqrt{n} \}} \) is hard.
We will be using the presumed hardness of \( \mathsf {SIVP}_{\gamma } \) for approximation factors \( \gamma = 2^{o(\sqrt{n})} \). The \( \mathsf {SIVP}_{\gamma } \) lattice dimension associated to RLWE will be \( n = \kappa ^c \) (for some constant \( c>2 \)); the dimension associated to 1D-SIS hardness will be \( n' = \kappa \). We first choose \(L= \kappa , \sigma = \mathsf {poly}(n) \) and \( \sigma ' = \sigma ^2 n^2 \cdot \kappa ^{\omega (1)} \), and then set \( q = p \cdot \prod _{i=1}^{n'} p_i \) by picking coprime \( p, p_1 , \dots , p_{n'} = \sigma ' \cdot \omega (\sqrt{n n' \log q \log n' }) \). Having made these choices, we argue that each of the three conditions are satisfied. We argue RLWE hardness via \( \mathsf {SIVP}_{} \) for sub-exponential approximation factors \( 2^{\widetilde{\mathcal {O}}(n^{1/c})} \) (for \( c > 2 \)), noting that \( \sigma = \mathsf {poly}(n) \) and
Now substituting in \( \ell = \log q \) implies that the second condition can be satisfied. Finally for the 1D-SIS condition, we note that \( q/p = \prod _{i=1}^{n'} p_i \) and
So we get hardness of our 1D-SIS instance via the presumed hardness of \( \mathsf {SIVP}_{} \) on \( n' \)-dimensional lattices for \( {(n')}^{\omega (1)} \cdot \mathsf {poly}(n') \) approximation factors. We summarise the parameters of our construction in Table 1.
To give a rough estimate for concrete bandwidth costs, we start by observing that we need \(q\) to be super-polynomial in \(\kappa \) for (a) PRF correctness and (b) noise drowning on the server side. We may pick \(\log q \approx 256\) for \(\kappa = 128\). Applying the “estimator” from [2] with the quantum cost model from [3] and noise standard deviation \(\sigma = 3.2\) suggests that \(n=16,384\) provides security of \(> 2^{128}\) operations (indeed, significantly more, suggesting room for fine tuning). Thus, a single RLWE sample takes about 0.5 MB. As specified in Sect. 3 our construction sends \(2\,\ell \) such samples. However, an implementation could send only two such samples (see Sect. 3.2). Thus, each party would send about 1MB of RLWE sample material. Of course, a more careful analysis and optimisation – picking parameters, analysing bounds, applying rounding, perhaps removing the need for super-polynomial drowning – would reduce this magnitude.
In addition to this, each party must send material for the zero-knowledge proofs. In the full version of this work, we show that the statement associated to the client proof may be written as an instance of \( \mathcal {R}^* \) consisting of more than \( m'=n \ell ^2 (L-1) \) equations where the witness has a dimension of more than \( n'= 4n\ell ^2(L-1) \). Additionally, there are at least \( |\mathcal {M}|:=4n \ell ^2 (L-1) \) constraints. This implies that the argument system of [47] requires the communication of at least \( m'+3n'+4|\mathcal {M}| = 9n \ell ^2 (L-1) \) integers modulo q per repetition. Using the concrete parameters laid out above, we require \(> 9 \cdot 16,384 \cdot 256^2 \cdot 127 > 2^{40}\) bits of communication per repetition. We remind the reader that choosing parameters of the ZKAoK of Yang appropriately would allow us to only repeat a small number of times and stress that this discussion gives a crude lower bound designed to give an intuition on the inefficiency of our scheme, rather than a formal analysis of the concrete cost of our scheme. We note that applying a SNARK or STARK would reduce the bandwidth requirement for proofs.
Notes
- 1.
A subsidiary of the Internet Research Task Force (IRTF).
- 2.
Note that using post-quantum secure VOPRF primitives in either the OPAQUE or Privacy Pass examples above would immediately result in PQ-secure alternatives.
- 3.
Meaning that only two messages are sent in the online (query) phase.
- 4.
Note that the output of \( \mathbb {S} (k) \) is \( \perp \) in our construction.
- 5.
Using the fact that \( x^2=x \bmod q \iff x\in \{0,1\} \) assuming q is a prime power.
References
Albrecht, M.R., Davidson, A., Deo, A., Smart, N.P.: Round-optimal verifiable oblivious pseudorandom functions from ideal lattices. Cryptology ePrint Archive, Report 2019/1271 (2019). https://eprint.iacr.org/2019/1271
Albrecht, M.R., Player, R., Scott, S.: On the concrete hardness of learning with errors. J. Math. Cryptol. 9(3), 169–203 (2015). http://www.degruyter.com/view/j/jmc.2015.9.issue-3/jmc-2015-0016/jmc-2015-0016.xml
Alkim, E., Ducas, L., Pöppelmann, T., Schwabe, P.: Post-quantum key exchange - a new hope. In: Holz, T., Savage, S. (eds.) USENIX Security 2016, pp. 327–343. USENIX Association (2016)
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Mathematische Annalen 296(1), (1993)
Banerjee, A., Peikert, C.: New and improved key-homomorphic pseudorandom functions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 353–370. Springer, Heidelberg (2014)
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012)
Beullens, W.: Sigma protocols for MQ, PKP and SIS, and Fishy signature schemes. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part III. LNCS, vol. 12107, pp. 183–211. Springer, Heidelberg (2020)
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press (1988)
Boneh, D., Dagdelen, Ö., Fischlin, M., Lehmann, A., Schaffner, C., Zhandry, M.: Random oracles in a quantum world. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 41–69. Springer, Heidelberg (2011)
Boneh, D., Kogan, D., Woo, K.: Oblivious pseudorandom functions from isogenies. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part II. LNCS, vol. 12492, pp. 520–550. Springer, Heidelberg (2020)
Boneh, D., Lewi, K., Montgomery, H.W., Raghunathan, A.: Key homomorphic PRFs and their applications. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 410–428. Springer, Heidelberg (2013)
Bootle, J., Lyubashevsky, V., Seiler, G.: Algebraic techniques for short(er) exact lattice-based zero-knowledge proofs. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 176–202. Springer, Heidelberg (2019)
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 575–584. ACM Press (2013)
Brakerski, Z., Tsabary, R., Vaikuntanathan, V., Wee, H.: Private constrained PRFs (and more) from LWE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 264–302. Springer, Heidelberg (2017)
Brakerski, Z., Vaikuntanathan, V.: Constrained key-homomorphic PRFs from standard lattice assumptions - or: How to secretly embed a circuit in your PRF. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 1–30. Springer, Heidelberg (2015)
Canetti, R., Chen, Y.: Constraint-hiding constrained PRFs for NC\(^{1}\) from LWE. In: Coron, J.S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 446–476. Springer, Heidelberg (Apr / May (2017)
CFRG: Cfrg pake selection process. Public GitHub repository (Summer 2019). https://github.com/cfrg/pake-selection. Accessed Jan 2020
Davidson, A., Goldberg, I., Sullivan, N., Tankersley, G., Valsorda, F.: Privacy pass: Bypassing internet challenges anonymously. PoPETs 2018(3), 164–180 (2018)
Davidson, A., Sullivan, N.: The privacy pass protocol. Internet-Draft draft-privacy-pass-0, IETF Secretariat (November 2019). https://datatracker.ietf.org/doc/draft-privacy-pass/
Davidson, A., Sullivan, N., Wood, C.: Oblivious pseudorandom functions (OPRFs) using prime-order groups. Internet-Draft draft-irtf-cfrg-voprf-01, IETF Secretariat (July 2019). http://www.ietf.org/internet-drafts/draft-irtf-cfrg-voprf-01.txt
Dodis, Y., Goldwasser, S., Kalai, Y.T., Peikert, C., Vaikuntanathan, V.: Public-key encryption schemes with auxiliary inputs. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 361–381. Springer, Heidelberg (2010)
Don, J., Fehr, S., Majenz, C., Schaffner, C.: Security of the Fiat-Shamir transformation in the quantum random-oracle model. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 356–383. Springer, Heidelberg (2019)
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO’86. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987)
Freedman, M.J., Ishai, Y., Pinkas, B., Reingold, O.: Keyword search and oblivious pseudorandom functions. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 303–324. Springer, Heidelberg (2005)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner, R.E., Dwork, C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press (2008)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013)
Goldreich, O., Micali, S., Wigderson, A.: How to prove all NP-statements in zero-knowledge, and a methodology of cryptographic protocol design. In: Odlyzko, A.M. (ed.) CRYPTO’86. LNCS, vol. 263, pp. 171–185. Springer, Heidelberg (1987)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems (extended abstract). In: 17th ACM STOC, pp. 291–304. ACM Press (1985)
Jarecki, S., Kiayias, A., Krawczyk, H.: Round-optimal password-protected secret sharing and T-PAKE in the password-only model. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014, Part II. LNCS, vol. 8874, pp. 233–253. Springer, Heidelberg (2014)
Jarecki, S., Kiayias, A., Krawczyk, H., Xu, J.: Highly-efficient and composable password-protected secret sharing (or: How to protect your bitcoin wallet online). In: EuroS&P, pp. 276–291. IEEE (2016)
Jarecki, S., Krawczyk, H., Xu, J.: OPAQUE: An asymmetric PAKE protocol secure against pre-computation attacks. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 456–486. Springer, Heidelberg (2018)
Jarecki, S., Liu, X.: Efficient oblivious pseudorandom function with applications to adaptive OT and secure computation of set intersection. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 577–594. Springer, Heidelberg (2009)
Keelveedhi, S., Bellare, M., Ristenpart, T.: Dupless: server-aided encryption for deduplicated storage. In: Presented as part of the 22nd USENIX Security Symposium (USENIX Security 13), pp. 179–194. USENIX, Washington, D.C. (2013)
Krawczyk, H.: The opaque asymmetric pake protocol. Internet-Draft draft-krawczyk-cfrg-opaque-02, IETF Secretariat (July 2019), http://www.ietf.org/internet-drafts/draft-krawczyk-cfrg-opaque-02.txt
Libert, B., Ling, S., Mouhartem, F., Nguyen, K., Wang, H.: Zero-knowledge arguments for matrix-vector relations and lattice-based group encryption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 101–131. Springer, Heidelberg (2016)
Libert, B., Ling, S., Nguyen, K., Wang, H.: Zero-knowledge arguments for lattice-based PRFs and applications to E-cash. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part III. LNCS, vol. 10626, pp. 304–335. Springer, Heidelberg (2017)
Liu, Q., Zhandry, M.: Revisiting post-quantum Fiat-Shamir. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 326–355. Springer, Heidelberg (2019)
Lyubashevsky, V.: Fiat-Shamir with aborts: applications to lattice and factoring-based signatures. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 598–616. Springer, Heidelberg (2009)
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012)
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010)
Micciancio, D., Peikert, C.: Trapdoors for lattices: Simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012)
Papadopoulos, D., Wessels, D., Huque, S., Naor, M., Včelák, J., Reyzin, L., Goldberg, S.: Making NSEC5 practical for DNSSEC. Cryptology ePrint Archive, Report 2017/099 (2017), http://eprint.iacr.org/2017/099
Peikert, C.: A decade of lattice cryptography. Cryptology ePrint Archive, Report 2015/939 (2015), http://eprint.iacr.org/2015/939
Peikert, C., Shiehian, S.: Privately constraining and programming PRFs, the LWE way. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 675–701. Springer, Heidelberg (2018)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press (May 2005)
Sullivan, N.: Cloudflare supports privacy pass. Cloudflare Blog (November 09 2017), https://blog.cloudflare.com/cloudflare-supports-privacy-pass/. Accessed Aug 2019
Yang, R., Au, M.H., Zhang, Z., Xu, Q., Yu, Z., Whyte, W.: Efficient lattice-based zero-knowledge arguments with standard soundness: construction and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 147–175. Springer, Heidelberg (2019)
Acknowledgements
We thank Ward Beullens for helpful discussions and advice on replacing Stern-based ZKAoKs with more efficient alternatives.
The research of Albrecht was supported by EPSRC grants EP/S020330/1 and EP/S02087X/1, and by the European Union Horizon 2020 Research and Innovation Program Grant 780701; the research of Deo was partially supported by the EPSRC and the UK government as part of the Centre for Doctoral Training in Cyber Security at Royal Holloway, University of London (EP/K035584/1), the European Union Horizon 2020 Research and Innovation Program Grant 780701, and BPI-France in the context of the national project RISQ (P141580); the research of Smart was supported by CyberSecurity Research Flanders with reference number VR20192203, by ERC Advanced Grant ERC-2015-AdG-IMPaCT and by the FWO under an Odysseus project GOH9718N.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Albrecht, M.R., Davidson, A., Deo, A., Smart, N.P. (2021). Round-Optimal Verifiable Oblivious Pseudorandom Functions from Ideal Lattices. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)







 when interacting directly with
when interacting directly with  .
. ; outputs
; outputs
 .
.




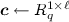 with a simulated proof
with a simulated proof 
