Abstract
A family \(\mathcal {R}\) of binary relations on a set X is called a relator on X, and the ordered pair \( X(\mathcal {R})=( X, \mathcal {R})\) is called a relator space. Sometimes relators on X to Y are also considered.
By using an obvious definition of the generated open sets, each generalized topology \(\mathcal {T}\) on X can be easily derived from the family  of all Pervin’s preorder relations R
V = V
2 ∪ V
c × X with \(V\in \mathcal {T}\), where \(V^{2}={}V\!\times \!V\) and V
c = X ∖ V .
of all Pervin’s preorder relations R
V = V
2 ∪ V
c × X with \(V\in \mathcal {T}\), where \(V^{2}={}V\!\times \!V\) and V
c = X ∖ V .
For a subset A of the relator space \(X(\mathcal {R})\), we define
and  . And, for instance, we write
. And, for instance, we write  if A ⊆ A
∘.
if A ⊆ A
∘.
Moreover, following some basic definitions in topological spaces, for a subset A of the relator space \(X(\mathcal {R})\) we write

The members of the above families will be called the topologically regular open, preopen, semi-open, α-open, β-open, a-open and b-open subsets of the relator space \(X(\mathcal {R})\), respectively.
In our former papers, having in mind the original definitions of N. Levine [49] and H. H. Corson and E. Michael [11], we have also investigated four further, closely related, families of generalized topologically open sets in \(X(\mathcal {R})\).
Now, we shall offer a general framework for studying these families. Moreover, motivated by a definition of Á. Császár [15] and his predecessors, we shall also consider a further important class of generalized topologically open sets.
For the latter purpose, for a subset A of the relator space \(X(\mathcal {R})\), we shall write
-
(8)
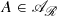 if A
− ∘⊆ A
∘ −.
if A
− ∘⊆ A
∘ −.
Thus, according to Császár’s terminology, the members of the family  should be called the topologically quasi-open subsets of the relator space \(X(\mathcal {R})\). However, in the earlier literature, these sets have been studied under different names.
should be called the topologically quasi-open subsets of the relator space \(X(\mathcal {R})\). However, in the earlier literature, these sets have been studied under different names.
While, for the former purpose, for any two subsets A and B of the relator space \(X(\mathcal {R})\) we shall write
-
(9)
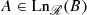 and
and 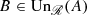 if A ⊆ B ⊆ A
−.
if A ⊆ B ⊆ A
−.
Moreover, for a family \(\mathcal {A}\) of subsets of \(X(\mathcal {R})\) we shall define
-
(10)
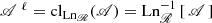 and
and  .
.
Thus, \(\mathcal {A}^{\hskip 1mm\ell }\) and \(\mathcal {A}^{{\hskip 1mm}u}\) may be called the lower and upper nearness closures of \(\mathcal {A}\), respectively. Namely, if  , then we may naturally say that A is near to B from below and B is near to A from above.
, then we may naturally say that A is near to B from below and B is near to A from above.
The most important particular cases are when \(\mathcal {A}\) is a minimal structure or a generalized topology on X. Or even more specially, \(\mathcal {A}\) is one of the families  ,
,  or
or  .
.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
M.E. Abd El-Monsef, S.N. El-Deeb, R.A. Mahmoud, β-open sets and β-continuous mappings. Bull. Fac. Sci. Assiut Univ. 12, 77–90 (1983)
P. Alexandroff, Zur Begründung der n-dimensionalen mengentheorischen Topologie. Math. Ann. 94, 296–308 (1925)
D. Andrijević, Semi-preopen sets. Mat. Vesnik 38, 24–32 (1986)
D. Andrijević, On b-open sets. Mat. Vesnik 48, 59–64 (1996)
N. Biswas, On some mappings in topological spaces. Bull. Cal. Math. Soc. 61, 127–135 (1969)
N. Bourbaki, General Topology, Chapters 1–4 (Springer, Berlin, 1989)
T.A. Chapman, A further note on closure and interior operators. Am. Math. Monthly 69, 524–529 (1962)
Ch. Chattopadhyay, Ch. Bandyopadhyay, On structure of δ-sets. Bull. Calcutta Math. Soc. 83, 281–290 (1991)
Ch. Chattopadhyay, U.K. Roy, δ-sets, irresolvable and resolvable spaces. Math. Slovaca 42, 371–378 (1992)
H. Choda, K. Matoba, On a theorem of Levine. Proc. Jpn. Acad. 37, 462–463 (1961)
H.H. Corson, E. Michael, Metrizability of countable unions. Ill. J. Math. 8, 351–360 (1964)
Á. Császár, Foundations of General Topology (Pergamon Press, London, 1963)
Á. Császár, Generalized open sets. Acta Math. Hungar. 75, 65–87 (1997)
Á. Császár, On the γ-interior and γ-closure of a set. Acta Math. Hungar. 80, 89–93 (1998)
Á. Császár, γ-quasi-open sets. Stud. Sci. Math. Hungar. 38, 171–176 (2001)
Á. Császár, Remarks on γ-quasi-open sets. Stud. Sci. Math. Hungar. 39, 137–141 (2002)
Á. Császár, Further remarks on the formula for the γ-interior. Acta Math. Hungar. 113, 325–332 (2006)
Á. Császár, Remarks on quasi-topologies. Acta Math. Hungar. 119, 197–200 (2008)
B.A. Davey, H.A. Priestley, Introduction to Lattices and Order (Cambridge University Press, Cambridge, 2002)
A.S. Davis, Indexed systems of neighbordoods for general topological spaces. Am. Math. Monthly 68, 886–893 (1961)
K. Dlaska, N. Ergun, M. Ganster, On the topology generated by semi-regular sets. Indian J. Pure Appl. Math. 25, 1163–1170 (1994)
J. Dontchev, Survey on preopen sets. Meetings on Topological Spaces, Theory and Applications, Yatsushiro College of Technology, Kumamoto, Japan (1998), 18 pp.
Z. Duszyński, T. Noiri, Semi-open, semi-closed sets and semi-continuity of functions. Math. Pannon. 23, 195–200 (2012)
V.A. Efremovič, The geometry of proximity. Mat. Sb. 31, 189–200 (1952) (Russian)
V.A. Efremović, A.S. Švarc, A new definition of uniform spaces. Metrization of proximity spaces. Dokl. Acad. Nauk. SSSR 89, 393–396 (1953) (Russian)
N. Elez, O. Papaz, The new operators in topological spaces. Math. Moravica 17, 63–68 (2013)
P. Fletcher, W.F. Lindgren, Quasi-Uniform Spaces (Marcel Dekker, New York, 1982)
M. Ganster, Preopen sets and resolvable spaces. Kyungpook J. 27, 135–143 (1987)
M. Ganster, I.L. Reilly, M.K. Vamanamurthy, Remarks on locally closed sets. Math. Pannon. 3, 107–113 (1992)
B. Ganter, R. Wille, Formal Concept Analysis (Springer, Berlin, 1999)
R. Gargouri, A. Rezgui, A unification of weakening of open and closed subsets in a topological spaces. Bull. Malays. Math. Sci. Soc. 40, 1219–1230 (2017)
S. Givant, P. Halmos, Introduction to Boolean Algebras (Springer, Berlin, 2009)
T. Glavosits, Generated preorders and equivalences. Acta Acad. Paed. Agrienses, Sect. Math. 29, 95–103 (2002)
W.H. Gottschalk, Intersection and closure. Proc. Am. Math. Soc. 4, 470–473 (1953)
W. Hunsaker, W. Lindgren, Construction of quasi-uniformities. Math. Ann. 188, 39–42 (1970)
D.H. Hyers, On the stability of the linear functional equation. Proc. Nat. Acad. Sci. U.S.A 27, 222–224 (1941)
Y. Isomichi, New concept in the theory of topological spaces–Supercondensed set, subcondensed set, and condensed set. Pac. J. Math. 38, 657–668 (1971)
Y.B. Jun, S.W. Jeong, H.j. Lee, J.W. Lee, Applications of pre-open sets. Appl. Gen. Top. 9, 213–228 (2008)
S.-M. Jung, Interiors and closure of sets and applications. Int. J. Pure Math. 3, 41–45 (2016)
S.-M. Jung, D. Nam, Some properties of interior and closure in general topology. Mathematics 7, 624 (2019)
J.L. Kelley, General Topology (Van Nostrand Reinhold Company, New York, 1955)
H. Kenyon, Two theorems on relations. Trans. Am. Math. Soc. 107, 1–9 (1963)
V.L. Kljushin, Al bayati J.H. Hussein, On simply-open sets. Vestnik UDC 3, 34–38 (2011). (Russian)
K. Kuratowski, Sur l’opération \(\overline {A}\) de l’analysis situs. Fund. Math. 3(1922), 182–199 (1922) (An English translation: On the operation \(\overline {A}\) in analysis situs, prepared by M. Bowron in 2010, is available on the Internet)
K. Kuratowski, Topology I (Academic Press, New York, 1966)
J. Kurdics, A note on connection properties. Acta Math. Acad. Paedagog. Nyházi. 12, 57–59 (1990)
J. Kurdics, Á. Száz, Well-chainedness characterizations of connected relators. Math. Pannon. 4, 37–45 (1993)
N. Levine, On the commutivity of the closure and interior operators in topological spaces. Am. Math. Montly 68, 474–477 (1961)
N. Levine, Semi-open sets and semi-continuity in topological spaces. Am. Math. Monthly 70, 36–41 (1963)
N. Levine, Some remarks on the closure operator in topological spaces. Am. Math. Monthly 70, 553 (1963)
N. Levine, On uniformities generated by equivalence relations. Rend. Circ. Mat. Palermo 18, 62–70 (1969)
N. Levine, On Pervin’s quasi uniformity. Math. J. Okayama Univ. 14, 97–102 (1970)
J. Mala, Relators generating the same generalized topology. Acta Math. Hungar. 60, 291–297 (1992)
J. Mala, Á. Száz, Properly topologically conjugated relators. Pure Math. Appl. Ser. B 3, 119–136 (1992)
J. Mala, Á. Száz, Modifications of relators. Acta Math. Hungar. 77, 69–81 (1997)
A.S. Mashhour, M.E. Abd El-Monsef, S.N. El-Deeb, On precontinuous and weak precontinuous mappings. Proc. Math. Phys. Soc. Egypt 53, 47–53 (1982)
S.A. Naimpally, B.D. Warrack, Proximity Spaces (Cambridge University Press, Cambridge, 1970)
H. Nakano, K. Nakano, Connector theory. Pac. J. Math. 56, 195–213 (1975)
A.A. Nasef, R. Mareay, More on simplly open sets and its applications. South Asian J. Math. 5, 100–108. (2015)
A.A. Nasef, R. Mareay, Ideals and some applications of simply open sets. J. Adv. Math. 13, 7264–7271 (2017)
A. Neubrunnová, On transfinite sequences of certain types of functions. Acta Fac. Rer. Natur. Univ. Commun. Math. 30, 121–126 (1975)
O. Njåstad, On some classes of nearly open sets. Pac. J. Math. 15, 195–213 (1965)
G. Pataki, Supplementary notes to the theory of simple relators. Radovi Mat. 9, 101–118 (1999)
G. Pataki, On the extensions, refinements and modifications of relators. Math. Balk. 15, 155–186 (2001)
G. Pataki, Á. Száz, A unified treatment of well-chainedness and connectedness properties. Acta Math. Acad. Paedagog. Nyházi. (N.S.) 19, 101–165 (2003)
W.J. Pervin, Quasi-uniformization of topological spaces. Math. Ann. 147, 316–317 (1962)
Th.M. Rassias, M. Salih, Á. Száz, Characterizations of generalized topologically open sets in relator spaces, in Recent Trends on Pure and Applied Mathematics, Special Issue of the Montes Taurus, ed. by G.V. Milovanovic, Thm. M. Rassias, Y. Simsek. J. Pure Appl. Math., Dedicated to Professor Hari Mohan Srivastava on the occasion of his 80th Birthday, Montes Taurus J. Pure Appl. Math. 3, 39–94 (2021)
Th.M. Rassias, M. Salih, Á. Száz, Set-theoretic properties of generalized topologically open sets in relator spaces, in Mathematical Analysis in Interdisciplinary Research, ed. by I.N. Parasidis, E. Providas, Th.M. Rassias, to appear
M. Salih, Á. Száz, Generalizations of some ordinary and extreme connectedness properties of topological spaces to relator spaces. Electron. Res. Arch. 28, 471–548 (2020)
P. Sivagami, Remarks on γ-interior. Acta Math. Hungar. 119, 81–94 (2008)
Yu.M. Smirnov, On proximity spaces. Math. Sb. 31, 543–574 (1952) (Russian)
M.H. Stone, Application of the theory of Boolean rings to general topology. Trans. Am. Math. Soc. 41, 374–481 (1937)
Á. Száz, Basic tools and mild continuities in relator spaces. Acta Math. Hungar. 50, 177–201 (1987)
Á. Száz, Directed, topological and transitive relators. Publ. Math. Debrecen 35, 179–196 (1988)
Á. Száz, Relators, Nets and Integrals. Unfinished doctoral thesis, Debrecen (1991), 126 pp.
Á. Száz, Structures derivable from relators. Singularité 3, 14–30 (1992)
Á. Száz, Refinements of relators. Tech. Rep., Inst. Math., Univ. Debrecen, vol. 76 (1993), 19 pp.
Á. Száz, Cauchy nets and completeness in relator spaces. Colloq. Math. Soc. János Bolyai 55, 479–489 (1993)
Á. Száz, Neighbourhood relators. Bolyai Soc. Math. Stud. 4, 449–465 (1995)
Á. Száz, Uniformly, proximally and topologically compact relators. Math. Pannon. 8, 103–116 (1997)
Á. Száz, Somewhat continuity in a unified framework for continuities of relations. Tatra Mt. Math. Publ. 24, 41–56 (2002)
Á. Száz, Upper and lower bounds in relator spaces. Serdica Math. J. 29, 239–270 (2003)
Á. Száz, Rare and meager sets in relator spaces. Tatra Mt. Math. Publ. 28, 75–95 (2004)
Á. Száz, Galois-type connections on power sets and their applications to relators. Tech. Rep., Inst. Math., Univ. Debrecen 2005/2 (2005), 38 pp.
Á. Száz, Minimal structures, generalized topologies, and ascending systems should not be studied without generalized uniformities. Filomat 21, 87–97 (2007)
Á. Száz, Galois type connections and closure operations on preordered sets. Acta Math. Univ. Comenian. (N.S.) 78, 1–21 (2009)
Á. Száz, Inclusions for compositions and box products of relations. J. Int. Math. Virt. Inst. 3, 97–125 (2013)
Á. Száz, A particular Galois connection between relations and set functions. Acta Univ. Sapientiae, Math. 6, 73–91 (2014)
Á. Száz, Generalizations of Galois and Pataki connections to relator spaces. J. Int. Math. Virtual Inst. 4, 43–75 (2014)
Á. Száz, Basic tools, increasing functions, and closure operations in generalized ordered sets, in Contributions in Mathematics and Engineering, ed. by P.M. Pardalos, Th.M. Rassias. In Honor of Constantion Caratheodory (Springer, Berlin, 2016), pp. 551–616
Á. Száz, Four general continuity properties, for pairs of functions, relations and relators, whose particular cases could be investigated by hundreds of mathematicians. Tech. Rep., Inst. Math., Univ. Debrecen, 2017/1 (2017), 17 pp.
Á. Száz, The closure-interior Galois connection and its applications to relational equations and inclusions. J. Int. Math. Virt. Inst. 8, 181–224 (2018)
Á. Száz, Corelations are more powerful tools than relations, in Applications of Nonlinear Analysis, ed. by Th.M. Rassias. Optimization and Its Applications, vol. 134 (Springer, Berlin, 2018), pp. 711–779
Á. Száz, Relationships between inclusions for relations and inequalities for corelations. Math. Pannon. 26, 15–31 (2018)
Á. Száz, Galois and Pataki connections on generalized ordered sets. Earthline J. Math. Sci. 2, 283–323 (2019)
Á. Száz, Birelator spaces are natural generalizations of not only bitopological spaces, but also ideal topological spaces, in Mathematical Analysis and Applications, Springer Optimization and Its Applications, ed. by Th.M. Rassias, P.M. Pardalos, vol. 154 (Springer, Switzerland, 2019), pp. 543–586
W.J. Thron, Topological Structures (Holt, Rinehart and Winston, New York, 1966)
H. Tietze, Beiträge zur allgemeinen Topologie I. Axiome für verschiedene Fassungen des Umgebungsbegriffs. Math. Ann. 88, 290–312 (1923)
A. Weil, Sur les espaces á structure uniforme et sur la topologie générale. Actual. Sci. Ind., vol. 551 (Herman and Cie, Paris 1937)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Rassias, T.M., Száz, Á. (2021). A General Framework for Studying Certain Generalized Topologically Open Sets in Relator Spaces. In: Rassias, T.M. (eds) Nonlinear Analysis, Differential Equations, and Applications. Springer Optimization and Its Applications, vol 173. Springer, Cham. https://doi.org/10.1007/978-3-030-72563-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-72563-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-72562-4
Online ISBN: 978-3-030-72563-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


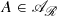 if A
− ∘⊆ A
∘ −.
if A
− ∘⊆ A
∘ −.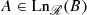 and
and 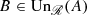 if A ⊆ B ⊆ A
−.
if A ⊆ B ⊆ A
−.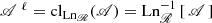 and
and  .
.