Optimal Time and EOQ for Inventory of Deteriorating Items with Variation and Leading Times

Abstract

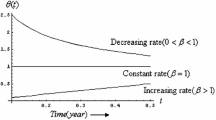
The proposed model represents the optimal time, EQO and optimal total cost, for two different time intervals as components of first run time under-considered constant demand, inventory is non-contact within the first component-time runs, constant within a second, purchasing cost is more than holding, the finite horizon planning, without shortage cost, replenishment required after the second component which is equal the first leading time of first run time. The inventory level is non-zero within a lengthier time on the horizon. Sensitivity analysis for the proposed model has represented the many values for varying demand; the deterioration rate lies in an assumed range. The represented figures explained the performance of optimal quantity and optimal total cost within the components of the first runtime (required time), the difference between the optimal total cost and the actual total cost was proposed.