Abstract
We prove that the module learning with errors (\(\mathrm {M\text {-}LWE}\)) problem with arbitrary polynomial-sized modulus p is classically at least as hard as standard worst-case lattice problems, as long as the module rank d is not smaller than the number field degree n. Previous publications only showed the hardness under quantum reductions. We achieve this result in an analogous manner as in the case of the learning with errors (\(\mathrm {LWE}\)) problem. First, we show the classical hardness of \(\mathrm {M\text {-}LWE}\) with an exponential-sized modulus. In a second step, we prove the hardness of \(\mathrm {M\text {-}LWE}\) using a binary secret. And finally, we provide a modulus reduction technique. The complete result applies to the class of power-of-two cyclotomic fields. However, several tools hold for more general classes of number fields and may be of independent interest.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The learning with errors (LWE) problem, introduced by Regev [Reg05], is used as a core computational problem in lattice-based cryptography. Given positive integers n (the dimension) and q (the modulus), and a secret vector \(\mathbf {s}\in \mathbb {Z}_q^n\), an \(\mathrm {LWE}_{n,q,\psi }\) sample is defined as \((\mathbf {a}, b = \frac{1}{q} \langle \mathbf {a}, \mathbf {s}\rangle + e)\), where \(\mathbf {a}\) is sampled from the uniform distribution on \(\mathbb {Z}_q^n\) and e (the error), is sampled from a probability distribution \(\psi \) on the torus \(\mathbb {T}=\mathbb {R}/\mathbb {Z}\). In many cases, the error distribution is given by a Gaussian distribution \(D_{\alpha }\) of width \(\alpha \), for a positive real \(\alpha \). The search version of \(\mathrm {LWE}\) asks to recover the secret \(\mathbf {s}\), given arbitrarily many samples of the \(\mathrm {LWE}\) distribution. Its decision variant asks to distinguish between \(\mathrm {LWE}\) samples and samples drawn from the uniform distribution on \(\mathbb {Z}_q^{n}\times \mathbb {T}\).
The LWE problem is fundamental in lattice-based cryptography as it allows to construct a wide range of cryptographic primitives, from the basic ones, as public-key encryption (e.g. [Reg05, MP12]), to the most advanced ones, as fully homomorphic encryption (e.g. [BGV12, BV14, DM15]) or non-interactive zero-knowledge proof systems (e.g. [PS19]). A very appealing aspect of \(\mathrm {LWE}\) is its connection to well-studied lattice problems. Lattices are discrete additive subgroups of \(\mathbb {R}^n\) and arise in many different areas of mathematics, such as number theory, geometry and group theory. There are several lattice problems that are conjectured to be computationally hard to solve, for instance, the problem of finding a set of shortest independent vectors (\(\mathrm {SIVP}\)) or the decisional variant of finding a shortest vector (\(\mathrm {GapSVP}\)). A standard relaxation of those two problems consists in solving them only up to a factor \(\gamma \), denoted by \(\mathrm {SIVP}_{\gamma }\) and \(\mathrm {GapSVP}_{\gamma }\), respectively. In the seminal work of Regev [Reg05, Reg09], a worst-case to average-case quantum reduction from \(\mathrm {GapSVP}_{\gamma }\) or \(\mathrm {SIVP}_{\gamma }\) to \(\mathrm {LWE}\) was established. In other words, if there exists an efficient algorithm that solves \(\mathrm {LWE}\), then there also exists an efficient quantum algorithm that solves \(\mathrm {GapSVP}_{\gamma }\) and \(\mathrm {SIVP}_{\gamma }\) in the worst-case. Later, Peikert [Pei09] showed a classical reduction from \(\mathrm {GapSVP}_{\gamma }\) to \(\mathrm {LWE}\), but requiring the resulting modulus q to be exponentially large in the dimension n. With the help of a modulus reduction, Brakerski et al. [BLP+13] proved the hardness of \(\mathrm {LWE}\) via a classical reduction from \(\mathrm {GapSVP}_{\gamma }\), for any polynomial-sized modulus q.
Structured Variants. Cryptographic protocols, whose security proofs rely on the hardness of \(\mathrm {LWE}\), inherently suffer from large public keys, usually consisting of m elements of \(\mathbb {Z}_q^n\), where \(m \in O(n \log _2 n)\). To improve their efficiency, structured variants of \(\mathrm {LWE}\) have been proposed, e.g., [SSTX09, LPR10, LS15]. Within this paper, we focus on the module learning with errors (\(\mathrm {M\text {-}LWE}\)) problem, first defined by Brakerski et al. [BGV12] and thoroughly studied by Langlois and Stehlé [LS15]. Instead of working over integers, it uses a more algebraic setting. Let K be a number field of degree n and R its ring of integers with dual \(R^{\vee }\). Further, let q and d be positive integers. Let \(\psi \) be a distribution on the torus \(\mathbb {T}_{R^{\vee }}=K_{\mathbb {R}}/R^{\vee }\), where \(K_{\mathbb {R}} = K \otimes _{\mathbb {Q}} \mathbb {R}\), and let \(\mathbf {s}\in (R^{\vee }_q)^d\) be a secret vector. An \(\mathrm {M\text {-}LWE}_{n,d,q,\psi }\) sample is given by \((\mathbf {a},b= \frac{1}{q} \langle \mathbf {a}, \mathbf {s}\rangle + e )\), where \(\mathbf {a}\leftarrow U((R_q)^{d})\) and \(e \leftarrow \psi \). Again, usually \(\psi \) is a Gaussian distribution \(D_{\alpha }\) of width \(\alpha \). We refer to the special case of \(d=1\) as the ring learning with errors (\(\mathrm {R\text {-}LWE}\)) problem.
Similar to its unstructured counterpart, \(\mathrm {M\text {-}LWE}\) also enjoys worst-case to average-case connections from lattice problems such as \(\mathrm {SIVP}_{\gamma }\) [LS15]. Whereas the hardness results for \(\mathrm {LWE}\) start from the lattice problem in the class of general lattices, the set has to be restricted to module lattices in the case of \(\mathrm {M\text {-}LWE}\). These module lattices correspond to modules in the ring R and we refer to the related lattice problem as Mod-SIVP\(_{\gamma }\) and \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\), respectively. Whereas both problems are conjectured to be hard to solve for \(\gamma \) polynomial in the lattice dimension, the problem \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) becomes easy in the special case of module lattices of rank 1 as their minimum can also be bounded below [PR07].
Since its introduction, the \(\mathrm {M\text {-}LWE}\) problem has enjoyed more and more popularity as it offers a fine-grained trade-off between concrete security and efficiency. Within the NIST standardization processFootnote 1, several third round candidates rely on the hardness of \(\mathrm {M\text {-}LWE}\), e.g., the signature scheme Dilithium [DKL+18] and the key encapsulation mechanism Kyber [BDK+18] from the CRYSTALS suite.
Binary Secret. Several variants of \(\mathrm {LWE}\) have been introduced during the last 15 years. One very interesting and widely-used version is the binary secret learning with errors (\(\text {bin-}\mathrm {LWE}\)) problem, where the secret vector \(\mathbf {s}\) is chosen from \(\{0,1\}^n\). Besides gaining in efficiency, this variant also plays an important role in some applications like fully homomorphic encryption schemes, e.g., [DM15]. A first study of this problem was provided by Goldwasser et al. [GKPV10] in the context of leakage-resilient cryptography. Whereas their proof structure has the advantage of being easy to follow, their result suffers from a large error increase. Informally, they showed a reduction from \(\mathrm {LWE}_{\ell ,q,D_{\alpha }}\) to \(\text {bin-}\mathrm {LWE}_{n,q,D_{\beta }}\), where \(\frac{\alpha }{\beta } = \text {negl}(n)\) and \(n \ge \ell \log _2 q + \omega (\log _2 n)\). Later, Brakerski et al. [BLP+13] improved the state of the art in order to show the classical hardness of LWE with a polynomial-sized modulus. Micciancio [Mic18] published another reduction from LWE to its binary version. Whereas the two reduction techniques differ, both paper achieved similar results. The dimension is still increased roughly by a factor \(\log _2 q\), but the error only by a factor of \(\sqrt{n}\), where n is the resulting LWE dimension. More concretely, in [BLP+13] a reduction from \(\mathrm {LWE}_{\ell ,q,D_{\alpha }}\) to \(\text {bin-}\mathrm {LWE}_{n,q,D_{\beta }}\) is shown, where \(\frac{\alpha }{\beta } \le \frac{1}{\sqrt{10n}}\) and \(n\ge (\ell +1)\log _2 q + \omega (\log _2 n)\). The increase in dimension from \(\ell \) to roughly \(\ell \log _2 q\) is reasonable, as it essentially preserves the number of possible secrets. As stated by Micciancio [Mic18], an important open problem is whether similar results carry over to the structured variants, in particular to \(\mathrm {M\text {-}LWE}\), which seems to be an interesting problem to use in practice.
Our Contributions. Our first main contribution is a reduction from \(\mathrm {M\text {-}LWE}\) to its binary secret version, \(\text {bin-}\mathrm {M\text {-}LWE}\), if the module rank d is at least of size \(\log _2 q\,+\,\omega (\log _2 n)\), where n denotes the degree of the underlying number field and q the modulus. To the best of our knowledge, this is the first result on the hardness of a structured variant of \(\mathrm {LWE}\) with binary secret. We then use this new result to show our second main contribution, the classical hardness of \(\mathrm {M\text {-}LWE}\) for any polynomial-sized modulus p and module rank d at least \(2n + \omega (\log _2 n)\), assuming the hardness of \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) with module rank at least 2. This was stated as an open problem by Langlois and Stehlé [LS15], as only quantum hardness of \(\mathrm {M\text {-}LWE}\) for any polynomial-sized modulus p was known.
Technical Overview. At a high level, we follow the structure of the classical hardness proof of \(\mathrm {LWE}\) from Brakerski et al. [BLP+13]. Overall, we need three ingredients: First, the classical hardness of \(\mathrm {M\text {-}LWE}\) with an exponential-sized modulus. As a second component, we need the hardness of \(\mathrm {M\text {-}LWE}\) using a binary secret, and finally, a modulus reduction technique.
We begin with the hardness of \(\text {bin-}\mathrm {M\text {-}LWE}\) in Sect. 3. We follow the original proof structure of Goldwasser et al. [GKPV10], while achieving much better parameters by using the Rényi divergence instead of the statistical distance. The improvement on the noise rate compared to [GKPV10] stems from the fact that the Rényi divergence only needs to be constant for the reduction to work, compared to negligibly close to 0 for the statistical distance. Using the Rényi divergence as a tool for distance measurement requires to move to the search variants of \(\mathrm {M\text {-}LWE}\) and its binary version, respectively. Additionally, it asks to fix the number of samples m a priori, which we denote by a suffix m, i.e., \(\mathrm {M\text {-}LWE}_{n,d,q,\psi }^m\). Throughout the paper, we assume that m is polynomial in the security parameter. At the core of the hardness proof of \(\text {bin-}\mathrm {M\text {-}LWE}\) lies a lossy argument, where the public matrix \(\mathbf {A}\) is replaced by a lossy matrix \(\mathbf {B}\cdot \mathbf {C}\,+\,\mathbf {Z}\), which corresponds to the second part of some multiple-secrets \(\mathrm {M\text {-}LWE}\) sample. To argue that an adversary cannot distinguish between the two cases, we need the hardness of the decisional \(\mathrm {M\text {-}LWE}\) problem as well. However, prior to our work, the hardness of decisional \(\mathrm {M\text {-}LWE}\) was only proven for polynomial-sized modulus, see [LS15]. For our purpose, we need the hardness of decisional \(\mathrm {M\text {-}LWE}\) with an exponential-sized modulus. We solve this problem by adapting the main result of Peikert et al. [PRS17] to the module setting (Lemma 12).
This leads us to the first ingredient, the classical hardness of \(\mathrm {M\text {-}LWE}\) with an exponential-sized modulus. In their introduction, Langlois and Stehlé [LS15] claimed that Peikert’s dequantization [Pei09] carries over to the module case. In this paper, we prove this claim in Theorem 4. The proof idea is the same as the one from Peikert, but with two novelties. First, we look at the structured variants of the corresponding problems, i.e., \(\mathrm {GapSVP}\) over module lattices and \(\mathrm {M\text {-}LWE}\), where the underlying ring R is the ring of integers of a number field K. Second, we replace the main component, a reduction from the bounded distance decoding (\(\mathrm {BDD}\)) problem to the search version of \(\mathrm {LWE}\), by the reduction from the gaussian decoding problem (\(\mathrm {GDP}\)) over modules to the decisional version of \(\mathrm {M\text {-}LWE}\) (Lemma 12, adapted from [PRS17]). Thus, we also generalize the hardness of the decisional variant of \(\mathrm {M\text {-}LWE}\) to all number fields K, not only cyclotomic fields as in [LS15].
Finally, we provide a modulus reduction technique, the last required ingredient, where the rank of the underlying module is preserved. This corresponds to the modulus reduction for \(\mathrm {LWE}\) shown by Brakerski et al. [BLP+13, Cor. 3.2]. Prior to this paper, Albrecht and Deo [AD17] adapted the more general result from [BLP+13, Thm. 3.1], from which the necessary Corollary 3.2 is deduced. Thus, in Sect. 4.1, we first recall their general result [AD17, Thm. 1] and then derive Corollary 1, that we need, from it. The quality of the latter depends on the underlying ring structure and how the binary secret distribution behaves. For the case of power-of-two cyclotomics, we provide concrete bounds. This involves the computation of lower and upper bounds of the singular values of the rotation matrix. Note that Langlois and Stehlé [LS15] proved a modulus switching result from modulus q to modulus p, but the error increases at least by a multiplicative factor \(\frac{q}{p}\), which is exponential if q is exponential-sized and p only polynomial-sized. Further note that the reason why we need to go through the binary variant of \(\mathrm {M\text {-}LWE}\) is because we want to keep the noise amplification during the modulus switching part as small as possible.
Putting the Ingredients Together. We now explain how to complete the proof of our second main contribution, the classical hardness of \(\mathrm {M\text {-}LWE}\) for any polynomial-sized modulus p and module rank d at least \(2n + \omega (\log _2 n)\), as stated in Theorem 2. See Fig. 1 for an overview of the full proof.
Overview of the complete classical hardness proof of \(\mathrm {M\text {-}LWE}\) for linear rank d and arbitrary polynomially large modulus \(\hat{p}\), as stated in Theorem 2 for K the \(\nu \)-th cyclotomic number field of degree n. The parameter \(\varDelta \) is determined by the underlying ring R and is \(\mathrm {poly}(n)\) for the case of power-of-two cyclotomics.
Step 1: Classical worst-case to average-case reduction. Our result holds for any number field K of degree n with ring of integers R. Let \(\ell \ge 2\) denote the rank of the R-module. Informally, Theorem 4 shows a reduction from \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) to \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\Upsilon _{\alpha }}\), where \(\alpha \in (0,1)\), \(\gamma \alpha \ge n \ell \sqrt{\ell }\) and the modulus \(q \ge 2^{\frac{n\ell }{2}}\). Here, \(\Upsilon _{\alpha }\) defines a distribution on some special elliptical Gaussian distributions in the canonical embedding, which we define properly later.
Step 2: Hardness of the binary secret variant. Theorem 1 shows a reduction from \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\mathcal {D}_{R^{\vee },\alpha 'q}}^{m,d}\) and \(\mathrm {M\text {-}SLWE}^m_{n,\ell ,q,\mathcal {D}_{R^{\vee },\beta q}}\) to \(\text {bin-}\mathrm {M\text {-}SLWE}_{n,d,q,\mathcal {D}_{R^{\vee },\beta q}}^{m}\), where the underlying number field \(K=\mathbb {Q}(\zeta )\) is a cyclotomic field, \(d \ge \ell \cdot \log _2 q + \omega (\log _2 n)\) and \(\beta \ge \alpha ' \cdot \sqrt{m} n^2 d\). Further, the modulus q has to be prime and is preserved by the reduction. The starting error distribution is given by a discrete Gaussian \(\mathcal {D}_{R^{\vee },\alpha ' q}\), where \(\alpha '=\alpha \cdot \omega (\log _2 n)\). We explain in Lemma 13 how to move from \(\Upsilon _{\alpha }\) to \(\mathcal {D}_{R^{\vee },\alpha 'q}\). Again, the Gaussian distribution is defined with regard to the canonical embedding, but the binary secret is taken with regard to the coefficient embedding as we argue below.
Step 3: Modulus reduction. Using Corollary 1, we show a reduction from the problem \(\text {bin-}\mathrm {M\text {-}SLWE}_{n,d,q,D_{\sqrt{2}\beta }}^{m}\) to \(\text {bin-}\mathrm {M\text {-}SLWE}_{n,d,p,D_{\beta '}}^{m}\), where \(q \ge p \ge 1\) and \((\beta ')^2 \ge (\sqrt{2}\beta )^2 + \varDelta .\) Note that we show in Lemma 14 how to move from \(\mathcal {D}_{R^{\vee },\beta q}\) to \(D_{\sqrt{2} \beta }\). In the case of power-of-two cyclotomics (Corollary 2) the additional error factor is \(\varDelta =2dr^2\), with r polynomial in n.
Step 4: Search to decision. To conclude the classical hardness result of decisional \(\mathrm {M\text {-}LWE}\) with polynomial-sized modulus p, we use the search to decision reduction from [LS15, Section 4.3], which is restricted to any \(\nu \)-th cyclotomic field such that p is prime and satisfies \(p=1 \bmod \nu \). Adding a modulus switching step [LS15, Thm. 4.8], we can then reduce to any polynomial-sized modulus \(\hat{p}\) close to p by increasing the noise from \(\beta '\) to \(\hat{\beta } \ge \beta ' \cdot \max (1,\frac{p}{\hat{p}}) \cdot n^{3/4} d^{1/2} \omega ( \log _2^2(nd)).\)
Canonical Versus Coefficient Embedding. In previous publications about structured variants of \(\mathrm {LWE}\), many authors argued in praise of the canonical embedding \(\sigma :K \rightarrow H\) for the sake of achieving tighter reductions, e.g. [LPR10]. That is also the reason why most of the former results that we use within our proofs are formulated in the canonical embedding. However, it should be questioned again for \(\mathrm {M\text {-}LWE}\) with a binary secret. In practice, a small secret means that its coefficients, when seen as a polynomial, are small. In particular, the coefficients of a binary secret are chosen from the set \(\{0,1\}\). For instance, for the security level 3, the signature scheme Dilithium [DKL+18] samples the coefficients of the secret vector of polynomials from the set \(\{-3,\dots ,3\}\). One big disadvantage of using the canonical embedding \(\sigma \) is that the preimage of the set \(\{0,1\}^n \cap H\) under \(\sigma \) does not necessarily lie in R. More concretely, for the case of power-of-two cyclotomics, one can show that the only elements in R that have binary coefficients under the canonical embedding are the elements 0 and 1. Going from the coefficient to the canonical representation can be done by the linear transformation defined by the Vandermonde matrix. Thus, the distortion between the two embeddings depends on the norm of the Vandermonde matrix. Even though there are nice classes where the perturbation is relatively small, see [RSW18], in general, the problem of a binary secret with regard to the canonical embedding does not translate to a binary secret in the coefficient embedding. That is why we keep the definition of the binary secret in Theorem 1 with regard to the coefficient embedding. In order to keep the parameters as small as possible, this implies that the whole classical hardness proof then needs to be restricted to the class of power-of-two cyclotomics, where both embeddings are nearly isometric. Furthermore, the leftover hash lemma over rings (Lemma 7) asks for the coefficient embedding. Note that elements sampled from a Gaussian distribution are still sampled with respect to the canonical embedding.
Classical Hardness of R-LWE. The first result about the classical hardness of \(\mathrm {R\text {-}LWE}\) with exponential-sized modulus has been informally mentioned in [BLP+13]. It can be achieved in two steps. First, by a dimension-modulus switching as in [BLP+13], \(\mathrm {LWE}\) in dimension d and modulus q can be reduced to \(\mathrm {LWE}\) in dimension 1 and modulus \(q^d\) with a slightly increased error rate. Then, by a ring switching technique as in [GHPS12], the latter one can be reduced to \(\mathrm {R\text {-}LWE}\) over a ring of any degree n and modulus \(q^d\), while keeping the same error rate. For more details on the second step, we refer to [AD17, App. B].
On the other hand, as a direct application of our classical hardness result of \(\mathrm {M\text {-}LWE}\), we can provide an alternative solution for the classical hardness result of \(\mathrm {R\text {-}LWE}\) with exponential-sized modulus. The idea is that, using a rank-modulus switching as in
[WW19], we can instead reduce from \(\mathrm {M\text {-}LWE}\) over d-rank modules of n-degree ring and modulus q, to \(\mathrm {R\text {-}LWE}\) with n-degree ring and modulus \(q^d\), with a slightly increased error rate. However, we remark that the underlying worst-case lattice problems are different for these two results. Suppose that we consider the classical hardness of \(\mathrm {R\text {-}LWE}\) over n-degree ring and \(q^d\) modulus where  . Then, the underlying problem is the standard \(\mathrm {GapSVP}\) over general lattices of dimension
. Then, the underlying problem is the standard \(\mathrm {GapSVP}\) over general lattices of dimension  for the first result, while it is \(\mathrm {Mod}\text {-}\mathrm {GapSVP}\) over rank-2 modules of
for the first result, while it is \(\mathrm {Mod}\text {-}\mathrm {GapSVP}\) over rank-2 modules of  -degree ring for the second one.
-degree ring for the second one.
Related Work. We now compare the results of Theorem 1 with the former results on \(\mathrm {LWE}\). The LWE problem can be seen as a special case of \(\mathrm {M\text {-}LWE}\), where the ring is \(\mathbb {Z}\) and the degree n equals 1. In this case, the rank \(\ell \) of the module corresponds to the dimension of the LWE problem and should be polynomial in the security parameter. Hence, the error-ratio is given by \(\beta \ge \alpha \sqrt{m} \cdot d\) and \(d \ge \ell \log _2 q + \omega (\log _2 \ell )\). Asymptotically, we lose a factor of \(\sqrt{d}\) in the error-ratio in our reduction compared to the former results for \(\mathrm {LWE}\) [BLP+13, Mic18]. However, our proof is as direct and short as the original one in [GKPV10]. We don’t need to define intermediate problems such as First-is-errorless \(\mathrm {LWE}\) and Extended-\(\mathrm {LWE}\) as in [BLP+13] and no gadget matrix construction as in [Mic18]. Note that adapting the proof of [Mic18] asks to define a corresponding gadget matrix, which does not seem to work in an obvious way and that adapting the proof of [BLP+13] asks to define a corresponding notion of (a constant) quality for binary secrets, which is not straightforward. By replacing the statistical distance by the Rényi divergence and switching to the search variants we obtain a much better result than in the original paper from Goldwasser et al. [GKPV10].
Open Problems. In the course of this paper, we incurred several restrictions on the class of number fields we look at. Lemma 10 restricts the hardness proof of \(\text {bin-}\mathrm {M\text {-}SLWE}\) (Theorem 1) to cyclotomic fields, in order to bound the norm of the Vandermonde matrix. The hardness of \(\text {bin-}\mathrm {M\text {-}SLWE}\) for a rank which is smaller than \(\log _2 q + \omega (\log _2 n)\), in particular for binary \(\mathrm {R\text {-}LWE}\), is still an open problem. In practice, we usually chose a small constant rank (<10), as for instance in the submission to the NIST standardization process Kyber [BDK+18]. Furthermore, adapting the techniques of Brakerski et al. [BLP+13] and Micciancio [Mic18] to the module setting may help to further improve the error-ratio by a factor of \(\sqrt{nd}\). Further, quantifying the error increase in the modulus reduction from Sect. 4.1 for other number fields than power-of-two cyclotomics may be interesting. The current bounds heavily depend on the singular values of the secret’s rotation matrix, which further depend on the underlying number field.
2 Preliminaries
Let q be a positive integer, then \(\mathbb {Z}_q\) denotes the ring of integers modulo q. For any \(n \in \mathbb {N}\), we represent the set \(\{1,\dots ,n\}\) by [n]. Vectors are denoted in bold lowercase and matrices in bold capital letters. By \(\mathbf {a}^T\) (resp. \(\mathbf {a}^{\dagger }\)) and \(\mathbf {A}^T\) (resp. \(\mathbf {A}^{\dagger }\)) we denote the transpose (resp. conjugate transpose) of the vector \(\mathbf {a}\) and the matrix \(\mathbf {A}\). The standard basis of \(\mathbb {C}^n\) is identified by \(\{\mathbf {e}_i\}_{i \in [n]}\). For \(\mathbf {a}\in \mathbb {C}^n\), we define \(\mathrm {diag}(\mathbf {a})=(a_i \delta _{ij})_{i,j\in [n]}\) to be the diagonal matrix whose diagonal entries are the entries of \(\mathbf {a}\), where \(\delta _{ij}\) denotes the Kronecker delta. The identity matrix of order n is denoted by \(\mathbf {I}_n\). For any \(\mathbf {a}\in \mathbb {R}^n\), we set \(\left\| \mathbf {a}\right\| _{\infty }\) and \(\left\| \mathbf {a}\right\| _{2}\) as the infinity and the Euclidean norm, respectively. For any matrix \(\mathbf {A}=(a_{ij})_{i \in [m], j \in [n]}\), we define the norm \(\left\| \mathbf {A}\right\| = \max _{j \in [n]} \left\| \mathbf {a}_j\right\| _2\), where \(\mathbf {a}_j\) is the j-th column vector of \(\mathbf {A}\) for \(j \in [n]\). Further, we denote by \(\left\| \mathbf {A}\right\| _F\) the Frobenius norm given by \(\left\| \mathbf {A}\right\| _F^2= \sum _{i \in [m]} \sum _{j \in [n]} {a_{ij}}^2~\) and, by \(\mathrm {GS}(\mathbf {A})=(\mathrm {GS}(\mathbf {a}_j))_{j\in [n]}\) the Gram–Schmidt orthogonalization of \(\mathbf {A}\) from left to right.
2.1 Algebraic Number Theory
A number field \(K=\mathbb {Q}(\zeta )\) of degree n is a finite extension of the rational number field \(\mathbb {Q}\) obtained by adjoining an algebraic number \(\zeta \). We define the tensor field \(K_{\mathbb {R}} = K \otimes _{\mathbb {Q}} \mathbb {R}\) which can be seen as the finite field extension of the reals by adjoining \(\zeta \). The set of all algebraic integers of K defines a ring, called the ring of integers which we denote R. It is always true that \(\mathbb {Z}[\zeta ] \subseteq R\), where this inclusion can be strict. Lemma 7 is restricted to the class of number fields where the equality \(R = \mathbb {Z}[\zeta ]\) holds. This is the case for some quadratic extensions (i.e., when \(\zeta =\sqrt{d}\) with d square-free and \(d \ne 1 \bmod 4\)), cyclotomic fields (i.e., when \(\zeta \) is a primitive root of the unity) and number fields with a defining polynomial f of square-free discriminant \(\varDelta _f\).
A subset \(M \subseteq K^d\) is an R-module of rank d if it is closed under addition by elements of M and under multiplication by elements of R. It is a finitely generated module if there exists a finite family \(\{ b_k \}_k\) of vectors in \(K^d\) such that \(M = \sum _k R \cdot b_k\).
Space \(\varvec{H.}\) We introduce the space \(H \subseteq \mathbb {R}^{t_1} \times \mathbb {C}^{2t_2}\), where \(n=t_1 + 2t_2\), as
For \(j \in [t_1]\), we set \(\mathbf {h}_j = \mathbf {e}_j\), and for \(j \in \{t_1+1, \dots , t_1 + t_2\}\), we set \(\mathbf {h}_j = \frac{1}{\sqrt{2}} (\mathbf {e}_j + \mathbf {e}_{j+t_2})\) and \(\mathbf {h}_{j+t_2} = \frac{i}{\sqrt{2}} (\mathbf {e}_j - \mathbf {e}_{j+t_2})\). The set \(\{ \mathbf {h}_j\}_{j \in [n]}\) forms an orthonormal basis of H as a real vector space, showing that H is isomorphic to \(\mathbb {R}^n\). The change of basis is given by the unitary matrix
Canonical Embedding. Any number field \(K=\mathbb {Q}(\zeta )\) of degree n has exactly n field homomorphisms \(\sigma _i :K \rightarrow \mathbb {C}\) fixing each element of \(\mathbb {Q}\), where \(i \in [n]\). Let \(\sigma _1, \dots , \sigma _{t_1}\) be the real embeddings and \(\sigma _{t_1+1}, \dots , \sigma _{t_1 + 2t_2}\) the complex embeddings. The complex ones come in conjugate pairs, thus \(\sigma _i = \overline{\sigma _{i+t_2}}\) for \(i \in \{t_1+1,\dots , t_1+t_2\}\). In the particular case of cyclotomic fields, all n embeddings are complex. The canonical embedding \(\sigma \) is defined as the map \(\sigma :K \rightarrow H\), where \(\sigma (x)=(\sigma _i(x))_{i \in [n]}\). It describes a field homomorphism, where multiplication and addition in H are component-wise. By abuse of notation, for an \(\mathbf {x}\in K^d\), we also write \(\sigma (\mathbf {x})\) to denote the vector \((\sigma (x_i))_{i\in [d]} \in \mathbb {C}^{n d}\). We can represent \(\sigma (x)\) via the real vector \(\sigma _H(x) \in \mathbb {R}^n\) through the change of basis described above, i.e., \(\sigma _H(x)=({\mathbf {U}_H})^{\dagger } \cdot \sigma (x)\). Note that multiplication is not component-wise for \(\sigma _H\). More concretely, in the basis \(\{\mathbf {e}_i\}_{i\in [n]}\), multiplication by \(x \in K\) can be described as the left multiplication by the matrix \(\mathbf {X}=(x_{ij})_{i,j \in [n]}\), where \(x_{ij} = \sigma _i(x) \cdot \delta _{ij}\). Hence, changing to the basis \(\{ \mathbf {h}_i \}_{i \in [n]}\) leads to the corresponding matrix of multiplication \(\mathbf {X}_H = ({\mathbf {U}_H})^{\dagger } \mathbf {X}\mathbf {U}_H\), having the same singular values as \(\mathbf {X}\), given by  .
.
The trace \(\text {Tr} :K \rightarrow \mathbb {Q}\) is defined as the sum of the embeddings, i.e., for any \(x \in K\), we have \(\text {Tr}(x) = \sum _{i \in [n]} \sigma _i (x)\). For any fractional ideal \(\mathcal {I}\subset K\), we define the dual \(\mathcal {I}^{\vee }\) of \(\mathcal {I}\) as \(\mathcal {I}^{\vee } = \left\{ x \in K :\text {Tr}(x\mathcal {I}) \subseteq \mathbb {Z}\right\} .\) In the case of \(R=\mathbb {Z}[\zeta ]\), it yields \(R^{\vee } = \frac{1}{f'(\zeta )} R,\) where f is the defining polynomial of K. In particular, for \(K \cong \mathbb {Q}[x]/ \langle x^n+1 \rangle \) the \(\nu \)-th cyclotomic field, where \(\nu \) is a power of two and \(n=\nu /2\), it holds \(R^{\vee } = \frac{1}{n}R\).
Coefficient Embedding. Every number field \(K=\mathbb {Q}(\zeta )\) of degree n defines an n-dimensional vector space over \(\mathbb {Q}\) with basis \(\{1,\zeta , \dots , \zeta ^{n-1} \}\). Thus, every element \(x \in K\) can be written as \(x=\sum _{i=0}^{n-1} x_i \zeta ^i\), where \(x_i \in \mathbb {Q}\). The coefficient embedding \(\tau :K \rightarrow \mathbb {R}^n\) is the map that sends every element \(x \in K\) to its coefficient vector \(\tau (x)=(x_0,\dots ,x_{n-1})^T\). Multiplication by x in the coefficient embedding can be represented by a matrix multiplication, where we denote the corresponding matrix by \(\mathrm {Rot}(x) \in \mathbb {R}^{n \times n}\). Note that the matrix \(\mathrm {Rot}(x)\) is invertible in K for every \(x\ne 0\) and that its concrete form depends on the field K. Again, looking at the example, where \(K=\mathbb {Q}(\zeta )\) is the \(\nu \)-th cyclotomic field, with \(\nu \) a power of two and thus \(K \cong \mathbb {Q}[x]/ \langle x^n+1 \rangle \) with \(n=\nu /2\), it yields
As both embeddings play an important role in this paper, we recall how to go from one to the other. For any \(x \in K\), the embeddings \(\sigma (x)\) and \(\tau (x)\) are linked through the Vandermonde matrix \(\mathbf {V}\) of the roots of the defining polynomial f. For \(i \in [n]\), we let \(\alpha _i = \sigma _i(\zeta )\) be the i-th root of f. Then, \(\sigma (x) = \mathbf {V}\cdot \tau (x)\), where

2.2 Lattices
An n-dimensional lattice \(\varLambda \subseteq \mathbb {R}^n\) is a discrete additive subgroup of \(\mathbb {R}^n\). Within this work, we assume \(\varLambda \) to be of full rank n, i.e., \(\text {span}_{\mathbb {Q}}(\varLambda )=\mathbb {R}^n\). It can be seen as the set of all linear integer combinations of some n linearly independent vectors \(\mathbf {B}=\{ \mathbf {b}_i\}_{i \in [n]} \subseteq \mathbb {R}^n\), thus \( \varLambda = \left\{ \sum _{i \in [n]} z_i \mathbf {b}_i :z_i \in \mathbb {Z}\right\} .\) We call \(\mathbf {B}\) a basis of \(\varLambda \). The minimum \(\lambda _1(\varLambda )\) of a lattice \(\varLambda \) is the Euclidean norm of any of its shortest nonzero vectors. The dual lattice \(\varLambda ^*\) is defined by \(\varLambda ^* = \left\{ \mathbf {x}\in \mathbb {R}^n :\langle \mathbf {x},\mathbf {y}\rangle \in \mathbb {Z}, \forall \mathbf {y}\in \varLambda \right\} \). If \(\mathbf {B}\) is basis of \(\varLambda \), then \(\mathbf {B}^*=(\mathbf {B}^T)^{-1}\) is a basis of \(\varLambda ^*\). The fundamental parallelepiped \(\mathcal {P}(\mathbf {B})\) of the lattice \(\varLambda \) generated by the basis \(\mathbf {B}=\{\mathbf {b}_i\}_{i \in [n]}\) is defined as \(\mathcal {P}(\mathbf {B}) = \left\{ \sum _{i \in [n]} z_i \mathbf {b}_i :z_i \in \left[ -\frac{1}{2},\frac{1}{2}\right) , \forall i \in [n] \right\} .\) For any \(\mathbf {w}\in \mathbb {R}^n\), we write \(\mathbf {x}= \mathbf {w}\bmod \mathbf {B}\) to denote the unique point \(\mathbf {x}\in \mathcal {P}(\mathbf {B})\) such that \(\mathbf {w}-\mathbf {x}\in \varLambda \). One of the most studied lattice problems is the shortest vector problem (SVP). It exists in both search and decisional versions, but within this paper we are only using the approximation variant of the latter.
Definition 1
(Shortest vector problem). Let \(\gamma = \gamma (n) \ge 1\) be a function in the dimension n. An input to the shortest vector problem \(\mathrm {GapSVP}_{\gamma }\) is a pair \((\mathbf {B},\delta )\), where \(\mathbf {B}\) is a basis of an n-dimensional lattice \(\varLambda \) and \(\delta >0\) is a real number. It is a YES instance if \(\lambda _1(\varLambda ) \le \delta \), and it is a NO instance if \(\lambda _1(\varLambda ) > \gamma \cdot \delta \). The problem asks to distinguish whether a given instance is a YES or a NO instance. If \(\lambda _1(\varLambda )\) falls in \((\delta , \gamma \cdot \delta ]\), we can return anything.
Let R be of degree n. Any rank d module \(M\subseteq K^d\) of R is mapped by the canonical embedding \((\sigma _H, \dots , \sigma _H) :K^d \rightarrow \mathbb {R}^{nd}\) to a lattice in \(\mathbb {R}^{nd}\). By abuse of notation, we simply write \(\sigma _H\). Such lattices are called module lattices. The \(\mathrm {GapSVP}_{\gamma }\) restricted to module lattices is denoted by \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\). For any \(\mathbf {x}\in K^d\), we define three different norms \(\Vert \mathbf {x}\Vert _2= \Vert (\sigma _H(x_k))_{k \in [d]} \Vert _2\), \(\Vert \mathbf {x}\Vert _{\infty }= \Vert (\sigma _H(x_k))_{k \in [d]} \Vert _{\infty }\) and \(\Vert \mathbf {x}\Vert _{2,\infty } = \max _{i \in [n]} ( \sum _{k \in [d]} | \sigma _i(x_k) |^2 )^{1/2}\). Within this paper, we further need two intermediate lattice problems, presented in the setting of module lattices.
Definition 2
(Bounded distance decoding). Let K be a number field with R its ring of integers of degree n and \(M \subseteq K^d\) be a module of R of rank d. Further, let \(\delta \) be a positive real number. An input to the bounded distance decoding problem \(\mathrm {BDD}_{M,\delta }\) is a point \(\mathbf {y}\in K^d\) of the form \(\mathbf {y}= \mathbf {x}+ \mathbf {e}\), where \(\mathbf {x}\in M\) and \(\Vert \mathbf {e}\Vert _{2,\infty } \le \delta \). The problem asks to find \(\mathbf {x}\).
By \(D_g\) we denote the continuous Gaussian distribution of width g on \(K_{\mathbb {R}}^d\), which we define properly in the next subsection.
Definition 3
(Gaussian decoding problem). Let K be a number field with R its ring of integers of degree n and \(M \subseteq K^d\) be a module of R of rank d. Further, let \(g>0\) be a Gaussian parameter. An input to the gaussian decoding problem \(\mathrm {GDP}_{M,g}\) is a coset \(\mathbf {y}+ M\), where \(\mathbf {y}\leftarrow D_g\). The goal is to find \(\mathbf {y}\).
Every \(\mathrm {GDP}_{M,g}\) instance defines a \(\mathrm {BDD}_{M,\delta }\) one with \(\delta =g \cdot \sqrt{d} \cdot \omega (\sqrt{\log _2 n})\). Note that \(\mathrm {GapSVP}\), \(\mathrm {BDD}\) and \(\mathrm {GDP}\) can also be defined with regard to other norms.
Lemma 1
([LLL82], [Bab85]). There exists a polynomial-time algorithm that solves \(\mathrm {BDD}_{M,\delta }\) for \(\delta = 2^{-\frac{N}{2}} \cdot \lambda _1(M)\), where \(N=nd\).
2.3 Probabilities
For a set S and a distribution \(\chi \) on S, we denote by \(x \leftarrow \chi \) the process of sampling \(x \in S\) according to \(\chi \). By U(S) we denote the uniform distribution on S. For \(s>0\) and a vector \(\mathbf {c}\in \mathbb {R}^n\), the Gaussian function \(\rho _{s,\mathbf {c}}\) is defined by \( \rho _{s,\mathbf {c}}(\mathbf {x}) = \exp \left( - \frac{\pi \Vert \mathbf {x}- \mathbf {c}\Vert _2^2}{s^2} \right) .\) By normalizing the Gaussian function, we obtain the density function of the n-dimensional continuous Gaussian distribution \(D_{s,\mathbf {c}}\) of width s and center \(\mathbf {c}\). If the center is the zero vector \(\mathbf{0} \), we simply omit the index \(\mathbf {c}\) and write \(D_{s}\). For an n-dimensional lattice \(\varLambda \subseteq \mathbb {R}^n\), the discrete Gaussian distribution \(\mathcal {D}_{\varLambda , s,\mathbf {c}}\) of width s and center \(\mathbf {c}\) for \(\varLambda ~\) is defined by its density function \(\mathcal {D}_{\varLambda ,s,\mathbf {c}} (\mathbf {x}) = \frac{D_{s,\mathbf {c}}(\mathbf {x})}{{D_{s,\mathbf {c}}(\varLambda )}}\), where \(D_{s,\mathbf {c}}(\varLambda ) = \sum _{\mathbf {y}\in \varLambda } {D_{s,\mathbf {c}}(\mathbf {y})}\). Again, if the center is \(\mathbf{0} \), we simply omit the index \(\mathbf {c}\) and write \(\mathcal {D}_{\varLambda ,s}\).
Using the identification of H as \(\mathbb {R}^n\), we can extend the definition of the continuous Gaussian distribution to an elliptical Gaussian distribution in the basis \(\{ \mathbf {h}_i \}_{i \in [n]}\) as follows. Let \(\mathbf {r}=(r_1,\dots ,r_n)^T \in \mathbb {R}^n\) be a vector such that \(r_i >0\) for all \(i \in [n]\) and \(r_{t_1+j} = r_{t_1+t_2+j}\) for all \(j \in [t_2]\), where \(n=t_1 + 2t_2\). A sample from \(D_{\mathbf {r}}\) on H is given by \(\sum _{i \in [n]} x_i \mathbf {h}_i\), where \(x_i \leftarrow D_{r_i}\) over \(\mathbb {R}\) for \(i \in [n]\). By applying the inverse of the canonical embedding \(\sigma \), this provides Gaussian distributions on \(K^d_{\mathbb {R}}\) for any d. For \(0 \le \alpha <\alpha '\), we define \(\Psi _{[\alpha ,\alpha ']}\) to be the set of Gaussian distributions \(D_{\mathbf {r}}\) with \(\alpha <r_i \le \alpha '\) for all \(i \in [n]\). If \(\alpha =0\), we simply write \(\Psi _{\le \alpha '}\). Further, for any positive real \(\alpha \), we define the distribution \(\Upsilon _{\alpha }\) on distributions on H as done by Peikert et al. [PRS17]. Fix an arbitrary \(f(n)=\omega (\sqrt{\log _2 n})\). A distribution sampled from \(\Upsilon _{\alpha }\) is an elliptical Gaussian \(D_{\mathbf {r}}\), where \(\mathbf {r}\) is sampled as follows: For \(i \in [t_1]\), sample \(x_i \leftarrow D_1\) and set \(r_i^2 = \alpha ^2 (x_i^2 + f^2(n))/2\). For \(i \in \{t_1+1,\dots ,t_1+t_2\}\), sample \(x_i, y_i \leftarrow D_{1/\sqrt{2}}\) and set \(r_i^2=r_{i+t_2}^2=\alpha ^2 (x_i^2 + y_i^2 + f^2(n))/2\). Additionally, we define the smoothing parameter \(\eta _{\varepsilon }(\varLambda )\) of a lattice \(\varLambda \) which was first introduced by Micciancio and Regev [MR07]. Informally, this gives a threshold above which many properties of the continuous Gaussian distribution also hold for its discrete counterpart.
Definition 4
(Smoothing parameter). Let \(\varLambda \) be an n-dimensional lattice and \(\varepsilon \) be a positive real number, the smoothing parameter \(\eta _{\varepsilon }(\varLambda )\) is defined as the smallest positive real s such that \(\rho _{1/s}(\varLambda ^*\setminus \{\mathbf {0}\}) \le \varepsilon \).
In particular, we need the following bounds on the smoothing parameter.
Lemma 2
(Lem. 1.5 [Ban93] and Claim 2.13 [Reg05]). Let \(\varLambda \) be an n-dimensional lattice and \(\varepsilon = \exp (-n)\), it holds \( \frac{\sqrt{n}}{\sqrt{\pi } \lambda _1(\varLambda ^*)} \le \eta _{\varepsilon }(\varLambda ) \le \frac{\sqrt{n}}{\lambda _1(\varLambda ^*)}.\)
The statistical distance is a widely used measure of distribution closeness.
Definition 5
(Statistical distance). Let P and Q be two discrete probability distributions on a discrete domain E. The statistical distance is defined as \( \varDelta (P,Q) = \frac{1}{2} \sum _{x \in E} \vert P(x)-Q(x) \vert .\)
The statistical distance fulfills the probability preservation property.
Lemma 3
Let P, Q be two probability distributions with  and
and  be an arbitrary event. Then, \(P(E) \le \varDelta (P,Q) + Q(E)\).
be an arbitrary event. Then, \(P(E) \le \varDelta (P,Q) + Q(E)\).
Within the paper, we need the following two results about the statistical distance of two Gaussian distributions.
Lemma 4
(Thm. 1.2 [DMR18]). Let \(D_g\) denote the continuous Gaussian distribution on \(K_{\mathbb {R}}\) and let \(z \in K\). The statistical distance between \(D_g\) and \(D_{g,z}\) is bounded above by \(\frac{\sqrt{2\pi } \Vert z \Vert _2}{g}\).
Lemma 5
(Claim 2.2 [Reg05]). Let \(\alpha \) and \(\beta \) be positive reals such that \(\alpha < \beta \). The statistical distance between \(D_{\alpha }\) and \(D_{\beta }\) is bounded above by \(10 \cdot \left( \frac{\beta }{\alpha }-1\right) \).
The following lemma describes the behavior of the sum of a continuous Gaussian and a discrete one.
Lemma 6
(Claim. 3.9 [Reg09]). Let \(\varLambda \) be an n-dimensional lattice, \(s>0\), \(r>0\) and \(t=\sqrt{r^2+s^2}\). Assume that \(\frac{r s}{t} \ge \eta _{\varepsilon }(\varLambda )\) for some \(\varepsilon \in (0,\frac{1}{2})\). Consider the distribution Y on \(\mathbb {R}^n\) obtained by sampling from \(\mathcal {D}_{\varLambda ,r}\) and then adding a vector taken from \(D_{s}\). Then, it yields \(\varDelta (Y,D_{t}) \le 2\varepsilon \).
Further, we need a ring version of the leftover hash lemma, where the secret vector contains binary polynomials. For this purpose, we adapt a result from Micciancio [Mic07]. A proof can be found in the full version [BJRW20].
Lemma 7
Let n, m, d, q be positive integers, with q prime. Further, let f be the defining polynomial of degree n of the number field \(K\cong \mathbb {Q}[x]/ \langle f \rangle \) such that its ring of integers is \(R= \mathbb {Z}[x]/ \langle f \rangle \). We set \(R_q=R / qR\) and \(R_2=R / 2R\). Then,
where \(\mathbf {A}\leftarrow U((R_q)^{d \times m})\), \(\mathbf {x}\leftarrow U((R_2)^m)\) and \(\mathbf {v}\leftarrow U((R_q)^d)\).
In order to guarantee a statistical distance negligibly small in n for a fixed rank d, we require \(m \ge d \log _2 q + \omega (\log _2 n)\). Note that the requirement \(\Omega (\log _2 n)\) is not strong enough as \(\lim _{n \rightarrow \infty }\left( 1 + \frac{1}{c\cdot n} \right) ^n=e^{\frac{1}{c}}\), for any positive constant c.
The Rényi divergence [R61, vEH14] defines another measure of distribution closeness and was thoroughly studied for its use in cryptography as a powerful alternative for the statistical distance measure by Bai et al. [BLL+15]. In this paper, it suffices to use the Rényi divergence of order 2.
Definition 6
(Rényi divergence of order 2). Let P and Q be two discrete probability distributions such that  . The Rényi divergence of order 2 is defined as
. The Rényi divergence of order 2 is defined as

The Rényi divergence is multiplicative and fulfills the probability preservation property, as proved by van Erven and Harremoës [vEH14].
Lemma 8
Let P, Q be two discrete probability distributions with  and
and  be an arbitrary event. Further, let \((P_n)_{n \in \mathbb {N}}, (Q_n)_{n \in \mathbb {N}}\) be two families of independent discrete probability distributions with
be an arbitrary event. Further, let \((P_n)_{n \in \mathbb {N}}, (Q_n)_{n \in \mathbb {N}}\) be two families of independent discrete probability distributions with  for all \(n \in \mathbb {N}\). Then, the following properties are fulfilled:
for all \(n \in \mathbb {N}\). Then, the following properties are fulfilled:
In Sect. 3, we need the Rényi divergence of two shifted discrete Gaussians.
Lemma 9
(Adapted from Lem. 4.2 [LSS14]). Let s and \(\varepsilon \) be positive real numbers with \(\varepsilon \in (0,1)\), \(\mathbf {c}\) be a vector of \(\mathbb {R}^n\) and \(\varLambda \) be a full-rank lattice in \(\mathbb {R}^n\). We assume that \(s \ge \eta _{\varepsilon }(\varLambda )\). Then,
2.4 The Module Learning with Errors Problem
The module variant of \(\mathrm {LWE}\) was first defined by Brakerski et al. [BGV12] and thoroughly studied by Langlois and Stehlé [LS15]. It describes the following problem. Let K be a number field of degree n and R its ring of integers with dual \(R^{\vee }\). Further, let d denote the rank and let \(\psi \) be a distribution on \(K_{\mathbb {R}}\) and \(\mathbf {s}\in (R^{\vee }_q)^d\) be a vector. We let \(A^{(R^d)}_{\mathbf {s},\psi }\) denote the distribution on \((R_q)^{d} \times \mathbb {T}_{R^{\vee }}\) obtained by choosing a vector \(\mathbf {a}\leftarrow U((R_q)^{d})\), an element \(e \leftarrow \psi \) and returning \((\mathbf {a}, \frac{1}{q}\langle \mathbf {a}, \mathbf {s}\rangle + e \bmod R^{\vee })\).
Definition 7
Let q, d be positive integers with \(q \ge 2\). Let \(\varPsi \) be a family of distributions on \(K_{\mathbb {R}}\). The search version \(\mathrm {M\text {-}SLWE}_{n,d,q,\varPsi }\) of the module learning with errors problem is as follows: Let \(\mathbf {s}\in (R^{\vee }_q)^d\) be secret and \(\psi \in \varPsi \). Given arbitrarily many samples from \(A^{(R^d)}_{\mathbf {s},\psi }\), the goal is to find \(\mathbf {s}\). Let \(\varUpsilon \) be a distribution on a family of distributions on \(K_{\mathbb {R}}\). Its decision version \(\mathrm {M\text {-}LWE}_{n,d,q,\Upsilon }\) is as follows: Choose \(\mathbf {s}\leftarrow U((R^{\vee }_q)^d)\) and \(\psi \leftarrow \varUpsilon \). The goal is to distinguish between arbitrarily many independent samples from \(A^{(R^d)}_{\mathbf {s},\psi }\) and the same number of independent samples from \(U((R_q)^d \times \mathbb {T}_{R^{\vee }})\).
Fixed Number of Samples. When using the Rényi divergence as a tool to measure the distance of two given probability distributions, we need to fix the number of requested samples a priori. Let m be the number of requested \(\mathrm {M\text {-}LWE}\) samples \((\mathbf {a}_i, \frac{1}{q}\langle \mathbf {a}_i, \mathbf {s}\rangle + e_i)\) for \(i \in [m]\), then we consider the matrix \(\mathbf {A}\in R_q^{m \times d}\) whose rows are the \(\mathbf {a}_i\)’s and we set \(\mathbf {e}=(e_1, \dots , e_m)^T\). We obtain the representation \((\mathbf {A},\frac{1}{q}\mathbf {A}\cdot \mathbf {s}+ \mathbf {e})\), where \(\mathbf {s}\in (R_q^{\vee })^d\). We denote this problem by \(\mathrm {M\text {-}LWE}^m_{n,d,q,\Upsilon }\).
Multiple Secrets. Let k, m be natural numbers, where m denotes the number of requested samples of \(A^{(R^d)}_{\mathbf {s},\psi }\). In the multiple secrets version, the secret vector \(\mathbf {s}\in (R_q^{\vee })^d\) is replaced by a secret matrix \(\mathbf {S}\in (R_q^{\vee })^{d \times k}\) and the error vector \(\mathbf {e}\leftarrow \psi ^m\) by an error matrix \(\mathbf {E}\leftarrow \psi ^{m \times k}\). There is a simple polynomial-time reduction from \(\mathrm {M\text {-}LWE}\) using a secret vector to \(\mathrm {M\text {-}LWE}\) using a secret matrix for any k polynomially large in d via a hybrid argument, as given for instance in [Mic18, Lem. 2.9]. We denote the corresponding problem by \(\mathrm {M\text {-}LWE}^{m,k}_{n,d,q,\Upsilon }\).
Binary Secret. Another possibility is to choose a small secret. We are interested in the case where the secret vector \(\mathbf {s}\) is a binary vector, thus chosen from the set \((R^{\vee }_2)^d\). We denote the corresponding problem by \(\text {bin-}\mathrm {M\text {-}LWE}_{n,d,q,\Upsilon }\). Note that \(R^{\vee }_2\) is defined with regard to the coefficient embedding \(\tau \), see Sect. 2.1.
Discrete Version. As pointed out by Lyubashevsky et al. [LPR10], sometimes it can be more convenient to work with a discrete variant, where the second component b of each sample \((\mathbf {a},b)\) is taken from a finite set, and not from the continuous domain \(\mathbb {T}_{R^{\vee }}\). Indeed, for the case of \(\mathrm {M\text {-}LWE}\), if the rounding function \(\left\lfloor \cdot \right\rceil _{} :K_{\mathbb {R}} \rightarrow R^{\vee }\) is chosen in a suitable way, see Lyubashevsky et al. [LPR13, Sec. 2.6] for more details, then every sample \((\mathbf {a}, b= \frac{1}{q} \langle \mathbf {a}, \mathbf {s}\rangle + e) \in (R_q)^d \times \mathbb {T}_{R^{\vee }}~\) of the distribution \(A^{(R^d)}_{\mathbf {s},\psi }\) can be transformed to \((\mathbf {a}, \left\lfloor q \cdot b \right\rceil _{}) =(\mathbf {a}, \langle \mathbf {a}, \mathbf {s}\rangle + \left\lfloor q \cdot e \right\rceil _{} \bmod q R^{\vee }) \in (R_q)^d \times R^{\vee }_q\). For technical reasons, we use the latter representation in Sect. 3.
3 Hardness of Binary M-LWE
In the following, we show a reduction from \(\mathrm {M\text {-}LWE}\) to its binary secret version, if the module rank d is at least of size \(\log _2 q + \omega (\log _2 n)\), where q is the modulus and n is the degree of the underlying number field.
Our proof follows the proof structure of Goldwasser et al. [GKPV10], but achieves better parameters by using the Rényi divergence, while being as direct and short as the original proof. The improvement on the noise rate \(\frac{\alpha }{\beta }\) compared to [GKPV10] stems from the fact that the Rényi divergence only needs to be constant for the reduction to work and not necessarily negligibly close to 1 (compared to negligibly close to 0 for the statistical distance). However, using the Rényi divergence as a tool for distance measurement requires to move to the search variants of \(\mathrm {M\text {-}LWE}\) and its binary version, respectively.
Within the proof of Theorem 1 we need to apply the leftover hash lemma over rings (Lemma 7), and thus need to require that the modulus q is prime. Further, we need Lemma 10, which only holds for cyclotomic number fields \(K=\mathbb {Q}(\zeta )\), where \(\zeta \) is a primitive root of unity. As stated in Sect. 2.1, in this case it holds \(R^{\vee }_q=\frac{1}{f'(\zeta )}R_q\) for all \(q \in \mathbb {Z}\). In order to ease notation, we set \(\lambda = {f'(\zeta )}\) and write \(x = \frac{1}{\lambda } \cdot \tilde{x}\) for every \(x \in R^{\vee }_q\), where \(\tilde{x} \in R_q\).
In the following, we study the \(\mathrm {M\text {-}LWE}\) problem in its discrete version, as introduced in Sect. 2.4. This is convenient as we replace in the course of the proof the public matrix \(\mathbf {A}\in (R_q)^{m \times d}\) by the second part of some multiple-secret \(\mathrm {M\text {-}LWE}\) sample. Thus, we need to ensure that the second part is also an element of \((R_q)^{m \times d}\). Hence, we represent m samples by \((\mathbf {A},\mathbf {A}\cdot \mathbf {s}+ \mathbf {e}\bmod qR^{\vee }) \in (R_q)^{m \times d} \times (R^{\vee }_q)^m\), with \(\mathbf {s}\in (R^{\vee }_2)^d\) and \(\mathbf {e}\leftarrow \psi \), where \(\psi \) is a distribution on \(R^{\vee }\). The theorem uses the discrete Gaussian distribution \(\psi = \mathcal {D}_{R^{\vee },\alpha q}\), for some positive real \(\alpha \).
Theorem 1
Let K be a cyclotomic number field of degree n with R its ring of integers. Let \(\ell ,d,m\) and q be positive integers with q prime and m polynomial in n. Further, let \(\alpha \) and \(\beta \) be positive real numbers such that \(\frac{\alpha }{\beta } \le \frac{1}{\sqrt{m}\cdot n^2 d}\). Let \(\varepsilon \) be a positive real number with \(\varepsilon \in [0,1)\) such that \(\beta q \ge \eta _{\varepsilon }(R^{\vee })\). and \(\varepsilon =O(\frac{1}{m})\). Then, for any \(d \ge \ell \cdot \log _2 q + \omega (\log _2 n)\), there is a probabilistic polynomial-time reduction from \(\mathrm {M\text {-}SLWE}^m_{n,\ell ,q,\mathcal {D}_{R^{\vee },\beta q}}\) and \(\mathrm {M\text {-}LWE}^{m,d}_{n,\ell ,q,\mathcal {D}_{R^{\vee },\alpha q}}\) to \(\text {bin-}\mathrm {M\text {-}SLWE}^m_{n,d,q,{\mathcal {D}_{R^{\vee },\beta q}}}\).
The degree n of the number field K and the number of samples m are preserved. The reduction increases the rank of the module from \(\ell \) to \(\ell \cdot \log _2 q + \omega (\log _2 n)\) and the Gaussian width from \(\alpha q\) to \(\alpha q \cdot \sqrt{m}\cdot n^2 d\). Further, \(\mathrm {M\text {-}LWE}^m_{n,\ell ,q,\mathcal {D}_{R^{\vee },\alpha q}}\) trivially reduces to \(\mathrm {M\text {-}SLWE}^m_{n,\ell ,q,\mathcal {D}_{R^{\vee },\beta q}}\), as \(\beta \ge \alpha \).
Proof
Fix any \(n,\ell ,d,m,q,\alpha ,\beta \) and \(\varepsilon \) as in the statement of the theorem. Given a \(\text {bin-}\mathrm {M\text {-}SLWE}^m_{n,d,q,\mathcal {D}_{R^{\vee },\beta q}}\) sample \((\mathbf {A},\mathbf {A}\cdot \mathbf {s}+ \mathbf {e}) \in (R_q)^{m \times d} \times (R^{\vee }_q)^m\), with \(\mathbf {s}\in (R^{\vee }_2)^d\) and \(\mathbf {e}\leftarrow (\mathcal {D}_{R^{\vee },\beta q})^m\), the search problem asks to find \(\mathbf {s}\) and \(\mathbf {e}\). In order to prove the statement, we define different hybrid distributions:
-
\(H_0:\) \((\mathbf {A},\mathbf {A}\cdot \mathbf {s}+\mathbf {e})\), as in \(\text {bin-}\mathrm {M\text {-}SLWE}^m_{n,d,q,\mathcal {D}_{R^{\vee },\beta q}}\),
-
\(H_1:\) \((\mathbf {A}'=\lambda (\mathbf {B}\mathbf {C}+\mathbf {Z}),\mathbf {A}' \cdot \mathbf {s}+\mathbf {e})\), where \(\mathbf {B}\leftarrow U((R_q)^{m \times \ell })\), \(\mathbf {C}\leftarrow U((R^{\vee }_q)^{\ell \times d})\), and \(\mathbf {Z}\leftarrow (\mathcal {D}_{R^{\vee },\alpha q})^{m \times d}\) and \(\mathbf {s},\mathbf {e}\) as in \(H_0\),
-
\(H_2:\) \((\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {B}(\lambda \mathbf {C}\mathbf {s}) + \mathbf {Z}(\lambda \mathbf {s}) + \mathbf {e})\), where \(\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {s},\mathbf {e}\) as in \(H_1\),
-
\(H_3:\) \((\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {B}(\lambda \mathbf {C}\mathbf {s}) + \mathbf {e}')\), where \(\mathbf {e}' \leftarrow (\mathcal {D}_{R^{\vee },\beta q})^m\) and \(\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {s}\) as in \(H_2\),
-
\(H_4:\) \((\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {B}\mathbf {s}'+\mathbf {e}')\), where \(\mathbf {s}' \leftarrow U((R_q^{\vee })^{\ell })\) and \(\mathbf {B},\mathbf {C},\mathbf {Z},\mathbf {e}'\) as in \(H_3\).
For \(i \in \{0,\dots ,4\}\), we denote by \(P_i\) the problem of finding the secret \(\mathbf {s}\) (resp. \(\mathbf {s}'\) in \(H_4\)), given a sample of the distribution \(H_i\). We say that problem \(P_i\) is hard if for any probabilistic polynomial-time attacker  the advantage of solving \(P_i\) is negligible, thus
the advantage of solving \(P_i\) is negligible, thus  , where n is the degree of K. The overall idea is to show that if \(P_4\) is hard, then \(P_0\) is hard as well.
, where n is the degree of K. The overall idea is to show that if \(P_4\) is hard, then \(P_0\) is hard as well.
Problem \(P_4\) is hard: By the hardness assumption of \(\mathrm {M\text {-}SLWE}^m_{n,\ell ,q,{\mathcal {D}_{R^{\vee },\beta q}}}\), it yields

From \(P_4\) to \(P_3\): By the probability preservation property of the statistical distance (Lemma 3), we have

The only difference between the distributions \(H_3\) and \(H_4\) is that the element \(\lambda \mathbf {C}\mathbf {s}\) in \(H_3\) is replaced by \(\mathbf {s}'\) in \(H_4\). Our aim is to show that \(\lambda \mathbf {C}\mathbf {s}\) is statistically close to the uniform distribution on \((R_q^{\vee })^{\ell }\). We set \(\tilde{\mathbf {C}}=\lambda \mathbf {C}\in (R_q)^{\ell \times d}\) and \(\mathbf {s}=\frac{1}{\lambda } \tilde{\mathbf {s}}\), where \(\tilde{\mathbf {s}} \in (R_2)^d\). By the leftover hash lemma (Lemma 7) it yields that the distribution \((\tilde{\mathbf {C}},\tilde{\mathbf {C}}\tilde{\mathbf {s}})\) is statistically close to the distribution \((\tilde{\mathbf {C}},\tilde{\mathbf {s}}')\), where \(\tilde{\mathbf {s}}' \leftarrow U((R_q)^{\ell })\), as \(d \ge \ell \log _2 q + \omega (\log _2 n)\). Dividing the first and the second part of both distributions by \(\lambda \) preserves the statistical distance and yields that the distribution \((\mathbf {C},\lambda \mathbf {C}\mathbf {s})\) is statistically close to the distribution \((\mathbf {C},\mathbf {s}')\), where \(\mathbf {s}' \leftarrow U((R_q^{\vee })^{\ell })\). Overall, it yields \( \varDelta (H_3,H_4) \le \frac{1}{2} \sqrt{( 1 + {q^{\ell }}/{2^d})^n -1}. \) As we require \(d \ge \ell \log _2 q + \omega (\log _2 n)\), we obtain \(\varDelta (H_3,H_4) \le n^{-\omega (1)}\).
From \(P_3\) to \(P_2\): By the probability preservation property of the Rényi divergence (Lemma 8), we have

In order to compute the Rényi divergence of \(H_2\) and \(H_3\), we need to compute the Rényi divergence of \(\mathbf {Z}(\lambda \mathbf {s}) +\mathbf {e}\) and \(\mathbf {e}'\). We claim that each of the m coefficients of \(\mathbf {Z}(\lambda \mathbf {s})\) is bounded above by \(\alpha qdn^2\) with probability \(1-2^{-\Omega (n)}\), and provide a detailed proof below in Lemma 10. Thus, it suffices to compute the Rényi divergence of \((D_{R^{\vee },\beta q,c})^m\) and \((D_{R^{\vee },\beta q})^m\), where \(c \in R^{\vee }\) with norm bounded above by \(\alpha q d n^2\). Using that \(\beta q \ge \eta _{\varepsilon }(R^{\vee })\), the multiplicativity of the Rényi divergence (Lemma 8) and the result of Lemma 9 about the Rényi divergence of shifted discrete Gaussians, we deduce
The last approximation comes from considering the function \(f(x)= \exp (x)\), developing its first-order Taylor expansion at the point 0, i.e. \( f(x) \approx 1 + x\), and evaluating the function f at the small point \(\frac{2\pi \Vert c \Vert ^2}{(\beta q)^2}\). By setting \( \frac{2\pi \Vert c \Vert ^2}{(\beta q)^2} \le \frac{2\pi }{m}\), which leads to \( \frac{\alpha }{\beta } \le \frac{1}{\sqrt{m} \cdot n^2d}\), we get \(\exp \left( \frac{2\pi \Vert c \Vert ^2}{(\beta q)^2} \right) ^m \approx e^{2\pi }\).
For the Rényi divergence to be bounded by a constant, we also need \(\varepsilon = O(\frac{1}{m})\). Indeed, we have \( \left( \frac{1+\varepsilon }{1-\varepsilon }\right) ^2 = \left( 1 + \frac{4\varepsilon /1-\varepsilon }{2}\right) ^2 < \exp \left( \frac{4\varepsilon }{1-\varepsilon } \right) \) as \(\left( 1 + \frac{x}{y}\right) ^y < \exp (x)\) for any \(x,y >0\). Without loss of generality, assume \(\varepsilon < \frac{1}{2}\), then \(\frac{1}{1-\varepsilon } < 2\) and thus, we get \(\left( \frac{1+\varepsilon }{1-\varepsilon }\right) ^{2m} < \exp (8m\varepsilon )\) and therefore \(\varepsilon =O(\frac{1}{m})\) suffices.
From \(P_2\) to \(P_1\): Since more information is given in distribution \(H_2\) than in distribution \(H_1\), the problem \(P_1\) is harder than \(P_2\) and hence

From \(P_1\) to \(P_0\): By the hardness assumption of \(\mathrm {M\text {-}LWE}^{m,d}_{n,\ell ,q,\mathcal {D}_{R^{\vee },\alpha q}}\), the distributions \(H_0\) and \(H_1\) are computationally indistinguishable. More concretely,

where d is the number of secret vectors, represented as the columns of the matrix \(\mathbf {C}\). Putting all equations from above together, we obtain

\(\square \)
To complete the proof above, we now show the following bound on the norm of the product of some discrete Gaussian matrix (in the canonical embedding) and a binary vector in the dual ring (in the coefficient embedding).
Lemma 10
Let K be a cyclotomic number field with R its ring of integers of degree n. Let \(\mathbf {Z}\leftarrow (\mathcal {D}_{R^{\vee },\alpha q})^{m \times d}\) and \(\mathbf {s}\leftarrow U( (R_2^{\vee })^{d})\), where \(R_2^{\vee } = \lambda R_2\) as in the statement of Theorem 1 above. We set \(\tilde{\mathbf {s}} = \lambda \mathbf {s}\). Then, with overwhelming probability \(\Vert \mathbf {Z}\tilde{\mathbf {s}} \Vert _2 \le \alpha q n^2 d \sqrt{m}\). In particular, the Euclidean norm of each coefficient \((\mathbf {Z}\tilde{\mathbf {s}})_{i}\) for \(i \in [m]\) is bounded above by \(\alpha q n^2 d\).
Proof
We want to bound the norm \(\Vert \mathbf {Z}\tilde{\mathbf {s}} \Vert _2 = \Vert \sigma _H(\mathbf {Z}\tilde{\mathbf {s}}) \Vert _{2}\), where the latter norm is taken in \(\mathbb {R}^{nm}\). Since \(\sigma \) and \(\sigma _H\) only differ by a unitary transformation, we can consider \(\sigma \) instead of \(\sigma _H\). For all \(i \in [m]\) it yields
Let \(\theta \) denote the ring homomorphism from \(K^{m \times d} \rightarrow \mathbb {C}^{nm \times nd}\), where
Then, \(\sigma (\mathbf {Z}\tilde{\mathbf {s}})=\theta (\mathbf {Z})\sigma (\tilde{\mathbf {s}})\) and thus \(\Vert \sigma (\mathbf {Z}\tilde{\mathbf {s}}) \Vert _2 \le \Vert \theta (\mathbf {Z}) \Vert _2 \cdot \Vert \sigma (\tilde{\mathbf {s}}) \Vert _2\). Using the Vandermonde matrix \(\mathbf {V}\) to switch from the coefficient embedding \(\tau \) to the canonical embedding \(\sigma \), we can bound \(\Vert \sigma (\tilde{\mathbf {s}}) \Vert _2 \le \Vert \mathbf {V}\Vert _2 \cdot \Vert \tau (\tilde{\mathbf {s}}) \Vert _2 \le n \cdot \sqrt{nd},\) where we use that for cyclotomic number fields it yields \(\Vert \mathbf {V}\Vert _2 \le \Vert \mathbf {V}\Vert _F = \left( \sum _{i,j \in [n]} |\alpha _i^{j-1}|^2 \right) ^{1/2} \le n\) (as \(\alpha \) is a unit) and that \(\tau (\tilde{\mathbf {s}})\) is a binary vector of dimension nd. Further, for each \(i \in [m]\) and \(j \in [d]\) it holds \(\Vert \sigma (z_{ij}) \Vert _2 \le \alpha q \sqrt{n}\) with probability \(1-2^{-\varOmega (n)}\). Hence,
Combining both bounds proves the claim. \(\square \)
4 Classical Hardness for Linear Rank Modules
In the following, we use the result from Sect. 3 to prove a classical reduction from \(\mathrm {Mod}\text {-}\mathrm {GapSVP}\) to \(\mathrm {M\text {-}LWE}\) for any polynomial-sized modulus \(\hat{p}\) and module rank d at least \(2n + \omega (\log _2 n)\), for the case of power-of-two cyclotomics.
Theorem 2
Let \(\nu \) be a power of 2, defining the \(\nu \)-th cyclotomic number field with R its ring of integers of degree \(n=\nu /2\). Let \(d,\hat{p},m\) be positive integers and \(\hat{\beta }\) and \(\gamma \) be positive reals. Fix \(\varepsilon \in (0,\frac{1}{2})\) such that \(\hat{\beta } \ge \sqrt{2} \cdot 2^{-n} \cdot \eta _{\varepsilon }(R^{\vee })\) and \(\varepsilon = O\left( \frac{1}{m}\right) \). There is a classical probabilistic polynomial-time reduction from \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) to \(\mathrm {M\text {-}LWE}^m_{n,d,\hat{p},\Upsilon _{\hat{\beta }}}\), where \(d \ge 2n + \omega (\log _2 n)\) and
We quickly recall the proof structure for Theorem 2 as pictured in Fig. 1 in the introduction:
-
1.
A reduction from \(\mathrm {Mod}\text {-}\mathrm {GapSVP}\) to \(\mathrm {M\text {-}LWE}\) with an exponential-sized modulus q in Theorem 4, Sect. 4.2,
-
2.
A reduction from \(\mathrm {M\text {-}LWE}\) and \(\mathrm {M\text {-}SLWE}\) to \(\text {bin-}\mathrm {M\text {-}SLWE}\) in Theorem 1, Sect. 3, still with an exponential-sized modulus q,
-
3.
A modulus reduction from \(\text {bin-}\mathrm {M\text {-}SLWE}\) with exponential-sized modulus q to \(\text {bin-}\mathrm {M\text {-}SLWE}\) with polynomial-sized modulus p in Corollary 1, Sect. 4.1 (Corollary 2 for the power-of-two cyclotomic case),
-
4.
A trivial reduction from \(\text {bin-}\mathrm {M\text {-}SLWE}\) to \(\mathrm {M\text {-}SLWE}\),
-
5.
A reduction from \(\mathrm {M\text {-}SLWE}\) to \(\mathrm {M\text {-}LWE}\) with polynomial-sized prime modulus p, satisfying \(p = 1 \bmod \nu \), using [LS15, Sec. 4.3],
-
6.
A reduction from \(\mathrm {M\text {-}LWE}\) with prime modulus p satisfying \(p=1 \bmod \nu \) to \(\mathrm {M\text {-}LWE}\) with arbitrary polynomially large modulus \(\hat{p}\).
We first provide a modulus reduction in Sect. 4.1, using the results of Albrecht and Deo [AD17]. Finally, we adapt in Sect. 4.2 the classical reduction from Peikert [Pei09] to the module setting. In Sect. 4.3, we explain how to switch between different error distributions.
4.1 Modulus Switching
In order to prove the classical hardness of \(\mathrm {M\text {-}LWE}\), we provide a modulus reduction, where the rank of the underlying module is preserved. This corresponds to the modulus reduction for \(\mathrm {LWE}\) shown by Brakerski et al. [BLP+13, Cor. 3.2]. Note that Langlois and Stehlé [LS15] proved a modulus switching result from \(\mathrm {M\text {-}LWE}_{n,d,q,\Upsilon _{\beta }}\) to \(\mathrm {M\text {-}LWE}_{n,d,p,\Upsilon _{\beta '}}\), but the error increases at least by a multiplicative factor \(\frac{q}{p}\), which is exponential if q is exponential-sized and p only polynomial-sized.
Prior to this paper, Albrecht and Deo [AD17] adapted the more general result from [BLP+13, Thm. 3.1], from which Corollary 3.2 is deduced. Thus, we first recall their general result [AD17, Thm. 1] and then derive the corollary we need from it. Let K be a number field and let R be its ring of integers.
Theorem 3
(Thm. 1 [AD17]). Let \(d,d',q,p\) be positive integers, \(\varepsilon \in (0,\frac{1}{2})\) and \(\mathbf {G}\in R^{d' \times d}\). Fix a vector \(\mathbf {s}=(s_1,\dots ,s_d)^T \in (R_q^{\vee })^d\). Further, let \(\varLambda \) be the lattice given by \(\varLambda =\frac{1}{p} \mathbf {G}_H^T R^{d'} + R^d\) with known basis \(\mathbf {B}_{\varLambda }\) in the canonical embedding, let \(\mathbf {B}_R\) be some known basis of R in H and let \(\mathbf {B}_{s_jR}\) be a known basis of \(s_jR\) in the canonical embedding for \(j \in [d]\). Let further be r a real number such that

There exists an efficient mapping \(\mathcal {F} :(R_q)^d \times \mathbb {T}_{R^{\vee }} \rightarrow (R_{p})^{d'} \times \mathbb {T}_{R^{\vee }}\) such that:
-
1.
The output distribution \(\mathcal {F}(U((R_q)^d\times \mathbb {T}_{R^{\vee }}))\) given uniform input is within statistical distance \(4\varepsilon \) of the uniform distribution on \((R_{p})^{d'} \times \mathbb {T}_{R^{\vee }}\).
-
2.
Set
 The output distribution \(\mathcal {F}(A_{q,\mathbf {s},D_{\beta }}^{(R^d)})\) is within statistical distance \((4d+6)\varepsilon \) of \(A_{p,\mathbf {G}\mathbf {s},D_{\beta '}}^{(R^{d'})}\), where
The output distribution \(\mathcal {F}(A_{q,\mathbf {s},D_{\beta }}^{(R^d)})\) is within statistical distance \((4d+6)\varepsilon \) of \(A_{p,\mathbf {G}\mathbf {s},D_{\beta '}}^{(R^{d'})}\), where 
for \(i \in [n]\) and \(\gamma \) satisfying \(\gamma ^2 \ge B^2d\).
4.1.1 General Case
Whereas Albrecht and Deo [AD17] proved a rank-modulus trade-off, defining a map from \(\mathrm {M\text {-}LWE}\) in module rank d to d/k and from modulus q to \(q^k\) for any divisor k of d, we are interested in another particular instance of Theorem 3 where the rank of the module is preserved. The following corollary specializes the general result to the case of \(\mathbf {G}= \mathbf {I}_d \in R^{d \times d}\) and its proof is essentially the same as in [AD17]. Overall, we obtain a modulus reduction, where the rank d is preserved.
Corollary 1
Let d, q, p be positive integers with \(q\ge p\), \(\varepsilon \) and \(\beta \) be real numbers with \(\varepsilon \in (0,\frac{1}{2})\) and \(\beta >0\) and \(\mathbf {G}= \mathbf {I}_d \in R^{d \times d}\). Let \(\chi \) be a distribution on \(R_q^{\vee }\) satisfying

for some non-negative real numbers \(B,B',\delta ,\delta '\). By \(\chi ^d\) we denote the distribution on \((R_q^{\vee })^d\), where every coefficient is sampled from \(\chi \) independently. Let further be r a real number such that
Then, there is a polynomial-time reduction from \(\mathrm {M\text {-}SLWE}^m_{n,d,q,D_{\beta }}(\chi ^d)\) to the problem \(\mathrm {M\text {-}SLWE}^m_{n,d,p,D_{\beta '}}(\chi ^d)\) for \( (\beta ')^2 \ge \beta ^2 + 2r^2B^2d.\) This reduction reduces the advantage by at most \(1-(1-\delta -\delta ')^d+ (4d+6)\varepsilon m\).
Proof
We use the transformation from Theorem 3 by taking \(\gamma ^2 = B^2d\) and replacing  for every \(i \in [n]\) by B. For all \(j \in [d]\) it holds
for every \(i \in [n]\) by B. For all \(j \in [d]\) it holds  . Thus, we can replace the maximum in the third condition on r of Theorem 3 by \(B'\Vert \tilde{\mathbf {B}}_{R} \Vert \). We can write \(\mathbf {G}\) in the coefficient embedding as \(\hat{\mathbf {G}}=\mathbf {I}_d \otimes \mathbf {I}_n = \mathbf {I}_{dn}\), defining the corresponding lattice \(\hat{\varLambda } = \frac{1}{p} {\hat{\mathbf {G}}}^T \mathbb {Z}^{dn} + \mathbb {Z}^{dn}\) with basis \({\mathbf {B}}_{\hat{\varLambda }}=\frac{1}{p} \mathbf {I}_{dn}\). To move from the coefficient embedding to the canonical embedding, we can simply multiply the basis by the matrix \(\mathbf {B}_{R^d} = \mathbf {I}_d \otimes \mathbf {B}_R\). The basis for \(\varLambda =\frac{1}{p} \mathbf {G}_H^T R^{d} + R^d\) given in the canonical embedding is thus given by
. Thus, we can replace the maximum in the third condition on r of Theorem 3 by \(B'\Vert \tilde{\mathbf {B}}_{R} \Vert \). We can write \(\mathbf {G}\) in the coefficient embedding as \(\hat{\mathbf {G}}=\mathbf {I}_d \otimes \mathbf {I}_n = \mathbf {I}_{dn}\), defining the corresponding lattice \(\hat{\varLambda } = \frac{1}{p} {\hat{\mathbf {G}}}^T \mathbb {Z}^{dn} + \mathbb {Z}^{dn}\) with basis \({\mathbf {B}}_{\hat{\varLambda }}=\frac{1}{p} \mathbf {I}_{dn}\). To move from the coefficient embedding to the canonical embedding, we can simply multiply the basis by the matrix \(\mathbf {B}_{R^d} = \mathbf {I}_d \otimes \mathbf {B}_R\). The basis for \(\varLambda =\frac{1}{p} \mathbf {G}_H^T R^{d} + R^d\) given in the canonical embedding is thus given by
using the mixed product property of the Kronecker product. Orthogonalizing from left to right gives \(\Vert \tilde{\mathbf {B}}_{\varLambda } \Vert = \frac{1}{p} \Vert \tilde{\mathbf {B}}_R \Vert \). As \(q \ge p\), we have \(\frac{1}{q} \Vert \tilde{\mathbf {B}}_R \Vert \le \frac{1}{p} \Vert \tilde{\mathbf {B}}_R \Vert = \Vert \tilde{\mathbf {B}}_{\varLambda } \Vert \) and we can thus merge the first and second condition on r of Theorem 3. The loss in advantage is the result of a simple probability calculus. Let E be the event that  , which happens with probability greater than \(1-\delta \), and F be the event that
, which happens with probability greater than \(1-\delta \), and F be the event that  , which happens with probability greater than \(1-\delta '\) for any \(s \leftarrow \chi \). It yields \(\mathrm {Pr}(E \cap F)=\mathrm {Pr}(E)+\mathrm {Pr}(F)-\mathrm {Pr}(E \cup F) \ge \mathrm {Pr}(E)+\mathrm {Pr}(F)-1 \ge 1-\delta -\delta '\). As the secret vector \(\mathbf {s}=(s_1,\dots ,s_d)^T \in (R_q^{\vee })^d\) is chosen by drawing d times independently from \(\chi \), we have to add the advantage loss of \(1-(1-\delta -\delta ')^d\) to the one coming from Theorem 3. \(\square \)
, which happens with probability greater than \(1-\delta '\) for any \(s \leftarrow \chi \). It yields \(\mathrm {Pr}(E \cap F)=\mathrm {Pr}(E)+\mathrm {Pr}(F)-\mathrm {Pr}(E \cup F) \ge \mathrm {Pr}(E)+\mathrm {Pr}(F)-1 \ge 1-\delta -\delta '\). As the secret vector \(\mathbf {s}=(s_1,\dots ,s_d)^T \in (R_q^{\vee })^d\) is chosen by drawing d times independently from \(\chi \), we have to add the advantage loss of \(1-(1-\delta -\delta ')^d\) to the one coming from Theorem 3. \(\square \)
4.1.2 Power-of-two Cyclotomic Rings
The quality of Corollary 1 depends on the factor \(\varDelta = 2r^2B^2d\), that we have to add to the error \(\beta ^2\). This factor is determined by the rank d, the first bound B on the secret distribution \(\chi \) and the number r, which itself is quantified by the second bound \(B'\) on the secret distribution \(\chi \), the field degree n, the starting modulus q, the reduced modulus p and the norm \(\Vert \tilde{\mathbf {B}}_R \Vert \). In the following, we give a concrete calculation example for those parameters in the case of power-of-two cyclotomic rings and where \(\chi ^d\) is the uniform distribution on \((R_2^{\vee })^d\), denoted by \(U((R_2^{\vee })^d)\). Let \(\nu \) be a power of two, defining the ring of integers of the \(\nu \)-th cyclotomic field, given by \(R=\mathbb {Z}[\zeta ] \cong \mathbb {Z}[x]/\langle f \rangle \), where \(f(x)=x^n+1\) and \(n=\nu /2\).
Corollary 2
Let R be the ring of integers of degree n, where n is a power of 2. Let d, q, p be positive integers with \(q\ge p\), \(\varepsilon \) and \(\beta \) be real numbers with \(\varepsilon \in (0,\frac{1}{2})\) and \(\beta >0\) and \(\mathbf {G}= \mathbf {I}_d \in R^{d \times d}\). Let further be r a real number such that
For \( (\beta ')^2 \ge \beta ^2 + 2dr^2,\) there is a probabilistic polynomial-time reduction from the problem \(\mathrm {M\text {-}SLWE}_{n,d,q,D_{\beta }}^{m}(U((R_2^{\vee })^d))\) to \(\mathrm {M\text {-}SLWE}_{n,d,p,D_{\beta '}}^{m}(U((R_2^{\vee })^d))\). This reduction reduces the advantage by at most \(1-(1-\frac{1}{2^n})^d + (4d+6)\varepsilon m\).
In order to guarantee a negligible loss in advantage, we require n and d to be polynomial in the security parameter and \(\varepsilon \) negligibly small. If q is exponentially large, as it is the case in the classical hardness result of Sect. 4.2, say \(q \ge 2^{n}\), then we know that r is polynomial in n.
Proof
Let R be the ring of integers of degree n, where n is a power of 2. Its dual \(R^{\vee }=\frac{1}{n} R\) is just a scaling of the ring R itself. Further, the map that takes the vector of an element in R defined by its canonical embedding to the vector corresponding to the coefficient embedding is a scaled isometry with scaling factor \(\frac{1}{\sqrt{n}}\). A basis \(\mathbf {B}_R\) for R in H is given by \(\sqrt{n} \cdot \mathbf {U}\), where \(\mathbf {U}\) is unitary.
For any element \(s \in R\), let \(\mathbf {S}_H\) be the matrix of multiplication by s in the canonical embedding written in the basis \(\{\mathbf {h}_i\}_{i \in [n]}\) of H. Let \(\mathrm {Rot}(s)\) be the matrix of multiplication by s in the coefficient embedding. As mentioned above, going from the coefficient embedding to the canonical embedding is a scaled isometry of scaling factor \(\sqrt{n}\). Thus,
where \(\mathbf {U}\) is unitary. As explained in the preliminaries, the singular values of \(\mathbf {S}_H\) are given by  . It yields
. It yields
As a conclusion, the singular values of \(\mathrm {Rot}(s)\) are exactly the values given by  . The smallest (resp. largest) singular value of \(\mathrm {Rot}(s)\) thus determines the minimum (resp. maximum) of the set
. The smallest (resp. largest) singular value of \(\mathrm {Rot}(s)\) thus determines the minimum (resp. maximum) of the set  .
.
We use this observation to compute the bounds B and \(B'\) of Corollary 1 for the case where \(\chi \) equals \(U((R_2^{\vee })^d)\). Note that we provide new bounds, as the ones calculated by Albrecht and Deo [AD17] hold for a Gaussian, and not a binary secret distribution.
Using the identity \(R_2^{\vee } = \frac{1}{n} R_2\), we know that \(\mathrm {Rot}(s)=\frac{1}{n}\mathrm {Rot}(\tilde{s}),\) where \(\tilde{s} \in R_2\) and \(\mathrm {Rot}(\tilde{s})\) only has entries from the set \(\{0, 1\}\). Let \(\mathrm {Rot}(\tilde{s})=\mathbf {U}\cdot \mathbf {\Sigma } \cdot \mathbf {V}^{\dagger }\) be the singular value decomposition of \(\mathrm {Rot}(\tilde{s})\), where \(\mathbf {U}\) and \(\mathbf {V}\) are unitary matrices over \(\mathbb {R}\) and \(\mathbf {\Sigma }\) is a diagonal matrix with the singular values of \(\mathrm {Rot}(\tilde{s})\) on its diagonal. The singular value decomposition of \(\mathrm {Rot}(s)\) is thus given by \(\mathrm {Rot}({s})=\mathbf {U}\cdot \frac{1}{n}\mathbf {\Sigma } \cdot \mathbf {V}^{\dagger }\) and we can deduce that the singular values of \(\mathrm {Rot}(s)\) are just the singular values of \(\mathrm {Rot}(\tilde{s})\), shrank by a factor of \(\frac{1}{n}\).
The largest singular value \(\mathfrak {s}_1(\mathrm {Rot}(\tilde{s}))\) of \(\mathrm {Rot}(\tilde{s})\) is bounded above by its Frobenius norm \(\Vert \mathrm {Rot}(\tilde{s}) \Vert _F\) and hence
It follows \(\mathfrak {s}_1(\mathrm {Rot}(s)) \le 1\).
The smallest singular value \(\mathfrak {s}_n(\mathrm {Rot}(\tilde{s}))\) of \(\mathrm {Rot}(\tilde{s})\) is bounded below by the following formula given in [PP02]:

The last equation stems from the fact that every entry of \(\mathrm {Rot}(\tilde{s})\) is an integer and \(\mathrm {Rot}(\tilde{s})\) is invertible (in K) for every nonzero \(\tilde{s}\), thus  for every \(\tilde{s} \ne 0\). It follows \(\mathfrak {s}_n(\mathrm {Rot}(s)) \ge \frac{1}{2^{(n-2)/2} \cdot n^2}.\) We can thus set \(B=1\) with \(\delta =0\) and \(B'=n^2 \cdot 2^{(n-2)/2}\) with \(\delta '=\frac{1}{2^n}\) as
for every \(\tilde{s} \ne 0\). It follows \(\mathfrak {s}_n(\mathrm {Rot}(s)) \ge \frac{1}{2^{(n-2)/2} \cdot n^2}.\) We can thus set \(B=1\) with \(\delta =0\) and \(B'=n^2 \cdot 2^{(n-2)/2}\) with \(\delta '=\frac{1}{2^n}\) as

for every \(s \ne 0\), which happens with probability \(1-\frac{1}{2^n}\). \(\square \)
As the bound on the smallest singular value of [PP02] does not take the nega-cyclic structure of \(\mathrm {Rot}(\tilde{s})\) for power-of-two cyclotomics into account, we conjecture that it is very loose. Experiments in dimensions up to \(2^{10}\) show that \(\mathrm {Rot}(\tilde{s})\) behaves as a random binary matrix and the smallest singular value \(\mathfrak {s}_n(\mathrm {Rot}(\tilde{s}))\) can thus with high probability be bounded below by \(\frac{1}{10 \sqrt{n}}\).Footnote 2 With this heuristic bound and requiring p to be large enough, we can achieve \(\varDelta = \beta ^2\). Overall, this leads to an error increase from \(\sqrt{2}\beta \) to \(\sqrt{3}\beta \) in Step 3 of Figure 1, as explained in the introduction. We refer to [vNG47] for more details on heuristic bounds on the smallest singular values of random sub-Gaussian matrices.
4.2 Classical Reduction for M-LWE
In this section, we adapt the classical hardness reduction of \(\mathrm {LWE}\) from Peikert [Pei09, Thm. 3.1] to the module setting. In their introduction, Langlois and Stehlé [LS15] claimed that Peikert’s dequantization [Pei09] carries over to the module case. We prove this claim in the following. By using the more recent results of Peikert et al. [PRS17], our reduction directly reduces \(\mathrm {Mod}\text {-}\mathrm {GapSVP}\) to the decisional variant \(\mathrm {M\text {-}LWE}\) and holds for any number field K.
Throughout this section, let K be a number field of degree n with R its ring of integers. Any module \(M \subseteq K^{\ell }\) of R of rank \({\ell } \ge 2\) can be identified with a module lattice \(\varLambda \) of dimension \(N=n{\ell }\). First, we recall the following results about sampling discrete Gaussians over lattices and about reducing the decisional variant of \(\mathrm {M\text {-}LWE}\) from the \(\mathrm {GDP}\) problem over modules.
Lemma 11
(Thm. 4.1 [GPV08] and Lem. 2.3 [BLP+13]). There exists a probabilistic polynomial-time algorithm \(\mathcal {D}\) that, given a basis \(\mathbf {B}\) of a lattice \(\varLambda \) of dimension N, \(r \ge \Vert \mathrm {GS}(\mathbf {B}) \Vert \cdot \sqrt{\ln (2N+4)/\pi }\) and a center \(\mathbf {c}\in \mathbb {R}^N\), outputs a sample whose distribution is \(D_{\varLambda ,r,\mathbf {c}}\).
Let \(n=t_1\,+\,2 t_2\). As in [PRS17], for any \(r>0,\zeta >0\), and \(T\ge 1\), we define the set of non-spherical parameter vectors \(W_{r,\zeta ,T}\) as the set of cardinality \((t_1 \,+\, t_2) \cdot (T\,+\,1)\), containing for each \(i \in [t_1 + t_2]\) and \(j \in \{0,\dots ,T\}\) the vector \(\mathbf {r}_{i,j}\) which is equal to r in all coordinates except in the i-th (and the \((i + t_2)\)-th if \(i>t_1\)), where it is equal to \(r \cdot (1+\zeta )^j\).
Lemma 12
(Adapted from Lem. 6.6
[PRS17]). There exists a probabilistic polynomial-time algorithm that, given an oracle that solves \(\mathrm {M\text {-}LWE}_{q,\Upsilon _{\alpha }}\), a real \(\alpha \in (0,1)\) and an integer \(q \ge 2\) together with its factorization, a rank \({\ell }\) module \(M\subseteq K^{\ell }\), a parameter \(r \ge \sqrt{2}q\cdot \eta _{\varepsilon }(M)\) for \(\varepsilon =\exp (-\ell n)\), and polynomially many samples from the discrete Gaussian distribution \(\mathcal {D}_{M,\mathbf {r}}\) for each \(\mathbf {r}\in W_{r,\zeta ,T}\) (for some  and
and  ), solves \(\mathrm {GDP}_{M^{\vee },g}\), for \(g=\alpha q / (\sqrt{2{\ell }}r)\).
), solves \(\mathrm {GDP}_{M^{\vee },g}\), for \(g=\alpha q / (\sqrt{2{\ell }}r)\).
A proof can be found in the full version [BJRW20].
Using these results, we are able to adapt the classical hardness result of \(\mathrm {LWE}\) from Peikert [Pei09, Thm. 3.1] to modules.
Theorem 4
Let \(\alpha ,\gamma \) be positive real numbers such that \(\alpha \in (0,1)\). Let \(n,\ell \) and q be positive integers and set \(N=n\ell \). Further, assume that \(\ell \ge 2\), \(q \ge 2^{\frac{N}{2}}\) and \(\gamma \ge \frac{N \sqrt{\ell }}{\alpha }\). Let \(M\subseteq K^{\ell }\) be a rank-\({\ell }\) module. There exists a probabilistic polynomial-time reduction from solving \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) in the worst-case to solving the problem \(\mathrm {M\text {-}LWE}_{n,{\ell },q,\Upsilon _{\alpha }}\), using \(\mathrm {poly}(N)\) samples.
The proof idea is the same as the one from Peikert, but with two novelties. First, we look at the structured variants of the corresponding problems, i.e., \(\mathrm {GapSVP}\) over module lattices (of rank \(\ge 2\)) and \(\mathrm {M\text {-}LWE}\), where the underlying ring R is the ring of integers of a number field K. Second, we replace the main component, a reduction from the \(\mathrm {BDD}\) problem to the search version of \(\mathrm {LWE}\) ([Pei09, Prop. 3.4], originally from [Reg05, Lem. 3.4]), by the reduction from the \(\mathrm {GDP}\) problem over modules to the decisional version of \(\mathrm {M\text {-}LWE}\) (Lemma 12).
Proof
Let \(M\subseteq K^{\ell }\) be a rank-\({\ell }\) module over R, such that the corresponding module lattice of dimension N has basis \(\mathbf {B}=(\mathbf {b}_i)_{i \in [N]}\). Further, let \(\delta \) be a positive real. The \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) problem asks to decide whether \(\lambda _1(M) \le \delta \) (YES instance) or \(\lambda _1(M) > \gamma \delta \) (NO instance). Without loss of generality, we assume that the basis \(\mathbf {B}\) is LLL-reduced (Lemma 1) and appropriately scaled, thus the following three conditions hold:
-
C1) \(\lambda _1(M) \le 2^{\frac{N}{2}}\),
-
C2) \(\min _{i \in [N]} \Vert \mathrm {GS}(\mathbf {b}_i) \Vert _2 \ge 1\),
-
C3) \(1 \le \gamma \delta \le {2^{\frac{N}{2}}}\).
Note for C3, that \(\mathrm {Mod}\text {-}\mathrm {GapSVP}_{\gamma }\) becomes trivial if \(\delta \) lies outside this range. The reduction executes the following procedure \(\mathrm {poly}(N)\) many times:
-
Choose \(\mathbf {w}\leftarrow D_{g'}\) with \(g'=\frac{\delta }{2} \cdot \sqrt{N}\),
-
Compute \(\mathbf {w}+ M\),
-
Run the \(\mathrm {GDP}_g\) oracle from Lemma 12 with \(\mathbf {w}+M\), \(r=\frac{q \sqrt{2N}}{\gamma \delta }\), \(g= \frac{\alpha q}{\sqrt{2{\ell }} r}\), and using the Gaussian sampler from Lemma 11,
-
Compare the output of the oracle with \(\mathbf {w}\).
If the oracle’s answer is always correct, output NO, otherwise YES.
First, we show that the Gaussian sampler from Lemma 11 always succeeds to provide polynomially many samples from the discrete Gaussian distribution \(\mathcal {D}_{M^{\vee },\mathbf {r}}\) for each \(\mathbf {r}\in W_{r,\zeta ,T}\) (for some  and
and  ), needed in Lemma 12. Note that for every \(\mathbf {r}= (r_i)_{i \in [n]} \in W_{r, \zeta ,T}\) it yields \(r_i \ge r\) for every \(i \in [n]\). Thus, it suffices to show that the Gaussian sampler succeeds for r. Let \(\mathbf {D}=(\mathbf {B}^{-1})^T\) denote the basis of the dual \(M^{\vee }\), where we denote by \(\mathbf {d}_i\) its column vectors for \(i \in [N]\). It yields for the \(\ell _2\)-norm that \(\Vert \mathrm {GS}(\mathbf {D}) \Vert _2 = \Vert \mathrm {GS}(\mathbf {B}) \Vert _2^{-1}\). As we require in condition C2 that \(\min _{i \in [N]} \Vert \mathrm {GS}(\mathbf {b}_i) \Vert _2 \ge 1\), it follows \(\max _{i \in [N]} \Vert \mathrm {GS}(\mathbf {d}_i) \Vert _2 \le 1\). Using the condition C3 and that \(q \ge 2^{\frac{N}{2}}\), it yields
), needed in Lemma 12. Note that for every \(\mathbf {r}= (r_i)_{i \in [n]} \in W_{r, \zeta ,T}\) it yields \(r_i \ge r\) for every \(i \in [n]\). Thus, it suffices to show that the Gaussian sampler succeeds for r. Let \(\mathbf {D}=(\mathbf {B}^{-1})^T\) denote the basis of the dual \(M^{\vee }\), where we denote by \(\mathbf {d}_i\) its column vectors for \(i \in [N]\). It yields for the \(\ell _2\)-norm that \(\Vert \mathrm {GS}(\mathbf {D}) \Vert _2 = \Vert \mathrm {GS}(\mathbf {B}) \Vert _2^{-1}\). As we require in condition C2 that \(\min _{i \in [N]} \Vert \mathrm {GS}(\mathbf {b}_i) \Vert _2 \ge 1\), it follows \(\max _{i \in [N]} \Vert \mathrm {GS}(\mathbf {d}_i) \Vert _2 \le 1\). Using the condition C3 and that \(q \ge 2^{\frac{N}{2}}\), it yields
and thus the Gaussian sampler always succeeds.
Now, we assume that the reduction is given a NO instance, i.e., \(\lambda _1(M) > \gamma \delta \). We claim that in this case, all requirements from Lemma 12 are fulfilled and thus the oracle always outputs the correct answer. Using Lemma 2 it yields \(\eta _{\varepsilon }(M^{\vee }) \le \sqrt{N} / \lambda _1(M)\) for \(\varepsilon = \exp (-N)\). Thus,
Further, \(\mathbf {w}\) is sampled from \(D_{g'}\) with
Additionally, \(\mathbf {w}\) is the unique solution to this problem as with high probability
If, on the other hand, the reduction is given a YES instance, i.e., \(\lambda _1(M) \le \delta \), we can consider the following alternate experiment. Let \(\mathbf {z}\) be a shortest vector in \(M\) with \(\Vert \mathbf {z}\Vert _2 = \lambda _1(M) \le \delta \). Now, we replace \(\mathbf {w}\) by \(\mathbf {w}'=\mathbf {w}+ \mathbf {z}\) in the second step of the reduction and thus hand in \(\mathbf {w}' + M\) to the \(\mathrm {GDP}\) oracle. Using the statistical distance of \(\mathbf {w}\) and \(\mathbf {w}'\), it yields
where \(\mathcal {R}\) denotes the \(\mathrm {GDP}\) oracle. Note that \(\mathbf {w}' + M= \mathbf {w}+ M\), so in the real experiment we have \(\Pr [\mathcal {R}(\mathbf {w}' + M)=\mathbf {w}] = \Pr [\mathcal {R}(\mathbf {w}+ M)=\mathbf {w}]\) and thus
Using the statistical distance of two Gaussian distributions with the same width but different means, Lemma 4, we obtain
and thus \( \Pr [\mathcal {R}(\mathbf {w}+ M)=\mathbf {w}] \le \frac{1}{2} + \frac{\sqrt{2 \pi }}{\sqrt{N}}\). For sufficiently many iterations, the oracle gives a wrong answer in at least one iteration and the reduction outputs YES. \(\square \)
4.3 Adapting the Error Distribution
In order to complete our classical hardness result for \(\mathrm {M\text {-}LWE}\), Theorem 2, we need to adapt twice the error distribution.
First, we have to move from the distribution \(\varUpsilon _{\alpha }\) on elliptical Gaussian distributions, as used within Sect. 4.2, to a discrete Gaussian distribution \(\mathcal {D}_{R^{\vee },\alpha 'q}\), as used in Sect. 3. To achieve this, we use the techniques of [LS15, Sec. 4.4].
Lemma 13
Let \(n,\ell ,q\) be positive integers and \(\alpha \) be a positive real. There exists a probabilistic polynomial-time reduction from \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\Upsilon _{\alpha }}\) to \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\phi }\), where \(\phi =\mathcal {D}_{R^{\vee },\alpha 'q}\) with \(\alpha '=\alpha \cdot \omega ({\log _2 n})\).
Proof
First, we reduce \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\varUpsilon _{\alpha }}\) to \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\varPsi _{\le \alpha '}}\), where \(\alpha '\) is given by \(\alpha \cdot \omega (\log _2 n)\). Recall, that \(\varUpsilon _{\alpha }\) is a distribution on elliptical Gaussian distributions \(D_{\mathbf {r}}\), where \(r_i^2\) is distributed as a shifted chi-squared distribution for the real embeddings (\(i \in [t_1]\)) and as a shifted chi-squared distribution with two degrees of freedom for complex embeddings (\(i \in \{ t_1 + 1, \dots , t_1+t_2\}\)). Using properties about chi-squared distributions (see for instance [LM00, Lem. 1]), it yields that \(r_i \le \frac{\alpha }{\sqrt{2}} \cdot \omega ( {\log _2 n}) \le \alpha \cdot \omega ( \log _2 n)= \alpha '\) with probability negligible close to 1. Thus, \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\varPsi _{\le \alpha '}}\) is not easier than \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\varUpsilon _{\alpha }}\). Second, we use the error re-randomization from Peikert [Pei10] to reduce the continuous version \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\varPsi _{\le \alpha '}}\) to the discrete version \(\mathrm {M\text {-}LWE}_{n,\ell ,q,\phi }\), where \(\phi =\mathcal {D}_ {R^{\vee },\alpha 'q}\). Let \(D_{\mathbf {r}}\) be arbitrarily chosen from \(\Psi _{\le \alpha '}\), thus \(\mathbf {r} =(r_i)_{i \in [n]}\) with \(r_i \le \alpha '\) for all \(i \in [n]\). For any \(e \leftarrow D_{\mathbf {r}}\), we sample \(e' \leftarrow e + \mathcal {D}_{\frac{1}{q}R^{\vee }-e,\mathbf {r}'}\), where \(\mathbf {r}'=(r_i')_{i \in [n]}\) with \(r_i'=\sqrt{(\alpha ')^2-(r_i)^2}\). Following Theorem 1 of [Pei10], the new error \(e'\) is statistically close to \(\mathcal {D}_{\frac{1}{q} R^{\vee },\alpha '}\). Multiplying by q completes the claim. \(\square \)
Second, we need to move from the discrete Gaussian \(\mathcal {D}_{R^{\vee },\beta q}\), as used in Sect. 3, back to the continuous Gaussian \(D_{\sqrt{2}\beta }\), as used in Sect. 4.1. To achieve this, we add a continuous noise of the same width and use Lemma 6.
Lemma 14
Let n, d, q be positive integers and \(\beta \) be a positive real such that \(\beta \ge \sqrt{2} \cdot \eta _{\varepsilon }(\frac{1}{q} R^{\vee })\) for some \(\varepsilon \in (0,\frac{1}{2})\). There is a probabilistic polynomial-time reduction from \(\mathrm {M\text {-}SLWE}_{n,\ell ,q,\phi }\) to \(\mathrm {M\text {-}SLWE}_{n,\ell ,q,D_{\sqrt{2} \beta }}\), where \(\phi =\mathcal {D}_{R^{\vee },\beta q}\).
Proof
Given a sample of \(\mathrm {M\text {-}SLWE}_{n,\ell ,q,\phi }\) with \(\phi =\mathcal {D}_{R^{\vee },\beta q}\), we first divide the second part of the instance by q, thus the noise is distributed as a vector drawn from \(\mathcal {D}_{\frac{1}{q} R^{\vee },\beta }\). Then, we add to the second part of the instance a vector drawn from \(D_{\beta }\). Now, we apply Lemma 6 with \(\sigma =r=\beta \) to obtain that this new sample is statistically close to a sample of \(\mathrm {M\text {-}SLWE}_{n,\ell ,q,D_{\sqrt{2} \beta }}\). \(\square \)
Notes
- 1.
- 2.
The Python code is publicly available on https://github.com/KatinkaBou/Probabilistic-Bounds-On-Singular-Values-Of-Rotation-Matrices.
References
Albrecht, M.R., Deo, A.: Large modulus ring-LWE \(\ge \) module-LWE. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 267–296. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_10
Babai, L.: On Lovász’ lattice reduction and the nearest lattice point problem. In: Mehlhorn, K. (ed.) STACS 1985. LNCS, vol. 182, pp. 13–20. Springer, Heidelberg (1985). https://doi.org/10.1007/BFb0023990
Banaszczyk, W.: New bounds in some transference theorems in the geometry of numbers. Math. Ann. 296(4), 625–635 (1993)
Bos, J.W.: CRYSTALS - kyber: a CCA-secure module-lattice-based KEM. In: 2018 IEEE European Symposium on Security and Privacy, EuroS&P 2018, London, United Kingdom, 24–26 April 2018, pp. 353–367 (2018)
Brakerski, Z., Gentry, C., Vaikuntanathan, V.: (Leveled) fully homomorphic encryption without bootstrapping. In: Innovations in Theoretical Computer Science 2012, Cambridge, MA, USA, 8–10 January 2012, pp. 309–325 (2012)
Boudgoust, K., Jeudy, C., Roux-Langlois, A., Wen, W.: Towards classical hardness of module-lwe: The linear rank case. IACR Cryptol. ePrint Arch. 2020:1020 (2020)
Bai, S., Langlois, A., Lepoint, T., Stehlé, D., Steinfeld, R.: Improved security proofs in lattice-based cryptography: using the rényi divergence rather than the statistical distance. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 3–24. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_1
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: Symposium on Theory of Computing Conference, STOC 2013, Palo Alto, CA, USA, 1–4 June 2013, pp. 575–584 (2013)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 43(2), 831–871 (2014)
Ducas, L., Kiltz, E., Lepoint, T., Lyubashevsky, V., Schwabe, P., Seiler, G., Stehlé, D.: Crystals-dilithium: A lattice-based digital signature scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018(1), 238–268 (2018)
Ducas, L., Micciancio, D.: FHEW: bootstrapping homomorphic encryption in less than a second. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 617–640. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_24
Devroye, L., Mehrabian, A., Reddad, T.: The Total Variation Distance Between High-dimensional Gaussians (2018)
Gentry, C., Halevi, S., Peikert, C., Smart, N.P.: Ring switching in BGV-style homomorphic encryption. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. Ring switching in bgv-style homomorphic encryption, vol. 7485, pp. 19–37. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32928-9_2
Goldwasser, S., Kalai, Y.T., Peikert, C., Vaikuntanathan, V.: Robustness of the learning with errors assumption. In: Innovations in Computer Science - ICS 2010, Tsinghua University, Beijing, China, 5–7 January 2010. Proceedings, pp. 230–240. Tsinghua University Press (2010)
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: Proceedings of the 40th Annual ACM Symposium on Theory of Computing, Victoria, British Columbia, Canada, 17–20 May 2008, pp. 197–206. ACM (2008)
Lenstra, A.K., Lenstra Jr., H.W., Lovász, L.: Factoring polynomials with rational coefficients. Math. Ann. 261(4), 515–534 (1982)
Laurent, B., Massart, P.: Adaptive estimation of a quadratic functional by model selection. Ann. Statist. 28(5), 1302–1338 (2000)
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 1–23. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_1
Lyubashevsky, V., Peikert, C., Regev, O.: On ideal lattices and learning with errors over rings. J. ACM 60(6), 43:1–43:35 (2013)
Langlois, A., Stehlé, D.: Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 75(3), 565–599 (2015)
Langlois, A., Stehlé, D., Steinfeld, R.: GGHLite: more efficient multilinear maps from ideal lattices. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 239–256. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_14
Micciancio, D.: Generalized compact knapsacks, cyclic lattices, and efficient one-way functions. Comput. Complex. 16(4), 365–411 (2007)
Micciancio, D.: On the hardness of learning with errors with binary secrets. Theory Comput. 14(1), 1–17 (2018)
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Micciancio, D., Regev, O.: Worst-case to average-case reductions based on gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007)
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem: extended abstract. In Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, Bethesda, MD, USA, 31 May–2 June 2009, pp. 333–342 (2009)
Peikert, C.: An efficient and parallel Gaussian sampler for lattices. In: Rabin, T. (ed.) CRYPTO 2010. An efficient and parallel gaussian sampler for lattices, vol. 6223, pp. 80–97. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_5
Piazza, G., Politi, T.: An upper bound for the condition number of a matrix in spectral norm. J. Comput. Appl. Math. 143(1), 141–144 (2002)
Peikert, C., Rosen, A.: Lattices that admit logarithmic worst-case to average-case connection factors. In: Proceedings of the 39th Annual ACM Symposium on Theory of Computing, San Diego, California, USA, 11–13 June 2007, pp. 478–487 (2007)
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of ring-LWE for any ring and modulus. In: Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2017, Montreal, QC, Canada, 19–23 June 2017, pp. 461–473 (2017)
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (Plain) learning with errors. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019. LNCS, vol. 11692, pp. 89–114. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_4
Rényi, A.: On measures of entropy and information. In: Proceedings of 4th Berkeley Symposium on Mathematical Statistics and Probability, vol. I, pp. 547–561. University of California Press, Berkeley, California (1961)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005, pp. 84–93 (2005)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 34:1–34:40 (2009)
Rosca, M., Stehlé, D., Wallet, A.: On the ring-LWE and polynomial-LWE problems. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. On the ring-lwe and polynomial-lwe problems, vol. 10820, pp. 146–173. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_6
Stehlé, D., Steinfeld, R., Tanaka, K., Xagawa, K.: Efficient public key encryption based on ideal lattices. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 617–635. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_36
van Erven, T., Harremoës, P.: Rényi divergence and kullback-leibler divergence. IEEE Trans. Inf. Theory 60(7), 3797–3820 (2014)
von Neumann, J., Goldstine, H.H.: Numerical inverting of matrices of high order. Bull. Amer. Math. Soc. 53, 1021–1099 (1947)
Wang, Y., Wang, M.: Module-lwe versus ring-lwe, revisited. IACR Cryptology ePrint Archive 2019:930 (2019)
Acknowledgments
This work was supported by the European Union PROMETHEUS project (Horizon 2020 Research and Innovation Program, grant 780701). It has also received a French government support managed by the National Research Agency in the “Investing for the Future” program, under the national project RISQ P141580-2660001/DOS0044216. Katharina Boudgoust is funded by the Direction Générale de l’Armement (Pôle de Recherche CYBER). We also thank our anonymous referees for their helpful and constructive feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Boudgoust, K., Jeudy, C., Roux-Langlois, A., Wen, W. (2020). Towards Classical Hardness of Module-LWE: The Linear Rank Case. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12492. Springer, Cham. https://doi.org/10.1007/978-3-030-64834-3_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-64834-3_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64833-6
Online ISBN: 978-3-030-64834-3
eBook Packages: Computer ScienceComputer Science (R0)



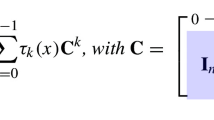


 The output distribution
The output distribution 
