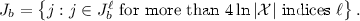On the Round Complexity of the Shuffle Model

Abstract

The shuffle model of differential privacy [Bittau et al. SOSP 2017; Erlingsson et al. SODA 2019; Cheu et al. EUROCRYPT 2019] was proposed as a viable model for performing distributed differentially private computations. Informally, the model consists of an untrusted analyzer that receives messages sent by participating parties via a shuffle functionality, the latter potentially disassociates messages from their senders. Prior work focused on one-round differentially private shuffle model protocols, demonstrating that functionalities such as addition and histograms can be performed in this model with accuracy levels similar to that of the curator model of differential privacy, where the computation is performed by a fully trusted party. A model closely related to the shuffle model was presented in the seminal work of Ishai et al. on establishing cryptography from anonymous communication [FOCS 2006].

Focusing on the round complexity of the shuffle model, we ask in this work what can be computed in the shuffle model of differential privacy with two rounds. Ishai et al. showed how to use one round of the shuffle to establish secret keys between every two parties. Using this primitive to simulate a general secure multi-party protocol increases its round complexity by one. We show how two parties can use one round of the shuffle to send secret messages without having to first establish a secret key, hence retaining round complexity. Combining this primitive with the two-round semi-honest protocol of Applebaum, Brakerski, and Tsabary [TCC 2018], we obtain that every randomized functionality can be computed in the shuffle model with an honest majority, in merely two rounds. This includes any differentially private computation.

We hence move to examine differentially private computations in the shuffle model that (i) do not require the assumption of an honest majority, or (ii) do not admit one-round protocols, even with an honest majority. For that, we introduce two computational tasks: common element, and nested common element with parameter $\alpha$. For the common element problem we show that for large enough input domains, no one-round differentially private shuffle protocol exists with constant message complexity and negligible $\delta$, whereas a two-round protocol exists where every party sends a single message in every round. For the nested common element we show that no one-round differentially private protocol exists for this problem with adversarial coalition size $\alpha n$. However, we show that it can be privately computed in two rounds against coalitions of size cn for every $c<1$. This yields a separation between one-round and two-round protocols. We further show a one-round protocol for the nested common element problem that is differentially private with coalitions of size smaller than cn for all $0<c<\alpha <1/2$.

1 Introduction

A recent line of work in differential privacy focuses on a distributed model where parties communicate with an analyzer via a random shuffle. The shuffle collects messages from the participating parties and presents them to the analyzer in a random order, hence potentially disassociating between messages and their senders [11, 16, 21]. The hope is that the shuffle model would be useful for the implementation of practical distributed differentially private statistical and machine learning analyses, and with accuracy comparable to that of centralized differential privacy solutions. The implementation of the shuffle itself is envisioned to be based on technologies such as secure enclaves, mix nets, and secure computation.

The theoretical work on the shuffle model has so far focused on developing protocols for the model formalized in [16]. In this synchronous one-round model, all the participating parties send their messages through the shuffle at once (parties may send one message or multiple messages). Already in this limited communication model there are fundamental statistical tasks for which differentially private shuffle model protocols exist with error comparable to that achievable in the (centralized) curator model of differential privacy [2, 4,5,6, 16, 23,24,25].

A model similar to the shuffle model was presented already in 2006 by Ishai, Kushilevits, Ostrovsky, and Sahai in the context of secure multiparty computation [27]. In particular, Ishai et al. presented a one-round secure summation protocol that has become one of the building blocks of noise efficient real summation differentially-private protocols, where each party holds a number $x_i \in [0,1]$ and the analyzer’s task is to estimate the sum $\sum x_i$ [4, 6, 23, 24]. Ishai et al. also presented a one-round protocol allowing any two parties to agree on a secret key, a step after which the parties can privately exchange messages. Combining this primitive with general constructions of secure multiparty computation protocols that rely on private or secure channels, Ishai et al. showed that it is possible to compute any (finite) function of the parties’ joint inputs in a constant number of rounds. In particular, we observe that combining the key agreement protocol of Ishai et al. [27] with the recent two-round secure multiparty protocol of Applebaum, Brakersky, and Tsabary [1] (denoted the ABT protocol), no more than three rounds suffice for computing any (finite) randomized function securely in the shuffle model, with semi-honest parties assuming an honest majority: one round for every pair of parties to setup a secret key, and hence private communication channels. Two more round to simulate the ABT protocol using these private channels. To conclude, the previous results imply that any randomized function (including, in particular, any curator model differential privacy computation) can be computed in the shuffle model with security against an honest majority.¹

1.1 Our Results

In this work, we focus on the shuffle model with semi-honest parties. We ask what can be computed in the shuffle model with one and two rounds of communication, and at the presence of coalitions of semi-honest parties that can put together their inputs, randomization, and messages they receive during the computation with the goal of breaching the privacy of other parties. We present new techniques for constructing round-efficient protocols in the shuffle models as well as new lowerbound techniques for studying the limitations of one-round protocols. In more detail:

One-Round Private Message Transmission. In Sect. 3.1 we present a new building block for shuffle model protocols. This is a protocol that allows a party $P_i$ to send a secret message to another party $P_j$ in one round. In the key agreement protocol of Ishai et al. [27], mentioned above, to agree on a bit b of the key, each of $P_i$ and $P_j$ selects and sends through the shuffle a random element chosen from a large set. Denoting the elements sent by $P_i, P_j$ as x, y resp., parties $P_i$ and $P_j$ can set the secret bit b to 0 if $x<y$ and to 1 if $x>y$. (The protocol fails if $x=y$.) The other parties cannot distinguish which of the two values is x and which is y and gain no information about the bit b. Using this protocol, party $P_i$ learns the secret key only after the conclusion of one communication round, and only then can $P_i$ use the key to encrypt a message. In contrast, our construction saves a round in the communication, as it allows $P_i$ to encrypt a message without having to first establish a key.

Generic Two-Round Secure MPC for the Shuffle Model. Using the one-round message transmission protocol, we show in Sect. 3.2 how to simulate the two-round semi-honest secure multi-party computation protocol with information theoretic security of Applebaum et al. [1].² The result is a general construction in the shuffle model of two-round honest majority protocols for the semi-honest setting, with information theoretic security. The construction is efficient in the size of the formula representing the functionality.

Our generic two-round construction shows that the shuffle model is extremely expressive: no more than two rounds suffice for computing any (finite) randomized function, including any curator level differential privacy computation, with semi-honest parties assuming an honest majority of players. We hence move to examine differentially private computations in the shuffle model that (i) do not require the assumption of an honest majority, or (ii) do not admit one-round protocols, even with an honest majority. To demonstrate our lowerbound and upperbound techniques, we introduce two computational tasks:

Common Element: Each of n parties holds an input $x_i$ taken from a large finite domain $\mathcal{X}$. The parties communicate with an analyzer via the shuffle. If all the parties hold the same input $x\in \mathcal{X}$ then the analyzer’s task is to output x. Otherwise, the analyzer’s outcome is not restricted.

Nested Common Element with Parameter ${\varvec{\alpha }}$: This is a variant of the common element problem, where parties $P_1,\ldots ,P_{\lfloor \alpha n\rfloor }$ each holds an input $x_i\in \mathcal{X}$. The other parties $P_{\lfloor \alpha n\rfloor + 1},\ldots ,P_n$ each holds a vector of $|\mathcal{X}|$ elements taken from some finite domain $\mathcal{Y}$, i.e., $\varvec{y}_i\in \mathcal{Y}^{|\mathcal{X}|}$. The parties communicate with an analyzer via the shuffle. If all the parties of the first type hold the same input $x\in \mathcal{X}$ and all the vectors held by parties of the second type have the same value z in their x-th entry, then the analyzer’s task is to output z (otherwise, the analyzer’s outcome is not restricted). We consider the case where $|\mathcal{X}|$ is polynomial in n, thus, the size of the inputs is polynomial in n even when $|\mathcal{Y}|$ is exponential in n.

Both tasks need to be performed with differential privacy, assuming semi-honest parties. We now describe the bounds we prove for these problems:

A Lowerbound on One-Round Shuffle Model Protocols for the Common Element Problem. In Sect. 4.1 we present a new lowerbound technique for one-round shuffle model protocols where the mutual information between input and output is high. Unlike other lowerbounds in the shuffle model of differential privacy that we are aware of, our lowerbound proof works for the multi-message setting, and does not require all parties to use the same randomizer.³

For the common element problem, we show a relationship between the message complexity $\ell$, the input domain size $|\mathcal X|$, and the privacy parameters $\varepsilon$ and $\delta$. In particular, for constant $\varepsilon$ and negligible $\delta$, our bound yields that for constant number of messages $\ell$ and domain size $|\mathcal{X}|> 2^{n^{O(\ell )}}$ the common element problem does not admit a one-round shuffle model protocol. At the heart of the lowerbound proof is a transformation from a shuffle model protocol into a local differential privacy randomizer, for which bounds on the mutual information between the input and output are known (see, e.g., [29]).

The one-round lowerbound is contrasted in Sect. 4.2 with a two-round protocol for the common element problem where each party sends a single message in each round. In this protocol, the parties need to communicate through the shuffle in only one of the rounds (and can either use the shuffle or a public channel in the other round).

An Impossibility Result for the Nested Common Element Problem. In Sect. 5.1 we show (for large enough $\mathcal{X}$, i.e., $|\mathcal{X}|=\tilde{\varOmega }(n^2)$) that, regardless of the number of messages sent by each party, no one-round shuffle protocol exists for the problem that is secure against coalitions of $\alpha n$ semi-honest parties, even when the domain $\mathcal{Y}$ is binary. We observe that for every $c<1$ the nested common element problem has a 2-round private protocol secure against a coalition of size cn. This gives a separation between what can be computed with coalitions of size up to $\alpha n$ in one- and two-round shuffle model protocols. Intuitively, the lowerbound follows from the fact that after seeing the shuffle outcome, a coalition covering $P_1,\ldots ,P_{\lfloor \alpha n\rfloor }$ can simulate the protocol’s execution for any possible value $x\in \mathcal{X}$ and hence learn all vector entries on which the inputs of parties $P_{\lfloor \alpha n\rfloor +1},\ldots ,P_n$ agree. When $\mathcal{Y}$ is binary, Bun et al. [13] have used fingerprinting codes to show that this task is impossible when the dimension of the vectors is $\tilde{\varOmega }(n^2)$, even in the curator model of differential privacy (in the setting of the nested common element the dimension corresponds to $|\mathcal{X}|$).⁴

A One-Round Protocol for the Nested Common Element Problem. A natural approach to solve the nested common element problem in two rounds is to execute a (one-round) protocol for the common element problem among parties $P_1,\ldots ,P_{\lfloor \alpha n\rfloor }$, then, if a common element x is found, repeat the protocol with parties $P_{\lfloor \alpha n\rfloor +1},\ldots ,P_n$ ignoring all but the x-th entry of their vectors. It may seem that any shuffle model protocol for the problem should require more than one round. We show that this is not the case. In fact, there is a one-round protocol that tightly matches the above impossibility result for $\alpha \le 1/2$. For all $c<\min \left\{ \alpha ,1-\alpha \right\}$ there exist one-round shuffle model protocols for the nested common element problem that are secure in the presence of coalitions of size up to cn.

1.2 Other Related Work

Private protocols for the common element problem in the shuffle model are implied by protocols for histograms [2, 16, 23]. Specifically, for all $c<1$, one-round shuffle model protocols for the common element problem that are secure in the presence of coalitions of size up to cn (provided that $n=\varOmega (\frac{1}{\varepsilon ^2} \log \frac{1}{\delta })$) are implied by the protocols of Balcer and Cheu [2]. While they only considered privacy given the view of the analyzer, their protocols are secure against coalitions containing a constant fraction of the parties.

Lowerbounds on the error level achievable in the one-round single message shuffle model for the problems of frequency estimation and selection were provided by Ghazi et al. [23]. Robustness against adversarial behaviour in the shuffle model was informally discussed by Balle et al. [6], when discussing the effect malicious parties can have on the accuracy guarantees in their protocols for addition of real numbers.

Closest to our interest are the recent lowerbounds by Balcer et al. [3]. They define robustly shuffle private one-round protocols, where privacy guarantees are required to hold if at least $\gamma n$ parties participate in the protocol. The other malicious parties avoid sending messages to the shuffle. While this model is equivalent to ours in the one-round setting, the lowerbound techniques in [3] are different from ours. In particular, they forge an interesting relationships between online pan-privacy [20] and robustly shuffle private one-round protocols and hence can use lowerbounds from pan-privacy to deduce lowerbounds for robustly shuffle private one-round protocols. Specifically, for estimating the number of distinct elements they prove that the additive error grows as $\varTheta _\varepsilon (\sqrt{k})$, and for uniformity testing they prove that the sample complexity grows as $\tilde{\varTheta }_{\varepsilon ,\delta }( k^{2/3})$. In both cases k is the domain size. (These bounds also hold in our model.) As with our bounds, the lowerbounds by Balcer et al. hold in the case where different parties may use different randomizers, and send multiple messages.

Independent and parallel to our work, Cheu and Ullman [17] and Chen et al. [15] presented strong impossibility results for 1-round shuffle model protocols. In particular, Cheu and Ullman [17] showed that every 1-round shuffle model protocol for private agnostic learning of parity functions over d bits requires $\varOmega (2^{d/2})$ samples, while O(d) samples suffice in the (centralized) curator model. Our work shows, in particular, that private agnostic learning of parity functions using O(d) samples can be done in the shuffle model in two rounds (with semi-honest parties assuming an honest majority). Hence, combined with our work, the results of [17] provide additional separations between one-round and two-round shuffle model protocols.

2 Preliminaries

2.1 The Communication Model

Let $\mathcal{X}$ be a data domain and let $\mathcal{M}$ be an arbitrary message domain (w.l.o.g., $\bot \in \mathcal{X}, \mathcal{M}$). We consider a model where the inputs and the computation are distributed among n parties $P_1,\ldots ,P_n$ executing a protocol $\varPi =(\bar{R}, S)$, where $\bar{R} = (R_1,\ldots ,R_n)$ are n stateful randomized functionalities and S is a stateless channel that acts either as a shuffle functionality or as a public channel. See Fig. 1 for a formal description of protocols in the shuffle model.

Fig. 1.

The communication model.

Definition 2.1

Consider an execution of a protocol in the shuffle model as described in Fig. 1. The message complexity of $\varPi$ is $\ell$, the number of messages that each party sends to the shuffle in each round. The round complexity of $\varPi$ is r. The shuffle complexity of $\varPi$ is the number of rounds where S is used as a shuffle.

Remark 2.2

A protocol that uses a public random string w can always be converted into a protocol that does not use a public random string, at the cost of one additional communication round in which party $P_1$ sends the string w (in the semi-honest setting). This additional communication round can be thought of as an “offline” round, as it is independent of the inputs and the function.

2.2 Differentially Private Shuffle Model Protocols

Definition 2.3

We say that input vectors $\varvec{x} = (x_1,\ldots ,x_n)\in \mathcal{X}^n$ and $\varvec{x'}=(x'_1,\ldots ,x'_n)\in \mathcal{X}^n$ are i-neighboring if they differ on exactly the i-th entry. We say that $\varvec{x}$ and $\varvec{x'}$ are neighboring if there exists an index i such that they are i-neighboring.

Definition 2.4

We say that two probability distributions $\mathcal{D}_0, \mathcal{D}_1\in \varDelta (\varOmega )$ are $(\varepsilon ,\delta )$-close and write $\mathcal{D}_0 \approx _{\varepsilon ,\delta } \mathcal{D}_1$ if for all events $T\subset \varOmega$ and for $b\in \left\{ 0,1 \right\}$,

$$\Pr _{t\sim \mathcal{D}_b}\left[ t\in T\right] \le e^{\varepsilon } \cdot \Pr _{t\sim \mathcal{D}_{1-b}}\left[ t\in T\right] + \delta .$$

Definition 2.5

(Differential privacy [18, 19]). An algorithm $\mathcal {A}$ is $(\varepsilon ,\delta )$ differentially private if for all neighboring $\varvec{x}, \varvec{x}'$ we have that $\mathcal {A}(\varvec{x}) \approx _{\varepsilon ,\delta } \mathcal {A}(\varvec{x}').$

We are now ready to define what it means for a protocol to be differentially private in the (semi-honest) shuffle model. Intuitively, this means that the view of every coalition $\mathcal{C}$ of up to t parties cannot depend too strongly on the input of a party $P_i\not \in \mathcal{C}$. More formally,

Definition 2.6

(View in shuffle model). The view of a coalition $\mathcal{C}$ on input $\varvec{x}$ in protocol $\varPi$, denoted $\mathrm{View}^\varPi _\mathcal{C}(\varvec{x})$, is the random variable consisting of the public randomness $w$, the inputs and local randomness of the parties in $\mathcal{C}$, and the output of the r rounds of $\varPi$ when executed on $\varvec{x}$, i.e., $s_1,\ldots ,s_r$.

Definition 2.7

(Multiparty semi-honest differential privacy[10, 29]). A protocol $\varPi$ is $(\varepsilon ,\delta )$-differentially private against coalitions of size t if for all $i\in [n]$, for all coalitions $\mathcal{C}$ of t parties s.t. $P_i\not \in \mathcal{C}$, and for all i-neighboring $\varvec{x}, \varvec{x}'$,

$$\mathrm{View}^\varPi _\mathcal{C}(\varvec{x}) \approx _{\varepsilon ,\delta } \mathrm{View}^\varPi _\mathcal{C}(\varvec{x}').$$

Observe that if a protocol is differentially private against coalitions of size t as in the definition above, then it also the case that $\mathrm{View}^\varPi _\mathcal{C}(\varvec{x}) \approx _{\varepsilon ,\delta } \mathrm{View}^\varPi _\mathcal{C}(\varvec{x}')$ for all coalitions $\mathcal{C}$ of size less than t.

Remark 2.8

• 1. The shuffle functionality $\varvec{S}$. It is not essential that the shuffle functionality S be randomized. The shuffle output s in Step (1d) of Protocol $\varPi$ in Fig. 1 can be replaced with any canonical representation of the multiset $\{\hat{m}_1,\ldots ,\hat{m}_{n\ell }\}$ (e.g., in lexicographic order) without affecting any of our results.

• 2. Hybrid-shuffle model. The shuffle model can equivalently be thought of as a hybrid model, where all parties have access to a shuffle functionality.

• 3. The local randomizers $\varvec{R_i}$. In deviation from most of prior work on the shuffle model, the randomizers $R_1,\ldots ,R_n$ need not be identical. In particular, the execution of $R_i$ may depend on the identity i of player $P_i$.

• 4. Local model protocols. An $(\varepsilon ,\delta )$-differentially private protocol $\varPi$ with zero shuffle complexity satisfies local differential privacy [28, 29].

• 5. Shuffle model with an analyzer. In prior work on the shuffle model one party, A, is an analyzer. The analyzer has no input ($x_A=\bot$) and does not send messages, i.e., ($m_{A,j}[1], \ldots , m_{A,j}[\ell ]) = \bot ^\ell$ for $1\le j \le r$. In this setting the local output of parties $P_1,\ldots ,P_n$ is $\bot$ and the outcome of the protocol is the local output of A. Sects. 4 and 5 consider the shuffle model with an analyzer.

2.3 Secure Computation Protocols with Semi-honest Parties

Let $f:\mathcal{X}^n\rightarrow \mathcal{Y}^n$ be a randomized functionality. We recall the definition from the cryptographic literature of what it means that a protocol $\varPi$ securely computes $f(x_1,\ldots ,x_n)$ with semi-honest parties. We will use this definition both in the shuffle model and in the setting where the parties communicate over a complete network of private channels. For the latter we define the view of a coalition as follows:

Definition 2.9

(View in a complete network of private channels). The view of a coalition $\mathcal{C}$ on input $\varvec{x}$ in protocol $\varPi$, denoted $\text {view}^\pi _\mathcal{C}(\varvec{x})$, is the random variable consisting of the inputs and local randomness of the parties in $\mathcal{C}$ and the messages the parties in $\mathcal{C}$ receive from the parties in $\overline{\mathcal{C}}= \{P_1,\ldots ,P_n\}\setminus \mathcal{C}$.

Definition 2.10

(Secure computation in the semi-honest model). A protocol $\varPi$ is said to $\delta$-securely compute f with coalitions of size at most t if there exists a simulator $\mathrm{Sim}^\varPi$ such that for any coalition $\mathcal{C}$ of at most t parties and every input vector $\varvec{x} = (x_1,\ldots ,x_n) \in \mathcal{X}^n$,

$$\left( \mathrm{Sim}^\varPi (\mathcal{C}, \varvec{x}[\mathcal{C}],\varvec{y}[\mathcal{C}]), \varvec{y}[\overline{\mathcal{C}}]\right) \approx _{0,\delta } \left( \mathrm{View}^\varPi _\mathcal{C}(\varvec{x}), {\mathrm {Output}}\,(\overline{\mathcal{C}})\right) ,$$

where $\varvec{y}=f(\varvec{x})$ and $\mathrm{Output}\, (\overline{\mathcal{C}})$ is the output of the parties in $\overline{\mathcal{C}}$ in the protocol. The probability distribution on the left is over the randomness of f and the randomness of the simulator, and the probability distribution on the right is over the randomness of the honest parties and the adversary. When $\delta =0$ we say that $\varPi$ provides perfect privacy.

Remark 2.11

In the shuffle model, $\mathrm{View}^\varPi _\mathcal{C}(\varvec{x})$ also includes the public random string w (if exists), and the probability distribution on the right in Definition 2.10 is also over the public random string.

We next state a composition theorem for differentially private protocols using secure protocols.

Lemma 2.12

Let $\varPi$ be a protocol with one invocation of a black-box access to some function f (the f-hybrid model). Let $\varPi _f$ be a protocol that $\delta '$-securely computes f with coalitions of size up to t. Let $\varPi '$ be as in $\varPi$, except that the call to f is replaced with the execution of $\varPi _f$. If $\varPi$ is $(\varepsilon ,\delta )$-differentially private with coalitions of size up to t, then $\varPi '$ is $(\varepsilon ,(e^\varepsilon +1)\cdot \delta ' + \delta )$-differentially private with coalitions of size up to t.

Proof

Consider a coalition $\mathcal{C}$ of up to t parties. The random variable $\mathrm{View}_\mathcal{C}^{\varPi '}(\varvec{x})$ consisting the view of coalition $\mathcal{C}$ in an execution of protocol $\varPi '$ can be parsed into the view of $\mathcal{C}$ in protocol $\varPi$, i.e., $\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x})$, and the view of $\mathcal{C}$ in the execution of protocol $\varPi _f$, i.e., $\mathrm{View}_\mathcal{C}^{\varPi _f}(\varvec{y})$. In the latter $\varvec{y}$ is the input to f in the execution of $\varPi$ on input $\varvec{x}$ (similarly, we will use $\varvec{y}'$ to denote the input to f in the execution of $\varPi$ on input $\varvec{x}'$). Note that, by Definition 2.10, $\mathrm{View}_\mathcal{C}^{\varPi _f}(\varvec{y})$ can be simulated as $\mathrm{Sim}^{\varPi _f}(\mathcal{C}, \varvec{y}[\mathcal{C}],f_\mathcal{C}(\varvec{y}))$ up to statistical distance $\delta '$. Observe that $\mathrm{View}_\mathcal{C}^\varPi$ contains the inputs $\varvec{y}_\mathcal{C}$ sent to f as well as the outcome seen by the coalition, $f_\mathcal{C}(\varvec{y})$. Hence, $\mathrm{Sim}^{\varPi _f}(\mathcal{C}, \varvec{y}[\mathcal{C}],f_\mathcal{C}(\varvec{y}))$ is a post-processing of $\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x})$. To emphasize this fact, we write $\mathrm{Sim}^{\varPi _f}(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x}))$ instead of $\mathrm{Sim}^{\varPi _f}(\mathcal{C}, \varvec{y}[\mathcal{C}],f_\mathcal{C}(\varvec{y}))$.

Let $P_i\not \in \mathcal{C}$. For all i-neighboring $\varvec{x},\varvec{x'}$ and all T we have that

$$\begin{aligned} \Pr [\mathrm{View}_\mathcal{C}^{\varPi '}(\varvec{x}) \in T]&= \Pr [(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x}), \mathrm{View}_\mathcal{C}^{\varPi _f}(\varvec{y})) \in T] \\&\le \Pr [(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x}), \mathrm{Sim}^{\varPi _f}(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x})))\in T] + \delta ' \\&\le e^\varepsilon \cdot \Pr [(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x'}), \mathrm{Sim}^{\varPi _f}(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x'})))\in T] + \delta + \delta ' \\&\le e^\varepsilon \cdot (\Pr [(\mathrm{View}_\mathcal{C}^{\varPi }(\varvec{x}'), \mathrm{View}_\mathcal{C}^{\varPi _f}(\varvec{y}')) \in T]+\delta ') + \delta + \delta '\\&= e^\varepsilon \cdot \Pr [\mathrm{View}_\mathcal{C}^{\varPi '}(\varvec{x}') \in T]+(e^\varepsilon + 1) \delta ' + \delta . \end{aligned}$$

The second step in the analysis follows from the fact that differential privacy is preserved under post-processing.    $\square$

2.4 Pairwise Independent Hash Functions

In our constructions We use pair pairwise independent hash functions, defined below.

Definition 2.13

(Pairwise independent hash functions). A family of hash functions $H = \left\{ h : \mathcal{X}\rightarrow R \right\}$ is said to be pairwise independent, if for any two distinct elements $x_1 \ne x_2 \in \mathcal{X}$, and any two (possibly equal) values $y_1, y_2 \in R$,

$$\Pr _{h\in H} [h(x_1) = y_1 \wedge h(x_2) = y_2] = \frac{1}{|R|^2},$$

where h is chosen with uniform distribution from H independently of $x_1,x_2$.

In particular, if H is a pairwise independent family, then for every $x_1 \ne x_2 \in \mathcal{X}$ it holds that $\Pr _{h\in H} [h(x_1) = h(x_2) ] = \frac{1}{|R|}$, and for every set $A \subseteq \mathcal{X}$ we have $\Pr _{h\in H} [\exists _{x_1 \ne x_2 \in A}\; h(x_1) = h(x_2) ] \le \frac{|A|^2}{|R|}$, in this case we say that A is perfectly hashed by h.

3 A Two-Round Secure MPC Protocol in the Shuffle Model

In this section we show that every functionality that can be computed with differential privacy in the centralized model can be computed with differential privacy in the shuffle model in two rounds assuming an honest majority. To achieve this result we first show a one-round protocol in the shuffle model for secure message transmission, that is, we show that how to emulate a private channel. This result together with an honest-majority two-round MPC protocol of [1] in the private channel model imply that every functionality (including differentially-private functionalities) can be securely computed in the shuffle model in two rounds assuming an honest majority.

3.1 A One-Round Secure Message Transmission Protocol

Assume that party $P_i$ wants to send a message to party $P_j$ using the shuffle such that any other party will not learn any information on the message. In [27] this was done in two rounds. In the first round $P_i$ and $P_j$ agree on a secret key, and in the second round $P_i$ encrypts the message using this key as a one-time pad. We present a protocol such that $P_i$ knows the key in advance and can encrypt the message already in the first round. The resulting protocol has statistical security.

We start by describing a variant of the protocol of [27] for key exchange. As a first step, we describe a key exchange protocol in which $P_i$ and $P_j$ agree with probability 1/2 on a random bit (and with probability 1/2 the output is “FAIL”). The protocol is as follows: Party $P_i$ samples a uniformly distributed bit a and sends to the shuffle the message (i, j, a). Similarly, party $P_j$ samples a uniformly distributed bit b and sends to the shuffle the message (i, j, b).⁵ If $a = b$ the protocol fails. Otherwise, the joint key is a. As both parties $P_i,P_j$ get the output of the shuffle, they both know if the protocol fails ($a=b$) or not, and if the protocol does not fail ($a\ne b$) they both know a – the common key. On the other hand, an adversary that sees the output of the shuffle when $a\ne b$, sees a shuffle of the two messages $\{(i,j,0),(i,j,1)\}$ and does not get any information on a. To generate a k-bit key, the above protocol is repeated 3k times in parallel with independent random bits $a_\ell ,b_\ell$ in each execution, and the shared key is the bits of $P_i$ in the first k indices where $a_\ell \ne b_\ell$. By a simple Chernoff-Hoefding bound, the probability that there are no such k indices is exponentially small. See Fig. 2 for a formal description of the protocol.

Fig. 2.

A one-round key exchange protocol.

To construct a one-round protocol for secure message transmission from $P_i$ to $P_j$, we want $P_i$ to know the key in advance so it can use the key to encrypt the message at the same time it sends the messages for the key exchange. In Protocol KeyExchange, party $P_i$ does not know the key in advance since it does not know the bits that $(a_1,\ldots ,a_{3k})$ and $(b_1,\dots ,b_{3k})$ disagree. To overcome this problem $P_i$ will use all the bits it generates as a pre-key K. In this case $P_j$ will know all bits of the pre-key K whereas an adversary will learn only about half of the bits of K. Parties $P_i$ and $P_j$ wish to agree on a key generated from the pre-key K without interaction such that the adversary gets negligible information about the agreed key. This is an instance of the privacy amplification problem and a simple solution is to sample a pairwise independent hash function h and set the key as h(K). It follows by the left-over hash lemma [26] that h(K) is close to uniform given h and the knowledge of the adversary about the pre-key K.

Theorem 3.1

(The left-over hash lemma [26]). Let m, n be integers and X be a random variable distributed over $\left\{ 0,1 \right\} ^n$ such that $\Pr [X=x]\le 2^{-m}$ for every $x \in \left\{ 0,1 \right\} ^n$. Let $\mathcal {H}$ be a family of pairwise independent hash functions from $\left\{ 0,1 \right\} ^n$ to $\left\{ 0,1 \right\} ^{m-2k}$. Then, for a random h uniformly distributed in $\mathcal {H}$ and independent of X,

where U is uniform over $\left\{ 0,1 \right\} ^{m-2k}$ and independent of h, and where denotes the statistical distance (total variation distance) (Fig. 3).

Fig. 3.

A one-round protocol for secure message transmission.

Theorem 3.2

Protocol SecureMessageTransmission is a correct and secure protocol for message transmission, that is (1) $P_j$ can always recover M, (2) For every two messages $M,M'$ the statistical distance between the views of the referee and all parties except for $P_i$ and $P_j$ in an executions of Protocol SecureMessageTransmission with M and Protocol SecureMessageTransmission with $M'$ is at most $3\cdot 2^{-k}$.

Proof

For the correctness of the protocol, as $P_j$ knows its messages, it can deduce for every $\ell$ the message $(i,j,\ell ,a_\ell )$ sent by $P_i$, hence compute the common key $h(a_1,\ldots ,a_{7k})$ and compute M.

For the security of the protocol, first note that by a Chernoff-Hoefding bound, the probability that there are less than 3k indices $\ell$ such that $a_\ell \ne b_\ell$ is less than $2^{-k}$, and such executions add at most $2^{-k}$ to the statistical distance. We continue the analysis assuming that such event did not occur.

We consider an execution of Protocol SecureMessageTransmission in which is Step (3) party $P_i$ sends the message $(i,j,\text {``message''},h,u\oplus M)$ for a uniformly sampled $u \in \left\{ 0,1 \right\} ^k$. In this case, the executions for M and $M'$ are equally distributed (as u acts as a one-time pad). To prove the security it suffices to prove that for every message M, the statistical distance in the view in the executions of Protocol SecureMessageTransmission and the modified Protocol SecureMessageTransmission (both with M) is at most $2^{-k}$. Fix a set $L \subset [7k]$ of size at least 3k, and consider all executions in which $a_\ell \ne b_\ell$ if and only if $\ell \in L$. For every index $\ell \in L$, the view discloses no information on $a_\ell$ in these executions (since an adversary sees a random shuffle of the two messages $(i,j,\ell ,0),(i,j,\ell ,1)$ and does not get any information on $a_\ell$). In other words, there are at least $2^{3k}$ strings $(a_1,\dots ,a_{7k})$ possible given the executions are consistent with L, and all strings are equiprobable. Thus, by Theorem 3.1, the statistical distance between u and $h(a_1,\dots ,a_{7k})$ is at most $2^{-k}$. This completes the proof of security.    $\square$

3.2 A Two Round MPC Protocol

We construct a two-round MPC protocol in the shuffle model for every functionality on inputs from a finite domain assuming an honest majority. The construction is via a combination of the two-round MPC protocol of Applebaum, Brakersky, and Tsabary [1] (Henceforth, Protocol ABT, see Theorem 3.3 below), which assumes private channels between every pair of parties, with Protocol SecureMessageTransmission executed in the shuffle model. The latter is used for simulating the private channels.

Theorem 3.3

(Protocol ABT [1, Theorem 1.1]). At the presence of honest majority, any function f can be computed with perfect privacy in a complete network of private channels in two rounds with polynomial efficiency in the number of parties and in the size of the formula that computes f.

Theorem 3.4

Let $f:\mathcal{X}^n\rightarrow \left\{ 0,1 \right\}$ be a function and $\gamma >0$ ($\gamma$ can depend on n and f). At the presence of honest majority, any function f can be computed with $\gamma$-statistical privacy in the shuffle model in two rounds with polynomial efficiency in the number of parties, in the size of the formula that computes f, and in $\log 1/\gamma$.

Proof

In Fig. 4, we describe Protocol MPCinShuffle – the two round MPC protocol in the shuffle model.

Fig. 4.

A two-round MPC protocol in the shuffle model for arbitrary functionalities.

As Protocol SecureMessageTransmission has perfect correctness, each party in Protocol MPCinShuffle can compute the messages it gets in Protocol ABT and compute f without any error.

For the security of the protocol, let $\mathcal{C}$ be a coalition of less than n/2 parties. We construct a simulator that generates a view for $\mathcal{C}$ that is $O(n^2 2^{-k})$ far from the view of $\mathcal{C}$ in the real-world execution of Protocol MPCinShuffle:

• Execute the simulator of Protocol ABT of Theorem 3.3 and generate a view for $\mathcal{C}$ that is identically distributed as the real view of $\mathcal{C}$ in Protocol ABT.

• For each round and for each pair $P_i,P_j$:

  • If at least one of $P_i,P_j$ is in $\mathcal{C}$ then let $M_{i,j}$ be the message that $P_i$ sends to $P_j$ in the simulated view.

  • Otherwise, let $M_{i,j}$ be some fixed arbitrary message.

  • Execute Protocol SecureMessageTransmission with the message $M_{i,j}$ and generate the messages that $P_i,P_j$ send to the shuffle.

• For each round, shuffle the messages generated by $P_i,P_j$ for every $i,j\in [n]$.

• Output: The shuffled messages of round 1 and the shuffled messages of round 2, the randomness of every $P_i$ generated by the simulator of Protocol ABT, and the randomness used by every $P_i \in \mathcal{C}$ in an execution of Protocol SecureMessageTransmission for which $P_i$ is either the sender or the receiver.

By Theorem 3.2, for every $P_i,P_j\notin \mathcal{C}$, the messages generated in the simulation (i.e., the messages of Protocol SecureMessageTransmission for the fixed message $M_{i,j}$ and the message that $P_i$ and $P_j$ send to the shuffle in the real world for the real message of the Protocol ABT of Theorem 3.3 are only $O(2^{-k})$ far. Thus, the output of the simulator we constructed is at most $O(n2^{-k})$ far from the view of $\mathcal{C}$ in the real execution of Protocol MPCinShuffle.    $\square$

Remark 3.5

• 1. In Protocol SecureMessageTransmission we use the shuffle in both rounds as we execute Protocol SecureMessageTransmission in each round. We can optimize the protocol and only use the shuffle in the first round. To achieve this, in the first round each ordered pair of parties $P_i,P_j$ also executes Protocol KeyExchange in round 1 and generate a key, which is used by $P_i$ to encrypt the message that it send to $P_j$ in round 2. The encrypted messages is sent on the public channel.

• 2. In a setting with an analyzer as in Remark 2.8, the protocol can be simplified, with the expense that we now need to assume that the number of colluding parties in $P_1,\ldots ,P_n$ is less than $(n-1)/2$. We execute Protocol ABT with $n+1$ parties, where the $(n+1)$-th party (i.e., the analyzer) has no input and is the only party that receives an output. Furthermore, we assume that the analyzer is always in the coalition, and, therefore, the messages that it sends and receives are public. As the analyzer cannot send messages to the shuffle, we use the public random string as the random string of the analyzer and the messages that the input-less analyzer sends in the first round to party $P_j$ in Protocol ABT are generated by $P_j$ without interaction using the random common string. Furthermore, in the second round each party only sends its message to the analyzer and this message is sent in the clear.

• 3. In Protocol SecureMessageTransmission the shuffle receives O(k) messages and shuffles them. We actually only need to shuffle every pair of messages $(i,j,\ell ,a_\ell ),(i,j,\ell ,b_\ell )$, thus, we can use many copies of 2-message shuffle. The same is true for Protocol MPCinShuffle.

Corollary 3.6

Let f be an $(\varepsilon ,\delta )$-differentially private functional (in the centralized model) acting on inputs from a finite domain and using a finite number of random bits and $\gamma >0$. At the presence of honest majority, the functionality f can be computed with $(\varepsilon ,\delta +(e^{\varepsilon }+1)\gamma )$-differential privacy in the shuffle model in two rounds with polynomial efficiency in the number of parties, in the size of the formula that computes f, and in $\log 1/\gamma$.

Proof

We use Protocol MPCinShuffle to compute the function f. By Lemma 2.12 the resulting protocol is private.    $\square$

4 The Common Element Problem

In this section we study the following problem.

Definition 4.1

(The common element problem). In the common element problem, there are n parties $P_1,\dots ,P_n$, where each party $P_i$ gets an input $x_i\in \mathcal{X}$, and there is an analyzer $P_0$ (with no input). If all inputs are equal, i.e., $x_1=x_2=\dots =x_n$, then with probability at least 3/4 the analyzer must output $x_1$ at the end of the execution. The outcome is not restricted otherwise.

4.1 An Impossibility Result for Single-Round Constant-Message Protocols

We present an impossibility result for 1-round protocols for the common element problem. Informally, we show that if the domain size $|\mathcal{X}|$ is large, then either the number of messages $\ell$ must be large, or else the privacy parameter $\delta$ must be “large”. Before we state and prove this impossibility result, we introduce the following bound on the mutual information between the input of a party in a 1-round differentially protocol and the messages she submits to the shuffle. This bound holds for any 1-round differentially protocol (not only for protocols for the common element problem).

Theorem 4.2

Let $\varPi$ be a 1-round shuffle model protocol for n parties satisfying $(\varepsilon ,\delta )$-differential privacy for coalitions of size 1, with message complexity $\ell$. Let $\mathcal{X}$ denote the input domain (i.e., the input of every party is an element of $\mathcal{X}$). Let $(Z_1,\dots ,Z_n)\in \mathcal{X}^n$ denote (possibly correlated) random variables. Consider the execution of $\varPi$ on inputs $x_1=Z_1,\dots x_n=Z_n$, and for $i\in [n]$ let $Y_i$ denote the vector of messages submitted by party $P_i$ to the shuffle, in lexicographic order. Also let $W$ be a random variable denoting the public randomness of the protocol. Then for every $i\in [n]$, if $Z_i$ is uniformly distributed over $\mathcal{X}$ then

$$ I(Y_i,W;Z_i)=O\left( (en)^{\ell }\cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log \frac{\varepsilon }{\delta } \right) + \ell \cdot \log \left( n\right) \right) . $$

In words, the theorem states that the mutual information between $Z_i$ (the input of party $P_i$), and $(Y_i,W)$ (the messages submitted by party $P_i$ and the public randomness) is bounded.

Before proving Theorem 4.2, we quote two basic results from information theory (see the full version of this work for the proofs of these lemmas, as well as additional preliminaries form information theory). Consider three random variables $Y_1,Y_2,Z$, where $Y_1$ and $Y_2$ are conditionally independent given Z. The following lemma shows that the amount of information that $(Y_1,Y_2)$ give about Z, is at most the amount that $Y_1$ gives on Z plus the amount that $Y_2$ gives on Z. (This is not necessarily true without the conditionally independent assumption.)

Lemma 4.3

Let $Y_1,Y_2,Z$ be random variables, where $Y_1$ and $Y_2$ are conditionally independent given Z. Then, $I(Z;Y_1) + I(Z;Y_2) \ge I(Z; Y_1,Y_2).$

The following lemma shows that if I(X; Y|Z) is high and if H(Z) is low, then I(X; Y) must also be high. That is, if X gives a lot of information on Y when conditioning on a random variable Z with low entropy, then X gives a lot of information on Y even without conditioning on Z.

Lemma 4.4

Let X, Y, Z be three random variables. Then, $I(X;Y)\ge I(X;Y|Z)-H(Z).$

We are now ready to prove Theorem 4.2.

Proof of Theorem 4.2. Let $R_1,\dots ,R_n$ denote the randomizers in the protocol $\varPi$, and fix $i\in [n]$. We use $\varPi$ and i to construct the following algorithm, which we call LocalRandomizer, that gets a single input $x_i$ and a public random string $w$.

• 1. Compute $\varvec{\widetilde{m}_i}\leftarrow R_i(w,x_i)$. That is, $\varvec{\widetilde{m}_i}$ is the vector of $\ell$ messages chosen by $R_i$.

• 2. For $j\ne i$, sample $x_j\in \mathcal{X}$ uniformly at random, and let $\varvec{\widetilde{m}_j}\leftarrow R_j(w,x_j)$.

• 3. For $j\in [n]$, we write $\varvec{\widetilde{y}_j}$ to denote $\varvec{\widetilde{m}_j}$ after sorting it in lexicographic order.

• 4. Let $\varvec{\widetilde{s}}$ be a random permutation of the collection of all messages in $\varvec{\widetilde{m}_1},\dots ,\varvec{\widetilde{m}_n}$.

• 5. Let $\varvec{\widetilde{y}}$ denote a (sorted) vector of $\ell$ messages chosen randomly (without repetition) from $\varvec{\widetilde{s}}$.

• 6. Return $\varvec{\widetilde{y}},w$.

Consider the execution of LocalRandomizer on a uniformly random input $x_i=\widetilde{Z}$ with the public randomness $\widetilde{W}$. We will use $\widetilde{Y},\widetilde{S}$ and $\left\{ \widetilde{M}_i\right\} _{i\in [n]}$ $\left\{ \widetilde{Y}_i\right\} _{i\in [n]}$ to denote the random variables taking values $\varvec{\widetilde{y}},\varvec{\widetilde{s}}, \{\varvec{\widetilde{m}_i}\}_{i\in [n]}$, and $\{\varvec{\widetilde{y}_i}\}_{i\in [n]}$ during the execution.

Observe that $\widetilde{S}$ is identically distributed to the outcome of the shuffler in an execution of $\varPi$ on random inputs, and observe that the outcome of LocalRandomizer is computed as a post-processing of $\widetilde{S}$ and $\widetilde{W}$. Algorithm LocalRandomizer is, therefore, $(\varepsilon ,\delta )$-differentially private (as a function of $x_i$). Since the mutual information between the input and the output of a differentially private algorithm is bounded (see, e.g., [8] or Theorem A.1), there exists a constant $\lambda$ such that

$$\begin{aligned} I\left( \widetilde{Y},\widetilde{W};\widetilde{Z}\right) \le \lambda \cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) . \end{aligned}$$

(1)

We now relate $I\left( \widetilde{Y},\widetilde{W};\widetilde{Z}\right)$ to $I\left( \widetilde{Y}_i,\widetilde{W};\widetilde{Z}\right)$. Intuitively, the connection is that with probability $\approx n^{-\ell }$ we get that $\widetilde{Y}=\widetilde{Y}_i$. Formally, let T be a random variable taking value 0 if $\widetilde{Y}=\widetilde{Y}_i$ and otherwise $T=1$, and denote $p=\Pr [T=0]=1/\left( {\begin{array}{c}\ell n\\ \ell \end{array}}\right)$. By Lemma 4.4 and using standard bounds on the entropy of a binary random variable we get that

(2)

So, combining Inequalities (1) and (2) we get that

$$\begin{aligned} I\left( \widetilde{Y}_i,\widetilde{W};\widetilde{Z}\right)&\le \frac{\lambda }{p}\cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) + \log \left( \frac{4}{p}\right) \\&\le \lambda \cdot (en)^{\ell }\cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) + \ell \cdot \log \left( 4en\right) . \end{aligned}$$

Finally, observe that the input $\widetilde{Z}$, the public randomness $\widetilde{W}$, and the (sorted) vectors of messages $\widetilde{Y}_i$ in the execution of LocalRandomizer are identically distributed to these variables in the execution of $\varPi$ on inputs $(Z_1,\dots ,Z_n)$ with the public randomness $W$. That is, the random variables $\left( \widetilde{Y}_i,\widetilde{W},\widetilde{Z}\right)$ and $\left( Y_i,W,Z_i\right)$ are identically distributed. Therefore,

$$\begin{aligned} I\left( Y_i,W;Z_i\right) \le \lambda \cdot (en)^{\ell }\cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) + \ell \cdot \log \left( 4en\right) . \end{aligned}$$

   $\square$

We next present our impossibility result for the common element problem.

Theorem 4.5

There exists a constant $\lambda >1$ such that the following holds. Let $\varepsilon \le 1$, let $\ell \in N$, and let $\mathcal{X}$ be such that $|\mathcal{X}|\ge 2^{\lambda (4en)^{\ell +1}}$. Let $\varPi$ be a 1-round protocol for the common element problem over the domain $\mathcal{X}$ with message complexity $\ell$, such that $\varPi$ is $(\varepsilon ,\delta )$-differentially private for coalitions of size 1. Then,

$$ \delta =\varOmega \left( (en)^{-\ell -1}\right) . $$

Proof

We first give a short overview of the proof. Recall that if all inputs are equal to some element $x\in \mathcal{X}$, then the analyzer must output x with high probability. This also holds when the (common) input x is chosen uniformly at random from $\mathcal{X}$, which means that the mutual information between the (common) input and the output of the analyzer must be high. We show that this means that there must be at least one party $P_{i^*}$ such that mutual information between the random (common) input and the messages submitted by $P_{i^*}$ must be high, which will contradict Theorem 4.2.

Let $R_1,\dots ,R_n$ denote the randomizers in the protocol $\varPi$. Let Z be a uniformly random element of $\mathcal{X}$ and consider the execution of $\varPi$ on inputs $x_1=x_2=\dots =x_n=Z$ with a public random string $W$. For $i\in [n]$, let $M_i$ denote a random variable representing the vector of $\ell$ messages submitted to the shuffler by party $P_i$, and let $Y_i$ be the same as $M_i$ after sorting it in lexicographic order. Let S be a random variable denoting the outcome of the shuffler. That is, S is a random permutation of all the messages in $M_1,\dots ,M_n$. Alternatively, S is a random permutation of all the messages in $Y_1,\dots ,Y_n$. We use A for the random variable denoting the outcome of the analyzer at the end of the execution.

Since $A=Z$ with probability at least 3/4, the mutual information between A and Z must be high. Specifically, Let B be a random variable taking value 0 if $A=Z$ and otherwise $B=1$. By Lemma 4.4

Recall that A is a (possibly randomized) function of the outcome of the shuffle S and the public randomness $W$. Hence, We now show that there must exist an index $i^*\in [n]$ such that

To that end, observe that since $\varPi$ is a 1-round protocol, then conditioned on Z and on the public randomness $W$ we have that the messages that party $P_i$ sends are independent of the messages that party $P_j$, where $j\ne i$, sends. That is, the random variables $Y_1,\dots ,Y_n$ are conditionally independent given $(Z,W)$. Therefore, by Lemma 4.3 we have that

Hence, there must exist an index $i^*$ such that

$$I(Y_{i^*},W;Z)\ge \frac{1}{n}\cdot I(S,W;Z)\ge \frac{1}{2n}\cdot \log |\mathcal{X}|.$$

We are now ready to complete the proof. Observe that it suffices to prove the theorem assuming that $\varepsilon =1$ and that $|\mathcal{X}|=2^{\lambda (4en)^{\ell +1}}$. The reason is that any $(\varepsilon ,\delta )$-differentially private protocol with $\varepsilon \le 1$ is also $(1,\delta )$-differentially private, and that a protocol for the common element problem over a domain $\mathcal{X}$ is, in particular, a protocol for the common element problem over subsets of $\mathcal{X}$. By Theorem 4.2 (our bound on the mutual information between the input and the messages submitted by any single party in a 1-round protocol), there exists a constant $\lambda >1$ such that

$$\begin{aligned} \frac{1}{2n}\cdot \log |\mathcal{X}|&\le I(Y_{i^*},W;Z)\\&\le \lambda \cdot (en)^{\ell }\cdot \left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) + \ell \cdot \log \left( 4en\right) . \end{aligned}$$

Substituting $\varepsilon =1$ and $|\mathcal{X}|=2^{\lambda (4en)^{\ell +1}}$, and solving for $\delta$, we get that $\delta \ge \frac{1}{8\lambda (en)^{\ell +1}}.$    $\square$

4.2 A Two-Round Protocol with Message Complexity 1

Intuitively, Theorem 4.5 shows that in any 1-round protocol for the common element problem, we either have that the message complexity is large, or we have that $\delta$ cannot be too small. In Fig. 5 we present a two round protocol for the common element problem, in which the message complexity is 1 and $\delta$ can be negligible. Our protocol, which we call Protocol CommonTwoRound, uses the shuffle channel in only one of the two rounds, and the communication in the second round is done via a public channel.

Theorem 4.6

Let $\delta \in (0,1)$. Protocol CommonTwoRound, described in Fig. 5, is $(O(1),O(\delta ))$-differentially private against coalitions of size 0.9n that solves the common element problem. The protocol uses two rounds (one via a public channel and one via the shuffle) and has message complexity 1.

Fig. 5.

A two-round protocol in the shuffle model for the common element problem with message complexity 1.

We begin with the privacy analysis of Protocol CommonTwoRound.

Lemma 4.7

Protocol CommonTwoRound is $(O(1),O(\delta ))$-differentially private against coalitions of size 0.9n.

Proof

Fix an index $i\in [n]$, fix two i-neighboring input vectors $\varvec{x}$ and $\varvec{x'}$, and fix a coalition $\mathcal{C}$ of size $|\mathcal{C}|=0.9n$ such that $P_i\notin \mathcal{C}$. We need to show that $\mathrm{View}^\varPi _\mathcal{C}(\varvec{x}) \approx _{\varepsilon ,\delta } \mathrm{View}^\varPi _\mathcal{C}(\varvec{x}').$ First observe that with probability at least $1-\delta$ over the choice of the hash function h, we have that h perfectly hashes all the different inputs in $\varvec{x},\varvec{x'}$ (note $\varvec{x},\varvec{x'}$ span at most $n+1$ different values). We proceed with the analysis after fixing such a hash function h.

We write $\varvec{x}_{\mathcal{C}}=\varvec{x'}_{\mathcal{C}}$ to denote the inputs of the parties in $\mathcal{C}$, and fix the internal randomness $r_{\mathcal{C}}$ of the parties in $\mathcal{C}$. Now let $S_1$ and $S_2$ be random variables representing the output of the public channel and the shuffle, respectively, during the execution on $\varvec{x}$, where we denote $S_2=\bot$ if the execution halted on Step (3). Similarly, $S'_1,S'_2$ denote the outputs of these channels during the execution on $\varvec{x'}$. With these notations we have that

$$\mathrm{View}^\varPi _\mathcal{C}(\varvec{x})=\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1,S_2\right) \qquad \text {and}\qquad \mathrm{View}^\varPi _\mathcal{C}(\varvec{x}')=\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1,S'_2\right) .$$

Observe that $S_1$ and $S'_1$ are computed using an $(\varepsilon ,0)$-differentially private protocol in the local model (see Theorem A.2), and hence,

$$\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1\right) \approx _{(\varepsilon ,0)}\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1\right) .$$

We next argue about $S_2$ and $S'_2$. For an element $x\in \mathcal{X}$ we write $f_{\varvec{x}}(x)$ to denote the number of occurrences of x in the input vector $\varvec{x}$. Also, let $x^*\in \mathcal{X}$ denote the most frequent element in $\varvec{x}$, that is, an element such that $f_{\varvec{x}}(x^*)$ is maximized.

Case (a)$\quad {\varvec{f_{\varvec{x}}(x^*)\le \frac{96\cdot n}{100}}}$: By the utility guarantees of the protocol for histograms (executed on Step (2)), each of the two executions terminates in Step (3) with probability at least $(1-\delta )$. This is because if $n=\varOmega (\frac{1}{\varepsilon ^2}\log (\frac{1}{\varepsilon \delta }))$ then with probability at least $(1-\delta )$ all of the estimates given by $D(\cdot )$ are accurate to within $\pm 0.01n$ (see Theorem A.2). Therefore, in case (a) we have

$$\begin{aligned} \mathrm{View}^\varPi _\mathcal{C}(\varvec{x})&=\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1,S_2\right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1,\bot \right) \\&\approx _{(\varepsilon ,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1,\bot \right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1,S'_2\right) =\mathrm{View}^\varPi _\mathcal{C}(\varvec{x}'). \end{aligned}$$

Case (b)$\quad {\varvec{f_{\varvec{x}}(x^*)>\frac{96\cdot n}{100}}}$: Fix any value $s_1$ for the outcome of the public channel, such that all the estimates given by the resulting data structure $D(\cdot )$ are accurate to within $\pm 0.01n$ w.r.t. $\varvec{x}$. We first show that conditioned on such an $s_1$ we have that

$$ \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S_2\right) \approx _{(\varepsilon ,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S'_2\right) . $$

To see this, observe that once we condition on $s_1$ then either both executions terminate on Step (3), or in the two executions we have that $y^*=h(x^*)$ (because $f_{\varvec{x}}(x^*)>0.96n$). If $s_1$ is such that the two executions terminate on Step (3), then (conditioned on $s_1$) we have $S_2=S'_2=\bot$ and so

$$ \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S_2\right) \equiv \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S'_2\right) . $$

Now suppose that the two executions do not halt prematurely, and that $y^*=h(x^*)$. In that case, the outcome of the shuffle contains (randomly permuted) copies of $\bot$ and copies of $x^*$. Note that since the outcome of the shuffle is randomly permuted, then the outcome distribution of the shuffle is determined by the number of occurrences of $x^*$.

Note that if $x_i$ and $x'_i$ are both equal to $x^*$, or are both different from $x^*$, then $S_2$ and $S'_2$ are identically distributed, which would complete the proof. We, therefore, assume that exactly one of $x_i,x'_i$ is equal to $x^*$. Suppose without loss of generality that $x_i=x^*$ and $x'_i\ne x^*$.

Since $f_{\varvec{x}}(x^*)>0.96n$ and since $|\mathcal{C}|=0.9n$, there is a set of parties $\mathcal{I}$ of size $|\mathcal{I}|=0.05n$ such that

• 1. $\mathcal{I}\cap (\mathcal{C}\cup \{i\})=\emptyset$.

• 2. For every $j\in \mathcal{I}$ we have that $x_j=x'_j=x^*$.

We show that the outcome of the shuffle preserves differential privacy (over the randomness of the parties in $\mathcal{I}$ and the randomness of the shuffle). Fix the randomness of all parties except for parties in $\mathcal{I}$. Note that this fixes the messages that these parties submit to the shuffle, and suppose that party $P_i$ submits $x^*$ during the first execution and submits $\bot$ during the second execution (if party $P_i$ submits $\bot$ during both execution then the outcome of the shuffle is, again, identically distributed). Let k denote the number of parties among the parties not in $\mathcal{I}$ that submitted $x^*$ to the shuffle during the execution on $\varvec{x}$. (So during the execution on $\varvec{x'}$ exactly $k-1$ such parties submitted $x^*$.)

Let us denote by Z the number of parties from $\mathcal {I}$ that submits $x^*$ to the shuffle. Note that $Z\equiv \text {Binomial}\left( |\mathcal{I}|,\frac{1}{2}\right)$. By the Hoeffding bound, assuming that $n=\varOmega (\ln (1/\delta ))$ (large enough), with probability at least $1-\delta$ we have that $\frac{9}{20}\cdot |\mathcal{I}|\le Z\le \frac{11}{20}\cdot |\mathcal{I}|$. In addition, by the properties of the Binomial distribution, for every $\frac{9}{20}\cdot |\mathcal{I}|\le z\le \frac{11}{20}\cdot |\mathcal{I}|$ we have that

$$ \frac{\Pr [Z=z]}{\Pr [Z=z+1]} =\frac{2^{-|\mathcal{I}|}\cdot \left( {\begin{array}{c}|\mathcal{I}|\\ z\end{array}}\right) }{2^{-|\mathcal{I}|}\cdot \left( {\begin{array}{c}|\mathcal{I}|\\ z+1\end{array}}\right) } =\frac{z+1}{|\mathcal{I}|-z}\in e^{\pm 1}. $$

Let us denote the number of occurrences of $x^*$ at the output of the shuffle during the two executions as $|S_2|$ and $|S'_2|$, respectively. So $|S_2|\equiv k+Z$ and $|S'_2|\equiv k-1+Z$. Fix a set $F\subseteq [n]$ of possible values for $|S_2|$, and denote

$$ T=\{(f-k):f\in F\} \qquad \text {and}\qquad T'=\{(f-k+1):f\in F\} $$

We have that

$$\begin{aligned} \Pr \left[ |S_2|\in F\right]&=\Pr [Z\in T] \le \delta +\Pr \left[ Z\in T\cap \left\{ z: \frac{9|\mathcal{I}|}{20}\le z\le \frac{11|\mathcal{I}|}{20}\right\} \right] \\&\le \delta +e^1\cdot \Pr \left[ Z-1\in T\cap \left\{ z: \frac{9|\mathcal{I}|}{20}\le z\le \frac{11|\mathcal{I}|}{20}\right\} \right] \\&\le \delta +e^1\cdot \Pr \left[ Z-1\in T\right] =\delta +e^1\cdot \Pr \left[ Z\in T'\right] \\&=\delta +e^1\cdot \Pr \left[ \left| S'_2\right| \in F\right] . \end{aligned}$$

A similar analysis shows that $\Pr \left[ |S'_2|\in F\right] \le \delta +e^1\cdot \Pr \left[ |S_2|\in F\right]$. This shows that conditioned on an output of the public channel $s_1$ such that $D(\cdot )$ is accurate for $\varvec{x}$, we have that

$$ \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S_2\right) \approx _{(1,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},s_1,S'_2\right) . $$

So far, we have established that the outcome of the first round (that uses the public channel) preserves $(\varepsilon ,0)$-differential privacy, and, conditioned on the outcome of the first round being “good” (i.e., the resulting data structure D is accurate) we have that the outcome of the second round (that uses the shuffle) preserves $(1,\delta )$-differential privacy. Intuitively, we now want to use composition theorems for differential privacy to show that the two rounds together satisfy differential privacy. A small technical issue that we need to handle, though, is that the privacy guarantees of the second round depend on the success of the first round. As the outcome of the first round is “good” with overwhelming probability, this technical issue can easily be resolved, as follows.

Consider two random variables $\tilde{S}_1$ and $\tilde{S'}_1$ that are identical to $S_1$ and $S'_1$, except that if the resulting data structure $D(\cdot )$ is not accurate, then the value is replaced such that the resulting data structure $D(\cdot )$ is exactly correct. Since the protocol for histograms fails with probability at most $\delta$, we have that

$$ \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},\tilde{S}_1\right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1\right) \approx _{(\varepsilon ,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1\right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},\tilde{S'}_1\right) . $$

In words, consider an imaginary protocol in which the outcome distribution of the first round during the two executions is replaced by $\tilde{S}_1$ and $\tilde{S'}_1$, respectively. The statistical distance between the outcome distribution of this imaginary protocol and the original protocol is at most $\delta$. In addition, for every possible fixture of the outcome of the first (imaginary) round we have the second round preserves differential privacy. Therefore, composition theorems for differential privacy show that the two rounds together satisfy differential privacy. Formally,

$$\begin{aligned} \mathrm{View}^\varPi _\mathcal{C}(\varvec{x})&=\left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S_1,S_2\right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},\tilde{S}_1,S_2\right) \\&\approx _{(1+\varepsilon ,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},\tilde{S'}_1,S'_2\right) \approx _{(0,\delta )} \left( h,r_{\mathcal{C}},\varvec{x}_{\mathcal{C}},S'_1,S'_2\right) =\mathrm{View}^\varPi _\mathcal{C}(\varvec{x}'). \end{aligned}$$

   $\square$

Lemma 4.8

Protocol CommonTwoRound solves the common element problem.

Proof

Fix an input vector $\varvec{x}=(x_1,\dots ,x_n)\in \mathcal{X}^n$ such that for every i we have $x_i=x$. By the utility guarantees of the locally-private protocol for histograms, with probability at least $1-\delta$ it holds that all of the estimates given by $D(\cdot )$ are accurate to within $\pm 0.01n$. In that case, we have that $y^*$ (defined in Step (3)) satisfies $y^*=h(x)$. Thus, every message submitted to the shuffle in the second round is equal to x with probability 1/2, and otherwise equal to $\bot$. Therefore, the analyzer fails to output x in Step (6) only if all of the parties submitted $\bot$ to the shuffle. This happens with probability at most $2^{-n}$. Overall, with probability at least $(1-\delta -2^{-n})$ the analyzer outputs x.    $\square$

Theorem 4.6 now follows by combining Lemma 4.7 and Lemma 4.8.

5 Possibility and Impossibility for the Nested Common Element Problem

In this section we define a nested version of the common element problem of Definition 4.1. This problem has a parameter $0< \alpha <1$. We show that this problem cannot be solved in the shuffle model in one round with differential privacy against coalitions of size $\alpha n$ (regardless of the number of messages each party can send). In contrast, we show that it can be solved with differential privacy in one round against coalitions of size cn for any constant $c < \min \left\{ \alpha ,1-\alpha \right\}$ and in two rounds against coalitions of size cn for any constant $c < 1$. The impossibility result for one round and the two round protocol imply a strong separation between what can be solved in one round and in two rounds.

Definition 5.1

(Nested common element problem with parameter $\alpha$). Let $0< \alpha < 1$. Consider n parties $P_1,\dots ,P_n$ and an analyzer $P_0$ (as in Remark 2.8). The input of each party in $P_1,\dots ,P_{\left\lfloor \alpha n \right\rfloor }$ is an element $x_i \in \mathcal{X}$ and the input of each party $P_{\left\lfloor \alpha n \right\rfloor +1},\dots ,P_{n}$ is a vector $\varvec{y_i}$ of $|\mathcal{X}|$ elements from some finite domain $\mathcal{Y}$. The analyzer $P_0$ has no input. If all inputs of $P_1,\dots ,P_{\left\lfloor \alpha n \right\rfloor }$ are equal (i.e., $x_1=x_2=\cdots =x_{\left\lfloor \alpha n \right\rfloor }$) and the $x_1$-th coordinate in all inputs of $P_{\left\lfloor \alpha n \right\rfloor +1},\dots ,P_{n}$ are equal (i.e., $\varvec{y_{\left\lfloor \alpha n \right\rfloor +1}}[x_1]=\varvec{y_{\left\lfloor \alpha n \right\rfloor +2}}[x_1]=\cdots =\varvec{y_{n}}[x_1]$), then the analyzer $P_0$ must output $\varvec{y_{\left\lfloor \alpha n \right\rfloor +1}}[x_1]$ with probability at least 3/4. The output is not restricted otherwise.

Remark 5.2

When $|\mathcal{X}|=\text {poly}(n)$ and $|\mathcal{Y}|$ is at most exponential in n, then the length of the inputs of all parties is polynomial in n. Our impossibility result for the nested common element problem holds in this regime (specifically, when $|\mathcal{X}| =\tilde{\varOmega }(n^2)$ and $|\mathcal{Y}|=2$). Our protocols are correct and private regardless of the size of $\mathcal{X}$ and $\mathcal{Y}$.

We prove the following three theorems.

Theorem 5.3

Let $|\mathcal{X}| = \tilde{\varOmega }(n^2)$. There is no one-round (1, o(1/n))-differentially private protocol in the shuffle model against coalition of size $\left\lfloor \alpha n \right\rfloor$ for the nested common element problem with parameter $\alpha$ (regardless of the number of messages each party can send).

Theorem 5.4

For every $0< c < 1$, $\varepsilon ,\delta \in [0,1]$, and $n \ge \frac{200}{(1-c)n}\ln \frac{4}{\delta }$ there exists a two-round $(\varepsilon ,\delta )$-differentially private protocol against coalitions of size cn that with probability at least $1-1/2^{n-1}$ solves the nested common element problem with parameter $\alpha$.

Theorem 5.5

For every constants $c,\alpha$ such that $0< c< \min \left\{ \alpha ,1-\alpha \right\} <1$, there exists a constant $\varepsilon _0$ such that there exits a one-round $(\varepsilon _0,\delta )$-differentially private protocol against coalitions of size cn that with probability at least 3/4 solves the nested common element problem with parameter $\alpha$, where $\delta =2^{-O(\min \left\{ \alpha ,1-\alpha \right\} -c)n)}$ and $n\ge 6 \cdot \max \left\{ 1/\alpha ,1/(1-\alpha ) \right\}$.

In the rest of this section we prove Theorem 5.3. The proofs of Theorems 5.4 and 5.5 are given in the full version of this paper.

5.1 An Impossibility Result for Private One-Round Protocols for the Nested Common Element Problem

We next show that the nested common element problem with parameter $\alpha$ cannot be solved privately against coalitions of size $\alpha n$ when $\mathcal{X}$ is large enough, namely, when $|\mathcal{X}|=\tilde{\varOmega }(n^2)$. The proof of the impossibility result is done by using an impossibility result to the vector common element problem (in the centralized model) defined below.

Definition 5.6

(The vector common element problem). The input of the problem is a database containing n vectors $(\varvec{y_1},\ldots ,\varvec{y_n})\in (\left\{ 0,1 \right\} ^d)^n$. For a given set of vectors $\varvec{y_1},\dots ,\varvec{y_n}$, define for every $b\in \left\{ 0,1 \right\}$

$$I_b=\left\{ j: \varvec{y_1}[j]=\cdots = \varvec{y_n}[j]=b \right\} .$$

To solve the the vector common element problem, an analyzer must output with probability at least $1-o(1/n)$ sets $J_0$ and $J_1$ such that $I_0\subseteq J_0$, $I_1\subseteq J_1$, and $J_0\cap J_1=\emptyset$.

In words, the task in the vector common element problem is to identify the coordinates in which the inputs vectors agree, that is, for each coordinate if all the vectors agree on the value of the coordinate then the algorithm should return this coordinate and the common value; if the vectors do not agree on this coordinate then the algorithm can say that this is either a zero-coordinate, a one-coordinate, or none of the above.

The following theorem is implied by the techniques of [14] (i.e., the reduction to fingerprinting codes).

Theorem 5.7

([14]). For every , any (1, o(1/n))-differentially private algorithm in the centralized model for the vector common element problem with vectors of length d has sample complexity $\tilde{\varOmega }(\sqrt{d})$.

We next prove our impossibility result, i.e., prove Theorem 5.3.

Proof of Theorem 5.3. We show that if for $|\mathcal{X}| = \tilde{\varOmega }(n^2)$ there is an n-party protocol, denoted $\varPi$, in the shuffle model for the nested common element problem with parameter $\alpha$ that is private against the coalition of parties holding the x-inputs, namely, $\mathcal{C}=\left\{ P_1,\ldots ,P_{\left\lfloor \alpha n \right\rfloor } \right\}$, then there is an algorithm in the centralized model for the vector common element problem with database of size $O(n^2 \log n)$ violating Theorem 5.7.

As a first step, consider the following algorithm $\mathcal {A}_1$ for the vector common element problem in the centralized model, whose inputs are $\varvec{y_{\left\lfloor \alpha n \right\rfloor +1}},\ldots ,\varvec{y_n}$ (each vector of length $|\mathcal{X}|$).

• 1. The analyzer chooses a public random string $w$.

• 2. For each $i \in \left\{ {\left\lfloor \alpha n \right\rfloor +1},\ldots ,n \right\}$, the analyzer simulates party $P_i$ in protocol $\varPi$ with the input $\varvec{y_i}$ and the public random string $w$, generating a vector of messages $\varvec{m_i}$.

• 3. The analyzer shuffles the messages in $\varvec{m_{\left\lfloor \alpha n \right\rfloor +1}},\cdots ,\varvec{m_n}$, denote the output of the shuffle by $\varvec{\tilde{m}}$.

• 4. For every $x \in \mathcal{X}$ do:

  • (a) For each $i \in \left\{ {1},\ldots ,{\left\lfloor \alpha n \right\rfloor } \right\}$, the analyzer simulates party $P_i$ in protocol $\varPi$ with the input x and the public random string $w$, generating a vector of messages $\varvec{m_i}$.

  • (b) The analyzer shuffles the messages in $\varvec{\tilde{m}},\varvec{m_1},\ldots ,\varvec{m_{\left\lfloor \alpha n \right\rfloor }}$, gives the shuffled messages to the analyzer of $\varPi$, and gets an output $z_x$.

• 5. The analyzer returns $I_b=\left\{ x:z_{x}=b \right\}$ for $b \in \left\{ 0,1 \right\}$.

First we argue that $\mathcal {A}_1$ is (1, o(1/n))-differentially private: The coalition $\mathcal{C}$ sees the output of the shuffle in $\varPi$ and can remove the messages it sent to the shuffle in $\varPi$, therefore computing $\varvec{\tilde{m}}$ from the view is a post-processing of an $(\varepsilon ,o(1/n))$-differentially private output. Second, notice that for every $x\in \mathcal{X}$, the shuffled messages that the analyzer of $\varPi$ gets in Step (4b) are distributed as in $\varPi$, thus, if $\varvec{y_{\left\lfloor \alpha n \right\rfloor +1}}[x]=\cdots =\varvec{y_{n}}[x]=b$, then $z_x=b$ with probability at least 3/4 (however for $x\ne x'$ these events might be independent).

The success probability of $\mathcal {A}_1$ is not enough to violate Theorem 5.3 and we repeat it $O(\log |\mathcal{X}|)$ times. This is done in $\mathcal {A}_2$, which preserves the privacy using sub-sampling:

• 1. Inputs: vectors $\varvec{y_1},\ldots ,\varvec{y_{t}}$, where $t=O(n\ln |\mathcal{X}|)$.

• 2. For $\ell =1$ to $4\ln |\mathcal{X}|$ do:

  • (a) Sample a set $T \subset [t]$ of size $\frac{t}{(3+\exp (1))4\ln |\mathcal{X}|}=n$ and execute $\mathcal {A}_1$ on the vectors $(\varvec{y_i})_{i \in T}$ and get sets $J_0^\ell ,J_1^\ell$.

• 3. For $b \in \left\{ 0,1 \right\}$, let

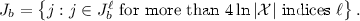
By Theorem A.3 (i.e., sub-sampling) and since $\mathcal {A}_1$ is $(1,o(\frac{1}{n}))$-differentially private, each execution of Step (2a) is $(\frac{1}{4\ln |\mathcal{X}|},o(\frac{1}{n \ln |\mathcal{X}|}))$-differentially private. By simple composition, algorithm $\mathcal {A}_2$ is (1, o(1/n))-differentially private.

We next argue that with probability at least $1-o(1/n)$ algorithm $\mathcal {A}_2$ outputs disjoint sets $J_0,J_1$ such that $I_0 \subseteq J_0$ and $I_1\subseteq J_1$. Fix j such that $\varvec{y_1}[j]=\cdots =\varvec{y_t}[j]=b$ for some b. By the correctness of $\mathcal {A}_1$, for every $\ell \in [4\ln |\mathcal{X}|]$ it holds that $j \in J_b^\ell$ with probability at least 3/4 and these events are independent. Thus, by the Hoeffding inequality, $j \in J_b^\ell$ for more than half of the values of $\ell$ with probability at least $1-1/|\mathcal{X}|^2$. By the union bound, the probability that the algorithm errs for some coordinate for which all vectors $\varvec{y_i}$ agree is at most $1/|\mathcal{X}|=\tilde{O}(1/n^2)=o(1/n)$.

To conclude, assuming that $\varPi$ as above exits, we constructed a (1, o(1/n))-differentially private algorithm $\mathcal {A}_2$ with database of size $O(n^2 \log n)$ and $d=|\mathcal{X}|=\tilde{\varOmega }(|\mathcal{X}|^2)$, contradicting Theorem 5.7.   $\square$

Additional Preliminaries from Differential Privacy

The following theorem bounds the mutual information between the input and the output of a differentially private algorithm (that operates on a database of size 1).

Theorem A.1

([8]). Let X be uniformly distributed over $\mathcal{X}$. Let $\mathcal {A}$ be an $(\varepsilon ,\delta )$-differentially private algorithm that operates on a single input (i.e., a database of size 1) from $\mathcal{X}$. Let Z denote $\mathcal {A}(X)$. Then,

$$ I(X;Z)=O\left( \varepsilon ^2 + \frac{\delta }{\varepsilon }\log |\mathcal{X}| + \frac{\delta }{\varepsilon }\log (\varepsilon /\delta ) \right) . $$

In our protocols we will use the following protocol in the local model for computing histograms.

Theorem A.2

(Histogram protocol [7, 8, 12]). Let $\beta ,\varepsilon \le 1$ and $\mathcal{X}$ be some finite domain. There exists a 1-round $(\varepsilon ,0)$-differentially private protocol in the local model for n parties with message complexity 1, in which the input of each agent is a single element from $\mathcal{X}$ and the outcome is a data structure $D:\mathcal{X}\rightarrow [n]$ such that for every input to the protocol $\varvec{x}\in \mathcal{X}^n$, with probability at least $1 - \beta$, for every input vector $x=(x_1,\dots ,x_n)\in \mathcal{X}$ we have

$$ \Big |\;D(x)-\left| \{i:x_i=x\}\right| \;\Big |\le O\left( \frac{1}{\varepsilon }\cdot \sqrt{n\cdot \log \left( \frac{|\mathcal{X}|}{\beta }\right) }\right) . $$

We next recall the sub-sampling technique from [9, 28].

Theorem A.3

(Sub-sampling [9, 28]). Let $\mathcal {A}_1$ be an $(\varepsilon ^*,\delta )$-differentially private algorithm operating on databases of size n. Fix $\varepsilon \le 1$, and denote $t=\frac{n}{\varepsilon }(3+\exp (\varepsilon ^*))$. Construct an algorithm $\mathcal {A}_2$ that on input a database $D=(z_i)_{i=1}^t$ uniformly at random selects a subset $T\subseteq \{1,2,...,t\}$ of size n, and runs $\mathcal {A}_1$ on the multiset $D_T=(z_i)_{i\in T}$. Then, $\mathcal {A}_2$ is $\left( \varepsilon ,\frac{4\varepsilon }{3+\exp (\varepsilon ^*)}\delta \right)$-differentially private.

Secure Addition Protocols in the Shuffle Model. Ishai et al. [27] gave a protocol where $n\ge 2$ parties communicate with an analyzer (as in Remark 2.8) to compute the sum of their inputs in a finite group G, in the semi-honest setting and in the presence of a coalition including the analyzer and up to $n-1$ parties. In their protocol, each participating party splits their input into $\ell =O(\log |G| + \log n + \sigma )$ shares and sends each share in a separate message through the shuffle. Upon receiving the $n\ell$ shuffled messages, the analyzer adds them up (in G) to compute the sum. Recent work by Ghazi et al. [24] and Balle et al. [6] improved the dependency of the number of messages on the number of participating parties to $\ell =O\left( 1+(\log |G| + \sigma )/\log n\right)$.

Theorem A.4

([6, 24, 27]). Let G be a finite group. There exist a one-round shuffle model summation protocol with n parties holding inputs $x_i\in G$ and an analyzer. The protocol is secure in the semi-honest model, and in the presence of coalitions including the analyzer and up to $n-1$ parties.