Mr NISC: Multiparty Reusable Non-Interactive Secure Computation

Abstract

Reducing interaction in Multiparty Computation (MPC) is a highly desirable goal in cryptography. It is known that 2-round MPC can be based on the minimal assumption of 2-round Oblivious Transfer (OT) [Benhamouda and Lin, Garg and Srinivasan, EC 2018], and 1-round MPC is impossible in general. In this work, we propose a natural “hybrid” model, called multiparty reusable Non-Interactive Secure Computation (mrNISC). In this model, parties publish encodings of their private inputs $x_i$ on a public bulletin board, once and for all. Later, any subset I of them can compute on-the-fly a function f on their inputs $\varvec{x}_I = {\{x_i\}}_{i \in I}$ by just sending a single message to a stateless evaluator, conveying the result $f(\varvec{x}_I)$ and nothing else. Importantly, the input encodings can be reused in any number of on-the-fly computations, and the same classical simulation security guaranteed by multi-round MPC, is achieved. In short, mrNISC has a minimal yet “tractable” interaction pattern.

We initiate the study of mrNISC on several fronts. First, we formalize the model of mrNISC protocols, and present both a UC security definition and a game-based security definition. Second, we construct mrNISC protocols in the plain model with semi-honest and semi-malicious security based on pairing groups. Third, we demonstrate the power of mrNISC by showing two applications: non-interactive MPC (NIMPC) with reusable setup and a distributed version of program obfuscation.

At the core of our construction of mrNISC is a witness encryption scheme for a special language that verifies Non-Interactive Zero-Knowledge (NIZK) proofs of the validity of computations over committed values, which is of independent interest.

1 Introduction

Reducing interaction in Multiparty Computation (MPC) is a highly desirable goal in cryptography, both because each round of communication is expensive and because the liveness of parties is hard to guarantee, especially when the number of participants is large. Contrary to throughput, latency is now essentially limited by physical constraints, and the time taken by a round of communication cannot be significantly reduced anymore. Moreover, non-interactive primitives are more versatile and more amenable to be used as powerful building blocks. Recent works [7, 21] constructed 2-round MPC protocols from the minimal primitive of 2-round Oblivious Transfer (OT), where in each round all participants simultaneously broadcast one message. Is it possible to further reduce interaction? The answer is no in general as any non-interactive (i.e., one-round) protocol is susceptible to the so-called residual attack, and cannot achieve the classical simulation security.

In this work, we introduce and study a natural “hybrid” model, between the 2-round and the 1-round settings, which gets us close to having non-interactive protocols while still providing classical security guarantees. We call this model multiparty reusable Non-Interactive Secure Computation (mrNISC). In this model, parties publish encodings of their private inputs $x_i$ on a public bulletin board, once and for all. Later, any subset I of them can compute on-the-fly a function f on their inputs ${\varvec{x}}_I = {\{x_i\}}_{i \in I}$ by just sending a single public message to a stateless evaluator, conveying the result $f({\varvec{x}}_I)$ and nothing else. Importantly, the input encodings are reusable across any number of computation sessions, and are generated independently of any information of later computation sessions—each later computation can evaluate any polynomial-time function, among any polynomial-size subset of participants. Figure 1 depicts the setting. The security guarantee is that an adversary corrupting a subset of parties, chosen statically at the beginning, learns no information about the private inputs of honest parties, beyond the outputs of the computations they participated in. This holds for any polynomial number of computation sessions.

Fig. 1.

mrNISC market (z is a public input to the function)

Our Contributions. We initiate the study of mrNISC at the following fronts:

• Modeling: We introduce the mrNISC model and formalize both UC security through an ideal mrNISC functionality, and a simpler game-based security notion that implies UC security. Our model aims for maximal flexibility. Consider the simplest form of 2-round MPC with reusable first messages, where the first messages could potentially depend on the number of parties, complexity of the computations, and potentially all parties must participate in all computations. mrNISC does not have such restriction. In addition, our model allows adaptive choices of inputs and computations, uses weak communication channels, and allows honest parties to individually opt out of computations.

• Construction: We construct the first mrNISC protocols based on SXDH in asymmetric (prime-order) pairing groups. Our protocols are in the plain-model (without any trusted setup), and satisfies semi-honest, and semi-malicious security. For malicious security, reliance on some trusted setups is inevitable. We use a CRS.

• Techniques: At the core of our construction is a witness encryption (WE) scheme for a special language that verifies non-interactive zero-knowledge (NIZK) proofs of the validity of computations over committed values. We construct it from bilinear groups. This significantly extends the range of languages for which we know how to construct WE from standard assumptions, which is a result of independent interest.

• Applications: We demonstrate the power of mrNISC protocols in two cryptographic applications. First mrNISC allows to generically transform non-interactive MPC protocols [5] using correlated randomness into non-interactive MPC protocols in the PKI plus CRS model. Second, mrNISC enables a secret-sharing analogue of Virtual Black-Box program obfuscation [4]—called secret sharing VBB.

Comparing with previous models of MPC with minimal interaction, mrNISC naturally generalizes the beautiful notion of reusable NISC by Ishai et al. [30] from two party to multiple parties. It differs from the notions of non-interactive MPC (NIMPC) [5] and Private Simultaneous Messages (PSM) [17, 29] which achieves weaker security or restricts the corruption pattern.

It is very plausible that multi-key fully-homomorphic encryption (MKFHE) with threshold decryption, which implies 2-round MPC [2, 13, 33], is sufficient for mrNISC. However, proving it is not straightforward. For instance, the current definitions of threshold decryption e.g., [3, 33] are insufficient for constructing mrNISC, as simulatability only ensures that a single partial decryption can be simulated (hence this definition does not allow to re-use ciphertexts.)

Organization of the Paper. Next we start with giving more details of our results. In Sect. 2, we formally define mrNISC schemes, and provide an overview of our construction of mrNISC from bilinear maps; the technical bulk of the construction is constructing WE for NIZK of commitments. Next, we define witness encryption for NIZK of commitments, and construct a scheme for $\mathrm {NC}^1$ in Sect. 3. Due to the lack of space, we refer the reader to the full version [8] for the following: 1) Bootstrapping WE for NIZK of commitments for $\mathrm {NC}^1$ to a scheme for $\mathrm {P}$, 2) the UC definition of mrNISC protocols, 3) The formal constructions of UC-secure mrNISC protocols from mrNISC schemes, 4) the applications of mrNISC, and 5) more detailed comparison with related works.

1.1 Our Results in More Detail

Definition. We start with defining a mrNISC scheme, consisting of an input encoding $\mathsf {Com}$, computation $\mathsf {Encode}$, and output $\mathsf {Eval}$ algorithms. An mrNISC scheme immediately yields an MPC protocol with minimal interaction pattern, called an mrNISC protocol. We formalize a game-based security notion for mrNISC scheme, as well as UC-security for mrNISC protocols, and show that the former implies the latter. We have both definitions since they each has its own advantage: UC security is the strongest security notion for MPC protocols, and implies security under composition. The ideal mrNISC functionality we define provides a simple interface for using our protocols in bigger systems. On the other hand, the game-based security notion is more succinct and easier to manipulate. By showing that game-based security implies UC security, we have the best of both sides.

mrNISC Scheme. A mrNISC scheme is defined by:

• Input Encoding: A party $P_i$ encodes its private input $x_i$ by invoking $(\hat{x}_i, s_i)\leftarrow \mathsf {Com}(1^\lambda , x_i)$. It then publishes the encoding $\hat{x}_i$ and keeps the secret state $s_i$.

• Computation: In order for a subset of parties ${\{P_i\}}_{i \in I}$ to compute the functionality f on their private inputs ${\varvec{x}}_I$ and a public input z, each party in I generates a computation encoding $\alpha _{i} \leftarrow \mathsf {Encode}(z, {\{\hat{x}_j\}}_{j \in I}, s_i)$ and sends it to the evaluator. Here, z can be viewed as part of the description of the function $f(z, \star )$ that is computed.

• Output: The evaluator reconstructs the output $y = \mathsf {Eval}(z, {\{\hat{x}_i\}}_{i \in I}, {\{\alpha _{i}\}}_{i \in I})$. (Note that reconstruction is public as the evaluator has no secret state.) Correctness requires that $y=f(z,{\{x_i\}}_{i\in I})$ when everything is honestly computed.

It is easy to see that an mrNISC scheme for f immediately gives an mrNISC protocol for f. Simulation-security requires that the view of an adversary corrupting the evaluator and any subset of parties, can be simulated using just the outputs of the computations that honest parties participate in. We consider static corruption: The set of corrupted parties C are chosen at the beginning and fixed; later, in a computation involving parties I, the corrupted and honest parties are respectively $I\cap C$ and $I \cap \bar{C}$.

The same security intuition can be formalized with different degree of flexibility. In the simplest selective setting, where the function f, parties’ inputs $x_1,\dots , x_m$, and $(z^1, I^1), \dots , (z^K, I^K)$ for different computations are all chosen selectively at the beginning, the view of corrupted parties in C is simulatable by a universal simulator $\mathcal {S}$ as follows.

where $\{x_i, r_i\}_{i \in C}$ are the inputs and randomness of corrupted parties, $\hat{x}_i$ is the input encoding of an honest party $P_i$, and $\alpha ^k_i$ the computation encoding from an honest party $P_i$ in session k. The above definition captures semi-honest security. In the stronger semi-malicious security [2], the corrupted parties still follow the protocol specification but are allowed to choose the randomness arbitrarily.

Dynamics in the mrNISC. The simple selective setting has several drawbacks undesirable for capturing a dynamic mrNISC setting we envision. Instead, in mrNISC, we have:

• Adaptive Choices: Each party’s input $x_i$ is chosen adaptively. Each computation specified by (z, I) is chosen adaptively, before it starts. Different computation can use the same z and/or I, or different ones. Parties outside I are not involved in and not even aware of computation (z, I). $f(z, \star )$ can be any polynomial time computable function, and I any polynomial size subset.

• Asynchronous P2P Communication: Parties have access to a common public bulletin board, but otherwise should only use asynchronous point-to-point authenticated channels. We do not assume any broadcast channel.

• Optional Participation: In a computation session $(z^k,I^k)$, honest parties in $I^k$ may opt in or out of any computation. We do not require all honest parties to participate. Furthermore, the output of a computation is revealed only after all parties in $I^k$ send their computation encoding. (This means that, in any computation session, the simulation of all but the last honest computation encoding must be done without knowing the output of the computation.)

Our mrNISC ideal functionality in the UC framework [11] captures all above features. Clearly, selective security is insufficient for implementing the mrNISC ideal functionality. We thus formalize a game-based adaptive-security of mrNISC schemes, Definition 3 in the overview (Sect. 2.1) and we show that it implies UC-security. We emphasize that our adaptive security does not mean security against adaptive corruptions.

Lemma 1 (Informal)

An mrNISC scheme for a function f satisfying adaptive semi-malicious (or semi-honest) privacy implies a protocol that UC-implements the mrNISC ideal functionality for f in the plain model with semi-malicious (or semi-honest) security.

Following standard techniques [2], semi-malicious UC protocols in the plain model can be transformed into malicious UC protocols in the CRS model using malicious UC-NIZK.

Plain-Model mrNISC from Bilinear Groups. We construct mrNISC schemes for polynomial time computable functions in the plain model from bilinear maps.

Theorem 1 (Informal)

There is an mrNISC scheme in the plain model for any function in $\mathrm {P}$, satisfying adaptive semi-malicious security, based on the SXDH assumption on asymmetric bilinear groups.

Our construction builds upon the construction of 2-round MPC protocols using general purpose WE and NIZK [24], which in turn improves upon the protocols of [18] based on indistinguishability obfuscation. (Unfortunately, follow-up works based on standard assumptions [7, 20, 21] do not have reusable first messages.)

So far, known WE schemes can be split into two categories. The first is WE for general NP language from very strong obfuscation-like assumptions, e.g., [19]. The second is WE from standard assumptions, but for very specific languages, such as, language of commitment (or hashes) of a given message, like in [15, 16], and languages of commitments that commit to value satisfying up to quadratic equations, like in [20, 21]. These functionality, however, is too weak for constructing 2-round MPC.

WE for NIZK of Com. We observe that it suffices to have witness encryption for a language that verifies NIZK proofs for the validity of computation over committed values. We then construct a commitment scheme $\mathsf {Com}$, a NIZK proof system $\mathsf {NIZK}$, and a WE scheme for the language $\mathcal {L}_{\mathrm {WE}}$ of statements of form $X_{\mathrm {WE}} = (\mathsf {crs}, c_1, \dots , c_m, G, y)$ (where $\mathsf {crs}$ is a CRS of $\mathsf {NIZK}$, every $c_i$ is a commitment of $\mathsf {Com}$, and G is an arbitrary polynomial-sized circuit). The statement is true if and only if there exists a NIZK proof $\pi$ (i.e., the witness) proving w.r.t. $\mathsf {crs}$ that G evaluated on the values $v_1, \dots , v_m$ committed in $c_1, \dots , c_m$ through $\mathsf {Com}$ outputs y, i.e., $G(v_1,\dots ,v_m) = y$. More precisely, the witness relations for WE and NIZK proof are:

$$\begin{aligned}&\mathcal R_{\mathrm {WE}}(X_{\mathrm {WE}} = (\mathsf {crs}, c_1, \dots , c_m, G, y), \; \pi ) = 1 \ \text { iff } \ \mathsf {NIZKVer}(\mathsf {crs}, X_{\mathsf {NIZK}}, \pi ) = 1 \end{aligned}$$

(1)

$$\begin{aligned}&\mathcal R_{\mathsf {NIZK}}(X_{\mathsf {NIZK}} = (c_1, \dots , c_m, G, y), \, ((v_1,\rho _1), \dots , (v_m, \rho _m))) = 1 \nonumber \\&\qquad \quad \text { iff }\ \forall i \in [m], \ (v_i, \rho _i) \text { is a valid opening of } c_i \text { and } G(v_1, \dots , v_m) = y \end{aligned}$$

(2)

We call such a triple $(\mathsf {Com}, \mathsf {NIZK}, \mathsf {WE})$ as WE for NIZK of commitments and construct it from bilinear pairing groups.

Theorem 2 (Informal)

There is a WE for NIZK of commitments $(\mathsf {Com}, \mathsf {NIZK}, \mathsf {WE})$ based on SXDH over asymmetric bilinear pairing groups.

We remark that our construction co-designs $(\mathsf {Com}, \mathsf {NIZK}, \mathsf {WE})$ together. It significantly extends the range of statements that WE supports, and is based on standard assumptions, which is of independent interest.

Fig. 2.

Construction of mrNISC schemes and protocols (mrNISC protocols implement the mrNISC ideal functionality; MPC$^\star$ is an MPC with some special properties). Citation [8] is the full version of the paper.

Applications. We show two applications of mrNISC. A summary of the applications is in Fig. 3.

Fig. 3.

Applications of mrNISC schemes (mrNISC protocols implement the mrNISC ideal functionality). See the full version [8].

[5] proposed the model of non-interactive MPC (NIMPC), where to jointly compute a function, each party sends a single message to an evaluator, without initially committing to their inputs. In this setting, adversaries can always evaluate the residual function where the inputs of the honest parties are fixed, on all possible inputs of the corrupted parties, a.k.a. the residual attack. Thus, NIMPC aims at achieving the best-possible security that the only information of honest parties’ inputs revealed is the residual function . NIMPC is a powerful and flexible concept equivalent, under different corruption models (i.e., what set C of parties can be corrupted), to garbled circuits, Private Simultaneous Messages [17, 29] protocols, and program obfuscation. Almost all NIMPC protocols are constructed in a model where parties receive correlated randomness sampled by a trusted third party from some distribution. However, correlated randomness is not reusable, and must be re-sampled independently for each computation session. So far, the only construction of NIMPC protocols with reusable setups is by [28], which makes use of a (reusable) PKI plus CRS, but is based on the sub-exponential security of IO and DDH. Using mrNISC, we give a generic transformation from any NIMPC protocols using correlated randomness to ones in the PKI plus CRS model.

Corollary 1

Applying our transformation to known NIMPC protocols [5, 6], gives the following NIMPC protocols in the PKI plus CRS model assuming mrNISC for $\mathrm {P}$ and UC-NIZK for $\mathrm {NP}$.

• 1. NIMPC for the iterated product function $f(x_1, \dots , x_n) = x_1 \cdots x_n$ over a group, against any number of corruption.

• 2. NIMPC for $\mathrm {P}$ from multi-input functional encryption, against any number of corruption.

• 3. NIMPC for $\mathrm {P}$, against a constant number of corruption (each holding a O(1)-bit input).

The first and third bullets are achieved for the first time, using only reusable setups. We weaken the assumption needed for the second bullet from sub-exponentially secure IO in [28] to polynomially secure IO, equivalent to multi-input functional encryption [23], which is a necessary assumption.

We propose a new primitive called secret-sharing VBB obfuscation. As the name suggests, it enables the owner of a private program M to secret share M among $N$ servers, where the i’th server holds share $M_i$. Later, the servers can evaluate the program on any input x, by sending one message, called the output shares, to an evaluator who learns the output M(x) and nothing else; this holds even if the evaluator colludes with all but one server. Analogous to VBB obfuscation, the secret shares of M are reusable and security is simulation-based. While VBB is impossible in general, secret-sharing VBB can be implemented using mrNISC in a simple way. Though the construction from mrNISC is simple, we found secret-sharing VBB conceptually interesting and it can be readily used to turn applications of VBB into their secret-sharing counterparts. For instance, for cryptographic primitives, such as, IBE, ABE, PE, and FE, where a central trusted authority issues secret keys for identities, key policies, and functions respectively, we can decentralize the trusted authority by creating a secret-sharing VBB obfuscation of the key generation algorithm among multiple servers. Importantly, the servers do not need to communicate with each other and only need to send a single message to the inquirer of a key.

The notion of secret-sharing VBB appears similar to the notions of Homomorphic Secret Sharing and Function Secret Sharing (HSS/FSS) [9, 10]. The main difference is that in secret-sharing VBB the evaluator may collude with all but one servers, whereas in HSS/FSS the evaluator is honest. Consequently, the security of secret-sharing VBB must hold even when all output shares are made public, whereas HSS/FSS does not guarantee security in this setting. Another similar notion is bit-fixing homomorphic sharing proposed in [31], which is tailor made for the construction there. Secret sharing VBB is simpler and more natural.

2 Technical Overview

2.1 Security Definition of mrNISC Schemes

We now present the game-based definition of adaptive security of mrNISC scheme. In the full version [8], we present the ideal mrNISC functionality and show that the definition below implies UC-security.

Definition 3

(Adaptive Security). An mrNISC scheme $\mathsf {mrNISC}$ for f is semi-honest (or semi-malicious) private if there exists a PPT simulator $\mathcal {S}$, such that, for all PPT adversary $\mathcal {A}$, the views of $\mathcal {A}$ in the following experiments $\mathsf {Exp}_{\mathcal {A},\mathcal {S}}(\mathsf {Real},\lambda , f)$ and $\mathsf {Exp}_{\mathcal {A}, \mathcal {S}}(\mathsf {Ideal},\lambda ,f)$ are indistinguishable.

Experiment $\mathsf {Exp}_{\mathcal {A},\mathcal {S}}(\mathsf {Real}, \lambda , f)$: $\mathcal {A}$ chooses the number of parties $M$ and the set of honest parties $H\subseteq [M]$; the set of corrupted parties is ${\bar{H}}$. It interacts with a challenger in an arbitrary number of iterations till it terminates. In every iteration k, it can submit one query of one of the following three types.

• Corrupt Input Encoding: Upon $\mathcal {A}$ sending a query $(\textsf {input}, P_i, x_i, \rho _i)$ for a corrupt party $i \in {\bar{H}}$, record $\hat{x}_i$ generated by $(\hat{x}_{i}, s_i) =\mathsf {Com}(1^\lambda , x_{i}; \rho _i)$. In the semi-honest case, $\rho _i$ is randomly sampled, whereas in the semi-malicious case, it is chosen by $\mathcal {A}$.

• Honest Input Encoding: Upon $\mathcal {A}$ choosing the input $(\textsf {input}, P_i, x_i)$ of an honest party $i \in H$, generate $(\hat{x}_{i}, s_i) \leftarrow \mathsf {Com}(1^\lambda , x_{i})$ and send $\hat{x}_i$ to $\mathcal {A}$. $\mathcal {A}$ is restricted to submit one input query for each party $P_i$.

• Honest Computation Encoding: Upon $\mathcal {A}$ querying $(\textsf {compute}, P_i, z, I)$ for an honest party $i \in H\cap I$, if the input encodings ${\{\hat{x}_j\}}_{j \in I}$ of all parties in $H\cap I$ have been generated, send $\mathcal {A}$ the computation encoding $\alpha _{i} \leftarrow \mathsf {Encode}(z, {\{\hat{x}_{j}\}}_{j \in I}, s_{i})$. ((z, I) is the unique identifier of a computation.)

Experiment $\mathsf {Exp}_{\mathcal {A},\mathcal {S}}(\mathsf {Ideal}, \lambda , f)$ : Same as the above experiment, except: Invoke $\mathcal {S}(1^\lambda , f)$.

• Corrupt Input Encoding: Additionally send query $(\textsf {input}, P_i,x_i,\rho _i)$ to $\mathcal {S}$.

• Honest Input Encoding: Upon $\mathcal {A}$ choosing $(\textsf {input}, P_i, x_i)$ for $i \in H$, send query $(\textsf {input}, P_i)$ to $\mathcal {S}$ who generates a simulated input encoding ${\tilde{x}}_i$ for $\mathsf {Adv}$.

• Honest Computation Encoding: Upon $\mathcal {A}$ choosing $(\textsf {compute}, P_i, z, I)$, if this is the last honest computation encoding to be generated for computation (z, I) (i.e., $\forall \ j \ne i \in I\cap H$, $\mathcal {A}$ has queried $(\textsf {compute}, P_j, z, I)$ before), send $\mathcal {S}$ the query $(\textsf {compute}, P_i,z,I)$ and the output $y = f(z, {\{x_{t}\}}_{t \in I})$; otherwise, send $\mathcal {S}$ the query $(\textsf {compute}, P_i,z,I)$ without y. $\mathcal {S}$ generates a simulated computation encoding ${\tilde{\alpha }}_i$ for $\mathsf {Adv}$.

We emphasize that the definition above captures all dynamic choices described in the introduction. For instance, in the ideal world, for each computation session, simulation of all but the last honest computation encoding do not use the output of that session, ensuring that the output remains hidden until all honest computation encodings are sent.

2.2 Overview of Our mrNISC Scheme

Our construction of mrNISC scheme follows the round collapsing approach for constructing 2-round MPC protocols started in [18]; in particular, we build on the work of [24].

The Round Collapsing Approach. The round-collapsing approach collapses a inner MPC protocol with a polynomial L number of rounds into a 2-round outer MPC protocol as follows. Assume that each party $P_i$ in the inner MPC broadcast one message $m_i^\ell$ in each round $\ell$. In the first round of outer MPC, each party $P_i$ commits $c_i \leftarrow \mathsf {COM}(x_i,r_i)$ to its input $x_i$ and some random tape $r_i$ to be used to execute the inner MPC protocol. In the second round, each party $P_i$ sends one garbled circuit $\hat{\mathsf {F}}_i^\ell$ per round $\ell \in [L]$ of the inner MPC protocol corresponding to the next message function $\mathsf {F}_i^\ell$ of $P_i$. This garbled circuit takes as input all the messages $\varvec{m}^{<\ell } = {\{m^{l}_j\}}_{l < \ell , j\in [n]}$ sent in previous rounds, and outputs the next message $m^\ell _i$ of $P_i$ of the inner MPC (or the output for the last round $\ell = L$).

To compute the output from all garbled circuits ${\{\hat{\mathsf {F}}_i^\ell \}}_{\ell \in [L], i \in [n]}$, each $P_i$ needs to provide a way to compute the labels of its garbled circuits $\hat{\mathsf {F}}_i^\ell$ that correspond to the correct messages of the inner MPC, where a message $m^l_j$ is correct if it is computed from $P_j$’s input and randomness $(x_j,r_j)$ committed to in the first round. For this, [24] proposed the following mechanism using a general purpose WE and NIZK. Let $k_0, k_1$ be two labels of $P_i$’s garbled circuit $\hat{\mathsf {F}}^\ell _i$ for an input wire that takes in the t’th bit $y = m^l_{j,t}$ of a message from $P_j$. Recall that $m^l_{j}$ is output by $P_j$’s garbled circuit $\hat{\mathsf {F}}^l_j$. The goal is translating the valid bit y to the corresponding label $k_y$—that is “let $\hat{\mathsf {F}}^l_j$ communicate y to $\hat{\mathsf {F}}^\ell _i$”. [24] modifies the garbled circuits as follows.

• To “receive” y, $\hat{\mathsf {F}}^{\ell -1}_i$ for round $\ell -1$ additionally outputs $\mathrm {ct}_y\leftarrow \mathsf {WEnc}(X_y,k_y)$ for $y \in {\{0,1\}}$, under the statement $X_y$ that there is a NIZK proof $\pi _y$ proving that $y=m^l_{j,t}$ is computed correctly from $P_j$’s input and randomness $(x_j,r_j)$ committed in $c_j$, according to the protocol specification and the partial transcript of messages $\varvec{m}^{<l}$ before round l.

• To “send” y, $\hat{\mathsf {F}}^l_j$ additionally outputs a NIZK proof $\pi$ that $y=m^l_{j,t}$ is computed correctly from $(x_j, r_j)$ committed in $c_j$.

For correctness, decrypting $\mathrm {ct}_y$ using $\pi$ as a witness reveals $k_y$. For security, $k_{1-y}$ remains hidden, thanks to the security of WE and soundness NIZK. Moreover, the ZK property of NIZK ensures that $P_j$’s committed input and randomness $(x_j, r_j)$ remains hidden, protecting $P_j$’s privacy.

Observe that the first messages of the [24] protocol consist of a commitment to parties’ input $x_i$ and randomness $r_i$. We show (as a corollary of our mrNISC construction) that the first messages can be made reusable if we replace $r_i$ with a PRF seed $s_i$ which can generate pseudo-random tapes for an unbounded number of computations.

Challenge and Our Method. The problem is we do not have general purpose WE from standard assumptions. Previous 2-round MPC constructions from standard assumptions circumvent this problem using weaker tools, namely functional commitment with witness encryption from OT in [7], or homomorphic proof commitment with encryption from bilinear pairing groups in [20], or achieving its effect using OT in [21]. Unfortunately, as we explain shortly, using these weaker tools kills the reusability of the first messages.

We restore the reusability of first messages using WE for NIZK of commitments, which suffices for the purpose of [24]. WE for NIZK of commitments is a triple $(\mathsf {Com}, \mathsf {NIZK}, \mathsf {WE})$ of commitment, NIZK, and WE schemes. It allows to commit to any values $c_1 \leftarrow \mathsf {Com}(v_1) \dots c_m \leftarrow \mathsf {Com}(v_m)$ and later reveal multiple NIZK proofs $\pi ^k$ w.r.t. a $\mathsf {crs}$ that $G^k(v_1 \dots v_m) = y^k$ for multiple polynomial-size circuits $G^k$ and outputs $y^k$. In addition, the proofs $\pi ^k$ can be used to decrypt ciphertexts $\mathsf {ct}\leftarrow \mathsf {WEnc}((\mathsf {crs}, c_1 \dots c_m, G^k,y^k), \mathsf {m})$ tied to a statement $X^k = (\mathsf {crs}, c_1 \dots c_m, G^k,y^k)$, so that, the message $\mathsf {m}$ is recovered if and only if $\pi ^k$ is an accepting proof that $G^k(v_1 \dots v_m) = y^k$ w.r.t. $\mathsf {crs}$. The formal witness relation for WE is in Eq. (1) and that for NIZK in Eq. (2).

The two key properties of WE for NIZK of commitments are i) reusability of commitments – one can generate an unbounded number of NIZK proofs and WE ciphertexts w.r.t. them while keeping committed values hidden (only information in the statements is revealed), and ii) support for $\mathrm {P}$ computation – the statements $X^k = (c, G, y)$ are about the correctness of arbitrary polynomial-sized circuits. These two properties are crucial for achieving the reusability of MPC first messages. Our specific definition and construction of WE for NIZK of commitments has an additional bonus feature that it is “dual-mode” in the sense that in a binding mode, binding of commitments, soundness of NIZK, and semantic security of WE are all information theoretic and perfect, and in a simulation mode, the commitments are perfectly equivocable, NIZK perfectly zero-knowledge. These two modes are controlled by how the CRS is sampled and are indistinguishable. The “dual-mode” feature is not necessary for mrNISC, but might be useful for other applications. We give an overview of our WE for NIZK of commitments in Sect. 2.3, and formal construction for $\mathrm {NC}^1$ in Sect. 3 and for $\mathrm {P}$ in the full version [8].

Combined with the round-collapsing approach of [24], we obtain semi-honest, in fact semi-malicious, mrNISC protocols in the CRS model from pairing groups. We can further remove the CRS, by letting each party $P_i$ sample a CRS in the binding mode for generating its own commitments and NIZK proofs, while generating WE ciphertexts w.r.t. other parties’ CRS, yielding protocols in the plain model. This does not hurt security because for every correctly generated binding CRS, the binding of commitments and the soundness of NIZK hold information theoretically; hence semi-malicious corrupted parties can’t cheat and the WE ciphertexts they receive are information theoretically secure. The simulator on the other hand can sample honest parties’ CRS in the simulation mode to simulate their commitments and NIZK proofs.

Implementing Additional Features in mrNISC. Beyond making the first messages reusable, we carefully implement features in mrNISC—namely, adaptive choices of inputs and computations, asynchronous P2P communication, and optional participation of honest parties. Technically, this means simulation of a message can only use information that is available to the simulator at the moment, e.g., only the last delivered honest message in a session can be simulated using the output of that session, all other honest messages are simulated with no information. We show this can be achieved if the inner MPC satisfies output-delayed simulatability—all but the last message from honest parties can be simulated without the output, which is the case w.r.t. the GMW protocol [22]. We then show that the resulting collapsed protocols achieves dynamics in mrNISC.

Comparison with Homomorphic Proof Commitments with Encryption. The homomorphic proof commitment with encryption of [20, 21] can be viewed as a WE for NIZK of the statement that (a linear combination of) committed values is 0 or 1. This in turns gives WE for NIZK of NAND, which verifies NIZK proofs that $c_1,c_2,c_3$ commit to three values $v_1,v_2,v_3$ such that $v_3 = \text {NAND}(v_1,v_2)$. The acute reader may remark that being able to prove NAND relations between committed values allow to prove any statement $X^k = (c,G^k,y^k)$, by including, in the NIZK proof, commitments to intermediate values in the computation of $G^k$, and proofs of correctness of every NAND gate computation w.r.t. them. This is the whole idea of GOS NIZK [25], on which [20] is based. However, we do not know how to construct WE for verifying such NIZK proofs, because checking these proofs require verifying quadratic relations among (committed) elements in the proof. The essence of the problem is that we do not how to construct WE verifying quadratic relations in the witness (i.e., the NIZK proof here); if we knew, we would have obtained general purpose WE. This should be distinguished from checking quadratic relations between (committed) elements in the statement. The latter is the case in [20] and is easier, because the WE encryption procedure knows the statement and can use it to create the ciphertext, but it cannot do the same with the witness.

2.3 Construction of WE for NIZK of Commitments

Key Ideas. Our key idea is to design NIZK proofs $\pi$ that can be verified by a linear equation, so that we can construct WE for verifying the proofs using a WE for linear languages, which are essentially hash proof systems (see, e.g., [1]). More specifically, we want to turn verifying a NIZK proof $\varvec{\pi }$ of a statement $X = (c, G, y)$ into verifying a system of linear equations $\varvec{\theta }= \varGamma \varvec{\pi }$. Crucially, $\varvec{\theta }$ and $\varGamma$, which describe the linear equations, must depend only on the statement X (independent of $\varvec{\pi }$). As such, $\varvec{\theta }, \varvec{\pi }$ are known at WE encryption time, and we can use hash proof systems to generate a WE ciphertext that reveals the message given a witness $\varvec{\pi }$ satisfying the linear system, and information theoretically hides the message if no such witness exists. More precisely, commitments and NIZKs are pairing group elements, and the linear equations are on values in the exponent; at the moment, we ignore this detail.

Unfortunately, verifying known NIZK proofs requires verifying quadratic relations between elements in the proof—the proof contains intermediate computation values, and verification checks the correctness of computation of each gate, which is quadratic. Designing WE for checking quadratic relations between elements in the witness is a barrier, which would give general purpose WE. Our next idea is leveraging that $\mathrm {NC}^1$ circuits can be represented as restricted multiplication straight-line (RMS) programs, where multiplication occurs between intermediate values and input elements; importantly, the latter are committed in c contained in the statement X. This asymmetry in multiplication allows to design NIZK proofs $\varvec{\pi }$ verified by a linear system $\varvec{\theta }, \varvec{\varGamma }$ defined by the statement. Roughly speaking, the proof $\varvec{\pi }$ contain (encodings of) intermediate values, while $\varvec{\theta }, \varvec{\varGamma }$ contain (encodings of) inputs elements. Then, multiplication between $\varvec{\varGamma }$ and $\varvec{\pi }$ captures multiplication between input elements and intermediate values in RMS programs. Hence, we can use WE for linear language to obtain WE for NIZK of commitments for $\mathrm {NC}^1$. Finally, we present a generic bootstrapping technique for lifting from a scheme for $\mathrm {NC}^1$, to a scheme for all polynomial-size circuits $\mathrm {P}$.

Our NIZK for $\mathrm {NC}^1$ with linear verification equations makes use of the homomorphic commitment schemes developed in existing NIZK proofs and some of the ideas behind these proofs [25, 27]. For simplicity, our description below uses GOS homomorphic proof commitments which are based on composite-order bilinear groups. Our final solution in Sect. 3 uses the same ideas but is based on the Groth and Sahai NIZK [27] which uses prime order bilinear groups.

WE for Linear Languages. We start with witness encryption for linear languages. A linear language over $\mathbb {Z}_p$ consists of tuples of a matrix $\varGamma \in \mathbb {Z}_p^{K \times k}$ and a vector $\varvec{\theta }\in \mathbb {Z}_p^K$ in the column span of $\varGamma$. A witness for $(\varvec{\theta }, \varGamma )$ is a vector $\varvec{\pi }$ s.t. $\varvec{\theta }= \varGamma \varvec{\pi }$. There is an extremely simple WE scheme for linear language: A ciphertext encrypting $m \in \mathbb {Z}_p$ consists of $\varvec{\alpha }^T \varGamma$ and $\varvec{\alpha }^T \varvec{\theta }+ m$ for a random row vector $\varvec{\alpha }^T$. When the statement is false, that is, $\varvec{\theta }$ is outside the column span of $\varGamma$, $\varvec{\alpha }^T \varGamma$ contains no information of $\varvec{\alpha }^T \varvec{\theta }$, which hides m.

$$\begin{aligned} \text {Linear WE} \qquad \mathsf {LWEnc}((\varvec{\theta }, \varGamma ), \mathsf {m}): \ \varvec{\alpha }\leftarrow \mathbb {Z}_p^K, \ \ \mathsf {ct}= \varvec{\alpha }^T \theta + \mathsf {m}, \varvec{\alpha }^T \varGamma \end{aligned}$$

Can we use linear WE to verify a complex computation $G(v)=y$ over committed values v? If we had a fully homomorphic commitment scheme for which verification of the opening (i.e., decommitment) is linear, we would solve the problem. Verifying that “$c$ opens to v and $G(v) = y$” is equivalent to that “$c'$ opens to y” w.r.t. $c'$ obtained from homomorphic evaluation of G on $c$. Now a message m can be encrypted using linear WE w.r.t. $c',y$ (which decides $\varvec{\theta }, \varGamma$) and a proof $\varvec{\pi }$ is simply an opening of $c'$ (ignoring ZK for now). Unfortunately, we do not know how to construct such commitment scheme.

Linear Proof for One Multiplication. GOS [25] constructed a commitment scheme with linear opening that can do one homomorphic multiplication, using pairing groups.

Let $(N,\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_t, e,g_1, g_2)$ describe a bilinear group of order N. We use the bracket notation in $G_b$ for $a \in \mathbb {Z}_N$ – referred to as an encoding of a, and write as applying group exponentiation in $G_b$ and as applying the pairing operation. GOS uses a composite order $N = pq$ symmetric bilinear group, where the two source groups are the same $\mathbb {G}= \mathbb {G}_1 =\mathbb {G}_2$; we simply write as a source group element.

The CRS of the commitment scheme contains for a random element in $\mathbb {Z}_N$ of order q. A commitment to $v$ in $\mathbb {Z}_p$ is simply using a random scalar $r \leftarrow \mathbb {Z}_N$. Such a commitment is perfectly binding, because h has order q, and $v$ is in $\mathbb {Z}_p$. Given two commitments and , we can compute a commitment of the product in the target group. Furthermore, we can prove that the product $v_1v_2$ is equal to some value $v_{12}$, and the verification is linear in the proof $\pi$:

In other words, the last equation shows that is a proof for the statement “ and commits to values $v_1$ and $v_2$ so that $v_1v_2 = v_{12}$.”

Since the verification is linear, combined with WE for linear language, this immediately gives a WE for NIZK of correctness of one multiplication. This approach was exploited in [20] for obtaining WE for NIZK of correctness of one NAND.

Going beyond one Multiplication (Step 1). The main issue of the above construction is that a GOS commitment only allows for the evaluation of a single multiplication gate (or equivalently a single NAND), as is now in the target group. To evaluate more complex functions G, we need to be able to make further multiplications. The idea is that the prover can commit to $v_1v_2$ in the source group: and then prove that indeed commits to the same value as :

(3)

(4)

Furthermore, by linearity of the GOS commitment, it is also possible to prove that a commitment commits to a value $v_+$ that is a linear combination of values $v_1$ and $v_2$ committed in and : $v_+ = \mu _1 v_1 + \mu _2 v_2$ (for some public scalars $\mu _1,\mu _2$).

(5)

(6)

To extend to proving $\mathrm {P}$ computations, we can proceed as follows. To commit a bitstring v, we commit each bit individually as a GOS commitment: . Then, to prove that $G(v) = y$, we represent G as a sequence of linear operations and multiplications, and introduce an intermediate commitment for each intermediate result. The proof consists of these intermediate commitments , intermediate proofs that they were computed properly (using Eq. (3) or Eq. (5)) and the opening $r'_o$ of the commitment corresponding to the output of G. Verification would consist of verifying the intermediate proofs (using Eqs. (4) and (6)) and the opening of the output commitment.

The final proof would actually be a zero-knowledge proof and would in essence be a GOS or a Groth-Sahai proof [25, 27]. The zero-knowledge property comes from the following two facts: (1) if is chosen to be of order N (instead of q), commitments are fully equivocable, and (2) there is a single proof (resp., satisfying the verification Eq. 3 (resp., Eq. (5)). Leveraging these two facts, a ZK simulator for a proof of, say one multiplication, can equivocate $c_1, c_2, c_\times$ to any values satisfying ${\tilde{v}}_\times = {\tilde{v}}_1 {\tilde{v}}_2$, the equivocation gives a fake witness for computing the unique proof.

Unfortunately, the final proof verification is not linear: if two intermediate values $v_1, v_2$ need to be multiplied, Eq. (4) would involve a product of the corresponding two commitments $c_1, c_2$, which is quadratic in the final proof.

Restricted Multiplication Program (Step 2). To keep verification linear in the final proof, we remark that we just need to ensure that every multiplication involves at least one input commitment, but never two intermediate commitments (which are part of the final proof). In that case Eq. (4) becomes linear in the intermediate commitment. Hence, we can use the above ideas to verify any restricted multiplication straight-line (RMS) computation [10, 14], which includes all $\mathrm {NC}^1$ computations. Indeed, in an RMS program, the only allowed operations are linear operations over inputs or intermediate values, and multiplications of one intermediate value $v'_j$ with one input $v_i$ (but not of two intermediate values).

Improved $\mathrm {NC}^1$ Scheme Based on $\mathsf {SXDH}$ . The above construction of WE for NIZK of commitments for $\mathrm {NC}^1$ uses composite group order with pairings which are notoriously inefficient. In Sect. 3, we propose a construction solely based on the standard assumption $\mathsf {SXDH}$ over asymmetric prime order pairing groups. The construction follows the same ideas described above, but is based on the Groth-Sahai NIZK proofs, which use vector subspaces to implement features of the subgroup structure. The scheme becomes more complex. That’s why we explain our ideas w.r.t. the simpler GOS NIZK system.

Polynomial-Size Circuits. We now present a generic bootstrapping technique from a WE scheme for NIZK of commitments for RMS to one for $\mathrm {P}$. We can encode any polynomial-size computation $y = G(v)$ into a randomized encoding $o = \mathsf {RE}(G, v; \mathsf {PRF}(k))$ that reveals only y (with randomness expanded from a seed k using a $\mathsf {PRF}$). Since both $\mathsf {RE}$ and $\mathsf {PRF}$ are computable in $\mathrm {NC}^1$, our RMS-scheme can verify whether o is correctly computed from v, k committed in some commitments c, but cannot verify that o indeed decodes to y (which belongs to $\mathrm {P}$). Instead, we use a garbled circuit to verify the latter and use WE to ensure that only labels corresponding to the correct RE encoding o are revealed. More precisely, a WE ciphertext of m w.r.t. (G, c, y) for a polynomial-size circuit G contains 1) a garbled circuit $\widehat{F}_{y,m}$ of $F_{y,m}$ that outputs m iff given an input $o'$ that decodes to y, and 2) WE encryption (using the RMS-scheme) of labels under statements that verify the computation of o from (k, v) committed in c. Decryption requires NIZK proofs certifying the correctness of o, which allows recovering labels for o, and then m.

Applications. Due to the lack of space, we refer the reader to the full version [8] for applications of mrNISC. At a very high-level, in scenarios where a set of parties need many copies of freshly sampled correlated randomness, we can use mrNISC to replace correlated randomness with reusable PKI and CRS setup: Parties’ public key in the PKI is simply an encoding of their private PRF key, later on, they can jointly run mrNISC to sample fresh correlated randomness using the pseudorandom coins generated from all parties’ PRF keys. In NIMPC, sampling correlated randomness and generating NIMPC message using this correlated randomness can be combined in one mrNISC computation.

3 WE for NIZK of Commitments: $\mathrm {NC}^1$

In this section, we define and construct our new primitive: witness encryption (WE) for NIZK of commitments (for the complexity class $\mathrm {P}$), which is the main component for the construction of our mrNISC scheme.

As explained in Sect. 2.3, from a high-level point of view, WE for NIZK of commitments combines the properties of homomorphic proof commitments with encryption [20] and of functional commitments with witness selector [7]. Compared with the former, it supports general statements in $\mathrm {P}$ (instead of a single NAND gate evaluation). Compared with the latter, it allows for zero-knowledge to hold when multiple NIZK proofs are generated.

3.1 Definition of Witness Encryption for NIZK of Commitments

We start by defining dual-mode commitment schemes (a.k.a., hybrid commitments [12]), where the CRS can be generated in two computationally indistinguishable ways: one yielding perfectly binding commitments and one yielding equivocal (a.k.a., simulatable or trapdoor) commitments. The term “dual-mode commitment” comes from [32].

We may not need dual-mode commitments to construct mrNISC, but just simulatable/equivocal commitments (without a perfectly binding setup). However using dual-mode commitments significantly simplifies definitions and proofs. Since our constructions achieve this stronger security notion, we use it. More precisely, without a dual-mode commitment, we could not use the standard definition of witness encryption: witness encryption indeed just ensures that ciphertexts related to a false statement (about the committed value, in our setting) cannot be decrypted. Without the dual mode, because of equivocality of the commitments, it would be possible to open any commitment to any value. Hence any statement about a committed value would be always true or always false (independently of the committed value).

Definition 4

(Dual-Mode Commitments). A (dual-mode) commitment scheme $\mathsf {COM}$ has a binding mode and a simulation mode, each involves three polynomial-time algorithms.

• Binding Setup: $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$ on input the security parameter $\lambda$ generates a binding CRS $\mathsf {crs}$.

• Commitment: $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$ on input the CRS $\mathsf {crs}$ and a message $v$ in some implicitly defined message set $\mathcal {V}$,¹ generates a commitment $c$ of $v$ and an associated decommitment (a.k.a., opening) $d$.

• Verification: on input the CRS $\mathsf {crs}$, a commitment $c$, a message $v\in \mathcal {V}$, and a decommitment $d$, outputs 1 if $c$ indeed commits to $v$, and 0 otherwise.

• Simulation Setup: $(\mathsf {crs}, \tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda )$ on input the security parameter $\lambda$ generates a simulation CRS $\mathsf {crs}$ and an associated trapdoor $\tau$.

• Commitment Simulation: $(c,\mathsf {aux}) \leftarrow \mathsf {CSimCom}(\tau )$ on input a simulation trapdoor $\tau$, generates a simulated commitment $c$ and some auxiliary data $\mathsf {aux}$.

• Opening Simulation: $d\leftarrow \mathsf {CSimOpen}(\tau ,\mathsf {aux},v)$ on input an auxiliary data $\mathsf {aux}$ and a message $v\in \mathcal {V}$, generates some decommitment $d$ corresponding to an opening of the associated commitment $c$ to $v$.

satisfying the following properties:

• Perfect Correctness: For every security parameter $\lambda \in \mathbb {N}$, CRS $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$ or $(\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda )$, message $v\in \mathcal {V}$, and commitment $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$, we have: $\mathsf {CVer}(\mathsf {crs},c,v,d) = 1$.

• Setup Indistinguishability: The following two distributions are computationally indistinguishable:

  $$\begin{aligned} {\left\{ \mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda ) \ : \ \mathsf {crs}\right\} }_{\lambda } \approx {\left\{ (\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda ) \ : \ \mathsf {crs}\right\} }_{\lambda } . \end{aligned}$$

• Perfect Binding in Binding Mode: For every security parameter $\lambda \in \mathbb {N}$, binding CRS $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$, message $v\in \mathcal {V}$, commitment $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$, message $v' \in \mathcal {V}$, bitstring $d'$, if $v' \ne v$: $\mathsf {CVer}(\mathsf {crs},c,v',d') = 0$.

• Perfect Equivocality in Simulation Mode: For every security parameter $\lambda \in \mathbb {N}$, simulation CRS $(\mathsf {crs}, \tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda )$, message $v\in \mathcal {V}$, the following two distributions are identical:

  $$\begin{aligned} \left\{ (c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v) \ : \ (c,d) \right\} , \\ \left\{ (c,\mathsf {aux}) \leftarrow \mathsf {CSimCom}(\tau ),\; d\leftarrow \mathsf {CSimOpen}(\tau ,\mathsf {aux},v)\ : \ (c,d) \right\} . \end{aligned}$$

We are interested in proving statements “in zero-knowledge” of the form: “$c$ commits to some value $v$ such that $G(v) = y$,” where $G$ is a circuit in some circuit class $\mathcal {G}$ and $y$ is the expected output of the function. In our construction, the trapdoor of the NIZK will actually be the trapdoor of the commitment. That is why we cannot easily rely on a generic definition of NIZK and instead introduce the notion of dual-mode NIZK of commitments. The binding setup yields perfectly sound NIZK proofs, while the simulation setup yields zero-knowledge proofs.

Definition 5

(Dual-Mode NIZK of Commitments). Let $\mathsf {COM}$ be as in Definition 4, and $\mathcal {G}$ be a class of polynomial-size circuits. A dual-mode NIZK $\mathsf {NIZK}$ associated with $\mathsf {COM}$ for $\mathcal {G}$ consists of two polynomial-time algorithms:

• Proof: $\pi \leftarrow \mathsf {CProve}(\mathsf {crs},c,G,v,d)$ on input the CRS $\mathsf {crs}$, a commitment $c$, a circuit $G\in \mathcal {G}$,² the committed message $v\in \mathcal {V}$, the decommitment $d$, as defined by $\mathsf {COM}$, generates a proof $\pi$ that G on input the value v committed in $c$ outputs $y = G(v)$. Refer to (c, G, y) as the statement and (v, d) the witness.

• Proof Verification: on input the CRS $\mathsf {crs}$, a statement (c, G, y), and a proof $\pi$, accepts or rejects the proof.

The algorithms satisfy the following properties:

• Perfect Proof Correctness: For every security parameter $\lambda \in \mathbb {N}$, CRS $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$ or $(\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda )$, message $v\in \mathcal {V}$, circuit $G\in \mathcal {G}$, commitment $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$ and proof $\pi \leftarrow \mathsf {CProve}(\mathsf {crs},c,G,v,d)$, we have: $\mathsf {CPVer}(\mathsf {crs},c,G(v),\pi ) = 1$.

• Perfect Soundness in Binding Mode: For every security parameter $\lambda \in \mathbb {N}$, binding CRS $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$, message $v\in \mathcal {V}$, commitment $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$, circuit $G\in \mathcal {G}$, incorrect output $y' \ne G(v)$, and bitstring $\pi$, $\mathsf {CPVer}(\mathsf {crs},c,y',\pi ) = 0$.

• Zero-Knowledge in Simulation Mode: There exists a PPT simulator algorithm $\mathsf {CPSim}$, such that for any PPT adversary $\mathcal {A}$, the quantity is negligible in $\lambda$:

  $$\begin{aligned} \Bigg | \Pr \left[ \begin{array}{l} (\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda ),\; (\mathsf {st},v) \leftarrow \mathcal {A}(\mathsf {crs},\tau ),\\ (c,\mathsf {aux}) \leftarrow \mathsf {CSimCom}(\tau ),\; d\leftarrow \mathsf {CSimOpen}(\tau ,\mathsf {aux},v) \end{array} \ : \ \mathcal {A}^{\mathsf {Prove}}(\mathsf {st}) = 1 \right] \\ - \Pr \left[ \begin{array}{l} (\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda ),\; (\mathsf {st},v) \leftarrow \mathcal {A}(\mathsf {crs},\tau ),\\ (c,\mathsf {aux}) \leftarrow \mathsf {CSimCom}(\tau ) \end{array} \ : \ \mathcal {A}^{\mathsf {Sim}}(\mathsf {st}) = 1 \right] \Bigg | , \end{aligned}$$

  where and .

We remark that our notion of zero-knowledge allows the adversary to see the trapdoor $\tau$ but not the auxiliary data $\mathsf {aux}$, that is why we let the adversary consider a single simulated commitment but as many simulated proofs as it wants. The reason that $\mathsf {aux}$ is not given to the adversary is because we need to store a PRF key in $\mathsf {aux}$, to generate the randomness for simulation, to be sure to use the same randomness if the simulation is called twice with the same circuit $G$ in the construction for $\mathrm {P}$.

Definition 6

(Witness Encryption for NIZK of Commitments). Let $\mathsf {COM}$, $\mathsf {NIZK}$, and $\mathcal {G}$ be as in Definition 4 and 5. A Witness Encryption $\mathsf {WE}$ associated with $\mathsf {COM}, \mathsf {NIZK}$ for $\mathcal {G}$ consists of two polynomial-time algorithms:

• Witness Encryption: $\mathsf {ct}\leftarrow \mathsf {CWEnc}(\mathsf {crs},c,G,y,\mathsf {m})$ on input the CRS $\mathsf {crs}$, a statement $(c,G,y)$ where $G\in \mathcal {G}$, and a bitstring $\mathsf {m}$, encrypts $\mathsf {m}$ into a ciphertext $\mathsf {ct}$, under that statement.

• Witness Decryption: on input the CRS $\mathsf {crs}$, a ciphertext $\mathsf {ct}$, a statement $(c,G,y)$, and a NIZK proof $\pi$, decrypts $\mathsf {ct}$ into the message $\mathsf {m}$, or outputs $\bot$.

The algorithms satisfy the following properties:

• Perfect Encryption Correctness: For every $\lambda \in \mathbb {N}$, CRS $\mathsf {crs}\leftarrow \mathsf {CSetup}_{\mathsf {bind}}(1^\lambda )$ or $(\mathsf {crs},\tau ) \leftarrow \mathsf {CSetup}_{\mathsf {sim}}(1^\lambda )$, message $v\in \mathcal {V}$, circuit $G\in \mathcal {G}$, commitment $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$ and proof $\pi \leftarrow \mathsf {CProve}(\mathsf {crs},c,G,v,d)$, bitstring $\mathsf {m}$, and ciphertext $\mathsf {ct}\leftarrow \mathsf {CWEnc}(\mathsf {crs},c,G,G(v),\mathsf {m})$, we have: $\mathsf {CWDec}(\mathsf {crs},\mathsf {ct},c,G,G(v),\pi ) = \mathsf {m}$.

• Semantic Security: For any PPT adversary $\mathcal {A}$, the following is negligible in $\lambda$:

  

  where $\rho$ denotes the random tape used by $\mathsf {CCom}$ to generate the commitment $c$ of the message $v$ ($\rho$ is provided by the adversary).

We remark that semantic security of our WE holds even when the binding CRS is generated semi-maliciously, i.e., the adversary chooses the random tape $\rho '$. This is important for our semi-malicious construction of mrNISC schemes, as the adversary generates itself the binding CRS. We also note that our construction for $\mathrm {NC}^1$ actually achieves perfect semantic security for binding CRS, however, our transformation from $\mathrm {NC}^1$ to $\mathrm {P}$ only achieves computational semantic security.

3.2 Bilinear Commitments with Proofs of Quadratic Relations

As a tool to construct witness encryption for NIZK of commitments, we first introduce the notion of bilinear commitments with proofs of quadratic relations. Such commitments essentially allow to “prove linearly and in a strong form of zero-knowledge” that one commitment $c_\times$ commits to the product of the values committed by two commitments $c_1$ and $c_2$ (quadratic proofs), and that one commitment $c_+$ commits to some linear combination of the values committed by two commitments $c_1$ and $c_2$ (linear proofs). These proofs are amenable to be verified by hash proof systems and can be combined to construct WE for NIZK of commitments.

Bilinear Groups and Notations. Denote by $(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t,e,g_1,g_2)$ a bilinear group where $e: \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_t$ is an efficiently computable bilinear map (called a pairing) such that $e(g_1,g_2)=g_T$ generates $\mathbb {G}_t$. We use the bracket notation to denote the element $g_\iota ^a$ in group $\mathbb {G}_\iota$ for $a \in \mathbb {Z}_p$ and write as applying group exponentiation in $\mathbb {G}_\iota$ and as applying the pairing operation. This notation extends to vectors and matrices. We assume the Symmetric External Diffie-Hellman assumption ( $\mathsf {SXDH}$ ) assumption over asymmetric bilinear pairing groups, which requires the Decisional Diffie-Hellman ($\mathsf {DDH}$) assumption to hold in each source group $\mathbb {G}_1$ and $\mathbb {G}_2$, namely, for any $\iota \in {\{1,2\}}$, , where r, s, t are random scalars sampled from $\mathbb {Z}_p$. All vectors are denoted by bold letters and all matrices are denoted by uppercase letters.

Bilinear Commitments. Our construction starts from the SXDH-based commitment scheme used in Groth-Sahai NIZK [26]. This commitment scheme allows to commit values both in $\mathbb {G}_1$ and $\mathbb {G}_2$. The resulting commitments are dual-mode and called type-1 and type-2 commitments respectively. More formally we define:

• Binding Setup: $\mathsf {crs}\leftarrow \mathsf {QSetup}_{\mathsf {bind}}(1^\lambda )$ generates a bilinear group $(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_t,e,g_1,g_2)$, and for $\iota \in \{1,2\}$, generates a random matrix $A_\iota \in \mathbb {Z}_p^{2 \times 2}$ of rank 1 such that the vector is not in the column span of $A_\iota$, and outputs .

• Simulation Setup: $(\mathsf {crs}, \tau ) \leftarrow \mathsf {QSetup}_{\mathsf {sim}}(1^\lambda )$ is identical to binding setup except that $A_1$ and $A_2$ are chosen of rank 2. The trapdoor is $\tau = (A_1, A_2)$. Note that $\varvec{1}$ is in the column spans of $A_1$ and $A_2$.

• Commitment: $(\varvec{c},\varvec{d}) \leftarrow \mathsf {QCom}_\iota (\mathsf {crs},v)$ generates a type-$\iota$ commitment of a message as follows: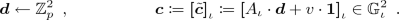

  

• Verification: checks whether $\varvec{c}$ is a valid type-$\iota$ commitment of $v$ as follows: it returns 1 if and only if:

  

  (7)

• Commitment Simulation: $(\varvec{c},\varvec{\mathsf {aux}}) \leftarrow \mathsf {QSimCom}_\iota (\tau )$ simulates a type-$\iota$ commitment as follows:

  

  (8)

• Opening Simulation: $\varvec{d}\leftarrow \mathsf {QSimOpen}_\iota (\tau =(A_1,A_2),\varvec{\mathsf {aux}},v)$ opens the type-$\iota$ commitment corresponding to $\varvec{\mathsf {aux}}$ as follows:

  

  (9)

We have the following lemma following directly from [26].

Lemma 2

(in [26]). The two commitment schemes $(\mathsf {QSetup}_{\mathsf {bind}},\mathsf {QCom}_\iota ,\mathsf {QVer}_\iota ,\mathsf {QSetup}_{\mathsf {sim}},\mathsf {QSimCom}_\iota ,\mathsf {QSimOpen}_\iota )$ (for $\iota \in \{1,2\}$) described above are both dual-mode commitments.

Remark 1

Jumping ahead, for semi-malicious security of mrNISC in the plain model, we want the binding of $\mathsf {COM}$, soundness of NIZK, and semantic security of WE to hold against every CRS in the support of $\mathsf {QSetup}_{\mathsf {bind}}$. This boils down to ensuring that the bilinear group generated by $\mathsf {QSetup}_{\mathsf {bind}}$ is always a valid one: p must be a prime number, $g_1,g_2$ generates the cyclic groups $\mathbb {G}_1$ and $\mathbb {G}_2$ of order p, and it is possible to check in polynomial time whether an element is in $\mathbb {G}_1$ or $\mathbb {G}_2$. This can be done, and we implicitly assume that this is the case.

Bilinear Commitments with Proofs of Linear Relations. We now show how to prove that a type-2 commitment $\varvec{c}_+$ commits to a given linear combination of values committed in two type-2 commitments $\varvec{c}_1$ and $\varvec{c}_2$. Concretely, we want to prove that $\varvec{c}_1,\varvec{c}_2,\varvec{c}_+$ respectively commit to values $v_1,v_2,v_+$ that satisfy the linear relation: $v_+ = \mu _1 v_1 + \mu _2 v_2$, where $\mu _1,\mu _2 \in \mathbb {Z}_p$ are some public parameters.

$$\begin{aligned} \text {Statement: } (\mathsf {Linear}, \mathsf {crs}, {\{\mu _i,\varvec{c}_i\}}_{i \in {\{1, 2\}}}, \varvec{c}_+),\qquad \text {Witness: } (v_1,\varvec{d}_1,v_2,\varvec{d}_2,\varvec{d}_+) \end{aligned}$$

The main idea of the construction is to remark that the commitments are linearly homomorphic and the above statement is equivalent to proving that is a commitment of 0, where for $i \in \{1,2,+\}$, . Hence the proof $\varvec{\pi }_+$ is the opening of this commitment to the value $v = 0$:

Zero-knowledge comes from the fact that this value $\varvec{\pi }_+$ always exists and is unique in the simulation mode, as the matrix $A_2$ is full rank in that mode.

Formally, the construction is as follows:

• Linear Proof: $\mathsf {QLinProve}(\mathsf {crs},{\{\mu _i,\varvec{c}_i,v_i,\varvec{d}_i\}}_{i\in [2]}, (\varvec{c}_+,\varvec{d}_+))$, given information of both statement and witness, outputs:

  

  (10)

• Linear Proof Verification: $\mathsf {QLinVer}(\mathsf {crs},{\{\mu _i,\varvec{c}_i\}}_{i\in [2]},\varvec{c}_+,\varvec{\pi }_+)$ returns 1 iff:

  

  (11)

  where for $i \in {\{1,2,+\}}$.

Lemma 3

For any security parameter $\lambda \in \mathbb {N}$, for any CRS $\mathsf {crs}\leftarrow \mathsf {QSetup}_{\mathsf {bind}}(1^\lambda )$ or $(\mathsf {crs},\tau ) \leftarrow \mathsf {QSetup}_{\mathsf {sim}}(1^\lambda )$, messages $v_1,v_2,v_+ \in \mathbb {Z}_p$, scalars $\mu _1,\mu _2,\mu _+ \in \mathbb {Z}_p$, bitstrings $\varvec{c}_1,\varvec{d}_1,\varvec{c}_2,\varvec{d}_2,\varvec{c}_+,\varvec{d}_+$ s.t. $\forall i\in \{1,2,+\}, \mathsf {QVer}_2(\mathsf {crs},\varvec{c}_i,v_i,\varvec{d}_i) = 1$,

• Perfect Correctness: If $v_+ = \mu _1 v_1 + \mu _2 v_2$, a proof $\pi _+ \leftarrow \mathsf {QLinProve}(\mathsf {crs},\{\mu _i,\varvec{c}_i,v_i,\varvec{d}_i\}_{i}, (\varvec{c}_+,\varvec{d}_+))$ passes verification: $\mathsf {QLinVer}(\mathsf {crs},{\{\mu _i,\varvec{c}_i\}}_{i \in [2]},\varvec{c}_+,\varvec{\pi }_+) = 1$

• Perfect Uniqueness: If $v_+ = \mu _1 v_1 + \mu _2 v_2$ and the CRS is simulated, then there is a unique vector $\varvec{\pi }_+ = (\tilde{\varvec{c}}_+ - \mu _1 \tilde{\varvec{c}}_1 - \mu _2 \tilde{\varvec{c}}_2)A_2^{-1} \in \mathbb {Z}_p^2$ that passes verification.

• Perfect Soundness: If $v_+ \ne \mu _1 v_1 + \mu _2 v_2$ and the CRS is binding, then no vector $\varvec{\pi }_+ \in \mathbb {Z}_p^2$ passes verification: $\mathsf {QLinVer}(\mathsf {crs},{\{\mu _i,\varvec{c}_i\}}_{i \in [2]},\varvec{c}_+,\varvec{\pi }_+) = 0$ for all $\varvec{\pi }_+ \in \mathbb {Z}_p^2$.

Proof

Perfect correctness is straightforward. Perfect uniqueness follows from Eq. (11) and the fact that when the CRS is simulated, the matrix $A_2$ is full rank. Perfect soundness comes from the fact that:

is a (perfectly binding) commitment of $\mu _1 v_1 + \mu _2 v_2 \ne v_+$.    $\square$

Remark 2

(Zero-knowledge of the linear proof $\varvec{\pi }_+$ in simulation mode). Perfect uniqueness of the proof $\varvec{\pi }_+$ in simulation mode is a very strong form of witness indistinguishability: whatever witness $(v_1,\varvec{d}_1,v_2,\varvec{d}_2,\varvec{d}_+)$ is used, the proof is exactly the same $\varvec{\pi }_+ = (\tilde{\varvec{c}}_+ - \mu _1 \tilde{\varvec{c}}_1 - \mu _2 \tilde{\varvec{c}}_2)A_2^{-1}$. To show further that it is ZK, we need to argue that $\varvec{\pi }_+$ is also efficiently computable. This the case when the commitments are simulated with $\mathsf {QSimCom}$, as the simulator can then equivocate $\varvec{c}_1,\varvec{c}_2,\varvec{c}_+$ to any $v'_1,v'_2,v'_+$ satisfying $v'_+ = \mu _1 v'_1 + \mu _2 v'_2$ with decommitments $\varvec{d}'_1, \varvec{d}'_2, \varvec{d}'_+$ using $\mathsf {QSimOpen}$. This gives a valid witness $(v'_1,\varvec{d}'_1,v'_2,\varvec{d}'_2,\varvec{d}'_+)$ for the statement and a simulated proof can be generated by running the honest prover algorithm $\mathsf {QLinProve}$ with this witness.

Bilinear Commitments with Proofs of Quadratic Relations. We now show how to prove that a type-2 commitment $\varvec{c}_\times$ commits to the product of values committed in a type-1 commitment $\varvec{c}_1$ and a type-2 commitment $\varvec{c}_2$. Concretely, we want to prove that $\varvec{c}_1,\varvec{c}_2,\varvec{c}_+$ respectively commit to values $v_1,v_2,v_\times$ that satisfy the quadratic relation $v_\times = v_1 \cdot v_2$.

$$\begin{aligned} \text {Statement: } (\mathsf {Mult}, \mathsf {crs}, {\{\varvec{c}_i\}}_{i \in {\{1, 2, \times \}}}),\qquad \text {Witness:} (v_1,\varvec{d}_1,v_2,\varvec{d}_2,\varvec{d}_\times ) \end{aligned}$$

(12)

The main idea of the construction is to construct from and a commitment of $v_1\cdot v_2$. Remember that in the technical overview Sect. 2.3, we could multiply commitments $\varvec{c}_1$ and $\varvec{c}_2$ directly (by using a pairing operation) to get a commitment of $v_1 \cdot v_2$, as commitments were a single group element. Intuitively, the equivalent of this multiplication to vector of group elements $\varvec{c}_1$ and $\varvec{c}_2$ is the tensor product operation $\otimes$. And we want to prove that is a “commitment” of 0 in $\mathbb {G}_t$, where $\varvec{1}$ is used as a type-1 commitment of 1.³ Similar to multiplication of commitments in Sect. 2.3, computing these tensor products uses pairings.

The basic idea is then that the proof is a decommitment of this commitment to 0. Unfortunately, this would not be zero-knowledge since there are multiple possible decommitments and choosing one may reveal information about the witness $(v_1,\varvec{d}_1,v_2,\varvec{d}_2,\varvec{d}_\times )$. To tackle this subtle issue (which does not happen with the commitments from the technical overview in Sect. 2.3 nor with proof of linear relations), the prover needs to rerandomize this decommitment, similarly to what is done in [26] to get perfect witness indistinguishability. This is the purpose of the vector $\varvec{\rho }$ in Eq. (14).

  We first need to briefly recall the notion of tensor products. The tensor product of two matrices $M \in \mathbb {Z}_p^{k \times m}$ and $M' \in \mathbb {Z}_p^{k' \times m'}$ is the matrix $T = M \otimes M' \in \mathbb {Z}_p^{kk' \times mm'}$ defined as:

$$ T = \begin{pmatrix} M_{1,1} \cdot M' &{} \cdots &{} M_{1,m} \cdot M' \\ \vdots &{} &{} \vdots \\ M_{k,1} \cdot M' &{} \cdots &{} M_{k,m} \cdot M' \end{pmatrix}. $$

We extensively use the following identity: if $M \in \mathbb {Z}_p^{k \times m}$, $M' \in \mathbb {Z}_p^{k' \times m'}$, $N \in \mathbb {Z}_p^{m \times n}$ and $N' \in \mathbb {Z}_p^{m' \times n'}$, then we have,

$$\begin{aligned} (M \otimes M') \cdot (N \otimes N') = (M \cdot N) \otimes (M' \cdot N') . \end{aligned}$$

(13)

Recall that the construction essentially consists of proving that is a commitment of 0, which is what Eq. (15) below ensures. To better understand how this value is computed (in term of group elements, pairings, and exponentiations), we explicitly write it down:

The construction is as follows:

• Quadratic Proof: $\varvec{\pi }_\times \leftarrow \mathsf {QQuadProve}(\mathsf {crs},{\{\varvec{c}_i,v_i,\varvec{d}_i\}}_{i \in [2]}, \varvec{c}_\times ,\varvec{d}_\times )$ picks $\varvec{\rho }\in \mathbb {Z}_p^4$ and outputs:

  

  (14)

  where $\mathsf {Id}\in \mathbb {Z}_p^{2 \times 2}$ is the identity matrix. Recall that the vector $\varvec{\rho }$ is used to randomize the proof so that it is uniformly random among the valid proofs, and hence is perfectly witness indistinguishable.

• Quadratic Proof Verification: returns 1 if and only if:

  

  (15)

  where $\mathsf {Id}\in \mathbb {Z}_p^{2 \times 2}$ is the identity matrix. Note that computing involves pairing operations between elements of vectors $\varvec{c}_1 \in \mathbb {G}_1^2$ and $\varvec{c}_2 \in \mathbb {G}_2^2$. Computing the right hand side also involves pairing operations.

Remark 3

Quadratic proof verification just consists of checking a linear equation in $(\varvec{c}_2,\varvec{c}_\times ,\varvec{\pi }_\times )$. Indeed, thanks to Eq. (13), Eq. (15) is equivalent to:

Lemma 4

For any security parameter $\lambda \in \mathbb {N}$, for any CRS $\mathsf {crs}\leftarrow \mathsf {QSetup}_{\mathsf {bind}}(1^\lambda )$ or $(\mathsf {crs},\tau ) \leftarrow \mathsf {QSetup}_{\mathsf {sim}}(1^\lambda )$, messages $v_1,v_2,v_\times \in \mathbb {Z}_p$, bitstrings $\varvec{c}_1,\varvec{d}_1,\varvec{c}_2,\varvec{d}_2,\varvec{c}_\times ,\varvec{d}_\times$ such that $\forall i\in \{1,2,\times \},\mathsf {QVer}_i(\mathsf {crs},\varvec{c}_i,v_i,\varvec{d}_i) = 1$, we have:

• Perfect Correctness: If $v_\times = v_1 v_2$, a proof $\mathsf {QQuadProve}(\mathsf {crs},\{\varvec{c}_i,v_i,\varvec{d}_i\}_{i\in [2]}, (\varvec{c}_\times ,\varvec{d}_\times ))$ passes verification: $\mathsf {QQuadVer}(\mathsf {crs},{\{\mu _i,\varvec{c}_i\}}_{i \in [2]},\varvec{c}_\times ,\varvec{\pi }_\times ) = 1$

• Perfect Uniformity: If $v_\times = v_1 v_2$ and the CRS is simulated, then the vector $\varvec{\pi }_\times$ generated by $\mathsf {QQuadProve}$ follows a uniform distribution among the solutions of Eq. (15).

• Perfect Soundness: If $v_\times \ne v_1 v_2$ and the CRS is binding, then no $\varvec{\pi }_\times \in \mathbb {Z}_p^8$ passes verification: $\mathsf {QQuadVer}(\mathsf {crs},\varvec{c}_1,\varvec{c}_2,\varvec{c}_\times ,\varvec{\pi }_\times ) = 0$ for all $\varvec{\pi }_\times \in \mathbb {Z}_p^8$.

Proof

To prove perfect correctness, we use Eqs. (13) and (14) and remark:

$$\begin{aligned}&\varvec{1} \otimes \tilde{\varvec{c}}_\times - \tilde{\varvec{c}}_1 \otimes \tilde{\varvec{c}}_2 = \varvec{1} \otimes (A_2 \varvec{d}_\times + v_\times \cdot \varvec{1}) - \tilde{\varvec{c}}_1 \otimes (A_2 \varvec{d}_2 + v_2 \cdot \varvec{1}) \nonumber \\&= \varvec{1} \otimes (A_2 \varvec{d}_\times ) + v_\times \cdot \varvec{1} \otimes \varvec{1} - \tilde{\varvec{c}}_1 \otimes (A_2 \varvec{d}_2) - (A_1 \varvec{d}_1 + v_1 \cdot \varvec{1}) \otimes (v_2 \cdot \varvec{1}) \nonumber \\&= \varvec{1} \otimes (A_2 \varvec{d}_\times ) - \tilde{\varvec{c}}_1 \otimes (A_2 \varvec{d}_2) - (A_1 \varvec{d}_1) \otimes (v_2 \cdot \varvec{1}) + (v_\times - v_1 v_2) \cdot (\varvec{1} \otimes \varvec{1}) \nonumber \\&= (\mathsf {Id}\otimes A_2) \cdot (\varvec{1} \otimes \varvec{d}_\times ) - (\mathsf {Id}\otimes A_2) \cdot (\tilde{\varvec{c}}_1 \otimes \varvec{d}_2) \nonumber \\&\qquad \qquad - (A_1 \otimes \mathsf {Id}) \cdot (v_2 \varvec{d}_1 \otimes \varvec{1}) + (v_\times - v_1 v_2) \cdot (\varvec{1} \otimes \varvec{1}). \end{aligned}$$

(16)

We conclude by remarking that $v_\times = v_1 v_2$ and that:

Perfect soundness follows from Eq. (16) and the fact that $\varvec{1}\otimes \varvec{1}$ is not in the subspace generated by the columns of the matrix

(17)

when the CRS is binding, because if $\varvec{a}_1,\varvec{a}_2 \in \mathbb {Z}_p^2$ are two vectors generating the column space of $A_1$ and $A_2$ respectively, then $(\varvec{a}_1 \otimes \varvec{a}_2,\ \varvec{a}_1 \otimes \varvec{1},\ \varvec{1} \otimes \varvec{a}_2, \ \varvec{1} \otimes \varvec{1})$ is a basis of $\mathbb {Z}_p^4$.

Finally, perfect uniformity comes from the fact that the kernel of the matrix B (from Eq. (17)) consists of all the vectors:

$$ \begin{pmatrix} (\mathsf {Id}\otimes A_2) \cdot \varvec{\rho }\\ - (A_1 \otimes \mathsf {Id}) \cdot \varvec{\rho }\end{pmatrix}, $$

for $\varvec{\rho }\in \mathbb {Z}_p^4$, since these elements are clearly in the kernel and form a subspace of dimension 4, and the kernel is of dimension 4 as $B \in \mathbb {Z}_p^{8 \times 4}$ is of rank 4 (because $A_1$ is of full rank and hence $A_1 \otimes \mathsf {Id}\in \mathbb {Z}_p^{4 \times 4}$ is of full rank).

Remark 4

(Zero-knowledge of the quadratic proof $\varvec{\pi }_\times$ in simulation mode). Perfect uniformity in the simulation mode is a very strong form of witness indistinguishability: whatever witness is used, the proof follows exactly the same uniform distribution over solutions of Eq. 15. To show that $\varvec{\pi }_\times$ is zero-knowledge, it remains to argue that this distribution can be efficiently sampled. This can be done similarly as in Remark 2: for simulated commitments $\varvec{c}_i$, the simulator can equivocate $\varvec{c}_1,\varvec{c}_2,\varvec{c}_\times$ to any $v'_1, v'_2, v'_\times$ satisfying $v'_\times = v'_1 v'_2$ with decommitment $\varvec{d}'_1, \varvec{d}'_2, \varvec{d}'_\times$ using $\mathsf {QSimOpen}$. This gives a valid witness $(v'_1,\varvec{d}'_1,v'_2,\varvec{d}'_2,\varvec{d}'_\times )$ for the statement and a simulated proof can be generated by running the honest prover algorithm $\mathsf {QQuadProve}$ with this witness.

3.3 WE for NIZK of Commitments for $\mathrm {NC}^1$

We now describe our construction of WE for NIZK of commitments for $\mathrm {NC}^1$. It follows the technical overview Sect. 2.3. The idea is to represent the function by a Restricted Multiplication Straight-line (RMS) Program [10, 14], which only performs multiplications or quadratic operations between an intermediate variable and an input. We start with defining a variant of RMS where operations are done modulo some prime number p.

Definition 7

(RMS Programs). Let p be a prime. A Restricted Multiplication Straight-line (RMS) program modulo p with input $v = v_1 \Vert \cdots \Vert v_n\in {\{0,1\}}^n$ and output $y= y_1 \Vert \cdots \Vert y_m \in {\{0,1\}}^m$ is a sequence of the following instructions:

• Load a constant $\omega \in \mathbb {Z}_p$ into the memory value $u_j$: $(u_j \leftarrow \omega )$.

• Linearly combine memory values $u_i$ and $u_j$ into the memory value $u_k$: $(u_k \leftarrow \mu u_i + \mu ' u_j \bmod p)$, with $(\mu ,\mu ') \in \mathbb {Z}^2_p \setminus {\{(0,0)\}}$ a non-zero pair of constants.

• Multiply the input value $v_i$ by the memory value $u_j$ into the memory value $u_k$: $(u_k \leftarrow v_i \cdot u_j \bmod p)$.

where each memory value is written at most once and each memory value that is read was written before. The program aborts if one memory value $u_k$ is not in ${\{0,1\}}$. If it does not abort, it outputs $y= y_1 \Vert \cdots \Vert y_m = u_1 \Vert \dots \Vert u_m$.

The size of an RMS is the number of instructions. Furthermore, any $\mathrm {NC}^1$ circuit $G$ can be written as an RMS program of polynomial size, because deterministic branching programs can be encoded into RMS with constant overhead [10, Claim A.2]. The resulting RMS program outputs the correct value when evaluated modulo any prime number p, as when evaluated without modulo, all the memory values are in ${\{0,1\}}$.

Construction. Let $\mathsf {QC}= (\mathsf {QSetup}_{\mathsf {bind}},\mathsf {QSetup}_{\mathsf {sim}},\{\mathsf {QCom}_i,\mathsf {QVer}_i,\mathsf {QSimCom}_i,$ ${\mathsf {QSimOpen}_i\}}_{i \in \{1,2\}},\mathsf {QQuadProve},\mathsf {QQuadVer})$ be the bilinear commitment scheme with proofs of quadratic relations from the previous section. We construct a witness encryption $\mathsf {WE}$ for NIZK of commitments for $\mathrm {NC}^1$ below. To help differentiate type-1 and type-2 commitments, all type-$\iota$ commitments have subscript starting with $\iota$, such as, $\varvec{c}_{\iota ,k}$.

• Commitment: $(c,d) \leftarrow \mathsf {CCom}(\mathsf {crs},v)$ for , generates type-1 commitments for each bit of $v= v_1 \Vert \dots \Vert v_n$. More formally, $c= (\varvec{c}_{1,1},\dots ,\varvec{c}_{1,n}$ and $d= (\varvec{d}_{1,1},\dots ,\varvec{d}_{1,n})$, where for $i \in [n]$, $(\varvec{c}_{1,i},\varvec{d}_{1,i}) \leftarrow \mathsf {QCom}_1(\mathsf {crs},v_i)$.

• Verification, Commitment Simulation and Opening: just consist in running the respective algorithms $\mathsf {QVer}_1,\mathsf {QSimCom}_1,\mathsf {QSimOpen}_1$ in parallel for each commitment $\varvec{c}_{1,i}$.

• Proof $\pi \leftarrow \mathsf {CProve}(\mathsf {crs},c,G,v,d)$, for an $\mathrm {NC}^1$ circuit $G$ represented as an RMS program with n-bit input and m-bit output works as follows. Let $S_\omega$, $S_+$, and $S_\times$ be the sets of memory indexes written by constant loading, linear, and multiplication instructions respectively. We suppose that the used memory values are $u_1,\dots ,u_L$. The proof $\pi$ is a tuple $({\{\varvec{c}_{2,k}\}}_{k \in [L]}, {\{\varvec{d}_{2,k}\}}_{k \in [m] \cup S_\omega }, {\{\varvec{\pi }_{k}\}}_{k \in S_+ \cup S_\times })$ where these values are generated as follows, for each instruction

  • $(u_k \leftarrow \omega )$: generate $(\varvec{c}_{2,k},\varvec{d}_{2,k}) \leftarrow \mathsf {QCom}_2(\mathsf {crs},\omega )$.

  • $(u_k \leftarrow \mu u_i + \mu ' u_j \bmod p)$: compute

    

  • $(u_k \leftarrow v_i \cdot u_j \bmod p)$: compute

    

    (Note that values $v_i$ and $u_j$ are known by the prover.)

• Proof Verification: just consists in verifying the provided openings and quadratic proofs. More formally, $\mathsf {CPVer}(\mathsf {crs},c,G,y,\pi )$ where $y= y_1 \Vert \cdots \Vert y_m$ returns 1 if and only if all the following tests pass:

  • For every $i \in [m]$, check that $\mathsf {QVer}_2(\mathsf {crs},\varvec{c}_{2,i},y_i,\varvec{d}_{2,i}) \overset{{}_{?}}{=}1$.

  • For every instruction:

  • * $(u_k \leftarrow \omega )$: check $\mathsf {QVer}_2(\mathsf {crs},\varvec{c}_{2,k},\omega ,\varvec{d}_{2,k}) \overset{{}_{?}}{=}1$.

  • * $(u_k \leftarrow \mu u_i + \mu ' u_j \bmod p)$: check $\mathsf {QLinVer}(\mathsf {crs},(\mu ,\varvec{c}_{2,i}),(\mu ',\varvec{c}_{2,j}),$ $\varvec{c}_{2,k},\varvec{\pi }_k) \overset{{}_{?}}{=}1$.

  • * $(u_k \leftarrow v_i \cdot u_j \bmod p)$: check $\mathsf {QQuadVer}(\mathsf {crs},\varvec{c}_{1,i},\varvec{c}_{2,j},\varvec{c}_{2,k},\varvec{\pi }_k) \overset{{}_{?}}{=}1$.

• Proof Simulation: $\pi \leftarrow \mathsf {CPSim}(\tau , \mathsf {aux}, c, G,y)$ where $c= (\varvec{c}_{1,1}, \dots , \varvec{c}_{1,n})$ are simulated with auxiliary data $\mathsf {aux}= (\varvec{\mathsf {aux}}_{1,1},\dots ,\varvec{\mathsf {aux}}_{1,n})$, simulates a proof $\pi = ({\{\varvec{c}_{2,k}\}}_{k \in [L]}, {\{\varvec{d}_{2,k}\}}_{k \in [m] \cup S_\omega }, {\{\varvec{\pi }_{k}\}}_{k \in S_+ \cup S_\times })$ as follows: Run through the instructions in RMS in order and for each instruction do:

  • $(u_k \leftarrow \omega )$: generate

    $$\begin{aligned} (\varvec{c}_{2,k},\varvec{\mathsf {aux}}_{2,k})\leftarrow \mathsf {QSimCom}_2(\tau )~, \quad \varvec{d}_{2,k} \leftarrow \mathsf {QSimOpen}_2(\tau ,\varvec{\mathsf {aux}}_{2,k},\omega )~. \end{aligned}$$

  • $(u_k \leftarrow \mu u_i + \mu ' u_j \bmod p)$: set if $k \in [m]$ or 0 otherwise, and let $u'_i,u'_j \in \mathbb {Z}_p$ be arbitrary scalars such that $\mu u'_i + \mu ' u'_j = u'_k$ (which is possible as $(\mu ,\mu ') \ne 0$), and compute:

    

    (18)
    

    Note: values $u'_i$, $u'_j$, $u'_k$ are local and may be different for different instructions.

  • $(u_k \leftarrow v_i \cdot u_j \bmod p)$: set is $k \in [m]$ or 0 otherwise, as well as and (so that $u'_k = u'_i u'_j$—again values $u'_i$, $u'_j$, $u'_k$ are local) and compute:

    $$\begin{aligned} (\varvec{c}_{2,k},\varvec{\mathsf {aux}}_{2,k})&\leftarrow \mathsf {QSimCom}_2(\tau ), \nonumber \\ \varvec{d}'_{1,i}&\leftarrow \mathsf {QSimOpen}_1(\tau ,\varvec{\mathsf {aux}}_{1,i},u'_i) \end{aligned}$$

    (19)
    $$\begin{aligned} \varvec{d}'_{2,\ell }&\leftarrow \mathsf {QSimOpen}_2(\tau ,\varvec{\mathsf {aux}}_{2,\ell },u'_\ell ) \quad \text {for } \ell \in \{j,k\}, \end{aligned}$$

    (20)
    

• Witness Encryption: Looking at Eqs. (7) and (11) and Remark 3, we remark that the proof verification $\mathsf {CPVer}(\mathsf {crs},c,G,y,\pi )$ is affine in the vector $\pi$. Concretely, there exists a matrix and a vector (both only depend on $\mathsf {crs},c,G,y$ and can be efficiently computed from these three values—the star $\star$ denotes the fact that elements are not necessarily in the same group), such that, seeing $\pi$ as a vector of elements in $\mathbb {Z}_p,\mathbb {G}_1,\mathbb {G}_2$ of length $\beta$, and denoting by ${\tilde{\varvec{\pi }}} \in \mathbb {Z}_p^\beta$ the vector derived from $\pi$ by replacing every $\mathbb {G}_\iota$ element with its discrete logarithm, we have:

  

  (Note: This is because: By Eq. 7and  11, verification of opening and verification of a linear proof are both linear equations whose coefficients are either constants or elements in $\mathsf {crs}$. By Remark 3, verification of a quadratic proof is a linear equation whose coefficients are constants, or elements in $\mathsf {crs}$, or commitments $\varvec{c}_{1,i}$ (as in Eq. 19) to the first operand in the multiplication. Since in RMS the first operand of multiplication is always an input bit, $\varvec{c}_{1,i}$ is contained in $c$.) The witness encryption then just uses hash proof systems from [1]. More formally, to encrypt a bit message $\mathsf {m}\in {\{0,1\}}$, $\mathsf {CWEnc}(\mathsf {crs},c,G,y,\mathsf {m})$ picks a uniformly random row vector $\varvec{\alpha }\in \mathbb {Z}_p^{1\times \nu }$, where $\nu$ is the number of rows of $\varGamma _{\mathsf {crs},c,G,y}$, and outputs the ciphertext where:

  

• Witness Decryption: Using the notation from witness encryption, $\mathsf {CWDec}(\mathsf {crs},\mathsf {ct},c,G,y,\pi )$ outputs $\mathsf {m}\in {\{0,1\}}$ satisfying

  

The algorithms $\mathsf {CSetup}_{\mathsf {bind}},\mathsf {CCom},\mathsf {CVer}$ (as well as the simulators $\mathsf {CSetup}_{\mathsf {sim}},\mathsf {CSimCom},\mathsf {CSimOpen}$) of the resulting WE for NIZK of commitments run in time polynomial in their inputs. The algorithms $\mathsf {CProve},\mathsf {CPVer},\mathsf {CWEnc},\mathsf {CWDec}$ run in time polynomial in their inputs and exponential in the depth of the circuit $G$. This exponential blow up is due to the representation by a RMS program and explains the restriction to $\mathrm {NC}^1$.

Theorem 8

Assuming SXDH over bilinear groups. The construction $\varPi$ described above is a WE for NIZK of commitments for $\mathrm {NC}^1$.

Proof

Perfect correctness of the commitment, setup indistinguishability, perfect binding, and perfect equivocality follow directly from the fact that $(\mathsf {QSetup}_{\mathsf {bind}},\mathsf {QSetup}_{\mathsf {sim}},\mathsf {QCom}_1,\mathsf {QVer}_1,\mathsf {QSimCom}_1,\mathsf {QSimOpen}_1)$ is a dual-mode commitment scheme. Perfect proof correctness follows from perfect correctness of linear and quadratic proofs. Perfect soundness follows from perfect binding of type-1 and type-2 commitments as well as perfect soundness of linear and quadratic proofs. Perfect encryption correctness and perfect semantic security follow immediately from correctness and smoothness of the hash proof systems in [1]. It remains to prove the perfect zero-knowledge property. This is where the uniqueness of linear proofs (Remark 2) and the perfect uniformity (Remark 4) of the quadratic proofs are used. We give a proof by games:

• Game 0 corresponds to the zero-knowledge game where proofs are honestly generated.

• Game 1 is similar to Game 0 except that all the commitments are simulated but still opened to the value a real prover would use. This game is perfectly indistinguishable from the previous one by perfect equivocality of type-1 and type-2 commitments.

• Game 2 is similar to Game 1, except that the decommitments $\varvec{d}_{2,k}$ for $k \in (S_+ \cup S_\times ) \setminus [m]$ (i.e., the ones which are not published) and $\varvec{d}'_{\star ,\star }$ used to generate the linear and quadratic proofs (see Eqs. (18) to (20)) are generated as by $\mathsf {CPSim}$. By perfect equivocality of type-1 and type-2 commitments, these values $\varvec{d}_{2,k}$ and $\varvec{d}'_{\star ,\star }$ are valid decommitments. Hence by uniqueness of linear proofs and perfect uniformity of quadratic proofs, the resulting proofs $\varvec{\pi }_k$ are perfectly indistinguishable between Game 1 and Game 2.

As Game 2 corresponds to the zero-knowledge game where proofs are simulated, this conclude the proof of perfect zero-knowledge.    $\square$