Abstract
Broadcast Encryption with optimal parameters was a long-standing problem, whose first solution was provided in an elegant work by Boneh, Waters and Zhandry [BWZ14]. However, this work relied on multilinear maps of logarithmic degree, which is not considered a standard assumption. Recently, Agrawal and Yamada [AY20] improved this state of affairs by providing the first construction of optimal broadcast encryption from Bilinear Maps and Learning With Errors (LWE). However, their proof of security was in the generic bilinear group model. In this work, we improve upon their result by providing a new construction and proof in the standard model. In more detail, we rely on the Learning With Errors (LWE) assumption and the Knowledge of OrthogonALity Assumption (KOALA) [BW19] on bilinear groups.
Our construction combines three building blocks: a (computational) nearly linear secret sharing scheme with compact shares which we construct from LWE, an inner-product functional encryption scheme with special properties which is constructed from the bilinear Matrix Decision Diffie Hellman (MDDH) assumption, and a certain form of hyperplane obfuscation, which is constructed using the KOALA assumption. While similar to that of Agrawal and Yamada, our construction provides a new understanding of how to decompose the construction into simpler, modular building blocks with concrete and easy-to-understand security requirements for each one. We believe this sheds new light on the requirements for optimal broadcast encryption, which may lead to new constructions in the future.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Broadcast encryption [FN94] (\(\mathsf {BE}\)) is a novel form of encryption that enables a sender to transmit a single ciphertext over a broadcast channel so that only an authorized subset S of total N users can decrypt and recover the message. Security requires that no collusion of unauthorized users can learn anything about the encrypted message with non-negligible advantage. Evidently, broadcast encryption is implied by public key encryption if no restriction is placed on the size of the ciphertext. However, the size of the ciphertext in broadcast encryption is of paramount importance, and is quantified in terms of ciphertext overhead, namely, the size of the ciphertext not counting the description of the recipient set S. Thus, in an optimal solution, the ciphertext overhead would be of size proportional to a symmetric encryption of the plaintext message (upto constant factors), aside from the description of S which is provided in the clear.
In a celebrated work, Boneh, Gentry and Waters [BGW05] provided the first construction of broadcast encryption which achieved both optimal (constant) ciphertext overhead and short secret keys, but suffered from large public parameters, namely, linear in the number of users N. A series of elegant works provided improvements to this scheme [GW09, DPP07, Del07, SF, AL10, BZ17, BZ17] achieving many interesting new features such as anonymity, adaptive security and such others, but failed to improve the size of the public parameters. In 2014, Boneh, Waters and Zhandry [BWZ14] provided the first solution to the long standing problem of BE with optimal parameters, but their construction relied on the existence of multilinear maps of degree \(\log N\), which is not considered a standard assumption. Recently, Agrawal and Yamada [AY20] improved the state of affairs by achieving the same parameters from the learning with errors assumption (\(\mathsf {LWE}\)) along with assumptions on bilinear maps. However, this construction [AY20] could only be proven secure in the generic bilinear group model. Independently, Brakerski and Vaikuntanathan [BV20] also provided a construction of BE with optimal parameters from new assumptions on lattices, but they were unable to provide a proof of security for their scheme.
While encouraging, this state of affairs nevertheless leaves much to be desired. It is evident that for a primitive as important as broadcast encryption, we would like to have a proof from well-studied standard assumptions, and in the standard model. However, so far such a construction has been elusive.
Our Results. In this work, we make further progress towards this goal and provide the first construction for broadcast encryption with optimal parameters, from Learning with Errors (LWE) [Reg09] and the Knowledge of OrthogonALity Assumption (KOALA) [BW19] in the standard model. While similar to that of Agrawal and Yamada, our construction provides a new understanding of how to decompose the construction into simpler, modular building blocks with concrete and easy-to-understand security requirements for each one. We believe this sheds new light on the requirements for optimal broadcast encryption, which may lead to new constructions in the future.
In more detail, as in [AY20], we provide a construction for ciphertext-policy attribute based encryption (\(\mathsf {cpABE}\)) for \({\mathsf {NC}}_1\) circuits, such that its ciphertext size, secret key size, and public key size are all independent of the size of the circuits supported by the scheme, and depend only on their input length and depth. Recall that in a \(\mathsf {cpABE}\) scheme, a ciphertext for a message m is associated with a function (policy) f, and secret keys are associated with public attributes \(\mathbf {x}\) from the domain of f. Decryption succeeds to yield the hidden message m if and only if the attribute satisfies the policy, namely \(f(\mathbf {x}) = 1\). To see \(\mathsf{BE}\) as a special case of \(\mathsf {cpABE}\), note that the circuit embedded in the ciphertext (\(F_S\), say) can check for membership of a given user index in a set of authorised recipients S, and the attributes \(\mathbf {x}\) may encode a user’s index in the set N. Thus, a user i holds a secret key for attributes i and can decrypt a ciphertext associated with S if and only if i is a member of S. As observed in [AY20], the depth and input length of the circuit \(F_S\) are logarithmic in N, so it suffices to construct \(\mathsf {cpABE}\) with parameters independent of the width of \(F_S\), which is linear in N.
Building upon the construction of [AY20], we provide a new \(\mathsf {cpABE}\) for \({\mathsf {NC}}_1\) from the Learning with Errors (LWE) [Reg09] and the Knowledge of OrthogonALity Assumption (KOALA) [BW19]. The LWE assumption introduced in the seminal work of Regev [Reg09] enjoys worst case to average case hardness guarantees and is widely considered a standard assumption in the literature. The KOALA assumption introduced by Beullens and Wee [BW19] (also implicitly present in prior work such as [CRV10]) may be viewed as a decisional analogue of the algebraic group model [FKL18], which posits that the only way an adversary can compute a new group element is to take a linear combination of group elements already provided. More specifically, the KOALA assumption asserts that any adversary that can distinguish \(g^{\mathbf {M}\mathbf {r}}\) from \(g^{\mathbf {v}}\) for some matrix \(\mathbf {M}\) and random vectors \(\mathbf {r}, \mathbf {v}\), must know some nontrivial vector \(\mathbf {z}\ne 0\) such that \(\mathbf {z}\;\mathbf {M}= 0\). Beullens and Wee provided a proof of the KOALA assumption in the generic group model. While KOALA is a “knowledge assumption” and therefore not considered a standard assumption, we believe it is a significant improvement over [AY20] to rely on the hardness of a specific assumption in the standard model, than to rely on the the generic group model for the security of the entire scheme.
Technical Overview. We proceed to outline the main ideas of our construction. As discussed above, we construct a ciphertext-policy attribute-based encryption (\(\mathsf {cpABE}\)) for \({\mathsf {NC}}_1\) circuits. The \(\mathsf {cpABE}\) is compact, meaning that the size of the ciphertexts and keys are all small, proportional only to the length of the inputs and the depth of the supported circuits, but independent of the circuit size. Our construction combines three building blocks: a (computational) nearly linear secret sharing scheme with compact shares, which we construct from Learning With Errors (LWE), a certain form of inner-product functional encryption (IPFE) [ABCP15, ALS16, LV16, Lin17, LL20], constructed from the bilinear Matrix Decision Diffie Hellman (MDDH) assumption, and a certain form of hyperplane obfuscation [CRV10], constructed using the KOALA assumption. Next, we describe each of these primitives individually and outline how they are combined to construct our \(\mathsf {cpABE}\).
Nearly Linear Secret Sharing. Our main building block is a new type of secret sharing scheme. Given a message \(\mathsf {\mu }\in \{0,1\}\) and a circuit C with \(\ell \)-bit input, the scheme outputs \(2\ell \) shares \(\{\mathsf {share}_{i,b}\}_{i \in [\ell ], b \in \{0,1\}}\). Each \(\mathsf {share}_{i,b}\) is a vector over \(\mathbb {Z}_p\). For any \(x \in \{0,1\}^\ell \), let \(\mathsf {share}_x = \{\mathsf {share}_{i,x_i}\}\), which we think of as a long vector produced by concatenating of all the component shares. If \(C(x)=0\) then \(\mathsf {share}_x\) computationally hides the message \(\mathsf {\mu }\), and moreover, \(\mathsf {share}_x\) is even indistinguishable from a uniformly random vector. On the other hand, if \(C(x)=1\) then there is an efficient method to reconstruct the message \(\mathsf {\mu }\) from \(\mathsf {share}_x\). Moreover, this reconstruction procedure is “nearly linear” in the sense that given C, x, one can efficiently determine some linear function f such that \(f(\mathsf {share}_x) = \mathsf {\mu }\cdot \lceil p/2 \rceil + e\), where \(|e| \ll p/2\) is some small polynomially bounded error.
We use LWE to construct this type of nearly linear secret sharing for all \({\mathsf {NC}}_1\) circuits, where the size of the shares only depends on the security parameter and the depth of the circuit, but is independent of the circuit size. The construction closely follows the ideas behind the ABE scheme of [QWW18] and the laconic function evaluation of [QWW18]. As in [AY20], we are restricted to \({\mathsf {NC}}_1\) because we require the magnitude of the error e to be polynomially bounded. The construction additionally relies on some uniformly random public parameters \(\mathsf {pp}\), which we will ignore throughout the introduction.
Towards \(\mathsf {cpABE}\) from Secret Sharing. In our \(\mathsf {cpABE}\) construction, to encrypt a message \(\mathsf {\mu }\) under a given policy specified by an \({\mathsf {NC}}_1\) circuit C, the encryptor creates a “nearly linear secret sharing” of the message resulting in shares \(\{\mathsf {share}_{i,b}\}_{i \in [\ell ], b \in \{0,1\}}\). At a high level, the encryptor then encrypts these shares using some form of functional encryption (\(\mathsf {FE}\)) and outputs the \(\mathsf {FE}\) ciphertext. Let us examine what kind of functional encryption would be helpful in this setting.
As a starting point, assume the shares are encrypted via an \(\mathsf {FE}\) scheme such that a decryptor with a secret key for x only learns the subset \(\mathsf {share}_x = \{\mathsf {share}_{i,x_i}\}\). Such an \(\mathsf {FE}\) scheme is easy to construct by encrypting each of the \(2\ell \) shares under a different public key of a standard public-key encryption scheme and giving the decryptor the \(\ell \) secret keys corresponding to the choice of x [SS10]. This would already provide security in the non-colluding setting – if the adversary has a secret key for a single value x such that \(C(x)=0\), then she cannot learn anything about the message by getting \(\mathsf {share}_x\). However, if the adversary has secret keys for even just two different values \(x_0,x_1\), such that \(C(x_0)= C(x_1)=0\), all bets are off; indeed, with our scheme, she could easily recover the message.
To fix the above problem, we rely on a more restricted form of \(\mathsf {FE}\) where the decryptor with a secret key for a value x would not learn \(\mathsf {share}_x\) in full, but rather only a hyperplane obfuscation of the vector \(\mathsf {share}_x\). A hyperplane obfuscation [CRV10] of a vector \(\mathbf {v}\) allows one to test whether various affine functions h evaluate to \(h(\mathbf {v})= 0\), but should not reveal anything else about the obfuscated vector beyond having black-box access to such tests. When \(C(x)=1\), a hyperplane obfuscation of \(\mathsf {share}_x\) is sufficient to decrypt the message \(\mathsf {\mu }\), since we have a linear function f such that \(f(\mathsf {share}_x) = \mathsf {\mu }\cdot \lceil p/2 \rceil + e\) and therefore, by testing whether \(f(\mathsf {share}_x) - e' = 0\) for all values \(e'\) in the polynomial range that e comes from, we can determine whether \(\mathsf {\mu }=0\) or \(\mathsf {\mu }=1\). For security, consider an adversary has secret keys for some q inputs \(x^{(1)},\ldots ,x^{(q)}\) such that \(C(x^{(i)})=0\) and learns the corresponding hyperplane obfuscations of the vectors \(\mathsf {share}_{x^{(i)}}\). We know that each of the vectors \(\mathsf {share}_{x^{(i)}}\) is individually computationally indistinguishable from uniform, but mutually the vectors have non-trivial correlations and can be used to recover \(\mathsf {\mu }\). We wish to conclude that the hyperplane obfuscations of \(\mathsf {share}_{x^{(i)}}\) are mutually indistinguishable from obfuscations of random and independent vectors. Indeed, this follows if we had a composable [CD08, BC10] virtual-black-box (VBB) hyperplane obfuscator since, given black box access to each of these vectors, an adversary will never be able to find an affine function evaluates to 0 on any of them. To make this approach work, we therefore need to instantiate an appropriate hyperplane obfuscator together with a matching \(\mathsf {FE}\) scheme that outputs a hyperplane obfuscations of \(\mathsf {share}_x\).
Hyperplane Obfuscation. We rely on the extremely simple hyperplane obfuscator of [CRV10]. Let G be a cyclic group of order p with a generator g. To obfuscate a vector \(\mathbf {v} \in \mathbb {Z}_p^n\), we choose a random \(\gamma \leftarrow \mathbb {Z}_p\) and output \(g^\gamma \), \(g^{\gamma \cdot \mathbf {v}}\). This allows one to test if an affine function h evaluates to \(h(\mathbf {v})=0\) by computing \(\gamma \cdot h(\mathbf {v})\) in the exponent. The work of [CRV10] shows that this is a VBB hyperplane obfuscator under a new assumption that they proposed, which can in retrospect be seen as a variant of the KOALA assumption restricted to spaces of dimension 1. However, they did not prove that the obfuscator is composable. In our work, we do not directly prove that this obfuscator satisfies composable VBB security, but rather prove that it satisfies a specialized property that suffices for us. Namely, we show that under the KOALA assumption the following holds: for any set of vectors that are individually indistinguishable from uniform but can be mutually correlated, one cannot distinguish between being given the hyperplane obfuscations of all the vectors in the set versus hyperplane obfuscations of uniformly random and independent vectors.
Functional Encryption for Inner Products. As the last step, we need to provide an appropriate (public-key) functional encryption (\(\mathsf {FE}\)) scheme. Such an \(\mathsf {FE}\) should allow us to encrypt a set of shares \(\{\mathsf {share}_{i,b}\}_{i \in [\ell ], b \in \{0,1\}}\), and give out secret keys for value \(x \in \{0,1\}^\ell \), so that such a ciphertext/key pair (only) reveals a fresh hyperplane obfuscation of \(\mathsf {share}_x\) and nothing else. We can simplify this problem by relying on a simpler “component” \(\mathsf {FE}\) scheme and then combining the component \(\mathsf {FE}\)s to get what we need. The component \(\mathsf {FE}\) should allow us to encrypt a scalar \(s \in \mathbb {Z}_p\) and give out secret keys for values \(g^\gamma \), so that such a ciphertext/key pair only reveals \(g^{\gamma \cdot s}\) and nothing else. We want to component \(\mathsf {FE}\) to satisfy unbounded-collusion simulation-based security. Given such a component \(\mathsf {FE}\) scheme, we can instantiate a separate copy of it for each \(i \in [\ell ], b \in \{0,1\}\) and each position in the share vector. The encryptor then encrypts each position of each share vector \(\mathsf {share}_{i,b}\) under the appropriate copy of the component scheme. To create a secret key for \(x \in \{0,1\}^\ell \) we choose a fresh random \(\gamma \leftarrow \mathbb {Z}_p\) and give out a secret key for \(g^\gamma \) for each of the component schemes in locations \((i, x_i)\). This would ensure that, given an encryption of \(\{\mathsf {share}_{i,b}\}_{i \in [\ell ], b \in \{0,1\}}\), a secret key for a value \(x \in \{0,1\}^\ell \) only allows one to recover the hyperplane obfuscation of \(\mathsf {share}_x\) given by \((g^{\gamma }, g^{\gamma \cdot \mathsf {share}_{x}})\).
The above almost works, up to one subtlety. When we instantiate the component \(\mathsf {FE}\) scheme, we do so using bilinear groups  of order p with corresponding generators \((g_1,g_2,g_T)\) and a bilinear map
of order p with corresponding generators \((g_1,g_2,g_T)\) and a bilinear map  . We can create an encryption of a scalar \(s \in \mathbb {Z}_p\) and give out a secret key for
. We can create an encryption of a scalar \(s \in \mathbb {Z}_p\) and give out a secret key for  so that the decryption of the ciphertext with the secret key reveals \(g_T^{\gamma \cdot s}\). However, we can only guarantee simulation based security when the simulator is given \(g_2^{\gamma \cdot s}\). In other words, there is a discrepancy between correctness (where the honest users decrypt the product in the exponent of \(g_T\)) and security (where the simulator needs to know the product in the exponent of \(g_2\)). It turns out that this suffices for us. For correctness, the decryptor gets a hyperplane obfuscation over
so that the decryption of the ciphertext with the secret key reveals \(g_T^{\gamma \cdot s}\). However, we can only guarantee simulation based security when the simulator is given \(g_2^{\gamma \cdot s}\). In other words, there is a discrepancy between correctness (where the honest users decrypt the product in the exponent of \(g_T\)) and security (where the simulator needs to know the product in the exponent of \(g_2\)). It turns out that this suffices for us. For correctness, the decryptor gets a hyperplane obfuscation over  , which suffices to recover the message. For security, we need to rely on the hyerplane obfuscation being secure even when given over
, which suffices to recover the message. For security, we need to rely on the hyerplane obfuscation being secure even when given over  , which just requires us to assume that KOALA holds over
, which just requires us to assume that KOALA holds over  . We instantiate the above type of component \(\mathsf {FE}\) in a black-box way using the recent primitive of “Slotted Inner Product Functional Encryption” [LV16, Lin17, LL20].Footnote 1
. We instantiate the above type of component \(\mathsf {FE}\) in a black-box way using the recent primitive of “Slotted Inner Product Functional Encryption” [LV16, Lin17, LL20].Footnote 1
2 Preliminaries
In this section, we define some notation and preliminaries that we require.
Notation. We use bold letters to denote vectors. We treat a vector as a row vector by default. The notation [a, b] denotes the set of integers \(\{k\in \mathbb {N}~|~a\le k\le b\}\). We use [n] to denote the set [1, n]. Throughout the paper, we use \(\lambda \) to denote the security parameter. We say a function \(f(\lambda )\) is negligible if it is \(O(\lambda ^{-c})\) for all \(c > 0\), and we use \({{\,\mathrm{negl}\,}}(\lambda )\) to denote a negligible function of \(\lambda \). We say \(f(\lambda )\) is polynomial if it is \(O(\lambda ^c)\) for some constant \(c > 0\), and we use \({{\,\mathrm{poly}\,}}(\lambda )\) to denote a polynomial function of \(\lambda \). Throughout the paper, we consider non-uniform adversaries that are modeled as polynomial-size circuits \(\mathcal {A}= \{ \mathcal {A}_\lambda \}_\lambda \) indexed by the security parameter. We often drop the subscript when it is clear from the context.
2.1 Bilinear Map Preliminaries
Here, we introduce our notation for bilinear maps and the bilinear generic group model following Baltico et al. [BCFG17], who specializes the framework by Barthe [Mau05] for defining generic k-linear groups to the bilinear group settings. The definition closely follows that of Maurer [Mau05], which is equivalent to the alternative formulation by Shoup [Sho97].
Notation on Bilinear Maps. A bilinear group generator \(\mathsf {GroupGen}\) takes as input \(1^\lambda \) and outputs a group description \(\mathbb {G}=(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e, g_1, g_2)\), where p is a prime of \(\varTheta (\lambda )\) bits, \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\) are cyclic groups of order p, \(e:\mathbb {G}_1\times \mathbb {G}_2 \rightarrow \mathbb {G}_T\) is a non-degenerate bilinear map, and \(g_1\) and \(g_2\) are generators of \(\mathbb {G}_1\) and \(\mathbb {G}_2\), respectively. We require that the group operations in \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\) as well as the bilinear map e can be efficiently computed. We employ the implicit representation of group elements: for a matrix \(\mathbf {A}\) over \(\mathbb {Z}_p\), we define \([ \mathbf {A}]_1 := g_1^{\mathbf {A}}\), \([ \mathbf {A}]_2 := g_2^{\mathbf {A}}\), \([ \mathbf {A}]_T := g_T^{\mathbf {A}}\), where exponentiation is carried out component-wise. We will use similar notation for vectors.
Generic Bilinear Group Model. Let \(\mathbb {G}=(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e, g_1, g_2)\) be a bilinear group setting, \(L_1\), \(L_2\), and \(L_T\) be lists of group elements in \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\) respectively, and let \(\mathcal{D}\) be a distribution over \(L_1\), \(L_2\), and \(L_T\). The generic group model for a bilinear group setting \(\mathbb {G}\) and a distribution \(\mathcal{D}\) is described in Fig. 1. In this model, the challenger first initializes the lists \(L_1\), \(L_2\), and \(L_T\) by sampling the group elements according to \(\mathcal{D}\), and the adversary receives handles for the elements in the lists. For \(s\in \{ 1,2,T \}\), \(L_s[h]\) denotes the h-th element in the list \(L_s\). The handle to this element is simply the pair (s, h). An adversary running in the generic bilinear group model can apply group operations and bilinear maps to the elements in the lists. To do this, the adversary has to call the appropriate oracle specifying handles for the input elements. The challenger computes the result of a query, stores it in the corresponding list, and returns to the adversary its (newly created) handle. Handles are not unique (i.e., the same group element may appear more than once in a list under different handles).
We remark that we slightly simplify the generic group model of Baltico et al. [BCFG17]. Whereas they allow the adversary to access the equality test oracle, which is given two handles \((s,h_1)\) and \((s,h_2)\) and returns 1 if \(L_s[h_1]=L_s[h_2]\) and 0 otherwise for all \(s\in \{1,2,T\}\), we replace this oracle with the zero-test oracle, which is given a handle (s, h) and returns 1 if \(L_s[h]=0\) and 0 otherwise only for the case of \(s=T\). We claim that even with this modification, the model is equivalent to the original one. This is because we can perform the equality test for \((s,h_1)\) and \((s,h_2)\) using our restricted oracles as follows. Let us first consider the case of \(s=T\). In this case, we can get the handle \((T,h')\) corresponding to \(L_T[h_1]-L_T[h_2]\) by calling \(\mathsf {neg}_T\) (see Fig. 1). We then make a zero-test query for \((T,h')\). Clearly, we get 1 if \(L_s[h_1]=L_s[h_2]\) and 0 otherwise. We next consider the case of \(s\in \{1,2\}\). This case can be reduced to the case of \(s=T\) by lifting the group elements corresponding to \(h_1\) and \(h_2\) to the group elements in \(\mathbb {G}_T\) by taking bilinear maps with an arbitrary non-unit group element in \(\mathbb {G}_{3-s}\), which is possible by calling \(\mathsf {map}_e\).
Symbolic Group Model. The symbolic group model for a bilinear group setting \(\mathbb {G}\) and a distribution \(\mathcal{D}_P\) gives to the adversary the same interface as the corresponding generic group model, except that internally the challenger stores lists of elements in the field \(\mathbb {Z}_p[X_1,\ldots , X_n]\) instead of lists of group elements. The oracles \(\mathsf {add}_s\), \(\mathsf {neg}_s\), \(\mathsf {map}\), and \(\mathsf {zt}\) computes addition, negation, multiplication, and equality in the field.
2.2 Slotted Inner Product Functional Encryption
We need slotted Inner Product Functional Encryption (IPFE) due to Lin and Vaikuntanathan [LV16, Lin17, LL20]. Slotted IPFE is a hybrid between a secret-key function-hiding IPFE and a public-key IPFE. In this scheme, a vector \(\mathbf {u}\in \mathbb {Z}_p^n\) is divided into a public and private part respectively \(\mathbf {u}= (\mathbf {u}_\mathsf{pub}, \mathbf {u}_\mathsf{priv})\) such that given the master secret key, the encryption algorithm can encrypt any vector \(\mathbf {u}\) of its choice, but given only the public key, it can encrypt only to the public slot, i.e. \(\mathbf {u}_\mathsf{priv} =0\). Slotted IPFE can guarantee function hiding only with respect to the private slot. We provide the definitions from [LL20].
Let \(\mathsf {GroupGen}\) be a group generator that outputs bilinear group \(\mathbb {G}=(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,[1]_1,[1]_2)\). A slotted inner-product functional encryption (IPFE) scheme based on \(\mathbb {G}\) consists of 5 efficient algorithms:
-
\(\mathsf{Setup}(1^\lambda , \mathfrak {s}_\mathsf{pub}, \mathfrak {s}_\mathsf{pri}) \rightarrow (\mathsf {mpk}, \mathsf {msk})\): The setup algorithm takes as input two disjoint index sets, the public slot \(\mathfrak {s}_\mathsf{pub}\) and the private slot \(\mathfrak {s}_\mathsf{pri}\), and outputs a pair of master public key and master secret key \((\mathsf {mpk}, \mathsf {msk})\). The whole index set \(\mathfrak {s}\) is \(\mathfrak {s}_\mathsf{pub}\cup \mathfrak {s}_\mathsf{pri}\).
-
\(\mathsf{KeyGen}(\mathsf {msk},{[\mathbf {v}]}_2) \rightarrow \mathsf{sk}_\mathbf {v}\): The key generation algorithm takes as input the master secret key and an encoding of a function vector \([\mathbf {v}]_2\), and outputs a secret key \(\mathsf{sk}_\mathbf {v}\) for \(\mathbf {v}\in \mathbb {Z}_p^\mathfrak {s}\).
-
\(\mathsf{Enc}(\mathsf {msk},{[\mathbf {u}]}_1)\rightarrow \mathsf {ct}_\mathbf {u}\): The encrypt algorithm takes input the master secret key and an encoding of a message vector \([\mathbf {u}]_1\) and outputs a ciphertext \(\mathsf {ct}_\mathbf {u}\) for \(\mathbf {u}\in \mathbb {Z}_p^\mathfrak {s}\).
-
\(\mathsf{Dec}(\mathsf{sk}_\mathbf {v}, \mathsf {ct}_\mathbf {u})\) \(\rightarrow T \vee \bot \): The decrypt algorithm takes as input a secret key \(\mathsf{sk}_\mathbf {v}\) and a ciphertext \(\mathsf {ct}_\mathbf {u}\), and outputs an element \(T \in \mathbb {G}_T\) or \(\bot \).
-
\(\mathsf {SlotEnc}( \mathsf {mpk}, {[\mathbf {u}_\mathsf{pub}]}_1)\rightarrow \mathsf {ct}_\mathbf {u}\): The slot encryption algorithm takes as input the master public key and a vector \(\mathbf {u}_\mathsf{pub}\in \mathbb {Z}_p^{\mathfrak {s}_\mathsf{pub}}\), sets \(\mathbf {u}= (\mathbf {u}_\mathsf{pub}, \mathbf{0}) \in \mathbb {Z}_p^{\mathfrak {s}}\) and outputs a ciphertext \(\mathsf {ct}_{\mathbf {u}}\).
Correctness. We say the slotted inner-product functional encryption scheme satisfies decryption correctness if for all \(\lambda \in \mathbb {N}\), all index sets \(\mathfrak {s}\) and all vectors \(\mathbf {u}, \mathbf {v}\in \mathbb {Z}_p^{\mathfrak {s}}\),

We say the slotted inner-product functional encryption scheme satisfies slot-mode correctness if for all \(\lambda \in \mathbb {N}\), all disjoint index sets \(\mathfrak {s}_\mathsf{pub}, \mathfrak {s}_\mathsf{pri}\) and all vectors \(\mathbf {u}\in \mathbb {Z}_p^{\mathfrak {s}_\mathsf{pub}}\), the following two distributions should be identical:

and

Slotted IPFE generalizes both secret-key and public-key IPFEs: we may obtain the former by setting \(\mathfrak {s}= \mathfrak {s}_\mathsf{pri}\) and the latter by setting \(\mathfrak {s}= \mathfrak {s}_\mathsf{pub}\).
Next, we define the adaptive function hiding property.
Definition 2.1
(Function Hiding Slotted IPFE). Let \((\mathsf{Setup}, \mathsf{KeyGen}, \mathsf{Enc}, \mathsf{Dec}, \mathsf {SlotEnc})\) be a slotted IPFE scheme as defined above. The scheme is function hiding if \(\mathsf {Exp}^0_\mathsf{FH}\) is indistinguishable from \(\mathsf {Exp}^1_\mathsf{FH}\) for all efficient adversary \(\mathcal {A}=\{ \mathcal {A}_\lambda \}_\lambda \) where \(\mathsf {Exp}^b_\mathsf{FH}\) for \(b \in \{0,1\}\) is defined as follows:
-
1.
Setup: Run the adversary \(\mathcal {A}_\lambda \) and obtain the disjoint index sets \(\mathfrak {s}_\mathsf{pub}, \mathfrak {s}_\mathsf{pri}\) from \(\mathcal {A}_\lambda \). Let \(\mathfrak {s}= \mathfrak {s}_\mathsf{pub}\cup \mathfrak {s}_\mathsf{pri}\). Let \((\mathsf {mpk}, \mathsf {msk}) \leftarrow \mathsf{Setup}(1^\lambda , \mathfrak {s}_\mathsf{pub}, \mathfrak {s}_\mathsf{pri}) \) and return
 to
to  .
. -
2.
Challenge: Repeat the following for arbitrarily many rounds determined by
 : In each round,
: In each round,  has 2 options:
has 2 options:-
\(\mathcal {A}_\lambda \) chooses \(\mathbf {v}_j^0, \mathbf {v}_j^1 \in \mathbb {Z}_p^\mathfrak {s}\) and submits \([\mathbf {v}_j^0]_2, [\mathbf {v}_j^1]_2\) for a secret key. Upon receiving this, compute \(\mathsf{sk}_j \leftarrow \mathsf{KeyGen}( \mathsf {msk},{[\mathbf {v}_j^b]}_2)\) and return this to \(\mathcal {A}_\lambda \).
-
\(\mathcal {A}_\lambda \) chooses \(\mathbf {u}_i^0, \mathbf {u}_i^1 \in \mathbb {Z}_p^\mathfrak {s}\) and submits \([\mathbf {u}_i^0]_1, [\mathbf {u}_i^1]_1\) for a ciphertext. Upon receiving this, compute \(\mathsf {ct}_i \leftarrow \mathsf{Enc}( \mathsf {msk},{[\mathbf {u}_i^b]}_1)\) and return this to \(\mathcal {A}_\lambda \).
-
-
3.
Guess:
 outputs its guess
outputs its guess  .
.
The outcome of the experiment is defined as \(b'\) if all the public components of the key queries are equal, i.e. \(\mathbf {v}^0_j\vert _{\mathfrak {s}_\mathsf{pub}} = \mathbf {v}^1_j\vert _{\mathfrak {s}_\mathsf{pub}}\) for all j and \(\langle \mathbf {u}^0_i,\;\mathbf {v}^0_j \rangle = \langle \mathbf {u}^1_i,\;\mathbf {v}^1_j \rangle \) for all i, j.
We will also require the following lemma by [ALS16, Wee17, LV16, Lin17, LL20]:
Lemma 2.2
Let \(\mathsf {GroupGen}\) be a group generator that outputs bilinear group \(\mathbb {G}=(p,\mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T,e,[1]_1,[1]_2)\) and \(k\ge 1\) an integer constant. If \(\mathsf{MDDH}_k\) holds in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\), then there is an (adaptively) function-hiding slotted IPFE scheme on \(\mathsf {GroupGen}\).
Note that the \(\mathsf{MDDH}_k\) assumption on \(\mathbb {G}_s\) (\(s\in \{1,2\}\)) says that a random group element \([\mathbf {r}]_s\) is indistinguishable from \([\mathbf {s}\mathbf {A}]_s\) given \([\mathbf {A}]\), where \(\mathbf {A}\leftarrow \mathbb {Z}_p^{k\times (k+1)}\), \(\mathbf {r}\in \mathbb {Z}_p^{k+1}\), and \(\mathbf {s}\in \mathbb {Z}_p^{k}\). The assumption is implied by the standard k-\(\mathsf {LIN}\) assumption, which becomes progressively weaker as k becomes larger.
2.3 Attribute Based Encryption
Let \(R=\{ R_\lambda : A_\lambda \times B_\lambda \rightarrow \{0,1\} \}_\lambda \) be a relation where \(A_\lambda \) and \(B_\lambda \) denote “ciphertext attribute" and “key attribute” spaces. An attribute-based encryption (ABE) scheme for R is defined by the following PPT algorithms:
-
 : The setup algorithm takes as input the unary representation of the security parameter \(\lambda \) and outputs a master public key
: The setup algorithm takes as input the unary representation of the security parameter \(\lambda \) and outputs a master public key  and a master secret key
and a master secret key  .
. -
 : The encryption algorithm takes as input a master public key
: The encryption algorithm takes as input a master public key  , a ciphertext attribute
, a ciphertext attribute  , and a message bit
, and a message bit  . It outputs a ciphertext \(\mathsf {ct}\).
. It outputs a ciphertext \(\mathsf {ct}\). -
 : The key generation algorithm takes as input the master public key
: The key generation algorithm takes as input the master public key  , the master secret key
, the master secret key  , and a key attribute \(Y \in B_\lambda \). It outputs a private key \(\mathsf{sk}_Y\).
, and a key attribute \(Y \in B_\lambda \). It outputs a private key \(\mathsf{sk}_Y\). -
 : The decryption algorithm takes as input the master public key
: The decryption algorithm takes as input the master public key  , a ciphertext \(\mathsf {ct}\), ciphertext attribute \(X\in A_\lambda \), a private key \(\mathsf{sk}_Y\), and private key attribute \(Y \in B_\lambda \). It outputs the message
, a ciphertext \(\mathsf {ct}\), ciphertext attribute \(X\in A_\lambda \), a private key \(\mathsf{sk}_Y\), and private key attribute \(Y \in B_\lambda \). It outputs the message  or
or  which represents that the ciphertext is not in a valid form.
which represents that the ciphertext is not in a valid form.
Definition 2.3
(Correctness). An ABE scheme for relation family R is correct if for all \(\lambda \in \mathbb {N}\), \(X\in A_\lambda , Y\in B_\lambda \) such that \(R(X,Y)=1\), and for all messages \(\mathsf {\mu }\in \mathcal {M}\),

where the probability is taken over the coins of \(\mathsf{Setup}\), \(\mathsf{KeyGen}\), and \(\mathsf {Enc}\).
Definition 2.4
(\(\mathsf {Sel}\text{- }\mathsf {IND}\) security for ABE). For an ABE scheme \({\mathsf {ABE}}=\{ \mathsf{Setup}, \mathsf {Enc}, \mathsf{KeyGen}, \mathsf{Dec}\}\) for a relation family \(R = \{ R_\lambda : A_\lambda \times B_\lambda \rightarrow \{0,1\} \}_\lambda \) and a message space \(\{\mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}\) and an efficient adversary \(\AA = \{ \mathcal {A}_\lambda \}_\lambda \), let us define \(\mathsf {Sel}\text{- }\mathsf {IND}\) security game as follows.
-
1.
Choosing the Target: At the beginning of the game, \(\mathcal {A}_\lambda \) chooses its target \(X^\star \in A_\lambda \) and sends to the challenger.
-
2.
Setup phase: On input \(1^\lambda \), the challenger samples
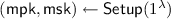 and gives
and gives  to
to  .
. -
3.
Query phase: During the game,
 adaptively makes the following queries, in an arbitrary order.
adaptively makes the following queries, in an arbitrary order.  can make unbounded many key queries, but can make only single challenge query.
can make unbounded many key queries, but can make only single challenge query.-
(a)
Key Queries: \(\mathcal {A}_\lambda \) chooses an input \(Y \in B_\lambda \). For each such query, the challenger replies with \(\mathsf{sk}_Y \leftarrow \mathsf{KeyGen}(\mathsf {mpk}, \mathsf {msk}, Y)\).
-
(b)
Challenge Query: At some point, \(\mathcal {A}_\lambda \) submits a pair of equal length messages \((\mathsf {\mu }_0, \mathsf {\mu }_1)\in (\mathcal {M})^2\) to the challenger. The challenger samples a random bit \(\beta \leftarrow \{0,1\}\) and replies to \(\mathcal {A}_\lambda \) with \(\mathsf {ct}\leftarrow \mathsf {Enc}(\mathsf {mpk}, X^\star , \mathsf {\mu }_\beta )\).
We require that
 holds for any Y such that \(\mathcal {A}_\lambda \) makes a key query for Y in order to avoid trivial attacks.
holds for any Y such that \(\mathcal {A}_\lambda \) makes a key query for Y in order to avoid trivial attacks. -
(a)
-
4.
Output phase:
 outputs a guess bit
outputs a guess bit  as the output of the experiment.
as the output of the experiment.
We define the advantage \(\mathsf {Adv}^{\mathsf {Sel}\text{- }\mathsf {IND}}_{{\mathsf {ABE}}, \mathcal {A}}(1^\lambda )\) of \(\mathcal {A}\) in the above game as

The ABE scheme \({\mathsf {ABE}}\) is said to satisfy \(\mathsf {Sel}\text{- }\mathsf {IND}\) security (or simply selective security) if for any efficient and stateful adversary \(\mathcal {A}=\{ \mathcal {A}_\lambda \}_\lambda \), there exists a negligible function \({{\,\mathrm{negl}\,}}(\cdot ) \) such that \(\mathsf {Adv}^{\mathsf {Sel}\text{- }\mathsf {IND}}_{{\mathsf {ABE}}, \mathcal {A}}(1^\lambda ) \ne {{\,\mathrm{negl}\,}}(\lambda )\).
We can consider the following stronger version of the security where we require the ciphertext to be pseudorandom.
Definition 2.5
(\(\mathsf {Sel}\text{- }\mathsf {INDr}\) security for ABE). We define \(\mathsf {Sel}\text{- }\mathsf {INDr}\) security game similarly to \(\mathsf {Sel}\text{- }\mathsf {IND}\) security game except that the adversary \(\mathcal {A}\) chooses single message \(\mathsf {\mu }\) instead of \((\mathsf {\mu }_0,\mathsf {\mu }_1)\) at the challenge phase and the challenger returns \(\mathsf {ct}\leftarrow \mathsf {Enc}(\mathsf {mpk}, X^\star , \mathsf {\mu })\) if \(\beta =0\) and a random ciphertext \(\mathsf {ct}\leftarrow \mathcal {CT}\) from a ciphertext space \(\mathcal {CT}\) if \(\beta =1\). We define the advantage \(\mathsf {Adv}^{\mathsf {Sel}\text{- }\mathsf {INDr}}_{{\mathsf {ABE}}, \mathcal {A}}(1^\lambda )\) of the adversary \(\mathcal {A}\) accordingly and say that the scheme satisfies \(\mathsf {Sel}\text{- }\mathsf {INDr}\) security if the quantity is negligible.
We also consider (weaker) version of the above notions, where \(\mathcal {A}\) specifies the set \(\mathcal{Y}\) of attributes for which it makes key queries along with \(X^\star \) at the beginning of the game.
Definition 2.6
(\(\mathsf {VerSel}\text{- }\mathsf {IND}\) security for ABE). We define \(\mathsf {VerSel}\text{- }\mathsf {IND}\) security game as \(\mathsf {Sel}\text{- }\mathsf {IND}\) security game with the exception that the adversary \(\mathcal {A}\) has to choose the set \(\mathcal{Y}\subseteq B_\lambda \) for which it makes key queries along with the challenge ciphertext attribute \(X^{\star }\) before the setup phase but the choice of \((\mathsf {\mu }_0,\mathsf {\mu }_1)\) can still be adaptive. After that, \(\mathcal {A}_\lambda \) can make key queries for \(Y_1,Y_2,\ldots \) adaptively, but we need \(Y_i \in \mathcal{Y}\) for all queries. We define the advantage \(\mathsf {Adv}^{\mathsf {VerSel}\text{- }\mathsf {IND}}_{{\mathsf {ABE}}, \mathcal {A}}(1^\lambda )\) of the adversary \(\mathcal {A}\) accordingly and say that the scheme satisfies \(\mathsf {VerSel}\text{- }\mathsf {IND}\) security (or simply very selective security) if the quantity is negligible.
In the following, we define standard notions of ciphertext-policy attribute-based encryption (CP-ABE) and broadcast encryption (BE) by specifying the relation R.
CP-ABE for Circuits. We define CP-ABE for circuit class \(\{ \mathcal{C}_\lambda \}_\lambda \) by specifying the relation. Here, \(\mathcal{C}_\lambda \) is a set of circuits with input length \(\ell (\lambda )\) and binary output. We define \(A_\lambda ^{\mathsf {CP}} = \mathcal{C}_\lambda \) and \(B_\lambda ^{\mathsf {CP}} = \{0,1\}^{\ell }\). Furthermore, we define the relation \(R_\lambda ^\mathsf {CP}\) as \(R_\lambda ^\mathsf {CP}( C, \mathbf {x})= \lnot C(\mathbf {x})\).Footnote 2
BE. To define BE, we define \(A_\lambda ^{\mathsf {BE}} = 2^{[N(\lambda )]}\) and \(B_\lambda ^{\mathsf {BE}} = [N(\lambda )]\), where \(N(\lambda )={{\,\mathrm{poly}\,}}(\lambda )\) is the number of users in the system and \(2^{[N(\lambda )]}\) denotes all subsets of [N]. We also define \(R_\lambda ^\mathsf {BE}: A_\lambda ^\mathsf {BE}\times B_\lambda ^\mathsf {BE}\rightarrow \{0,1\}\) as \(R_\lambda ^\mathsf {BE}( S , i )= 1\) when \(i\in S\) and \(R_\lambda ^\mathsf {BE}( S , i )= 0\) otherwise. For BE, we typically require that the ciphertext size should be \(o(N) \cdot {{\,\mathrm{poly}\,}}(\lambda )\), since otherwise we have a trivial construction from plain public key encryption.
Remark 2.7
We note that very selective security and selective security are in fact equivalent in the case of BE since one can convert selective adversary into very selective adversary as follows. Namely, if the selective adversary chooses its target \(S\subseteq [N]\), the very selective adversary chooses the same target S and specifies the set of user indices for which it makes key queries as \([N]\backslash S\). Then, the very selective adversary can simulate the game for the selective adversary using the secret keys given by the challenger.
3 Computational Secret Sharing Scheme with Short Shares
We will use secret sharing scheme with special properties that we are going to define here. Let \(\mathcal{C}=\{ \mathcal{C}_\lambda \}_\lambda \) be a circuit class. A secret sharing scheme for the circuit class \(\mathcal{C}\) is defined by the following PPT algorithms:
-
\(\mathsf {SS.Setup}(1^\lambda , p)\rightarrow \mathsf {pp}\): The setup algorithm takes as input the unary representation of the security parameter \(\lambda \) and the modulus p and outputs public parameter \(\mathsf {pp}\).
-
\(\mathsf {SS.Share}(\mathsf {pp}, C, \mathsf {\mu })\): The sharing algorithm takes as input the public parameter \(\mathsf {pp}\), a circuit \(C\in \mathcal{C}_\lambda \) that specifies access policy, and a message \(\mathsf {\mu }\in \{0,1\}\) to be shared and outputs a set of shares \( \{ \mathsf {share}_{i,b} \in \mathbb {Z}_p^m \}_{i\in [\ell ], b\in \{0,1\}}\), where \(\ell \) is the input length of C and m is a parameter specified by \(\lambda \) and p.
-
\(\mathsf {SS.Recon}(\mathsf {pp}, C, x, \{ \mathsf {share}_{i,x_i} \}_{i\in [\ell ]} )\rightarrow \mathsf {\mu } \text{ or } \bot \): The reconstruction algorithm takes as input the public parameter \(\mathsf {pp}\), a circuit C, an input \(x\in \{0,1\}^\ell \) to the circuit, and shares \(\{ \mathsf {share}_{i,x_i} \}_{i\in [\ell ]}\) and outputs message \(\mathsf {\mu }\) or \(\bot \).
We require correctness and security for the secret sharing scheme as defined in the following.
Definition 3.1
(Correctness). We say that a secret sharing scheme \(\mathsf {SS} = (\mathsf {SS.Setup}, \mathsf {SS.Share}, \mathsf {SS.Recon})\) for circuit class \(\mathcal{C}\) has correctness if there exists a function \(p_0(\lambda )\) specified by the circuit class \(\mathcal{C}\) such that for any \(p > p_0(\lambda )\), \(C\in \mathcal{C}\) with input length \(\ell \), \(x\in \{0,1\}^\ell \) satisfying \(C(x)=1\), and \(\mathsf {\mu }\in \{0,1\}\), we have
Definition 3.2
(Security). We say that a secret sharing scheme \(\mathsf {SS} = (\mathsf {SS.Setup}, \mathsf {SS.Share}, \mathsf {SS.Recon})\) for circuit class \(\mathcal{C}= \{ \mathcal{C}_\lambda \}_\lambda \) is secure if for any \(C\in \mathcal{C}_\lambda \) with input length \(\ell =\ell (\lambda )\), \(x\in \{0,1\}^\ell \) satisfying \(C(x)=0\), \(\mathsf {\mu }\in \{0,1\}\), \(p\in \mathbb {N}\), and for any efficient adversary \(\mathcal {A}= \{ \mathcal {A}_\lambda \}\), we have
where the probability is taken over the choice of \(\mathsf {pp}\leftarrow \mathsf {SS.Setup}(1^\lambda , p)\), \(\{\mathsf {share}_{i,b}\}_{i, b} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \mathsf {\mu })\), \(\mathbf {v}_i \leftarrow \mathbb {Z}_p^m\) for \(i\in [\ell ]\), and the internal coin of \(\mathcal {A}_\lambda \).
We note that in the above, we not only require that the shares do not reveal \(\mathsf {\mu }\) if \(C(x)=0\), but also require that they look random.
We furthermore require following structural properties for the construction. First, we require that \(\mathsf {pp}\) is a random string.
Definition 3.3
(Random Public Parameters). We require that \(\mathsf {pp}\) output by \(\mathsf {SS.Setup}(1^\lambda ,p)\) is statistically close to uniformly random, where the length of the string is deterministically determined by p.
Looking ahead, the above property is crucial when we prove the security of our ABE scheme. If the public parameter of the secret sharing scheme was chosen from a structured distribution, we would have to rely on the bilinear KOALA assumption (Definition 4.1) with auxiliary input chosen from the same distribution. However, we cannot hope the assumption to hold for auxiliary input with general distribution as we will discuss in Remark 4.3.
We also require that the reconstruction algorithm is structured as two steps: a function evaluation step that computes the circuit on the shares to yield the message along with noise, followed by a rounding step that removes the noise. We require that the first step is linear. We refer to such a reconstruction algorithm as being “almost linear”, and define it formally next.
Definition 3.4
(Almost Linear Reconstruction). We say that a secret sharing scheme \(\mathsf {SS} = (\mathsf {SS.Setup}, \mathsf {SS.Share}, \mathsf {SS.Recon})\) has almost linear reconstruction if the reconstruction algorithm is divided into two steps:
-
Step 1 takes as input the public parameter \(\mathsf {pp}\), the circuit C, and the input x. It outputs a set of coefficients \(\{ a_{i,j} \in \mathbb {Z}_p \}_{i\in [\ell ], j\in [m]}\). We denote this step as an algorithm \(\mathsf {SS.FindCoef}( \mathsf {pp}, C, x )\).
-
Step 2 takes as input the set of shares \(\{ \mathsf {share}_{i,x_i} \}_{i\in [\ell ]}\) that corresponds to x and a set of linear coefficients \(\{ a_{i,j } \}_{i\in [\ell ],j\in [m]}\) and computes
$$ d:=\sum _{ i\in [\ell ], j\in [m] } a_{i,j} \mathsf {share}_{i,x_i,j} \mod p $$where \(\mathsf {share}_{i,x_i,j} \in \mathbb {Z}_p\) is the j-th entry of the vector \(\mathsf {share}_{i,x_i}\). It then outputs 1 if d is closer to p/2 and 0 otherwise.
We require the following property, which implies the correctness: For any \(x\in \{0,1\}^\ell \) and \(C \in \mathcal{C}\) satisfying \(C(x)=1\) and \(p>p_0\), if we have:
where \({i\in [\ell ], j \in [m]}\), then there exists \(e\in [-B,B]\) such that
where \(B(\lambda )\) is an integer specified by \(\mathcal{C}\).
The following theorem asserts that we can construct a secret sharing scheme with the desired properties under the LWE assumption.
Theorem 3.5
For circuit class \(\mathcal{C}_{\ell , d} = \{ \mathcal{C}_{\lambda , \ell (\lambda ), d(\lambda )} \}_{\lambda \in \mathbb {N}}\) consisting of circuits whose input length is \(\ell (\lambda ) = {{\,\mathrm{poly}\,}}(\lambda )\) and depth \(d(\lambda ) = O(\log \lambda )\), we have secret sharing scheme that satisfies almost linear reconstruction (Definition 3.4) for \(p_0 = {{\,\mathrm{poly}\,}}(\lambda , 2^d, \ell )\) and has random public parameters (Definition 3.3). We can prove the security of the scheme (Definition 3.2) under the LWE assumption with approximation factor \(p^{\epsilon } \cdot {{\,\mathrm{poly}\,}}(\lambda )\) for some constant \(\epsilon <1\). Furthermore, the size of the parameters in the construction is as follows:
In particular, \(B(\lambda )\) is bounded by a polynomial in \(\lambda \) since \(d=O(\log \lambda )\).
Proof
The construction is based on the ABE scheme for circuit class \(\{ \mathcal{C}_{\ell ,d} \}\) by [GV15]. Here, we first show a construction that almost works but has a problem. We then fix the problem by slightly modifying the construction. In our first construction, we put the master public key and a secret key for circuit C of the ABE scheme into \(\mathsf {pp}\), where the former consists of set of random matrices \(\mathbf {A}\) and \(\{ \mathbf {B}_{i,b} \}_{i,b}\) along with a random vector \(\mathbf {u}\). To generate \(\{ \mathsf {share}_{i,b} \}_{i,b}\), we generate LWE samples using corresponding matrices in \(\{ \mathbf {B}_{i,b} \}_{i,b}\) with respect to the same secret, so that \(\{ \mathsf {share}_{i,x_i} \}_{i}\) constitutes a valid ABE ciphertext for attribute x and message \(\mathsf {\mu }\) to be shared.Footnote 3 Most of the properties we require for the secret sharing scheme are directly implied by the corresponding properties of the ABE scheme. The correctness (Definition 3.1) and the security (Definition 3.2) of the secret sharing scheme are implied by the corresponding properties of the ABE scheme, where for the latter we use \(\mathsf {Sel}\text{- }\mathsf {INDr}\) security of the ABE scheme. The size requirements for the parameters (Eq. (3.1)) are satisfied by the efficiency of the ABE scheme. The almost linear reconstruction property (Definition 3.4) is also satisfied by the structure of the decryption algorithm of the ABE scheme.
However, the above construction does not have the property of random public parameters (Definition 3.3) and we have to change it slightly. In particular, in the above, \(\mathsf {pp}\) is chosen as follows: We first sample random matrices \(\mathbf {A}\) and \(\{ \mathbf {B}_{i,b} \}_{i,b}\) and a random vector \(\mathbf {u}\), where \(\mathbf {A}\) is chosen along with a trapdoor. We then compute a matrix \(\mathbf {B}_C\) corresponding to the circuit C from the matrices \(\{ \mathbf {B}_{i,b} \}_{i,b}\) and then generate a vector \(\mathbf {r}\) from a Gaussian distribution over the integer lattice with the restriction
using the trapdoor. We then set \(\mathsf {pp}=(\mathbf {A},\mathbf {B},\mathbf {u},\mathbf {r})\). Because of the above relation between \(\mathbf {r}\) and \(\mathbf {u}\), \(\mathsf {pp}\) is not random.
To address this issue, we first remove \(\mathbf {u}\) from \(\mathsf {pp}\). We now have that the distribution of \(\mathbf {r}\) is statistically close to the Gaussian distribution over the integer lattice (without the restriction), since for a vector \(\mathbf {r}\) chosen from (sufficiently wide) Gaussian distribution over the integer lattice, \(\mathbf {u}\) defined as \(\mathbf {u}= [ \mathbf {A}| \mathbf {B}_C ]\mathbf {r}\mod q\) is statistically close to uniform. Now, such \(\mathbf {r}\) can be chosen from randomness of fixed polynomial length, in particular, without a trapdoor. We then put the randomness R used for sampling \(\mathbf {r}\) into \(\mathsf {pp}\) instead of \(\mathbf {r}\) itself. We now have that \(\mathsf {pp}\) is statistically close to random as desired.
It is easy to see that this change does not affect the properties that we want from the secret sharing scheme. In particular, the correctness is not lost since \(\mathbf {u}\) can be recovered from \(\mathbf {r}\). We note that for the security to be preserved, we need an efficient reverse sampling algorithm that is given \(\mathbf {r}\) and samples randomness R conditioned that the Gaussian sampler outputs \(\mathbf {r}\) on input R. The reason why we need this property is that the reduction algorithm that breaks the ABE scheme using the adversary against the secret sharing scheme should simulate the randomness R for sampling \(\mathbf {r}\) only given \(\mathbf {r}\), which is the secret key of the ABE scheme.
This property is satisfied by efficient Gaussian samplers such as [GPV08]. To see this, let us recall the procedure of sampling Gaussian on integer lattice in [GPV08] (See Lemma 4.3 in the paper). Without loss of generality, we can consider one-dimensional case since multi-dimensional case can be handled by running the algorithm for one-dimensional case in parallel. The sampling algorithm by [GPV08] was based on rejection sampling. The algorithm first samples a candidate for the output uniformly at random and outputs it with certain probability. This step is repeated until it outputs something or the number of times it repeats the procedure exceeds predetermined number. The idea for the reverse sampling is to first run the algorithm until it outputs something and then replace the randomness that was used for the output with that which leads to the intended output. The former step can be done straightforwardly since it is exactly the same as the original sampling algorithm. The purpose of performing this step is to simulate the failure. The latter step can be performed efficiently as well, since the randomness that leads to the output consists of the output value itself along with the randomness that allows the sampler to accept and output the value (rather than to reject). It is easy to see that this algorithm indeed works. This completes the proof of Theorem 3.5.
The complete description of the secret sharing scheme will appear in the full version.
4 Our Security Assumptions
In this section, we will introduce the bilinear knowledge of orthogonality (KOALA) assumption, which is an analogue of the KOALA assumption introduced in [BW19]. Looking ahead, the assumption will be used to prove the security of our ABE scheme in Sect. 5.1. We then introduce weak KOALA assumption (\(\mathsf {wKOALA}\)) and show that it is implied by the bilinear KOALA assumption. While the former assumption is implied by the latter, the former is handier to use and would be of independent interest.
4.1 Bilinear KOALA Assumption
Here, we introduce bilinear KOALA assumption, which is an analogue of the KOALA assumption introduced in [BW19].
Definition 4.1
(Bilinear KOALA Assumption). Let \(\mathsf {Samp}= \{ \mathsf {Samp}_\lambda \}_\lambda \) be an efficient sampling algorithm that takes as input an integer p and a string \(\mathsf {aux}\) and outputs a matrix \(\mathbf {V}\in \mathbb {Z}_p^{\ell _1 \times \ell _2}\) with \(\ell _1 < \ell _2\). For an efficient adversary \(\mathcal {A}= \{ \mathcal {A}_{\lambda } \}\), let us define
where the probabilities are taken over the choice of uniformly random \(\mathsf {aux}\), \(\mathbb {G}= (p, \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, e, [1]_1, [1]_2) \leftarrow \mathsf {GroupGen}(1^\lambda )\), \(\mathbf {V}\leftarrow \mathsf {Samp}(p, \mathsf {aux}) \), \(\mathbf {s}\leftarrow \mathbb {Z}_p^{\ell _1}\), \(\mathbf {r}\leftarrow \mathbb {Z}_p^{\ell _2}\), and the coin of \(\mathcal {A}_\lambda \).
Furthermore, for an efficient adversary \(\mathcal {B}=\{ \mathcal {B}_\lambda \}_{\lambda }\), we also define
where the probability is taken over the choice of uniformly random \(\mathsf {aux}\), \(\mathbb {G}= (p, \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, e, [1]_1, [1]_2) \leftarrow \mathsf {GroupGen}(1^\lambda )\), \(\mathbf {V}\leftarrow \mathsf {Samp}_\lambda (p, \mathsf {aux}) \), and the coin of \(\mathcal {B}_\lambda \).
We say that the bilinear KOALA assumption holds with respect to \(\mathsf {GroupGen}\) if for any efficient adversary \(\mathcal {A}\) and efficient sampler \(\mathsf {Samp}\), there exists another efficient adversary \(\mathcal {B}\) and a polynomial function \(Q(\lambda )\) such that
Remark 4.2
Our definition of the bilinear KOALA assumption differs from the original KOALA assumption defined by Beullens and Wee [BW19] in several points. First, we consider the assumption in groups equipped with bilinear maps whereas they consider the assumption in groups without bilinear maps.
Second, in our assumption, the adversary is given an auxiliary input \(\mathsf {aux}\) and \(\mathbf {V}\) is chosen from a distribution specified by \(\mathsf {Samp}\) whereas there is no any auxiliary information and \(\mathbf {V}\) is fixed in [BW19]. This change is necessary to prove the security of our ABE scheme in Sect. 5, since we will use an adversary \(\mathcal {B}\) that is obtained from \(\mathcal {A}\) to break a computational assumption, where we put the problem instance of the assumption into \(\mathsf {aux}\).
Remark 4.3
One could consider simpler and stronger variant of the above assumption where \(\mathsf {Samp}\) chooses \(\mathsf {aux}\) along with \(\mathbf {V}\) instead of letting \(\mathsf {aux}\) to be a random string that is not controlled by \(\mathsf {Samp}\). However, we cannot hope this variant of the assumption to hold for all efficient samplers. For example, let us consider a sampler that outputs random \(\mathbf {V}\) along with auxiliary information \(\mathsf {aux}= \mathcal{O}(C_\mathbf {V})\), which is an obfuscation of circuit \(C_\mathbf {V}\) that takes as input group description \(\mathbb {G}\) and elements \([\mathbf {v}]_2\) and returns whether \(\mathbf {v}\) is in the space spanned by the rows of \(\mathbf {V}\) or not. Using \(\mathcal{O}(C_\mathbf {V})\), one can easily distinguish \([\mathbf {s}\mathbf {V}]_2\) from \([\mathbf {r}]_2\) with high probability. However, an efficient adversary may not be able to find a vector \(\mathbf {x}\ne \mathbf {0}\) that satisfies \(\mathbf {x}\mathbf {V}=\mathbf {0}\) even given \(\mathcal{O}(C_\mathbf {V})\), if we use sufficiently strong obfuscator to obfuscate the circuit \(C_\mathbf {V}\). Our assumption above excludes this kind of attack by making \(\mathsf {aux}\) to be public randomness that is not touched by the sampler. Our definition is inspired by that of public coin differing input obfuscation [IPS15], where the authors exclude similar kind of attacks [GGHW14] in the context of differing input obfuscations by restricting the distribution of auxiliary input to be random.
The following theorem justifies the bilinear KOALA assumption on the bilinear generic group model. The proof is almost the same as that for the KOALA assumption in [BW19], but we have to adjust it into the setting where the groups are equipped with bilinear maps and the adversary is given auxiliary input.
Theorem 4.4
The bilinear KOALA assumption holds under the bilinear generic group model, where \(\mathcal {A}\) has access to the generic group oracles but \(\mathsf {Samp}\) does not.
Proof
Let us fix PPT sampler \(\mathsf {Samp}\) and an adversary \(\mathcal {A}\). We also let \(Q_{\mathsf {zt}}(\lambda )\) be the upper bound on the number of zero test queries that \(\mathcal {A}\) makes. To prove the theorem, we consider following sequence of games. Let us denote the event that \(\mathcal {A}\) outputs 1 at the end of \(\mathbf {Game}_\mathrm{x}\) as \(\mathsf {E}_\mathrm{x}\).
-
\(\mathbf {Game}_1\): In this game, \(\mathsf {Samp}\) takes as input the order of groups p and a random string \(\mathsf {aux}\) and outputs \(\mathbf {V}\in \mathbb {Z}_p^{\ell _1\times \ell _2}\). By assumption, \(\mathsf {Samp}\) does not have access to the generic group oracles. Then, the adversary \(\mathcal {A}\) is given \(\mathsf {aux}\), handles corresponding to the group elements \([\mathbf {r}]_2\), where \(\mathbf {r}=(r_1,\ldots , r_{\ell _2})\leftarrow \mathbb {Z}_p^{\ell _2}\), and access to the oracles in generic group model and outputs a bit at the end of the game.
-
\(\mathbf {Game}_2\): In this game, we switch to symbolic group model and replace \(r_1,\ldots , r_{\ell _2} \in \mathbb {Z}_p\) with formal variables \(R_1,\ldots , R_{\ell _2}\). Note that all handles given to \(\mathcal {A}\) during the game refer to a group element that is represented as
$$ x_0 + \sum _{j\in [\ell _2]} x_j R_j \in \mathbb {Z}_p[ R_1,\ldots , R_{\ell _2} ] $$where the challenger computes coefficients \(\{ x_j\in \mathbb {Z}_p \}_{j\in [0,\ell _2]}\) by keeping track of the group operations performed by \(\mathcal {A}\). We observe that this game differs from the previous game only when \(\mathcal {A}\) makes a zero test query for \(x_0 + \sum _{j\in [\ell _2]} x_j R_j \) such that \(x_0 + \sum _{j\in [\ell _2]} x_j R_j \ne 0\) but \(x_0 + \sum _{j\in [\ell _2]} x_j r_j \). However, this occurs with probability at most 1/p since \(\mathbf {r}\) is chosen uniformly at random independently from anything else. Therefore, we have
$$\begin{aligned} \left| \Pr [\mathsf {E}_2] - \Pr [\mathsf {E}_1] \right| = {{\,\mathrm{negl}\,}}(\lambda ). \end{aligned}$$ -
\(\mathbf {Game}_3\): In this game, we replace the formal variable \(R_j\) with
$$\begin{aligned} \sum _{i\in [\ell _1]} v_{i,j} S_{i} \end{aligned}$$for all \(j\in [\ell _2]\), where \(v_{i,j}\) is the (i, j)-th entry of \(\mathbf {V}\) and \(S_1,\ldots , S_{\ell _1}\) are set of formal variables.
-
\(\mathbf {Game}_4\): In this game, we switch back to the generic group model (rather than the symbolic group model) and provide the adversary with handles for \([\mathbf {s}\mathbf {V}]_2\) as input. By the same reason as the game hop from \(\mathbf {Game}_1\) to \(\mathbf {Game}_2\), we have
$$\begin{aligned} \left| \Pr [\mathsf {E}_4] - \Pr [\mathsf {E}_3] \right| = {{\,\mathrm{negl}\,}}(\lambda ). \end{aligned}$$
By the definition of the games, we have \(|\Pr [\mathsf {E}_4] - \Pr [\mathsf {E}_1]| = \mathsf {Adv}^{\mathsf {BKOALA,dist}}_{\mathcal {A},\mathbb {G},\mathsf {Samp}}( \lambda )\). Let us define \(\epsilon := | \Pr [\mathsf {E}_2] - \Pr [\mathsf {E}_3] |\). By triangular inequality, we have
Therefore, it suffices to prove the following lemma to finish the proof of Theorem 4.4.
Lemma 4.5
There exists an efficient adversary \(\mathcal {B}\) that has access to the bilinear generic group oracles and \(\mathsf {Adv}^{\mathsf {BKOALA,find}}_{\mathcal {B},\mathbb {G},\mathsf {Samp}}( \lambda ) \ge \epsilon /Q_{\mathsf {zt}}\).
Proof
We first observe that the oracle response to \(\mathcal {A}\) in \(\mathbf {Game}_2\) and \(\mathbf {Game}_3\) differs only when \(\mathcal {A}\) makes a zero-test query for a handle that corresponds to \(x_0 + \sum _{j \in [\ell _2]} x_j R_j \) such that \(x_0 + \sum _{j\in [\ell _2]} x_j R_j \ne 0\) over \(\mathbb {Z}_p[ R_1,\ldots , R_{\ell _2} ]\) and
over \(\mathbb {Z}_p[ S_1,\ldots , S_{\ell _1} ]\). We call such a query bad query. We can see that \(\mathcal {A}\) makes a bad query with probability at least \(\epsilon \) in \(\mathbf {Game}_2\). We observe that for a bad query, we have \(x_0=0\), \(\mathbf {x}\mathbf {V}^\top = \mathbf {0}\), and \(\mathbf {x}\ne \mathbf {0}\) for \(\mathbf {x}=(x_1,\ldots , x_{\ell _2})\).
To prove the theorem, we further consider the following sequence of games. In the following, let us denote \(\mathsf {F}_{\mathrm {x}}\) the event that \(\mathcal {A}\) makes a bad query and the challenger does not output \(\bot \) in \(\mathbf {Game}_{\mathrm {2,x}}\).
-
\(\mathbf {Game}_{2,1}\): This is the same as \(\mathbf {Game}_2\). Without loss of generality, we assume that the challenger simulates the generic group oracles for \(\mathcal {A}\). By definition, we have
$$\begin{aligned} \Pr [\mathsf {F}_{1}]\ge \epsilon . \end{aligned}$$ -
\(\mathbf {Game}_{2,2}\): In this game, we change the previous game so that the challenger picks a random guess \(k^*\) for the first bad query as \(k^*\leftarrow [Q_{\mathsf {zt}}]\) at the beginning of the game. Furthermore, we change the game so that the challenger outputs \(\bot \) at the end of the game if the \(k^*\)-th zero-test query is not the first bad query. Since \(k^*\) is chosen uniformly at random and independent from the view of \(\mathcal {A}\), the guess is correct with probability \(1/Q_{\mathsf {zt}}\) conditioned on \(\mathsf {F}_1\). Therefore, we have
$$\begin{aligned} \Pr [ \mathsf {F}_2 ] \ge \Pr [\mathsf {F}_1] /Q_{\mathsf {zt}}. \end{aligned}$$ -
\(\mathbf {Game}_{2.3}\): This game is the same as the previous game except that the challenger aborts the game and outputs \(\bot \) immediately after \(\mathcal {A}\) makes the \(k^*\)-th zero-test query. Since whether \(\mathsf {F}_2\) occurs or not is irrelevant to how the game proceeds after the \(k^*\)-th zero-test query is made by \(\mathcal {A}\), we clearly have
$$ \Pr [\mathsf {F}_3] = \Pr [\mathsf {F}_2]. $$
We then construct \(\mathcal {B}\), which acts as the challenger in \(\mathbf {Game}_{2,3}\) for \(\mathcal {A}\) as follows.
\(\mathcal {B}\) takes \(\mathsf {aux}\) as input and then chooses random \(k^* \leftarrow [Q_{\mathsf {zt}}]\). It then runs \(\mathcal {A}\) on input \(\mathsf {aux}\) and handles for symbols \(R_1,\ldots ,R_{\ell _2}\). \(\mathcal {B}\) then answers generic oracle queries made by \(\mathcal {A}\) honestly until the \(k^*\)-th zero test query. When \(\mathcal {A}\) makes the \(k^*\)-th zero test query, \(\mathcal {B}\) extracts \((x_0,x_1,\ldots , x_{\ell _2})\) such that the query corresponds to the handle of \(x_0+ \sum _{j\in [\ell _2]}x_jR_j\). This is possible by keeping track of \(\mathcal {A}\)’s group operations while simulating the generic group oracles. If \(x_0\ne 0\), \(\mathcal {B}\) aborts and outputs \(\bot \). Otherwise, it outputs the vector \(\mathbf {x}=(x_1,\ldots , x_{\ell _2})\).
Since \(\mathcal {B}\) perfectly simulates \(\mathbf {Game}_{2,3}\) and thus the probability that \(\mathcal {B}\) outputs \(\mathbf {x}\) such that \(\mathbf {x}\mathbf {V}^\top = 0\) and \(\mathbf {x}\ne \mathbf {0}\) is \(\Pr [\mathsf {F}_3]=\epsilon /Q_{\mathsf {zt}}\). This completes the proof of Lemma 4.5.
This completes the proof of Theorem 4.4.
4.2 Our New Assumption \(\mathsf {wKOALA}\)
Here, we introduce our new assumption that we call \(\mathsf {wKOALA}\) (for “weak” KOALA) that will be used to prove the security of our ABE scheme in Sect. 5. The assumption essentially says that for a sampler that outputs a set of vectors such that the vectors are individually pseudorandom but mutually correlated, it holds that the vectors appear mutually pseudorandom when they are lifted to the exponent and randomized by vector-wise randomness. We require that this hold even in the presence of random auxiliary input as is assumed for the case of the bilinear KOALA assumption.
Definition 4.6
Let \(\mathsf {Samp}= \{ \mathsf {Samp}_\lambda \}_\lambda \) be an efficient sampling algorithm that takes as input an integer p and a string \(\mathsf {aux}\) and outputs a set of vectors \(\{ \mathbf {u}^{(j)}\in \mathbb {Z}_p^m \}_{j\in [t]}\). For an efficient adversary \(\mathcal {A}=\{ \mathcal {A}_\lambda \}_{\lambda }\) and \(i:= i(\lambda )\in \mathbb {N}\), let us define
where the probabilities are taken over the choice of uniformly random \(\mathsf {aux}\), \(\mathbb {G}= (p, \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, e, [1]_1, [1]_2) \leftarrow \mathsf {GroupGen}(1^\lambda )\), , \(\{ \mathbf {u}^{(j)} \}_{j\in [t]} \leftarrow \mathsf {Samp}_\lambda (p,\mathsf {aux})\), \(\mathbf {v}\leftarrow \mathbb {Z}_p^m\), and the coin of \(\mathcal {A}_\lambda \). In the above, we set \(\mathbf {u}^{(i)}:= \mathbf {v}\) if \(i>t\). Furthermore, for an efficient adversary \(\mathcal {B}= \{ \mathcal {B}_{\lambda } \}\), we define
where the probabilities are taken over the choice of uniformly random \(\mathsf {aux}\), \(\mathbb {G}\), \(\{ \mathbf {u}^{(j)} \}_{j\in [t]} \leftarrow \mathsf {Samp}_\lambda (p,\mathsf {aux})\), \(\gamma ^{(j)} \leftarrow \mathbb {Z}_p\), \(\mathbf {v}^{(j)} \leftarrow \mathbb {Z}_p^m\) for \(j\in [t]\), and the coin of \(\mathcal {B}_\lambda \). We say that \(\mathsf {wKOALA}\) holds with respect to \(\mathsf {GroupGen}\) if for any efficient sampler \(\mathsf {Samp}\) such that \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {single}}_{\mathcal {A},\mathbb {G},\mathsf {Samp}, i }( \lambda )\) is negligible for any efficient adversary \(\mathcal {A}\) and \(i(\lambda )\), \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {multi}}_{\mathcal {B},\mathbb {G},\mathsf {Samp}}( \lambda )\) is also negligible for any efficient adversary \(\mathcal {B}\).
The following theorem shows that \(\mathsf {wKOALA}\) is in fact implied by the bilinear KOALA assumption.
Theorem 4.7
If the bilinear KOALA assumption holds with respect to \(\mathsf {GroupGen}\), so does \(\mathsf {wKOALA}\).
Proof
For the sake of contradiction, let us assume that \(\mathsf {wKOALA}\) does not hold with respect to \(\mathsf {GroupGen}\), but the bilinear KOALA assumption holds with respect to \(\mathsf {GroupGen}\). The former assumption implies that there exists an efficient sampler \(\mathsf {Samp}\) such that \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {single}}_{\mathcal {A},\mathbb {G},\mathsf {Samp},i }( \lambda )\) is negligible for any efficient adversary \(\mathcal {A}\) and \(i=i(\lambda )\), but there exists an efficient adversary \(\mathcal {B}\) such that \(\epsilon (\lambda ):= \mathsf {Adv}^\mathsf{{wKOALA}, \mathsf {multi}}_{\mathcal {B},\mathbb {G},\mathsf {Samp}}( \lambda )\) is non-negligible.
We then consider another sampler \(\mathsf {Samp'}\) that takes as input p and \(\mathsf {aux}\) and outputs matrix \(\mathbf {V}\) defined as
where \(\{ \mathbf {u}^{(j)} \}_{j\in [t]} \leftarrow \mathsf {Samp}(p,\mathsf {aux}) \). For this sampler \(\mathsf {Samp'}\), we have
which follows from the definition of \(\mathsf {Adv}^{\mathsf {BKOALA,dist}}_{\mathcal {B},\mathbb {G},\mathsf {Samp}' }( \lambda )\) (See Definition 4.1). This further implies that there exists another adversary \(\mathcal {B}'\) and polynomial function \(Q(\lambda )\) such that
from the bilinear KOALA assumption. By the definition, \(\mathcal {B}'\) takes as input \(\mathsf {aux}\) and \(\mathbb {G}\) and outputs a vector \(\mathbf {x}\in \mathbb {Z}_p^{(1+m)t}\) such that \(\mathbf {x}\mathbf {V}^\top = \mathbf {0}\) and \(\mathbf {x}\ne \mathbf {0}\) with probability \(\epsilon '(\lambda ) ;= \epsilon (\lambda )/Q(\lambda ) - {{\,\mathrm{negl}\,}}(\lambda )\). Let us denote
where \(x^{(i)} \in \mathbb {Z}_p\) and \(\mathbf {x}^{(i)} \in \mathbb {Z}_p^{m}\) for \(i\in [t]\). Then, for such vector \(\mathbf {x}\), we have
for some \(i\in [t]\) by the structure of \(\mathbf {V}\). This further implies that there exists fixed \(i^*=i^*(\lambda )\) such that \(x^{(i^*)} + \langle \mathbf {x}^{(i^*)}, \mathbf {u}^{(i^*)} \rangle = 0 \mod p\) and \((x^{(i^*)}, \mathbf {x}^{(i^*)})\ne \mathbf {0}\mod p\) hold with probability at least \(\epsilon '/t\).
We then use \(\mathcal {B}'\) to construct an adversary \(\mathcal {A}\) such that \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {single}}_{\mathcal {A},\mathbb {G},\mathsf {Samp}, i^* }( \lambda )\) is non-negliglble, which contradicts our assumption. \(\mathcal {A}\) takes as input the group description \(\mathbb {G}\), auxiliary information \(\mathsf {aux}\) and a vector \(\mathbf {v}\), which is either \(\mathbf {v}\leftarrow \mathbb {Z}_p^m\) or \(\mathbf {v}=\mathbf {u}^{(i^*)}\) with \(\{ \mathbf {u}^{(j)} \}_{j\in [t]} \leftarrow \mathsf {Samp}(p,\mathsf {aux})\). Then, \(\mathcal {A}\) runs \(\mathcal {B}'\) on input \(\mathsf {aux}\) and \(\mathbb {G}\). If \(\mathcal {B}'\) outputs something outside of \(\mathbb {Z}_p^m\), \(\mathcal {A}\) outputs 0. Otherwise, let \(\mathbf {x}\in \mathbb {Z}_p^m\) be the output by \(\mathcal {B}'\). If \( ( x^{(i^*)},\mathbf {x}^{(i^*)} ) = \mathbf {0}\), \(\mathcal {A}\) outputs 0. Otherwise, \(\mathcal {A}\) checks whether
It outputs 1 if it holds and 0 otherwise.
We evaluate the probability that \(\mathcal {A}\) outputs 1. There are two cases to consider.
-
If \(\mathbf {v}= \mathbf {u}^{(i^*)}\), \(\mathcal {B}'\) outputs non-zero vector \( ( x^{(i^*)},\mathbf {x}^{(i^*)} ) \) satisfying Eq. (4.3) with probability at least \(\epsilon '/t\). \(\mathcal {A}\) outputs 1 with the same probability.
-
If \(\mathbf {v}\) is chosen uniformly at random from \(\mathbb {Z}_p^m\), Eq. (4.3) holds for \(( x^{(i^*)},\mathbf {x}^{(i^*)} ) \) output by \(\mathcal {B}'\) with probability at most 1/p unless \(( x^{(i^*)},\mathbf {x}^{(i^*)} ) = \mathbf {0}\mod p\), since \(\mathbf {v}\) is information theoretically hidden from \(\mathcal {B}'\). Since \(\mathcal {A}\) outputs 1 only when \(( x^{(i^*)},\mathbf {x}^{(i^*)} ) \ne \mathbf {0}\) and Eq. (4.3) holds, the probability that \(\mathcal {A}\) outputs 1 is at most 1/p.
We finally observe that
where the probabilities are taken over the choice of \(\mathbb {G}\leftarrow \mathsf {GroupGen}(1^\lambda )\), \(\mathbf {v}\leftarrow \mathbb {Z}_p^n\), random \(\mathsf {aux}\), \(\{ \mathbf {u}^{(j)} \}_{j\in [t]} \leftarrow \mathsf {Samp}(p,\mathsf {aux})\) and the internal coin of \(\mathcal {A}\). Since \(\epsilon /tQ -{{\,\mathrm{negl}\,}}\) is non-negligible, this contradicts our initial assumption. This completes the proof of Theorem 4.2.
5 Our CP-ABE Scheme
In this section, we provide our construction of CP-ABE scheme for \({\mathsf {NC}}_1\) whose sizes of the parameters are independent from the size of the circuits supported by the scheme and only dependent on the input length and depth of the circuits. This efficiency property is not satisfied by most of the existing schemes except for [AY20, BV20]. Unlike [AY20, BV20], we provide the security proof in the standard model. We then show that the CP-ABE scheme can be used to construct BE with optimal efficiency. This provides the first optimal BE scheme whose security is proven in the standard model.
5.1 Construction
Here, we provide our construction of CP-ABE scheme that supports the circuit class \(\mathcal{C}_{\ell , d}= \{ \mathcal{C}_{\lambda , \ell (\lambda ), d(\lambda )} \}_\lambda \), which is a set of all circuits with input length \(\ell (\lambda )\) and depth at most \(d(\lambda )\) with arbitrary \(\ell (\lambda )= {{\,\mathrm{poly}\,}}(\lambda )\) and \(d(\lambda ) = O( \log \lambda )\). For our construction, we will use public key slotted IPFE scheme \(\mathsf {IPFE}= (\mathsf {IPFE.Setup}, \mathsf {IPFE.KeyGen}, \mathsf {IPFE.Enc}, \mathsf {IPFE.SlotEnc}, \mathsf {IPFE.Dec})\), which is proposed by Lin and Luo [LL20], which is secure under the MDDH assumption, and a secret sharing scheme \(\mathsf {SS} = (\mathsf {SS.Setup}, \mathsf {SS.Share}, \mathsf {SS.Recon})\) for \(\mathcal{C}_{\ell (\lambda ),d(\lambda )}\) that is provided in Sect. 3.
-
\(\mathsf {ABE.Setup}(1^\lambda )\): On input \(1^\lambda \), the setup algorithm proceeds as follows.
-
1.
Run \(\mathbb {G}= (p, \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, e, [1]_1, [1]_2) \leftarrow \mathsf {GroupGen}(1^\lambda )\). Note that p and \(\lambda \) specify the parameter \(m:=m(\lambda )\) (See syntax of secret sharing scheme in Sect. 3).
-
2.
Run \(\mathsf {pp}\leftarrow \mathsf {SS.Setup}(1^\lambda , p)\).
-
3.
Run \((\mathsf {IPFE.mpk}_{i,b,j}, \mathsf {IPFE.msk}_{i,b,j}) \leftarrow \mathsf {IPFE.Setup}(1^\lambda , \{1\}, \{2\} )\) for \(i\in [\ell ]\), \(b\in \{0,1\}\), and \(j\in [m]\). Note that here we generate slotted IPFE instances whose the first entry is for public slot and the second entry is for private slot.
-
4.
Output \( \mathsf {ABE.mpk}=( \mathbb {G}, \mathsf {pp}, \{ \mathsf {IPFE.mpk}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} ) \) and \( \mathsf {ABE.msk} = \{ \mathsf {IPFE.msk}_{i,b,j} \}_{ i\in [\ell ], b\in \{0,1\},j\in [m] } \).
-
1.
-
\(\mathsf {ABE.KeyGen}(\mathsf {ABE.mpk}, \mathsf {ABE.msk}, x )\): The key generation algorithm takes as input the master public key \(\mathsf {ABE.mpk}\), the master secret key \(\mathsf {ABE.msk}\), and an attribute \(x \in \{0,1\}^\ell \) and proceeds as follows.
-
1.
Let \(x_1\cdots x_\ell \in \{0,1\}^\ell \) be the binary representation of \(x\in \{0,1\}^\ell \).
-
2.
Pick \(\gamma \leftarrow \mathbb {Z}_p\) and compute \([\gamma ]_T\).
-
3.
Sample \(\mathsf {IPFE.sk}_{i,x_i,j} \leftarrow \mathsf {IPFE.KeyGen}( \mathsf {IPFE.msk}_{i,x_i,j}, [(\gamma , 0)]_2 ) \) for all \(i\in [\ell ]\) and \(j\in [m]\).
-
4.
Output \(\mathsf {ABE.sk}= ( [\gamma ]_T, \{ \mathsf {IPFE.sk}_{i,x_i,j} \}_{ i\in [\ell ],j\in [m] } )\).
-
1.
-
\(\mathsf {ABE.Enc}(\mathsf {ABE.mpk}, C, \mathsf {\mu })\): The encryption algorithm takes as input the master public key \(\mathsf {ABE.mpk}\), a circuit C, and the message \(\mathsf {\mu }\) and proceeds as follows.
-
1.
Run \(\{\mathsf {share}_{i,b}\}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \mathsf {\mu })\).
-
2.
Parse each \(\mathsf {share}_{i,b}\) as \(\mathsf {share}_{i,b} = \{ \mathsf {share}_{i,b,j} \in \mathbb {Z}_p \}_{j \in [m]}\).
-
3.
Run \(\mathsf {IPFE.ct}_{i,b,j}\leftarrow \mathsf {IPFE.SlotEnc}( \mathsf {IPFE.mpk}_{i,b,j}, [\mathsf {share}_{i,b,j} ]_1 )\) for \(i \in [\ell ]\), \(b\in \{0,1\}\), \(j \in [m]\).
-
4.
Output \(\mathsf {ABE.ct}= \{ \mathsf {IPFE.ct}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} \).
-
1.
-
\(\mathsf {ABE.Dec}(\mathsf {ABE.mpk}, \mathsf {ABE.sk}, x, \mathsf {ABE.ct}, C )\): The decryption algorithm takes as input the master public key \(\mathsf {ABE.mpk}\), the secret key \(\mathsf {ABE.sk}\) along with x, the ciphertext \(\mathsf {ABE.ct}\) along with C and does the following:
-
1.
Parse the ciphertext as \(\mathsf {ABE.ct}\rightarrow \{ \mathsf {IPFE.ct}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} \) and the secret key as \(\mathsf {ABE.sk}\rightarrow ( [\gamma ]_T, \{ \mathsf {IPFE.sk}_{i,x_i,j} \}_{ i\in [\ell ],j\in [m] } ) \).
-
2.
Run \(\mathsf {IPFE.Dec}( \mathsf {IPFE.sk}_{i,x_i,j}, \mathsf {IPFE.ct}_{i,x_i,j} ) \rightarrow [d_{i,j}]_T \) for \(i\in [\ell ]\) and \(j\in [m]\).
-
3.
Run \(\mathsf {SS.FindCoef}(\mathsf {pp}, C, x ) \rightarrow \{ a_{i,j} \in \mathbb {Z}_p \}_{i\in [\ell ], j\in [m] }\).
-
4.
Compute \( [d']_T = [ \sum _{ i\in [\ell ], j\in [m] } a_{i,j}d_{i,j} ]_T \) from \(\{ [d_{i,j}]_T \}_{i,j}\) and \(\{ a_{i,j} \}_{i,j}\).
-
5.
Find \(e\in [-B,B]\) and \(\mathsf {\mu }\in \{0,1\}\) such that \([d']_T = [ \gamma ( \mathsf {\mu }\lceil p/2 \rceil + e ) ]_T\) by Brute-force search using \([\gamma ]_T\). If such a pair does not exist, output \(\bot \). Otherwise, output \(\mathsf {\mu }\).
-
1.
Correctness. To show correctness of the scheme, we first observe that \(d_{i,j}= \gamma \cdot \mathsf {share}_{i,x_i,j}\) by the correctness of \(\mathsf {IPFE}\). We then observe that \(d' = \sum _{ i\in [\ell ], j\in [m] } \gamma a_{i,j}\mathsf {share}_{i,x_i,j} = \gamma ( \mathsf {\mu }\cdot \lceil p/2 \rceil + e ) \) for some \(e\in [-B,B]\) by the almost linear reconstruction property (Definition 3.4) of \({\mathsf {ABE}}\). Since B is polynomially bounded by Theorem 3.5, the last step in the decryption algorithm works in polynomial time and recovers the message \(\mathsf {\mu }\).
Efficiency. The master public key of the ABE consists of \(O(\ell m)\) master public keys of the IPFE and the public parameter \(\mathsf {pp}\) of the secret sharing scheme. The ciphertext and secret key of the ABE contain \(O(\ell m)\) ciphertexts and secret keys of the IPFE, respectively. By the efficiency of the secret sharing scheme, m and the size of \(\mathsf {pp}\) are bounded by \({{\,\mathrm{poly}\,}}(\lambda )\). Furthermore, each instance of IPFE only deals with constant dimension of vectors, which means that sizes of all the parameters of each instance of the IPFE scheme are bounded by \({{\,\mathrm{poly}\,}}(\lambda )\). Therefore, we can see that sizes of all the parameters in the ABE scheme are bounded by \({{\,\mathrm{poly}\,}}(\lambda ,\ell )\).
5.2 Security Proof
Here, we prove the security of our ABE scheme in Sect. 5.1. Before doing so, we prove the following lemma.
Lemma 5.1
Let \(C \in \mathcal{C}_{\lambda , \ell (\lambda ), d(\lambda )}\) be a circuit and \(X \subseteq \{0,1\}^{\ell (\lambda )} \) be a set of strings that satisfies \(C(x)=0\) for all \(x \in X\), and \(\mathsf {SS} = (\mathsf {SS.Setup}, \mathsf {SS.Share}, \mathsf {SS.Recon})\) be a secure secret sharing scheme for this circuit class as per Definition 3.2. Then, for any efficient adversary \(\mathcal {A}= \{ \mathcal {A}_\lambda \}\), we have
under the bilinear KOALA assumption, where the probabilities are taken over the choice of \(\mathbb {G}= (p, \mathbb {G}_1,\mathbb {G}_2,\mathbb {G}_T, e, [1]_1, [1]_2) \leftarrow \mathsf {GroupGen}(1^\lambda )\), \(\gamma ^{(x)} \leftarrow \mathbb {Z}_p\) and \(\mathbf {w}^{(x)}_i \leftarrow \mathbb {Z}_p^m\) for \(x\in X\), \(\mathsf {pp}\leftarrow \mathsf {SS.Setup}(1^\lambda , p)\), and \( \{ \mathsf {share}_{i,b} \}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \mathsf {\mu })\).
Proof
To prove the theorem, we set \(\mathsf {Samp}\) to be an algorithm that takes as input an integer p and a random string \(\mathsf {aux}\), sets \(\mathsf {pp}:= \mathsf {aux}\), runs \( \{ \mathsf {share}_{i,b} \}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \mathsf {\mu })\), and outputs
Then, we argue that \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {single}}_{\mathcal {A},\mathbb {G},\mathsf {Samp}, i }( \lambda )\) defined in Eq. (4.1) is negligible for any i and any efficient adversary \(\mathcal {A}\). To show this, we first fix i and \(\mathcal {A}\) and observe that the quantity is negligible if we replace \(\mathsf {aux}\) that is input to \(\mathcal {A}\) with \(\mathsf {pp}\) output by \(\mathsf {SS.Setup}(1^\lambda , p)\), which follows from the security of \(\mathsf {SS}\) (Definition 3.2) and from the fact that \(C(x)=0\) holds for all \(x\in X\). We then observe that the adversary will not notice even if we replace \(\mathsf {pp}\) with \(\mathsf {aux}\) since the distributions of them are statistically close by the random public parameter property (Definition 3.3) of \(\mathsf {SS}\). We therefore have \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {single}}_{\mathcal {A},\mathbb {G},\mathsf {Samp}, i }( \lambda ) = {{\,\mathrm{negl}\,}}(\lambda )\). This implies that \(\mathsf {Adv}^\mathsf{{wKOALA},\mathsf {multi}}_{\mathcal {B},\mathbb {G},\mathsf {Samp}}( \lambda )\) defined in Eq. (4.2) is negligible for any efficient adversary \(\mathcal {B}\) by \(\mathsf {wKOALA}\), which is implied by the bilinear KOALA assumption. Finally, by replacing \(\mathsf {aux}\) with \(\mathsf {pp}\) output by \(\mathsf {SS.Setup}(1^\lambda , p)\) in Eq. (4.2), we have that Eq. (5.1) is negligible for any efficient adversary as desired.
The next theorem establishes the security of our ABE scheme.
Theorem 5.2
Our ABE scheme satisfies very selective security under the MDDH assumption, the bilinear KOALA assumption, and the LWE assumption.
Proof
To prove the theorem, we fix a PPT adversary \(\AA = \{ \mathcal {A}_\lambda \}\). Without loss of generality, we make some simplifying assumptions on \(\mathcal {A}\). First, we assume that \(\mathcal {A}\) always chooses \((\mu _0,\mu _1)=(0,1)\) as its target message at the challenge phase. This can be assumed without loss of generality since our scheme is a single-bit scheme. Second, we assume that the adversary does not make key queries for the same attribute x twice. The adversary that makes key queries for the same attribute more than once can be dealt with by making the key generation algorithm deterministic by changing the scheme so that it derives randomness using a PRF, which can be instantiated from any one-way functions. Third, we assume that the adversary chooses fixed challenge attribute \(C= \{ C_\lambda \}\) and key queries \(X= \{ X_\lambda \}\). This can be assumed without loss of generality because they are chosen by the adversary at the beginning of the game only depending on the security parameter and we can derandomize \(\mathcal {A}\) by choosing the best randomness that maximizes the advantage of \(\mathcal {A}\).
In order to prove the security, we consider following sequence of games. Let us denote the event that \(\mathcal {A}\) outputs correct guess for b at the end of \(\mathbf {Game}_\mathrm{x}\) as \(\mathsf {E}_\mathrm{x}\).
-
\(\mathbf {Game}_1\): This is the real very selective security game. To fix the notation and for the sake of concreteness, we briefly describe the game here. At the beginning of the game, the adversary chooses C and \(X\subseteq \{0,1\}^\ell \). Then, the challenger first chooses the master public key \(\mathsf {ABE.mpk}\) and the master secret key \(\mathsf {ABE.msk}\) of the ABE scheme. It then generates the challenge ciphertext as follows. It first chooses the message \(\beta \leftarrow \{0,1\}\) and runs \(\{\mathsf {share}_{i,b}\}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \beta )\). It then runs
$$ \mathsf {IPFE.ct}_{i,b,j}\leftarrow \mathsf {IPFE.SlotEnc}( \mathsf {IPFE.mpk}_{i,b,j}, [\mathsf {share}_{i,b,j} ]_1 ) $$for \(i \in [\ell ]\), \(b\in \{0,1\}\), \(j \in [m]\) and sets the challenge ciphertext to be \(\mathsf {ABE.ct}= \{ \mathsf {IPFE.ct}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} \). It also generates secret key \(\mathsf {ABE.sk}_x\) for all \(x\in X\) as follows. It first generates \(\gamma ^{(x)} \leftarrow \mathbb {Z}_p\) and
$$\begin{aligned} \mathsf {IPFE.sk}_{i,x_i,j} \leftarrow \mathsf {IPFE.KeyGen}( \mathsf {IPFE.msk}_{i,x_i,j}, [(\gamma ^{(x)}, 0)]_2 ) \end{aligned}$$for all \(i\,{\in }\, [\ell ]\) and \(j\,{\in }\, [m]\). It then sets \(\mathsf {ABE.sk}_x \,{=}\, ( [\gamma ]_T, \{ \mathsf {IPFE.sk}_{i,x_i,j} \}_{ i\in [\ell ],j\in [m] } )\). Finally, the challenger returns \(\mathsf {ABE.mpk}\), \(\mathsf {ABE.ct}\), and \(\{ \mathsf {ABE.sk}_x \}_{x\in X}\) to \(\mathcal {A}\), which then outputs a bit \(\widehat{\beta }\) as a guess for \(\beta \). By definition, the advantage of \(\mathcal {A}\) against the scheme is
$$ \left| \Pr [\mathsf {E}_1] - \frac{1}{2} \right| . $$ -
\(\mathbf {Game}_2\): In this game, we change the game so that the challenger generates the challenge ciphertext as follows. It first chooses the message \(\beta \leftarrow \{0,1\}\) and runs \(\{\mathsf {share}_{i,b}\}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \beta )\). It then generates
$$ \mathsf {IPFE.ct}_{i,b,j}\leftarrow \mathsf {IPFE.Enc}( \mathsf {IPFE.msk}_{i,b,j}, [(\mathsf {share}_{i,b,j},0)]_1 ) $$for \(i \in [\ell ]\), \(b\in \{0,1\}\), \(j \in [m]\) and sets the challenge ciphertext to be \(\mathsf {ABE.ct}= \{ \mathsf {IPFE.ct}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} \). By the slot-mode correctness of the IPFE, we have
$$ \Pr [\mathsf {E}_1] = \Pr [\mathsf {E}_2]. $$ -
\(\mathbf {Game}_3\): In this game, we change the way the challenge ciphertext and the secret keys are generated. In this game, the challenger generates the challenge ciphertext as follows. It first chooses the message \(\beta \leftarrow \{0,1\}\) and runs \(\{\mathsf {share}_{i,b}\}_{i\in [\ell ], b\in \{0,1\}} \leftarrow \mathsf {SS.Share}(\mathsf {pp}, C, \beta )\). However, it ignores theses values and generates
$$ \mathsf {IPFE.ct}_{i,b,j}\leftarrow \mathsf {IPFE.Enc}( \mathsf {IPFE.msk}_{i,b,j}, [(0,1)]_1 ) $$for \(i \in [\ell ]\), \(b\in \{0,1\}\), \(j \in [m]\) and sets the challenge ciphertext to be \(\mathsf {ABE.ct}= \{ \mathsf {IPFE.ct}_{i,b,j} \}_{i\in [\ell ], b\in \{0,1\}, j\in [m]} \). We also change the way the challenger generates the secret keys as follows. For \(x\in X\), it first generates \(\gamma ^{(x)} \leftarrow \mathbb {Z}_p\) and
$$\begin{aligned} \mathsf {IPFE.sk}_{i,x_i,j} \leftarrow \mathsf {IPFE.KeyGen}( \mathsf {IPFE.msk}_{i,x_i,j}, [(\gamma ^{(x)}, \gamma ^{(x)} \mathsf {share}_{i,x_i,j})]_2 ) \end{aligned}$$for all \(i\in [\ell ]\) and \(j\in [m]\), where we use \(\mathsf {share}_{i,x_i,j}\) that is generated when creating the challenge ciphertext. It then sets \(\mathsf {ABE.sk}_x = ( [\gamma ^{(x)}]_T, \{ \mathsf {IPFE.sk}_{i,x_i,j} \}_{ i\in [\ell ],j\in [m] } )\). We can observe that for each instance of IPFE, the inner products between the vector that is encoded in the ciphertext and the vectors encoded in the secret keys are unchanged. Furthermore, the values in the public slots of the vectors encoded in the secret keys are unchanged. Therefore, this game is indistinguishable from the previous game for \(\mathcal {A}\) by the security of the IPFE, which follows from the MDDH assumption. We therefore have
$$ \left| \Pr [\mathsf {E}_2] - \Pr [\mathsf {E}_3] \right| = {{\,\mathrm{negl}\,}}(\lambda ). $$ -
\(\mathbf {Game}_4\): In this game, we further change the way the secret keys are generated as follows. The challenger first generates \(\gamma ^{(x)} \leftarrow \mathbb {Z}_p\) and chooses \(\mathbf {w}_{i}^{(x)} \leftarrow \mathbb {Z}_p^m\) for \(i\in [\ell ]\). It then generates
$$\begin{aligned} \mathsf {IPFE.sk}_{i,x_i,j} \leftarrow \mathsf {IPFE.KeyGen}( \mathsf {IPFE.msk}_{i,x_i,j}, [(\gamma ^{(x)}, w_{i,j}^{(x)} )]_2 ) \end{aligned}$$for all \(i\in [\ell ]\) and \(j\in [m]\), where \(w^{(x)}_{i,j}\) is the j-th entry of the vector \(\mathbf {w}^{(x)}_i\), and sets \(\mathsf {ABE.sk}_x = ( [\gamma ]_T, \{ \mathsf {IPFE.sk}_{i,x_i,j} \}_{ i\in [\ell ],j\in [m] } )\). We claim that this game is indistinguishable from the above game. To see this, let us assume that \(\mathcal {A}\) distinguishes the games with non-negligible advantage for the sake of contradiction. Then, for \(C=\{ C_\lambda \}\) and \(X = \{ X_\lambda \}\) chosen by \(\mathcal {A}\), we can construct another adversary \(\mathcal {B}= \{ \mathcal {B}_\lambda \}\) that distinguishes two distributions in Eq. (5.1) with non-negligible advantage as follows. \(\mathcal {B}\) takes as input \(\mathbb {G}\), \(\mathsf {pp}\), \(\left\{ [\gamma ^{(x)}]_2, \{ [ \mathbf {w}^{(x)}_{i} ]_2 \}_{i\in [\ell ]} \right\} _{x\in X}\), where \(\mathbf {w}^{(x)}_{i}\) is either random or \(\mathbf {w}^{(x)}_i = \gamma ^{(x)}\mathsf {share}_{i,x_i}\). It chooses \((\mathsf {IPFE.mpk}_{i,b,j}, \mathsf {IPFE.msk}_{i,b,j}) \leftarrow \mathsf {IPFE.Setup}(1^\lambda , \{1\}, \{2\} )\) for all i, b, and j and sets the \(\mathsf {ABE.mpk}\) and \(\mathsf {ABE.msk}\) accordingly. It generates the challenge ciphertext using \(\mathsf {ABE.msk}\). It also generates a secret key for x using \([\gamma ^{(x)}]_2, \{ [\mathbf {w}^{(x)}_{i} ]_2 \}_{i\in [\ell ]}\) and \(\mathsf {ABE.msk}\). In particular, the syntax of the slotted IPFE allows us to generate the secret key for the vector \([(\gamma ^{(x)}, w^{(x)}_{i,j})]_2\) without knowing the corresponding discrete logarithm, which \(\mathcal {B}\) does not know. \(\mathcal {B}\) then inputs \(\mathsf {ABE.mpk}\), \(\mathsf {ABE.ct}\), and \(\{\mathsf {ABE.sk}_x\}\) to \(\mathcal {A}\) and outputs what \(\mathcal {A}\) outputs. Clearly, \(\mathcal {B}\) simulates \(\mathbf {Game}_3\) for \(\mathcal {A}\) if \(\mathbf {w}^{(x)}_i = \gamma ^{(x)}\mathsf {share}_{i,x_i}\) and \(\mathbf {Game}_4\) if \(\mathbf {w}^{(x)}_i\) is random. Thus, \(\mathcal {B}\) can distinguish the two distributions with the same advantage as \(\mathcal {A}\). This contradicts the bilinear KOALA assumption and the security of the secret sharing scheme by Lemma 5.1, where the latter follows from the LWE assumption by Theorem 3.5. Therefore, we have
$$ \left| \Pr [\mathsf {E}_3] - \Pr [\mathsf {E}_4] \right| = {{\,\mathrm{negl}\,}}(\lambda ). $$
We can easily observe that the view of \(\mathcal {A}\) in \(\mathbf {Game}_4\) is independent from \(\beta \) and \(\Pr [\mathsf {E}_4] = 1/2.\) Therefore, we have
as desired. This completes the proof of Theorem 5.2.
5.3 Implication to Broadcast Encryption
Here, we show that our CP-ABE scheme implies BE by restricting the circuit class of the scheme to be some specific one as was observed in [AY20, BV20]. Let us consider the following circuit class \(\mathcal{F}_{\mathsf {BE}}\):
Here, we identify a user index \(i\in [N]\) and elements in S with binary strings in \( \{0,1\}^{\lceil \log N \rceil }\) by a natural bijection map between \(\{0,1\}^{\lceil \log N \rceil }\) and \([ 2^{\lceil \log N \rceil } ] \supseteq [N]\). Since the depth of \(F_S\) affects the efficiency of the DBE scheme, we want \(F_S\) to be as shallow as possible. For this purpose, we compute \(F_S\) by first computing \(b_j := (i {\mathop {=}\limits ^{?}} j ) \) for all \(j\in S\) in parallel and then computing \(\vee _{j\in S} b_j \). The first step can be implemented with depth \(O(\log \log N)\) and the second step with \(O(\log N )\). This allows us to implement \(F_S\) with depth \(O(\log |S|) \le O(\log N)\). Therefore, our CP-ABE scheme indeed supports this circuit class. Furthermore, by the definition of \(F_S\), one can see that this CP-ABE scheme implements the functionality of BE. The obtained BE scheme has optimal efficiency in the sense that the size of the master public key, secret key, and the ciphertext is bounded by \({{\,\mathrm{poly}\,}}(\lambda , \ell , d) = {{\,\mathrm{poly}\,}}(\log N, \lambda ) = {{\,\mathrm{poly}\,}}(\lambda )\), which is independent of the number of users N in the system. The scheme satisfies very selective security since so is the underlying CP-ABE. We note that our scheme indeed satisfies selective security since very selective security is equivalent to selective security in the setting of BE (See Remark 2.7).
Notes
- 1.
In the technical sections we use \(\mathsf {IPFE}\) directly rather than first showing that it provides an \(\mathsf {FE}\) scheme with the above discrepancy between correctness and security and then relying on such an \(\mathsf {FE}\). This is purely to avoid proliferation of additional definitions/abstractions.
- 2.
Here, we follow the standard convention in lattice-based cryptography where the decryption succeeds when \(C(\mathbf {x})=0\) rather than \(C(\mathbf {x})=1\).
- 3.
In fact, the ABE ciphertext also has to include the LWE samples with respect to the matrix \(\mathbf {A}\) and the vector \(\mathbf {u}\), where the latter will be used to mask the message. These LWE samples are put into both of \(\mathsf {share}_{1,0}\) and \(\mathsf {share}_{1,1}\).
References
Abdalla, M., Bourse, F., De Caro, A., Pointcheval, D.: Simple functional encryption schemes for inner products. Cryptology ePrint Archive, Report 2015/017 (2015). http://eprint.iacr.org/. To appear in PKC 2015
Attrapadung, N., Libert, B.: Functional encryption for inner product: achieving constant-size ciphertexts with adaptive security or support for negation. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 384–402. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_23
Agrawal, S., Libert, B., Stehle, D.: Fully secure functional encryption for linear functions from standard assumptions, and applications. In: Crypto (2016)
Agrawal, S., Yamada, S.: Optimal broadcast encryption from pairings and LWE. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part I. LNCS, vol. 12105, pp. 13–43. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45721-1_2
Bitansky, N., Canetti, R.: On strong simulation and composable point obfuscation. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 520–537. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_28
Baltico, C.E.Z., Catalano, D., Fiore, D., Gay, R.: Practical functional encryption for quadratic functions with applications to predicate encryption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 67–98. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_3
Barthe, G., Fagerholm, E., Fiore, D., Mitchell, J., Scedrov, A., Schmidt, B.: Automated analysis of cryptographic assumptions in generic group models. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 95–112. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_6
Boneh, D., et al.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Gentry, C., Waters, B.: Collusion resistant broadcast encryption with short ciphertexts and private keys. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 258–275. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_16
Brakerski, Z., Vaikuntanathan, V.: Lattice-inspired broadcast encryption and succinct ciphertext-policy ABE. IACR Cryptol. ePrint Arch. 2020: 191 (2020)
Lin, H., Luo, J.: Compact adaptively secure ABE from k-Lin: beyond NC1 and towards NL. In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020, Part III. LNCS, vol. 12107, pp. 247–277. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_9
Boneh, D., Waters, B., Zhandry, M.: Low overhead broadcast encryption from multilinear maps. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 206–223. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_12
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. Algorithmica 79(4), 1233–1285 (2017)
Canetti, R., Dakdouk, R.R.: Obfuscating point functions with multibit output. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 489–508. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_28
Canetti, R., Rothblum, G.N., Varia, M.: Obfuscation of hyperplane membership. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 72–89. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_5
Delerablée, C.: Identity-based broadcast encryption with constant size ciphertexts and private keys. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 200–215. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_12
Delerablée, C., Paillier, P., Pointcheval, D.: Fully collusion secure dynamic broadcast encryption with constant-size ciphertexts or decryption keys. In: Takagi, T., Okamoto, E., Okamoto, T., Okamoto, T. (eds.) Pairing 2007. LNCS, vol. 4575, pp. 39–59. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73489-5_4
Fuchsbauer, G., Kiltz, E., Loss, J.: The algebraic group model and its applications. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 33–62. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_2
Fiat, A., Naor, M.: Broadcast encryption. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 480–491. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_40
Garg, S., Gentry, C., Halevi, S., Wichs, D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 518–535. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_29
Gentry, C., Peikert, C., Vaikuntanathan, V.: Trapdoors for hard lattices and new cryptographic constructions. In: STOC, pp. 197–206 (2008)
Gorbunov, S., Vinayagamurthy, D.: Riding on asymmetry: efficient ABE for branching programs. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 550–574. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48797-6_23
Gentry, C., Waters, B.: Adaptive security in broadcast encryption systems (with short ciphertexts). In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 171–188. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01001-9_10
He, K., Weng, J., Liu, J.-N., Liu, J.K., Liu, W., Deng, R.H.: Anonymous identity-based broadcast encryption with chosen-ciphertext security. In: Proceedings of the 11th ACM on Asia Conference on Computer and Communications Security, ASIA CCS 2016 (2016)
Ishai, Y., Pandey, O., Sahai, A.: Public-coin differing-inputs obfuscation and its applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 668–697. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_26
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Lin, H., Luo, J.: Compact adaptively secure ABE from \(k\)-Lin: beyond \(\sf {NC}^{\sf 1}\) and towards \(\sf {NL}\). In: Canteaut, A., Ishai, Y. (eds.) EUROCRYPT 2020. LNCS, vol. 12107, pp. 247–277. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-45727-3_9
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: FOCS (2016)
Maurer, U.: Abstract models of computation in cryptography. In: Smart, N.P. (ed.) Cryptography and Coding 2005. LNCS, vol. 3796, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/11586821_1
Quach, W., Wee, H., Wichs, D.: Laconic function evaluation and applications. In: 2018 IEEE 59th Annual Symposium on Foundations of Computer Science (FOCS), pp. 859–870. IEEE (2018)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 1–40 (2009). Extended abstract in STOC 2005
Sakai, R., Furukawa, J.: Identity-based broadcast encryption. IACR Cryptology ePrint Archive (2007)
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Sahai, A., Seyalioglu, H.: Worry-free encryption: Functional encryption with public keys. In: Proceedings of the 17th ACM Conference on Computer and Communications Security, CCS 2010 (2010)
Wee, H.: Attribute-hiding predicate encryption in bilinear groups, revisited. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 206–233. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_8
Acknowledgement
We thank the anonymous reviewers of TCC 2020 for their helpful comments. Dr. Agrawal is supported by the DST “Swarnajayanti” fellowship, an Indo-French CEFIPRA project and an “Indo-Israel” ISF-UGC project. Daniel Wichs is supported by NSF grants CNS-1314722, CNS-1413964, CNS-1750795, and the Alfred P. Sloan Research Fellowship. Shota Yamada is supported by JST CREST Grant Number JPMJCR19F6 and JSPS KAKENHI Grant Number 19H01109. This work was done in part while the first and the third authors were visiting the Simons Institute for the Theory of Computing.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Agrawal, S., Wichs, D., Yamada, S. (2020). Optimal Broadcast Encryption from LWE and Pairings in the Standard Model. In: Pass, R., Pietrzak, K. (eds) Theory of Cryptography. TCC 2020. Lecture Notes in Computer Science(), vol 12550. Springer, Cham. https://doi.org/10.1007/978-3-030-64375-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-64375-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64374-4
Online ISBN: 978-3-030-64375-1
eBook Packages: Computer ScienceComputer Science (R0)



 to
to  .
. : In each round,
: In each round,  has 2 options:
has 2 options: outputs its guess
outputs its guess  .
. : The setup algorithm takes as input the unary representation of the security parameter
: The setup algorithm takes as input the unary representation of the security parameter  and a master secret key
and a master secret key  .
. : The encryption algorithm takes as input a master public key
: The encryption algorithm takes as input a master public key  , a ciphertext attribute
, a ciphertext attribute  , and a message bit
, and a message bit  . It outputs a ciphertext
. It outputs a ciphertext  : The key generation algorithm takes as input the master public key
: The key generation algorithm takes as input the master public key  , the master secret key
, the master secret key  , and a key attribute
, and a key attribute  : The decryption algorithm takes as input the master public key
: The decryption algorithm takes as input the master public key  , a ciphertext
, a ciphertext  or
or  which represents that the ciphertext is not in a valid form.
which represents that the ciphertext is not in a valid form.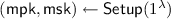 and gives
and gives  to
to  .
. adaptively makes the following queries, in an arbitrary order.
adaptively makes the following queries, in an arbitrary order.  can make unbounded many key queries, but can make only single challenge query.
can make unbounded many key queries, but can make only single challenge query. holds for any Y such that
holds for any Y such that  outputs a guess bit
outputs a guess bit  as the output of the experiment.
as the output of the experiment.