Keywords

1 Introduction

Linear algebra problems, such as solving a linear system of equations, are the backbone of modern scientific computing and data-intensive tasks. Among these, machine learning is currently the discipline with most effort of study from scientists and engineers, to unleash the full power of computational algorithms with applications to any aspect of our life. These powerful algorithms, such as linear and logistic regression, are usually executed in conventional digital hardware by combining sequences of boolean functions on binary data. Thus, computing complicated operations requires a large memory and many computing steps. These problems are encoded in matrix form and executed by iteratively performing matrix-vector multiplications [7, 36], resulting in a polynomial computational time complexity, for example \(O(N^3)\) where N is the size of the problem. In this chapter, novel analog circuits for the solution of matrix equations in one step will be presented. Thanks to the in-memory computing framework, the problem implementation does not require data transfer between memory and processing unit, resulting in unprecedented speed. With nanoscale crosspoint resistive memories, the novel circuit requires also less area compared to traditional technology. The results pave the way for the development of memory computing unit to overcome the limitation of current accelerators.

Fig. 6.1
figure 1

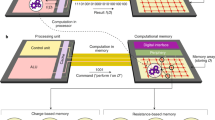
a Comparison between the exponential growth of Moore’s Law (red) and the required performance for executing modern artificial intelligence (AI) algorithms (blue), b conventional von-Neumann architecture suffering from a bottleneck when transferring data between memory and processing unit and c in-memory computing concept

Full size image

2 In Memory Computing

Technology scaling has been driven by Moore’s law [21] in the last decades, predicting that the number of transistors per \(mm^2\) of an integrated circuit doubles every 18 months. Figure 6.1a depicts in red the exponential growth fitted from real data of different technology node of the last 25 years and the confirmed prediction from the future releases [28]. It is already possible to see a deviation from the ideal exponential scaling, as the some technologies will see the market with significant delay. Moore’s law is in fact slowing down, due to physical limits of devices scaling and increased cost manufacturing [28]. It has also been observed [13] that the energy dissipated by transistors has decreased exponentially with the technology node until the late 80’s. However, by now this energy should have reached the thermal fluctuation kT, known as Landauer limit [13], which is impossible with modern Complementary-Metal-Oxide-Semiconductor (CMOS) technologies. Even future predictions are far away from the Landauer limit. It is thus evident that new computing technologies need to be developed to keep the pace with Moore’s Law and reduce the energy dissipation. Among this, novel memory devices have attracted research interest also from the computing community [39], in fact they have been demonstrated able of performing traditional computing tasks such as boolean function [31].

However Moore’s law speed is not enough. Figure 6.1a shows a comparison of Moore’s law (in red) with the performance required for executing state of the art algorithms (in blue) developed across the last years [3]. It is possible to see that with an exponential growth of the number of floating point operations per second (FLOP/s) that doubles every 3.4 months, the required resources scaling outperforms Moore’s Law. This suggest that not only new materials and devices are needed to fulfill Moore’s law requirements, but a shift of paradigm in architecture is needed to outperform traditional computing systems. Figure 6.1b shows the conventional von-Neumann architecture [22], where the processing unit (blue) is responsible only for executing operations whereas the memory unit (red) is responsible for storing them. Most of nowadays computers are based on this architecture, where one or multiple types of memory store the data with the central processing units (CPU) or graphic processing units (GPU) performing computation. When a lot of data need to be analyzed this architecture exposes a bottleneck in computation, known as von-Neumann bottleneck [19], due to the time and energy spent for handling data travelling from memory to processor and back. A new computing architecture that avoids the bottleneck is then desired.

In-memory computing with novel resistive memories [10, 11] has been proposed as a solution to overcome the limitation of both Moore’s law speed and von Neumann bottleneck. The idea is to harness intrinsic materials properties of such memories to create new computing paradigms based on physical laws and known as physical computing [11, 44]. By organizing memories in crosspoint arrays it is possible then to have a compact accelerator known as memory processing unit (MPU) [44], which does not require data transfer and can perform computations within the memory. Figure 6.1c shows a conceptual representation of a MPU architecture, with many memory cores interconnected with each other. The novel computing unit have been shown to have unprecedented speed up compared with traditional and specific circuit for acceleration [25].

Fig. 6.2
figure 2

Adapted from [33]

a Resistive Random Access Memory (RRAM) I-V characteristics. By applying a positive voltage it is possible to set the memory device into a low resistance state (LRS) whose conductance is controlled by the maximum compliance current \(I_C\) flowing during the set operation, while by applying a negative voltage it is possible to reset the device into a high resistance state (HRS) whose depth is controlled by the maximum applied negative voltage. Inset shows the fabricated Ti-HfO\(_x\)-C RRAM device. b Different conductance achieved by modulating \(I_C\) during the set operation. c Crosspoint memory architecture for multiply-accumulate operation. RRAM devices are organized in an array representing an analog matrix A, by applying a voltage vector V on the columns, the current vector I at the rows is the matrix-vector multiplication result \(I=GV\). Inset represent a measured programmed matrix A. d Measured (circles) and calculated (lines) currents vector I as function of the parameter \(\alpha \) controlling the applied voltage vector \(V=\alpha [0.2,0.3,0.4]\) with \(-1\le \alpha \le 1\).

Full size image

3 In-Memory Matrix-Vector-Multiplication Accelerator

Emerging memory devices, commonly referred as memristors, have recently attracted interest for their application both as memory and computing elements. Among these, resistive random access memories (RRAM) are a promising candidate for computing, due to their low energy operation, high endurance, small area and cost-effective fabrication [9]. Figure 6.2a shows a typical current-voltage characteristic of a RRAM device which is depicted in the inset and made of a Ti top electrode (TE) deposited on a HfO\(_x\) layer and a C bottom electrode (BE) [2]. After a forming process it is possible to change and modulate the conductance of the device. A positive pulse applied from the TE to the BE will result in a filament growth from TE to BE, or set transition, bringing the device into a low resistance state (LRS). By fixing the maximum current flowing to the RRAM during the set transition, namely compliance current (\(I_C\)), it is possible to avoid hard breaks of the device oxide and modulate the LRS conductance. \(I_C\) can be fixed by an external circuit, such a Source Measurement Unit (SMU), or with a transistor connected with the drain at the BE, that can also be used as selector device in an array configuration. By applying a negative pulse the RRAM undergoes a reset, resulting in the filament rupture and a gap formation in the conductive path, thus an high resistance state (HRS). The gap width can be controlled by the maximum applied negative voltage during reset and can be used as well to modulate the conductance. Figure 6.2b shows different measured conductance states demonstrating the possibility of analog programming of the RRAM device. Given the possibility of representing in principle any given number, applications in analog operation acceleration with RRAM devices have rapidly arisen. Different architectures have been presented to accelerate analog problems such as crosspoint arrays [40] and content addressable memories [17]. Figure 6.2c shows a crosspoint array implementation where memristive devices are arranged in a matrix form to directly write an algebraic matrix of real positive numbers G into the RRAM conductance. By applying a input voltage vector V on the crosspoint columns, the current flowing through the crosspoint rows is \(I=GV\) or the dot product of matrix G by vector V. In this way, it is possible to accelerate dot product, also referred as matrix-vector-multiplication (MVM), in one step [10, 11]. Memristive crosspoint has been shown able to accelerate different problems based on MVM, such as the training [16, 27, 38] and inference [20, 41] of neural networks, image processing [18], sparse coding [29], optimization problems [6, 24] and the solution of linear equations through iterative numerical approaches [14, 43]. Integrated circuits comprising memristive arrays and the circuitry need to generate the input, such as digital-analog-converters (DAC), sense and read the outputs, such as transimpedance amplifiers (TIA) and analog-digital-converters (ADC), and cell selecting and routing, able to accelerate MVM have been proposed [5, 37, 42], outperforming modern processor both in throughput and energy saving [42].

4 One Step in-Memory Solution of Inverse Algebraic Problems

Crosspoint arrays offer the analog capability of writing arbitrary positive real matrixes coefficients, however iterative operations are usually performed in conventional digital hardware [6, 43]. To harness the full potential of the analog approach, iterations can be performed in the analog domain through feedback connected operational amplifiers [23, 33, 34]. By properly programming the conductance matrix and connecting the feedback amplifiers, one can solve different inverse problems such as linear systems [33], eigenvectors calculation and pageranking[32], linear and logistic regressions [34].

Fig. 6.3
figure 3

Adapted from [33]

a Circuit for solving a linear system in one step comprising a cross-point array of RRAM devices (red cylinders) programmed with the conductance matrix A (inset), connected with the rows (blue bars) at the negative input of operational amplifiers. By injecting a current I through the rows, the columns (green lines) connected to the operational amplifier outputs will stabilized to a voltage vector \(V = A^{-1}I\) which is the solution of a linear system. b Measurements of output voltages (circles) and analytical (lines) solution of the linear systems \(AV=I\) with \(I=\beta [0.2;1;1]\) and \(-1\le \beta \le 1\) as function of the controlling parameter \(\beta \). The comparison of the measured voltages with the analytical solution support the accuracy of the system. c Hardware implementation of the circuit for solving linear systems with HfO\(_x\) devices arranged on a printed circuit board with commercial operational amplifiers controlled with an external arbitrary waveform generator. d 1-dimensional Fourier equation encoded with 21 points in a \(21\times 21\) conductance matrix. e Output voltages V (circle) simulated with SPICE for a larger circuit showing the solution of the 1-D Fourier heat equation confirming a good agreement with the analytical result (lines).

Full size image

4.1 In-Memory Solution of Linear Systems in One-Step

Operational amplifiers in negative feedback configuration offer analog implementation of loops. Solving a system of linear equation is the equivalent matrix operation of performing a division between two scalars. This is the role of a TIA, an operational amplifier with a feedback resistance R connected between the negative input and the output. Grounding the positive input and injecting a current I on the negative input, the output voltage will adjust on \(V=IR\) or \(V=I/G\) with \(G=1/R\) conductance of the resistance R. This is due to the negative feedback effect and the nature of the operational amplifier that has a very large input impedance. By considering a matrix version of this circuit, it is then possible to calculate the solution of a linear system encoded in a matrix of conductance G, which is connected in feedback with operational amplifiers [33]. Figure 6.3a shows the circuit schematic for a 3 equations linear system. The system coefficients are encoded in the conductance matrix A (Fig. 6.3a inset) measured on 9 HfO\(_x\) RRAM devices arranged in crosspoint configuration. The crosspoint rows are connected to the negative input of the operational amplifiers, the columns to the output of the operational amplifiers while the positive input of the operational amplifiers is kept connected to ground. By injecting a current I on the rows representing the known vector of the linear system the output voltage vector will be the solution of the linear system \(V=A^{-1}I\), which is computed in one step without digital iteration [33]. Figure 6.3b demonstrate the concept showing the measured voltage V and the analytical solution of the linear system \(AV=I\) with \(I=\beta [0.2;1;1]\) as function of the controlling parameter \(\beta \), indicating a good agreement between electrical measurements and analytical result. The measurements were performed on a printed circuit board (PCB) with Ti/Hf\(O_x\)/C RRAM devices [2] arranged on a crosspoint configuration and connected in feedback with commercial operational amplifiers (Fig. 6.3c). The known vector is given as voltage with an arbitrary waveform generator and then converted to current with input resistance connected to the negative input of the operational amplifiers. The output voltage is monitored with an external oscilloscope. To represent both positive and negative coefficients of the linear system, it is possible to use two separated crosspoint that represent the matrixes B and C, with \(A = B - C\). By connecting matrix B to the circuit of Fig. 6.3a, the output voltage to the matrix C through negative buffers and feeding both matrix B and matrix C with the same input current representing the known vector, one can solve an arbitrary linear system \((B-C)V=AV=I\) where A has both positive, negative and zero coefficients [33]. As an example, this circuit can be used to solve differential equations such as the Fourier heat equation [33]. Figure 6.3d shows a 1-D Fourier heat equation encoded in its \(21\times 21\) discretized matrix form, that can directly be mapped in a crosspoint array and be solved in one step. Figure 6.3e shows the output voltage vector V simulated with in SPICE representing the solution of the problem in Fig. 6.3d for different starting temperature compared with the analytical results and as function of the distance.

The results shows a good match supporting the use of the circuit for solving large systems of equations. In fact, interestingly the solution time does not depends on the matrix, thus linear system, dimension [35]. One can think about the operational amplifier in negative feedback configuration, where the bandwidth is limited by the loop gain and equal to \(f_{max}=GBWP\cdot \frac{R_{in}}{R_{in}+R_f}\) where GBWP is the gain bandwidth product of the operational amplifiers, \(R_{in}\) the input resistance and \(R_f\) the feedback resistance. By considering a feedback matrix, it is possible to demonstrate that the settling time, thus the bandwidth, is solely limited by the minimal eigenvalue of the matrix [35] and not by its size making the time complexity O(1). This is an unprecedented speedup compared with conventional conjugate gradient solvers [30], where time complexity is O(N) at its best and quantum computing [8], where the best time complexity is O(log(N)) where N is the size (i.e. the number of equations) in the linear system. The result supports the use of the circuit for solving systems of linear equations in one step, outperforming digital and quantum computers.

Fig. 6.4
figure 4

Adapted from [33]

a Circuit for solving the eigenvector equation \(Ax=\lambda x\), where x is the eigenvector and \(\lambda \) the maximum positive eigenvalue. With an input current \(I=0\), the operational amplifier corresponding to the maximum value of the eigenvector x saturates. By normalizing the output voltages, the eigenvector is found. Inset shows a \(3\times 3\) matrix encoded in RRAM conductance. b Experimental solution of the eigenvector corresponding to the highest positive (red) and lowest negative (blue) eigenvalue, as function of the analytical solution. The eigenvalues are encoded in the feedback conductance \(G_{\lambda }\). c Illustration of Pagerank algorithm, web pages are represented by green circles and the corresponding citation with blue arrows. d Stochastic link matrix corresponding to the problem in (c), which is calculated by normalizing the boolean link matrix by the sum over each column. e Simulation (circles) results of Pagerank problem in (c) as function of the ideal ranking.

Full size image

4.2 In-Memory Eigenvectors Calculation in One-Step

Many scientific and machine learning problems, such as the solution of differential equations, require not the simple solution of a linear system, but the eigenvector computation. Mathematically speaking, this means to solve the equation \(Ax=\lambda x\), which can be arranged such as \((A-\lambda I)x=0\). It is possible to observe that by encoding on a crosspoint the matrix A and on a second crosspoint the diagonal matrix \(\lambda I\), with the mixed matrix configuration it is possible to compute the eigenvectors with the feedback circuit of Sect. 6.4.1 [32, 33]. Figure 6.4a shows a compact circuit schematic for calculating the eigenvector solution where the diagonal matrix is represented with feedback conductance \(G_{\lambda }\). To guarantee the stability of the circuit, only the eigenvectors corresponding to highest positive and lower negative eigenvalue can be computed. In fact the circuit works at the boundary of stability with a loop gain \(G_{Loop}=1\). Without any input current the opamp corresponding to the maximum value of the eigenvector saturates while the others adjust resulting in an output voltage vector V, which normalized by the supply voltage, it is equal to the normalized eigenvector x corresponding to the non-trivial solution of \((A-\lambda I)x=0\). Figure 6.4a-inset shows a programmed conductance matrix A and Fig. 6.4b the measured eigenvectors calculation corresponding to the highest positive (red) and lowest negative (blue) eigenvalue as function of the analytical solution, showing a good agreement. It has to be noted that to compute the eigenvector corresponding to the negative eigenvalue the analog inverter of Fig. 6.4 should be removed with the output voltages of the operational amplifiers directly connected to the crosspoint array A. Unfortunately, in any case the highest eigenvalue \(\lambda _1\) must be known. To do that it is possible to apply iterative solution such as power iteration, or a sweep the conductance \(G_{\lambda }\) until one of the operational amplifier saturates. However, for some applications such as Pagerank the algorithm at the backbone of Google search engine [4], the maximum eigenvalue is always known a priori. Figure 6.4c shows an illustration of a web pages network with pages represented with green circles and citation represented by blue arrows. Goal of pageranking is to give a score to every webpage corresponding to its authority, namely how many citation receives from other pages with high authority. To do that it is possible to compute the eigenvector corresponding to the maximum eigenvalue of a stochastic matrix, namely the boolean link matrix between webpages normalized by the sum over each column [32, 33]. Interestingly, the maximum eigenvalue of such matrix is always known and \(\lambda _1=1\), making the system highly feasible for giving such solution. Figure 6.4d shows the stochastic matrix corresponding to the network in Fig. 6.4c, whose SPICE simulated eigenvector solution is plotted in Fig. 6.4e as function of the ideal solution showing good agreement. The circuit was also simulated with measured RRAM conductance tuned with a program and verify algorithm showing good agreement with the Hardvard500 dataset results [32]. As the circuit in Sect. 6.4.1, the circuit for eigenvector computation shows a constant time complexity O(1) [32], making it aggressively interesting for machine learning and scientific applications compared with other computing technologies.

4.3 In-Memory Regression and Classification in One-Step

Many computing problems have more unknowns than equations or more equations than unknowns. The latter is the case of regression problem, which is a fundamental machine learning model for predicting a certain data behavior or classify its class. Linear and logistic regression are among the most used ML algorithms [1]. A linear regression problem can be described with the overdetermined linear system \(Xw=y\), where X is a \(N\times M\) matrix with \(N>M\), y is known vector of size \(N\times 1\) and w is the unknown weight vector of size \(M\times 1\). There is no exact solution to this problem, but the best solution can be calculated with the least squares error approach, that minimizes \(||\epsilon ||=||Xw-y||_2\) which is the euclidean norm of the error. This can be done through the Moore-Penrose pseudoinverse [26] solving the equation

$$\begin{aligned} w = (X^TX)^{-1}X^Ty. \end{aligned}$$
(6.1)

To calculate w is one step, it is possible to cascade multiple analog stages representing all the parts of the equation. Figure 6.5a shows a schematic of the realized circuit for calculating linear regression weights in one step [34]. The conductance matrix X encodes the explanatory variables while the dependent variables are injected as current I. The output voltage of the rows amplifier will then adjust on \(V_{row}=(VX+I)/G_{TI}\), thanks to the transimpedance configuration. Being the columns of the right crosspoint array connected to the input of the columns operational amplifier the current should be equal to zero, such as

$$\begin{aligned} \frac{(VX+I)}{G_{TI}}X^T=0. \end{aligned}$$
(6.2)
Fig. 6.5
figure 5

Adapted from [34]

a Circuit for calculating regressions operation trough the Moore-Penrose pseudo inverse. Inset shows a programmed linear regression problem. b Experimental results and analytical calculation of the linear regression of 6 data points. c Neural network topology implemented for the weights optimization in one step. d Simulated weights as function of the analytical weights for the training of the neural network classification layer.

Full size image

By rearranging equation (6.2), it is possible to observe that the weights of equation (6.1) are obtained in one step, without iterations as voltage V [34]. The inset of Fig. 6.5a shows a programmed conductance matrix on HfO\(_x\) arranged in a double array configuration and representing the linear regression problem of Fig. 6.5b, which shows a comparison of the experimental linear regression and the analytical one, evidencing a good agreement. Interestingly, with the same circuit is also possible to compute logistic regression in one step, thus classify data. By encoding in the conductance matrix the explanatory variables and injecting the class as input current, indeed it is possible to obtain the weights corresponding to a binary classification of data. To illustrate such concept it is possible for example to train an output layer of a neural network in one step. Figure 6.5c shows a neural network topology, namely an extreme learning machine (ELM) used as example for neural network training. The network is made of 196 input neurons (corresponding to the pixels of an input image from the MNIST dataset reshaped on a \(14\times 14\) size), 784 hidden neurons on a single hidden layer and 10 output neurons corresponding to the numbers from 0 to 9 of the MNIST dataset [15]. The first layer weights are randomized with a uniform distribution between 1 and −1 and the output last layer is trained with logistic regression. By encoding in the conductance matrix the dataset evaluated on the hidden layer it is possible to use the circuit for calculating the weights of the second layer corresponding to a single output neuron in one step [34]. Figure 6.5d shows a comparison between the analytical weights and the simulated weights with a SPICE circuit simulation, showing little differences. The accuracy of the network trained with the circuit in recognizing the MNIST dataset is 92% which is equivalent to the ideal result for such network.

To evaluate the performance of the circuit it is possible to consider the number of computing steps required for training such neural network on a von Neumann architecture. With conventional computing approach, the complexity for calculating the logistic regression weights of equation (6.1) is composed by \(O(M^2N)\) to multiply \(X^T\) by X, O(MN) to multiply \(X^T\) by y and \(O(M^3)\) to compute the LU factorization of \(XX^T\) and use it to calculate \((XX^T)^{-1}\). Thus, \(M^2N+MN+M^3\) floating points operations are required. In the case of the training of the neural network classification layer of Fig. 6.5c, 2.335\(\times \)10\(^9\) operations are required. Given that the simulated weight training with the in-memory closed loop crosspoint circuit required 145 us [34], the circuit has an equivalent throughput of 16.1 TOPS. The overall power consumption of the simulated circuit is calculated to be 355.6 mW [34] per training operation assuming a conductance unit of 10\(\mu \)S in the circuit. As a result the efficiency of the circuit is calculated to be 45.3 TOPS/W. As an approximate comparison the energy efficiency of Google TPU is 2.3 TOPS/W [12] while the energy efficiency of an in-memory open loop circuit is 7.02 TOPS/W [29], evidencing that the in-memory closed loop solution is 19.7 and 6.5 times more efficient, respectively. The results show the appealing feasibility of the in-memory computing circuit for solving machine learning tasks, such as training a neural network with unprecedented throughput.

5 Conclusions

In this chapter in-memory circuit accelerators for inverse algebra problems have been presented. Compared to previous results, thanks to operational amplifiers connected in feedback configuration, it is possible to solve such problems in just one step. First the open loop crosspoint circuit for matrix vector multiplication is illustrated. Then, the novel crosspoint closed loop circuits are demonstrated able of solving linear systems and computing eigenvectors, in one step without iterations. Finally, the concept is extended to machine learning tasks such as linear regression and neural networks training in one step. These results supports in-memory computing as a future computing paradigm to obtain size independent time complexity solution of algebraic problems in a compact and low energy platform.