Abstract
The goal of cooperative verification is to combine verification approaches in such a way that they work together to verify a system model. In particular, cooperative verifiers provide exchangeable information (verification artifacts) to other verifiers or consume such information from other verifiers with the goal of increasing the overall effectiveness and efficiency of the verification process.
This paper first gives an overview over approaches for leveraging strengths of different techniques, algorithms, and tools in order to increase the power and abilities of the state of the art in software verification. To limit the scope, we restrict our overview to tools and approaches for automatic program analysis. Second, we specifically outline cooperative verification approaches and discuss their employed verification artifacts. Third, we formalize all artifacts in a uniform way, thereby fixing their semantics and providing verifiers with a precise meaning of the exchanged information.
A preliminary version of this article appeared as technical report [30].
Funded in part by the Deutsche Forschungsgemeinschaft (DFG) – 418257054 (Coop)
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Cooperative verification
- Software verification
- Conditional model checking
- Verification witness
- Exchange format
- Partial verification
- Reducer
- Execution report
- Tool combination
1 Introduction
The area of software verification studies methods and constructs tools for automatically proving program properties. The recent past has seen an enormous improvement in this area, in particular with respect to scalability, precision, and the handling of different programming-language features. Today’s software-verification tools employ a variety of different techniques, ranging from data-flow analysis [69] over symbolic execution [70] to SAT-based approaches [16, 33]. As all these techniques have their particular strengths and weaknesses, a number of tools tightly integrate different —usually two— approaches into one tool (see [17] for an overview). For instance, the integration of techniques that under- and over-approximate the state space of the program is a frequent combination. Such combinations typically improve over pure approaches. However, such conceptual integrations also require new tool implementations for every additional integration of techniques. Portfolio combinations loosely integrate different tools: There is no communication between the approaches and the resulting combination can be composed from off-the-shelf components. Algorithm selection combines different approaches into one by first analyzing the input problem and then choosing the approach that will most likely (according to some heuristics) succeed.
In contrast to these extremely tight or extremely loose combinations, cooperative verification is a combination of approaches that cooperate, that is, work together to achieve the verification goal, but leave the existing tools (mostly) untouched. Cooperative verifiers communicate with each other in order to maximize the common strength, in particular, by exchanging information about intermediate results. In a framework for cooperative verification, the integration of a new technique might require some implementation to make it understand the communication, viz. be able to use intermediate results, but it can avoid a new re-implementation of the combination — from the conceptual as well as from the practical viewpoint. If the intermediate results come in a format already accepted by the tool (e.g. as a program), the tool can even be employed as is.
In this paper, we provide a classification of verification approaches according to the interface and type of combination employed; we briefly survey combination approaches, for portfolio, selection, cooperative, and conceptual combination of verification approaches. We then discuss a number of aspects relevant to cooperative verification, in particular its objectives and prerequisites.
2 Classification of Verification Approaches
In the following, we provide a classification of verification approaches according to their way of interfacing and combining verification components. By the term “verification approach” we understand an automatic or automatable formal method for solving verification tasks, i.e., for evaluating the proposition “Program p satisfies behavioral specification \(\varphi _b\)” and returning a result r, which can be  ,
,  , or \(\textsc {unknown} \), and an (optional) witness \(\omega \), which contains proof hints, as depicted in Fig. 1.
, or \(\textsc {unknown} \), and an (optional) witness \(\omega \), which contains proof hints, as depicted in Fig. 1.
2.1 Overview over Interfaces
Output. The goal of a verification tool is to solve a verification task and to deliver the computed results to either a verification engineer for manual inspection or to a machine for further automated processing (Fig. 2). Depending on how the results are consumed (by human or by machine), the tool needs to use different formats.
While researchers mainly concentrated on improving the (internal) verification algorithms during the past two decades, it is understood since recently that it is (at least) equally important to provide not only true/false answers, but more details about the reasoning and the process of the verification.
Human. Almost all verification tools provide some kind of statistics to the user, for example, about the number of iterations, of number of proof facts, or consumed resources. Execution reports [34] present an underapproximation of the successfully verified state space to the user. There are also approaches to support interactive inspection of verification results, e.g., by visualization of error paths [81] and verification-aided debugging [11].
Machine. In order to make it possible to validate verification results in an automated way, verification witnesses were introduced [8, 31], a machine-readable exchange format (XML based). Verification witnesses make it possible to independently re-verify the program based on knowledge that another verifier has produced. This can increase trust in the results, can spread the risk of verification errors, and can help making internal knowledge from the verification engine accessible for the user (error paths, program invariants). Violation witnesses [14] enhance the answer false by a description of the state space that contains an error path (a program path that violates the specification), while correctness witnesses [13] enhance the answer true by a description of program invariants that are helpful to prove that the program satisfies the specification. It is known since 15 years that test cases can be derived from error paths [9, 96], but this approach was rarely used in practice and only since recently it is possible to output and exchange this kind of information via a standard format.
While the previous approaches, as the name indicates, witness the verification result, it is also important to make intermediate results and partial results accessible to further processing. Conditional model checking [19] reads as input and writes as output a description of the already verified state space. That is, a conditional verifier outputs a condition that describes the work already done, i.e, the parts of the state space that are already verified. Another kind of intermediate output for machines to later reuse is the abstraction precision [23, 29, 86]. In CEGAR-based approaches [38] an abstract model is automatically constructed by finding abstraction facts in refinement steps which are added to the precision of the analysis (the more abstraction facts are added to the precision, the finer the abstract model). Full abstract models can be used as certificate of correctness [66] or in order to speed up later verification runs for different versions of the same program during regression verification [60].
Input. Similar to the output, there are different interfaces for the kind of input that is given to the verification tools, some from users, some from machines, see Fig. 3.
Human. From the very beginning of programming, assertions were added to programs [94] in order to make it easier to prove correctness. Nowadays, assertions, invariants, pre- and post-conditions, are annotated in programs in a way that machines (interactive verifiers) can read [5, 59]. There are several languages and tools that support this, and a nice overview over such tools and their application opportunities are given in the annual competition on interactive software verification VerifyThis [49].
There were also attempts to support the splitting of specifications and programs into modular parts, in order to make the verification task for the model checkers easier, such as in the
 query language
[10, 87]. There are also testing and analysis tools which ask the user for help
[98]. Last not least, and this is one of the most difficult parts, each verifier expects a set of parameters that the user has to set, in order to choose how the verifier should solve its task. However, finding the right parameters is a challenging task, which could use tool support itself (such as SMAC
[64] or Tuner
[92]).
query language
[10, 87]. There are also testing and analysis tools which ask the user for help
[98]. Last not least, and this is one of the most difficult parts, each verifier expects a set of parameters that the user has to set, in order to choose how the verifier should solve its task. However, finding the right parameters is a challenging task, which could use tool support itself (such as SMAC
[64] or Tuner
[92]).
Machine. A classic approach to make additional information available to a tool is by transforming the original input, e.g., by simplification or enhancement. The advantage is that there is no additional input (no extra parser, no need to implement additional features). For example, the first software model checkers did not have a specification language, but the specification was weaved into the program in a preprocessing step (as was done for the
 [3] specification language
[3] specification language
 [2] and the
[2] and the
 [18] query language
[10]). Even programs were made simpler
[78].
[18] query language
[10]). Even programs were made simpler
[78].
Verification witnesses and conditions were discussed already above as example implementations for output interfaces. Verification witnesses can be taken as input by validation tools that re-establish the verification result using independent technology. Also, the error path described by the violation witness can be replayed and a test case can be derived from the path constraints along the found error path [15].
Conditional model checking is not widespread yet because it was considered difficult to extend a verifier such that it understands conditions as input and reduces the state space accordingly before running the verification engine. This problem was solved by the reducer-based construction of conditional verifiers: Reducers [25, 45] can be used to construct (without implementation effort) conditional model checkers from off-the-shelf verifiers that do not understand conditions themselves, by reducing the original input program to a residual program that contains all the behavior that is not yet covered by the condition and removes as much as possible from the already-verified state space.
2.2 Overview over Combinations
In the early days of automatic program verification, tools implemented a single technique for verification (e.g., explicit enumeration of state space or data-flow analysis using a fixed abstract domain). In our classification (see Fig. 4) these are represented as Basic. Later, the tools implementing these techniques were considerably generalized, for instance by allowing abstract domains to be flexibly set via tool parameters. Still, during one verification run a single basic technique was employed.
It soon turned out that a single verification technique may work well for some verification tasks, but fail for others. This immediately triggered the application of Combination techniques, in order to benefit from the different strengths. Combinations can come in two sorts: A combination either treats techniques or tools as Black Box objects and runs them (mainly) as they are without implementation-specific integrations for which it matters what’s inside the box, or a combination views a component as White Box, conceptually integrating two or more techniques within a new tool. We distinguish three forms of black-box combinations, without and with communication, and classify all white-box approaches into one category.
Portfolio combinations are motivated by the portfolio idea from economics [63], which is a means for distributing the risk: if one investment (here: of computational resources in a certain technique) fails, there are other investments (techniques) that will be successful. A portfolio combination has a number of approaches available, and on a given verification task executes the approaches in a fixed order sequentially (Fig. 5, top), or runs all approaches in parallel (Fig. 5, bottom). The overall approach terminates if one component analysis was successful in obtaining the result. The big advantage of this approach is that it requires no knowledge about the components and there is almost no effort for implementing the combination. Therefore, we placed this most loosely coupled approach on the very left in the bottom row of Fig. 4. The big disadvantage of portfolio approaches is that the resources invested on unsuccessful tools or approaches are lost.
Algorithm Selection [85] is a solution to the problem of wasted resources of portfolio approaches: Algorithm-selection approaches have a number of approaches available, and on a given verification task choose one and execute it (Fig. 6). That is, before starting an approach, a selection model is extracted from the input, based on which a selector function predicts which approach would be best, and only the potentially best approach is selected and executed. This requires some knowledge about the (black box) characterization of the components, but does not require any change of the implementation of the components.
Portfolio and selection approaches run the component tools independently from each other, without any form of information exchange between the approaches. The goal of combining strengths of different approaches and at the same time avoiding to waste resources inspired the development of cooperative combinations of verification approaches.
Cooperation approaches enable the possibility of solving the problem together. Typically, tools exchange intermediate results (e.g., the state space which has already been searched) in order to achieve a division of labor. Such cooperative combinations range from two or more basic techniques running in parallel and combining the information obtained for certain program locations (e.g., combining partial verification results to proof witnesses [67]) to approaches executing different tools in turns with each specializing to specific tasks (e.g., a testing tool trying to achieve coverage together with a model checker constructing counter examples to non-reachability [46]).
Conceptual Integration is the most intensively coupled approach and therefore put on the very right end of the bottom row in Fig. 4. The components are not communicating via clear interfaces, but are tightly integrated and exchange data structures via procedure calls and not via interfaces that could be externalized [17].
In the following subsections, we describe some forms of non-cooperative verification approaches in more detail. In the next section we explain some examples for cooperative verification approaches.
2.3 Examples for Portfolio Combinations
While it seems obvious that portfolio combinations of verification techniques have a large potential, the topic has not yet been systematically investigated for software verification, although it is used in other areas since many years [63].
Sequential Combinations. Examples of sequential combinations are SDV and
 . The static driver verification (SDV)
[4] tool chain at Microsoft used a sequential combination (described in
[93]) which first runs Corral
[71] for up to 1 400 s and then Yogi
[80].
. The static driver verification (SDV)
[4] tool chain at Microsoft used a sequential combination (described in
[93]) which first runs Corral
[71] for up to 1 400 s and then Yogi
[80].
 [26] won the competition on software verification 2013 (SV-COMP’13,
[7]) using a sequential combination
[97] that started with explicit-state model checking for up to 100 s and then switched to a predicate analysis
[27].
[26] won the competition on software verification 2013 (SV-COMP’13,
[7]) using a sequential combination
[97] that started with explicit-state model checking for up to 100 s and then switched to a predicate analysis
[27].
Parallel Combinations. Examples of parallel combinations are the verifiers
 [57] and
[57] and
 [77], which start several different strategies simultaneously and take the result from the approach that terminates first.
[77], which start several different strategies simultaneously and take the result from the approach that terminates first.
2.4 Examples for Algorithm Selection
Algorithm selection [85] first extracts a selection model from the input. In the case of software verification, the input is the verification task (program and its specification). The selection model describes some characteristics of the verification task, for example, feature vectors (measurement values for certain measures that map verification tasks to values). Based on the selection model, the strategy selector chooses one strategy from a set of given verification strategies.
Approaches without Machine Learning. Strategy selection can be very simple and yet effective. For example, a recent work has shown that it is possible with a few boolean features to effectively improve the overall verification progress [12]. The disadvantage is that the strategy selector needs to be explicitly defined by the developer or user. This leads to approaches that use machine learning, in order to automatically learn the strategy selector from training instances.
Machine-Learning-Based Approaches. The technique MUX [93] can be used to synthesize a strategy selector for a set of features of the input program and a given number of strategies. The strategies are verification tools in this case, and the feature values for the selection model are statically extracted from the source code of the input program. Later, a technique that uses more sophisticated features was proposed [47, 48]. While the above techniques use explicit features (defined by measures on the source code), a more recently developed technique [44] leaves it up to the machine learning to obtain insights from the input program. The advantage is that there is no need to define the features: the learner is given the control-flow graph, the data-dependency graph, and the abstract syntax tree, and automatically derives internally the characteristics that it needs. Also, the technique predicts a ranking, that is, the strategy selector is not a function that maps verification tasks to a strategy, but to a sequence of strategies.
2.5 Examples for Conceptual Integrations
Conceptual integrations tightly combine two or more approaches into a new tool, typically re-implementing the basic techniques. A frequent combination of this type is integrating an overapproximating (static) may-analysis with an underapproximating (dynamic) must-analysis. The tool SMASH [54] at the same time maintains an over- and an under-approximation of the state space of programs. Building on the same idea, Yogi [6] (first proposal of the algorithm was under the name Synergy [55]) in addition specifically employs testing to derive alias information which is costly to precisely compute by a static analysis.
A second form of conceptual integration is offered by tools running different analysis in parallel in a form of “product” construction. For example, the verification framework
 [26] provides the possibility of specifying and running composite analyses. A composite analysis could for instance combine two sorts of data-flow analyses (e.g., an interval analysis and an available-expression analysis). The analyses are then jointly run and jointly derive analysis information for program locations. The same idea was classically hard-coded as reduced product
[40] and further improved
[22, 39, 43, 50, 56, 72].
[26] provides the possibility of specifying and running composite analyses. A composite analysis could for instance combine two sorts of data-flow analyses (e.g., an interval analysis and an available-expression analysis). The analyses are then jointly run and jointly derive analysis information for program locations. The same idea was classically hard-coded as reduced product
[40] and further improved
[22, 39, 43, 50, 56, 72].
All those combinations have in common that they exchange information, but they are configured, intertwined, or even hardcoded combinations, rather than interface-based black-box combinations. More approaches are described in the Handbook on Model Checking, in the chapters on combining model checking with data-flow analysis [17], with deductive verification [88], and with testing [53].
2.6 Verification as a Web Service
Orthogonally to the above combinations, approaches can be combined by providing them as web services. The Electronic Tools Integration platform (ETI)
[91] was developed for experimenting with, presenting, evaluating, conserving, and coordinating tools. Later, the approach was extended to make it possible to use the tools via a web site
[74,75,76], such that the user does not need to install any software. ETI uses LTL as specification language, and the systems to be verified can be software systems or models of systems (e.g., times automata). The central point of information of ETI is important, as otherwise, it is time-consuming to collect the URLs of web services to different tool providers, such as, for example,
 Footnote 1,
Footnote 1,
 Footnote 2, and
Footnote 2, and
 Footnote 3. It is even more difficult to get them to cooperate if the tools are distributed, using different interfaces. Unfortunately, the ETI initiative was discontinued, according to Steffen
[90] because of the manual integration effort at the ETI site in Dortmund and because tool providers hesitated to provide their tools.
Footnote 3. It is even more difficult to get them to cooperate if the tools are distributed, using different interfaces. Unfortunately, the ETI initiative was discontinued, according to Steffen
[90] because of the manual integration effort at the ETI site in Dortmund and because tool providers hesitated to provide their tools.
3 Cooperative Verification Approaches
In the following, we discuss approaches for cooperative verification, structured according to the kind of information objects that are exchanged, and then explain a few applications and their effects.
3.1 Exchangeable Objects for Communication and Information Transfer
We now classify the approaches for cooperative verification according to the kinds of communication interfaces that they use. While our text always refers to software verification for concrete examples, cooperative verification is in no way limited to software.
Conditions and Residual Programs. Conditional model checking (CMC)
[19] means to produce a condition as output that describes the state-space that was successfully verified. The (temporal) condition can be represented as an automaton. This information can be passed on to another verifier as input, instructing this verifier to not verify again those parts of the state space that are covered by the condition. Using a reducer
[25], a program can be reduced to those parts of its state space that still has to be verified; the result is called residual program. Symbiotic
[36] can be seen as reducer-based cooperation (slicer +
 ). Inspired by CMC, comprehensive failure characterization (CFC)
[51] computes a condition that represents failure paths, using several tools that cooperate on the task. Alternating conditional analysis (implemented in the tool ALPACA
[52]Footnote 4) is a generalization of CFC and involves a portfolio of 14 tools for program analysis.
). Inspired by CMC, comprehensive failure characterization (CFC)
[51] computes a condition that represents failure paths, using several tools that cooperate on the task. Alternating conditional analysis (implemented in the tool ALPACA
[52]Footnote 4) is a generalization of CFC and involves a portfolio of 14 tools for program analysis.
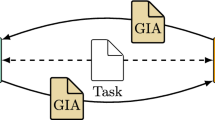
Witnesses. Exchangeable witnesses serve as envelopes for error paths and invariants in a way that makes it possible to exchange the information between different tools. A violation witness [8, 14, 31] explains the specification violation, by describing a path through the program that violates the specification. A correctness witness [13] explains why the program satisfied the specification, by describing invariants that are useful to have in a correctness proof. Figure 7 illustrates the process: The first analyzer verifies the program p according to specification \(\varphi _b \), and produces a result r and a witness \(\omega \). The second analyzer (re-)verifies the same program and specification using information from the witness. If the result r matches the result r’, then the result is confirmed.
Precisions. Verification approaches that are based on counterexample-guided abstraction refinement (CEGAR) [38] iteratively construct an abstract model of the system. The “abstraction facts” that define the level of abstraction are often formalized and expressed as precision [23, 29, 31, 86]. The precision can be exported as output, such that later verification runs can start from such a given definition of the abstraction level.
Abstract States / Certificates. Extreme model checking [60] dumps the abstract reachability graph (ARG) to a file when the verification process terminates. Configurable certificates [66] are sets of abstract states that cover all reachable states of the system. ARGs and configurable certificates can be used by a different verifier to check their validity (completeness and soundness).
Path Programs and Path Invariants. Path programs [21] are programs (for example, written in the same programming language as the input program) that were invented to incorporate external invariant generators into CEGAR-based approaches and are produced after a verifier has found an infeasible error path (often called infeasible counterexample). The path program contains that path in question, but usually also longer paths that use the same program operations, that is, unrollings of a certain loop. The path program can now be given to a tool for invariant synthesis (e.g., [20]) in order to obtain path invariants [21], which are invariants for the whole path program, but in particular also for the original path. The path invariants can then be fed back into the CEGAR-based approach that was encountering the original path.
Taint-Analysis Queries and Answers. Taint analyses perform a specific sort of software verification. They do not look at the satisfaction of behavioral specifications, but at the flow of information (typically within smartphone applications) from private sources to public sinks. In this area of software analysis, numerous tools with complementary strengths exist which has already lead to the proposal of a cooperative taint-analysis tool [83]. Information exchange among tools is therein performed via the AQL (Android-App Analysis Query Language [82]) which allows to state task queries as well as answers to these queries.
Evidential Tool Bus. The evidential tool bus [41, 42] is a tool-integration framework, which is based on a variant of Datalog [1, 35] as a meta language. Artifacts like claims, rules, and evidence are described in this language, as well as verification workflows. The idea is to compose assurance claims (certificates) based on evidence artifacts contributed by different tools, which interact in the evidential tool bus using scripts, queries, and evidence artifacts. Artifacts for models and programs are stored together with evidence artifacts. The intended application area is not only software verification, but the verification of systems in general (that is, models of systems).
Program Annotations. Assertions [94] and other information about the behavior of the program can be added to the program as annotations [5]. An overview over behavioral interface specification languages can be found in the literature [59].
3.2 Objectives and Applications
Having exchangeable objects about (partial) verification results [32] available is important to overcome a variety of practical problems. In the following, we highlight a few of the objectives and applications that we can aim for.
Improvement of Effectiveness and Efficiency. Storing intermediate results can be used to improve the effectiveness and efficiency of the verification process.
Stateful Verification and Reuse. Storing (exchangeable) objects that contain information about intermediate verification results can be considered as a state of the verification process, i.e., making the verification process stateful.
Precisions that are stored and in later verification runs read and reused can significantly improve the performance of regression verification [29, 86]. The setup of this strategy is the following: the first version of a module is verified and at the end, the precision is written to a file. When the i-th version is verified, then the verifier reads the precision that the verification run for version \(i-1\) has written, in order to save time discovering the right abstraction level for the abstract model.
Configurable certificates [66] can reduce the validation time, because the verifier that performs the validation of the certificate “only” needs to check for the set of abstract states that all initial states are contained and that the set is closed under successor transitions.
Also caching-based approaches to improve the efficiency can be seen as a stateful way of performing computation. For example, Green [95] makes symbolic execution more efficient by caching previous intermediate results.
Stateless Verification and Parallelization. The previous argument was based on having a state that contains the intermediate results. It is also possible to speed up verification processes in a stateless way. The technique of conditional model checking is used to split programs into parts that can be independently verified [89].
Improvement of Precision and Confidence. Witness-based results validation [13, 14] can be used to increase the confidence in the results of verification tools, because it is possible to take a witness-based results validator to “replay” the verification. That is, for a violation witness, the validator tries to find and confirm the error path that the witness describes, and for a correctness witness, the validator tries to use the invariants in the witness to re-establish the proof of correctness.
Execution-based results validation [15] extracts a test case from a violation witness and executes it, in order to confirm that the specification violation is observable in the executed program as well.
Explainability. The existence and availability of exchangeable objects with information about the verification process makes it possible to develop approaches for explaining what the verification process did and why the user should be more confident about the verification result. There are preliminary results on explaining and visualizing counterexamples, e.g., for SPIN models [73] and for C programs [11, 81], but due to the exchangeable witness format, many more approaches are possible.
4 Verification Artifacts
This section outlines a construction framework for cooperation. We study verification artifacts, classify several verification tools as verification actors according to their usage of artifacts, and define the semantics of some important artifacts.
4.1 Artifacts of Verification Tools
Verification artifacts are central to cooperation as they provide the means of information exchange. A number of artifacts exist already, most notably of course the programs themselves. We identified the following artifacts:
-
Program p. Defines the implemented behavior of the system. Syntax: C programming language (for example). We represent programs as control-flow automata in Sect. 4.3.
-
Behavior Specification \(\varphi _b \). Defines requirements that all executions of a given program have to satisfy, often as conjunction of several properties. Syntax: The competition SV-COMP established a minimal set of properties that participants of the competition have to supportFootnote 5, which is based on LTL [84], but some tools also support monitor automata as specification. We represent properties by property automata in Sect. 4.3.
-
Test Specification \(\varphi _t \). Defines requirements that a given test suite has to satisfy. Syntax: The competition Test-Comp established a minimal set of coverage criteria that participants of the competition have to supportFootnote 6, which is based on FQL [61, 62]; some tools offer parameters for hard-coded coverage criteria. We represent coverage criteria by test-goal automata in Sect. 4.3.
-
Verification Result r. Verification tools return an evaluation of the statement “Program p satisfies specification \(\varphi _b \).” as answer. Syntax: The answer is from the set \(\{\textsc {true}, \textsc {false}, \textsc {unknown} \}\).
-
Witness \(\omega \). Verification witnesses are used to witness an outcome of a verification run, and thus can come in the form of violation and correctness witnesses. Syntax: XML-based witness formatFootnote 7 that is supported by all available validators of verification results.
-
Test case t. Defines a sequence of values for all calls of external functions, i.e., inputs for the program. Syntax: XML-based test-case formatFootnote 8 that is supported by all test-case generators that participate in Test-Comp.
-
Condition \(\psi \). Defines the part of the program behavior that does not need to be further explored. For verification, \(\psi \) describes the already verified parts. For testing, \(\psi \) describes the parts of the program that are already covered by an existing test suite. Syntax: Condition automata using a notation similar to the
 query lang.
[10] for verification and test-goal sets for testing
[28].
query lang.
[10] for verification and test-goal sets for testing
[28].
We use the corresponding capital letters to denote the types (i.e., sets of artifacts of a kind), for example, the type P is the set of all C programs. Many tools generate different forms of verification artifacts, but currently only very few understand more than the artifact “program” as input.
4.2 Classification of Verification Tools as Actors
Based on the identified artifacts, we classify existing tools according to their usage of artifacts into three sorts of verification actors:
-
Analyzers. Produce new knowledge about programs, for example verification results or test suites.
-
Transformers. Translate one artifact into another, in order to implement a certain feature or support cooperation.
-
Presenters. Prepare information from artifacts such that it can be presented in a human-readable form.
To convey a better understanding of these concepts, consider the following examples: A verifier is an analyzer of type \(P \times \varPhi _b \rightarrow R \times \varOmega \), which takes as input a program p and a behavior specification \(\varphi _b \), and produces as output a result r and a witness \(\omega \)Footnote 9. A conditional verifier is of type \(P \times \varPhi _b \times \varPsi \rightarrow R \times \varOmega \times \varPsi \), i.e., a verifier that supports also input and output conditions. A validator is of type \(P \times \varPhi _b \times \varOmega \rightarrow R \times \varOmega \), i.e., a verifier that takes as input in addition a witness. A test-case generator is also an analyzer, but of type \(P \times \varPhi _t \rightarrow 2^T\), which takes as input a program p and a test specification \(\varphi _t \), and produces as output a set \(ts \in 2^T\) of test cases.
Transformers are largely lacking today, only a few exist already [15, 25, 58, 79]. Transformers are, however, key to cooperation: only if a transformer can bring the artifact into a form understandable by the next tool without implementing an extension of this tool, cooperation can be put into practice. A test-case extractor is a transformer of type \(P \times \varPhi _b \times \varOmega \rightarrow T\), which translates a program, specification, and violation witness to a test case. The identity function is also a transformer (for any given type). A reducer is a transformer of type \(P \times \varPsi \rightarrow P\), which takes a program and a condition as input, and transforms it to a residual program.
Presenters form the interface to the user. A test-case executor is a presenter of type \(P \times T \rightarrow \{\}\), which takes a program p and a test case t as input, and shows a particular program execution (perhaps with a crash) to the software engineer.
Now we can construct, for example, a conditional verifier from a reducer \( red \) and an off-the-shelf verifier \( ver \) by composition. For inputs p, \(\varphi _b \), and \(\psi \), the expression \( ver ( red (p, \psi ), \varphi _b)\) runs the construction. For a verification with an execution-based result validation based on a given verifier \( ver \), test extractor \( wit2test \), and test executor \( exec \), we can write \( exec (p, wit2test (p, \varphi _b, ver (p, \varphi _b).\omega ))\). Figure 8 shows a graphical visualization of the individual components and the two mentioned constructions.
With our construction framework, it is possible to identify the gaps of meaningful transformers, and propose solutions to close these gaps, as far as needed for cooperation.
4.3 Semantics of Verification Artifacts
We now develop the theoretical foundations of artifacts and actors. Artifacts describe some information about a program (or a program itself), and for sound cooperation we need to define the semantics of artifacts. For instance, a violation witness of a program describes a path of the program on which a specific specification is violated, a condition describes a set of paths of a program which have (or have not been) inspected by an analyzer. When employing cooperation as a means for sharing the work load of validation, the cooperating tools need to agree on the meaning of the exchanged artifacts. Without this, cooperation might easily get unsound, e.g., returning a result true for a program and specification although the combined usage of tools has failed to inspect the whole state space of the program. By defining the semantics of artifacts, we also implicitly define the desired semantics of the various actors operating on artifacts.
All of the artifacts given below are a variation of finite-state automata. The reasons for choosing automata as our formalization are twofold: First, artifacts arising in software verification naturally incorporate the sequencing of actions or events as specifiable via automata (e.g., programs have control flow, paths or counterexamples are sequences of operations), and second, a number of verification tools already accept or produce artifacts which are some sort of automata (e.g., violation or correctness witnesses).
We start the formalization of artifacts with the definition of programs, our prime artifact. We denote the set of all program locations by Loc. Formally, a program p is described by a control-flow automaton (CFA) \(A_p=(L,\ell _0,G)\) that consists of a set of locations \(L \subseteq Loc\), an initial location \(\ell _0 \in L\), and a set of control-flow edges \(G \subseteq L \times Ops \times L\), where Ops is the set of operations. Operations can be (a) assignments, (b) assume statements (arising out of branches), and (c) calls to functions retrieving inputs. Here, we assume to have a single such function, called input. We let \({\mathcal {G}}= L \times Ops \times L\) be the set of all control-flow edges.
We let X be the set of variables occurring in the operations Ops. For simplicity, we restrict the type of variables to integers. A concrete data state \(c: X \;\longrightarrow \!\!\!\!\!\!\!\!\circ \;\;\;\mathbb {Z}\) is thus a partial mapping from X to \(\mathbb {Z}\). In the left of Fig. 9 we see our running example of the simple program p and its control-flow automaton on the right. The program starts by retrieving an input for variable x, sets variables a and b to 0, and then increments both while the value of a is less than that of x.
A concrete program path of a program \(A_p=(L,\ell _0,G)\) is a sequence
 , where the initial concrete data state \(c_0 = \emptyset \) assigns no value, \(g_i = (\ell _{i-1},op_i,\ell _i) \in G\), and
, where the initial concrete data state \(c_0 = \emptyset \) assigns no value, \(g_i = (\ell _{i-1},op_i,\ell _i) \in G\), and
 , i.e., (a) in case of assume operations, \(c_{i-1} \models op_i\) (\(op_i\) is a boolean condition) and \(c_{i-1} = c_i\), (b) in case of assignments, \({c_i = \mathsf {SP}_{op_i}(c_{i-1})}\), where \(\mathsf {SP}\) is the strongest-post operator of the operational semantics, and (c) in case of inputs of the form \(x=\) input(), \(c_i(x) \in \mathbb {Z}\) (nondeterministic choice of input) and \(c_i(y) = c_{i-1}(y)\) for all \(y \ne x\). An edge g is contained in a concrete program path
, i.e., (a) in case of assume operations, \(c_{i-1} \models op_i\) (\(op_i\) is a boolean condition) and \(c_{i-1} = c_i\), (b) in case of assignments, \({c_i = \mathsf {SP}_{op_i}(c_{i-1})}\), where \(\mathsf {SP}\) is the strongest-post operator of the operational semantics, and (c) in case of inputs of the form \(x=\) input(), \(c_i(x) \in \mathbb {Z}\) (nondeterministic choice of input) and \(c_i(y) = c_{i-1}(y)\) for all \(y \ne x\). An edge g is contained in a concrete program path
 if \(g = g_i\) for some \(i \in [1, n]\). We let \( paths (A_p)\) be the set of all concrete program paths.
if \(g = g_i\) for some \(i \in [1, n]\). We let \( paths (A_p)\) be the set of all concrete program paths.
We allow artifacts to state assumptions and invariants on program variables. These are given as state conditions (from a set \(\varPhi \) of predicates over a certain theory). We write  and
and  to say that a concrete state c satisfies an assumption \(\psi \in \varPhi \) and an invariant \(\varphi \in \varPhi \), respectively.
to say that a concrete state c satisfies an assumption \(\psi \in \varPhi \) and an invariant \(\varphi \in \varPhi \), respectively.
Artifacts on a program \(\textit{p} \) are represented by protocol automata [14]:
Definition 1
A protocol automaton \(A = (Q,\varSigma ,\delta ,q_0,F)\) for a program CFA \(A_p=(L,\ell _0,G)\) consists of
-
a finite set \(Q \subseteq \varOmega \times \varPhi \) of states, each being a pair of a name and an invariant, and an initial state \(q_0 \in Q\),
-
an alphabet \(\varSigma \subseteq 2^G \times \varPhi \),
-
a transition relation \(\delta \subseteq Q \times \varSigma \times Q\), and
-
a set \(F \subseteq Q\) of final states.
We write
 for \((q,(D,\psi ),q') \in \delta \). In figures, we often elide invariants at states and assumptions at edges when they are \( true \). We furthermore elide the set notation when the element of \(2^G\) is a singleton.
for \((q,(D,\psi ),q') \in \delta \). In figures, we often elide invariants at states and assumptions at edges when they are \( true \). We furthermore elide the set notation when the element of \(2^G\) is a singleton.
Protocol automata describe paths of a program.Footnote 10 Depending on the sort of protocol automaton, these could for instance be paths allowed or disallowed by a specification, or paths already checked by a verifier. A path of the program can be accepted (if the automaton reaches a final state) or covered by the automaton.
Definition 2
A protocol automaton \(A = (Q,\varSigma ,\delta ,q_0,F)\) matches a path
 if there is a run
if there is a run
 in A, with \(k \in [0, n]\), s.t.
in A, with \(k \in [0, n]\), s.t.
-
1.
\(\forall i \in [1, k]: g_i \in G_i\),
-
2.
 and
and -
3.
 .
.
The protocol automaton A accepts the path \(\pi \) if A matches \(\pi \) and \(q_k \in F\), and A covers \(\pi \) if A matches \(\pi \) and \(k = n\).
We let L(A) be the set of paths accepted by the automaton A (its language) and \( paths (A)\) be the set of paths covered by A. As we will see below, some protocol automata might have an empty set of final states and just describe a set of paths that they cover.
Protocol Automata as Representation of Artifacts. We consider different specializations of protocol automata and use the notation \(A_s\) to denote the automaton that represents the syntactical object s.
(1) A property automaton (or, observer automaton) \(A_{\lnot \varphi _b} = (Q,\varSigma ,\delta ,q_0,F)\) is a protocol automaton that satisfies the following conditions:
-
1.
 ,
, -
2.

(assuming \(\bigvee \emptyset = false \)).
Condition 2 ensures that property automata only observe the state of the program (when running in parallel with the program). They do not block, except for the case when the final state is reached where blocking is allowed. Final states denote the reaching of property violations (or, targets).
(2) A test-goal automaton \(A_{\varphi _t} = (Q,\varSigma ,\delta ,q_0,F)\) is a protocol automaton that has only trivial state invariants, i.e.,
 If a final state is reached, the test goal is fulfilled.
If a final state is reached, the test goal is fulfilled.
Figure 10 shows two specification automata: In Fig. 10a we see a property automaton specifying that variables a and b have to be equal when the loop terminates, i.e., the error state is reached if there is a transition from location 3 to 6 at which \(a \ne b\). The label o/w (otherwise) denotes all transitions other than the ones explicitly depicted. Figure 10b depicts a test-goal automaton for the branch condition entering the loop.
Automata for a correctness witness for program p and a violation witness for p without line 5, both wrt. behavior specification \(\varphi _b \) of Fig. 10a
(3) A violation-witness automaton \(A_\omega = (Q,\varSigma ,\delta ,q_0,F)\) is a protocol au tomaton with trivial state invariants only, i.e.,

Violation witnesses are used to describe the part of a program’s state space which contains the error. The final state is reached if an error is detected. Counterexamples are a specific form of violation witnesses which describe a single path.
(4) A correctness-witness automaton \(A_\omega = (Q,\varSigma ,\delta ,q_0,F)\) is a protocol automaton that has only trivial transition assumptions, that is,
 , and all states are final states (
, and all states are final states (
 ). A correctness witness typically gives information about the state space of the program (like a loop invariant) in order to facilitate its verification.
). A correctness witness typically gives information about the state space of the program (like a loop invariant) in order to facilitate its verification.
In Fig. 11 we see both a correctness and a violation witness. The correctness witness belongs to program p and, e.g., certifies that at location 3 variables a and b are equal (via the invariant for \(q_3\)). The violation witness on the right belongs to program p with line 5 removed, i.e., a program which does not satisfy the property stated in Fig. 10a. The violation witness states that an input value of x being greater or equal to 1 is needed for directing the verifier towards the error.
(5) A condition automaton \(A_\psi = (Q,\varSigma ,\delta ,q_0,F)\) is a protocol automaton that satisfies
-
1.
 (no invariants at states) and
(no invariants at states) and -
2.
 (no transitions leaving final states).
(no transitions leaving final states).
A condition is typically used to describe parts of the state space of a program, e.g., the part already explored during verification. Final states are thus used to fix which paths have already been explored.
A test case is a sequence of input values consecutively supplied to the calls of function input. Such a test case is encoded as protocol automaton using a special template variable \(\chi \) that can be instantiated with every program variable.
(6) A test-case automaton \(A_t = (Q,\varSigma ,\delta ,q_0,F)\) for a test case \(\langle z_1, \ldots , z_n \rangle \) is a protocol automaton with the following components:
 ) and
) and
 . For matching these special transitions \((G_i,\psi _i) = \) \(\big ((\cdot ,\chi =\texttt {input()},\cdot ),\chi =z\big )\) with program paths, the program transitions \(g_i\) have to be of the form \((\ell ,x=\texttt {input()},\ell ')\) and the next state needs to satisfy \(c_i(x)=z\), \(c_i(y) = c_{i-1}(y)\) for \(y\ne x\).
. For matching these special transitions \((G_i,\psi _i) = \) \(\big ((\cdot ,\chi =\texttt {input()},\cdot ),\chi =z\big )\) with program paths, the program transitions \(g_i\) have to be of the form \((\ell ,x=\texttt {input()},\ell ')\) and the next state needs to satisfy \(c_i(x)=z\), \(c_i(y) = c_{i-1}(y)\) for \(y\ne x\).
Figure 12a gives a condition stating the exploration of the state space for inputs less or equal to 0. This could for instance be the output of a verifier having checked that the property holds for inputs \(x \le 0\). Figure 12b is the test-case automaton for the test case \(\langle 4 \rangle \).
Semantics of Protocol Automata. The above definitions fix the syntactical structure of protocol automata. In addition, we need to state their semantics, i.e., the meaning of particular artifacts for a given program. In the following, we let \(A_p=(L,\ell _0,G)\) be the CFA for a program \(\textit{p} \) and \(A_{\lnot \varphi _b}\), \(A_\omega \), and \(A_{\varphi _t}\) be protocol automata.
(i) The program \(\textit{p} \) fulfills a property specification \(\varphi _b \) if
 . Our running example p fulfills the property of Fig. 10a.
. Our running example p fulfills the property of Fig. 10a.
(ii) A correctness witness \(\omega \) is valid for a program \(\textit{p} \) and property specification \(\varphi _b \) if
 . We see here that a correctness witnesses can thus be used to facilitate verification: when we run program, property, and correctness witness in parallel in order to check the emptiness of \( paths (A_p) \cap L(A_{\lnot \varphi _b})\), the correctness witness helps in proving the program correct. The correctness witness in Fig. 11a is valid for p and the property in Fig. 10a.
. We see here that a correctness witnesses can thus be used to facilitate verification: when we run program, property, and correctness witness in parallel in order to check the emptiness of \( paths (A_p) \cap L(A_{\lnot \varphi _b})\), the correctness witness helps in proving the program correct. The correctness witness in Fig. 11a is valid for p and the property in Fig. 10a.
(iii) A violation witness \(\omega \) is valid for a program \(\textit{p} \) and a property specification \(\varphi _b \) if
 . During verification, violation witnesses can thus steer the state-space exploration towards the property violation. Looking again at the running example: If we elide the statement in location 5 of our program, the automaton in Fig. 11b is a valid violation witness. It restricts the state-space exploration to inputs for variable x which are greater or equal to 1.
. During verification, violation witnesses can thus steer the state-space exploration towards the property violation. Looking again at the running example: If we elide the statement in location 5 of our program, the automaton in Fig. 11b is a valid violation witness. It restricts the state-space exploration to inputs for variable x which are greater or equal to 1.
(iv) A condition \(\psi \) is correct for a program \(\textit{p} \) and property \(\varphi _b \) if
 . All program paths accepted by the condition fulfill the specification given by the property automaton. The condition in Fig. 12a describes all paths of the program \(\textit{p} \) which initially started with input \(x\) less or equal to 0. This condition is correct for \(\textit{p} \) and the property automaton in Fig. 10a.
. All program paths accepted by the condition fulfill the specification given by the property automaton. The condition in Fig. 12a describes all paths of the program \(\textit{p} \) which initially started with input \(x\) less or equal to 0. This condition is correct for \(\textit{p} \) and the property automaton in Fig. 10a.
(v) A test-case t for a program \(\textit{p} \) covers a goal of a test-goal specification \(\varphi _t \) if
 . Basically, we require that the inputs provided by the test case guarantee the program execution to reach (at least one) test goal. If there are more than one final state in the test-goal automaton (or the final state can be reached via different paths), the test-goal automaton specifies several test goals. In this case, the test case covers only some of these goals. The test-case automaton in Fig. 12b for p covers the (single) goal of the test-goal automaton in Fig. 10b.
. Basically, we require that the inputs provided by the test case guarantee the program execution to reach (at least one) test goal. If there are more than one final state in the test-goal automaton (or the final state can be reached via different paths), the test-goal automaton specifies several test goals. In this case, the test case covers only some of these goals. The test-case automaton in Fig. 12b for p covers the (single) goal of the test-goal automaton in Fig. 10b.
5 Conclusion
Different verification approaches have different strengths, and the only way to benefit from a variety of approaches is to combine them. The two classic approaches of combining approaches either in white-box manner via a tight conceptual integration or in black-bock manner via loosely coupled combinations, such as portfolio or selection, are both insufficient.
We propose that cooperation is the right direction to go: a loosely-coupled combination of tools that interact via clear interfaces and exchange formats, in order to achieve the verification goal together. To this end, we provide a classification and an overview of existing techniques, which we briefly describe, while giving most importance to cooperative approaches. We add definitions of several useful artifacts, actors, and their semantics.
As future work we see the development of tool combinations putting the outlined cooperation approach into practice. Since a number of tools already generate some of the discussed artifacts, they are “ready for cooperation”. Ultimately, we aim at assembling a pool of actors which can be combined in various ways and where some combination can be easily defined by users, e.g., with the help of a domain-specific combination language.
Notes
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
All verifiers that participate in the competition SV-COMP are analyzers of this form.
- 10.
Note: Each CFA \((L,\ell _0,G)\) induces a protocol automaton (where \(\top \) denotes true) \(\big (L\times \{\top \}, \{(\{g\},\top ) \,|\, g\!\in \! G\}, \{(l, (\{g\}, \top ), l') \,|\, g\!=\!(l, op , l')\in G\}, (\ell _0, \top ), L\times \{\top \} \big )\).
References
Abiteboul, S., Hull, R., Vianu, V.: Foundations of Databases. Addison-Wesley (1995)
Ball, T., Rajamani, S.K.: SLIC: A specification language for interface checking (of C). Technical report MSR-TR-2001-21, Microsoft Research (2002)
Ball, T., Rajamani, S.K.: The SLAM project: Debugging system software via static analysis. In: Proc. POPL, pp. 1–3. ACM (2002). https://doi.org/10.1145/503272.503274
Ball, T., Bounimova, E., Kumar, R., Levin, V.: SLAM2: Static driver verification with under 4% false alarms. In: Proc. FMCAD, pp. 35–42. IEEE (2010)
Baudin, P., Cuoq, P., Filliâtre, J.C., Marché, C., Monate, B., Moy, Y., Prevosto, V.: ACSL: ANSI/ISO C specification language version 1.15 (2020)
Beckman, N.E., Nori, A.V., Rajamani, S.K., Simmons, R.J., Tetali, S., Thakur, A.V.: Proofs from tests. IEEE Trans. Softw. Eng. 36(4), 495–508 (2010). https://doi.org/10.1109/TSE.2010.49
Beyer, D.: Second competition on software verification (Summary of SV-COMP 2013). In: Proc. TACAS. LNCS, vol. 7795, pp. 594–609. Springer (2013). https://doi.org/10.1007/978-3-642-36742-7_43
Beyer, D.: Software verification and verifiable witnesses (Report on SV-COMP 2015). In: Proc. TACAS. LNCS, vol. 9035, pp. 401–416. Springer (2015). https://doi.org/10.1007/978-3-662-46681-0_31
Beyer, D., Chlipala, A.J., Henzinger, T.A., Jhala, R., Majumdar, R.: Generating tests from counterexamples. In: Proc. ICSE, pp. 326–335. IEEE (2004). https://doi.org/10.1109/ICSE.2004.1317455
Beyer, D., Chlipala, A.J., Henzinger, T.A., Jhala, R., Majumdar, R.: The Blast query language for software verification. In: Proc. SAS. LNCS, vol. 3148, pp. 2–18. Springer (2004). https://doi.org/10.1007/978-3-540-27864-1_2
Beyer, D., Dangl, M.: Verification-aided debugging: An interactive web-service for exploring error witnesses. In: Proc. CAV (2). LNCS, vol. 9780, pp. 502–509. Springer (2016). https://doi.org/10.1007/978-3-319-41540-6_28
Beyer, D., Dangl, M.: Strategy selection for software verification based on Boolean features: A simple but effective approach. In: Proc. ISoLA. LNCS, vol. 11245, pp. 144–159. Springer (2018). https://doi.org/10.1007/978-3-030-03421-4_11
Beyer, D., Dangl, M., Dietsch, D., Heizmann, M.: Correctness witnesses: Exchanging verification results between verifiers. In: Proc. FSE, pp. 326–337. ACM (2016). https://doi.org/10.1145/2950290.2950351
Beyer, D., Dangl, M., Dietsch, D., Heizmann, M., Stahlbauer, A.: Witness validation and stepwise testification across software verifiers. In: Proc. FSE, pp. 721–733. ACM (2015). https://doi.org/10.1145/2786805.2786867
Beyer, D., Dangl, M., Lemberger, T., Tautschnig, M.: Tests from witnesses: Execution-based validation of verification results. In: Proc. TAP. LNCS, vol. 10889, pp. 3–23. Springer (2018). https://doi.org/10.1007/978-3-319-92994-1_1
Beyer, D., Dangl, M., Wendler, P.: A unifying view on SMT-based software verification. J. Autom. Reasoning 60(3), 299–335 (2018). https://doi.org/10.1007/s10817-017-9432-6
Beyer, D., Gulwani, S., Schmidt, D.: Combining model checking and data-flow analysis. In: Handbook of Model Checking, pp. 493–540. Springer (2018). https://doi.org/10.1007/978-3-319-10575-8_16
Beyer, D., Henzinger, T.A., Jhala, R., Majumdar, R.: The software model checker Blast. Int. J. Softw. Tools Technol. Transf. 9(5–6), 505–525 (2007). https://doi.org/10.1007/s10009-007-0044-z
Beyer, D., Henzinger, T.A., Keremoglu, M.E., Wendler, P.: Conditional model checking: A technique to pass information between verifiers. In: Proc. FSE. ACM (2012). https://doi.org/10.1145/2393596.2393664
Beyer, D., Henzinger, T.A., Majumdar, R., Rybalchenko, A.: Invariant synthesis for combined theories. In: Proc. VMCAI. LNCS, vol. 4349, pp. 378–394. Springer (2007). https://doi.org/10.1007/978-3-540-69738-1_27
Beyer, D., Henzinger, T.A., Majumdar, R., Rybalchenko, A.: Path invariants. In: Proc. PLDI, pp. 300–309. ACM (2007). https://doi.org/10.1145/1250734.1250769
Beyer, D., Henzinger, T.A., Théoduloz, G.: Lazy shape analysis. In: Proc. CAV. LNCS, vol. 4144, pp. 532–546. Springer (2006). https://doi.org/10.1007/11817963_48
Beyer, D., Henzinger, T.A., Théoduloz, G.: Program analysis with dynamic precision adjustment. In: Proc. ASE, pp. 29–38. IEEE (2008). https://doi.org/10.1109/ASE.2008.13
Beyer, D., Jakobs, M.C.: CoVeriTest: Cooperative verifier-based testing. In: Proc. FASE. LNCS, vol. 11424, pp. 389–408. Springer (2019). https://doi.org/10.1007/978-3-030-16722-6_23
Beyer, D., Jakobs, M.C., Lemberger, T., Wehrheim, H.: Reducer-based construction of conditional verifiers. In: Proc. ICSE, pp. 1182–1193. ACM (2018). https://doi.org/10.1145/3180155.3180259
Beyer, D., Keremoglu, M.E.: CPAchecker: A tool for configurable software verification. In: Proc. CAV. LNCS, vol. 6806, pp. 184–190. Springer (2011). https://doi.org/10.1007/978-3-642-22110-1_16
Beyer, D., Keremoglu, M.E., Wendler, P.: Predicate abstraction with adjustable-block encoding. In: Proc. FMCAD, pp. 189–197. FMCAD (2010)
Beyer, D., Lemberger, T.: Conditional testing: Off-the-shelf combination of test-case generators. In: Proc. ATVA. LNCS, vol. 11781, pp. 189–208. Springer (2019). https://doi.org/10.1007/978-3-030-31784-3_11
Beyer, D., Löwe, S., Novikov, E., Stahlbauer, A., Wendler, P.: Precision reuse for efficient regression verification. In: Proc. FSE, pp. 389–399. ACM (2013). https://doi.org/10.1145/2491411.2491429
Beyer, D., Wehrheim, H.: Verification artifacts in cooperative verification: Survey and unifying component framework. arXiv/CoRR 1905(08505), May 2019. https://arxiv.org/abs/1905.08505
Beyer, D., Wendler, P.: Reuse of verification results: Conditional model checking, precision reuse, and verification witnesses. In: Proc. SPIN. LNCS, vol. 7976, pp. 1–17. Springer (2013). https://doi.org/10.1007/978-3-642-39176-7_1
Beyer, D.: Partial verification and intermediate results as a solution to combine automatic and interactive verification techniques. In: Proc. ISoLA. LNCS, vol. 9952, pp. 874–880. Springer (2016). https://doi.org/10.1007/978-3-319-47166-2
Biere, A., Cimatti, A., Clarke, E.M., Zhu, Y.: Symbolic model checking without BDDs. In: Proc. TACAS. LNCS, vol. 1579, pp. 193–207. Springer (1999). https://doi.org/10.1007/3-540-49059-0_14
Castaño, R., Braberman, V.A., Garbervetsky, D., Uchitel, S.: Model checker execution reports. In: Proc. ASE, pp. 200–205. IEEE (2017). https://doi.org/10.1109/ASE.2017.8115633
Ceri, S., Gottlob, G., Tanca, L.: What you always wanted to know about Datalog (and never dared to ask). IEEE Trans. Knowl. Data Eng. 1(1), 146–166 (1989)
Chalupa, M., Vitovská, M., Strejcek, J.: Symbiotic 5: Boosted instrumentation (competition contribution). In: Proc. TACAS. LNCS, vol. 10806. Springer (2018). https://doi.org/10.1007/978-3-319-89963-3_29
Christakis, M., Müller, P., Wüstholz, V.: Guiding dynamic symbolic execution toward unverified program executions. In: Proc. ICSE, pp. 144–155. ACM (2016). https://doi.org/10.1145/2884781.2884843
Clarke, E.M., Grumberg, O., Jha, S., Lu, Y., Veith, H.: Counterexample-guided abstraction refinement for symbolic model checking. J. ACM 50(5), 752–794 (2003). https://doi.org/10.1145/876638.876643
Codish, M., Mulkers, A., Bruynooghe, M., de la Banda, M.G., Hermenegildo, M.: Improving abstract interpretations by combining domains. In: Proc. PEPM, pp. 194–205. ACM (1993). https://doi.org/10.1145/154630.154650
Cousot, P., Cousot, R.: Systematic design of program-analysis frameworks. In: Proc. POPL, pp. 269–282. ACM (1979). https://doi.org/10.1145/567752.567778
Cruanes, S., Hamon, G., Owre, S., Shankar, N.: Tool integration with the Evidential Tool Bus. In: Proc. VMCAI. LNCS, vol. 7737, pp. 275–294. Springer (2013). https://doi.org/10.1007/978-3-642-35873-9_18
Cruanes, S., Heymans, S., Mason, I., Owre, S., Shankar, N.: The semantics of Datalog for the Evidential Tool Bus. In: Specification, Algebra, and Software, pp. 256–275. Springer (2014)
Cuoq, P., Kirchner, F., Kosmatov, N., Prevosto, V., Signoles, J., Yakobowski, B.: Frama-C. In: Proc. SEFM, pp. 233–247. Springer (2012). https://doi.org/10.1007/978-3-642-33826-7_16
Czech, M., Hüllermeier, E., Jakobs, M., Wehrheim, H.: Predicting rankings of software verification tools. In: Proc. SWAN, pp. 23–26. ACM (2017). https://doi.org/10.1145/3121257.3121262
Czech, M., Jakobs, M., Wehrheim, H.: Just test what you cannot verify! In: Proc. FASE. LNCS, vol. 9033, pp. 100–114. Springer (2015). https://doi.org/10.1007/978-3-662-46675-9_7
Daca, P., Gupta, A., Henzinger, T.A.: Abstraction-driven concolic testing. In: Proc. VMCAI. LNCS, vol. 9583, pp. 328–347. Springer (2016). https://doi.org/10.1007/978-3-662-49122-5_16
Demyanova, Y., Pani, T., Veith, H., Zuleger, F.: Empirical software metrics for benchmarking of verification tools. In: Proc. CAV. LNCS, vol. 9206, pp. 561–579. Springer (2015). https://doi.org/10.1007/978-3-319-21690-4_39
Demyanova, Y., Pani, T., Veith, H., Zuleger, F.: Empirical software metrics for benchmarking of verification tools. Formal Methods Syst. Des. 50(2–3), 289–316 (2017). https://doi.org/10.1007/s10703-016-0264-5
Ernst, G., Huisman, M., Mostowski, W., Ulbrich, M.: VerifyThis: Verification competition with a human factor. In: Proc. TACAS. LNCS, vol. 11429, pp. 176–195. Springer (2019). https://doi.org/10.1007/978-3-030-17502-3_12
Fischer, J., Jhala, R., Majumdar, R.: Joining data flow with predicates. In: Proc. FSE, pp. 227–236. ACM (2005). https://doi.org/10.1145/1081706.1081742
Gerrard, M.J., Dwyer, M.B.: Comprehensive failure characterization. In: Proc. ASE, pp. 365–376. IEEE (2017). https://doi.org/10.1109/ASE.2017.8115649
Gerrard, M.J., Dwyer, M.B.: ALPACA: A large portfolio-based alternating conditional analysis. In: Proc. ICSE, pp. 35–38. IEEE (2019). https://doi.org/10.1109/ICSE-Companion.2019.00032
Godefroid, P., Sen, K.: Combining model checking and testing. In: Handbook of Model Checking, pp. 613–649. Springer (2018). https://doi.org/10.1007/978-3-319-10575-8_19
Godefroid, P., Nori, A.V., Rajamani, S.K., Tetali, S.: Compositional may-must program analysis: unleashing the power of alternation. In: Proc. POPL, pp. 43–56. ACM (2010). https://doi.org/10.1145/1706299.1706307
Gulavani, B.S., Henzinger, T.A., Kannan, Y., Nori, A.V., Rajamani, S.K.: Synergy: A new algorithm for property checking. In: Proc. FSE, pp. 117–127. ACM (2006). https://doi.org/10.1145/1181775.1181790
Gulwani, S., Tiwari, A.: Combining abstract interpreters. In: Proc. PLDI, pp. 376–386. ACM (2006). https://doi.org/10.1145/1133981.1134026
Gurfinkel, A., Albarghouthi, A., Chaki, S., Li, Y., Chechik, M.: Ufo: Verification with interpolants and abstract interpretation (competition contribution). In: Proc. TACAS. LNCS, vol. 7795, pp. 637–640. Springer (2013). https://doi.org/10.1007/978-3-642-36742-7_52
Harman, M., Hu, L., Hierons, R.M., Wegener, J., Sthamer, H., Baresel, A., Roper, M.: Testability transformation. IEEE Trans. Softw. Eng. 30(1), 3–16 (2004). https://doi.org/10.1109/TSE.2004.1265732
Hatcliff, J., Leavens, G.T., Leino, K.R.M., Müller, P., Parkinson, M.: Behavioral interface specification languages. ACM Comput. Surv. 44(3) (2012). https://doi.org/10.1145/2187671.2187678
Henzinger, T.A., Jhala, R., Majumdar, R., Sanvido, M.A.A.: Extreme model checking. In: Verification: Theory and Practice, pp. 332–358 (2003). https://doi.org/10.1007/978-3-540-39910-0_16
Holzer, A., Schallhart, C., Tautschnig, M., Veith, H.: Query-driven program testing. In: Proc. VMCAI. LNCS, vol. 5403, pp. 151–166. Springer (2009). https://doi.org/10.1007/978-3-540-93900-9_15
Holzer, A., Schallhart, C., Tautschnig, M., Veith, H.: How did you specify your test suite. In: Proc. ASE, pp. 407–416. ACM (2010). https://doi.org/10.1145/1858996.1859084
Huberman, B.A., Lukose, R.M., Hogg, T.: An economics approach to hard computational problems. Science 275(7), 51–54 (1997)
Hutter, F., Hoos, H.H., Leyton-Brown, K.: Sequential model-based optimization for general algorithm configuration. In: Proc. LION. LNCS, vol. 6683, pp. 507–523. Springer (2011). https://doi.org/10.1007/978-3-642-25566-3_40
Jakobs, M.C.: Speed up configurable certificate validation by certificate reduction and partitioning. In: Proc. SEFM. LNCS, vol. 9276, pp. 159–174. Springer (2015). https://doi.org/10.1007/978-3-319-22969-0_12
Jakobs, M.C., Wehrheim, H.: Certification for configurable program analysis. In: Proc. SPIN, pp. 30–39. ACM (2014). https://doi.org/10.1145/2632362.2632372
Jakobs, M.: PART\(_{PW}\) : From partial analysis results to a proof witness. In: Proc. SEFM. LNCS, vol. 10469, pp. 120–135. Springer (2017). https://doi.org/10.1007/978-3-319-66197-1_8
Jakobs, M., Wehrheim, H.: Compact proof witnesses. In: Proc. NFM. LNCS, vol. 10227, pp. 389–403. Springer (2017). https://doi.org/10.1007/978-3-319-57288-8_28
Kildall, G.A.: A unified approach to global program optimization. In: Proc. POPL, pp. 194–206. ACM (1973). https://doi.org/10.1145/512927.512945
King, J.C.: Symbolic execution and program testing. Commun. ACM 19(7), 385–394 (1976). https://doi.org/10.1145/360248.360252
Lal, A., Qadeer, S., Lahiri, S.K.: A solver for reachability modulo theories. In: Proc. CAV. LNCS, vol. 7358, pp. 427–443. Springer (2012). https://doi.org/10.1007/978-3-642-31424-7_32
Lerner, S., Grove, D., Chambers, C.: Composing data-flow analyses and transformations. In: Proc. POPL, pp. 270–282. ACM (2002). https://doi.org/10.1145/503272.503298
Leue, S., Befrouei, M.T.: Counterexample explanation by anomaly detection. In: Proc. SPIN. LNCS, vol. 7385, pp. 24–42. Springer (2012). https://doi.org/10.1007/978-3-642-31759-0_5
Margaria, T., Nagel, R., Steffen, B.: Remote integration and coordination of verification tools in jETI. In: Proc. ECBS, pp. 431–436 (2005). https://doi.org/10.1109/ECBS.2005.59
Margaria, T.: Web services-based tool-integration in the ETI platform. Softw. Syst. Modeling 4(2), 141–156 (2005). https://doi.org/10.1007/s10270-004-0072-z
Margaria, T., Nagel, R., Steffen, B.: jETI: A tool for remote tool integration. In: Proc. TACAS. LNCS, vol. 3440, pp. 557–562. Springer (2005). https://doi.org/10.1007/978-3-540-31980-1_38
Müller, P., Peringer, P., Vojnar, T.: Predator hunting party (competition contribution). In: Proc. TACAS. LNCS, vol. 9035, pp. 443–446. Springer (2015). https://doi.org/10.1007/978-3-662-46681-0_40
Necula, G.C., McPeak, S., Rahul, S.P., Weimer, W.: Cil: Intermediate language and tools for analysis and transformation of C programs. In: Proc. CC. LNCS, vol. 2304, pp. 213–228. Springer (2002)
Necula, G.C., McPeak, S., Weimer, W.: CCured: Type-safe retrofitting of legacy code. In: Proc. POPL, pp. 128–139. ACM (2002). https://doi.org/10.1145/503272.503286
Nori, A.V., Rajamani, S.K., Tetali, S., Thakur, A.V.: The Yogi Project: Software property checking via static analysis and testing. In: Proc. TACAS. LNCS, vol. 5505, pp. 178–181. Springer (2009). https://doi.org/10.1007/978-3-642-00768-2_17
Novikov, E., Zakharov, I.S.: Towards automated static verification of GNU C programs. In: Proc. PSI. LNCS, vol. 10742, pp. 402–416. Springer (2017). https://doi.org/10.1007/978-3-319-74313-4_30
Pauck, F., Bodden, E., Wehrheim, H.: Do Android taint-analysis tools keep their promises? In: Proc. ESEC/FSE, pp. 331–341. ACM (2018). https://doi.org/10.1145/3236024.3236029
Pauck, F., Wehrheim, H.: Together strong: Cooperative Android App analysis. In: Proc. ESEC/FSE, pp. 374–384. ACM (2019). https://doi.org/10.1145/3338906.3338915
Piterman, N., Pnueli, A.: Temporal logic and fair discrete systems. In: Handbook of Model Checking, pp. 27–73. Springer (2018). https://doi.org/10.1007/978-3-319-10575-8_2
Rice, J.R.: The algorithm selection problem. Adv. Comput. 15, 65–118 (1976). https://doi.org/10.1016/S0065-2458(08)60520-3
Rothenberg, B., Dietsch, D., Heizmann, M.: Incremental verification using trace abstraction. In: Proc. SAS. LNCS, vol. 11002, pp. 364–382. Springer (2018). https://doi.org/10.1007/978-3-319-99725-4_22
Serý, O.: Enhanced property specification and verification in Blast. In: Proc. FASE. LNCS, vol. 5503, pp. 456–469. Springer (2009). https://doi.org/10.1007/978-3-642-00593-0_32
Shankar, N.: Combining model checking and deduction. In: Handbook of Model Checking, pp. 651–684. Springer (2018). https://doi.org/10.1007/978-3-319-10575-8_20
Sherman, E., Dwyer, M.B.: Structurally defined conditional data-flow static analysis. In: Proc. TACAS (2). LNCS, vol. 10806, pp. 249–265. Springer (2018). https://doi.org/10.1007/978-3-319-89963-3_15
Steffen, B.: The physics of software tools: SWOT analysis and vision. Int. J. Softw. Tools Technol. Transf. 19(1), 1–7 (2017). https://doi.org/10.1007/s10009-016-0446-x
Steffen, B., Margaria, T., Braun, V.: The Electronic Tool Integration platform: Concepts and design. STTT 1(1–2), 9–30 (1997). https://doi.org/10.1007/s100090050003
Torsney-Weir, T., Saad, A., Möller, T., Hege, H., Weber, B., Verbavatz, J.: Tuner: Principled parameter finding for image segmentation algorithms using visual response surface exploration. IEEE Trans. Vis. Comput. Graph. 17(12), 1892–1901 (2011). https://doi.org/10.1109/TVCG.2011.248
Tulsian, V., Kanade, A., Kumar, R., Lal, A., Nori, A.V.: MUX: Algorithm selection for software model checkers. In: Proc. MSR. ACM (2014). https://doi.org/10.1145/2597073.2597080
Turing, A.: Checking a large routine. In: Report on a Conference on High Speed Automatic Calculating Machines, pp. 67–69. Cambridge Univ. Math. Lab. (1949)
Visser, W., Geldenhuys, J., Dwyer, M.B.: Green: Reducing, reusing, and recycling constraints in program analysis. In: Proc. FSE, pp. 58:1–58:11. ACM (2012). https://doi.org/10.1145/2393596.2393665
Visser, W., Păsăreanu, C.S., Khurshid, S.: Test-input generation with Java PathFinder. In: Proc. ISSTA, pp. 97–107. ACM (2004). https://doi.org/10.1145/1007512.1007526
Wendler, P.: CPAchecker with sequential combination of explicit-state analysis and predicate analysis (competition contribution). In: Proc. TACAS. LNCS, vol. 7795, pp. 613–615. Springer (2013). https://doi.org/10.1007/978-3-642-36742-7_45
Xie, T., Zhang, L., Xiao, X., Xiong, Y., Hao, D.: Cooperative software testing and analysis: Advances and challenges. J. Comput. Sci. Technol. 29(4), 713–723 (2014). https://doi.org/10.1007/s11390-014-1461-6
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Beyer, D., Wehrheim, H. (2020). Verification Artifacts in Cooperative Verification: Survey and Unifying Component Framework. In: Margaria, T., Steffen, B. (eds) Leveraging Applications of Formal Methods, Verification and Validation: Verification Principles. ISoLA 2020. Lecture Notes in Computer Science(), vol 12476. Springer, Cham. https://doi.org/10.1007/978-3-030-61362-4_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-61362-4_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-61361-7
Online ISBN: 978-3-030-61362-4
eBook Packages: Computer ScienceComputer Science (R0)











 query lang.
[
query lang.
[

 and
and .
.
 ,
,

 (no invariants at states) and
(no invariants at states) and (no transitions leaving final states).
(no transitions leaving final states).