Formation of a Nanostructured Hardened Surface Layer on the TiC-(Ni-Cr) Metal-Ceramic Alloy by Pulsed Electron-Beam Irradiation

Abstract

The efficiency and service life of products made from metal-ceramic tool alloys and used as cutting tools and friction units are determined by a combination of physical and strength properties of their surface layers with a thickness of up to 200 μm. Therefore, much attention is paid to their improvement at the present time. An effective way to increase the operational properties of the metal-ceramic alloy products is to modify the structure and the phase composition of the surface layers by forming multi-scale internal structures with a high proportion of low-dimensional (submicro and nano) components. For this purpose, surfaces are treated with concentrated energy fluxes. Pulse electron-beam irradiation (PEBI) in an inert gas plasma is one of the most effective methods. This chapter presents results of theoretical and experimental studies of this process. An example is the nanostructured hardened surface layer on the TiC-(Ni-Cr) metal-ceramic alloy (ratio of components 50:50) formed by PEBI in the plasma of argon, krypton, and xenon. Its multi-level structure, phase composition, as well as tribological and strength properties are shown.

1 Introduction

Processing materials and products with concentrated energy fluxes to modify the structure, physical and strength characteristics of their surface layers is one of the effective ways to improve operational properties of metals and alloys. High-frequency [1,2,3,4,5,6,7], plasma [8,9,10,11,12,13,14,15], laser [16,17,18,19,20,21,22,23], ion- and electron-beam treatment [24,25,26,27,28,29] are widely used. The technological advantages of these methods include locality and non-contact heating of the surface layers. Each of these methods has its own features determined by the depth and the maximum temperature of the heated surface layer, heating and cooling rates, as well as duration and frequency of pulses. The purpose of the above surface hardening methods is to form multi-scale structures and phase compositions in the surface layer that determine a higher level of physical and strength properties. These structures and the phase compositions enable to decrease local plastic deformations and contribute to a more uniform distribution of elastic stresses in the material volume [30]. As a result, an energy level required to form stress concentrators in the nanostructured surface layer increases, and the probability of defects decreases. Also, a transition zone (instead of an interface) appears between the surface layer and the base material (they smoothly pass into each other). This determines the damping properties of the surface layer with respect to the base material under external shock mechanical and thermal loads. The transition zone prevents premature nucleation and propagation of microcracks from the surface into the material volume which cause its failure. The high-strength nanostructured surface layer, even having multiple micro-cracks, reduces the probability of the crack formation due to increased ductility.

Pulsed electron-beam irradiation (PEBI) has particular advantages for the modification of the structure and the phase composition of the surface layers of metals and alloys. It makes possible to treat a rather large surface area per one pulse with a power density of more than $10^{6} \,{\text{W/cm}}^{ 2}$. Also, PEBI has some another benefits such as pulse frequency up to $10\,{\text{s}}^{ - 1}$, the low reflection coefficient from the irradiated metal surfaces (less than 10%) and high efficiency (more than 90%), as well as possibility to modify the surface layers up to several tens of micrometers in depth.

One of the first comprehensive studies of the metals treated by PEBI has been carried out by scientists of the Tomsk Scientific Center of the Siberian Branch of the USSR Academy of Sciences in the mid-1970s [31]. A little bit later, in the 1980s and subsequent years, some investigations have been done related to the impact of the high-energy electron beams on inorganic materials (Kurchatov Institute of Atomic Energy, Russia; D.V. Efremov Research Institute of Electrophysical Equipment, Russia; The Chernyshev Moscow Machine-Building Enterprise, Russia [30,31,34], and Sandia National Laboratory, USA [35, 36] have been devoted to amorphization and surface hardening of the materials. However, many important relationships and mechanisms of the formation of the phase composition and the substructure in the surface layer of the metals and the alloys after PEBI are still unclear. In particular, the modes that make possible to initiate the dynamic recrystallization and the subsequent formation of nano- and submicroscale multiphase structures have not been established.

The mentioned possibilities to modify the surface layer of the metal and the alloys by PEBI are in many ways superior to other hardening technologies, such as deposition of wear-resistant coatings, ion irradiation and implantation, pulsed plasma and laser surface treatment [37,38,39]. The results of preliminary experimental studies have enabled to make conclusions that the development of an industrial technology for the modification of the surface layers is especially relevant for the manufacturing of metal-ceramic alloy tools. These alloys, based on refractory and high-hardness chemical compounds (carbides, nitrides, carbonitrides, and oxides) with a metal binder, are up-to-date dispersion-strengthened composite materials. They have high mechanical and tribological properties, such as strength, hardness, fracture toughness, wear resistance, and thermal stability. In this regard, the metal-ceramic alloys are widely used in various industries as functional materials for heavily loaded tribological units, machine parts, cutting elements operating under conditions of abrasive action, high temperatures and aggressive environments.

World-wide market analysis results show that about 67% of the total number of the metal-ceramic alloys is used for metal cutting tools, 13% is for drilling and rock cutting, 11% is for woodworking, and 9% is for chipless material-removal. At the same time, global consumption of the metal-ceramic alloy tools has doubled over the past 5 years.

Nowadays, the main direction of improving the operational properties of the metal-ceramic alloys is the development of technologies for sintering particles of highly hard components with a size of less than 1 μm (down to 100 nm). This increases the dispersion of the structure, hardness and strength of the alloys [40, 41]. Despite these advantages of the nanostructured hard alloys, their widespread implementation in the industries is hampered by the lack of effective technologies for mass production by the powder metallurgy method. Therefore, the widely used materials for the critical heavily loaded mechanisms are conventional metal-ceramic materials with particle sizes ranging from units to several tens of micrometers.

The operational efficiency of the metal-ceramic alloys in the mentioned conditions is determined by a set of mechanical properties of the surface layer with a thickness of 100–200 µm (the maximum permissible wear of a tool in the industries). Therefore, recent approaches to increase their lifecycle are based on the improvement of the surface layer characteristics. The main challenge is to eliminate powder sintering defects, including thermally activated micro- and macro-discontinuities of the solid structure. This is achieved by the interfacial interaction of the components under non-equilibrium thermodynamic conditions when heating to critical temperatures and then cooling at ultrahigh rates. The interaction of the metal and ceramic components of the alloys occurs at the peak of heating in the pulsed mode and, as a result, non-equilibrium structures are formed having new physical and strength properties. They remain in the surface layer after cooling at ultrahigh rate. A facility, designed and implemented in the Institute of High Current Electronics (Tomsk, Russia), makes it possible to modify the surface by PEBI [42]. The material is heated at a rate of up to $10^{9} \,{\text{K/s}}$ and, then, cooled at a rate of $10^{4} - 10^{9} \,{\text{K/s}}$ forming temperature gradients in the surface layer up to $10^{7} - 10^{8} {\text{ K/m}}$ [43]. To date, in collaboration with the Institute of Strength Physics and Materials Science SB RAS (Tomsk, Russia), a new approach has been developed to increase the depth of the surface layer on the metal-ceramic alloys which has a high content of nanoscale components. This is achieved by simultaneous pulsed irradiation with electron and ion beams in a single cycle. Inert gases (krypton and xenon), having higher atomic masses and lower ionization energy levels than argon (Table 1), are used as plasma-forming gas. Heavy ions interact with the surface of the irradiated material, increase the effective energy density in the electron beam, form a high level of radiation defects in the surface layer, and accelerate the processes of mass transfer and atom redistribution [43, 44].

Table 1 Atomic mass and ionization energy of the plasma-forming gases

This chapter presents the results of the studies of the nanostructured hardened surface layer on the TiC-(Ni-Cr) metal-ceramic alloy (ratio of components 50:50) formed by PEBI in the plasma of argon, krypton, and xenon. Its multi-level structure, phase composition, as well as tribological and strength properties are shown.

2 Temperature Fields in the Surface Layer under Pulsed Electron-Beam Irradiation

Temperature fields in the surface layer of the TiC-(Ni-Cr) metal-ceramic alloy heated by irradiation with high-energy beams of a rather large diameter can be quantified with a high degree of reliability using a one-dimensional model [45]. The model is based on PEBI of a cylindrical sample of radius $r$ and length $X$ from the end side. Denote electron-beam energy density $E_{s}$, pulse duration $t_{i}$, and pause between pulses $t_{0}$. An approximation has been made in the model that the energy density distribution over the cross section of the electron beam is uniform. Therefore, the sample heating by the electron beam is determined by the equation [46]:

$$ c\rho \frac{\partial T}{\partial t} = \lambda \frac{{\partial^{2} T}}{{\partial x^{2} }} - \frac{\chi }{{x_{0} }}(T - T_{0} ) - \frac{\delta }{{x_{0} }}(T^{4} - T_{0}^{4} ),\;0 \le x \le X, $$

(1)

where $T$ is temperature; $t$ is time; $c, \, \lambda$ are heat capacity and thermal conductivity, respectively, in the solid material as a function of temperature; $\rho$ is density; $\chi$ is the convective heat transfer coefficient; $\delta$ is the radiation heat transfer coefficient; $T_{0}$ is ambient temperature; $x$ is longitudinal coordinate.

According to the additivity law, the heat capacity, thermal conductivity and density values of composite materials are calculated as:

$$ \begin{gathered} c = v_{{Ni - Cr}} c_{{Ni - Cr}} + v_{{TiC}} c_{{TiC}} ,\lambda = v_{{Ni - Cr}} \lambda _{{Ni - Cr}} + v_{{TiC}} \lambda _{{TiC}} , \hfill \\ \rho = v_{{Ni - Cr}} \rho _{{Ni - Cr}} + v_{{TiC}} \rho _{{TiC}} ,c_{{Ni - Cr}} = (c_{{Ni}} a_{{Ni}} + c_{{Cr}} a_{{Cr}} )/(a_{{Ni}} + a_{{Cr}} ), \hfill \\ c_{{TiC}} = (c_{{Ti}} a_{{Ti}} + c_{C} a_{C} )/(a_{{Ti}} + a_{C} ), \hfill \\ \lambda _{{Ni - Cr}} = (\lambda _{{Ni}} a_{{Ni}} + \lambda _{{Cr}} a_{{Cr}} )/(a_{{Ni}} + a_{{Cr}} );\lambda _{{TiC}} = (\lambda _{{Ti}} a_{{Ti}} + \lambda _{C} a_{C} )/(a_{{Ti}} + a_{C} ), \hfill \\ \rho _{{Ni - Cr}} = (\rho _{{Ni}} a_{{Ni}} + \rho _{{Cr}} a_{{Cr}} )/(a_{{Ni}} + a_{{Cr}} );\rho _{{TiC}} = (\rho _{{Ti}} a_{{Ti}} + \rho _{C} a_{C} )/(a_{{Ti}} + a_{C} ), \hfill \\ \end{gathered} $$

(2)

where $c_{j} , \, \lambda_{j} , \, \rho_{j, \, } v_{j}$ are the heat capacity, thermal conductivity, density and relative mass fraction of the j-th component of the composite (the TiC-(Ni-Cr) metal-ceramic alloy in the investigated case).

For a single electron pulse, boundary conditions on the irradiated surface $\left( {x = 0} \right)$ are represented as:

$$ - \lambda \frac{\partial T}{\partial x} = \left\{ {\begin{array}{*{20}c} {E_{s} /t_{i} > 0,t \in [(n - 1)(t_{i} + t_{0} ),\;(n - 1)t_{0} + nt_{i} ]} \\ {0,t \notin [(n - 1)(t_{i} + t_{0} ),\;(n - 1)t_{0} + nt_{i} ]\;} \\ \end{array} } \right.,x = X:\quad \frac{\partial T}{\partial x} = 0 $$

(3)

where n is the number of pulses.

The initial data for the TiC-(Ni-Cr) metal-ceramic alloy having the ratio of the components 50:50 are [47,48,49]: $c_{NiCr} = 452\,{\text{J/kgK}}$, $c_{TiC} = 408\,{\text{J/kgK}}$, $\lambda_{NiCr} = 88.5\,{\text{J/sKm}}$, $\lambda_{TiC} = 42\,{\text{J/sKm}}$, $\rho_{NiCr} = 8800\,{\text{kg/m}}^{ 3}$, $v_{NiCr} = v_{TiC} = 0.5$, $\chi = 10\,{\text{J/sKm}}^{ 2}$, $\delta = 3 \times 10^{ - 7} \,{\text{J/sK}}^{ 4} {\text{m}}^{ 2}$, $T_{0} = 300\,{\text{K}}$, $r = 0.01\,{\text{m}}$, $x = 0.001\,{\text{m}}$.

An increase in pulse duration causes a significant decrease in temperature of the surface layer and an increase in its depth. When pulse duration is 200 μs, the surface layer temperature achieves 550 K and its depth slightly increases. The electron-beam energy density values have a strong effect on the temperature profile in the surface layer. Both temperature and depth of the surface layer rise simultaneously with an increase in electron-beam energy density. For example, the surface layer temperature rises from 760 to 1250 K when electron-beam energy density enhances from $5\;{\text{to}}\;10\,{\text{J/cm}}^{ 2}$. Its further increase up to $40\,{\text{J/cm}}^{ 2}$ raises the surface layer temperature up to 4250 K. This effect becomes stronger with increasing pulse duration.

At a constant energy density value, an increase in the number of pulses up to 300 enhances the heated surface layer depth by more than two times. Then, upon reaching a certain number of pulses, the surface layer depth remains constant rising only with an increase in electron-beam energy density. At a frequency of $1\,{\text{s}}^{ - 1}$, an increase in the number of pulses up to 50 has almost no effect on the surface layer temperature which increases only after 100 pulses. The temperature profile in the surface layer changes little with increasing pulse frequency from 1 to $20\,{\text{s}}^{ - 1}$.

The temperature gradient under PEBI significantly affects structural and phase transformations in the surface layer. The calculated dependences of the temperature gradient in the surface layer of the TiC-(Ni-Cr) metal-ceramic alloy from pulse frequency and duration, the number of pulses, as well as electron-beam energy density show that an increase in pulse duration sharply decreases the temperature gradient while, on the contrary, an increase in electron-beam energy density enhances it. Rising pulse frequency and the number of pulses do not affect the temperature gradient in the surface layer. Thus, the main patterns of the structural and phase transformations in the surface layer of the TiC-(Ni-Cr) metal-ceramic alloy under PEBI are determined primarily by electron-beam energy density, as well as the number of pulses and pulse duration. A weak correlation of the temperature distribution in the surface layer with the number of pulses and pulse frequency means that the temperature profiles are formed during the first pulse and remains almost unchanged with an increase in these parameters. Raising the number of pulses enhances duration of the surface layer existence in non-equilibrium temperature–time conditions. It also determines the interfacial interaction of the surface layer components and, as a result, the formed structure.

An analysis of the temperature profiles and the surface layer depth enables to estimate the ranges of the experimental parameters (electron-beam energy density, the number of pulses and pulse duration) for the surface layer structure modification by PEBI. The main criteria are the modified surface layer depth (from 100 to 200 µm), an increase in its temperature during the first pulse (up to 3000 K), and a minimum temperature gradient. Electron-beam energy density of $40 - 50\,{\text{J/cm}}^{ 2}$ and pulse duration of 100–200 µs correspond to these criteria. Taking into account that the temperature profiles in the surface layer are formed precisely during the first pulse and remain almost unchanged then, an increase in the number of pulses changes only the duration of the interfacial interaction of the components in the TiC-(Ni-Cr) metal-ceramic alloy under non-equilibrium temperature–time conditions for the specified electron-beam energy density and pulse duration values. Thus, the results of the surface layer temperature profile calculations enable to verify their compliance with the general patterns. However, an increase in the content of the ceramic component in the TiC-(Ni-Cr) metal-ceramic alloy enhances the maximum heating temperature in the surface layer, as well as the temperature gradient in the surface layer.

3 The Effect of Pulsed Electron-Beam Irradiation in Different Plasma-Forming Gases on the Surface Layer Structure and Properties

3.1 Material and Experimental Methods

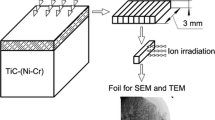
Samples (10 × 10 × 4 mm plates) were made from the TiC-(Ni-Cr) metal-ceramic alloy. The flat sample surfaces were polished to a mirror shine before irradiation. PEBI was performed using a plasma cathode setup [50, 51]. Argon, krypton, and xenon were used as a plasma-forming gas; their atomic mass and ionization energy are presented in Table 1. The values of electron-beam energy density, pulse duration, and frequency are presented in Table 2. The wide-aperture electron beam covered the entire sample surfaces.

Table 2 PEBI parameters

Specimens for the microstructure analysis were prepared by the focused ion beam method using an ‘Jeol EM-09100IS’ setup (accelerating voltage 8 kV, ion beam incidence angle 4°).

Three-point bending tests were carried out using an ‘Instron-3369’ machine under continuous loading at a speed of 0.2 mm/min in accordance with ISO 3327-82. Transverse bending strength was calculated without taking into account any possible plastic deformations by the formula $\sigma = 3Pl/2h^{2} b$, where $P$ was force corresponding to the sample failure; $l$ was the distance between the pillars; $h$ was the sample height (the size coincided with the force direction); $b$ was the sample width (perpendicular to height).

X-ray phase analysis of the surface layers of the samples having the minimum and maximum values of transverse bending strength after PEBI in different plasma-forming gases was carried out using a ‘Shimadzu XRD 6000’ X-ray diffractometer in Cu radiation (accelerating voltage 40 kV, current 30 mA).

Microhardness values on the surface layers were measured using a ‘DM 8B’ microhardness tester in accordance with ISO 14577-1:2015. Nanohardness and Young’s modulus of the surface layers were investigated using a ‘CSEM Nano Hardness Tester’ facility in accordance with ISO 14577-1:2015.

Wear resistance of the surface layers and the friction coefficients on the sample surfaces were studied using a ‘CSEM Tribometer High Temperature S/N 07-142’ tribometer (CSEM Instruments, Switzerland). The samples were rotated on the stationary counterpart (a diamond cone) during the tests. Load on the diamond cone was 5 N, the number of the sample revolutions was 2500. Friction force was continuously measured using a ‘Micromesure System STIL’ micrometer system (Science et Techniques Industrielles de la Lumere. STILS. A, France). Then, absolute friction coefficient values were calculated. The surface profiles (the depth and the cross-section area of grooves made with the diamond cone) were identified using a ‘MICRO MEASURE 3D station (STIL)’ profiler after the end of the tests.

Also, abrasive wear resistance of the sample surfaces was investigated in accordance with ASTM G65. The flat samples were pushed down to a rotated rubber lined wheel with a diameter of 218 mm. Load was 36 N, rotating speed was 200 revolutions per minute. An abrasive powder (13A electrocorundum with a particle size of $200 - 250\,{{\upmu \text{m}}}$) was supplied to the friction surface. The abrasive flow rate was $270 - 280\,{\text{g/min}}$.

3.2 Changes in the Structure and the Properties of the Surface Layer after Pulsed Electron-Beam Irradiation

The study of the TiC-(Ni-Cr) metal-ceramic alloy microstructure by scanning electron microscopy (SEM) showed that titanium carbide particles in the initial state (after sintering) had pronounced unequal shapes (Fig. 1a). The average particle size was $2.7 \pm 1.2{{ \upmu \text{m}}}$, the maximum size was 7.6 μm (Fig. 1b). The alloy in the initial state had three main structural components:

Fig. 1

SEM images of the structure of the metal-ceramic alloy polished surface in the initial state (a) and the element distribution in the TiC-(Ni-Cr) metal-ceramic alloy at the interface between titanium carbide particles and the nickel-chrome binder (b)

• (1) high-strength titanium carbide particles with a size of 1–10 microns;

• (2) interparticle layers of the metal binder;

• (3) “particles–binder” transition zones with a width of about four microns.

Fracture surfaces of the samples had a brittle intergranular appearance (Fig. 2). Figure 3 shows SEM images of the alloy structure in the initial state, as well as titanium carbide particles and the nickel-chrome binder.

Fig. 2

The fracture surface of the TiC-(Ni-Cr) metal-ceramic alloy in the initial state

Fig. 3

TEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy in the initial state

After PEBI, the shapes of titanium carbide particles smoothed and became more rounded (especially of small ones) in the surface layer (Fig. 4a). In addition, their average sizes changed (Fig. 4b). As electron-beam power density $\left( {W_{S} } \right)$ increases, their average and maximum sizes changed along curves with a maximum at $3.2 \times 10^{5} \,{\text{W/cm}}^{ 2}$ (Fig. 5, curve 1 and 2, respectively).

Fig. 4

The structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI $\left( {W_{s} = 2.5 \times 10^{5} \,{\text{W/cm}}^{ 2} } \right)$ in the argon plasma (a) and the size distribution of titanium carbide particles $\left( {b,D = 2.8 \pm 1.7 \, {{ \upmu \text{m}}}} \right)$

Fig. 5

The average (curve 1) and maximum (curve 2) titanium carbide particle sizes on the irradiated surface versus electron-beam power density

PEBI caused high-rate melting and subsequent solidification of the nickel-chrome binder in the surface layer. As a result, titanium carbide particles were refined by partially dissolving in the molten nickel-chrome binder and simultaneous large particle cracking due to high thermal stresses (Figs. 6 and 7).

Fig. 6

The structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI $\left( {W_{S} = 6.0 \times 10^{5} {\text{ W/cm}}^{ 2} } \right)$ in the argon plasma (a), and the distribution of the titanium carbide particle sizes $\left( {b,D = 1.9 \pm 1.2 \, {{ \upmu \text{m}}}} \right)$

Fig. 7

Failure types of titanium carbide particles under thermo-elastic stresses versus electron-beam power density after irradiation in the argon plasma

In addition to microcracking, PEBI changed the structure and the phase composition of the surface layer. The next process options occurred depending on the PEBI parameters: the nickel-chrome binder melted and solidified, or the primary titanium carbide particles partially dissolved and the secondary titanium carbide precipitated, or large carbide particles cracked and these microcracks were filled with the molten nickel-chrome binder. Figures 8 and 9 show microphotographs of the surface layer after PEBI that demonstrate the results of the mentioned processes. The various stages of the interaction of titanium carbide particles with the molten nickel-chrome binder are illustrated by the micrographs in Fig. 8. The initial stage of the titanium carbide particle melting was at $2 \times 10^{5} \,{\text{W/cm}}^{ 2}$ (Fig. 8a). Then, the sizes of the primary titanium carbide particles and their volume fraction decreased with increasing electron-beam power density (Fig. 8b, c). Finally, the process completed with the partial dissolution of titanium carbide particles in the molten nickel-chrome binder and the formation of a nanostructure in the surface layer (Fig. 8d).

Fig. 8

The surface structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI in the argon plasma at an electron-beam power density from $2 \times 10^{5}$ up to $10 \times 10^{5} \,{\text{W/cm}}^{ 2} :\;a - E_{S} = 40.0\,{\text{J/m}}^{ 2}$, $t_{i} = 200.0\,{\upmu }{\text{s}}$, $W_{S} = 2 \times 10^{5} \,{\text{W/cm}}^{2}$; $b - E_{S} = 40.0\,{\text{J/cm}}^{ 2}$, $t_{i} = 80.0\,{{\upmu \text{s}}}$, $W_{S} = 4 \times 10^{5} \,{\text{W/cm}}^{ 2}$, $c - E_{S} = 40.0\,{\text{J/cm}}^{ 2}$, $t_{i} = 50.0\,{{\upmu \text{s}}}$, $W_{S} = 8 \times 10^{5} \,{\text{W/cm}}^{ 2}$; $d - E_{S} = 2.5\,{\text{J/cm}}^{ 2}$, $t_{i} = 2.5\,{{\upmu \text{s}}}$, $W_{S} = 10 \times 10^{5} \,{\text{W/cm}}^{ 2}$

Fig. 9

TEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI $\left( {E_{S} = 40\,{\text{J/cm}}^{2} ,\,t_{i} = 50\,{{\upmu \text{s}}},\,V = 1\,{\text{s}}^{ - 1} ,\,n = 15\,{\text{pulses}}} \right)$: a—titanium carbide particles; b—the nickel-chrome binder

The partial dissolution of the primary titanium carbide particles and the formation of titanium carbide dissolution zones in the molten nickel-chrome binder occurred in the surface layer at an electron-beam power density of $2 \times 10^{5} \,{\text{W/cm}}^{ 2}$ (Fig. 8a). Rising electron-beam power density up to $4 \times 10^{5} \,{\text{W/cm}}^{ 2}$ caused an increase in dissolution rate of the primary titanium carbide particles in the molten nickel-chrome binder, the formation of the extensive titanium carbide dissolution zones, and the release of the secondary titanium carbide nanoparticles inside them (Fig. 8b). A subsequent increase in electron-beam power density up to $8 \times 10^{5} \,{\text{W/cm}}^{2}$ resulted in the almost complete dissolution of the primary titanium carbide particles in the surface layer, and the subsequent formation of a supersaturated titanium-carbon solid solution in the nickel-chromium binder at $10 \times 10^{5} \,{\text{W/cm}}^{ 2}$ (Fig. 8c, d).

A glass-like structure formed in the surface layer. In this structure, titanium carbide particles were almost completely dissolved in the molten nickel-chrome binder (Fig. 9). Microdiffraction studies showed that the glass-like structure consisted of the submicron (200–250 nm) titanium carbide particles and the nanostructured nickel-chrome binder (crystallite size was in the range of 10–30 nm).

Figure 10 shows typical surface layer structures after PEBI using various pulse durations with constant other energy parameters (electron-beam energy density was $40\,{\text{J/cm}}^{ 2}$, pulse frequency was $1\,{\text{s}}^{ - 1}$, the number of pulses was 15). Almost complete dissolution of the primary titanium carbide particles occurred in the molten nickel-chrome binder, and a titanium-carbon solid solution was formed in the surface layer at a pulse duration of 50 μs. An increase in pulse duration up to 100 μs caused the formation of a fine-grain structure with residues of the primary titanium carbide particles in the central part of each grain. The uniform structure was formed at a pulse duration of 150 μs. It included the primary titanium carbide microparticles and interlayers of the nickel-chrome binder saturated with the secondary titanium carbide nanoparticles.

Fig. 10

SEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI $\left( {E_{S} = 40\,{\text{J/cm}}^{ 2} ,\,v = 1\,{\text{s}}^{ - 1} ,\,n = 15\,{\text{pulses}}} \right)$: $\textbf{a} \; t_{i} = 50\,{{\upmu \text{s}}}$, $\textbf{b} \; t_{i} = 100\,{{\upmu \text{s}}}$, $\textbf{c} \; t_{i} = 150\,{{\upmu \text{s}}}$, $\textbf{d} \; t_{i} = 200\,{{\upmu \text{s}}}$

The dependence of the dimension of the titanium carbide particles on electron-beam power density is shown in Fig. 11. At low electron-beam power density values, large titanium carbide particles were refined due to thermal shock and partially dissolved in the molten nickel-chrome binder. Then, this effect intensified to a large extent with an increase in electron-beam power density. As a result, a supersaturated titanium-carbon solid solution in the nickel-chrome binder was formed at electron-beam power density of $8 \times 10^{5} \,{\text{W/cm}}^{ 2}$ and higher.

Fig. 11

Average titanium carbide particle sizes versus electron-beam power density

Finally, the secondary titanium carbide nanoparticles precipitated in the nickel-chrome binder upon cooling (Fig. 12).

Fig. 12

The structure of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI $\left( {\textbf{a}, E_{S} = 40\,{\text{J/cm}}^{2} ,\,t_{i} = 200\,{{\upmu \text{s}}},\,v = 1\,{\text{s}}^{ - 1} ,\,n = 15\,{\text{pulses}}} \right)$, and the effect of the distance from titanium carbide particles on the nickel, titanium, and chromium content (b, numbers indicate the measurement points and the results of local quantitative X-ray spectral analysis)

It was found by the local X-ray spectral analysis that the titanium concentration in the nickel-chrome binder interlayers varied within 19–29 wt% and increased significantly near the interface between titanium carbide particles and the nickel-chrome binder. The values were maximum at the surfaces of titanium carbide particles (Fig. 13). These results indicated the intensive dissolution of titanium carbide particles in the molten nickel-chrome binder and its excessive saturation with titanium and carbon, as well as proved the inevitability of the formation of the multiphase composition in the surface layer during its high-rate cooling after electron-beam pulses. In this regard, it was suggested that one of the reasons for the nanostructure (Fig. 10a) formation in the surface layer after PEBI $\left( {E_{S} = 40\,{\text{J/cm}}^{2} ,t_{i} = 50\,{{\upmu \text{s}}}\;{\text{and}}\;15\,{\text{pulses}}} \right)$ was the supersaturation of the nickel-chromium binder with carbon and titanium.

Fig. 13

SEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy surface after PEBI: $\textbf{a}\;{\text{and}}\;\textbf{b} - E_{S} = 40\,{\text{J/cm}}^{2} ,t_{i} = 50\,{{\upmu \text{s}}}, n = 15\,{\text{pulses}}$; $c\;{\text{and}}\;d - E_{S} = 40\,{\text{J/cm}}^{2} ,t_{i} = 200\,{{\upmu \text{s}}}, n = 15\,{\text{pulses}}$

These features were revealed by the results of the SEM investigations (Fig. 13). Dendritic structures typical for high-rate solidification were formed at the mentioned PEBI parameters. However, there were some differences depended on the PEBI mode due to various heat input rates characterized by electron-beam power density. In the formed structure, titanium carbide particles with a size of ${0}{.5 - 1}{{.5 \upmu \text{m}}}$ had an almost equiaxial shape at a pulse duration of 50 μs (Fig. 13a, b). An increase in pulse duration up to 200 μs decreased cooling rate of the surface layer. Therefore, a dendritic structure with clearly defined first and second order axes was formed during solidification (Fig. 13c, d). Carbide particle shapes varied from an isotropic type with a size of $0.5 - 1.5\,{{\upmu \text{m}}}$ to a highly anisotropic one having a length of $1.5 - 6\,{{\upmu \text{m}}}$ and a width of $0.5 - 0.8{{ \upmu \text{m}}}$.

Thus, the phase composition, the defective substructure state, and the solid solution in the gradient structure formed by PEBI depended on the location of the initial structure with respect to titanium carbide particles. The whole thickness of the modified surface layer increased from $13\;{\text{to}}\;40\,{{\upmu \text{m}}}$ with rising pulse duration from $50\;{\text{to}}\;200\,{{\upmu \text{s}}}$, but the thickness of its glass-like part continuously decreased down to zero at a pulse duration of 200 μs.

Modification of the structure and the phase composition in the surface layer changed the mechanism of its failure. Fractography analysis of the surface layer after PEBI with a pulse duration of 200 μs and an electron-beam energy density of $40\,{\text{J/cm}}^{ 2}$ (Fig. 14) showed that failures had occurred by the ductile-brittle mechanism (numerous plastic deformation steps were on the facets) while the initial sample fracture type was brittle.

Fig. 14

The fracture surface of the TiC-(Ni-Cr) metal-ceramic alloy in the initial state (a and b, the arrows indicate the irradiation surface) and after PEBI $\left( {c\;{\text{and}}\;d,E_{S} = 40\,{\text{J/cm}}^{2} ,\,t_{i} = 200\,{{\upmu \text{s}}},\,n = 15\,{\text{pulses}}} \right)$

The revealed diversity of the structures and the phase composition in the surface layer after PEBI was due to a high level of temperature gradients and the distribution of the alloying elements. The basic indication of the non-equilibrium state achievement in the surface layer was the formation of the modified structure included titanium carbide submicroparticles and the nanostructured nickel-chrome binder. The nickel-chrome binder nanostructuring changed the fracture mechanism from the brittle type to the ductile-brittle one. In this case, the brittle component was determined by the titanium carbide particle failures, and the ductile one was driven by the failure of the nanostructured nickel-chrome binder.

3.3 Theoretical Assessment of the Effect of Plasma-forming Gases on the Pulsed Electron-Beam Irradiation Process

An integral part of the PEBI process is the plasma formation by the inert gas ionization in a vacuum chamber. The inert gas plasma is also an electron source in the case of using a plasma-cathode setup. Additionally to electrons, inert gas ions interact with the irradiated material surface and enhance the surface layer modification. Argon is typically used as a plasma-forming gas for PEBI. However, krypton and xenon are also of significant interest. They differ significantly from argon in terms of atomic mass [52] and ionization energy [53] (Table 1).

It can be assumed that atomic mass and ionization energy of a plasma-forming gas affects the result of the surface layer modification by PEBI at the same pressure in the electron-beam setup chamber. In order to verify or disproof this, PEBI of the end surface of a round plate TiC-(Ni-Cr) metal-ceramic alloy sample with a radius of r and a thickness of $X$ is considered. When the energy density distribution in the electron-beam cross section is uniform, the thermal-conductivity equation is similar to the Eq. (1).

For a single electron pulse, boundary conditions on the irradiated surface $\left( {X = 0} \right)$ are represented as:

$$ - \lambda \frac{\partial T}{\partial x} = \left\{ {\begin{array}{*{20}l} {E_{S} (g)/t_{i} > 0,} \hfill & {0 < t \le t_{i} } \hfill \\ {0,} \hfill & {t > t_{i} } \hfill \\ \end{array} } \right., $$

(4)

and at the end $\left( {x = X} \right)$

$$ - \lambda \frac{\partial T}{\partial x} = \chi (T - T_{0} ) + \varepsilon (T_{{}}^{4} - T_{0}^{4} ) $$

(5)

In Eqs. (4) and (5), the following notations are used: $t_{i}$ is pulse duration; $E_{S} \left( g \right)$ is effective electron-beam energy density in an inert gas plasma. In order to determine $E_{S} \left( g \right)$, it was assumed that an additional ion flux, formed in the inert gas plasma due to electron-beam energy exposure, increases effective (total) radiation density. It is presented in the following approximated form:

$$ E_{S}^{{}} (g) \approx E_{S} (Ar) + \Delta E(g) $$

(6)

where $E_{S} \left( {Ar} \right)$ is electron-beam energy density in the argon plasma, $\Delta E\left( g \right)$ is electron-beam energy density increment due to additional ionization in the krypton or xenon plasma $\left( {g = Kr\;{\text{or}}\;Xe} \right)$. It is also suggested that a decrease in ionization energy of the inert gas increases the number of ions in the electron-plasma flow and, accordingly, the value of $\Delta E\left( g \right)$. Hence, effective electron-beam energy density increases with decreasing gas ionization energy and increasing $\Delta E\left( g \right)$. Since $E_{iAR} > E_{iKr} > E_{iXe}$ (according to Table 1), the next condition $0 < \Delta E\left( {Kr} \right) < \Delta E\left( {Xe} \right)$ is satisfied, which can be rewritten as

$$ E_{s} \left( {Ar} \right) < E_{s} \left( {Kr} \right) < E_{s} \left( {Xe} \right) $$

(7)

Numerical calculations were carried out using the system of the Eqs. (2)–(5) and the relations (6) and (7). Heat capacity and thermal conductivity of the TiC-(Ni-Cr) metal-ceramic alloy were taken constant. The values of thermo-physical properties are represented in paragraph 2 and in [54,55,56,58].

In order to facilitate the analysis of the effect of the plasma-forming gas on the possibility and intensity of the structure and phase transformations in the surface layer under PEBI, the characteristic temperature index $T^{*}$ has been used. Structural and phase transformations are negligible when $T < T^{*}$, and are quite intense when $T \ge T^{*}$. Figure 15 shows the dependence of the surface layer depth heated up to $T^{*} = 1500\,{\text{K}}$ under single electron-beam pulse with a duration of 150 μs on effective electron-beam energy density for argon, krypton and xenon used as a plasma-forming gas. It increases with the change of the plasma-forming gas from argon to krypton, and, then, to xenon at constant pulse duration and electron-beam energy density. Accordingly, there is also a high probability of an increase in the intensity of the interfacial interaction of the TiC-(Ni-Cr) metal-ceramic alloy components in the surface layer and its depth.

Fig. 15

Depth of the TiC-(Ni-Cr) metal-ceramic alloy surface layer heated up to a temperature of 1500 K by PEBI (argon, krypton, and xenon plasma, $t_{i} = 150\,{{\upmu \text{s}}}, n = 1\,{\text{pulse}}$) versus energy density

3.4 The Effect of the Plasma-Forming Gases on the Structure and the Properties of the Modified Surface Layer

The results of the SEM studies of the modified surface layer structure after PEBI in the different plasma-forming gases showed their patterns in terms of heterogeneity and diversity in the quantitative structure parameters. All modified layers consisted of a set of sublayers. The top sublayer, directly adjacent to the irradiated surface, had a nanosized metal-ceramic columnar structure oriented perpendicular to the outer sample surface (Figs. 16 and 17, sublayer 1). Below, a thicker sublayer was formed with a coarser columnar metal-ceramic structure (Figs. 16 and 17, sublayer 2). Columns were mostly oriented perpendicular to the outer sample surface. The next sublayer had a dendritic type structure. It was a transition layer to the initial metal-ceramic structure (Figs. 16 and 17, sublayer 3). The thicknesses of the mentioned sublayers depended on the PEBI parameters and the plasma-forming gas. Figure 18 shows the dependences of the thickness of the top sublayer and the whole modified surface layer on pulse duration at electron-beam energy densities of $40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$ using argon, krypton, and xenon as a plasma-forming gas. The effect of the electron-beam energy density on the whole modified surface layer thickness was minimal. However, it significantly increased in the krypton plasma, and even more in the xenon one. The range of the maximum thicknesses of the modified surface layer varied from 35 μm in the argon plasma to 40 μm in the krypton one, and 47 μm in the xenon plasma at an electron-beam energy density of $60\,{\text{J/cm}}^{ 2}$ (Fig. 18). An increase in pulse duration caused an increase in the thickness of both the top sublayer and the whole modified surface layer (Figs. 16 and 17). However, the top sublayer thickness was almost independent of both the plasma-forming gas and the electron-beam energy density values.

Fig. 16

SEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy surface layer after PEBI (argon plasma, $E_{S} = 60{\text{ J/cm}}^{ 2}$)

Fig. 17

SEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy surface layer after PEBI: a and b—krypton plasma, $E_{S} = 40\,{\text{J/cm}}^{ 2}$; c and d—xenon plasma, $E_{S} = 60\,{\text{J/cm}}^{ 2}$

Fig. 18

The thickness of the upper part of the surface layer having the columnar nanostructure (curves 1 and 2) and the whole thickness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer having the modified structure (curves 3 and 4) versus pulse duration (argon, krypton, and xenon plasma, $E_{S} = 40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2} ,\,n = 15\,{\text{pulses}}$)

Figure 19 shows histograms of the size distribution of titanium carbide particles in the top, middle, and bottom sublayers modified in the plasma of argon, krypton, and xenon at an electron-beam energy density of $40\,{\text{J/cm}}^{ 2}$. The size distribution of titanium carbide particles varied with enhancing distance from the surface to the sample depth. In addition, their average size became larger. It should be noted that this effect was minimal after PEBI in the xenon plasma. The dispersion of the titanium carbide particles almost did not change in the top and middle sublayers, but became a little bit larger in the bottom one. In addition, the greatest thickness of the modified layer was also in the xenon plasma.

Fig. 19

The histograms of the titanium carbide particle size distribution in the upper, middle and lower parts of the TiC-(Ni-Cr) metal-ceramic alloy modified surface layer after PEBI (argon, krypton, and xenon plasma, $E_{S} = 40\,{\text{J/cm}}^{ 2}$)

Changes in the structure and the phase composition in the surface layer were due to the dissolution of titanium carbide particles in the molten nickel-chrome binder and the formation of a supersaturated with titanium and carbon dissolution at the maximum temperature. Also, the secondary titanium carbide nanoparticles precipitated in zones of the primary titanium carbide highest concentration at the interfaces between primary titanium carbide particles and the molten nickel-chrome binder. As a result, a metal-ceramic structure oriented perpendicular to the irradiated surface was formed during solidification under conditions of high temperature gradients. It is shown in Fig. 20 the red line. The primary titanium carbide particles on the surface, where the secondary titanium carbides nanoparticles were formed, are shown by arrows below the red line.

Fig. 20

SEM images of the structure of the TiC-(Ni-Cr) metal-ceramic alloy surface layer after PEBI. Nanosized titanium carbide particles at the interface between the primary titanium carbide particles and the nickel-chrome binder are shown by the arrows

A layer having a metal-ceramic dendrite structure was between the top nanostructured layer and the primary titanium carbide particles partially dissolved in the molten nickel-chrome binder. Elongated titanium carbide particles oriented in different directions were in it (Fig. 21).

Fig. 21

The dendrite structure of the TiC-(Ni-Cr) metal-ceramic alloy surface layer after PEBI (krypton plasma, $E_{S} = 60\,{\text{J/cm}}^{2} ,\,t_{i} = 150\,{{\upmu \text{s}}},\,n = 15\,{\text{pulses}}$)

The same results were obtained by transmission electron microscopy (TEM). Large titanium carbide particles dispersed to a nanoscale level in the surface layer after PEBI in different plasma-forming gases are shown in Fig. 22. The dispersion of the primary titanium carbide particles occurred by dissolving them in the molten nickel-chrome binder, as well as releasing titanium carbide nanoparticles from a supersaturated with titanium and carbon solid solution in the molten nickel-chrome binder during PEBI in the plasma of argon (a) and krypton (b). The titanium and carbon concentrations in the molten nickel-chrome binder were maximum at the surfaces of the primary titanium carbide particle. Therefore, the number of titanium carbide nanoparticles was also maximum at the interface between the primary titanium carbide particles and the nickel-chrome binder after solidification (Fig. 22, shown by arrows). As their number increases in the nickel-chrome binder interlayers, the dendritic structure included titanium carbide nanoparticles oriented perpendicular to the irradiated surface that had formed by the temperature field (Fig. 20). The dispersion of the primary titanium carbide particles, as the mentioned mechanism of the titanium carbide nanoparticle formation, apparently occurred by mechanical refining as a result of thermal shock, followed by filling of the discontinuities with the molten nickel-chrome binder upon PEBI in the xenon plasma (Fig. 22c, shown by the arrows). Thus, it can be concluded that the heterophase nanostructure was formed in the surface layer of the TiC-(Ni-Cr) metal-ceramic alloy under PEBI in the plasma of light (argon) and heavy (krypton and xenon) inert gases. The modified layer depth increased with the change of the plasma-forming gas from argon to krypton and xenon.

Fig. 22

TEM images of dispersed titanium carbide particles in the initial structure of the TiC-(Ni-Cr) metal-ceramic alloy surface layers after PEBI: a—argon plasma, $E_{S} = 60\,{\text{J/cm}}^{2} , t_{i} = 150\,{{\upmu \text{s}, }}n = 15\,{\text{pulses}}$; b—krypton plasma, $E_{S} = 60\,{\text{J/cm}}^{2} ,\,t_{i} = 150\,{{\upmu \text{s},}}\,n = 15\,{\text{pulses}}$; c—xenon plasma, $E_{S} = 60{\text{ J/cm}}^{2} {, }t_{i} = 150\,{{ \upmu \text{s}, }}n = 15{\text{ pulses}}$. Nanosized titanium carbide particles formed from a supersaturated solid solution of carbon and titanium on the surface of the primary titanium carbide particles are shown by small arrows. The mechanical failures of the primary carbide particles are shown by the large arrows

Let us consider X-ray diffraction data. From Table 3, it follows that the phase composition of the material in the initial state (the ceramic to metal component ratio) corresponded to the specified values for the sintered titanium carbide and nickel-chrome powder mixture. There was no texture in the surface layer of the sample.

Table 3 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer in the initial state

PEBI significantly changed the ratio of the ceramic and metal components in the surface layer, as well as formed the (002) texture (Table 4). The presented data were verified by the results of the above numerical estimation of the relative component content in the surface layer. Also, there were a decrease in the nickel-chrome binder content with a corresponding increase in the titanium carbide content, as well as an increase in the lattice parameters of the nickel-chrome binder and titanium carbide. The reason was the mutual solubility of the components when the surface layer was heated under PEBI.

Table 4 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (argon plasma, $E_{S} = 60\,{\text{J/cm}}^{ 2} , t_{i} = 150\,{{\upmu \text{s}}} , n = 15\,{\text{pulses}}$)

Tables 5 and 6 show diffraction patterns and tables of the structure and phase composition parameters of the surface layers after PEBI in the krypton plasma at electron-beam energy densities of $40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$ The main features of the structure and the phase composition were a decrease in the titanium carbide content from 90.08 down to 82.51 wt% and corresponding increase in the nickel-chrome binder content from 9.92 up to 17.49 wt%. In addition, the titanium carbide lattice parameter increased from 0.43037 up to 0.43152 nm. Also, the size of the coherent scattering regions of the ceramic component decreased from 187.79 down to 20.31 nm. These features became more pronounced after PEBI in the xenon plasma. This can be concluded from the diffraction patterns, as well as the tables of the structure and phase composition parameters presented in Tables 7 and 8 (electron beam energy densities was $40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$, respectively). An increase in electron-beam energy density from $40\;{\text{up}}\;{\text{to}}\;60\,{\text{J/cm}}^{ 2}$ reduced the ceramic content from 93.33 down to 65.00 wt%. This value almost corresponded to the level of its content in the initial state. The lattice parameters increased from 0.35798 up to 0.35920 nm for the nickel-chrome binder and from 0.42844 up to 0.43157 nm for titanium carbide. In addition, the coherent scattering regions for the nickel-chrome binder decreased from 39.01 to 14.36 nm. The lattice microdistortions also decreased from $7.242 \times 10^{ - 3}$ down to $1.242 \times 10^{ - 3}$; texture of the surface layer was the same (002).

Table 5 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (krypton plasma, $E_{S} = 40\,{\text{J/cm}}^{2} , t_{i} = 200\,{{\upmu \text{s}}}, n = 15\,{\text{pulses}}$)

Table 6 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (krypton plasma, $E_{S} = 60\,{\text{J/cm}}^{2}, t_{i} = 200\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$)

Table 7 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (xenon plasma, $E_{S} = 40\,{\text{J/cm}}^{2}, t_{i} = 150\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$)

Table 8 The parameters of the structure and the phase composition in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (xenon plasma, $E_{S} = 60\,{\text{J/cm}}^{2} , t_{i} = 150\,{{\upmu \text{s} }}, n = 150\,{\text{pulses}}$)

Summarized results of the X-ray phase analysis are presented in Figs. 23 and 24. PEBI in the argon plasma caused a significant decrease in the nickel-chrome binder content in the surface layer, but increased this value by changing the plasma-forming gas to krypton. The nickel-chrome binder content in the surface layer was about the initial state level when the heaviest xenon plasma had been used (Fig. 23a).

Fig. 23

The relative content of the nickel-chrome binder in the TiC-(Ni-Cr) metal-ceramic alloy surface layer (a) and the crystal lattice parameter of titanium carbide (b) after PEBI $\left( {E_{S} = 60\,{\text{J/cm}}^{2} {, }t_{i} = 150 \ldots 200\,{{\upmu \text{s}, }} n = 15\,{\text{pulses}}} \right)$ versus plasma-forming inert gas: 1—the initial state, 2—argon, 3—krypton, 4—xenon

Fig. 24

The lattice parameter (a), the lattice micro-distortion (b), and the size of the coherent scattering regions (c) in the TiC-(Ni-Cr) metal-ceramic alloy surface layer after PEBI $\left( {E_{S} = 60\,{\text{J/cm}}^{2} , t_{i} = 150 \ldots 200\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}} \right)$ versus plasma-forming inert gas: 1—the initial state, 2—argon, 3—krypton, 4—xenon

A feature of the structure and the phase composition of the surface layer after PEBI was an increase in the crystal lattice parameter. This effect intensified with increasing atomic mass of the plasma-forming gas. For example, the titanium carbide crystal lattice parameter reached 0.43157 nm after PEBI in the xenon plasma. This corresponded to the $C/Ti \approx 0.65$ ratio at the maximum titanium carbide hardness.

Figure 24 shows the effect of the plasma-forming gas on the crystal lattice parameters, the lattice microdistortions, and the size of the coherent scattering regions in the nickel-chrome binder. The crystal lattice parameters increased with an increase in atomic mass of the plasma-forming gas as a result of doping of the nickel-chrome binder during its interaction with titanium carbide particles. However, the lattice microdistortions and the sizes of the coherent scattering regions in the nickel-chrome binder decreased with increasing atomic mass of the plasma-forming gas.

3.5 The Effect of the Plasma-Forming Gases on the Nano- and Microhardness, and Wear Resistance of the Modified Surface Layer

Figure 25 shows dependences of nanohardness values in the surface layer after PEBI in the plasma of argon, krypton, and xenon from electron-beam energy density for pulse durations of 100, 150, and 200 μs. Based on their comparison, it can be concluded that the plasma-forming gas had a significant effect on the nanohardness values in the surface layer. They decreased with increasing electron-beam energy density up to $40\,{\text{J/cm}}^{ 2}$, but then enhanced significantly with rising electron-beam energy density up to $50\,{\text{J/cm}}^{ 2}$ (regardless of the plasma-forming gas). However, this effect was greater after PEBI in the plasma of krypton or xenon. The maximum nanohardness values were after PEBI in the xenon plasma.

Fig. 25

Nanohardness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer versus electron-beam energy density (argon, krypton, and xenon plasma, $t_{i} = 100,\,150\;{\text{and}}\;200\,{{\upmu \text{s}}}$)

A similar dynamics of the change in the nanohardness values was more concise with a change in pulse duration when electron-beam energy densities were $40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$ (Fig. 26). Nanohardness values decreased with an increase in pulse duration up to 150 μs (regardless of the plasma-forming gas). Then, they enhanced slightly as pulse duration increased up to 200 µs.

Fig. 26

Nanohardness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer versus pulse duration (argon, krypton, and xenon plasma, $E_{S} = 40\;{\text{and}}\;60{\text{ J/cm}}^{ 2}$)

Figure 27 shows dependences of microhardness values in the surface layer after PEBI from pulse duration in the plasma of argon, krypton, and xenon for various values of electron-beam energy density. They have common patterns with the same number of pulses. Initially, the microhardness values enhanced with increasing electron-beam energy density.

Fig. 27

Microhardness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer versus pulse duration (argon, krypton, and xenon plasma, $E_{S} = 20, \, 40, \, 50\;{\text{and}}\;60\,{\text{J/cm}}^{ 2} , n = 15\,{\text{pulses}}$)

However, they change along a curve with a maximum at 150 μs as pulse duration increased, regardless of the plasma-forming gas (Fig. 28). The maximum microhardness values were after PEBI in the plasma of the lightest inert gas (argon). They decreased as the plasma-forming gas changed to krypton and xenon.

Fig. 28

Microhardness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer versus electron-beam energy density (argon, krypton, and xenon plasma, $t_{i} = 50,100, 150\;{\text{and}}\;200\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$)

The presented data on the effect of atomic mass of the plasma-forming gases on the microhardness values in the surface layer after PEBI enabled to make conclusions that the best results were obtained at electron-beam energy densities of $40,\;50\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$ (Fig. 29).

Fig. 29

Microhardness of the TiC-(Ni-Cr) metal-ceramic alloy surface layer versus pulse duration (argon, krypton, and xenon plasma, $E_{S} = 20,40\;{\text{and}}\;60\,{\text{J/cm}}^{ 2} , n = 15\,{\text{pulses}}$). The ovals highlight the areas of greatest values

Figure 30 presents dependences of the groove depth from electron-beam energy density after PEBI in the plasma of argon, krypton, and xenon. Modification of the surface layer greatly increased its wear resistance regardless of the plasma-forming gas. However, it increased with enhancing electron-beam energy density. The plasma-forming gas also had a significant effect. The maximum wear resistance values were after PEBI in the xenon plasma at an electron beam energy density of $60\,{\text{J/cm}}^{ 2}$. It decreased with a change in the plasma-forming gas to krypton and reached the minimum values after PEBI in the argon plasma (Fig. 30).

Fig. 30

Depth of the track on the surface of the TiC-(Ni-Cr) metal-ceramic alloy cut with a diamond counterpart after PEBI (argon, krypton, and xenon plasma, $t_{i} = 150\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$) versus energy density

The presented results were verified by the abrasion test results in accordance with ASTM G65. In the initial period, wear resistance of the samples after PEBI was several times higher than that of the samples in the initial state. The maximum wear resistance was after PEBI in the xenon plasma. However, the modified layer became thinner as the number of revolutions of the abrasive disk increased. As a result, the dendritic structure began to interact with the counterpart and wear resistance of the surface layer decreased to the level of the sample in the initial state.

Figure 31 shows dependence of the friction coefficient on pulse duration. The main feature of these dependences was a sharp strong decrease in the friction coefficient after PEBI for all studied parameters (regardless of the plasma-forming gas) as compared with the sample in the initial state.

Fig. 31

The friction coefficient of the TiC-(Ni-Cr) metal-ceramic alloy surface after PEBI (argon, krypton, and xenon plasma, $E_{S} = 20,40,50\;{\text{and}}\;60\,{\text{J/cm}}^{ 2} , n = 15\,{\text{pulses}}$) versus pulse duration

At a pulse duration of 150 μs, the general pattern of dependences shown in Fig. 32 was the invariance of the friction coefficient with changes in electron-beam energy density and pulse duration in all the plasma-forming gases studied. This means the invariance of the type of the structure and the phase composition of the top part of the surface layer with a change in the PEBI energy parameters.

Fig. 32

The friction coefficient of the TiC-(Ni-Cr) metal-ceramic alloy surface after PEBI (argon, krypton, and xenon plasma, $t_{i} = 150\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$) versus electron-beam energy density

One of the important parameters of the effect of the surface layer nanostructuring on its tribological properties was the dependence of the friction coefficient on temperature. Figure 33 shows the temperature dependences of the friction coefficient in the initial state and after PEBI by pulses of various durations in the plasma of argon, krypton, and xenon. Modification of the surface layer significantly reduced the friction coefficient over the entire studied temperature range up to 600 °C (especially at room temperature). The friction coefficient increased with rising temperature for all samples after PEBI. The friction coefficient of the sample in the initial state changed along a curve with a maximum at 200 °C. However, it was larger than that of the samples after PEBI in the entire studied temperature range. The samples after PEBI in the xenon plasma had the smallest values among others.

Fig. 33

The friction coefficient of the TiC-(Ni-Cr) metal-ceramic alloy surface after PEBI (argon, krypton, and xenon plasma, $E_{S} = 60\,{\text{J/cm}}^{2} {,}\,t_{i} = 150\;{\text{and}}\;200\,{{\upmu \text{s} }}, n = 15\,{\text{pulses}}$) versus temperature

3.6 The Effect of the Nanostructured Surface Layer on Transverse Bending Strength

It follows from the distribution of the titanium carbide particle sizes, that the top part of the surface layers had the structure included columnar titanium carbide nanoparticles oriented perpendicular to the irradiated surface and the nickel-chrome binder interlayers. It is obvious that an increase in the nanostructuring level in the top part of the surface layer lowered the friction coefficient, and also increased its wear resistance and ductility. As a result, transverse bending strength of the samples increased under loading from the side of the irradiated surface. Figure 34 shows a dependence of transverse bending strength from pulse duration after PEBI. Electron-beam energy density was $40 , { }50\;{\text{and}}\;60\,{\text{J/cm}}^{ 2}$, the number of pulses was 15, the plasma-forming gases were argon, krypton, and xenon. Modification of the surface layer increased transverse bending strength in all investigated cases. The maximum values (indicated by the ellipses in the graphs) were after PEBI in the xenon plasma with the following combinations of electron-beam energy density and pulse duration: $40\,{\text{J/cm}}^{ 2}$ and 100 μs, $50\,{\text{J/cm}}^{ 2}$ and 200 μs, as well as $60\,{\text{J/cm}}^{ 2}$ and $150\,{{\upmu \text{s}}}$.

Fig. 34

Bending strength of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI (argon, krypton, and xenon plasma, $E_{S} = 20, \, 40, \, 50\;{\text{and}}\;60\,{\text{J/cm}}^{ 2} ,\,n = 15\,{\text{pulses}}$, loading to the irradiated side) versus pulse duration

4 Conclusions

The results of the studies of the structure and the phase composition, as well as the physical, mechanical, and tribological properties of the surface layer of the TiC-(Ni-Cr) metal-ceramic alloy after PEBI the inert gas plasma enabled to draw the following conclusions.

• 1. PEBI in the plasma of the light (argon) and heavy (krypton, xenon) inert gases formed the nanostructured heterophase structure in the surface layer.

• 2. The modified layer depth increased with the change of the plasma-forming gas from argon to krypton and xenon.

• 3. Analysis of the results of the electron microscopic studies of the surface layer microstructure showed various mechanisms of the surface layer nanostructuring with an increase in atomic mass of the plasma-forming gas. Formation of titanium carbide nanoparticles directly at the interface of the carbide particles and the molten nickel-chromium binder was supplemented by the mechanical dispersion of titanium carbide particles and filling gaps with the molten nickel-chromium binder.

• 4. The change in the plasma-forming gas had the significant effect on the nanohardness values in the surface layer after PEBI. They increased greatly with rising atomic mass of the inert gas.

• 5. The nanohardness values decreased with increasing electron-beam energy density up to $40\,{\text{J/cm}}^{ 2}$, but then enhanced significantly with rising electron-beam energy density up to $50\,{\text{J/cm}}^{ 2}$ (regardless of the plasma-forming gas). However, this effect was greater after PEBI in the plasma of krypton or xenon. The maximum nanohardness values were after PEBI in the xenon plasma.

• 6. Typically, the microhardness values changed along the curve with the as pulse duration increased, regardless of the plasma-forming gas. The maximum microhardness values were after PEBI in the plasma of the lightest inert gas (argon). They decreased as the plasma-forming gas changed to krypton and xenon.

• 7. PEBI in the plasma of the heavy inert gases formed the thicker modified surface layers having lower microhardness values and, accordingly, higher ductility.

• 8. Modification of the surface layer greatly increased its wear resistance regardless of the plasma-forming gas. However, it increased with enhancing electron-beam energy density. The plasma-forming gas also had a significant effect. The maximum wear resistance values were after PEBI in the xenon plasma at an electron beam energy density of $60\,{\text{J/cm}}^{ 2}$.

• 9. The friction coefficient of the nanostructured modified surface layers decreased after PEBI for all studied parameters (regardless of the plasma-forming gas).

• 10. The general pattern was the invariance of the friction coefficient with changes in electron-beam energy density and pulse duration in all the plasma-forming gases studied. This means the invariance of the type of the structure and the phase composition of the top part of the surface layer with a change in the PEBI energy parameters.

• 11. Modification of the surface layer by PEBI in the plasma of the inert gases enhanced transverse bending strength of the samples under loading from the side of the irradiated surface.

• 12. The maximum values of the transverse bending strength were after PEBI in the xenon plasma with the following combinations of electron-beam energy density and pulse duration: $40\,{\text{J/cm}}^{ 2}$ and 100 μs, $50\,{\text{J/cm}}^{ 2}$ and 200 μs, as well as $60\,{\text{J/cm}}^{ 2}$ and 150 μs.

• 13. The maximum values of the transverse bending strength were after PEBI in the xenon plasma when electron-beam energy density was $60\,{\text{J/cm}}^{ 2}$. Transverse bending strength increased from 570 MPa in the initial state up to 1061 after PEBI (almost doubled).