Microstructure-Based Computational Analysis of Deformation and Fracture in Composite and Coated Materials Across Multiple Spatial Scales

Abstract

A multiscale analysis is performed to investigate deformation and fracture in the aluminum-alumina composite and steel with a boride coating as an example. Model microstructure of the composite materials with irregular geometry of the matrix-particle and substrate-coating interfaces correspondent to the experimentally observed microstructure is taken into account explicitly as initial conditions of the boundary value problem that allows introducing multiple spatial scales. The problem in a plane strain formulation is solved numerically by the finite-difference method. Physically-based constitutive models are developed to describe isotropic strain hardening, strain rate and temperature effects, Luders band propagation and jerky flow, and fracture. Local regions experiencing bulk tension are found to occur during compression that control cracking of composites. Interrelated plastic strain localization in the steel substrate and aluminum matrix and crack origination and growth in the ceramic coating and particles are shown to depend on the strain rate, particle size and arrangement, as well as on the loading direction: tension or compression.

1 Introduction

Actual materials have essentially inhomogeneous microstructure (Fig. 1). According to the concepts of physical mesomechanics, stress concentrators of different physical origin are a major factor influencing the deformation pattern in nonhomogeneous materials. The effects are most conspicuous in composite materials (metal-matrix composites, coated and surface-hardened materials, doped alloys, etc.) because of differences in the mechanical properties (density, elastic moduli, and strength and plasticity characteristics) of their constituent elements. Thus, basic research along these lines is of great practical importance for development of advanced structural and functional materials.

Fig. 1

Microstructures of an Al/Al₂O₃ composite (a) and steel coated by diffusion borating (b) [16, 34]

The foundations of the physical mesomechanics of materials as a consistent methodology were laid more than 35 years ago [1]. At this time, the basic principles underlying the scientific approach have been formulated and developed [2, 3]. Early theoretical studies helped outline the range of immediate tasks and determined modeling and simulation techniques capable of solving these problems [2, 4,5,6,7,8,9,10]. New deformation and fracture mechanisms operative at macro-, meso- and microscales in solids were identified and accounted for [4]. Development of techniques for computer-aided design of materials and software enabled deformation and fracture processes to be simulated [2, 4,5,6,7,8,9,10].

At present, the problem of an adequate consideration of the multiscale nature of solids is recognized internationally as the first-priority line of investigations aimed at developing new-generation materials, and there is an increasing interest in theoretical studies in this research area—see e.g. [11,12,13,14,15,16,17,18,19,20,21,22]. This has been due to a general awareness that a correct prediction of the macroscopic properties of solids is hardly possible without hierarchy of structural levels and scales in the materials under study.

Nowadays, there are a large number of studies addressing multiscale numerical simulation and modeling, with an explicit consideration of the microstructure being taken into account. Material components are associated with proper constitutive models. For instance, some papers involve artificial models of real microstructures in studying micro-, meso- and homogenized macromechanical response of materials [2], [4, 9,10,11, 15, 17,18,19, 23,24,25,26,27,28,29,30,31,32]. Other authors reported results on the stress-strain analysis of experiment-based microstructure models [2, 6, 8, 12,13,14, 16, 20,21,22, 33,34,35,36,37,38,39]. All these and related works extend our understanding of the relationship between the microstructure and mechanical properties of materials. A special attention is given to interfaces. A majority of contributions devoted to the interfacial problem considers the interfacial fracture, decohesion and debonding [40,41,42,43,44,45,46,47,48]. Nevertheless, a comprehensive study of the phenomena related to the irregular interface geometry effects is often neglected.

The main purpose of this contribution is to show that, from the standpoint of mechanics stress concentration in local regions of a composite at different scale levels could be of the same origin. It is controlled by the irregular geometry of microstructural elements making up the composition (ductile matrix/substrate, brittle ceramic particles/coatings/hardened interlayers, etc.) and the difference in their mechanical properties.

It is found out that the value of local stresses in composites might, by a large factor, exceed the average level of the load applied. The evolution of this effect is attributed to the presence of inhomogeneities with characteristic sizes corresponding to different scales—macro, meso and micro. It is demonstrated that the regions of stress concentration might undergo both compressive and tensile stresses irrespective of the type of external loading. The larger the difference in the mechanical properties of the constituents, the higher is the level of stress concentration developed in the vicinity of inhomogeneities of certain geometry.

The main aim of the paper is to investigate mechanisms of deformation and fracture which are related to complex geometry of interfaces in a composite material. Multiscale analysis of deformation and fracture in composites is performed. A dynamic boundary-value problem is solved numerically by the finite-difference method. Constitutive models for the elastic-plastic deformation and elastic-brittle fracture are developed to describe the mechanical response of steel substrate/aluminum matrix and boride coating/alumina particles. Interface geometries correspond to the configurations found experimentally and are accounted for explicitly in the calculations.

2 Numerical Modelling Across Multiple Spatial Scales

In the frame of the proposed formulation, a multiscale numerical analysis implies at least two factors (Fig. 2): (1) the use of different models to describe the mechanical response of different constituent elements of a composite material under load in order to characterize the physical processes developing in the components and their interplay (Fig. 3), and (2) an explicit consideration of the microstructure of the material that provides information on the characteristic scales for which the models used are valid (Fig. 4).

Fig. 2

Schematics of multiscale numerical simulation

Fig. 3

A set of constitutive models for composite material constituents

Fig. 4

Microstructure of steel with a hardened boride surface layer to be simulated and characteristic sizes of structure inhomogeneities at different scale levels

It is suggested that deformation of composite materials can be described by a system of equations using the laws of conservation of mass and momentum, strain equations, and constitutive relations for the material constituents complemented with initial and boundary conditions (Fig. 3). The models presented in Fig. 3 enable us to handle only particular problems. Notably, the models under discussion have already been tested. The list of those accounting for the great diversity of the physical phenomena and processes observed in loaded solids is by no means complete.

The choice of particular elastoplastic response models numbered 1 through 6 in Fig. 3 depends on the material used as a substrate or a matrix (aluminum-based alloys, different types of steel, etc.) and on the applied loading conditions (high strain rate deformation, quasi-static loading, etc.). Fracture models, such as model 7, are required to describe the mechanical behavior of brittle and viscobrittle inclusions, coatings, and intermediate subsurface layers. Purely elastic or perfectly plastic descriptions (model 1 and 2) can be used as a first approximation.

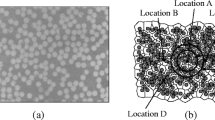
An explicit consideration of the material microstructure makes it possible to introduce a scale factor and specify the length scales where one or another model can successfully be employed (Fig. 4). Figure 1b shows the mesostructure of a coated material, which was used in the calculations and corresponds to that observed experimentally (see Fig. 1). For the case in question, where the interface has a serrated profile and irregular geometry, we might single out certain types of inhomogeneities at different scale levels and their respective characteristic sizes. In particular, boride teeth proper, whose size is ~50–100 μm (Fig. 4b), are independent stress concentrators. A quasiperiodic alternation of boride and steel teeth results in the formation of a peculiar stress-strained state at mesoscale II.

The shape of an individual tooth, is not perfect and exhibits fine structure at a lower scale level. Throughout the interface profile, there are convexities and concavities. The characteristic size of these inhomogeneities is within 5–10 μm (Fig. 4c). The regions of “intrusion” of ductile steel into a more brittle and strong boride material are sources of geometrical stress concentration at mesoscale I. Let us single out two types of such regions with respect to the direction of applied loading: types C and A, along (Fig. 4c) and perpendicular (Fig. 4d) to the x-direction.

The local fracture zone has a characteristic size of ~1 μm (Fig. 4d) and gives rise to stress concentration at the microscale.

A homogenized stress-strain curve reflects the mechanical behavior of the mesovolume at the macroscale. Thus, an introduction of the mesovolume with a boride hardened layer of a complicated geometry in an explicit form allows us to prescribe the length scales—a scale hierarchy of inhomogeneities, whose characteristic sizes might differ by two orders of magnitude.

3 Governing Equations and Boundary Conditions

Let us formulate the governing equations (Fig. 3) in terms of plane strain. In this case there are the following non-zero components of the strain rate tensor:

$$ \dot{\varepsilon }_{xx} = \dot{u}_{x,x} ,\;\dot{\varepsilon }_{yy} = \dot{u}_{y,y} \;\dot{\varepsilon }_{xy} = \frac{1}{2}\left( {\dot{u}_{x,y} + \dot{u}_{y,x} } \right), $$

(1)

where $u_{x}$ and $u_{y}$ are the components of the displacement vector, $\varepsilon_{xx}$, $\varepsilon_{yy}$ and $\varepsilon_{xy}$ are the strain tensor components, the upper dot and comma in the notations stand for the time and space derivatives, respectively.

The mass conservation law and the equations of motion take the forms

$$ {{\dot{V}} \mathord{\left/ {\vphantom {{\dot{V}} V}} \right. \kern-0pt} V} = \dot{\varepsilon }_{xx} + \dot{\varepsilon }_{yy} , $$

(2)

$$ \sigma_{xx,x} + \sigma_{yx,y} = \rho \ddot{u}_{x} ,\;\sigma_{xy,x} + \sigma_{yy,y} = \rho \ddot{u}_{y} , $$

(3)

where $\sigma_{xx}$, $\sigma_{yy}$ and $\sigma_{xy}$ are the stress tensor components, $V$ is the specific volume and $\rho$ is the mass density.

Taking into account the resolution of the stress tensor in the spherical and deviatoric parts

$$ \sigma_{ij} = - P\delta_{ij} + S_{ij} $$

(4)

the pressure and the stress deviator components are written as follow

$$ \begin{aligned} & \dot{S}_{xx} = 2\mu \left( {\dot{\varepsilon }_{xx}^{{}} - \frac{1}{3}\dot{\varepsilon }_{kk}^{{}} - \dot{\varepsilon }_{xx}^{p} } \right),\;\dot{S}_{yy} = 2\mu \left( {\dot{\varepsilon }_{yy}^{{}} - \frac{1}{3}\dot{\varepsilon }_{kk}^{{}} - \dot{\varepsilon }_{yy}^{p} } \right), \\ & \dot{S}_{zz} = 2\mu \left( { - \frac{1}{3}\dot{\varepsilon }_{kk} } \right) = - (\dot{S}_{xx} + \dot{S}_{yy} ),\;\dot{S}_{xy} = 2\mu \left( {\dot{\varepsilon }_{xy}^{{}} - \dot{\varepsilon }_{xy}^{p} } \right),\;\dot{P} = - K\dot{\varepsilon }_{kk} , \\ \end{aligned} $$

(5)

where $K$ and $\mu$ are the bulk and shear moduli, $\dot{\varepsilon }_{ij}^{p}$ is the plastic strain rate tensor, and $\delta_{ij}$ is the Kronecker delta.

To eliminate an increase in stress due to rigid rotations of medium elements, we define deviatoric stresses through the Jaumann derivative

$$ \dot{S}_{ij}^{*} = \dot{S}_{ij} - S_{ik} \omega_{jk} - S_{jk} \omega_{ik} , $$

(6)

where $\omega_{ij} = \frac{1}{2}\left( {\dot{u}_{i,j} - \dot{u}_{j,i} } \right)$ is the material spin tensor.

The strain tensor is the sum of elastic and plastic strain $\varepsilon_{ij} = \varepsilon_{ij}^{e} + \varepsilon_{ij}^{p}$, and $\dot{\varepsilon }_{kk}^{p} = 0$ is the hypothesis of plastic incompressibility. Unloading is elastic.

The boundary conditions on the surface $B_{1}$ and $B_{3}$ simulate uniaxial tension parallel to the X-axis, whereas on the bottom and top surfaces, they correspond to symmetry and free surface conditions, respectively (Fig. 4b). We obtain

$$ \begin{aligned} & \dot{u}_{x} = const = - v\;{\text{for}}\;(x,y) \in B_{1} \;\dot{u}_{x} = const = v\;{\text{for}}\;(x,y) \in B_{3} ,\;\dot{u}_{y} \\ & \quad = 0\;{\text{for}}\;(x,y) \in B_{4} ,\;\sigma_{ij} \cdot n_{j} = 0\;{\text{for}}\;(x,y) \in B_{2} \;\sigma_{xy} \\ & \quad = 0\;{\text{for}}\;(x,y) \in B_{1} \cup B_{3} \cup B_{4} \\ \end{aligned} $$

(7)

Here $B = B_{1} \cup B_{2} \cup B_{3} \cup B_{4}$ is the boundary of the computational domain, $t$ is the computation time, $v$ is the load velocity and $n_{j}$ is the normal to the surface $B_{2}$.

The system of Eqs. (1–7) have to be completed with a formulation for plastic strain rates $\dot{\varepsilon }_{ij}^{p}$.

4 Constitutive Modelling for Plasticity of the Substrate and Matrix Materials

4.1 Physically-Based Strain Hardening

Depending on the loading strain rate and material to be used as a substrate or matrix, different formulations of the constitutive models (models 2–6 in Fig. 3) have to be applied. To describe plasticity (model 3 in Fig. 3), use was made of the plastic flow law

$$ \dot{\varepsilon }_{ij}^{p} = \dot{\lambda }\frac{\partial f}{{\partial S_{ij} }} $$

(8)

associated with the yield condition

$$ f(S_{ij} ) = \sigma_{eq} - \sigma_{A} (\varepsilon_{eq}^{p} ) = 0. $$

(9)

Here $\lambda$ is a scalar parameter, $\sigma_{eq}$ and $\varepsilon_{eq}^{p}$ are the equivalent stress and accumulated equivalent plastic strain

$$ \sigma_{eq} = \frac{1}{\sqrt 2 }\sqrt {\left( {S_{11} - S_{22} } \right)^{2} + \left( {S_{22} - S_{33} } \right)^{2} + \left( {S_{33} - S_{11} } \right)^{2} + 6(S_{12}^{2} + S_{23}^{2} + S_{31}^{2} )} $$

(10)

$$ \varepsilon_{eq}^{p} = \frac{\sqrt 2 }{3}\int\limits_{0}^{t} {\sqrt {\left( {\varepsilon_{11}^{p} - \varepsilon_{22}^{p} } \right)^{2} + \left( {\varepsilon_{22}^{p} - \varepsilon_{33}^{p} } \right)^{2} + \left( {\varepsilon_{33}^{p} - \varepsilon_{11}^{p} } \right)^{2} + 6\left( {\varepsilon_{12}^{p2} + \varepsilon_{23}^{p2} + \varepsilon_{31}^{p2} } \right)} } dt $$

(11)

The function $\sigma_{A} (\varepsilon_{eq}^{p} )$ prescribes isotropic strain hardening in the steel substrate or aluminium matrix. The following phenomenological function can be selected:

$$ \sigma_{A} = \sigma_{s} - \left( {\sigma_{s} - \sigma_{0} } \right)\exp ( - \varepsilon_{eq}^{p} /\varepsilon_{r}^{p} ) , $$

(12)

where $\sigma_{0}$ is the yield point and $\sigma_{s}$ is the strength, $\varepsilon_{r}^{p}$ is the reference value of plastic strain. Model 2 in Fig. 3 describes perfect plasticity at $\sigma_{A} = \sigma_{0}$.

For a more detailed description, $\sigma_{A}$ can be obtained from physical consideration of dislocation dynamics. $\sigma_{A}$ is the athermal part of the stress $\sigma_{eq}$ and associated with long-range obstacles to the dislocation motion. It is independent of the strain rate and mainly depends on the microstructure of the material: the dislocation density and substructures, grain sizes, point defects and various solute atoms. The current yield stress is proposed to be defined in the following way:

$$ \sigma_{A} = \sigma_{0} + \alpha \mu b\sqrt {N (\varepsilon_{eq}^{p} )} + \sum\limits_{j} {\alpha_{1j} P_{j} (\varepsilon_{eq}^{p} )} , $$

(13)

with the Hall-Perth dependence being introduced

$$ \sigma_{0} = \sigma_{0}^{0} + kd^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} $$

(14)

where $\sigma_{0}^{0}$ is the yield point of the single crystal and $d$ is the grain size.

The addend in Eq. (13) is a familiar dependence from physics of plasticity that accounts for a microscopic contribution from a forest of dislocations, where $N$ is the dislocation density. The third summand is associated with the formation of substructures: dislocation cells, band and fragmented substructures, where $\alpha_{1i}$ denotes coefficients accounting for dislocation substructure contributions to strengthening, and the probability functions $P_{j} (\varepsilon_{eq}^{p} )$ are connected with volume fractions of the substructures. Based on the experimental evidence the following form of the exponential law is proposed:

$$ P_{j} (\varepsilon_{eq}^{p} ) { = }\int\limits_{ 0}^{{\varepsilon_{eq}^{p} }} {\lambda_{\text{j}} {\text{exp(}}\eta - { \exp }\eta )d\varepsilon_{eq}^{p} } . $$

(15)

Here $\eta = - \lambda_{j} (\varepsilon_{eq}^{p} - \varepsilon_{eqj}^{p} )$, $\varepsilon_{eqj}^{p}$ is a parameter associated with deformation giving rise to formation of the i-th substructure, and $\lambda_{j}$ specifies the strain range wherein the substructure exists. The volume fraction of the substructure of interest is determined via the distribution function (15) to give

$$ P_{j}^{\nu } (\varepsilon_{eq}^{p} )= {\text{exp(}}1 + \eta - { \exp }\eta ). $$

(16)

For instance, for the only dislocation cell substructure Eq. (13) takes the form

$$ \sigma_{A} = \sigma_{0} + \alpha \mu b\sqrt {N (\varepsilon_{eq}^{p} )} + \alpha_{c} P_{c} (\varepsilon_{eq}^{p} ). $$

(17)

Comparing Eq. (17) with the well-known experimental evidence $\sigma_{A} \propto d_{c}^{ - 1}$ [49], which is similar to Eq. (14), and taking into account the fact that the dislocation cell diameter $d_{c}$ decreases during plastic deformation reaching the saturation point where its value does not depend on the stacking fault energy ($d_{c}^{sat} \approx 0.2\,\upmu{\text{m}}$ for many materials [50, 51]), the following expression can be obtained

$$ d_{c} (\varepsilon_{eq}^{p} ) = \frac{{d_{c}^{sat} }}{{P_{c} (\varepsilon_{eq}^{p} )}} . $$

(18)

The physically-based expression (13) includes microscopic parameters such as elastic moduli, dislocation density, grain size and dislocation cell diameter, module of Burgers vector b, empirical strength coefficient $\alpha$, while purely phenomenological Eq. (12) operates with macroscopic yield point and strength.

4.2 Strain Rate and Temperature Effects

To describe strain rate and temperature sensitivity of steel or aluminum, it is necessary to develop a relaxation constitutive equation (model 4 in Fig. 3). Substituting (8) in the equation for the equivalent plastic strain (11), it can be found

$$ \dot{\varepsilon }_{ij}^{p} = \frac{3}{2}\frac{{\dot{\varepsilon }_{eq}^{p} }}{{\sigma_{eq} }}S_{ij} . $$

(19)

In order to describe the equivalent plastic strain rate $\dot{\varepsilon }_{eq}^{p}$, let us continue proceeding from a dislocation concept of plastic flow. Kinetic equations for the plastic strain rate based on the motion of dislocations are the subject of a considerable amount of literature. Theoretical concepts relevant to the discussion are in part summarized in [52]. Following the model let us define

$$ \dot{\varepsilon }_{eq}^{p} = \dot{\varepsilon }_{r}^{p} \exp \left\{ { - \frac{{G_{0} }}{kT}\left[ {1 - \left( {\frac{{\sigma_{vis} }}{{\tilde{\sigma }}}} \right)^{w} } \right]^{z} } \right\}, $$

(20)

$$ \sigma_{vis} = \sigma_{eq} - \sigma_{A} \left( {\varepsilon_{eq}^{p} } \right)\;T = T_{0} + \int_{0}^{{\varepsilon_{eq}^{p} }} {\frac{\beta }{{\rho C_{v} }}} \sigma_{eq} d\varepsilon_{eq}^{p} . $$

Here $G_{0}$ is the energy that a dislocation must have to overcome its short-range barrier solely by its thermal activation, $\tilde{\sigma }$ is the stress above which the barrier is crossed by a dislocation without any assistance from thermal activation, $k$ is the Boltzmann constant, $\dot{\varepsilon }_{r}^{p}$ is the reference value of the plastic strain rate, $T_{0}$ is the test temperature, $C_{v}$ is the heat capacity, $\beta$ is the fraction of plastic work which is converted into heat. $\beta \cong 1$, $z = 2/3$ and $w = 2$ for many metals [52].

Parameters of the model were derived by solving an initial value problem and by fitting the calculation results to the experimental stress-strain curves under tension at different strain rates and temperatures. For uniaxial loading in the X-direction $\sigma_{xx} = \sigma_{eq}$ and $\varepsilon_{xx} = \varepsilon_{eq}$. In this case the constitutive Eq. (4) takes the form

$$ \sigma_{eq} = E(\varepsilon_{eq} - \varepsilon_{eq}^{p} ) , $$

(21)

where $E$ is the Young’s module. Equations (20), (21) and (12) were solved numerically by a fourth-order Runge–Kutta method.

The results obtained are presented in Fig. 5. In order to validate the model, Eqs. (19) and (20) were introduced into the commercial software ABAQUS and the tension of steel H418 plates was simulated in a plane stress formulation. Here and in what follows, stress $\left\langle \sigma \right\rangle$ was computed as the equivalent stress $\sigma_{eq}$ averaged over the mesovolume $\left\langle \sigma \right\rangle = {{\sum\nolimits_{k = 1,n} {\sigma_{eq}^{k} s^{k} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{k = 1,n} {\sigma_{eq}^{k} s^{k} } } {\sum\nolimits_{k = 1,N} {s^{k} } }}} \right. \kern-0pt} {\sum\nolimits_{k = 1,N} {s^{k} } }}$, where $n$ is the number of computational mesh cells and $s^{k}$ is the k-th cell area. Strain $\varepsilon$ corresponds to the relative elongation of the computational domain in the X-direction $\varepsilon = {{(L - L_{0} )} \mathord{\left/ {\vphantom {{(L - L_{0} )} {L_{0} }}} \right. \kern-0pt} {L_{0} }},$ where $L_{0}$ and $L$ are the initial and current lengths of the computational domain along X. The results show good agreement between the calculations and experiment (Fig. 5d). Model parameters are presented in Table 1. Strain rate effects were not taken into account for Al6061 alloy.

Fig. 5

Predicted mechanical properties of austenitic steels in comparison with the experimental data (a–c) and comparison of the calculation results for H418 steel with those obtained by ABAQUS (d)

Table 1 Material constants and model parameters for different steels and an Al6061 alloy

For the investigated steels, $G_{0} /k = 10.6 \times 10^{ - 5} \,{\text{K}}^{ - 1}$ and $\tilde{\sigma } = 1450$ MPa are the constants which reflect the temperature sensitivity of the material. They were extracted from experimental mechanical tests at different test temperatures. Since corresponding experiments for the austenitic steels were not available, the values of these parameters are suggested to be the same as for HSLA-65 steel defined in [52].

Experimental and calculated stress-strain curves for HSLA-65 steel are presented in Fig. 6. It can be seen that for $\varepsilon < 10 \div 20\%$ Eq. (20) overestimates the current stress and fails to give a correct description of the shape of the stress-strain curve. The overestimation may be due to the fact that the parameter $\dot{\varepsilon }_{r}^{p}$ is assumed as the constant value which is proportional to the density of mobile dislocations $N_{m} \cong 10^{11} \,{\text{cm}}^{ - 2}$ [52], although it is well known that $N_{m}$ changes with the plastic deformation development and reaches its saturation at total strains of 10 ÷ 40% for different steels.

Fig. 6

Stress-strain curves for steel HSLA-65 [52]. Dots—experiment, lines—calculations, using Eq. (20)

In order to take into account the evolution of the dislocation continuum, the plastic strain rate is proposed to be as follows

$$ \dot{\varepsilon }_{eq}^{p} = \dot{\varepsilon }_{r}^{p} F(\varepsilon_{eq}^{p} )\exp \left\{ { - \frac{{G_{0} }}{kT}\left[ {1 - \left( {\frac{{\sigma_{vis} }}{{\tilde{\sigma }}}} \right)^{w} } \right]^{z} } \right\} $$

(22)

where

$$ F(\varepsilon_{eq}^{p} ) = F^{*} + (1 - F^{*} ) \cdot \exp \left( { - \frac{B}{\left| g \right|b}\varepsilon_{eq}^{p} } \right) $$

(23)

is the fraction of mobile dislocations (Kelly and Gillis 1974) which decreases at the initial stages of plastic flow due to stalemating events. Here $\left| g \right| = 0.5$ is the orientation factor, $b \cong 3.3{\text{\AA}}$ is the magnitude of the Burgers vector, $F^{*}$ is the minimum value of $F$.

It is suggested for $F^{*}$ and $B$ to be connected with the reciprocal mean free path for stalemating events as follows. Parameter $B$ is attributed to the initial state of the material, when the free path is a half of an average grain size $d$

$$ B = \frac{2}{{dN^{0} }}, $$

(24)

where $N^{0}$ is the initial dislocation density.

In the equation for $F^{*}$, the free part is calculated from some intermediate state, using the dislocation cell diameter $d_{c}^{sat}$ formed inside the grains

$$ F^{*} = \frac{{N^{0} d}}{{N^{*} d_{c}^{sat} }}, $$

(25)

where $N^{*}$ is the maximum dislocation density. In this formulation the density of mobile dislocations

$$ N_{m}^{*} = N^{*} F^{*} $$

(26)

is a measure for the saturation density. Defining $N^{*} = 5 \times 10^{12} \,{\text{cm}}^{ - 2}$, we obtain from Eq. (26) $F^{*} = 0.02$. The grain size $d = 15\,\upmu{\text{m}}$ for HSLA-65 steel [52], hence $N^{0} \cong 1.33 \times 10^{9} \,{\text{cm}}^{ - 2}$ from Eq. (25) and $B = 0.01\,\upmu{\text{m}}$ from Eq. (24).

The system of Eqs. (1)–(7), (12) and (22) for a rectangular homogeneous region was solved numerically by the finite-difference method (Sect. 6). Figure 7 shows the results of plane strain calculations for varying strain rate and temperature. For reference, a dotted curve (296 К, 8000/s) is plotted in the figure to present calculations according to the model, where $\dot{\varepsilon }_{eq}^{p}$ was computed, using Eq. (20). Relation (22) is seen to provide a more accurate description of stress-strain curves than Eq. (20) for small deformations ($\varepsilon \le 20\%$).

Fig. 7

Stress strain curves calculated using Eq. (22) for different temperatures (a) and strain rates (b)

4.3 Lüders Band Propagation and Jerky Flow

Experimental stress-strain curves for HSLA-65 steel are characterized by the upper and lower yield stresses (Fig. 6), which could be an evidence of Lüders band propagation.

The jerky-flow phenomenon in alloys has been well studied experimentally, for instance in [52,53,54,55,56,57,58,59], and attributed to the formation of localized deformation bands at the mesoscale. As a special case of such an anomalous behavior, Lüders band propagation is characterized by single displacement of macroscopic localization zone along the test piece. It is generally agreed that the microscopic essence of the discontinuous yielding is the dynamic aging of dislocations by diffusing solute atoms. There are some physically based attempts to simulate the propagation of bands of localized plastic deformation [60,61,62].

In this paper, to describe Lüders band propagation (model 5 in Fig. 3), use was made of a phenomenological approach [63]. It is suggested that the methods of continuum mechanics and discrete cellular automata can be used in combination. The approach relies on the experimentally established fact that the plastic deformation originates near surfaces and interfaces and subsequently propagates from the surface sources as localized deformation front.

Each cell of the computational grid is treated as a cellular automaton which can be either in elastic or plastic state. Initially all cells are elastic. Elastic-to-plastic transition of a certain computational cell is controlled by both the stress value in this local point and the deformation behavior of the neighboring computational cells. Noteworthy, different yield criteria are formulated for the surface cells and for local regions in the bulk of the material. In the former case, a local region near the surface becomes plastic if the equivalent stress acting there reaches its critical value; the stress-based criterion is used for the surface and interface cells. The response of an internal region is elastic until two conditions are satisfied: the equivalent stress in this cell achieves the yield limit and the plastic deformation accumulated in any of the neighboring cells amounts to its critical value. In such a way, the internal regions are successively involved in plastic deformation by flows propagating from the surface and interface sources.

Mathematically, the stress-based yield criterion given by a physically-based constitutive model for any local internal region $D$ is complemented with the necessary condition whereby there must be plastic deformation at least in one of the regions $D^{*}$ adjacent to $D$:

$$ \varepsilon_{eq}^{p*} = \varepsilon_{0} . $$

(27)

Here, $\varepsilon_{0}$ is the new parameter that reflects material properties associated with the strain aging effects. This is a critical value of the equivalent plastic strain accumulated in the $D^{*}$ region, which is necessary for the onset of plastic flow in the region $D$.

Using the criterion (27) and the constitutive model (22) in combination, we have performed numerical simulations of Lüders band propagation in a wide range of strain rates and temperatures. Figure 8 demonstrates calculated stress-strain curves at early deformation stages ($\varepsilon \le 3\%$). The computational domain is approximated by a regular mesh consisting of 600 cells, $n_{x} = 80,n_{y} = 20$. The parameter $\varepsilon_{0} = 8 \times 10^{ - 4}$. For comparison, the dashed curve in Fig. 8b ($T_{0}$ = 296 K, the strain rate is 1000 $s^{ - 1}$) shows the initial portion of the curve calculated in the assumption of homogeneous deformation (see Fig. 7b).

Fig. 8

Initial portions of stress-strain curves calculated using Eqs. (27) and (22) for different temperatures (a) and strain rates (b)

The combined approach is seen to provide a more accurate description of the experimental stress-strain relations for HSLA-65 steel (see Fig. 6). Plastic flow first originates near the left boundary of the computational domain where load is applied and propagates along the specimen in the form of a localized plastic deformation front (Fig. 9a). The material ahead of the front is elastic and the plastic strain is accumulated behind the moving Lüders band front. Similar behavior was observed in experiments. Presented in Fig. 9b are the experimental data on Lüders band propagation in a steel plate surface-hardened by the electron-beam-induced deposition [64]. This process leads to the occurrence of the upper and lower yield points in the macroscopic stress-strain curve and a zone of slow variation in the current resistance to load—the yield plateau (Fig. 8).

Fig. 9

Equivalent plastic strain distributions for Lüders band propagation: calculation results (a) where A–E are the material states corresponding to the points A–E in Fig. 8b and experimental data [64] (b)

On further loading, the stress relaxation in the elastic region slows down (Fig. 10). Simultaneously, the strain hardening in the expanding plastic flow region makes an increasingly greater contribution to the macroscopic stress. Therefore, the yield plateau appears which is characterized by a slow variation in the current resistance to deformation (Fig. 8). In this stage, the relative elongation of the specimen occurs primarily by plastic deformation of the zone located behind the front.

Fig. 10

Equivalent stress filed at a compressive strain corresponding to the point A in Fig. 8b

The approach discussed was further developed to account for the Portevin-Le Chatellier effect (model 6 in Fig. 3) associated with sequential propagation of multiple localized deformation bands from the specimen ends (model 6 in Fig. 3). Experimental observations of unstable deformation effects [55,56,57,58,59] show that propagation of a localized deformation band corresponds to each drop in stress seen in the stress-strain curve. As a rule, the stress amplitude at that point and the average quasi-homogeneous deformation during time intervals between the sequential band formation are found to increase with strain hardening. Therefore, condition (27) was modified to

$$ \varepsilon_{eq}^{p*} = \varepsilon^{*} (\xi ,\varepsilon_{0} ),\;\xi = {{\sigma_{A} (\varepsilon_{eq} ,\sigma_{0} )} \mathord{\left/ {\vphantom {{\sigma_{A} (\varepsilon_{eq} ,\sigma_{0} )} {\sigma_{0} }}} \right. \kern-0pt} {\sigma_{0} }}. $$

(28)

The localized-deformation bands are formed near specimen loaded ends at regular intervals with the proviso that $\Delta \varepsilon_{eq}^{p\min } = \varepsilon^{\Delta } (\xi ,\varepsilon_{0} )$. Here, $\Delta \varepsilon_{eq}^{p\min }$ is a minimum increase in the equivalent plastic deformation as the result of propagation of the previous band. Thus, in the model proposed, the drop in stress and the periodic generation pattern of the localized deformation bands are expressed by some dimensionless parameter $\xi$ accounting for the strain hardening. The simple relations

$$ \varepsilon^{*} = \varepsilon_{0} \exp \left( {\frac{\xi }{1 - \xi }} \right),\;\varepsilon^{\Delta } = \varepsilon_{0} (\xi - 1), $$

(29)

were derived in numerical simulations of loading of an Al6061 alloy that exhibits unstable plastic flow [55]. The parameters for a hardening function of the type given in Eq. (12) were chosen according to the experiments performed in [55] (see Table 1). The calculated results demonstrated in Figs. 11 and 12 are an evidence for an essentially nonhomogeneous stressed-strained state at the yield point. The stress-strain curve is a serrated line (Fig. 11).

Fig. 11

Calculated stress-strain curve for an Al6061 alloy (a) and three selected sections shown at enlarged scales (b–c)

Fig. 12

Equivalent plastic strain rate distributions for strain states 1–14 in Fig. 11

Each drop in the curve (Fig. 11d) corresponds to the formation and propagation of one or two localized deformation bands (Fig. 12). According to Eq. (29), the quantities $\varepsilon^{*} (\xi ,\varepsilon_{0} )$ and $\varepsilon (\xi ,\varepsilon_{0} )$ are rather small in early plastic flow stages, as a result of which the stress amplitude during the drastic decrease in the equivalent stress is low (Fig. 11c). On further loading, the deformation fronts are set in a regular motion as a consequence of hardening and nonhomogeneous deformation due to propagation of the previous localized-deformation band. The band can move faster or slower or can even cease to move (Figs. 12 and 14), which causes oscillations in the stress-strain curves (Fig. 11b and d). Propagation of one deformation band is responsible for oscillations of larger amplitude (Figs. 12 (8–14), 11d), whereas formation of two deformation fronts propagating from the boundaries of the computational domain in opposite directions is associated with oscillations of smaller amplitude (Figs. 12 (1–7) and 11d).

4.4 Brittle Fracture of Ceramic Particles and Coatings

A distinctive feature of deformation of brittle materials is the fact that under compression their fracture can occur along planes where the macroscopic stresses are thought to be zero [65], so that the crack can propagate along the direction of the applied loading (the X-direction in Fig. 13). For instance, for particle-reinforced metal matrix composites and coated materials it was experimentally shown that cracks in the particles and in the coating under compression are largely oriented along the direction of compression [66, 67]. For the case of modeling of a homogenous specimen, however, the stress tensor components in the transverse direction, $Y$, which are supposed to open this crack, are identically equal to zero. Thus, in experiments, cracks propagate under stresses that are zero from the standpoint of mechanics. To describe fracture in this case use is made of strain-based criteria. The simplest one is the criterion of positive elongation along the planes normal to the above-mentioned cross-section, [65], i.e., along $Y$.

Fig. 13

Fracture under tension and compression

In what follows, we are going to show that in simulation of composites the stress tensor components along $Y$ are nonzero in contrast to the case of a homogeneous material. Moreover, at the interfaces there are localized regions oriented with respect to the direction of externally applied compression so that they experience tensile stresses. It is these stresses that can give rise to crack opening and propagation along the direction of external loading.

To describe fracture of the boride coating and corundum particles (model 7 in Fig. 3) use was made of the maximum distortion energy criterion. The criterion is thought to poorly describe fracture of brittle materials. In this work, we show that when it is applied to composite materials with realistically simulated interface geometry, where the calculations contain localized regions of tensile stresses under any type of external loading, the maximum distortion energy criterion works fairly well and provides a correct description of brittle materials and composites. We have modified the criterion to account for the difference in strength values of the tensile and compressive regions:

$$ \sigma_{eq} = \left\{ {\begin{array}{*{20}l} {C_{ten} ,} \hfill & {if\;\varepsilon_{kk} > 0} \hfill \\ {C_{com} ,} \hfill & {if\;\varepsilon_{kk} < 0,} \hfill \\ \end{array} } \right. $$

(30)

where $C_{com}$ and $C_{ten}$ are the values of the tensile and compressive strengths. According to the criterion, Eq. (30), fracture occurs in the local regions undergoing bulk tension. The following fracture conditions are prescribed for any local region of the coating: if the cubic strain $\varepsilon_{kk}$ has a negative value and $\sigma_{eq}$ reaches its critical value $C_{com}$, then all components of the deviatoric stress tensor in this region are taken to be zero, and in the case of $\varepsilon_{kk} > 0$ and $\sigma_{eq} \ge C_{ten}$, pressure $P$ is equal to zero as well. Elastic modules for the composite constituents and strength parameters for the boride coating and corundum particles are presented in Table 2.

Table 2 Elastic modules, densities and strength constants [15, 68]

5 Finite-Difference Numerical Procedure

The boundary-value problems in terms of the plane strain were solved numerically by the finite difference method (FDM) [69, 70]. In contrast to the finite-element method (FEM), where the solution of the system is approximated, the FDM approximates the derivatives entering this system.

Let us look at a microstructure region near the base of one of the teeth (Fig. 14a). The region is approximated by a mesh containing $N$ uniform rectangular cells $N = N_{x} \times N_{y}$ (Fig. 14b). The mesh is “frozen” into the material and is deformed together with it. The system of equations for this mesh is replaced by a difference analog. Use is made of an explicit conditionally stable scheme of the second order of accuracy. For the time step, it is necessary that the Courant criterion is satisfied as follows:

Fig. 14

A-type region of the composite structure (a) and discretization of the region (b)

$$ \Delta t = k_{C} \frac{{h_{\min } }}{{C_{l} }}, $$

(31)

where $h_{\min }$ is the minimum step of the mesh, $C_{l}$ is the longitudinal velocity of sound, and $0 < k_{C} < 1$ is the Courant ratio. The stability condition, Eq. (31), implies that an elastic wave within one time step does not cover the distance longer than the minimum mesh step.

The values of stress $\sigma_{ij}$, strain $\varepsilon_{ij}$, and density $\rho$ are computed in the cell centers (points I, II …. in Fig. 15), while those of the displacements $u_{i}$ and velocities $\dot{u}_{i}$ correspond to the mesh nodes (points 1, 2 …. in Fig. 15). Let us use the following definition of partial derivatives:

Fig. 15

Schematic representation of approximating the space derivatives

$$ \frac{\partial F}{\partial x} = \mathop {\lim }\limits_{D \to 0} \frac{{\int_{B} {F\left( {\bar{n} \cdot \bar{i}} \right)ds} }}{D},\frac{\partial F}{\partial y} = \mathop {\lim }\limits_{D \to 0} \frac{{\int_{B} {F\left( {\bar{n} \cdot \bar{j}} \right)ds} }}{D}, $$

(32)

where $B$ is the boundary of region $D$, $s$ is the arc length, $\bar{n}$ is the normal vector, and $\bar{t}$ is the tangent vector (Fig. 15).

$$ \bar{n} = \frac{\partial x}{\partial n}\bar{i} + \frac{\partial y}{\partial n}\bar{j} = \frac{\partial y}{\partial S}\bar{i} - \frac{\partial x}{\partial S}\bar{j} . $$

(33)

Applying Eqs. (32)–(33) to the rectangular regions bounded by dashed lines (Fig. 15), we obtain for the case of stress derivatives corresponding to, e.g., node $k$

$$ \int\limits_{C} {\sigma_{ij} \left( {\bar{n} \cdot \bar{i}} \right)ds} = \int\limits_{C} {\sigma_{ij} \frac{\partial y}{\partial S}ds} , $$

from which

$$ \left( {\sigma_{ij,x} } \right)^{k} = \frac{1}{D}\left( {\sigma_{ij}^{I} (y_{2} - y_{1} ) + \sigma_{ij}^{II} (y_{3} - y_{2} ) + \sigma_{ij}^{III} (y_{4} - y_{3} ) + \sigma_{ij}^{IV} (y_{1} - y_{4} )} \right) $$

(34)

and

$$ \int\limits_{C} {\sigma_{ij} \left( {\bar{n} \cdot \bar{j}} \right)ds} = \int\limits_{C} {\sigma_{ij} \frac{\partial x}{\partial S}ds} , $$

whence

$$ \left( {\sigma_{ij,y} } \right)^{k} = \frac{1}{D}\left( {\sigma_{ij}^{I} (x_{2} - x_{1} ) + \sigma_{ij}^{II} (x_{3} - x_{2} ) + \sigma_{ij}^{III} (x_{4} - x_{3} ) + \sigma_{ij}^{IV} (x_{1} - x_{4} )} \right) . $$

(35)

Derivatives $u_{i,j}$, in their turn, correspond to the cell centers and are calculated from the values of $u_{i}$ in the surrounding nodes. In particular, for cell $m$, we have

$$ \left( {u_{{i,x}} } \right)^{m} = \frac{1}{{2D}}\left( {\begin{array}{*{20}c} {\left( {u_{i}^{5} + u_{i}^{6} } \right)(y_{6} - y_{5} )\left( {u_{1}^{6} + u_{i}^{7} } \right)(y_{7} - y_{6} )\, + } \\ {\left( {u_{i}^{7} + u_{i}^{8} } \right)(y_{8} - y_{7} )\left( {u^{8} + u_{i}^{5} } \right)(y_{5} - y_{8} )} \\ \end{array} } \right) $$

(36)

$$ \left( {u_{{i,y}} } \right)^{m} = \frac{1}{{2D}}\left( {\begin{array}{*{20}c} {\left( {u_{i}^{5} + u_{i}^{6} } \right)(x_{6} - x_{5} )\left( {u_{1}^{6} + u_{i}^{7} } \right)(x_{7} - x_{6} )\, + } \\ {\left( {u_{i}^{7} + u_{i}^{8} } \right)(x_{8} - x_{7} )\left( {u^{8} + u_{i}^{5} } \right)(x_{5} - x_{8} )} \\ \end{array} } \right) $$

(37)

where $D$ is the area of the respective quadrangle. The computation is performed in time steps, moving from one layer $n$ to another $n + 1$.

$$ \dot{u}_{i} = \frac{{u_{i}^{n + 1} - u_{i}^{n} }}{\Delta t} $$

(38)

In modeling multi-phase materials, the interface between the microstructure constituents goes across the computational mesh nodes (Fig. 15, thick solid line), with the properties of the two materials prescribed on either side of this interface. The continuity of displacements and normal stresses at this interface is, therefore, preserved, i.e., the conditions of an ideal mechanical contact are satisfied. It is shown in [69] that in the case where the densities of the two materials differ only slightly, the approximating equations, Eqs. (34) and (35), at this interface could be used without any changes. Inaccuracies might appear if we consider, e.g., a solid–liquid interface. In the latter case, it is reasonable to use a formula taking into account both left and right limits in the approximation.

6 Coated Materials

6.1 Overall Plastic Strain and Fracture Behavior Under Tension of the Coated Material with Serrated Interface

In this Section a model microstructure of coated steel DC04 (Fig. 5) with a toothed interface is investigated under tension (Fig. 16a). Figure 16b illustrates a macroscopic stress-strain curve for the mesovolume. The stages in the stress-strain curve are due to the fact that the substrate and coating materials behave in different ways in the corresponding deformation stages: 1—the substrate and coating experience elastic strain, 2—plastic flow develops in the substrate, whereas the coating is still in the elastic state, 3—a cracking of the coating.

Fig. 16

Computational mesovolume (a) and its stress-strain curve under tension (b)

Because of the difference in the elastic moduli between the coating and the substrate, the stress and strain distributions are nonuniform even at stage 1. At stage 2, in turn, two stages of plastic deformation can be distinguished. Initially, plastic strains are initiated near the stress concentrators at the root of boride teeth (Fig. 17a). As the loading increases, plastic deformation propagates deep into the specimen, gradually covering the steel-base regions between the boride teeth (Fig. 17b). Thus, at stage 2.1 (Fig. 16b), plastic flow is localized near the teeth-concentrators and the main part of the base material is still in the elastic state. When an average stress level in the steel base exceeds the yield point, the main part of the base material becomes plastic—stage 2.2 is realized (Fig. 16b) at which the macroscopic stress-strain curve sharply changes the slope. As the plastic flow develops from stage 2.1 to stage 2.2, localized shear bands are formed from the stress concentrators near the boride teeth (Fig. 17c). The bands develop at an angle of about 45° to the axis of loading. Under further loading the average level of plastic strain in the substrate, as well as the degree of strain localization in the bands is increased.

Fig. 17

Equivalent plastic strain distributions for tensile strains of 0.08 (a), 0.1, (b) and 0.16% (c) shown in Fig. 16

A similar conclusion can be drawn relative to a value of the stress concentration at the “coating–base material” interface. Local concentrations of stresses arise at stage 1. Their distribution is due to the geometry of boride teeth. At the elastic stage, values of local stresses relative to an average level of the equivalent stress do not change in the coating. As plastic flow in the base material develops, the stress concentration increases. At stage 2.1, this effect is less pronounced—the patterns given in Fig. 18a are close to the corresponding distributions at stage 1. An intensive straining of the base material at stage 2.2 leads to a sharp nonlinear increase of local stresses (Fig. 18c).

Fig. 18

Equivalent stress distributions at tensile strains lettered by A and A in Figs. 16 and 17

In this case, the rate of increase of the equivalent stresses can differ for various concentrators. For example, we can see from Fig. 18 that at the stage close to elasticity three stress concentrators lying at the center of the investigated region have almost the same power (Fig. 18a). As plastic flow develops, the stresses in one of these concentrators increase relatively quicker and at the prefracture stage reache a maximum (Fig. 18c).

Stage 3 is the stage of composite failure. Plastic deformation in the base material and cracking in the coating develop simultaneously. These processes are interrelated and interconsistent. When $\sigma_{eq}^{\max }$ exceeds a value of $C_{ten}$, a first local fracture zone forms in the coating. The surrounding regions of the material begin to intensely deform and the crack propagates toward the free surface perpendicular to the direction of tension (Fig. 19). The crack formation is a dynamic process: there appears a new free surface from which release waves propagate, causing an unloading of the coating material (Fig. 19a). A descending portion is observed on the stress-strain curve (Fig. 16, stage 3). A localized plastic flow enhances in the steel base near the place of crack insipience (Fig. 19b).

Fig. 19

Equivalent stress (a) and plastic strain distributions (b) (cracked regions in the coating are given in black) for the state D presented in Fig. 16. Total strain—0.19%

6.2 Interface Asperities at Microscale and Mesoscale I. Convergence of the Numerical Solution

Let us examine the loading of two different-scale regions of the coated H418 steel (Fig. 5). The first region is shown in Fig. 14. It is an A-type region at mesoscale I (see Fig. 4). The results of calculations under tensile conditions are given in Figs. 20 and 21. The crack nucleates at the hump of the convexity and propagates towards the specimen surface. Crack propagation is a purely dynamic process occurring at velocities approximating that of sound. The time of crack propagation from the interface to the specimen surface is small compared to the characteristic time of quasistatic loading. The cracking can be regarded as a formation of new free surfaces, from which elastic release waves begin to propagate. The wave dynamics of crack propagation is clearly shown in Fig. 20, where equivalent stress patterns are presented.

Fig. 20

Mesh-dependent equivalent stress and fracture patterns in the region presented in Fig. 14 in tension

Fig. 21

Homogenized stress-strain curves (a) and the stress maximum values versus the number of cells in the X-direction (b)

To verify the solution convergence, a set of calculations was performed with the step varying in space (Figs. 20 and 21). The total number of cells $N$ in the computational mesh in each case was: 1222, 5035, 8820, 12,768, 19,950, 35,420 and 79,800. The computations showed that the fracture region has a physically-based size that is controlled by the interface geometry—its curvature, and only weakly depends on the size of a local fracture region.

Shown in Fig. 21a are the respective stress-strain curves. The drooping part of the curves corresponds to the initiation and propagation of a unit crack. Figure 21b depicts the dependence of the maximum value of $\left\langle \sigma \right\rangle$, corresponding to the onset of crack propagation, on the computational mesh size. It is evident that the solution is convergent and well approximated by the exponential law (dotted line)

$$ \left\langle \sigma \right\rangle_{\max } = \sigma_{act} + \sigma_{mesh} \exp \left( {{\raise0.7ex\hbox{${N_{x} }$} \!\mathord{\left/ {\vphantom {{N_{x} } {N_{ref} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${N_{ref} }$}}} \right), $$

(39)

where $\sigma_{act}$ = 556 MPa is the actual stress, $\sigma_{mesh}$ = 140 MPa is the mesh dependent overestimation and $N_{ref}$ = 79 is the reference number of cells.

For the second computational run, we selected a larger region (Fig. 22). This region is part of the structure given in Fig. 4; it includes the region in Fig. 14, and contains both A- and C-type inhomogeneities. Figure 23 is an illustration of the computation results under different types of external loading: tension and compression. It is evident that initiation and propagation of cracks under tensile and compressive loading occurs in different places. Under tension, cracks primarily propagate from the teeth to the specimen surface, while under compression—from one lateral face of a tooth to the other. This phenomenon is discussed in Sect. 7.4 in details.

Fig. 22

Calculated region containing characteristic A- and C-type inhomogeneities

Fig. 23

Mesh-dependent equivalent stress and fracture patterns for a region containing A- and C-type inhomogeneities under tension and compression

The investigations of mesh convergence showed that in the case where a step in space is quite small, in other words when an A-type characteristic convexity of the least curvature is approximated by as many as 10 computational cells, the character of fracture changes, but only slightly. In Fig. 24a the curves under both tension and compression are presented with the convergence parameters shown in Table 3. Figure 24b shows an averaged estimation of the convergence. An average error $\delta$ connected with the mesh size effects is calculated as

Fig. 24

Stress maximum values under tension and compression (a) and an average error (b) versus the number of cells in the X direction

Table 3 Convergence exponential parameters for the crack initiation in the coated steel

$$ \delta = \frac{{\left\langle \sigma \right\rangle_{\max } - \sigma_{act} }}{{\sigma_{act} }} \cdot 100\% . $$

(40)

The dependence is approximated by the following formula (dotted line in Fig. 24b)

$$ \delta = 28.5\exp \left( { - \frac{{N_{x} }}{136}} \right). $$

(41)

The calculations discussed in this paragraph yield the following conclusions. Interface convexities are sources of unit cracks in the coating. The mesh-convergence analysis showed that the solution for this system of primary cracks converges when the step in space is decreased. The finer the mesh, the more detailed the fracture pattern, while the general behavior is similar for different meshes. There are limiting real stress and strain values for the onset of fracture, which are controlled by the physical geometry of concavities and their curvature. For the investigated microstructure and properties of contacting materials, the maximum mesh size error is about 28%.

6.3 Fracture of the Coating with Plane Interface. Macroscale Simplification

In this Section, the fracture criterion, Eq. (30), is shown to provide an adequate description of directions of crack propagation under different types of external loading: tension and compression. Let us simulate tension and compression of a specimen with a plane interface, i.e., excluding the interface curvature factor. Since the interface is plane, there is no concentration of tensile stresses. Fracture would not appear locally as we have excluded the cause for its local initiation. In this case, we have to artificially nucleate cracking by initially introducing a single fractured zone at the steel–boride coating interface. Even if an interface does not exhibit any serrated structure and appears to be regular at a certain scale, in the places of its adhesion to the substrate there could be various inhomogeneities, including cracks and discontinuities.

In Fig. 25, we show the results of computations under tensile and compressive loading. The differences in the direction of crack propagation are clearly seen: propagation is along the interface in the case of compression and perpendicular to it in the case of tension. For the latter, the coating separates along the interface due to the absence of boride teeth grown into the steel substrate. Thus, the fracture criterion, Eq. (30), correctly describes the direction of crack propagation in a brittle material, and its use, combined with an explicit interface of a complicated geometry, would allow us (as it will be shown later in Sect. 7.4) to interpret a possible mechanism of fracture initiation. This mechanism, according to our simulation results, is associated with the mechanical concentration of tensile stresses in the places where the interface curvature changes.

Fig. 25

Crack propagation in the coating with a plane interface under tension and compression

6.4 Plastic Strain Localization and Fracture at Mesoscale II. Effects of the Irregular Interfacial Geometry Under Tension and Compression of Composites

In the following sections we consider a real microstructure of a coated material with an interface of irregular geometry (Fig. 4b). Steel STE250 (Fig. 5) was selected as a substrate to be coated by diffusion borating. A macroscopic response of the composite microstructure under different external loading conditions is presented in Fig. 26.

Fig. 26

Calculated stress-strain curves of the coated material under tension and compression. The respective stress and strain distributions in the mesovolume for states 1–13 are given in Figs. 27, 28 and 29

According to the calculated dependences, the coated material shows higher tolerance to compressive stresses than to external tensile loading: the macroscopic yield strength, both in terms of stress and strain, is higher in the case of compression (see Fig. 26). This mechanical behavior is typical for composite materials and, as the calculations show, is associated with the principal difference of fracture processes in the coating under different external loading conditions.

Figure 27 shows the distribution of the stress tensor components under external compressive loading for the cases of needle-like and plane “coating-substrate” interfaces. It can be seen that under uniaxial loading of a coated material with the plane interface along the X-direction, only the values of $\sigma_{xx}$ remain nonzero throughout the computational domain. In contrast, the serrated shape of the substrate–coating interface favors the development of a complex stressed state with nonzero values of the stress component $\sigma_{yy}$. Note that it is in the Y-direction that the material experiences both compressive and tensile stresses which are in their absolute values comparable to the values of external compressive loads. Thus, the regions of the steel substrate located between the boride teeth are subjected to compressive stresses while the teeth themselves experience tensile stresses.

Fig. 27

Distributions of stress tensor components (×100 MPa) for needle-like (a) and plane “coating-substrate” interfaces (b) at a strain corresponding to point (1) in Fig. 26

Should we change the direction of external loading and address tension rather than compression, the pattern presented in Fig. 27 would be the same both qualitatively and quantitatively, the difference being in the sign of the stress tensor components. Thus, the local tensile stresses develop in different places under tension and compression. This fact is responsible for the difference in fracture processes under tension and compression (Fig. 28).

Fig. 28

Equivalent stress distributions for compressive (2–7) and tensile (8–13) strains (cf. Fig. 26)

Both tension and compression cracks originate in the local tensile regions. Under compression, the regions are situated at the lateral side of the boron teeth (red color regions in Fig. 27). Cracks successively nucleate on boride tooth sides and propagate along the axis of compression (Fig. 28, states 2–7). No formation of the main longitudinal crack is, however, observed. The upper coating layer maintains its stressed state and resists to the load, while multiple cracking of a boride tooth unloads the composite in the intermediate sublayer (Fig. 28, state 7). Thus, the presence of a serrated structure grown into the steel substrate prevents the coating from spalling. The stress-strain curve in this case exhibits local drops of the averaged stress, whose general level, however, continues to increase, and no catastrophic loss of strength is observed (see Fig. 26b).

A different fracture pattern is found under external tension (Fig. 28, states 8–13). The crack nucleates in the local region of highest concentration of tensile stress, which is situated at a boron tooth base, and propagates in the boride coating towards the free surface of the specimen. This unloads the material along the direction of applied tension. A descending portion appears in the stress-strain curve (points 8–13 in Fig. 26).

The formation of longitudinal and transverse cracks was found experimentally during nanoindentation (Fig. 29b), which, due to its specific geometry, gives rise both to tensile and compressive conditions in the coating within one and the same experiment. Cracks in this experiment propagate in different ways: perpendicular and parallel to the direction of applied tensile and compressive loading, respectively. The same result was obtained in the discussed simulations of two different experiments on uniaxial compression/tension (Fig. 29a). Note that the key role belongs to the complicated geometry of the interface and the presence of regions undergoing localized tensile stresses.

Fig. 29

Equivalent plastic strain distributions for states 2 and 13 (see Figs. 26 and 28) (a) and microscopic section of a TiN coating deposited on stainless steel after nanoindentation [67] (b)

6.5 Dynamic Deformation of the Coated Material

To describe the mechanical response of the steel substrate under dynamic loading use was made of the constitutive Eq. (20) taking into account plastic strain rate and temperature in an explicit form. This equation allows a prediction of the mechanical properties of austenitic steels (Fig. 5). Boron coating is elastic-brittle. Experimental evidence shows that the elastic modules as well as the strength of brittle ceramics weakly depend on the strain rate. Therefore, strain rate sensitivity for the boron material was not introduced into the model formulation.

A series of numerical compression and tension tests were carried out by varying the strain rate externally applied (Fig. 30). The calculations show a difference between the composite responses under different types of loading: tension and compression. The following conclusions can be made.

Fig. 30

Homogenized stress-strain curves under compression and tension at different strain rates

First, under the high-strain-rate tension the fracture process intensifies in comparison with that observed under quasistatic loading. Figure 31 shows the simulation of crack initiation and growth under strain rate of $24 \times 10^{3} \,{\text{s}}^{ - 1}$. Comparing the results with those presented in Fig. 28 (states 8–13), it can be seen that under quasistatic loading only one crack propagates, whereas under a high strain rate multiple cracks arise. The stress under a high strain rate increases rapidly, and release waves from the first crack formation are not in time for unloading the nearby A-type stress concentration regions, i.e. the equivalent stress in one of these regions reaches the strength value $C_{ten}$ before the release wave arriving (see Fig. 31, states 2–3).

Fig. 31

Coating cracking at a strain rate of $24 \times 10^{3} \,{\text{s}}^{ - 1}$. Equivalent stress and fracture patterns correspond to states 1–6 shown in Fig. 30

The second conclusion is that the macroscopic strength under tension changes, but only slightly with the strain rate increasing, while both the total strain and homogenized stress of the fracture onset strongly depend on the value of the compression strain rate (Fig. 30). Figure 32 shows the stress, plastic strain and fracture patterns under compression at different strain rates. The simulations show that the higher the strain rate, the less intensive the cracking of the coating and, as a result, the higher the dynamic strength of the coated material (see Fig. 30). The explanation is the following. The value of stress concentration in C-type regions depends on the difference between mechanical properties of the steel and boron ceramics. According to the model formulation, the stress in the boron material does not change but the current dynamic yield stress of the steel increases with the strain rate increasing (Fig. 5). Therefore, the stress difference at a certain macroscopic strain decreases, and this arises only due to plasticity of the steel substrate. As the analysis of the calculation results showed, the fracture of the coating under tension develops at the elastic stage of composite deformation. The difference discussed does not change with the strain rate increasing at the elastic stage, and there is no change in the macroscopic strength.

Fig. 32

Distributions of equivalent stresses and the equivalent plastic strains (fractured regions in the coating are marked by black color) for different strain rates of compression. Total strain—0.37% (see Fig. 30)

The dependence of the macroscopic stress on the compression strain rate is shown in Fig. 33a for different strains (Fig. 30). The curves are well approximated by the exponential law (dotted lines)

Fig. 33

Homogenized stress values for different compressive strains (a) and relative increase in the stress (b) versus the strain rate of compression

$$ \left\langle \sigma \right\rangle = \sigma_{dyn} - (\sigma_{dyn} - \sigma_{stat} )\exp \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {\dot{\varepsilon }_{ref} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\dot{\varepsilon }_{ref} }$}}} \right), $$

(42)

where $\sigma_{dyn}$ is the saturation dynamic stress, $\sigma_{stat}$ is the stress under quasistatic loading, and $\dot{\varepsilon }_{ref}$ is the reference strain rate. Considering the relative value, the formula can be rewritten as

$\varSigma = \Delta \varSigma \exp \left( {{\raise0.7ex\hbox{${\dot{\varepsilon }}$} \!\mathord{\left/ {\vphantom {{\dot{\varepsilon }} {\dot{\varepsilon }_{ref} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\dot{\varepsilon }_{ref} }$}}} \right)$, where $\varSigma = \frac{{\sigma_{dyn} - \left\langle \sigma \right\rangle }}{{\sigma_{dyn} }}$, $\Delta \varSigma = \frac{{(\sigma_{dyn} - \sigma_{stat} )}}{{\sigma_{dyn} }}$.

The obtained dependence presented in Fig. 33b shows that there is a possibility to predict the strain rate dependent increase in the compressive strength of a composite based on the quasistatic experiments.

7 Metal-Matrix Composites

A mesovolume of a metal matrix composite is represented schematically in Fig. 34a. The microstructure was chosen according to the experiments reported in [35]. Figure 34b illustrates the macroscopic response of the mesovolume in tension and compression. Similar to the coated material, the composite under study is seen to withstand a higher load in compression than in tension. At first glance, this difference could be due to the substantial difference in the tensile and compressive strength values of the particles: since $C_{com} \gg C_{ten}$, it must take a much higher average stress level for local regions to fail in compression than in tension. However, a proportional increase in the macroscopic yield stress (relative to the ratio between aluminum and alumina volume fractions) does not occur for two reasons. First, plastic deformation in aluminum causes the total stress level to decrease (stress deviator is constrained), and free surfaces are a hindrance to a build-up of pressure. Second, the calculations for Al/Al₂O₃ under different types of applied loading have shown that $C_{com}$ is not reached.

Fig. 34

Calculated composite microstructure (a) and its tensile and compressive stress-strain curves (b)

Again, for the composite the microstructural inhomogeneity and interfacial effect are responsible for the formation of tensile regions, while the mesovolume is subjected to compression, and it is essential that the required values of tensile stresses are obtained in these regions. This conclusion is of critical importance for an analysis of the resulting plastic deformation of the matrix and of crack growth in brittle particles. It is necessary to stress that in simulation of uniaxial loading of a homogeneous material the stress tensor components along the direction perpendicular to the loading axis are assumed to be zero over the entire region of interest.

In the case of the metal-matrix composite the following types of inhomogeneities referred to the meso II, meso I, and microscales by their characteristic sizes can be singled out: (1) $\approx 20\,\upmu{\text{m}}$ for the particles, (2) $\approx 2\,\upmu{\text{m}}$ for the matrix-particle interfacial asperities, and (3) $\approx 250\,{\text{nm}}$ for a local fracture zone. The particle is a mesoscale stress concentrator responsible for the formation of macroscopic localized shear bands in the matrix. The type 2 inhomogeneities will result in the stress concentration at the mesoscale I. As a consequence, plastic deformation will be localized in the matrix in the vicinity of interfacial asperities, and primary fracture zones will be formed in the particle.

Ideally the inhomogeneities can be assumed to take the form of a true circle. Hence, the stress concentration and corresponding types of the stressed state can be estimated using an analytical solution obtained in [71] for a round inclusion embedded in a matrix. The materials for the matrix and inclusion are chosen arbitrarily. For inhomogeneities of type 1, a solution for a stiff inclusion surrounded by a comparatively soft matrix material is valid. For inhomogeneities of type 2, on the contrary, a relatively soft inclusion will be found in a rigid matrix. Finally, in the limiting case 3, we will have to solve the classical elasticity theory problem on the influence of a round hole on the stress distribution in a plate (Fig. 35). Our analytical and numerical estimations have shown that the maximum values of $\sigma_{eq}$ for $\varepsilon_{kk} > 0$ are obtained at points of the A-type in tension, and at points of the C-types in compression (Fig. 35).

Fig. 35

Schematics of crack propagation in aluminum-alumina composite in different loading conditions

The first fracture zone nucleates in the vicinity of a hump of the interface concavities (Fig. 35). The fracture zone is a new stress concentrator. A new interface between fractured material and ceramics is characterized by a higher curvature due to a smaller area and by a larger difference in mechanical characteristics than the aluminum–alumina interface, since the fractured material no longer resists shear. This is a more powerful stress concentrator at the microscale than a concavity at the mesoscale I but it is formed following the same principle. Under external tension, the maximum value of the equivalent stress is observed in the A type tensile regions near the new fractured material—alumina interface (Fig. 35a), while under external compressive loading it is the C regions that undergo tensile stresses, in whose vicinity the second fracture zone is formed (Fig. 35b). Further, the process is repeated, and the crack propagates perpendicular to the direction of applied loading in the case of tension, and parallel to it—under compression.

Deformation and fracture of the composite are illustrated in Fig. 36, where the equivalent stress and strain distributions and velocity fields superimposed on a microstructure map are shown. The calculated results are presented for compression (1–6) and tension (7–12). The corresponding states (7–12) in the stress-strain curves are shown in Fig. 34b on an enlarged scale.

Fig. 36

Equivalent stress and plastic strain distributions and velocity fields in tension (1–6) and in compression (7–12) for the stress-strain curves in Fig. 34b

It is obvious from Fig. 36 (1) that in tension, the primary crack is initiated in the largest particle in the neighborhood of point A (Fig. 34a), where the stress concentration $\sigma_{eq}$ is at its maximum. The crack propagates in the direction normal to that of tensile load and reaches the opposite side of the interface (Fig. 36 (1–4)). As this takes place, the adjacent regions are unloaded due to release waves propagating from newly formed free surfaces. This is supported by the descending portion of the stress-strain curve (Fig. 34(1–4)). The velocity fields in Fig. 36 (1–3) illustrate the crack opening process. Interactions of elastic waves with interfaces give rise to formation of a complex stressed state and may be responsible for generation of vortex structures. Rotations of local regions contribute to further increase in the stress concentration (Fig. 36 (3)). On further loading the average stress level in the region of interest is increased. Another stress concentrator is formed in a particle of smaller size, and new cracks are initiated (Fig. 36 (4–6)) with the resulting unloading of the material (Fig. 34 (2, 5, 6)). Figure 36 (4–6) shows the equivalent plastic strain distributions. The fracture regions corresponding to a maximum value of plastic strain are shown in black. The tension crack nucleation and growth in the mesovolume are seen to occur essentially in the elastic deformation stage. This is attributed to the fact that the average stress level in the matrix is below the yield point $\sigma_{0} = 62$ MPa (see Table 1), whereas the stress concentration in the local regions of the particles (points A in Fig. 34a) may be above a critical point $C_{ten} = 260$ MPa (see Table 2). Moderate plastic strain is seen in the neighborhood of points where local fracture zones are generated localized (Fig. 36 (1–4)).

In compression (Fig. 36 (7–12)), cracks are initiated at points of the maximum tensile stress concentration (points C in Fig. 34a). Notably, the equivalent stress at points of local compression (points A) is much higher than at points C. Thus, the compression fracture of the particle occurs at a much higher total stress level than that involved in tension (Fig. 34b) and is accompanied by high-intensity plastic deformation in the matrix (Fig. 36 (10–12)).

The compression cracks propagate in the loading direction. However, unlike the case of tensile load the crack propagation exhibits an oscillatory pattern. Severe plastic deformation of the matrix hinders fast increasing of the stress concentration. That is why the average velocity of compression-induced crack propagation through particles is much lower than in the case of tension-induced cracks. In consequence, cracking of the particles may occur in a switching mode. The regime in question can easily be traced by examining field velocities (Fig. 36 (7–9)). The first crack is initiated to produce an unloading effect of the mesovolume (Fig. 36 (7)). Then, the crack ceases to propagate, and the average stress level is seen to rise thereafter for a fairly long period of time due to strain hardening of the matrix (Fig. 34 (2, 7)). A new local fracture zone is formed in another particle. When a second crack ceases to grow the primary crack resumes its growth, propagating slowly (Fig. 34 (9–11)) to the opposite side of the interface (Fig. 36 (9–11)). Next, a third crack is formed (Fig. 36 (12)) and the process recurs.

In the calculations presented in Fig. 36, both for tension and for compression, the largest, medium-size, and the smallest particles are involved successively in the fracture process. Similar situations where the largest grains undergo the largest deformations and, in consequence, suffer the greatest damage have been observed experimentally. However, for an arbitrary microstructure of the type studied here (Fig. 34a), the sequence of events may be due to other reasons in addition to the size factor: different shape of the interface segments at points of crack nucleation and different types of the stressed-strained state of particles by virtue of their particular relative positions. We looked for ways to avoid the effects of the geometry and the loading conditions. To this end, a series of calculations were performed for composite microstructures subjected to tension. In the calculations, particles of the same shape and varying size (centers of masses of the particles) were aligned at the center of the computational domain. There are six independent combinations of relative positioning of particles according to this principle (Fig. 37). As in the former calculation presented in Fig. 36, the order of failure of the particles (the largest—medium-size—the smallest particles) is the same in all cases at hand. Such a fracture pattern is accounted for on the basis of the foregoing analysis of the calculated results and analytical estimation of the stress concentration: the larger the particle, the closer the stress concentration near the type II inhomogeneity approaches a maximum value obtained from an analytical solution for an infinite domain, and hence the sooner a local fracture zone is formed.

Fig. 37

Fracture patterns in composite mesovolumes with particles of the same shape and different size for 6 independent combinations of relative positions of the particles