Keywords

1 Introduction and Model Assumptions

Hydrodynamic lubrication [1, 2] is one of the classic topics contributing to the field of fluid mechanics that is of considerable relevance; for example, in technological terms in connection with the design of lubricated contacts such as plain bearings or ball joints [3] and more specifically, in bio-engineering terms, in the context of joint replacement [4]. In the present work, a model, based on a potential field description is presented for the case of a lubricated contact consisting of two contiguous immiscible layers, located one on top of the other. In a general sense, both layers can be considered as purely viscous liquids and/or viscoelastic layers, depending on the application of interest.

Different aspects of film flows involving two or more immiscible liquid layers have been investigated in [5,6,7] with a focus on both confined shear-driven flows, the topic of interest here, and free-surface flows due to their relevance in the production and deposition of functional coatings [8]. Current studies addressing the material modelling of articular cartilage, see for example [9], reveal an appreciable complexity of material behaviour, which among other things includes chemo-elastic effects and anisotropy; here standard simplified viscoelastic models are considered as a first step.

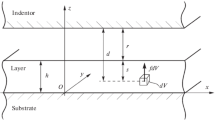
The model problem considered is that of an idealised system of two-dimensional steady Couette flow, as illustrated in Fig. 1: the lower, flat surface translates with speed \( v_{0} \) while the upper, corrugated, one remains stationary. The region separating the surfaces, which are in parallel alignment, is taken to be filled with contiguously contacting, immiscible liquids or viscoelastic layers, having different dynamic viscosity η and Young’s modulus \( E \); the case shown is for a bilayer system , mimicking the more general case of a joint in which the synovia meets a protective layer exhibiting viscoelastic properties. While at outset the general case is formulated, the focus of the results presented and discussed subsequently is restricted to the simpler case of two Newtonian liquid layers.

Fig. 1
figure 1

Model of a periodic two-phase system (a), consisting of a layer of viscous liquid lying on top of a viscoelastic one, both confined between non-compliant rigid surfaces; the lower one is flat and translating while the upper one is profiled/contoured and stationary. The model is based on the natural form of biological joints (b), [10] and is a key feature of the planned investigation

Full size image

The two-phase system is defined in terms of a number of non-dimensional parameters, the most relevant of these being the ratios of the two layer thicknesses, \( H_{1} /H_{2} \), and of their fluid properties, namely the viscosities \( \eta_{1} /\eta_{2} \) and the densities \( \rho_{1} /\rho_{2} \). The shape of the periodic profile defining the upper corrugated surface is given by the function:

$$ b(x) = - 2a\frac{{\ln \left( {2 - 2s\cos x} \right) - \ln \left( {1 + \sqrt {1 - s^{2} } } \right)}}{{\ln \left( {1 + s} \right) - \ln \left( {1 - s} \right)}}. $$
(1)

It depends on two parameters: the dimensionless amplitude \( a = 2\pi A/\lambda \) and \( s \in \left( { - 1,1} \right) \) determining the shape. Figure 2 illustrates three potential shapes, demonstrating the role of the shape parameter \( s \). In the limiting case \( s \to 0 \) the surface shape becomes a cosine function, \( b(x) = - a\cos x \), for positive values of \( s \) the corrugations form pronounced peak asperities while for negative values they result in a smoother levelling.

Fig. 2
figure 2

Surface profile shapes obtained for different values of the shape parameters. The red curve, with \( s = 0.9 \), results in peak asperities while the blue one, with \( s = - 0.9 \), (phase shift π) leads to smoother ones. The cosine function (green curve) is shown as a reference for the limit \( s \to 0 \)

Full size image

If the upper layer is assumed to be viscoelastic, the Deborah number \( De = \eta_{1} v_{0} /E\lambda \) enters the problem as an additional parameter, while the Reynolds number is so small that it can be taken to be zero.

The focus here, from a bio-engineering viewpoint, is the determination of the normal and shear stresses along the interface separating the two layers: normal stresses, especially when periodically varying with time, have a positive influence on the nutrient supply to the articular cartilage by promoting the exchange of substances between the nutrient-containing synovial fluid and the partially porous articular cartilage; shear stresses, on the other hand, cause wear and thus have a detrimental effect [4].

2 Mathematical Formulation

The field equations for the different layer types, together with the boundary and interface conditions, are formulated below, making use of the first integral approach [11,12,13]. The benefits of the latter are: (i) an elegant implementation for arbitrary rheological models; (ii) a beneficial form for the dynamic condition at the interface separating the two layers.

2.1 Field Equations for Newtonian Layer Types

When one, or both layers, is assumed to be an incompressible viscous Newtonian liquid, resolving the associated flow requires a solution of the governing Navier-Stokes equations and accompanying continuity equation:

$$ \rho \left( {\vec{v} \cdot \nabla } \right)\vec{v} = - \nabla p + \eta \nabla^{2} \vec{v}, $$
(2)
$$ \nabla \cdot \vec{v} = 0, $$
(3)

respectively, to obtain the velocity \( \vec{v} = v_{x} \left( {x,y} \right)\vec{e}_{x} + v_{y} \left( {x,y} \right)\vec{e}_{y} \) and scalar pressure \( p = p\left( {x,y} \right) \) fields. Defining a complex coordinate and complex velocity as:

$$ \xi = x + iy, $$
(4)
$$ v = v_{x} + iv_{y} , $$
(5)

and introducing the scalar potential Φ as an auxiliary unknown, facilitates integration of Eq. (2), leading finally to the following two complex field equations [14]:

$$ \frac{\rho }{2}v^{2} = 2\eta \frac{\partial v}{{\partial \bar{\xi }}} - 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }^{2} }}, $$
(6)
$$ \frac{\rho }{2}\bar{v}v = - p + 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }\partial \xi }}. $$
(7)

The continuity equation is fulfilled identically on introduction of the streamfunction \( \varPsi \), according to \( v = - 2i\partial \varPsi /\partial \bar{\xi } \).

Note that the above approach originates from two-dimensional elasticity theory [15, 16], where the scalar potential Φ plays the role of Airy’s stress function. This prominent complex variable approach was adopted subsequently by several authors, e.g. [17], for the solution of Stokes flow problems, before being generalised for the case of inertial flows in [11].

2.2 Field Equations for Viscoelastic Layer Types

A complex variable formulation of the governing evolution equations, as in the case of Newtonian liquids and Hookean materials, is also available for any generalised material [18] with an elegant embodiment of the respective rheological model equations in the first integral approach. By applying the complex transformations (4) and (5) to the general momentum balance in place of the Navier-Stokes equations and following the procedure described in [14], one obtains the following complex equations:

$$ \frac{\rho }{2}v^{2} = \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } - 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }^{2} }}, $$
(8)
$$ \frac{\rho }{2}\bar{v}v = \sigma_{0} + 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }\partial \xi }}, $$
(9)

where \( \sigma_{0} = \frac{{\sigma_{x} + \sigma_{y} }}{2} \) is the isotropic part of the stress tensor of the respective material, while the complex quantity \( \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } = \frac{{\sigma_{x} - \sigma_{y} }}{2} + i\tau_{xy} \) is its traceless part. The adoption of a corresponding rheological model, given as a relationship between the stress \( \sigma \), the deformation \( \varepsilon \), together with their time derivatives, can be implemented by formal substitutions according to the rules listed in Table 1.

Table 1 Substitution rules for the implementation of generalised rheological models
Full size table

Here \( u = u_{x} + iu_{y} \) denotes the complex displacement field. Note also, the kinematic constraint \( v = v\frac{\partial u}{\partial \xi } + \bar{v}\frac{\partial u}{{\partial \bar{\xi }}} \) between the velocity and displacement fields.

Implementation of the above methodology is demonstrated for a Kelvin-Voight model \( \sigma = E\varepsilon + \eta \dot{\varepsilon } \) with Young’s modulus \( E \) and viscosity \( \eta \) [19]. Following substitution, according to Table 1, Eqs. (8) and (9) become:

$$ \frac{\rho }{2}v^{2} = 2E\frac{\partial u}{{\partial \bar{\xi }}} + 2\eta \frac{\partial v}{{\partial \bar{\xi }}} - 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }^{2} }}, $$
(10)
$$ \frac{\rho }{2}\bar{v}v = E\left( {\frac{\partial u}{\partial \xi } + \frac{{\partial \bar{u}}}{{\partial \bar{\xi }}}} \right) + \eta \left( {\frac{\partial v}{\partial \xi } + \frac{{\partial \bar{v}}}{{\partial \bar{\xi }}}} \right) + 4\frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }\partial \xi }}, $$
(11)

which are generalised forms of Eqs. (6) and (7), respectively; the latter equations result in the limit case of a viscous liquid when \( E = 0 \).

Note that the above procedure can be applied to any arbitrary rheological model, using the formal substitution rules in Table 1 with respect to the general complex momentum Eqs. (8) and (9).

2.3 Boundary and Interface Conditions

Along both the stationary profiled surface, given by the function \( b(x) \), and the moving flat surface no-slip/no-penetration conditions have to be fulfilled:

$$ u\left( {x,b\left( x \right)} \right) = 0, $$
(12)
$$ v\left( {x,H_{1} + H_{2} } \right) = v_{0} . $$
(13)

Periodic boundary conditions at inflow and outflow, to the left and right, are enforced. At the interface separating the layers, \( y = f\left( x \right) \), the shape of which is unknown a priori, the velocity field has to be continuous:

$$ \left[ {\left[ v \right]} \right] = 0, $$
(14)

with the double square brackets denoting the discontinuity of the associated term. Moreover, the kinematic boundary condition there:

$$ v_{y} - f'\left( x \right)v_{x} = 0, $$
(15)

can be used to determine the shape of the interface. Finally, the dynamic interface condition:

$$ \left[ {\underline{\underline{T}}_{2} - \underline{\underline{T}}_{1} } \right] \cdot \vec{n} = \sigma_{S} \kappa \vec{n}, $$
(16)

accounts for the equality in stress at the interface; \( \sigma {}_{S} \) is the interfacial tension, \( \kappa \) the curvature, \( \vec{n} \) the vector normal to the interface and \( \underline{\underline{T}}_{1,2} \) the stress tensor associated with the materials forming the respective layers. Using a conventional description, the treatment of the dynamic interface condition is a challenging task, since the viscous or viscoelastic stresses present lead to combinations of different derivatives of different components of the displacement and velocity field and therefore to a mathematically unfavourable form. Using the first integral approach, the unfavourable terms involved in the interface condition (16) can be replaced by second order derivatives of the scalar potential \( \Phi \) and the interface condition integrated [14], leading finally to the simple jump condition:

$$ \left[ {\left[ {\frac{\partial \Phi }{{\partial \bar{\xi }}}} \right]} \right] = \frac{{\sigma_{S} n}}{4}, $$
(17)

where \( n = n_{x} + in_{y} \) is the complex equivalent of the normal vector. It is shown in [14] that, after re-transformation to a real-valued representation, the two conditions resulting from (17) can be formulated in standard Dirichlet/Neumann form. Among various other benefits, the reduction of the complicated dynamic interface condition (16) to the significantly simpler jump condition (17) for the potential \( \Phi \) justifies its introduction as an additional auxiliary field and demonstrates its use.

3 Methods of Solution

The problem is formulated in three different ways: via a Lubrication approximation allowing for an analytical solution; a numerical finite-element FE approach; a semi-analytical one benefitting from the use of complex variables. The FE approach enables Reynolds number effects to be investigated and, more generally, the validity of the two simpler models to be assessed. In terms of the adopted first integral approach, the standard mathematical form of the jump conditions (17) is advantageous, since the resulting friction coefficient can be calculated conveniently from the auxiliary potential field \( \Phi \) based on the first integral formulation without the need to approximate velocity derivatives in a post-processing step as would be the case if a primitive variable formulation had been adopted.

3.1 Lubrication Approximation

The first integral Eq. (6) can be simplified based on a Lubrication approximation, noting that the same applies to the Navier-Stokes equations, [20,21,22,23], leading to a single equation for the local film thickness; the velocity field to leading order being locally parabolic. The requirement underpinning its applicability in the case of surface contours exhibiting rapid changes is that the commensurate interface disturbance is slowly varying.

Applying the Lubrication approximation to the real-valued decomposed Eq. (6) leads to:

$$ \begin{aligned} & \frac{\rho }{2}\left( {v_{x}^{2} - v_{y}^{2} } \right) + \frac{\partial }{\partial x}\left[ {\frac{\partial \Phi }{\partial x} - \eta v_{x} } \right] - \frac{\partial }{\partial y}\left[ {\frac{\partial \Phi }{\partial y} - \eta v_{y} } \right] = 0, \\ & \rho v_{x} v_{y} + \frac{\partial }{\partial y}\left[ {\frac{\partial \Phi }{\partial x} - \eta v_{x} } \right] + \frac{\partial }{\partial x}\left[ {\frac{\partial \Phi }{\partial y} - \eta v_{y} } \right] = 0. \\ \end{aligned} $$
(18)

Next, by neglecting \( \partial v_{y} /\partial x \) compared to \( \partial v_{x} /\partial y \) and omitting inertial terms, the set of PDEs is reduced to one that can be solved by successive integration, as shown in detail in [24], leading to the following general solution:

$$ v_{x} = \frac{1}{2}F^{\prime\prime}_{1 \, } \left( x \right)y^{2} + F^{\prime}_{2} \left( x \right)y + F_{3} \left( x \right), , $$
(19)
$$ \psi = F^{\prime\prime}_{1 \, } \left( x \right)\frac{{y^{3} }}{6} + F^{\prime}_{2} \left( x \right)\frac{{y^{2} }}{2} + F_{3} \left( x \right)y + F_{4} \left( x \right), $$
(20)

for the velocity \( v_{x} \) and the streamfunction \( \psi \), involving four integration functions \( F_{1} (x), \, F_{2} (x), \, F_{3} (x) \) and \( F_{4} (x) \); while the gradient of the potential results in:

$$ \begin{aligned} & \frac{2}{\eta }\frac{\partial \Phi }{\partial x} = \frac{1}{2}F^{\prime\prime}_{1 \, } \left( x \right)y^{2} + F^{\prime}_{2} \left( x \right)y + F_{3} \left( x \right) + F_{1} (x), \\ & \frac{2}{\eta }\frac{\partial \Phi }{\partial y} \approx F^{\prime}_{1} \left( x \right)y + F_{2} \left( x \right). \\ \end{aligned} $$
(21)

Note that four integration functions occur with respect to each layer m, thus for a bilayer system eight functions \( F_{mi} \left( x \right) \) with \( m = 1,2 \) and \( i = 1, \ldots ,4 \) have to be considered. Together with the shape of the interface, \( f\left( x \right) \), nine unknown functions have to be determined from the boundary and interface conditions (12)–(15) and (17), considering that each of the complex conditions delivers two real-valued conditions after decomposition into real and imaginary parts.

By successive elimination of unknown functions, the resulting set of nine ODEs can be reduced to three nonlinear ODEs for the functions \( F_{11} \left( x \right), \, F_{21} \left( x \right) \) and \( f\left( x \right). \) In non-dimensional form, taking \( L = \lambda /2\pi \) as the characteristic length with \( \lambda \) the wavelength and \( v_{0} \) as a characteristic velocity, the resulting equations read:

$$ \frac{{2Q_{2} }}{h - f\left( x \right)} - \frac{{2Q_{1} }}{f\left( x \right) - b\left( x \right)} - \frac{{\left[ {f\left( x \right) - b\left( x \right)} \right]^{2} }}{6}F^{\prime\prime}_{11} \left( x \right) + \frac{{\left[ {h - f\left( x \right)} \right]^{2} }}{6}F^{\prime\prime}_{21} \left( x \right) = 1 $$
(22)
$$ \left( {1 - n} \right)\left[ {\frac{{2Q_{1} }}{f\left( x \right) - b\left( x \right)} + \frac{{\left[ {f\left( x \right) - b\left( x \right)} \right]^{2} }}{6}F^{\prime\prime}_{11} \left( x \right)} \right] + F_{21} \left( x \right) - nF_{11} \left( x \right) = 0 $$
(23)
$$ \begin{aligned} & \frac{{Q_{2} }}{{\left[ {h - f\left( x \right)} \right]^{2} }} + \frac{{nQ_{1} }}{{\left[ {f\left( x \right) - b\left( x \right)} \right]^{2} }} + n\frac{f\left( x \right) - b\left( x \right)}{3}F^{\prime\prime}_{11} \left( x \right) \\ & \quad + \frac{h - f\left( x \right)}{3}F^{\prime\prime}_{21} \left( x \right) = \frac{1}{h - f\left( x \right)} \\ \end{aligned} $$
(24)

where \( Q_{1} = \psi \left( {x,f\left( x \right)} \right) \) and \( Q_{2} = \psi \left( {x,h} \right) - Q_{1} \) are the constant partial flow rates of the two different layers and \( n = \eta_{1} /\eta_{2} \) is the viscosity ratio. In contrast to the conventional Lubrication model derived starting from the original Navier-Stokes equations leading to the well-known Reynold’s equation [3], the first integral approach yields the equation set (22)–(24) comprising three equations for the interface shape \( f\left( x \right) \) and the two functions \( F_{11} \left( x \right), \, F_{21} \left( x \right) \) which are connected with the curvatures of the respective velocity profiles within the two layers. Having once determined these three functions by solving (22), (23) and (24), the streamfunction results for the two layers, as:

$$ \begin{aligned} & \psi^{\left( 1 \right)} = \frac{{\left[ {y - b\left( x \right)} \right]^{2} }}{2}\left[ {\frac{y - f\left( x \right)}{3}F^{\prime\prime}_{11} \left( x \right) + \frac{{2Q_{2} }}{{\left[ {f\left( x \right) - b\left( x \right)} \right]^{2} }}} \right]{ ,} \\ & \psi^{\left( 2 \right)} = Q_{1} + \left[ {1 - \frac{{\left( {h - y} \right)^{2} }}{{\left[ {h - f\left( x \right)} \right]^{2} }}} \right]\left[ {Q_{2} - h + f\left( x \right)} \right] \\ & \quad + \frac{{\left( {h - y} \right)^{2} }}{6}\left[ {y - f\left( x \right)} \right]F^{\prime\prime}_{21} \left( x \right) \, , \\ \end{aligned} $$
(25)

where the numbers 1, 2 in the brackets denote the respective layer.

The above set of nonlinear equations, (22), (23) and (24), can be solved numerically in their given form or asymptotically after linearization, as shown below. The latter approach is briefly demonstrated in the following. By introducing:

$$ \varphi \left( x \right): = f\left( x \right) - h_{1} , $$
(26)

as the deviation of the interface from its mean value and assuming that the functions \( b\left( x \right), \, \varphi \left( x \right), \, F^{\prime\prime}_{11} \left( x \right) \) and \( F^{\prime\prime}_{21} \left( x \right) \) depend linearly on the amplitude \( a \) of the profiled upper surface, an asymptotic expansion of Eqs. (22) and (24) with respect to powers of \( a \) leads, to zeroth order, to:

$$ \begin{aligned} Q_{1} = \frac{{h_{1} }}{{h_{1} + nh_{2} }}\frac{{h_{1} }}{2}{ ,} \hfill \\ Q_{2} = \frac{{2h_{1} + nh_{2} }}{{h_{1} + nh_{2} }}\frac{{h_{2} }}{2}{ , } \hfill \\ \end{aligned} $$
(27)

as solutions for the flow rates in the case of bilayer flow between two parallel planar walls. The first order contribution of the same equations resulting from linearization with respect to \( a \):

$$ \begin{aligned} & \frac{{h_{1} }}{3}\left( {h_{1} + nh_{2} } \right)F^{\prime\prime}_{11} \left( x \right) = \frac{{2h_{1} + nh_{2} }}{{h_{1} \left( {h_{1} + nh_{2} } \right)}}\left[ {\varphi \left( x \right) - b\left( x \right)} \right] + \frac{{3h_{1} + 2nh_{2} }}{{h_{2} \left( {h_{1} + nh_{2} } \right)}}\varphi \left( x \right) ,\\ & \frac{{h_{2} }}{3}\left( {h_{1} + nh_{2} } \right)F^{\prime\prime}_{21} \left( x \right) = - \frac{{n\left[ {\varphi \left( x \right) - b\left( x \right)} \right]}}{{h_{1} + nh_{2} }} - \frac{{h_{1}^{2} + 4nh_{1} h_{2} + 2n^{2} h_{2}^{2} }}{{h_{2}^{2} \left( {h_{1} + nh_{2} } \right)}}\varphi \left( x \right) ,\\ \end{aligned} $$
(28)

allow the two functions \( F^{\prime\prime}_{11} \left( x \right) \) and \( F^{\prime\prime}_{21} \left( x \right) \) to be expressed in terms of \( \varphi \left( x \right) \) and \( b\left( x \right) \). By computing the linear part of (23), taking the second order derivative with respect to \( x \) and eliminating \( F^{\prime\prime}_{11} \left( x \right) \) and \( F^{\prime\prime}_{21} \left( x \right) \) by means of (28), one ends up with a second order ODE of the form:

$$ A_{1} \varphi^{\prime\prime}\left( x \right) + A_{2} \varphi \left( x \right) = A_{3} b^{\prime\prime}\left( x \right) + A{}_{4}b\left( x \right) , $$
(29)

with the four coefficients given by:

$$ \begin{aligned} & A_{1} = - \left( {1 - n} \right)\left( {3h_{1}^{2} + 2nh_{1} h_{2} - nh_{2}^{2} } \right) \\ & A_{2} = 6\left( {\frac{{h_{1} }}{{h_{2} }} + \frac{{nh_{2} }}{{h_{1} }}} \right)^{2} + 12n\left[ {2\frac{{h_{1} }}{{h_{2} }} + \left( {1 + n} \right)\left( {1 + \frac{{h_{2} }}{{h_{1} }}} \right)} \right] \\ & A_{3} = n\left( {1 - n} \right)h_{2}^{2} \\ & A_{4} = 6n\left[ {1 + 2\frac{{h_{2} }}{{h_{1} }} + n\frac{{h_{2}^{2} }}{{h_{1}^{2} }}} \right] \\ \end{aligned} $$
(30)

Since the above ODE (29) is linear and of second order, it allows for a closed form analytic solution for any prescribed profile shape \( b\left( x \right) \). Note that the latter need not to be periodic at this stage; apart from the examples considered in the results section, any profile shape can be considered, including step and trench geometries as in [24].

3.2 Finite Elements Approach

For validation purposes numerical calculations are obtained, in the case of two viscous layers, by using existing and established practices based on classical FE formulations for the original Eqs. (2) and (3) in terms of “primitive variables”, namely velocity and pressure, see e.g. [25, 26] or [27]; an alternative approach would have been to use a streamfunction and vorticity formulation as adopted by [28, 29] or [30].

A challenging task is the a priori unknown shape \( f\left( x \right) \) of the interface separating the two layers, requiring an iterative approach in which the calculation for the two system components, no matter whether they are fluid or viscoelastic, is carried out separately, assuming a starting value for \( f\left( x \right) \) and calculating the velocity/displacement field for both layers without considering the kinematic boundary condition (15). Following this, a new interface shape \( f\left( x \right) \) is calculated separately as the limiting streamline. The iteration process is repeated until either the change in the interface shape from one iteration step to the next falls below a prescribed tolerance or if the ratio of the normal velocity to the tangential one along the current interface shape is smaller than a tolerable value, typically 0.25% [31]. Implementation of the methodology was performed using standard libraries for efficient FE Galerkin solvers, making use of the packages ‘numpy’, ‘scipy’ and ‘matplotlib’, accessed via Python and the ‘Triangle’ mesh generator [32].

3.3 Complex-Variable Approach with Spectral Solution Method

For completeness and different to the above aforementioned approaches, direct use can be made of the complex formulation (10) and (11) of the field equations. On neglecting the nonlinear inertial terms, Eq. (10) becomes integrable with respect to \( \bar{\xi } \), implying:

$$ Eu + \eta v = 2\frac{\partial \Phi }{{\partial \bar{\xi }}} - 4g_{0} \left( \xi \right), $$
(31)

containing the integration function \( g_{0} \left( \xi \right) \). After inserting this into Eq. (11), the identity:

$$ g^{\prime}_{0} \left( \xi \right) + \overline{{g^{\prime}_{0} \left( \xi \right)}} = \frac{{\partial^{2} \Phi }}{{\partial \bar{\xi }\partial \xi }} , $$
(32)

is obtained, which is again integrable. Further integration and noting that the potential \( \Phi \) is real-valued, finally leads to:

$$ \Phi = 2\Re \left[ {\bar{\xi }g_{0} \left( \xi \right) + g_{1} \left( \xi \right)} \right], $$
(33)

yielding a second integration function \( g_{1} \left( \xi \right) \). Thus, the entire problem has been reduced to one of determining the two holomorphic functions \( g_{0} \left( \xi \right) \) and \( g_{1} \left( \xi \right) \), frequently referred to as Goursat functions .

For the incompressible flow of a Newtonian liquid \( v = - 2i\partial \psi /\partial \bar{\xi } \) and \( E = 0 \), in which case Eq. (31) can be integrated a second time leading, together with expression (33), to the advantageous form:

$$ \Phi + i\eta \psi = \bar{\xi }g_{0} \left( \xi \right) + g_{1} \left( \xi \right), $$
(34)

of the solution for both the streamfunction and the scalar potential [12].

Since the Goursat functions are functions of only one complex variable, the mathematical problem is elegantly reduced from a two- to a one-dimensional problem. While in the classical literature a purely analytical approach via conformal mappings is preferred, which is limited to finding approximate solutions for simple geometries, a spectral method based on a Fourier expansion of either the Goursat functions directly or their boundary values enables fulfillment of the boundary conditions for arbitrary profile shapes with arbitrary accuracy, depending of the truncation order of the Fourier series. Although not considered in the context of the result presented and discussed below, further details of the use of this elegant semi-analytical method and its application to free surface flows and Couette flows for Newtonian liquids can be found in [31, 33, 34].

4 Results

In the present work bilayer flow is explored, for a stationary upper surface having a particular contoured shape, utilising the Lubrication approach with the results validated via corresponding FE-calculations.

4.1 Sinusoidal Upper Surface Shapes

Assuming a sinusoidally shaped profile for the upper stationary surface, \( b\left( x \right) = - a\cos x \), resulting as the limit case \( s \to 0 \) of the more general shape (1), the solution of the ODE (29) is obtained straightforwardly by assuming a corresponding harmonic form for the interface shape, i.e.: \( \varphi \left( x \right) = - \hat{\varphi }a\cos x \), with the amplitude factor \( \hat{\varphi } \) resulting in:

$$ \hat{\varphi } = \frac{{A_{4} - A_{3} }}{{A_{2} - A_{1} }}, $$
(35)

and with the coefficients \( A_{1} , \ldots ,A_{4} \) given according to (30). From the above solution the interface function \( f\left( x \right) \) and the two functions \( F_{11} \left( x \right), \, F_{21} \left( x \right) \) are obtained from (26) and (28) and finally the streamfunction from (25).

This closed form analytic solution for a viscous bilayer flow is visualised via streamlines in the left column of Fig. 3 for a fixed thickness ratio of \( h_{1} /h_{2} = 2/3 \) and a fixed amplitude \( a = 1/2 \) for varying viscosity ratio \( n \). Corresponding FE solutions are provided in the right column.

Fig. 3
figure 3

Streamline plots of bilayer flow for the case of a sinusoidally profiled upper surface, with fixed geometry and varying viscosity ratio. The analytical results stem from the linearized Lubrication approximation (left column) and are compared to their corresponding FE solutions (right column)

Full size image

The calculations reveal a clear dependence of the interface shape on the viscosity ratio \( n \): if the viscosity \( \eta_{1} \) of the layer adjacent to the profiled surface is much larger than the viscosity \( \eta_{2} \) of the layer adjacent to the planar translating one, the interface shape mimics the upper surface profile. Comparing the resulting flow for \( n = 2 \) with the corresponding one for \( n = 500 \), a minimal change only is apparent, indicating that for a very large ratio a limit case exists. If, vice versa, the viscosity of the lower layer is larger than the viscosity of the upper one, the interface becomes smoother. For \( n \) with a very small value, the second layer acts effectively as a continuation of the translating planar surface and the interface approaches a straight line. For the present geometry this induces the onset of a small eddy in the troughs of the profiled surface, which is a well-known observation in monolayer Couette flow, see e.g. [35], or [36].

The above results show that the solution obtained via an asymptotic analysis, although slightly overestimating the slope of the interface shape, leads to a good approximation for bilayer flow in the presence of a sinusoidally profiled surface; its limitations are due primarily to the prerequisite of a small corrugation amplitude \( a. \) Additionally, one has to keep in mind that the lubrication analysis is effectively a long-wave approximation [21] requiring the film thickness not to exceed the wavelength of the upper surface profile.

As mentioned in the introduction, the shear stress \( \tau_{f} \) along the interface \( y = f\left( x \right) \) is of particular interest and can, in general, be calculated as:

$$ \tau_{f} = 2\eta \left[ {\frac{\partial v}{\partial y} - \frac{\partial u}{\partial x}} \right]\frac{{f^{\prime}\left( x \right)}}{{1 + f^{\prime}\left( x \right)^{2} }} + \eta \left[ {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right]\frac{{1 - f^{\prime}\left( x \right)^{2} }}{{1 + f^{\prime}\left( x \right)^{2} }}. $$
(36)

Two examples of the resulting distribution of the shear stress along the interface over one wavelength of the bilayer flow are presented in Fig. 4, for the same layer thicknesses \( h_{1} = 1.2 \) and \( h_{2} = 1.8 \) considered when generating the streamline patterns for the flows in Fig. 3 but with a viscosity ratio \( n = 1/3 \) and for two different profile amplitudes.

Fig. 4
figure 4

Resulting shear stress along the interface of a bilayer flow over one wavelength; the layer thicknesses are h1 = 1.2, h2 = 1.8 and n = 1/3, for two different amplitudes, a = 0.1 (left) and a = 0.3 (right), calculated via the Lubrication and FE approaches

Full size image

As expected, the maximum shear stress coincides with the peak value of the upper surface profile where the local film thickness is a minimum. Furthermore, for the smaller of the two amplitudes, \( a = 0.1 \), the agreement between the analytically calculated shear stress and the comparative FE solution is excellent; while for the larger amplitude, \( a = 0.3 \), the shear stress is underestimated by the Lubrication approach.

4.2 Inharmonic Periodic Upper Surface Profiles

Due to the linearity of the ODE (29), the result obtained for sinusoidally profiled upper surfaces can be adapted to generally periodic profiles by utilizing a spectral decomposition:

$$ b\left( x \right) = a\sum\limits_{k = 1}^{\infty } {\beta_{k} \cos \left( {kx} \right)} , $$
(37)

of the respective profile shape function. For the shape given by Eq. (1), the Fourier coefficients read [37]:

$$ \beta_{k} = \frac{{4\left( {1 - \sqrt {1 - s^{2} } } \right)^{k} }}{{k\left[ {\ln \left( {1 + s} \right) - \ln \left( {1 - s} \right)} \right]s^{k} }} . $$
(38)

This allows the ODE (29) to be solved separately for each spectral component and the writing of the solution for the interface shape as the superposition:

$$ \varphi \left( x \right) = a\sum\limits_{k = 1}^{\infty } {\varphi_{k} \beta_{k} \cos \left( {kx} \right)} , $$
(39)

where:

$$ \varphi_{k} = \frac{{A_{4} - k^{2} A_{3} }}{{A_{2} - k^{2} A_{1} }}. $$
(40)

FE solutions were generated in the same manner as above. Figure 5 shows the streamline patterns obtained for a bilayer flow in the presence of an upper surface profile given by the analytic form (1), with \( a = 0.5 \) and a shape parameter \( s = 0.9 \) and as before layer thickness of \( h_{1} = 1.2 \) and \( h_{2} = 1.8 \), for three different values of \( n \). The corresponding interface shape given by the Lubrication approximation is shown as a dashed line in each case.

Fig. 5
figure 5

Streamline plots for bilayer flow, obtained using the FE approach, in the presence of an inharmonic upper surface profile, with fixed geometry and three different viscosity ratios. The interface shape in each case, obtained analytically via the Lubrication approximation with linearization, is shown for comparison purposes as a dashed line

Full size image

As can be seen the results obtained are qualitatively similar to those of Fig. 3 for the case of a sinusoidally shaped upper surface profile: for the larger of the three \( n \) values the interface disturbance is greater, while for the smaller of the two \( n \) values the interface tends to a straight line when \( n = 0.05 \), and for which case distinct eddies are observed to exist in the troughs of the profiled surface. As for the case of a sinusoidally profiled upper surface, it can be seen that the curvature of the interface is overestimated by the Lubrication approach.

5 Conclusions and Perspectives

Three different approaches are presented as solutions to the problem of bilayer flow for the case of two immiscible Newtonian liquids confined between an upper profiled surface at rest and a lower translating planar surface. The FE approach enables sufficiently accurate solutions of the Navier-Stokes equations to be obtained, that provide a reliable means of validating the predictions of the other two methods. The latter originate from a potential-based first integral formulation of Navier-Stokes equation. In the present work only the Lubrication approach in combination with linearization of the resulting ODEs is considered. This allows for closed form analytic solutions, which are compared in detail with corresponding FE solutions. Although overestimating the curvature of the interface between the two fluid layers and underestimating the shear stress along the latter, the Lubrication approach provides results of quantitatively acceptable accuracy if the amplitude of the profiled upper surface is sufficiently small. A potential improvement of the method could be realised by solving the nonlinear Eqs. (22), (23) and (24) without linearization.

For both biomedical and advanced technological applications, the consideration of non-Newtonian materials is an essential next step. In this context the complex variable approach outlined above provides an interesting perspective towards the implementation of viscoelastic models within a first integral framework; further details of which will appear in forthcoming articles.