Fault Sliding Modes—Governing, Evolution and Transformation

Abstract

A brief summary of fundamental results obtained in the IDG RAS on the mechanics of sliding along faults and fractures is presented. Conditions of emergence of different sliding regimes, and regularities of their evolution were investigated in the laboratory, as well as in numerical and field experiments. All possible sliding regimes were realized in the laboratory, from creep to dynamic failure. Experiments on triggering the contact zone have demonstrated that even a weak external disturbance can cause failure of a “prepared” contact. It was experimentally proven that even small variations of the percentage of materials exhibiting velocity strengthening and velocity weakening in the fault principal slip zone may result in a significant variation of the share of seismic energy radiated during a fault slip event. The obtained results lead to the conclusion that the radiation efficiency of an earthquake and the fault slip mode are governed by the ratio of two parameters—the rate of decrease of resistance to shear along the fault and the shear stiffness of the enclosing massif. The ideas developed were used to determine the principal possibility to artificially transform the slidding regime of a section of a fault into a slow deformation mode with a low share of seismic wave radiation.

1 Introduction

One of the important areas of Professor S. G. Psakhie’s activities was studying regularities of deformation of hierarchical blocky media. His interest in these problems arose, among other things, under the influence of Academician S. V. Goldin. Sergey Grigorievich took active part in his seminar. Special attention in his works was paid to the possibility of altering the regime of blocky medium deformation to prevent powerful seismic impacts [1,2,3]. Starting with the application of the method of movable cellular automata [4] to the problems of deformation of contact areas between rock blocks, S. G. Psakhie and his colleagues conducted a series of experimental works, including investigations of the reaction of a natural fault to dynamic disturbances and watering [5,6,7]. Especially a big cycle of works should be noted that had been performed on the ice cover of the Lake of Baikal, which was used as a model to study the tectonic processes in the Earth’s crust [8, 9].

Authors of this paper were lucky to take part in experiments that were held under the guidance of S. G. Psakhie at a segment of the Angarskiy seismically active fault (Baikal Rift zone) [10]. The device constructed in IDG RAS—the Borehole Generator of Seismic Waves (BGSW, Fig. 1)—was mounted there to disturb the fault. The device was used to produce periodical explosions of the air-fuel mixture in a specially drilled borehole [11]. The results of observations showed that after the active disturbance the nature of movements along the fault changed. Precise measurements of the parameters of displacement along the fault showed that the disturbance triggered movements along strike, which manifested as a left-side shear. The quasi-dynamic micro-displacements which were detected many times in the records after actions with a drop-hammer, explosions and BGSW coincided with the macro-displacement in direction. Approximately in a day after the action of BGSW had been terminated the background direction of the creep and the average velocity of sliding (~4÷5 μm/day) restored [12].

Fig. 1

The Borehole Generator of Seismic Waves (BGSW) mounted at one of the sides of the Angarsky fault

Approaches that were developed in those works had a clear physical sense. Injecting water and the effect of vibrations can both change the parameters of friction during the shear along the fault and increase the pore pressure. These changes may result in emergence of conditions that correspond to the Mohr–Coulomb failure criterion. It means that a movement can be provoked at a fault that hasn’t reached the ultimate state yet. Though the mechanics of the process seemed evident, it remained unclear whether the triggered movement would be a “quasi-viscous” one (in terms of V. V. Ruzhich with co-authors [7]) and no dynamic failure would occur. Let us cite Sh. Mukhamediev: “Here the clarity in fault’s behavior ends. Further development of the artificially triggered movement (velocity of its propagation and its size) is not so evident. Here the non-uniformities of properties and stresses along the existing fault or its future trajectory play the most important role” [13]. The macroscopic conditions of different sliding modes on faults remained uncertain at that time. For the last 10–15 years the geophysical community has essentially advanced in many components of fault mechanics—cumulating information about the structure of segments where slip localizes [14,15,16], conditions of dynamic slip to be initiated [17, 18], in situ observations [19, 20] and laboratory modeling of slip episodes on faults [21,22,23]. We are going to present some of these data in this chapter.

2 Fault Slip Modes

In the very beginning of instrumental observations over deformations of the Earth’s surface it became clear that stresses cumulated in tectonically active regions relax not only through dynamic failure of some sections of the Earth’s crust, but through continuous aseismic sliding (creep) along existing faults, too. Earthquakes were interpreted as a quasi-brittle failure of rock, while creep—as a plastic deformation. It was believed that in the areas where the rate of deformation is high enough, accumulation of elastic stresses occurs with further dynamic failure of rock accompanied by intensive emission of seismic waves. In case the rate of deformation of a limited volume of the medium is so low that stresses have time to relax on all the structural inhomogeneities, regimes of deformation at a constant velocity without destruction (creep) occur [24]. Thus, it was believed that the earthquake and the asesimic sliding are two opposite phenomena that take place under different loading conditions in the medium.

As the observation data were cumulated and measuring facilities were upgraded, qualitative and quantitative differences between seismic events of one and the same rank were detected. For example, it turned out that seismic energies emitted in earthquakes with approximately equal seismic moments can differ by several orders of magnitude [25, 26].

Sensitive deformographs and tiltmeters periodically registered displacements and deformations at velocities several orders of magnitude higher than the background ones, but essentially slower than the velocity of rupture propagation in an “ordinary” earthquake. However, the low installation density of such devices didn’t allow to summarize the data being obtained, especially as the attention of investigators was concentrated primarily on post-seismic and pre-seismic deformations.

The situation changed qualitatively when dense networks of GPS sensors and broadband sensitive seismic stations were launched to operation in a continuous regime [27, 28]. As a result, in the last 25–30 years the fault slip modes were detected and classified as what can be treated as transitional from the stable sliding (creep) to the dynamic failure (earthquake). Discovering these phenomena changed to a great extent the understanding of how the energy cumulated during the Earth’s crust deformation releases—slow slippage along faults are apprehended not as a special sort of deformation, but they span a continuum of slip modes from creep to earthquake [29].

Studying the conditions of occurrence and evolution of transitional slip modes can give new important information about structure and laws of fault behavior. That is why investigations of these “unusual” movements on faults have become one of the leading trends. Detecting the phenomenon of episodic tremor and slip (ETS) in many subduction zones is believed to be one of the most important advances of geophysics in recent history [30].

Developing observation systems has allowed to reveal a number of new deformation phenomena associated with discontinuities of the Earth’s crust—subduction zones [31], continental fault zones [32], tectonic fractures [10], fractures in large ice masses [33] and even with micro-cracks in hydrocarbon reservoirs [34].

The classification of deformation events along tectonic discontinuities adopted currently is based primarily on duration of the process in the source [29, 35]. Only several percent of the released deformation energy are emitted in the form of seismic waves in a ‘normal’ earthquake (duration of the process in the source 0.1–100 s). This turns out to be enough for the strongest macroscopic manifestations of powerful earthquakes to occur. The ratio of the emitted seismic energy E_s to the seismic moment M₀ varies in the range of E_s/M₀ ~ 10⁻⁶–10⁻³, the average value being ~$2 \times 10^{ - 5}$ [25, 26].

Under some conditions, the slip velocity may not reach seismic slip rates, but nevertheless, low amplitude low-frequency seismic waves are emitted. These are the so called Low Frequency Earthquakes (LFE) and Very Low Frequency Earthquakes (VLFE) [29]. The spectrum of these vibrations is depleted with high frequencies which testifies a longer (than it follows from standard relations) duration of the process in the source—up to hundreds of seconds. The ratio of the emitted seismic energy to seismic moment, specific for LFEs, is about E_s/M₀ ~ $5 \times 10^{ - 8} - 5 \times 10^{ - 7}$, and the velocity of rupture propagation is V_r ~ 100–500 m/s [36,37,38]. VLFEs have durations in the source of about tens to hundreds of seconds, a velocity of rupture propagation of about V^r ~ 10–100 m/s and an energy-to-moment ratio of E_s/M₀ ~ 10⁻⁹–10⁻⁷ [39].

In some cases, the peak slip velocity is so low that seismic waves which could be recorded instrumentally are not emitted at all. Nevertheless, the slip velocity in these deformation phenomena noticeably exceeds typical velocities of aseismic creep along faults which is, on average, several centimeters a year. Such deformation events that can last from several hours to several years are called Slow Slip Events (SSE).

First reports in which the phenomena of aseismic sliding were for the first time interpreted as “slow earthquakes” came after observations at the Izu Peninsula in Japan [40]. But perhaps for the first time, an episode of slow slip as a self-contained event that had a start and a termination was described by A. T. Linde with co-authors [32]. The authors presented a recorded deformation event about a week in duration. They called it a “slow earthquake” and proposed to characterize such events quantitatively, just like ordinary earthquakes, with the value of seismic moment M₀ or moment magnitude M_w, which is linked to the seismic moment by the well known relation [41]:

$$ M_{w} = 2/3(\lg M_{0} - 9.1) $$

(1)

The velocity of rupture propagation along the fault strike for SSEs lies in the range from several hundreds of meters a day to 20–30 km a day [39]. Despite small displacements, an appreciable seismic moment accumulates at the expense of a large fault area, at which the displacements take place. An essential part of energy cumulated in the course of deformation releases through slow movements. For example, in New Zeeland about 40% of seismic moment release through SSEs [42]. Slow displacements are registered there with durations from several months to a year and with moment magnitudes up to M_w ~ 7. Such SSEs repeat with a period of 5 years. Less scale events with durations of several weeks have a recurrent time of 1–2 years [43, 44].

Large scale SSEs last for months and even years. The seismic moment released in them is comparable to the one of the most powerful earthquakes. For example, from 1995 to 2007 more than 15 events were registered in different regions around the world, each of them with the released seismic moment of more than M₀ ~ $5 \times 10^{19} \;{\text{Nm}}$, which corresponds to the moment magnitude of M_w ~ 7 [39]. Their durations were from a month to one year and a half, and the amplitude of displacement along the fault reached 300 cm. It should be noted that some of these SSEs were not independent events, but episodes of post-seismic sliding.

The results of studying slow movements along faults show that these specific deformations are widespread all around the world and to a great extent at their expense stress conditions of many segments of the Earth’s crust are regulated. Though initially it was thought that periodical slow slip is specific mainly for depths of several tens of kilometers in the subduction zones, installation of dense networks of seismic and geodetic observations allowed to detect similar phenomena at shallow sections of submerging plates and continental faults [45]. It is not impossible, that as the density and sensitivity of installed devices increase, sections of periodic slow slips with small moment magnitudes will be detected at numerous tectonic structures, including areas of high anthropogenic activities. Slope phenomena have also much in common with slow tectonic slip along faults [46].

The importance of studying the slow slip modes bases on several reasons. Investigating mechanisms and driving forces of these processes will allow to advance essentially in understanding regularities of interactions of blocks in the Earth’s crust, and, consequently, in assessing risks of natural and man-caused catastrophes linked to movements along interfaces—earthquakes, fault-slip rock bursts, landslides, etc.

Slow movements along faults can, beyond all doubt, be triggers of dynamic events. Detecting transitional slip modes all around the world has led many investigators into the attempt of linking the slow slip phenomena to powerful earthquake triggering [47,48,49,50], but the mechanics of this process is not developed so far. There are only few works, in which sequences of deformation events of different modes were registered instrumentally, and their interrelations were soundly demonstrated [51, 52]. Manifestations of seismicity were registered most reliably after slow slip [53], or manifestations of seismicity in the form of non-volcanic tremor against the background slow slip [54]. Geodetic and seismic observations can give only a confined insight into the physical mechanism of slow sliding. For example, though it is admitted that an asesimic slip preceded the Tohoku 2011 earthquake [55], it remains uncertain, how and why the sliding regime altered just before the main shock. Taking measurements near the surface, it is actually impossible to detect small spots of “accelerated slip” at a seismogenic depth [56].

Last but not least, a problem which regularly attracts the attention of the scientific community shall be mentioned—the possibility to alter the seismic regime of some area or the deformation regime of a specific fault segment through some external actions [57]. Therefore, it is important to investigate the conditions under which different slip modes emerge and evolve in fault zones.

3 Localization of Deformations and Hierarchy of Faults

Applying the ideas of self-similar blocky structure of Earth’s crust [58] inevitably leads to the necessity of introducing a hierarchy of interblock gaps—tectonic fractures and faults. Meanwhile the situation seems unobvious for these objects. At first glance, it is hard to reveal a similarity between a closed crack in a rock mass and a large fault zone, as opposed to the rock blocks they bound.

Unlike blocks whose linear sizes can be reliably measured, it is often impossible to estimate unambiguously the geometric characteristics of discontinuities. Analysis of any tectonic map shows that prolonged linear structures can be considered to be single objects only partially. Each of these structures is a concatenation of separate sections adjoining distinctly detectable blocks of certain ranks. Widening of the zones of active faults, as well as delta-wise and trapezium-wise sections of fault splitting can be observed in tectonic junctions.

The size of an active zone can be limited to a local section, even though a rather long linear structure may be available. As a rule, sizes of active zones match well with the sizes of structural blocks, which corresponds to the classical concept that the energy of an earthquake is controlled by a certain size of a block being unloaded. Actually, it means that the length of a linear structure should be characterized by the length of its active section, which in its turn manifests quasi-independently in the geodynamic sense. The hierarchical rank of a fault zone is determined by the rank of the blocks it separates.

Despite many publications, the relationship between parameters of fault zones such as length, width (the size across strike), amplitude of displacement are being discussed actively. Empirical scale relations linking fault length L, fault width W and amplitude of displacement along rupture are widely used in describing structural characteristics of fault zones [59, 60]. Power relations of the following types are often used to establish links between these parameters:

$$ W = \alpha \cdot D^{a} ,\quad D = \beta \cdot L^{b} ,\quad W = \chi \cdot L^{c} $$

(2)

In many publications the indexes in Eqs. (2) are more often close to one, while the factors $\alpha ,\beta$ and $\chi$ vary in a wide range. Some authors expressed essential doubts in applicability of Eqs. (2). The doubts based mainly on a noticeable dispersion of experimental data [61, 62]. Closeness of indexes in Eqs. (2) to one means fulfillment of similarity relations for the process of faulting—all the linear sizes are linked to each other through direct proportionalities.

More detailed investigations of the last years [63, 64] have shown that there are several hierarchical levels, in which alterations of parameters of the events with scale occur according to different laws, which differ very often strongly from the similarity relations. Figure 2a presents maximum displacement along a fault versus fault length. The plot uses the data of several investigations.

Fig. 2

Structural and mechanical characteristics of faults versus fault length. a Cumulative slip along a fault. References [1,2,3,4,5,6,7,8,9,10,11] are presented in [65]. Lines—best fit of the data in the range L < 500 m and L > 500 m. b Shear stiffness of a fault. Crosses in circles—the data were obtained with the method of seismic illumination. The point in the frame was not used in constructing the regression dependence. Black stars—the data were obtained with the method of trapped waves [65]

By all appearances the linear size L ~ 500–1000 m is a transitional zone, a specific boundary between two bands, in which the scale relations differ. Faults that have reached this stage of evolution may be called the “mature” ones. In [63] for example, a relation linking the width of the influence zone to the fault length was suggested:

$$ W = \left\{ {\begin{array}{*{20}c} {0.15 \cdot L^{0.63} ,\,\;\,L \le 500 \div 1000\,{\text{m}}} \\ {0.85 \cdot L^{0.42} ,\;\,\,L > 500 \div 1000\,{\text{m}}} \\ \end{array} } \right. $$

(3)

Here, the width of the influence zone is the width of the cross-section with higher fracturing.

It is important to emphasize that the change of mechanical characteristics of faults (fault stiffness) with scale demonstrates the presence of approximately the same transitional zone (Fig. 2b).

Further alteration of scaling relations is observed for the most powerful deformation events with characteristic sizes exceeding the thickness of the crust.

Investigations performed for the last 20–30 years have allowed to essentially widen and clarify the knowledge about the inner structure of fault zones. New data have been acquired in the frames of the international program of “fast drilling” of a fault zone after an earthquake [66]. Similar projects of drilling through fault zones have already been fulfilled in several regions [67, 68]. Together with the results of traditional geologic explorations at the surface and in mines [14,15,16, 69, 70] these data allow to acquire a rather orderly notion about the structure of faults’ central parts.

The damage zone is located at the periphery of the fault. Its width may vary from meters to hundreds of meters. It is usually associated with a higher fracture density, if compared to the intact massif. The damage zone contains distributed fractures of a wide range of sizes. It is structured to a great extent and usually contains a standard set of discontinuity types [71].

Cataclastic metamorphism becomes more intensive in the direction to the fault core. One or several sub-zones of intensive deformations can usually be detected there. Their widths may be from centimeters to meters. They are usually composed of gouge, cataclasite, ultracataclasite or of their combination. Deformations can either be distributed uniformly over the fault core, or be localized inside a narrow shear zone. This zone of intensive grain grinding is the principal slip zone (PSZ). Its width is usually from one millimeter to decimeters [14, 16].

The structure of a fault zone depends on depth, properties of enclosing rock, tectonic conditions (shear, compression, tension), cumulated deformations, hydrogeological conditions and type of the deformation process. In slow aseismic creep the principal slip zone is often represented by a set of individual slip zones and zones of distributed shear deformations. Some secondary shears (they are often of oscillatory origin) can be localized along discrete fracture plains. The width of shear zones in the sections of aseismic creep of such faults as Hayward fault and San Andreas lie in the range of meters—tens of meters, the average value at the surface being 15 m [14]. There are suggestions that this zone becomes narrower with depth and its width reduces to about 1 m deep in the rock massif.

An essentially higher degree of localization is observed in seismically active fault zones, where most deformations are, presumably, of coseismic origin. For example, investigations of shears in Punchbowl and San Gabriel faults in California have detected the thickness of the principal slip zone to be not wider than 1–10 cm. Note that cumulative displacements along these faults reach tens of kilometers [16, 71,72,73].

Chester and Chester [16] showed that it is in the principal slip zone that displacements of sides of large faults localize. According to their data, concerning one of the segments of the Punchbowl fault, only 100 m of displacement (of the total displacement length of 10 km) localized in the zone of fracturing about 100 m thick, while the rest occurred inside a narrow ultracataclasite layer from 4 cm to 1 m thick. A continuous, rather plane interface about 1 mm thick was detected inside this core. This interface was the principal slip zone of the last several kilometers of displacement [74].

In fault zones, whose cores consist of cataclastic rocks, coseismic ruptures often occur along one and the same interface, formed of ultracataclasites that have emerged at previous deformation stages [14]. Displacements along secondary, novel discontinuities are small and have a negligible contribution to the cumulative amplitude of fault side displacement.

Individual zones of the PSZ can rarely be traced longer than for several hundred meters, though it is suggested that their lengths can reach several kilometers [14]. In all likelihood PSZs may interact at some deformation stages through the zones of distributed cataclastic deformations without clear signs of a single rupture in latter. An analogy with laboratory sample destruction comes to mind here [75]. Such linear conglomerates of separate PSZs and sections of heterogeneous fracturing can make up an integrated fault core.

Geophysical investigations in wells that penetrate through fault zones at appreciable depths have also demonstrated an extreme degree of localization not only of deformation structure, but such parameters as porosity, permeability, velocity of propagation of elastic vibrations [19, 68].

Thus, the results of geological description of exhumed fault segments, the data on deep drilling of fault zones, as well as detailed investigations of seismic sources located with high accuracy [76] allow to speak about an extreme degree of localization of coseismic displacements. Macroscopic interblock displacements are not distributed over the thickness of material crushed in the course of shear, but are localized along a narrow interface of sliding. It means that with some conditionality, a dynamic movement along a fault can be considered as a relative displacement of two blocks, and their interaction is determined mainly by forces of friction.

4 Frictional Properties of Geomaterial and the Slip Mode

Investigating exhumed segments of fault zones has shown that the structural heterogeneity of large fault zones results in appreciable spatial variations in rheology and deformation rate at one and the same segment [77]. The evolution of frictional properties of rocks composing the massif and their spatial distribution play an important role in the processes of nucleation, localization and propagation of rupture in seismic events [78]. It has been shown in several works that the mineral composition affects the frictional strength and the sliding regime of the fault [79], and frictional stability depends on the evolution of structural properties of the fault during deformation [80].

Models that interpret emergence of different slip modes base on dependences of frictional properties of the sliding interface on velocity, displacement and P-T conditions revealed in laboratory experiments [81, 82].

These dependences are different for different geomaterials. Over the past years, a great number of experiments have been performed with materials collected while drilling fault zones. These experiments have shown that there exist materials with a pronounced property of velocity strengthening (VS). For example, saponite (a material with a low friction factor, which increases as sliding velocity grows), determines the deformation behavior of the creeping segment of the San Andreas fault [83]. Judging by the results of laboratory experiments weak materials rich with phyllosilicates manifest only stable sliding (corresponds to velocity strengthening), at least until the mineral composition of geomaterial in the principal slip zone alters with time. Stronger materials rich with quartz and feldspar, after creeping for a while, become ‘velocity weakening’ (VW) and provide unstable sliding [84].

VS- and VW-wise behavior can take place at different segments of one and the same fault zone. A complex topography of the fault interface leads to emergence of areas of stress concentration and rather unloaded areas. The probability of stick-slip to realize increases essentially in the areas of stress concentration. Deposition of minerals drawn by fluids takes place in unloaded areas, which in many cases promotes formation of layers composed of weak materials rich with phyllosilicates that manifest velocity strengthening. Thus, in many cases it is the contacts of rough surfaces (areas of stress concentration) that turn out to be dynamically unstable in sliding along a fault, while fault segments located between rough surfaces in contact manifest frictional properties of stable sliding. It is likely that these segments preserve their properties during, at least, several seismic cycles. This is supported by, the so called, repeated earthquakes (events identical in locations, energy and waveforms) [85]. These events repeatedly break again and again one and the same spot or asperity on the fault. These repeaters, whose manifestations are now found all around the world, have in most cases small magnitudes, but there are powerful ones too, with magnitudes higher than M6. These observations lead to the conclusion that different sliding regimes are determined by the non-uniform distribution of frictional properties and stress conditions over the fault interface.

It is convenient to demonstrate the effect of spatial non-uniformity of frictional properties on integral characteristics of the sliding process by the example of a numerical calculation of the relative shear of two elastic blocks separated by a sliding interface. The friction between blocks was described by a rate-and-state friction law [81, 82]. According to relations of this empirical model, the coefficient of friction μ depends on the running velocity of sliding V and on the variable of state θ:

$$ \mu = \mu_{0} - a\ln \left( {\frac{{V_{0} }}{V} + 1} \right) + b\ln \left( {\frac{{V_{0} \theta }}{{D_{c} }} + 1} \right) $$

(4)

Here, μ₀ is the constant corresponding to stable sliding at a low velocity V₀; a, b, D_c are empirical constants, V is the running velocity of displacement, θ is the variable of state, which is determined by the kinetic equation:

$$ \dot{\theta } = 1 - \left( {\frac{\left| V \right|\theta }{{D_{c} }}} \right) $$

(5)

When (b − a) > 0 the regime of velocity strengthening realizes. The case of (b − a) < 0 leads to velocity weakening and provides conditions for stick-slip to occur.

One or several spots with “true” condition of velocity weakening but different values of the friction parameter $\Delta = (b - a) < 0$ were “installed” into the sliding interface when the boundary conditions were set. A typical computation scheme is given in Fig. 3.

Fig. 3

Simulating the process of relative shear of two elastic blocks separated by a sliding interface: computation scheme. The block is pressed to the half-space by the normal stress. The upper right corner of the block is being pulled at a constant velocity u_s

The rate-and-state law used here differed from the traditional one by the fact that after the instability has arisen the factors a and b in Eq. (4) were considered to be zero. It was done to avoid repeated dynamic failures triggered by the waves reflected from the boarders of the mesh.

At the rest sliding interface the force of friction was described either by the Coulomb’s law with the same friction factor μ₀ (i.e., there was no dependence on velocity and displacement) or by law (4) with constants that provided velocity strengthening $\Delta = b - a > 0$. Kinematic parameters of motion, components of stress tensor, spatial distribution of alteration of power density of shear deformation of blocks, kinetic energy at different moments of time from the rupture start were controlled.

The size of the upper block (width, length) varied from 50 × 100 m to 200 × 600 m. The lower block was a half-space with the same elastic characteristics (the density 2.5 g/cm³, velocity of P-wave propagation C_p = 3000 m/s, shear modulus G = 52 MPa). The coefficients used in the main series of computations provided the regime of velocity weakening: µ₀ = 0.3, a = 0.0002, b = 0.0882, D_c = 1 μm, V₀ = 0.002 mm/s.

Figure 4 shows the hodograph of a rupture propagating along a fault segment including 1 weakening spot. One can see that the rupture starts at a non-uniformity and propagates away from both sides of the spot. The velocity of rupture propagation along the interface of Coulomb friction is close to the one of P-wave, while at the interface with strengthening the velocity of rupture propagation is noticeably lower than that of the S-wave.

Fig. 4

Hodograph of the first onset of relative block motion. The size of the upper moveable block is 50 × 100 m. The lower block with the size of 400 × 800 m is immovable. Blue line—Δ = 0 at the surface outside the spot; red line—velocity strengthening (Δ = 0.024) is “switched on” at the surface outside the spot

In the case of a contact with strengthening the amplitude of the velocity of displacement decays essentially faster in both directions. For example, at a distance of 100 diameters of the spot in the direction normal to the fault the maximum velocity of displacement in the case of interface with strengthening approximately 6 times lower than in the case of Coulomb friction.

Figure 5 shows the seismic moment $M_{0} = G \cdot L \cdot U$ and kinetic energy of the block versus time for several variants of simulations. In the relation of seismic moment: L is the block length and U is the relative displacement. When friction between blocks increases as velocity and displacement grow (variant 2, 3), then the value of kinetic energy (the analogue of emitted energy) becomes lower than in the case of Coulomb friction. The final values of seismic moment are close for all the three variants, though the rate of growth of the value of M₀ is noticeably lower in the case of strengthening. It means that the energy of elastic deformation cumulated in the course of the interseismic period releases to a great extent during a rather slow sliding. It is this slow sliding that the dynamic rupture degenerates to, when it reaches the contact segment exhibiting velocity strengthening. This is well seen in the computation variant with several spots of weakening (Fig. 6). Again, the rupture starts at one of the spots of velocity weakening and propagates away from both sides of the spot. Outside the spot of weakening the velocity decays rapidly even in absence of segments with strengthening, speeding up again at neighboring VW spots. Though the maximum velocity of sliding decreases rapidly outside the spot of weakening, the integral value of relative ‘fault side’ displacement (the sum of dynamic slip and slow pre- and post-seismic slips) in this computation statement remains almost the same. The higher the total share of the VW spots is, the higher is the share of deformation energy spent to emission of the elastic wave in the high-frequency band of the spectrum.

Fig. 5

Kinetic energy of the block and seismic moment versus time. The upper block is of the size of 150 × 450 m. a, b The centre of the single spot of velocity weakening of the size of l = 1 m is located in the point x = 225 m. 1—friction outside the spot doesn’t depend on velocity (Δ = 0). 2, 3—friction outside the spot increases as the velocity and displacement grow (Δ = −0.008 and Δ = −0.024, relatively), c the number of velocity weakening spots is shown by corresponding numbers near the curves; parameters a and b in the R&S law vary in a random way in the limits: a = 0.0002–0.0006, b = 0.0071–0.0084

Fig. 6

Waveforms of particle velocity in the direction parallel to the sliding interface for the computation variant with four identical spots of velocity weakening. Locations of the VW spots are shown with bold segments at the left axis. Coulomb friction acts outside the spots. Numbers near the curves are the distances from the point of rupture start scaled by the spot diameter D. Solid lines are the epures corresponding to points inside the spots; dashed lines are the epures corresponding to points outside the spots. The amplitude of particle velocity is scaled by the velocity, at which the upper side of the block is pulled. Only first phases of motion are shown for better readability

For a great number of “spots-asperities” the rupture may start almost simultaneously at several spots. As far as the particle velocity is concerned, two types of segments can be clearly detected, just like in the case of several spots. The first one includes the spots themselves and their closest vicinity. Maximum velocity there reaches the values of 0.1–0.2 m/s. All over the rest contact the maximum particle velocity is 10–20 times lower.

Increasing quantity and density of asperities leads to an abrupt growth of the kinetic energy of block gained for the first 100 ms, i.e., the energy emitted in the high-frequency band of the spectrum. Meanwhile the integral value of seismic moment increases essentially slower.

Thus, the presence of VW spots determines the possibility of dynamic rupture to emerge. Their density and mutual locations govern the amount of energy emitted in the high-frequency band. Location and size of zones exhibiting velocity strengthening affect the velocity of rupture propagation, the scaled seismic energy (the ratio of E_s/M₀) and the size of the “earthquake”. Under the adopted statement of computations, termination of the dynamic rupture corresponds to a radical decrease of the velocity of sliding. The rupture propagates along a stressed tectonic fault to the zone, in which the contact exhibits velocity strengthening—velocity of displacement, emitted energy and rate of seismic moment growth harshly decrease. If the size of the strengthening zone is big enough, the “earthquake” degenerates into a “slow slip event” or the rupture terminates completely. The rupture crosses small zones, then again speeding up at VW spots. If there are no big strengthening segments at fault interface, in this statement all the length of the block becomes involved in sliding, though in nature the rupture is usually terminated at some structural barrier [86].

5 Generating Different Slip Modes in Laboratory Experiments

Experiments on investigating regularities of emergence of different slip modes on a fracture with filler were performed on a well known slider-model set-up, in which a block under normal and shear loads slides along an interface (Fig. 7). A granite block (B) 8 × 8×3 cm in size was put on an immoveable granite base. The contact between rough surfaces (the average depth of roughness was 0.5–0.8 mm) was filled with a layer of discrete material (S), imitating the PSZ of a natural fault. The layer thickness was about 2.5 mm. The normal load σ_n was applied to the block through a thrust bearing. σ_n varied in the range of 1.2 × 10⁴ to 1.5 × 10⁵ Pa. The shear load τ_s was applied to the block through a spring block. Its stiffness could vary. The set-up was equipped with an electromotor with a reducer that allowed to maintain the velocity of loading u_s with high accuracy in the range of 0.08–25 μm/s. The shear force was controlled with a force sensor. Displacements of the block relative the base were measured with LVDT sensors with the accuracy of 1 μm and with laser sensors (D) in the frequency range of 0–5 kHz and with the accuracy of 0.1 μm.

Fig. 7

Photo of the slider-model setup and the scheme of the experiments. B—movable block, S—layer of filler, D—laser sensor, K—spring element, F—force sensor, AE—acoustic emission sensor

Filling the contact with mixtures of different materials, we managed to realize a wide spectrum of slip modes in the experiments, which correspond qualitatively to all types of interblock movements observed in nature—from aseismic creep to earthquakes. Examples of slip episodes realized in experiments are shown in Fig. 8. The figure also shows the recorded pulses of acoustic emission radiated during sliding.

Fig. 8

Examples of diagrams of block velocity corresponding to different deformation events and their acoustic signal portraits. a fast mode (corresponds to normal earthquake); b medium mode (corresponds to slow earthquake); c slow mode (corresponds to slow slip event)

Let’s consider the conditions for slip to occur. A necessary condition for a slip to occur is closeness of effective stresses, tangential to fault plane, to the local or running ultimate strength:

$$ \tau \ge \tau_{0} $$

(6)

We use the term “local ultimate strength” because slip can occur under tangential stresses knowingly lower than the Coulomb strength $\,\tau_{p}$.

Another necessary condition is the weakening of the sliding area as the velocity v and/or amplitude D of fault side displacement grows:

$$ \frac{\partial \tau }{\partial v} < 0\,;\,\,\,\frac{\partial \tau }{\partial D} < 0\, $$

(7)

It is clear that if the contact strength will not decrease during shear, a dynamic slip will be actually impossible.

And, at last, the third condition: the rate of decrease of stresses in the enclosing massif, tangential to sliding interface (this is the shear stiffness of the massif K) should be lower than the rate of decrease of resistance to shear (this is the modulus of fault stiffness k_s at the post-critical section of the rheologic curve):

$$ \left| {k_{s} } \right| = \left| {\frac{\partial \tau }{\partial D}} \right| \ge K = \eta \frac{G}{{\hat{L}}} $$

(8)

G is the shear modulus of the enclosing massif, $\eta \sim 1$ is the shape factor [75], and $\hat{L}$ is a specific size linked to the magnitude of the earthquake.

It is convenient to demonstrate the meaning of relations (6)–(8) at the scheme shown in Fig. 9. After the stress has reached the running strength of the contact (τ_p corresponds to the maximum of rheological curve τ(D) in Fig. 9, though it is not obligatory) the contact strength starts to decrease as the relative displacement and velocity grow. If condition (8) is true (black solid line in Fig. 9), a dynamic instability occurs and the energy is emitted outside the system. The amount of emitted energy in this simple example corresponds to the area bounded by the rheologic curve and the solid line of unloading of the enclosing massif. In the case when condition (8) is not true (dashed line in Fig. 9) the dynamic slip and, consequently, emission of energy are impossible.

Fig. 9

Scheme of the slip emerging on a fault. Red line is the rheologic dependence stress-displacement; black straight lines are the lines of enclosing massif unloading in the course of relative fault side displacement. Black solid line—the rate of massif unloading is lower than the rate of decrease of resistance to shear along the fault. This case corresponds to emergence of dynamic slip. The energy emitted by a unit area of the sliding interface corresponds to the hatched area. Black dashed line—the rate of massif unloading is higher than the rate of decrease of resistance to shear along the fault. The fault remains stable in this case. Blue line is the decrease of effective friction during sliding at the expense of frictional melting, thermal effects, etc. It is well seen that these processes can change the parameters of an earthquake, but not the moment of dynamic slip start

In the course of sliding at velocities of ~1–10 m/s and in P-T conditions specific for seismogenic depths, a number of processes severely affecting the parameters of resistance to shear can occur at the interacting surfaces. These are the effects of friction lowering either because of thermal effects or due to effects produced by the high velocity of sliding: frictional melting [87], dynamic lubrication with solid materials [88], localization of heating in the area of “real” contact [89], macroscopic rise of temperature and the effect of velocity weakening [90], thermal decomposition of minerals leading to growth of pore pressure and generation of weak material [91], generation of silica gel during quartz amorphization under high pressure and large deformations [92], neo-mineralization of the sliding interface at the nano-crystal level [93].

All these effects are very important because they lead to a decrease of residual friction τ_r (blue line in Fig. 9) and, consequently, a decrease of the amplitude of stress drop Δτ and of the amount of emitted energy (magnitude of the earthquake). However, as these phenomena have no effect on fulfillment of conditions (6)–(8), they are of no use in searching for the signs of dynamic failure preparation.

Thus, it seems reasonable to select the modulus of the rate of decrease of resistance to shear (fault stiffness |k_s| at the beginning of the post-critical section of the rheologic curve) as the characteristics which controls the initial stage of earthquake rupture nucleation. The ratio $\psi = {{\left| {k_{s} } \right|} \mathord{\left/ {\vphantom {{\left| {k_{s} } \right|} K}} \right. \kern-0pt} K}$ determines not only the possibility of sliding, but its character as well.

A certain slip mode realized in fault deformation is determined by structural, physical and mechanical properties of the filler. In a regular stick-slip repeated slip events take place with close parameters, while in irregular regimes stochastic events are observed, and their statistics obeys a power law.

For example, increasing the share of smooth grains (glass beads) leads to jamming of the granular layer and transition from stable sliding to stick-slip (Fig. 10). Earlier a similar result was obtained in [94]. In absence of smooth grains 90% of all the events have peak velocity of only 0.1–0.2 mm/s, while events with peak velocities exceeding 0.5 mm/s are absolutely absent. Thus, we can say that the steady sliding mode is realized.

Fig. 10

Transformation of sliding regime. a Displacement versus time for experiments with filler consisting of quartz sand with different admixtures of glass beads. (1) pure sand, (2) 20% of glass beads, (3) 40% of glass beads, (4) pure glass beads. b The variations in peak velocity versus changes in the gouge texture

When the share of glass beads reaches 40–50% of filler mass the motion becomes the stick slip with a relatively small value of stress drop. A further increase of the amount of smooth grains changes only the amplitude of displacement during a failure. When the filler consists only of glass beads the value of stress drop Δτ reaches approximately 15% of the maximum value of shear strength τ₀, and the peak velocity of blocks reaches the value of 60–80 mm/s.

The emergence of a certain slip mode is determined not only by the grain geometry, but also by their chemical and physical properties. For example, for monocomponent low dispersion fillers consisting of angulated grains with ionic bonds between molecules (sodium chloride, corundum, magnesium oxide) realization of dynamic failures is much more probable than for fillers with covalent or metallic bonds between molecules (dry quartz sand, graphite and others) under similar loading parameters [95]. Probably the ionic bonds provide a stronger adhesive interaction of the filler grains in contact.

Moistening of the filler has an essential effect on the slip mode. It is well known that adding even a small amount of liquid to a granular media changes its collective stability [96, 97]. It is interesting that the value of stress drop changes non-monotonically as the viscosity of the moistening fluid grows (Fig. 11).

Fig. 11

Variations of shear stress drop versus fluid viscosity. Red symbols correspond to experiments with post-critical values of viscosity

Varying interstitial fluid viscosity, we traced the transformation of the sliding regime. The mass humidity of gouge was 1%. Variation of liquid viscosity $\eta$ from 3 × 10⁻⁴ to 2 × 10¹ Pa s caused a 15 times change of static stress drop. At the same time relative change of $\tau_{s}$ was only 25%. The value of $\Delta \tau /\tau_{s}$ gradually increases with increasing liquid viscosity up to the critical value η_cr ≈ 1 Pa·s and then sharply drops by almost one order of magnitude, after which the value of $\Delta \tau /\tau_{s}$ gradually decreases with increasing viscosity up to 20 Pa s. At the range of after-critical values of viscosity the peak velocity decrease is approximately inversely proportional to the value of viscosity, and growth of slip duration is observed.

The presence of a small amount of interstitial liquid promotes jamming of the model fault. Probably, fault jamming is caused by the emergence of an additional intergrain force. The higher the force is, the higher is the value of elastic energy accumulated and, consequently, the higher are the stress drop and peak velocity during the slip episode. The cohesive force between gouge grains initially increases sharply for very small volumes of liquid because of the roughness of grains, further cohesiveness is effectively constant at least up to the stage when the liquid occupies about 35 percent of the available pore space [98, 99].

During the slip episode a reorganization of the meso-scale fault structure takes place, manifested in intergrain slipping. [95, 100]. At the stage of rest, when velocity is low, the intergrain contact dewets, which is accompanied by the accumulation of excess liquid in the pore space. But during the slip episode the liquid can penetrate into the grain contact at “critical” slip velocity conditions [101]. Probably, in the presented experiments, in the case of pre-critical viscosity (η ≤ 1 Pa s) the slip velocity is not high enough for the “lubrication effect” to occur. But when η > 1 Pa s liquid penetration takes place, provoking damping of stick-slip events and the higher value of viscosity corresponds to the lower value of peak velocity. According to [102], when the fluid viscosity is about 10⁵ Pa s, the occurrence of steady sliding must be observed.

The effect of filler properties on the sliding regime can be traced if one uses low dispersion mixtures of different grain materials as fracture filler. Variations of clay content in the moistening sand/clay mixture provided considerable changes of the fault slip modes. Figure 12 shows the dependences of slip episode parameters for different content of clay in the gouge moistened with water and glycerol. As clay content was increasing, transformation from stick-slip to steady sliding was observed. For the clay content of less than 15% a regular regime of fast slip episodes took place. Increasing clay content up to 20% led to the formation of irregular regime consisting of fast and slow slip episodes. The average values of slip episode parameters varied relatively slow (about an order of magnitude) in the range of clay content of ν = 0–25%. When clay content was increased from 25 to 28% of mass, the decrease of average value of peak velocity by more than two orders of magnitude (from ~7 mm/s to ~0.04 mm/s) occurred and shear stress drop decreased 5 times. For mixtures with clay content of 30% rare slow slip episodes were observed, and for mixtures with clay content exceeding 35% the sliding became steady.

Fig. 12

Variation of shear stress drop (blue), peak slip velocity (black) and the slip episode duration (red) versus clay content in the gouge moistened with water (a) and glycerol (b). Vertical solid lines are standard deviations, vertical dashed lines show the range of variation of slip event parameters for irregular slip regimes

A similar pattern of changes in the fault behavior, but more drastic, was observed in experiments with glycerol. In the range of clay content of ν = 0–1% the peak velocity decreased 3 times, further increase of clay content from 1 to 3% resulted in the drop of peak velocity by approximately 3 orders of magnitude. For mixtures with clay content exceeding 5% sliding became steady.

A wide spectrum of shear deformation regimes was realized in the presented experiments by changing the filler properties or the stiffness of loading—from dynamic failures to stable sliding. It should be emphasized that slow slip modes have all the phases intrinsic for stick-slip—acceleration, prolonged sliding, braking, stopping and the phase of rest. This suggests the idea that all the slip modes on faults span a continuum—they may be considered as a single set of phenomena.

Interesting consequences follow from comparison of the laboratory experimental data to results of numerical simulation basing on the rate-and-state frictional law—Eqs. (4) and (5). By overrunning the constants in the rate-and-state relations a, b and D_c the best fit of simulated and experimental data was provided.

Figure 13a compares the simulated and experimental dependences of block slip velocity on time for the contact filled with quartz sand. For convenience, here and below the time is counted from the moment of velocity maximum. The following parameters of the rate-and-state model were used in simulations: a = 0.0002, b = 0.00109, D_c = 10 μm. The characteristics of slider model corresponded to experiment. The figure confirms that in the case of a pronounced stick-slip the simulated epure reproduces the experimental one rather well. Comparing the results of simulations to the experiment at the diagram force-displacement also demonstrates good correspondence. Calculations made for numerous experiments have shown that failure episodes during stick-slip (“laboratory earthquakes”) can be satisfactorily simulated with the canonical rate-and-state law (4).

Fig. 13

a Block velocity versus time for the contact filled with quartz sand. R&S parameters of simulation: K = 17 kN/m; µ = 0.61; D_c = 10 µm; a = 2 × 10⁻⁴; b = 1.09 × 10⁻³. Solid line is the simulation, dashed line is the experiment. b Block velocity versus time. The contact is filled with dry fire clay. The stiffness of the spring is K = 17 kN/m; (1)—experiment; (2)—simulation with η_d= 0 in Eq. (9); (3)—simulation with η_d= 1000 Pa s. Parameters of the R&S model: Δ_c = 6.5 × 10⁻⁴; µ = 0.7; D_c= 50 μm; a = 1.2 × 10⁻⁴; b = 1.35 × 10⁻³

Attempts to simulate the slow sliding regimes (laboratory “slow earthquakes” and “episodes of slow slip events”) have met certain difficulties. This is well seen in the example presented in Fig. 13b, which shows the results of calculation of the block slipping slowly along the contact filled with dry clay, the stiffness of loading element being equal to 17 kN/m. In this experiment the duration of sliding has increased, if compared to the contact filled with dry quartz sand, approximately by an order of the magnitude, along with a corresponding decrease of both the maximal and the average slip velocities (curve 1 in Fig. 13b).

We failed to reproduce such a signal in simulations involving only the canonical rate-and-state model (curve 2 in Fig. 13b). Varying the parameters, one can only fit the amplitude of the signal, but the “fullness” of the epure, i.e., the value of displacement, is controlled mainly by block mass and spring stiffness (parameters rigorously defined for each experiment). We could only “dilute” the onset of the peak by changing D_c. The simulated peak of the dynamic failure for a given amplitude always remained essentially narrower than the one obtained in experiment.

We managed to better fit the results of simulating “slow” movements to experiment by introducing a term to the canonical R&S Eq. (4) that takes into account the emergence of additional resistance to shear produced by the “dynamic viscosity” of the contact:

$$ F_{s} = \sigma_{N} \cdot S \cdot \left[ {\mu_{0} + a\ln \left( {\frac{{|\dot{x}|}}{{u^{*} }}} \right) + b\ln \left( {\frac{{u^{*} \theta }}{{D_{c} }}} \right)} \right] + \frac{{\eta_{d} \cdot S \cdot \dot{x}}}{d} $$

(9)

where η_d is the factor of dynamic viscosity of interblock contact; S and d are the area and thickness of the contact zone. Results of simulations with account for the dynamic viscosity are presented in Fig. 13b by the line 3. One can see that introducing the “dynamic viscosity” of the contact into the equation of motion allows to reproduce the slow slip mode in simulations with satisfactory accuracy, too.

Equation (9) allowed to satisfactorily reproduce the character of motion in all the experiments by fitting the effective viscosity. Figure 14 gives examples of epures of slip velocities of the block in two experiments—with the contact filled with watered fire clay and with the contact filled with quartz sand with an admixture of 25% of talc. In both cases the slippages have long phases (~30–40 s) of gradual velocity increase, and then phases of deceleration of about the same duration. The maximum velocity of displacement decreases to 10–100 μm/s. For best fitting of simulated and experimental results the factor of effective viscosity η was increased by more than an order of a magnitude if compared to the simulation of experiment with dry fire clay (Fig. 13b).

Fig. 14

Block velocity versus time for the slow slip mode. a contact filled with watered fire clay; (1) experiment; (2) simulation; Parameters of modified R&S model: K = 10 kN/m; Δ_c = 6.5 × 10⁻⁴; µ = 0.56; D_c= 90 мкм; a = 1.0 × 10⁻⁴; b = 3.5 × 10⁻³; η_d= 2.76 × 10⁴ Pa s. b contact filled with mixture of quartz sand (75%) and talc (25%). (1) experiment; (2) simulation; Parameters of modified R&S model (9): K = 16.56 kN/m; Δ_c = 2.3·10⁻⁴; µ = 0.61; D_c= 18 μm; a = 1.0 × 10⁻⁵; b = 8.5 × 10⁻⁴; η_d= 3.94 × 10⁴ Pa s

It is well known that the generalized viscosity of a rigid body is not the property of the material itself, as for example, the viscosity of Newtonian fluid. This parameter is a characteristics of the rigid body rheology, depending on the specific time of deformation process, or, to be more precise, on the deformation rate.

Figure 15 shows the dependence of the factor of effective viscosity η_d on the peak velocity of block displacement. The effective viscosity was obtained by fitting the results of simulations to the ones of experiments, the simulations being performed according to the modified Rate-and-State law (9). Symbols show the results for different fillers and stiffnesses of the loading device. The line shows the best fit by the following power function:

Fig. 15

Effective viscosity versus peak velocity of block displacement. The line shows the best fit by the Eq. (10) with R²= 0.94

$$ \eta_{d} = 235 \cdot u_{\max}^{ - 0.97} $$

(10)

Thus, the conducted laboratory and numerical experiments have demonstrated that the effective viscosity is a conventional parameter with the dimensionality of Pa s. This parameter is convenient to describe the alterations of fault slip modes. The factor of dynamic viscosity depends both on the properties of the filler and on the stiffness of the loading system. A verification of the results of simulations involving the rate-and-state model allows to conclude that to have the opportunity of modeling all the spectrum of fault slip modes the empirical Dieterich’s law [81, 82] should be supplemented by a term that takes into account the emergence of additional resistance to shear produced by the dynamic viscosity of the fault interface, or, to be more precise, by the fact that the force of resistance to shear depends on the velocity of interblock motion. After this the episodes of slow slip observed in experiment can be reproduced with an appropriate accuracy. The obtained results agree with the data presented in the works [103, 104], where the dependence of viscosity factor on specific time of deformation is close to a linear one.

6 Radiation Efficiency of Slip Episodes

It is evident that in different slip modes different shares of deformation energy are emitted as seismic waves. It is a common thing that seismic events produced by the processes of deformation and destruction of a rock massif are described by two parameters: seismic moment (M₀) and seismic energy (E_s). The scalar seismic moment:

$$ M_{0} = \mu \cdot D_{S} \cdot S $$

(11)

is a generally recognized measure of the event size. This value does not depend on details of the process in the source, because it is determined by the asymptotics of the spectrum of displacements in the low-frequency band. It is proportional to the amplitude of the low-frequency band of the spectrum, and, provided that up-to-date equipment and processing methods are used, it can be estimated rather reliably. In Eq. (11), μ is the shear modulus of rock in the source, D_s is the displacement along the rupture, S is the area of the source. The divergence of estimations made by different authors for powerful earthquakes rarely exceeds 2–3 times.

The seismic energy E_s, i.e., the part of the deformation energy emitted in the form of seismic waves, on the contrary, is determined by the dynamics of rupture development and depends on velocity of rupture propagation, balance of energy in the source, etc. The value of seismic energy is usually determined by integrating the recorded vibrations.

In laboratory experiments the following product can be considered as the analogue of seismic moment: $M_{lab} = K \cdot D \cdot L$. Indeed, in nature the seismic moment is the product of shear force drop $\Delta F_{s}$ acting at the fault plane by the fault length Ls:

$$ M_{0} = \mu \cdot D_{S} \cdot L_{s}^{2} = \mu \frac{D}{{L_{S} }}L_{S}^{3} = \Delta \tau \cdot S \cdot L_{S} = \Delta F_{s} \cdot L_{S} $$

(12)

In this relation D_s is the displacement produced by slip events, $S \approx L_{s}^{2}$ is the area of rupture, $\Delta \tau$ is the tangential stress drop at the fault due to slip. For laboratory experiments with the spring-block model the single shear force drop can be written as $\Delta F = K \cdot D$, where K is the spring stiffness, D is the block displacement.

Then, comparing the energy budgets for earthquake and for laboratory slip event [23], we may consider the relation $e_{lab} = {{E_{k} } \mathord{\left/ {\vphantom {{E_{k} } {\left( {K \cdot D \cdot l} \right)}}} \right. \kern-0pt} {\left( {K \cdot D \cdot l} \right)}}$ as the analogue of the energy/moment ratio e = E_s/M₀, which is used in seismology to characterize the seismic efficiency of an earthquake. Here l is the block size.

It is convenient to estimate the share of deformation energy that transited to the kinetic energy of block motion (emitted in a laboratory “earthquake”) using the experimental dependence of the measured shear force on block displacement. Examples of such dependences are given in Fig. 16.

Fig. 16

Examples of experimental diagrams ‘shear stress—displacement’. Solid line is the frictional resistance of the contact. Dashed line is the force applied by the spring. Shaded areas correspond to the values of kinetic energy of the block. a Fast mode (laboratory earthquake). The filler is quartz sand moistened with glycerol (1% of the mass). b Slow mode (laboratory slow slip event). The filler is watered mixture of quartz sand (70%) and clay (30%)

When stresses, tangential to fault interface, reach the ultimate strength of the contact τ₀ and the condition (6) is true, the resistance to shear $\tau_{fr} (x) = {{R\left( x \right)} \mathord{\left/ {\vphantom {{R\left( x \right)} {l^{2} }}} \right. \kern-0pt} {l^{2} }}$ starts to decrease with displacement faster than the applied load $\tau_{s} \left( x \right) = {{F_{s} \left( x \right)} \mathord{\left/ {\vphantom {{F_{s} \left( x \right)} {l^{2} }}} \right. \kern-0pt} {l^{2} }}$. As a result a slip starts, which is described by the equation:

$$ m \cdot \frac{{\partial^{2} x}}{{\partial t^{2} }} = \left[ {\tau_{s} (x) - \tau_{fr} (x)} \right] \cdot l^{2} $$

(13)

where m is the mass of moveable block, x is the relative displacement of blocks. After a certain displacement D_c has been reached (its value depends on roughness of fault walls, filler properties, etc.) the value of τ_fr comes to the residual (dynamic) value and stops changing.

After the following condition becomes true:

$$ \int\limits_{0}^{x} {\left[ {\sigma_{s} (\chi ) - \tau_{fr} (\chi )} \right]} {\text{d}}\chi = 0 $$

(14)

block slippage along the interface ceases ($x_{tot} = D_{tot}$ in Fig. 16a) and a new cycle of cumulating the deformation energy starts.

If the character of the dependence $\tau_{fr} (x)$ is such that the difference $\tau_{s} (x) - \tau_{fr} (x)$ becomes negative earlier than the minimum possible value of the friction force is reached (Fig. 16b), the contact actually doesn’t come to the slip regime fully, which results in a small stress drop. Such an effect is most pronounced for fractures with high content of ductile grains (clay, talc).

The energy E_s, emitted during a slip event, was determined by integrating the difference of experimental dependences of the applied load $\tau_{s} (x)$ and resistance to shear $\tau_{fr} (x)$:

$$ E_{s} = \int\limits_{0}^{{D_{0} }} {\left[ {\tau_{s} (\varsigma ) - \tau_{fr} (\varsigma )} \right]} \cdot l^{2} \cdot {\text{d}}\varsigma $$

(15)

where D₀ is the displacement, for which $\tau (D_{0} ) - \tau_{fr} (D{}_{0}) = 0$. Shaded areas in the examples presented in Fig. 16 correspond to the values of E_s.

Thus, the ratio of the stiffness of fault to the one of enclosing massif (fracture and spring in laboratory experiment) $\psi = \left| {k_{s} } \right|/K$ determines not only the possibility of slippage, but its character as well. The dependence of scaled emitted energy $e_{lab}$ on this parameter, plotted according to the results of laboratory experiments is shown in Fig. 17.

Fig. 17

Scaled emitted energy versus ratio of the stiffnesses of fault to enclosing massif. Symbols are the results of laboratory experiments. The area bounded by two horizontal dashed lines corresponds to dynamic failures. Slow events are to the left from the vertical dashed line

It is well seen that stick-slip takes place in a rather wide range of the values of $\psi$, while slow slip modes realize in a narrow area of the values of |k_s|/K ~ 1÷2. It means that at “brittle” faults, whose stiffnesses (the rate of decrease of resistance to shear) are rather high, the deformation energy releases solely in dynamic failures—normal earthquakes. Slow slip events can take place at faults with low stiffnesses. As massif stiffness in the crust alters slightly for different regions and different depths, it is the fault stiffness k_s that should be taken as governing parameter.

7 On Artificial Transformation of the Slip Mode

The main anthropogenic factors that can trigger movements on a prepared fault are variations of fluid-dynamic regime in the fault zone, effect of seismic vibrations, excavation and displacement of large amounts of rock in mining. Irrespective of what factor we are speaking about, the geomechanical criteria (6)–(8) formulated above should be true at a certain fault segment and in the enclosing rock massif. It makes sense to assume that the specific size of the segment should exceed the size of the, so called, “zone of earthquake nucleation”—the section where the rupture rate reaches the dynamic value [75]. Currently this value can be estimated only roughly. According to seismological data [103,104,105,106,107], the size of nucleation zone L_n can reach about 10% of the length of future rupture, i.e., for M = 6 $L_{n} \le { 1000}\,{\text{m}}$. Let us consider possibilities of realization of the formulated criteria under anthropogenic factors.

7.1 Changing the Fluid Dynamics

The effect of injection/withdrawal of fluid in/out of rock masses on seismicity has been studied in numerous works. One can find citations of corresponding publications, for example, in monographs and reviews [108, 109]. Rising pore or formation pressure and corresponding decrease of the effective Coulomb strength of faults and fractures is considered to be the main physical mechanism. However, there are many evidences [109, 110] that very weak variations of hydrostatic pressure (about millibar) affect seismicity. It is unlikely that the Coulomb model can be applicable here. It has been established in in situ experiments that the size of the area where parameters of sliding regime along a fault change can exceed several times the radius of the zone of pore pressure alterations [57]. It means that injection or withdrawal of fluid can change the characteristics of geomaterial.

The frictional parameter—the difference (a − b) from Eq. (4)—decreases abruptly, i.e., velocity weakening becomes more pronounced even when a small portion of fluid is injected. In the laboratory experiments described above adding fluid weighing 0.1% of the mass of laboratory fault filler is enough for a radical change of the character of sliding from creep to pronounced stick-slip [65].

Injecting fluid is, probably, one of the few possibilities to change the frictional parameter in situ. Such an effect was observed in the above laboratory experiments, in which the stick-slip of a granite block on a thin layer of granular material was investigated. Increasing fluid content, when its volume share had already reached ζ ≈ 0.1%, resulted in a rather abrupt transition from stable sliding to stick-slip. In the presence of glycerol the maximum velocity of sliding increased more than 300 times. In case the humidity was further increased the regime stabilized and up to ζ ≈ 10% the deformation regime exhibited almost no dependence on content of fluid in the filler. Most likely, this phenomenon results from the character of interaction of particles in the fracture filler. After adding a small amount of fluid a thin film of sub-micron thickness emerged at the surfaces of filler grains. This film smoothed roughness and promoted good contacts between separate grains. The deformation regime on the fracture depends essentially on the effective viscosity of the fluid (Fig. 11). The performed estimations show that in nature colloidal films covering filler grains may emerge during the processes of aggregation—formation of enlarged structural elements as a result of adhesion of separate grains. Judging by the results of the performed experiments, viscosity of these films, i.e., the chemical content of clays, may affect the regime of fault deformation.

In laboratory tests described in [111], fast injection of fluid into the contact zone resulted in alteration of such sliding parameters as velocity of movement, stress drop, emitted energy. Alteration of pore pressure was negligible in comparison to the normal stress on the fault, i.e., it is the changed frictional properties of the contact that led to alteration of the slip mode. It should be emphasized that in this case the effect was observed after an appreciable amount of fluid had been injected (~20% of fracture volume, the porosity of the filler being about 35%), so, the fluid spread to about 80% of the contact area.

Injecting noticeably less amount of water in experiments on loading a monolithic heterogeneous sample [112] resulted in appreciable variations of the regime of acoustic emission and kinetics of the process of macro-destruction. These processes, probably, caused by physical and chemical interactions in fracture snouts of the type of Rehbinder effect, had no relation to the effect of alteration of parameters of velocity weakening during sliding, being discussed here.

Thus, though an anthropogenic change of fluid dynamics hypothetically can lead to triggering a dynamic movement, one should keep in mind that this change should involve a rather big fault area.

7.2 Effect of Seismic Vibrations

Triggering seismic events by vibrations of earthquakes that occurred at distances of hundreds and thousands of kilometers is an admitted example of the trigger effect [18]. As far as the data of numerous investigations of the so called “dynamic triggering” is concerned, we should note that in most cases the minimum strain level needed for initiation is estimated to be about ~5 × 10⁻⁷–10⁻⁶, though some authors give less estimations [113]. In most cases occurrence of dynamically triggered seismicity is linked to the effect of low-frequency surface waves with periods of 20–40 s. It is generally admitted that triggering with high-frequency body waves seems hardly probable. A detailed review of this topic is given, for example, in [18] and in the monograph [65].

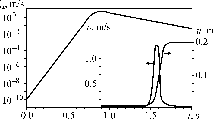
Explosions turn out to be less effective from the point of view of triggering dynamic movements, than powerful distant earthquakes. The results of measuring parameters of seismic vibrations produced by ripple-fired explosions (for example, in [112]) allow to estimate the maximum particle velocity of the wave at different distances. For delay-fired explosions with typical parameters used in mining, maximum particle velocity at the distance of R ~ 3÷5 km does not exceed the value of V_m~ 0.3–0.6 mm/s. The characteristic frequency of vibrations is about f ~ 0.1–0.5 Hz, while the duration of the wave-train may reach 100 s. It should be emphasized that increasing the integral energy of a delay-fired explosion leads (at distances of several kilometers) only to an increase of duration of the signal, but actually has no effect on the values of peak ground velocity (PGV). Therefore, dynamic stresses in seismic waves at the depth of 3–5 km can reach the values of only several kPa, and strains—~10⁻⁷.

Estimations [65] and the data of precise measurements of residual displacements on faults, produced by seismic vibrations from explosions, show (Fig. 18) that the expected value of a residual displacement on a fault under the effect of such a disturbance can be from sub-microns to tens of microns, and only in extreme cases it can reach 1 mm. Under such displacements a direct triggering of earthquake of an appreciable magnitude by seismic waves from explosions is hardly to be expected, because according to seismological data the value of critical displacement for an earthquake of average size (M ~ 6) is about 10 cm [75, 105]. It can be seen in Fig. 18 that for a noticeable effect to occur the PGV at an appreciable part of the fault area should be about 10 cm/s and even more. It means that the charge should be installed rather close to a fault that have reached the ultimately stressed state. An example of such an event is the April 16, 1989 earthquake in Khibiny Mountains [113].

Fig. 18

Residual displacements registered on discontinuities versus the value of peak ground velocity (PGV) in seismic wave

7.3 Excavation and Displacement of Rock in Mining

Perhaps the most powerful anthropogenic triggering factor is the displacement of rock in mining. Considering this question is out of the frames of this article. We should only note that excavation of material from a large operating quarry with the sizes of kilometers in plane and hundreds of meters in depth leads to a reduction of Coulomb stresses up to 1 MPa at the planes of faults located at depths of several kilometers [114]. This value is negligible compared to the level of lithostatic stresses. But it may turn to be enough to trigger a seismogenic movement along a stressed fault. This is supported by the well known calculations of the field of static stresses in the vicinity of hypocenters of aftershocks of powerful earthquakes [115]. It is important to emphasize that for large quarries the size of the zone, in which the change of Coulomb stresses at fault plane exceeds 10⁻¹ MPa, is essentially bigger than the size of the nucleation zone of an earthquake with magnitude $M \le 6$.

Open (surface) mining operations in most cases only bring the moment of the earthquake closer, while underground developing of deposits changes effective elastic moduli of the rock massif in the vicinity of an active fault [116]. Therefore, it seems probable that without the anthropogenic effect the cumulated deformation energy would have released not through a dynamic movement (earthquake), but in another way, e.g., through slow creep or a series of slow slip events.

8 Conclusion

Discovery and classification of sliding regimes on faults and fractures, that are transitional from stable sliding (creep) to dynamic failure (earthquake), alter to a great extent the understanding of how the energy cumulated in the process of the Earth’s crust deformation is released. Slow movements along faults are now perceived not as a special sort of deformations, but together with earthquakes span a continuum of slip modes.

Judging by the results of laboratory tests, small variations of material content of the fault principal slip zone can lead to an appreciable change of the part of seismic energy emitted in dynamic unloading of the adjacent section of the rock massif. Regimes of interblock sliding with values of scaled kinetic energy differing by several orders of magnitude, while differences of contact strengths are small, have been reproduced in experiments. The obtained results allow to conclude that the sliding regime and, in particular, the part of deformation energy that goes to seismic emission, is determined by the ratio of two parameters – stiffness of the fault and stiffness of the enclosing massif. A particular consequence of this statement is the well known condition of stick-slip occurrence.

It means that for episodes of slow movements to occur it is not obligatory that the fault is in a transitional state from brittle to plastic, as it happens either at large depths (25–45 km) between the seismogenic zone (beneath the zone) and the zone of stable sliding in subduction zones, where slow slip events are observed most often, or at shallow depths (~5 km) between the seismogenic zone (above the zone) and the surface zone of continuous creep [43]. Presence of watered clays in the principal slip zone, or of some amount of talc, which often substitutes the minerals of serpentite group along fracture walls in chemical reaction of serpentite with the silicon dioxide contained in thermal fluids, decreases harshly the shear stiffness of the fault, so that its value can be essentially lower than 10% of the normal one. In this situation the effective gradient of shear strength of the fault may turn to be close to the stiffness of the massif, which, can lead to occurrence of slow movements on faults. That is why similar effects can be observed at all depths in the crust.

As far as the possibility of artificial change of the slip mode on a fault is considered, the aim of external action should be not the removal of excessive stresses, but the decrease of fault zone stiffness. The change of sliding conditions should involve a rather big area, appreciably bigger that the size of the zone of earthquake nucleation. For example, pumping a clay-containing suspension into a fault zone may provide such a result, but this difficult scientific and engineering problem demands the development of a detailed technique of fulfilling the operation and methods to estimate its consequences.