Keywords

1 Introduction. General Consideration

In past few decades, the nature and salient features of plastic deformation in solids were investigated. A wealth of new experimental data has been collected, which add strong support to our understanding of plasticity problem. Naturally, we can do no more than mention a few experimental and theoretical studies related to dislocation physics and solids mechanics, e.g. [1,2,3,4,5,6,7,8,9,10,11,12,13,14]. We have recently made a significant discovery that the deforming medium is a self-organizing system, which is in a state far from thermodynamic equilibrium; such media are addressed by [15,16,17,18,19,20,21,22,23,24]. Moreover, the plastic flow in solids is found to have a space-time periodic nature, which is discussed at length by [25,26,27,28]. On the macro-scale level the plastic deformation exhibits an inhomogeneous localization behavior from yield point to failure. Hence, localization is a general feature of the plastic flow process, which should be taken properly into account to markedly advance our understanding of the deforming medium stratification into alternating deforming and non-deforming layers about 10−2 m thick. Similar layers form localized plasticity pattern.

In this line of research, considerable experimental study has been given to the problem of plastic deformation macrolocalization; the investigation results were summarized in a monograph by [29].Footnote 1 In what follows, we discuss new approaches to the same problem.

1.1 Experimental Technique

The experimental procedure was as follows. The flat samples having work part 50 × 6 × 2 mm were tested in tension along the axis x at a rate of 3.5 × 10−5 s−1 in a test machine at 300 K. The non-metallic materials were subjected to compression. Traditional ‘stress–strain’, \(\sigma \left( \varepsilon \right)\), diagrams recording were completed by double-exposure speckle photography [30] for reconstruction of the displacement vector field \({\varvec{r}}\left( {x,y} \right)\). Special device for these purposes has field of vision ~100 mm, real-time mode of operation and spatial resolution ~1…2 μm. According to [31], the plastic distortion tensor for plane stressed state is

$$ \beta^{\left( p \right)} = \nabla {\varvec{r}}\left( {x,y} \right) = \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{xy}^{{}} } \\ {\varepsilon_{yx} } & {\varepsilon_{yy} } \\ \end{array} } \right] + \omega_{z} . $$
(1)

Longitudinal, \(\varepsilon_{xx}\), transverse, \(\varepsilon_{yy}\), shear \(\varepsilon_{xy} = \varepsilon_{yx}\) components and rotation ones, \(\omega_{z}\) can be calculated for different points of the test sample.

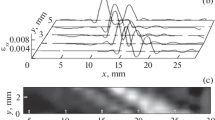
This developed method enables visualization of the deformation inhomogeneities. Thus, Fig. 1a demonstrates a macro-photograph of the deforming material structure and \(\varepsilon_{xx} \left( {x,y} \right)\) distribution for this case. The diagram \(X\left( t \right)\) is shown in Fig. 1b (here X is the x-coordinate of deformation nucleus and t is time); it illustrates the procedure employed for measuring the spatial and temporal periods of the deformation process, i.e. the values \(\lambda ,T\) and rate of the strain nucleus, \(V_{aw} = {\lambda \mathord{\left/ {\vphantom {\lambda T}} \right. \kern-\nulldelimiterspace} T}\).

Fig. 1
figure 1

Localized plastic flow pattern observed for the test sample of Fe-3 wt% Si alloy: a macrophotograph and distribution of strains \(\varepsilon_{xx}\) (halftone photograph) b illustration of the method for measuring \(\lambda\) and T values

Full size image

1.2 Studied Materials

We have studied by now nearly forty single-crystal and polycrystalline metals, alloys and other materials, which differ in chemical composition, crystal lattice type (FCC, BCC or HCP), grain size and deformation mechanism, i.e. dislocation glide [32], twinning [33] or phase transformation induced plasticity [34]. Later our study has been extended to ceramics, single alkali halide crystals and rocks.

1.3 Preliminary Results

The localization behavior of plastic deformation is its most salient feature. Thus, space-time periodic structures, so-called deformation patterns, emerge in the deforming sample from the yield limit to failure by constant-rate tensile loading. The following features are common to all the localization patterns observed thus far:

  • localization structures will occur spontaneously in the sample by constant-rate loading in the absence of any specific action from the outside;

  • in the course of plastic deformation a changeover in the types of localized plasticity patterns is observed;

  • due to work hardening, the deforming medium’s defect structure undergoes irreversible changes, which are suggestive of its non-linearity and are reflected in the emergent patterns.

Recent independent evidence supports the validity of the present conception about the macroscopic localization by deformation [35,36,37]. Acharia et al. [38] observed a localization nucleus traveling along the extension axis in the single Cu crystal at the linear work hardening stage; a stationary localization pattern at the parabolic work hardening stage in the samples of Fe-Mn alloy was described by [39].

2 Deformation Pattern. Localized Plastic Flow Viewed as Autowaves

The plastic flow has an attribute, which is common to all deforming solids. On the macro-scale level, the deformation is found to exhibit a localization behavior from the yield point to failure. In the cause of plastic flow, plastic flow curve would occur by stages; each work hardening stage involves a certain dislocation mechanism [40,41,42]. To gain an insight about the nature of plasticity, the existence of explicit connection between the above two attributes must be discovered.

2.1 Plastic Flow Stages and Localized Plasticity Patterns

We focused our efforts on proving this connection. To provide a proof for this assertion, a localized plasticity pattern was matched against the respective work hardening stage. These can be readily distinguished on the stress-strain curve \(\sigma \left( \varepsilon \right)\), describing by the Lüdwick equation [43]

$$ \sigma \left( \varepsilon \right) = \sigma_{y} + K\varepsilon^{n} , $$
(2)

where \(\sigma_{y}\) is the yield point and K is hardening coefficient. The convenient characteristic of the deformation process is the exponent \(n = \left( {\ln \varepsilon } \right)^{ - 1} \cdot \ln \left[ {\left( {\sigma - \sigma_{y} } \right)/K} \right]\).

According to [43] and [44], the exponent n varies with the stages of plastic deformation process as

  • for the yield plateau or easy glide stage, n ≈ 0;

  • for the linear stage of work hardening, n = 1;

  • for the parabolic stage of work hardening, n = ½,

  • for the prefailure stage, ½ > n > 0.

A set of kinetic diagrams \(X\left( t \right)\) was obtained simultaneously for the above stages; it is schematized in Fig. 2. Similar sets were plotted for all deforming materials, no matter what their microstructure or deformation mechanism. The localization patterns arise in a consecutive order that is governed by the work hardening law \(\theta \left( \varepsilon \right)\) alone. The emergent localization patterns can be distinguished from the dependencies \(X\left( t \right)\) obtained for the work hardening stages. The distinctive features of localization patterns remain the same; differences are quantitative ones. It should be pointed out that plastic deformation inhomogeneities have to be correlated for the entire material volume. The localized plasticity nuclei are distributed periodically; in all studied materials the distance between nuclei \(\lambda \approx 10^{ - 2} \;{\text{m}}\).

Fig. 2
figure 2

Plastic flow development. Schematic representation of autowave evolution process

Full size image

A qualitative analysis of experimental data rests on the observation that these regularities serve to provide a unified explanation of the plastic flow behavior. A total of four types of localized plasticity patterns have been observed experimentally for all studied materials. A definite type of localization pattern would emerge at each flow stage. It is thus asserted that

  • yield plateau is identified with a single mobile plastic flow nucleus;

  • linear work hardening stage, with a set of equidistant moving nuclei;

  • parabolic work hardening stage, with a set of equidistant stationary nuclei;

  • prefailure stage, with a set of moving nuclei, which are forerunners of failure.

Taken together, these results provide a reliable proof that one-to-one correspondence exists between the localization patterns on the one hand, and the respective plastic flow stages on the other.

2.2 Localized Plastic Flow Autowaves

A key aspect of this many-faceted problem to be dealt with is the nature of localized plasticity. Our basic viewpoint is that there are striking parallels between the localized plasticity patterns described herein and the dissipative structures synergetics deals with. We suggest that the dissipative structures are autowaves [45], self-excited waves [46] or pseudo-waves [15]. Special modes of these structures, which are also known as switching autowaves, phase autowaves or stationary dissipative structures, have been studied in detail for a number of chemical and biological systems.

The difference between the wave and autowave processes needs careful explanation. The majority of well-known wave processes are described by functions \(\sin \left( {\omega t - kx} \right)\), which are solutions of hyperbolic differential equations of the type \(\ddot{Y} = c^{2} Y^{\prime\prime}\). Here the value c is wave propagation rate, which is a finite quantity determined by material characteristics. The second derivative with respect to time is applicable to reversible physical processes alone, e.g. elastic deformation.

The autowaves have long been recognized as solutions to parabolic differential equations of the type \(\dot{Y} = \varphi \left( {x,y} \right) + \kappa Y^{\prime\prime}\) [47]. These equations can be derived formally by adding to the right part of the equation \(\dot{Y} = \kappa Y^{\prime\prime}\) the nonlinear function \(\varphi \left( {x,y} \right)\); the value κ is a transport coefficient having the dimensionality L2 · T−1. The availability of the first derivative with respect to time implies that the above equations are suitable for addressing irreversible processes similar to those involved in the plastic deformation.

The speculation that the localization patterns in question are equivalent to autowaves was originally prompted by a formal resemblance between the two kinds of phenomena. In what follows, we provide unequivocal physical evidence for the validity of this viewpoint by focusing our attention on the autowave nature of processes of interest. Thus, the well-known Lüders front can be regarded as a boundary between the elastically and plastically deforming material volumes. As the Lüders front propagates along the tensile sample, it leaves behind an ever increasing volume of deformed material [48]. Due to the structural changes, the deforming material volume acquires a new state, which is characterized by increasing density of defects; its deformation occurs via dislocation glide mechanism. With growing total deformation, the plastic flow will exhibit an intermittent behavior on the macro-scale level. Therefore, the Lüders band propagation is regarded as a switching autowave. A different scenario is realized at the linear work hardening stage where a set of mobile nuclei is observed. The nuclei move at a constant rate along the test sample (see Fig. 2). In this case, the phase constancy condition is fulfilled, i.e. \(\omega t - kx = const\). This pattern will be designated a phase autowave. The linear stage over, the parabolic stage of work hardening begins for n = ½ and \(V_{aw} = 0\) (see Fig. 2). At this stage the emergent localization pattern fits the definition of a stationary dissipative structure [15, 16]. At the prefailure stage the deformation development is nearing completion. For n < ½, collapse of the autowave would be observed [49, 50]. Thus, the types of localized plasticity patterns have been unambiguously identified with the respective modes of autowave processes.

It is therefore concluded that

  • a solitary localized deformation nucleus traveling at the yield plateau is a switching autowave;

  • a set of equidistant localization nuclei propagating at a constant rate along the sample at the linear work hardening stage is a phase autowave;

  • a set of stationary equidistant localization nuclei emergent at Taylor’s stage corresponds to a stationary dissipative structure;

  • a pattern of synchronously moving nuclei, which finally merge at the prefailure stage, fits neatly the definition of collapse of localized plasticity autowave.

Taken together, these regularities are Correspondence rule. Accordingly, it can thus be asserted that the plastic flow process occurring in the deforming can be addressed as continuous evolution of localized plastic flow autowaves. Hence, it can be claimed with confidence that the transition from one flow stage to the next involves a changeover in the types of autowaves generated by the deformation. With due regard to the correspondence rule, it is maintained that the plastic flow stages and the respective autowaves modes are closely related. This is favorable ground for inferring that the process of localized plastic flow is evolution of autowave patterns. Due to a changeover in the flow stages, the autowaves will emerge from a random strain distribution in an orderly sequence (Fig. 2): elastic wave → switching autowave → phase autowave → stationary dissipative structure → collapse of autowave. In some materials, however, individual stages might be missing and this sequence can be broken.

It is necessary to remind here that a special-purpose reaction cell has to be designed for carrying out experimental investigations of autowaves in chemistry or biology. Such cells differ widely in type and size, depending on the kind of studied system and its chemical composition as well as the kinetics of chemical reactions involved, temperatures employed, etc. However, it is found for plastic deformation that the autowaves will be generated spontaneously in the tensile sample practically at any temperature. From this point of view, the deforming solid can be regarded as a universal reaction cell [51], which can be conveniently used for modelling and studying the generation and evolution of various autowave modes.

2.3 Autowaves Observed for the Linear Work Hardening Stage

The plastic flow exhibit generally a regular localization behavior, which is markedly pronounced at the linear work hardening stage. In this case, the localization nuclei move in a concerted manner at a constant rate along the sample, forming a phase autowave. The experimental data on propagation rate, dispersion and material structure response obtained for these autowaves are demonstrated in Fig. 3.

Fig. 3
figure 3

Characteristics of localized plastic flow autowaves: a autowave rate as a function of work hardening coefficient for all studied materials; b dispersion observed for γ-Fe single crystals (2) and polycrystalline Al (1); c autowave length as a function of grain size plotted for polycrystalline Al

Full size image

The propagation rates of localized plasticity autowaves in all studied materials are in the range \(10^{ - 5} \le V_{aw} \le 10^{ - 4}\); they depend solely upon the work hardening coefficient, \(\theta = E^{ - 1} \cdot {\text{d}}\sigma /{\text{d}}\varepsilon\), and are given as (Fig. 3a)

$$ V_{aw} \left( \theta \right) = V_{0} + \Xi /\theta \sim \theta^{ - 1} , $$
(3)

where \(V_{0} <\) and Ξ are empirical constants, having the dimensionality of rate.

We have also obtained dispersion relation, \(\omega \left( k \right)\) (here \(\omega = 2\pi /T\) is frequency and \(k = 2\pi /\lambda\) is wave number) for localized plasticity autowaves [29, 52,53,54,55]. This relation has quadratic form (Fig. 3b)

$$ \omega \left( k \right) = \omega_{0} + \alpha \left( {k - k_{0} } \right)^{2} . $$
(4)

Using the values \(\omega = \omega_{0} \cdot \tilde{\omega }\) and \(k = k_{0} + \frac{{\tilde{k}}}{{\sqrt {\alpha /\omega_{0} } }}\) (here \(\tilde{\omega }\) and \(\tilde{k}\) are dimensionless frequency and wave number), Eq. (4) can reduce to the form \(\tilde{\omega } = 1 + \tilde{k}^{2}\).

Finally, the grain size dependence of autowave length illustrated in Fig. 3c has the form of logistic curve

$$ \lambda \left( \delta \right) = \lambda_{0} + \frac{{a_{1} /a_{2} }}{{1 + C \cdot \exp ( - a_{1} \delta )}}, $$
(5)

where \(a_{1}\), and \(a_{2}\) are empirical coefficients, \(\lambda_{0} \approx 5\;{\text{mm}}\) and C ≈ 2.25. The inflection point of Eq. (5) is found from the condition \({\text{d}}^{2} \lambda /{\text{d}}\delta^{2} = 0\); this corresponds to the boundary value of grain size \(\delta = \delta_{0} \approx 0.15 \ldots 0.2\;{\text{mm}}\). The dependence \(\lambda \left( \delta \right)\) has two limiting cases, i.e. \(\lambda \sim \exp \left( {\delta /\delta_{0} } \right)\) for \(\delta < \delta_{0}\) and \(\lambda \sim \ln \left( {\delta /\delta_{0} } \right)\) for \(\delta > \delta_{0}\). The quantity \(\lambda\) generally depends only weakly on the structural characteristics of the deforming medium. Thus variation in the grain size of polycrystalline Al from 5 μm to 5 mm corresponds to a 2.5-fold increase in the value \(\lambda\) [56].

Thus, the most significant features of localized plastic flow at the linear stage of work hardening are specified herein by Eqs. (3) through (5). By way of summing up our findings, we contend that in the course of plastic flow a large-scale deformation structure would form. Its elements are characterized by the nontrivial dependence \(V_{aw} \left( \theta \right)\sim \theta^{ - 1}\), the quadratic dispersion law \(\tilde{\omega } = 1 + \tilde{k}^{2}\) and the logistic dependence of autowave length on material structure, \(\lambda \left( \delta \right)\).

2.4 Plastic Flow Viewed as Self-organization of the Deforming Medium

We hypothesize herein that the localization of plastic flow might be regarded as a process of self-organization occurring spontaneously in an open thermodynamic system. The validity of our hypothesis can be objectively confirmed by the observations of localized plasticity patterns emergent at the linear stage of work hardening, which provide strong indications that the medium is separating into deforming and undeforming layers. The fruitful concept of self-organization has been proposed by [17], which states that a self-organizing system can attain spatial, temporal or functional inhomogeneity in the absence of any specific action from the outside. Note that the definition is used in a restricted, phenomenological, meaning; it implies no concrete underlying mechanism responsible for the realization of self-organization process.

The concept of self-organization is frequently and successfully used for explanation of the formation of structure in active media studied in physics, chemistry, materials science or biology. The deforming medium can be similar to an active medium far from thermodynamic equilibrium in which the sources of energy are distributed over material volume.

We furnish strong evidence that the plastic flow also involves self-organization phenomena. According to [57], the generation of localized plastic flow autowaves causes a decrease in the entropy of the deforming system, which is the principal attribute of self-organization processes.

2.5 Autowave Equations

To offer adequate tools for describing autowave processes, a set of two equations has to be produced [45, 58] to describe the rate of change in the catalytic and damping factors. The justification of the choice of these two factors is far from to be trivial. By addressing plasticity, it is convenient to introduce plastic deformation, ε, and stress, σ, as catalytic and damping factors, respectively. Hence, equations for the rates \(\dot{\varepsilon }\) and \(\dot{\sigma }\) have to be derived on the base of general principles. The equation for \(\dot{\varepsilon }\) is deduced from the condition of deformation flow continuity [43] as

$$ \dot{\varepsilon } = \nabla \cdot (D_{\varepsilon } \nabla \varepsilon ), $$
(6)

where the value \(D_{\varepsilon }\) is a transport coefficient and the term \(D_{\varepsilon } \nabla \varepsilon\) is the deformation flow in the deformation gradient field \(\nabla \upvarepsilon\); the coefficient \(D_{\varepsilon }\) depends on coordinates. By restricting our analysis to the case of uniaxial deformation along the axis x, we obtain

$$ \partial \varepsilon /\partial t = \partial \varepsilon /\partial x \cdot \partial D_{\varepsilon } /\partial x + D_{\varepsilon } \partial^{2} \varepsilon /\partial x^{2} = f\left( \varepsilon \right) + D_{\varepsilon } \partial^{2} \varepsilon /\partial x^{2} , $$
(7)

where \(f\left( \varepsilon \right) = \partial \varepsilon /\partial x \cdot \partial D_{\varepsilon } /\partial x\) is a non-linear strain function.

The equation for \(\dot{\sigma }\) can be derived from Euler’s equation for hydrodynamic flow [59] as

$$ \frac{\partial }{\partial t}\rho V_{i} = - \frac{{\partial \Pi_{ik} }}{{\partial x_{k} }}. $$
(8)

In the case of viscous medium, the momentum flux density tensor is given as \(\Pi_{ik} = p\delta_{ik} + \rho V_{i} V_{k} - \sigma_{vis} = \sigma_{ik} - \rho V_{i} V_{k}\); the value \(\delta_{ik}\) is unit tensor and \(V_{i}\) and \(V_{k}\) are flow rate components. The stress tensor \(\sigma_{ik} = - p\delta_{ik} + \sigma_{vis}\) includes viscous stresses. By plastic deformation, \(- p\delta_{ik} \equiv \sigma_{el}\); hence, \(\sigma = \sigma_{el} + \sigma_{vis}\) or \(\dot{\sigma } = \dot{\sigma }_{el} + \dot{\sigma }_{vis} = g\left( \sigma \right) + \dot{\sigma }_{vis}\).

The origination of viscous stresses, \(\sigma_{vis}\), is due to plastic deformation inhomogeneity; the value \(\sigma_{vis}\) is related to variation in the rate of elastic waves propagating in the deforming medium, i.e. \(\sigma_{vis} = \hat{\eta }\nabla V_{t}\). Here \(\hat{\eta }\) is the dynamic viscosity of the medium and \(V_{t}\) is the propagation rate of transverse ultrasound waves. The equation \(\sigma_{vis} = \hat{\eta }\nabla V_{t}\) can be written as \(\partial \sigma_{vis} /\partial t = V_{t} \nabla \cdot \left( {\hat{\eta }\nabla V_{t} } \right) = \hat{\eta }V_{t} \partial^{2} V_{t} /\partial x^{2}\). The value \(V_{t}\) depends on the acting stresses as \(V_{t} = V_{*} + \varsigma \sigma\) [60]. Hence, equation for describing the rate of stress change may have the form analogous to that of Eq. (7), i.e. \(\partial \sigma_{vis} /\partial t = \hat{\eta }V_{t} \partial^{2} V_{t} /\partial x^{2} = \hat{\eta }\varsigma V_{t} \partial^{2} \sigma /\partial x^{2}\). Thus, we obtain

$$ \dot{\sigma } = g\left( \sigma \right) + D_{\sigma } \partial^{2} \sigma /\partial x^{2} , $$
(9)

where \(D_{\sigma } = \hat{\eta }\varsigma V_{t}\) is the transport coefficient. It was shown in [60] that Eqs. (7) and (9) can be used to adequately describe plastic flow regimes.

2.6 On the Relation of Autowave Equations to Dislocation Theory

The problem of plasticity can be addressed in the frame of two different approaches, i.e. the autowave model proposed herein and dislocation theory. Of particular importance is the possible interrelation between the two approaches. Almost all the dislocation theories of plasticity are based on the Taylor-Orowan equation, which is used to describe the dislocation mechanism of plasticity [32], i.e.

$$ \dot{\varepsilon } = b\rho_{m} V_{disl} , $$
(10)

where b is the Bürgers vector and \(\rho_{m}\) is the density of dislocations moving at rate \(V_{disl} \left( \sigma \right)\) under the action of applied stress. The first term in the right side of Eq. (7) is transformed by assuming that dislocation distribution is homogeneous and \({\text{d}}\varepsilon /{\text{d}}x \approx 1/s \cdot b/s \approx b\rho_{m}\). Here s is the distance between dislocations; the quantity \(b/s\) has the meaning of shear strain for dislocation path s and \(s^{ - 2} \approx \rho_{m}\). For the case of plastic flow, it may be written \(\eta_{\varepsilon } \approx L_{disl} \cdot V_{disl}\) (here \(L_{disl} \approx \zeta x\) and \(V_{disl} = const\) are, respectively, dislocation path and rate). Hence,

$$ \dot{\varepsilon } = \zeta b\rho_{m} V_{disl} + D_{\varepsilon } \partial^{2} \varepsilon /\partial x^{2} . $$
(11)

The right part of Eq. (11) accounts for two deformation flows, i.e. \(\zeta b\rho_{m} V_{disl} \sim V_{disl}\) and \(D_{\varepsilon } \partial^{2} \varepsilon /\partial x^{2}\). The former flow is ‘hydrodynamic’ in character [59] and the latter is a ‘diffusion’ one.

Evidently, elimination of the second term will transform Eq. (11) into Eq. (10); hence, the Taylor-Orowan equation might be regarded as a special case of Eq. (11). Clearly, Eq. (10) finds limited use for plastic flow description, since it describes chaotic distributions of dislocations, which form no complex ensembles; hence, Eq. (10) corresponds to work hardening due to long-range stress fields alone. Dislocation theory based on long-range stress fields might be called a linear one, while theory describing both flows from Eq. (11) might be regarded as an extended version of the dislocation theory.

A thorough analysis of Eq. (11) suggests that an appropriate dislocation model can be developed with the proviso that both terms in the right side of Eq. (11) are taken into account. In case the term \(D_{\varepsilon } \partial^{2} \varepsilon /\partial x^{2}\) is not eliminated from Eq. (11), it will initiate non-linear corrections of dislocation theory equations and thus expand significantly the area of application of dislocation theory. Such corrections might be of significance for crystals having high dislocation density.

Thus, the application of new experimental technique for plastic flow investigation enabled discovery of a new class of deformation phenomena—localized plastic deformation autowaves. These phenomena are addressed above, taking different but complementary approaches, i.e. autowave plasticity theory and dislocation theory. There is good reason to believe that compelling evidence has been provided for the existence of localized plasticity autowaves.

3 Elastic-Plastic Strain Invariant

The uniformity of localized plasticity phenomena observed for a wide range of materials suggests the existence of a general law for the localized plastic flow autowaves. This section focuses on the search for a quantitative relationship between the characteristics of elastic waves and autowaves.

3.1 Introduction of Elastic-Plastic Strain Invariant

We suggest a link between plastic flow macro-parameters and crystal lattice characteristics. For this purpose, two products are matched, i.e. \(\lambda V_{aw}\) and \(\chi V_{t}\), which characterize plastic flow and elastic deformation, respectively. The quantities \(\chi\) and \(V_{t}\) are interplanar spacing of crystal lattice and transverse ultrasound wave velocity, respectively. Numerical analysis was performed using experimentally obtained values \(\lambda\) and \(V_{aw}\) as well as hand-book values \(\chi\) and \(V_{t}\). The data listed in Table 1 allow one to write the equality

Table 1 Data for verification of Eq. (12) for the elastic-plastic invariant of strain (data for \(\lambda V_{aw}\) and \(\chi V_{t}\) are multiplied by 107 m2/s)
Full size table
$$ \left\langle {\frac{{\lambda V_{aw} }}{{\chi V_{t} }}} \right\rangle = \widehat{Z} \approx const. $$
(12)

It can be seen from Fig. 4 that Eq. (12) holds true for all studied materials. The averaging of the value \(\alpha\) was performed for seventeen materials to give \(\left\langle {\widehat{Z}} \right\rangle = 0.49 \pm 0.05 \approx 1/2 < 1\). This result constitutes both formal and physical proofs that the elastic and plastic processes involved in the deformation are closely related. Therefore, Eq. (12) has been labeled as The elastic-plastic strain invariant.

Fig. 4
figure 4

Verification of invariant (12). The quantities \(\chi\), \(V_{t}\) (left) and \(\lambda\), \(V_{aw}\) (right) are grouped in logarithmic coordinates in the neighborhood of average values

Full size image

Apparently, \(V_{t} \approx \chi \omega_{D}\) (here \(\omega_{D}\) is the Debye frequency); hence, we write

$$ \lambda V_{aw} \approx \widehat{Z}\frac{{V_{t}^{2} }}{{\omega_{D} }} \approx \widehat{Z}\frac{G}{{\omega_{D} \rho }} \approx \widehat{Z}\frac{{\partial^{2} W/\partial \upsilon^{2} }}{{\left( {\omega_{D} \chi } \right)\rho }} \approx \widehat{Z}\frac{{\partial^{2} W/\partial \upsilon^{2} }}{{\xi_{1} }}, $$
(13)

where \(\upsilon \ll \chi\) is atomic displacement near interparticle potential minimum (W); the elastic modulus is expressed in terms of interparticle potential as \(G = \chi^{ - 1} \partial^{2} W/\partial \upsilon^{2}\) [61] and the value \(\xi_{1} = \left( {\omega_{D} \chi } \right)\rho = V_{t} \rho\) is specific acoustic resistance of the medium, which is shown to be related to crystal lattice perturbation due to dislocation motion [28]. The interparticle potential from Eq. (13) is

$$ W\left( \upsilon \right) \approx \frac{1}{2} \cdot \left( {\partial^{2} W/\partial \upsilon^{2} } \right)\upsilon^{2} + \frac{1}{6}\left( {\partial^{3} W/\partial \upsilon^{3} } \right)\upsilon^{3} = \frac{1}{2}p\upsilon^{2} - \frac{1}{3}q\upsilon^{3} , $$
(14)

where p is the coefficient of quasi-elastic coupling and q is anharmonicity coefficient. With the proviso that \(\frac{1}{2}p \cdot \upsilon^{2} \gg \left| { - \frac{1}{3}q\upsilon^{3} } \right|\), Eq. (13) assumes the form

$$ \lambda V_{aw} \approx p/\xi_{1} \approx p/V_{t} \rho , $$
(15)

where \(\lambda V_{aw}\) can be taken as a criterion of plasticity [29].

3.2 Generalization of Elastic-Plastic Strain Invariant

The criterion \(\lambda V_{aw}\) from Eq. (15) also holds good for deformation initiated by chaotically distributed dislocations. Let mobile dislocation density be \(\rho_{m}\); then the average distance between dislocations, which is equal to the dislocation path, is given as \(\left\langle s \right\rangle = \rho_{m}^{ - 1/2}\). According to [32], \(\sigma \approx \left( {Gb/2\pi } \right)\rho_{m}^{1/2}\); hence, we can write \(\rho_{m}^{ - 1/2} = \left\langle s \right\rangle = Gb/2\pi \sigma \sim \sigma^{ - 1}\). The rate of quasi-viscous motion of dislocations is \(V_{disl} = \left( {b/B} \right) \cdot \sigma\). Here B is the coefficient of dislocation drag by the phonon and electron gases [62]. Hence,

$$ l \cdot V_{disl} \approx const = \frac{{Gb^{2} }}{2\pi \cdot B}. $$
(16)

Using the values \(G \approx 40\;{\text{GPa}}\) and \(B \approx 10^{ - 4} \;{\text{Pa s}}\), which are conventionally employed for dislocation motion descriptions, we obtain \(lV_{disl} \approx 10^{ - 6} \;{\text{m}}^{2} /{\text{s}}\). The latter value is close to the calculated value of the product \(\widehat{Z}\chi V_{t}\) obtained for studied materials (see Table 1).

The above suggests that we have established a reliable quantitative criterion for analyzing the interaction between the elastic deformation, which occurs on the micro-scale level, and the macro-scale plastic deformation. This criterion, in its universal form, applies to autowaves in question as well as to elastic and plastic deformation via dislocation motion. Therefore, this criterion is considered as a more general form of the elastic-plastic strain invariant:

$$ \lambda V_{aw} = lV_{disl} = \hat{Z}\chi V_{t} \approx {1}0^{{ - {6}}} \;{\text{m}}^{{2}} /{\text{s}}. $$
(17)

To provide a framework for validating the proposed strain invariant, a special-purpose series of experiments were carried on for polycrystalline aluminum samples having grain sizes in the range \(5 \times 10^{ - 3} \le \delta \le 5\;{\text{mm}}\). We obtained grain size dependencies of strength limit, \(\sigma_{B} \left( \delta \right)\). The Hall-Petch relation \(\sigma_{B} \left( \delta \right) = \sigma_{0} + k_{B} \delta^{ - 1/2}\) [63] has been plotted; it is illustrated in Fig. 5a. It can be seen that for \(\delta_{0} \approx 0.1 \ldots 0.2\;{\text{mm}}\), a jump-wise variation occurs in the value \(\sigma_{B} \left( \delta \right)\). The dependence \(V_{aw} \left( \delta \right)\) demonstrated in Fig. 5b has a similar form. The value \(V_{aw}\) would also vary over the entire range of grain sizes; however, the surprising thing is that the ratio \(\lambda V_{aw} /\chi V_{t} \approx 1/2\) would remain constant for both \(\delta > \delta_{0}\) and \(\delta < \delta_{0}\).

Fig. 5
figure 5

Characteristics of autowaves obtained for polycrystalline Al: a strength limit as a function of grain size; b autowave rate as a function of grain size (sections 1 and 2 correspond, respectively, to the ranges \(0.005 \le \delta \le 0.15\;{\text{mm}}\) and \(0.15 \le \delta \le 5\;{\text{mm}}\))

Full size image

In view of the above, invariant (12) shows promise for gaining an insight into the nature of localized plastic flow. All the basic regularities of localized plastic flow autowaves can be deduced from Eq. (12). Therefore, the invariant is expected to play an important role in the development of new notions of plasticity.

3.3 On the Strain Invariant and Autowave Equations

Now certain theoretical considerations concerning the origin of invariant (12) will be explored. Particular emphasis is placed upon the fact that the quantities \(\lambda V_{aw}\) and \(\chi V_{t}\) from Eq. (12) have evidently the dimension L2 T−1. Note that in the right sides of Eqs. (7) and (9) the coefficients \(D_{\varepsilon }\) and \(D_{\sigma }\) for the terms containing second-order derivatives \(\partial^{2} /\partial x^{2}\) have the same dimension.

In view of the above, we assume that

$$ \lambda V_{aw} \equiv D_{\varepsilon } $$
(18)

and

$$ \chi V_{t} \equiv D_{\sigma } . $$
(19)

The above identification is valid, considering the dimensions of the quantities \(\lambda V_{aw}\) and \(\chi V_{t}\); moreover, Eq. (9) contains expression for the coefficient \(D_{\sigma }\) in which velocity \(V_{t}\) appears. According to Eq. (12), \(\widehat{Z} < 1\), i.e. \(D_{\sigma } > D_{\varepsilon }\). Hence, the condition required for the autowave generation is satisfied [45].

Given their dimensions, these quantities may be either diffusion coefficients or kinematic viscosities of a media. In what follows, the reasoning behind the latter suggestion is formulated. Using the dimensionality analysis, we write \(\lambda \approx \sqrt {2\eta \cdot t}\); here the value \(\eta \approx 10^{ - 6} \;{\text{m}}^{2} /{\text{s}}\) and the value \(t \approx T_{aw} \approx 10^{2} \;{\text{s}}\). Apparently, \(\lambda \approx 10^{ - 2} \;{\text{m}}\), which is identical to the autowave length.

3.4 Some Consequences of the Strain Invariant

Implicitly, it is generally assumed that the total deformation is a sum of elastic and plastic strains, i.e. \(\varepsilon_{tot} = \varepsilon_{e} + \varepsilon_{p}\). By virtue of \(\varepsilon_{e} \ll \varepsilon_{p}\) and \(\varepsilon_{tot} \approx \varepsilon_{p}\), the contribution of elastic strain is frequently neglected altogether. However, invariant (12) implies that the quantities \(\varepsilon_{e}\) and \(\varepsilon_{p}\) are closely related; hence, these quantities should be taken properly into account by addressing plastic flow localization. A model for simulation of plastic deformation should be based on the fundamental assumption that plastic form changing involves both elastic and plastic deformation mechanisms that are interdependent in principle.

To provide arguments in favor of the strain invariant, its consequences have been analyzed. It is found that the regularities of plastic flow localization, which are given by Eqs. (3) through (5), can be derived from Eq. (12) as well. Consider the respective procedures step by step.

It follows from Eq. (3) that the propagation rate of localized plasticity autowave is inversely proportional to the work hardening coefficient. To prove it, we differentiate Eq. (12) with respect to deformation \(\varepsilon\)

$$ \lambda \frac{{{\text{d}}V_{aw} }}{{{\text{d}}\varepsilon }} + V_{aw} \frac{{{{\text{d}}\lambda }}}{{{\text{d}}\varepsilon }} = \widehat{Z}\chi \frac{{{{\text{d}}V_{t} }}}{{{\text{d}}\varepsilon }} + \widehat{Z}V_{t} \frac{{{\text{d}}\chi }}{{{\text{d}}\varepsilon }}. $$
(20)

Hence,

$$ V_{aw} = \left( {\frac{{{\text{d}}\lambda }}{{{\text{d}}\varepsilon }}} \right)^{ - 1} \left( {\widehat{Z}\chi \frac{{{\text{d}}V_{t} }}{{{\text{d}}\varepsilon }} + \widehat{Z}V_{t} \frac{{{\text{d}}\chi }}{{{\text{d}}\varepsilon }} - \lambda \frac{{{\text{d}}V_{aw} }}{{{\text{d}}\varepsilon }}} \right). $$
(21)

Since the interplanar spacing of crystal is independent of plastic deformation, in Eq. (21) \(\widehat{Z}V_{t} \frac{{{\text{d}}\chi }}{{{\text{d}}\varepsilon }} \approx 0\). Hence,

$$ V_{aw} = \widehat{Z}\chi \frac{{{\text{d}}V_{t} }}{{{\text{d}}\lambda }} - \lambda \frac{{{\text{d}}V_{aw} }}{{{\text{d}}\lambda }}. $$
(22)

Further we shall refer to [32] who reasoned that work hardening coefficient can be expressed as a ratio of two parameters of the deforming medium structure, e.g. \(\chi \ll \lambda\), i.e. \(\theta \approx \chi /\lambda\) and \({\text{d}}V_{aw} /{\text{d}}\lambda < 0\). Thus, rearrangement of Eq. (22) yields the same result as the experiment does, i.e.

$$ V_{aw} = \widehat{Z}\chi \frac{{{\text{d}}V_{t} }}{{{\text{d}}\lambda }} - \chi \frac{{{\text{d}}V_{aw} }}{{{\text{d}}\lambda }}\frac{\lambda }{\chi } \approx V_{0} + \frac{\Xi }{\theta }. $$
(23)

Equation (4) also follows from Eq. (12), which can be rewritten as

$$ V_{aw} = \frac{\Theta }{\lambda } = \frac{\Theta }{2\pi }k, $$
(24)

where \(\Theta = \chi V_{t} /2\). If \(V_{aw} = {\text{d}}\omega /{\text{d}}k\), then \({\text{d}}\omega = \left( {\Theta /2\pi } \right) \cdot k \cdot {\text{d}}k\). Integration of the latter equality is performed:

$$ \int\limits_{{\omega_{0} }}^{\omega } {{\text{d}}\omega } = \frac{\Theta }{2\pi }\int\limits_{0}^{{k - k_{0} }} {k{\text{d}}k} $$
(25)

to yield dispersion law of quadratic form

$$ \omega = \omega_{0} + \frac{\Theta }{4\pi }\left( {k - k_{0} } \right)^{2} , $$
(26)

which is equivalent to Eq. (4) with the proviso that \(\alpha = \Theta /4\pi\).

The grain size dependence of autowave length, \(\lambda \left( \delta \right)\), given by Eq. (5) also follows from invariant (12). Indeed, Eq. (12) can be rewritten as

$$ \lambda = \widehat{Z}\chi \frac{{V_{t} }}{{V_{aw} }}. $$
(27)

By virtue of the fact that the quantities \(V_{t}\) and \(V_{aw}\) depend on grain size, \(\delta\), [54, 64], differentiation of Eq. (12) is performed with respect to \(\delta\) as

$$ \frac{{{\text{d}}\lambda }}{{{\text{d}}\delta }} = \widehat{Z}\chi \frac{{\text{d}}}{{{\text{d}}\delta }}\left( {\frac{{V_{t} }}{{V_{aw} }}} \right) = \widehat{Z}\chi \left( {\frac{{V_{aw} {\text{d}}V_{t} /{\text{d}}\delta - V_{t} {\text{d}}V_{aw} /{\text{d}}\delta }}{{V_{aw}^{2} }}} \right). $$
(28)

With the proviso that \(V_{aw} = \alpha \chi V_{t} /\lambda\), Eq. (28) can be rewritten as

$$ {\text{d}}\lambda = \widehat{Z}\chi \left( {\frac{{{\text{d}}V_{t} }}{{{\text{d}}\delta V_{aw} }} - V_{t} \frac{{{\text{d}}V_{aw} }}{{{\text{d}}\delta V_{aw}^{2} }}} \right){\text{d}}\delta = \left( {\frac{{{\text{d}}V_{t} }}{{{\text{d}}\delta V_{t} }}\lambda - \frac{1}{{\alpha \chi V_{t} }}\frac{{{\text{d}}V_{aw} }}{{{\text{d}}\delta }}\lambda^{2} } \right){\text{d}}\delta , $$
(29)

or

$$ {\text{d}}\lambda = \left( {a_{1} \lambda - a_{2} \lambda^{2} } \right){\text{d}}\delta . $$
(30)

A solution of Eq. (30) yields Eq. (5). Taking into account Eq. (29), the coefficients of Eq. (5) take on the meaning: \(a_{1} = \frac{{{\text{d}}V_{t} }}{{V_{t} {\text{d}}\delta }} = \frac{{{\text{d}}\ln V_{t} }}{{{\text{d}}\delta }}\) and \(a_{2} = \frac{{2{\text{d}}V_{aw} }}{{\chi V_{t} {\text{d}}\delta }}\).

Thus, Eqs. (3)–(5) follow from elastic-plastic invariant (12) and depend on the lattice properties of the deforming medium. It can thus be concluded that the elastic and plastic processes occurring in the deforming solid are closely related.

Plastic flow occurring in a medium is described by Eq. (7), which can be derived from invariant (12) as well. To do this, Eq. (12) is rewritten as

$$ \frac{\lambda }{\chi } = \widehat{Z}\frac{{V_{t} }}{{V_{aw} }}, $$
(31)

where the term \(\lambda /\chi \equiv \varepsilon\) is assumed to be deformation. By applying the differential operator \(\partial /\partial t = D_{\varepsilon } \partial^{2} /\partial x^{2}\) to the right and left sides of Eq. (31), we obtain

$$ \frac{\partial \varepsilon }{{\partial t}} = \widehat{Z}D_{\varepsilon } \frac{{\partial^{2} }}{{\partial x^{2} }}\left( {V_{t} /V_{aw} } \right). $$
(32)

Differentiation of Eq. (32) yields

$$ \frac{\partial \varepsilon }{{\partial t}} = \widehat{Z}D_{\varepsilon } \left( { - V_{t} \frac{{\partial^{2} V_{aw}^{ - 1} }}{{\partial x^{2} }} + V_{aw}^{ - 1} \frac{{\partial^{2} V_{t} }}{{\partial x^{2} }}} \right) $$
(33)

According to [56], the ultrasound rate \(V_{t}\) varies in an intricate fashion in the deforming medium, while the autowave propagates at a constant rate at the linear stage of work hardening. Thus, reduction of Eq. (33) yields

$$ \frac{\partial \varepsilon }{{\partial t}} = - \widehat{Z}D_{\varepsilon } V_{t} \frac{{\partial^{2} V_{aw}^{ - 1} }}{{\partial x^{2} }} + D_{\varepsilon } \frac{{\partial^{2} \varepsilon }}{{\partial x^{2} }} = f\left( \varepsilon \right) + D_{\varepsilon } \frac{{\partial^{2} \varepsilon }}{{\partial x^{2} }}, $$
(34)

which is equivalent to Eq. (7).

Thus, the main features of localized plastic flow are described by Eqs. (7) through (9), which are derived from invariant (12) obtained on the base of experimental evidence. Equation (12) states that the characteristics of localized plastic flow are determined by the lattice characteristics of the medium. This thesis in the form of logical implication would assert that the processes involved in elastic and plastic deformation in solids are closely related. It must be admitted that among the factors governing the processes of elastic deformation are not only the crystal lattice properties, but also its interparticle potential, whereas the processes of plastic deformation are governed by the behavior of lattice defects alone.

4 The Model of Localized Plastic Flow

By addressing the localization behavior of plastic deformation in solids, the acoustic characteristics manifested by the deforming medium also call for further investigation. Up to now, the acoustic characteristics of the deforming medium were addressed in terms of energy dissipation, in particular, in internal friction studies and related problems. In what follows, this subject is discussed at greater length.

4.1 Plastic and Acoustic Characteristics of the Deforming Medium

We are dealing here with the rate of transverse elastic waves, \(V_{t}\), which appears in Eq. (12) for strain invariant and in the expression of acoustic resistance of the medium, which enters into Eq. (13). It is also shown above that the coefficient Ξ from Eq. (3), which describes the autowave propagation rate, depends on the rate of transverse elastic waves [60].

One must take into account another characteristic of the deforming medium, i.e. phonon gas viscosity [65] which appears in Eq. (16). At first glance, this quantity seems to be out of place in the analysis of slow processes of localized plasticity autowave propagation. This value is generally determined for a sample under impact loading by addressing high rate motion of dislocations. Nonetheless, phonon gas viscosity made its appearance in our discussion from the following considerations. The development of plastic deformation is due to dislocation motion. Dislocations move over the local obstacles [32], the rate of dislocation motion is given as \(V_{disl} \approx \left( {b/B} \right)\sigma\) and is controlled by the phonon gas (see above). The appearance of the quantity B in the latter relation is accounted for by the occurrence of moving dislocations within the localized plasticity nuclei.

The mechanical and acoustic characteristics of the deforming medium are found to be closely related [28]. This finding is supported by the experimental evidence, which strongly suggests that acoustic processes play an important role in the development of localized plastic flow. Available acoustic emission data suggests that structural inhomogeneities would emerge in the deforming medium due to a traveling deformation front. Thus, the acoustic emission sources occurring in material bulk have to be linked to the localized plastic flow nuclei emergent in the deforming solid [56]. To address the nature of localized plasticity, a two-component model has been formulated, in which a key role is assigned to the acoustic properties of the deforming solid. Acoustic emission pulses play the role of information system and control the dynamics of form changing.

4.2 Two-Component Model of Localized Plasticity

In the conceptual framework used to address the basic problem of autowave formation is the nature of self-organization, which manifests itself in the deforming medium as a spontaneous emergence of autowave structure. Physical interpretation of Eqs. (7) and (9) might prove productive for elucidation of the problem. Kadomtsev [49] advanced the idea that a self-organizing system will separate spontaneously into dynamic and information subsystems, interacting with one another.

The idea of the proposed model is as follows. In the course of plastic deformation local stress concentrators would form and disintegrate; these are considered as slowed-down shears. Elementary stress relaxation act is due to breaking from a local obstacle, which involves acoustic emission [66]. These acoustic signals will activate other stress concentrators, to so that the same process is repeated over and over again. Thus acoustic emission signals propagating in the deforming medium play the role of information subsystem; dislocation shears are involved in the plastic deformation proper and operate as a dynamic subsystem. The model developed is made up of two components: acoustic emission and dislocation mechanisms of plasticity, which have been studied sufficiently, although in different contexts. The generation of acoustic signals was considered in connection with the initiation of dislocation shears, while the reverse process, i.e. initiation of shears due to acoustic pulses, has not been touched on thus far.

In what follows, the performance of the proposed model is assessed. Acoustic signal can propagate in non-uniform dislocation substructure, which forms by deformation and is observable by transmission electron microscopy, e.g. dislocation cell having size \(R \approx 0.01\;{\text{mm}}\). It is proposed by [56] that such cell be regarded as acoustic lens, which has focal length, \(f_{l}\), given as

$$ f_{l} \approx \frac{R}{{V_{t}^{{\left( {def} \right)}} /V_{t} - 1}}, $$
(35)

where the ratio of ultrasound rates, \(V_{t}^{{\left( {def} \right)}} /V_{t}\), observed for non-deformed and deformed volumes plays the role of acoustic refractive index. The initiation of plastic deformation is due to the ultrasound waves focusing at distance \(\lambda \approx f_{l} \approx 10^{ - 2} \;{\text{m}}\) from the active localized plasticity nucleus.

Now lets estimate acoustic emission pulses in terms of energy expenditure required for activating dislocation shears. According to [67], the time needed for dislocations to move over barriers during thermally activated motion, is \(\tau \approx \exp \left( {\frac{{U_{0} - \gamma \sigma }}{{k_{B} T}}} \right)\). Here \(U_{0} - \gamma \sigma = H\) is the process enthalpy and \(k_{B}\) is the Boltzmann constant. Generally, \(H \approx 1\;{\text{eV}}\) and τ ≈ 10−6 s. For the case of \(H = U_{0} - \gamma \sigma - \varepsilon_{ph}\), where the phonon energy is given as \(\varepsilon_{ph} = \hbar \omega_{D} \approx 0.3\;{\text{eV}}\), \(\tau \approx 5 \times 10^{ - 7} \;{\text{s}}\). The generation of a new front is presented schematically in Fig. 6.

Fig. 6
figure 6

Scheme of autowave formation

Full size image

It is an established fact that the perfect crystal lattice is a source of crystal defects responsible for plastic form changing; therefore, its properties must be taken into account by addressing self-organization processes as well. Hence, the basic premise of the given paper is that the regular features of plastic flow macrolocalization are directly related to the lattice characteristics.

5 Plastic Flow Viewed as a Macroscopic Quantum Phenomenon

An innovative approach to the plasticity problem can be developed using elastic-plastic strain invariant (12), which has a deep physical meaning.

5.1 Localized Plastic Flow Autowaves and the Planck Constant

In the course of plastic flow the autowave processes are generated in the deforming medium. This mechanism has been established experimentally for all the plastic flow stages. The findings are giving us a clue to the most distinctive features of the plastic flow and thus provide additional insights into basic plasticity problems. Clearly, the next step in the development of this model is a quantum representation of the plastic flow. This necessitates introduction of a quasi-particle corresponding to the localized plastic flow autowave. The strong evidence that lends support to this idea is considered below.

Numerical analysis was performed for the experimental data on \(\lambda\) and \(V_{aw}\), which produced an unexpected result. Thus it is found that the product \(\lambda V_{aw} \rho r_{ion}^{3}\) (here \(\rho\) is metal density and \(r_{ion} \approx \chi\) is ion radius of metal) is close to the Planck constant h = 6.63 × 10−34 J s [68]. Hence, we write

$$ \lambda V_{aw} \rho r_{ion}^{3} \approx h. $$
(36)

The validity of Eq. (36) is justified by the data listed in Table 2 (note: handbook values of ion radii are used herein). On the base of these data the average value of the Planck constant was calculated for thirteen metals; the resultant value \(\left\langle h \right\rangle = (6.9 \pm 0.45) \times 10^{ - 34} \;{\text{J}}\;{\text{s}}\), with the ratio \(\left\langle h \right\rangle /h = 1.04 \pm 0.06 \approx 1\), i.e. \(\left\langle h \right\rangle = h\).

Table 2 Estimation of the Planck constant with the help of Eq. (36)
Full size table

Using a standard statistical procedure [69], the quantities \(\left\langle h \right\rangle\) and h were matched. Let the value \(\left\langle h \right\rangle\) be defined as the average of thirteen measurements (\(n_{1} = 19\)). On the other hand, we operated on the premise that the value h was determined in a single measurement (\(n_{2} = 1\)) in the absence of dispersion. The statistical significance of coincidence of the quantities \(\left\langle h \right\rangle\) and h was determined with 95% confidence level by Student’s t-test as

$$ t = \frac{\left\langle h \right\rangle - h}{{\hat{\sigma }}} \cdot \sqrt {\frac{{n_{1} n_{2} }}{{n_{1} + n_{2} }}} , $$
(37)

where the value \(\hat{\sigma }\) is the square root of the overall estimate of dispersion. This procedure shows that the values \(\left\langle h \right\rangle\) and h are statistically identical, i.e. \(\left\langle h \right\rangle = h\). It is pertinent to note that h is the fundamental constant; hence, its appearance in Eq. (36) is in no way accidental—this suggests that plastic deformation physics is related to quantum mechanics.

5.2 Introduction of a New Quasi-particle and Its Applications

Further on, the plasticity problem is approached using quantum ideas. By further elaborating the autowave concept of localized plasticity, we were guided by the fundamentals of modern condensed-state physics where quasi-particle concept is generally introduced and freely employed for simplifying description of solids [70]. Our consideration of localized plastic flow autowaves is based on the concept of wave-particle dualism.

In the first place, the mass of the hypothetical quasi-particle is of principal importance. Clearly, the characteristics of the quasi-particle have to be related to those of the autowave. Thus the quasi-particle mass is defined as follows. On the base of data obtained for dispersion autowaves in Al and γ-Fe, we write

$$ m_{ef} = \left( {\frac{{{\text{d}}^{2} U}}{{{\text{d}}p^{2} }}} \right)^{ - 1} = \hbar \frac{{{\text{d}}^{2} }}{{{\text{d}}k^{2} }}\left[ {\omega \left( k \right)} \right], $$
(38)

where the values U and p denote, respectively, the energy and quasi-momentum of the quasi-particle. Another way of looking at it is proposed by [71, 72]. Thus the de Broglie formula can be employed to address localized plastic flow autowaves as

$$ m_{ef} = \frac{h}{{\lambda V_{aw} }}. $$
(39)

An alternative method is the use of the term from Eq. (36)

$$ \rho r_{ion}^{3} = m_{ef} . $$
(40)

Apparently, the effective mass of a quasi-particle having size \(\sim r_{ion}\) can also be defined from Eqs. (39) and (40).

Using Eqs. (38) through (40), the mass of the quasi-particle was found; the values obtained are in the range \(0.5 \le m_{ef} \le 1.5\;{\text{a.m.u.}}\) (atomic mass unit). The averaged value \(\left\langle {m_{ef} } \right\rangle \approx 1\;{\text{a.m.u.}}\) is a rough estimate of the quantity \(m_{ef}\).

The hypothetic quasi-particle is named auto-localizon. The next task is equating the propagation rates of the autolocalizon and the autowave. The mobility of autolocalizon is affected by the phonon and electron gases in solids. Thus the effective mass of the auto-localizon is regarded as its virtual mass, which is defined by the resistance of both gases to the motion of auto-localizon. Strong evidence was recently obtained in support of this conjecture. The effective mass was calculated from Eq. (38) for a range of metals.

We will now look at some possibilities offered by this approach. Using Eq. (38), the formula for elastic-plastic strain invariant (12) can be rewritten as

$$ \frac{h}{{\lambda V_{aw} }} \approx \widehat{Z}^{ - 1} \frac{h}{{\chi V_{t} }}, $$
(41)

where \(h/\chi V_{t} = m_{ph}\) and \(h/\lambda V_{aw} = m_{a - l}\) are, respectively, the phonon and the auto-localizon masses. Evidently, Eq. (41) is equipotent to the equality \(m_{a - l} \approx \widehat{Z}^{ - 1} m_{ph}\). Hence, Eq. (41) accounts for the mechanism, which is responsible for the generation of dislocations due to phonon condensation [73].

This concept is elaborated in the frame of conventional approach adopted in the solids physics, which involves introduction of a quasi-particle for description of wave processes. By way of an example, it well suffices to mention elementary excitations in media [70]. One of the first attempts of this kind was made by [74] who introduced a quasi-particle named crackon in order to address mechanisms of brittle crack propagation.

It should be reminded that such ideas have long been in the air; therefore, attempts at introducing quantum concepts into the physics of plasticity are by no means scarce. Thus the quantum tunneling effect was used by [2, 75, 76] in descriptions of low-temperature processes involving dislocations breakaway from pinning points. Later on, [77] supplied a detailed explanation of this phenomenon for the case of dislocation motion in the Peierls-Nabarro potential relief. Steverding [78] made use of quantization of elastic waves propagating by material fracture. Zhurkov [79] introduced the notion of elemental excitation in crystals, which was termed as dilaton. Later on, the possible existence of a specific precursor of deformation or fracture was hypothesized by [80] who coined the name frustron for this phenomenon. It has been shown that an elementary act of interatomic bond rupture has activation volume close to that of an atom. Evidently, ideas of this kind are transparent enough; the underlying theoretical premises are based on the discreteness of crystal lattice in which generation and evolution of elementary acts of plasticity takes place. The autowave and quasi-particle concepts are distinct, though complementary and interrelated approaches.

In the frame of quasi-particle concept, the length of localized plasticity autowave can be estimated. With this aim in view, the motion of autolocalizon in the phonon gas is considered. In view of the fluctuations of phonon gas density, it is proposed that the autolocalizon be involved in the Brownian motion. In accordance with Einstein’s theory, the free path of the Brownian particle is

$$ s \approx \sqrt {\frac{{k_{B} T}}{{\pi \hat{\eta }r_{a - l} }}t} , $$
(42)

where \(\hat{\eta }\) is the dynamic viscosity of the phonon gas and t is the time given as \(t \approx {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \omega }} \right. \kern-\nulldelimiterspace} \omega }\) (here ω is the frequency of localized plastic flow autowave).

Hence, the free path of the quasi-particle is presented as autowave length λ and is given as follows. Assume that T = 300 K; the autolocalizon has size \(r_{a - l} \approx 10^{ - 10} \;{\text{m}}\); the autowave period is \(t \approx 10^{3} \;{\text{s}}\) and \(\hat{\eta } \approx 10^{ - 4} \;{\text{Pa}}\;{\text{s}}\) (the latter value was obtained by [62] in high-velocity dislocation motion tests). The resultant value \(s \approx 10^{ - 2} \;{\text{m}}\), which is evidently close to the autowave length, \(\lambda\). Thus the application of Eqs. (35) and (42) yields equivalent numerical estimates.

5.3 Plasticity Viewed as a Macro-scale Quantum Phenomenon

A close relation has been established between the deformation and acoustic characteristics of the deforming medium, which suggests that the deformation processes can be described by a hybridized excitation spectrum (Fig. 7). Such a spectrum is obtained by the imposition of the linear dispersion relation \(\omega \approx V_{t} k\) for elastic waves and quadratic the same \(\omega = \omega_{0} + \alpha \left( {k - k_{0} } \right)^{2}\) for localized plasticity autowaves.

Fig. 7
figure 7

Generalized dispersion curve obtained for elastically and plastically deforming solids (insert similar dependencies obtained for high-frequency oscillation spectrum)

Full size image

For validation the coordinates \(\hat{\omega }\) and \(\hat{\lambda }\) were estimated for the point of intersection of the plots in a high-frequency spectral region. The frequency \(\hat{\omega } \approx \omega_{D}\) and the wave number \(\hat{k}\) correspond to the minimal length of elastic wave, which is of the order of distance between close packed planes, i.e. \(\hat{k} \approx 2\pi /\chi\). The above evidence indicates that the generalized dispersion relation holds good for both the phonons and the auto-localizons.

The dispersion curve illustrated in Fig. 7 is suggestive of a remarkable analogy with the dispersion relation obtained for superfluid 4He [70, 81]. The latter dispersion relation shows a minimum corresponding to the origination of ‘rotons’, i.e. quasi-particles having effective mass \(m_{rot} \approx 0.64\;{\text{a.m.u.}}\); moreover, the quadratic dispersion law obtained for rotons is similar to Eq. (4). The above analogy is indicative of a similarity of localized plasticity and superfluidity. Whether this is a formal similarity or whether it has a physical meaning, remains to be seen.

Additional argument in favor of this attractive conjecture is as follows. The superfluidity of 4He is attributed to the occurrence of normal and superfluid components in liquid 4He at \(T \le 2.17\;{\text{K}}\); the respective dynamic viscosities obtained for these components are \(\hat{\eta }_{n}\) and \(\hat{\eta }_{sf} \ll \hat{\eta }_{n}\). The plastic flow occurring in the deforming medium would involve both slow motion of individual material volumes, which undergo form changing, and fast dislocation motion. Slow process corresponds to high viscosity of material, \(\hat{\eta }_{mat} = G\tau \approx 10^{10} \;{\text{Pa s}}\) (here \(\tau \approx 10^{3} \;{\text{s}}\) is a characteristic time). The velocity of dislocation motion, \(V_{disl} \approx \left( {b/B} \right) \cdot \sigma\), is controlled by the phonon gas viscosity, \(B \approx 10^{ - 4} \;{\text{Pa}}\;{\text{s}}\) [62], i.e. \(\hat{\eta }_{mat} /B \approx 10^{14}\).

Three macroscopic quantum effects are well-known in physics, i.e. superconductivity, superfluidity and the quantum Hall effect [82]. The characteristics of these effects are listed in Table 3. On the base of data obtained in this study, the localized plasticity phenomenon might be included in the same ‘short list’. In what follows, we shall attempt to apply a quasi-particle approach to the analysis of serrated plastic deformation similar to the Portevin-Le Chatelier effect [83,84,85]. Assume that autowaves having length \(\lambda\) are arranged along sample length, L. Then the number of autowaves is given as \(\lambda = L/n\) where n = 1, 2, 3 …. The deformed sample has length \(L \approx L_{0} + \delta L\) (here \(L_{0}\) is initial length); hence, \(\delta L \approx \lambda\). Thus from Eq. (35) follows

Table 3 The macroscopic quantum phenomena
Full size table
$$ \delta L \approx \frac{h}{{\rho \chi^{3} V_{aw} }}n \approx \frac{h}{{m_{a - l} V_{aw} }}n. $$
(43)

The autolocalizon mass \(m_{a - l} \approx \rho \chi^{3} \approx \rho r_{ion}^{3}\) appears in Eq. (43) which states that a jump-wise elongation of the tensile sample is necessary, i.e. \(\delta L\sim n\). For the linear work hardening stage, \(V_{aw} = const\); hence, \(\frac{h}{{\rho \chi^{3} V_{aw} }} = const\). Given sufficient instrumentation sensitivity, the recorded curves \(\sigma \left( \varepsilon \right)\) will invariably exhibit a serrated behavior; moreover, accommodation of the sample length will occur to fit the general autowave pattern. Numerical estimates were made which suggest that for n = 1, \(\rho \approx 5 \times 10^{3} \;{\text{kg}}/{\text{m}}^{3}\) and \(\chi \approx 3 \times 10^{ - 10} \;{\text{m}}\) hence, the elongation jump \(\delta L_{m = 1} \approx 10^{ - 4} \;{\text{m}}\). For the sample length \(L \approx 10^{ - 1} \;{\text{m}}\) the elongation jump corresponds to the deformation jump \(\delta \varepsilon_{m = 1} \approx 10^{ - 3}\), which is a close match of the experimentally obtained value.

It also follows from Eq. (43) that an increase in the loading rate would cause a decrease in the deformation jump value, i.e. \(\delta L\sim V_{aw}^{ - 1}\). This inference is supported by the experimental results obtained for Al samples tested at 1.4 K at different loading rates [86]. Thus, the autowave rate was found to be proportional to the motion velocity of the testing machine crossheads, i.e. \(V_{aw} \sim V_{mach}\). According to Eq. (43), the velocity \(V_{aw}\) will increase with rate \(V_{mach}\), while the deformation jumps will grow smaller.

6 Conclusions

  1. 1.

    The discussion of factual evidence cited herein enables formulation of a new idea of the nature of plasticity. In the frame of proposed concept, the plastic flow localization is due not only to the formation and to redistribution of defects (dislocations) in the deforming medium, but also to the lattice and material characteristics related to quantum mechanics. It is found that the parameters of plastic flow localization are related to the quantities h, \(\chi\) and \(V_{t}\). This relation is a qualitative one, while material structure plays a subordinate, quantitative role.

  2. 2.

    An analysis of the plastic flow suggests that regular features, which are manifested in all deforming solids, distinguish the deformation process. The kinetics of plastic flow is determined by a regular changeover in the localization patterns (autowave modes).

  3. 3.

    Elastic-plastic strain invariant is introduced to relate the processes involved in plastic and elastic deformation. It is shown that the main laws of autowave plastic deformation are corollaries of this invariant.

  4. 4.

    A well-founded conjecture is proposed that the localized plasticity phenomenon belongs to the category of quantum effects manifested on the macro-scale level. Validation of this hypothesis is also provided. To advance this idea, a quasi-particle of localized plastic deformation (auto-localizon) is introduced.