Keywords

1 Introduction

The need for rehabilitation of hand-fractures origins from two sources. One is hand-fractures, in general occurring among all ages including boys and girls, among which one third face fractures before the age of 17 [1, 2]. The second source is rehabilitation after surgery or plastering to regain mobility. The traditional method usually requires the active involvement of a physiotherapist and requires a lot of time with repetitive training. Due to a lack of resources for therapy, new methods and equipment such as rehabilitation robots and actuated home-rehabilitation [3, 4] are under strong development.

Acceptance of such active systems is usually good if the patient feels to be in charge due to understandable and expectable motions and the possibility for an emergency stop. An additional benefit is always the opportunity to record and collect data about the progress of therapy. Combining robotic therapy with other methods, such as motor learning, control or bio-signal processing, helps to develop the potentiality of rehabilitation [5]. Although some items such as device-accuracy in the medical robots need to be considered, a large number of clinical studies confirmed the efficiency of robotic rehabilitation robots [6].

Coming into technical details, a lot of different systems for hand and finger-rehabilitation were proposed by researchers and commercial vendors for therapeutic systems. A device-taxonomy can be given by the number of actuated DOFs, the physiological joints in therapeutic focus, whether they are grounded or wearable, mode of rehabilitation exercises and in general the complexity of the device according to Table 1.

Table 1. Main features of some of the most common previous devices for wrist and finger rehabilitation
Full size table

The scope of this paper is about a combined wrist and finger rehabilitation robot with the capability to exercise each phalanx individually, with a maximum of multi DOFs combined in one device at an affordable price-point. Despite all systems from Table 1 have their benefits, nearest to the scope of this paper is [12, 16], and [19] from different points of view. [16] shows a reconfigurable system but it was not for fingers. [12] is for the rehabilitation of wrist and fingers and it differs from our system because it was not for each finger individually. [19] is for each finger but it was not for each phalanges.

Concerning the underlying control algorithm especially [20] shows an interesting approach by force control and [19] due to using impedance control, in this system an adaptive fuzzy sliding mode controller is used which will be described in the following.

2 Design and Prototyping

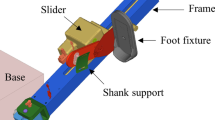
Figure 1a shows the schematic view of the designed wrist and finger rehabilitation robot, which moves finger joints and wrist with two motors. As can be seen in Fig. 1a, the hand is located in the upper section that includes the green finger part and two ball bearings. Because during the rotation, the joints center of motion changes, a flexible system is used for the finger part. In this system, the first motor (motor 1) moves the cable and rotates the finger. The wrist is rotated by the second motor (motor 2) while the ball bearings and a shaft transfer the rotation of the motor to the wrist [21, 22].

A detailed view of the finger part is shown in Fig. 1b. There is a bar at the backside of the system to lock or unlock the joints. The configuration of the bar shown in Fig. 1b is for DIP training of the index finger. The finger part is adjusted by changing the engaged track (Fig. 1b) and the circular end of the bar is for making the movement of the bar easier. By changing the unlocked joint, the rehabilitation can be applied to each phalanx. As it is shown in Fig. 1c, DIP sits at the tip of the finger part and according to the size of the finger, the tracks will be fixed. The cable connected to the tip of the system moves the finger to the palm and the spring moves it in the reverse direction.

Fig. 1.
figure 1

Schematic design of the system.

Full size image

In Fig. 2 the manufactured robot and rehabilitation procedure of the wrist and finger are shown. The system includes two actuators, rotating and fixed plates. Furthermore, an emergency key is designed to stop the system in an emergency condition. Due to the decoupled degrees of freedom, the actuation system moves the fingers and wrist separately. For rehabilitation, the patient’s hand should be placed at the hand holder and according to the desired movement, finger or wrist will be trained.

Fig. 2.
figure 2

Prototype of the rehabilitation robot

Full size image

3 Mathematical Model of the Device and SMC Design

The dynamic equation of the rehabilitation robot is the result of Newton’s law applied to the fingertip. The overall equation of the system is obtained as follows:

$$\begin{aligned} {I}{\ddot{\theta }} = T&\times \sin (\alpha ) \times {l}_{3} + T \times \cos (\alpha ) \times E- K \times ((\sqrt{A}-\sqrt{B})\times \cos (\beta )\times {l}_{3} \nonumber \\&+ \, (\sqrt{A}-\sqrt{B})\times \sin (\beta )\times G)- C {\dot{\theta }} - {K}_{1} {\theta } \end{aligned}$$
(1)
$$\begin{aligned} A=({H}+{l}_{3} \sin (\theta ))^{2}+ ({l}_{1}+{l}_{2}+{l}_{3} \cos (\theta ))^{2} \end{aligned}$$
(2)
$$\begin{aligned} B={H}^{2}+({l}_{1}+{l}_{2}+{l}_{3})^{2} \end{aligned}$$
(3)
$$\begin{aligned} {I}{\ddot{\theta }} = T \times R . \end{aligned}$$
(4)

Figure 3a shows the simplified kinematic model of the robot for Fig. 1 and E, G, and H are the distances shown in the picture. In Eq. 1, \({l}_{1}\), \({l}_{2}\), and \({l}_{3}\) are the length of the phalanges, I is the inertia of the rotating part, R is the motor shaft, and \(\theta \) is the rotation angle of the finger. C, \({K}_{1}\), and K represent the damping and stiffness of the robot and stiffness of the spring. I is the system’s moment of inertia and T shows the force of the cable. \(\alpha \) and \(\beta \) have the following relations and the distance between the finger part and the connection point of the cable with the system is shown by D in Fig. 3b.

Fig. 3.
figure 3

Simplified kinematic model of the robot

Full size image
$$\begin{aligned} \alpha = \theta + \mathrm {atan}(\frac{D-{l}_{3}\sin (\theta )-E\cos (\theta )}{{l}_{1}+{l}_{2}+{l}_{3} \cos (\theta )-E\sin (\theta )}) \end{aligned}$$
(5)
$$\begin{aligned} \beta = \theta + \mathrm {atan}(\frac{{l}_{1}+{l}_{2}+{l}_{3} \cos (\theta )+G\sin (\theta )}{H+{l}_{3} \sin (\theta )-G\cos (\theta )}) \end{aligned}$$
(6)

In Eq. 1, \(\theta \) is the finger rotation angle, l is the cable length, x and y are the horizontal and vertical axes of the cable length respectively. Because of unknown parameters and uncertainties in the mechanical model identification of the system, a sliding mode controller (SMC) has been used. This controller can reduce the effects of parameter variations, uncertainties, and disturbances.

For designing the SMC, it should be considered that the sliding mode controller could guarantee the stability of the system and it consists of two sub-controllers \({u}_{eq}\) and \({u}_{rb}\). To make the system stable in the Lyapunov sense, \(S\dot{S}\) should be less than zero. \({u}_{eq}\) is the equivalent controller and \({u}_{rb}\) is used to control the uncertainties and disturbances. In this system, \({u}_{eq}\) and \({u}_{rb}\) are considered as Eq. 8 and Eq. 9. The final design of the SMC found as follows [23].

$$\begin{aligned} {u}={u}_{eq} + {u}_{rb} \end{aligned}$$
(7)
$$\begin{aligned} {u}_{eq} = g ^ {-1} ({\ddot{{x}}_d}-f- k (\dot{{x}} - \dot{{x}}_d) - \eta {s}) \end{aligned}$$
(8)
$$\begin{aligned} {u}_{rb} = -g ^ {-1} {\rho }. \text {sgn}{({s}) } \end{aligned}$$
(9)

In which, \(\eta \) is a positive constant. If we consider the general equation of the system as Eq. 10 and Eq. 11, g and f formula for this system would be obtained as Eq. 12 and Eq. 13.

$$\begin{aligned} {\ddot{x}} = f({x},t) + g({x},t){u} + {\lambda } \end{aligned}$$
(10)
$$\begin{aligned} {y} = {x} \end{aligned}$$
(11)
$$\begin{aligned} g =( \frac{1}{I}) (\sin (\alpha ) {l}_{3}+ \cos (\alpha ) E) \end{aligned}$$
(12)
$$\begin{aligned} \begin{aligned} \begin{gathered} f = ( \frac{1}{I}) (- K \times ((\sqrt{A}-\sqrt{B})\times \cos (\beta )\times {l}_{3}\\ + \, (\sqrt{A}-\sqrt{B})\times \sin (\beta )\times G ) - C {\dot{\theta }} - {K}_{1} {\theta }) \end{gathered} \end{aligned} \end{aligned}$$
(13)

Where g(x, t) and f(x, t) are unknown functions of the system dynamic equation. Moreover, \(\lambda \) is unknown disturbances satisfying Eq. 14.

$$\begin{aligned} {|}{\lambda }{|}<\rho \end{aligned}$$
(14)

4 Adaptive Fuzzy Sliding Mode Controller Design

The sliding mode controller reduces the error of the system. But it has a sign function which leads to an undesired chattering phenomenon. To overcome this error, fuzzy controller design is proposed. In the previous work [23], a fuzzy sliding mode controller (FSMC) is designed for the rehabilitation robot by integrating a fuzzy controller into an SMC. S(t) and \(\dot{S}(t)\) are the inputs of the fuzzy system and the output of the system is \({u}_{fa}\) [23].

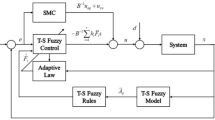
In this configuration, undesired chattering is overcome. However, during the experiments, it is shown that due to the different stiffness of the patients’ hands, various interactive forces are entered into the hand and robot. To overcome this, the robot needs an adaptive controller according to Fig. 4.

Fig. 4.
figure 4

The overall block diagram of the system containing adaptive controller

Full size image

The adaptive controller tuning law is derived based on the Lyapunov theory to guaranty the system stability. This adaptive law is designed to approximate the indeterminacy and the interaction force and drives the trajectory tracking error to zero. After considering disturbances, unknown parameters, and patients’ interaction force, the mathematical model of the system can be expressed as follows.

$$\begin{aligned} {x}_{1} = \theta \end{aligned}$$
(15)
$$\begin{aligned} \dot{{x}_{1}} = {x}_{2} \end{aligned}$$
(16)
$$\begin{aligned} \begin{aligned} \begin{gathered} {\ddot{x}} = ( \frac{1}{I})(T \times \sin (\alpha ) \times {l}_{3} + T \times \cos (\alpha ) \times E- K \times ((\sqrt{A}-\sqrt{B})\times \cos (\beta )\times {l}_{3}\\ + \, (\sqrt{A}-\sqrt{B})\times \sin (\beta )\times G ) - C {\dot{\theta }} - {K}_{1} {\theta }+{F}_{int}+{\lambda }) \end{gathered} \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned} y = {x}_{1} \end{aligned}$$
(18)

Where \({x}_{1}\),\({x}_{2}\), and y are the state vectors and \({F}_{int}\) is the interaction force of the robot and the hand. We also suppose that the interaction force changes slowly.

$$\begin{aligned} \dot{{F}}_{int} = 0 \end{aligned}$$
(19)

The proposed Lyapunov function is defined as follow.

$$\begin{aligned} v = (\frac{1}{2}) (s^{2})+(\frac{1}{2})(\tilde{F}^{2}) \end{aligned}$$
(20)
$$\begin{aligned} \tilde{F} ={F}_{int} - \hat{F} \end{aligned}$$
(21)

In which \(\hat{F}\) is the estimation of the interaction force(\({F}_{int}\) ), and \(\tilde{F}\) is the error of this estimation. Thus,

$$\begin{aligned} \dot{\tilde{F}} =\dot{{F}}_{int} - \dot{\hat{F}}=- \dot{\hat{F}} \end{aligned}$$
(22)
$$\begin{aligned} \dot{V} = S \times \dot{{S}} + \tilde{F} \times \dot{\tilde{F}}= S \times \dot{{S}} - \tilde{F} \times \dot{\hat{F}} \end{aligned}$$
(23)
$$\begin{aligned} \dot{V} = S \times ((\ddot{x}_{1}-\ddot{x}_{d})+K (\dot{x}_{1}-\dot{x}_{d}))- \tilde{F} \times \dot{\hat{F}} \end{aligned}$$
(24)
$$\begin{aligned} {\ddot{x}_{1}} = f({x},t) + g({x},t){u} + {\lambda } + \frac{{F}_{int} }{I} . \end{aligned}$$
(25)

Taking Eq. 25 into Eq. 24, then

$$\begin{aligned} \dot{{V}} = {s} \times g {u}_{ad} + \frac{(\tilde{F}+\hat{F}) }{I} {s} - \tilde{F} \times \dot{\hat{F}} + [-\eta {s}^{2} -\rho {|}{s}{|} + {\lambda } {s}] . \end{aligned}$$
(26)

The Eq. 27 was reached in the sliding mode section.

$$\begin{aligned} -\eta {s}^{2} -\rho {|}{s}{|} + {\lambda } {s} < 0 \end{aligned}$$
(27)

So,

$$\begin{aligned} \dot{{V}} < {s} \times g \times {u}_{ad} + \frac{(\tilde{F}+\hat{F}) }{I} {s} - \tilde{F} \times \dot{\hat{F}} \end{aligned}$$
(28)
$$\begin{aligned} {u}_{ad}=-\frac{\hat{F} }{I \times {g} } \end{aligned}$$
(29)
$$\begin{aligned} \hat{F} = \int {\frac{s}{I}} \end{aligned}$$
(30)
$$\begin{aligned} {u}_{ad}=-\frac{1 }{{l}_{3}\sin (\alpha ) + E \cos (\alpha ) } \int {\frac{s}{I}} \end{aligned}$$
(31)

Thus, with this adaptive signal which is added to the other signals, \(\dot{V}\) is always negative and the system stability is guaranteed.

5 Experiments and Results

Our robot design was developed with the focus on easy application in daily professional life and by advice from physiotherapists. Two trajectory tracking experiments were done to validate the controlling system and robot. The first one was for wrist and the second one was for fingers. In the first experiment, ten subjects (seven males and three females) did the tracking training three times and every training session takes time between 2 to 4 min. Each volunteer was encouraged to keep relaxed for training. In this experiment, a cosine wave function is defined as the desired trajectory for the wrist. Figure 5 shows the average error of the experiments and depicts that the error of the system for wrist trajectory tracking is reduced and the movement of the system became smooth and near to the desired. As shown in this figure, the fuzzy sliding mode controller reduced the error and the measured trajectory follows the desired trajectory better. But adaptive fuzzy SMC can reduce the errors resulting from the differences between patients. Therefore, this controller is used to reduce the effects of the different patients’ interactions with the robot.

Fig. 5.
figure 5

Different controllers error

Full size image
Fig. 6.
figure 6

Trajectory (blue line), output of the system with SMC (red line), and adaptive fuzzy SMC (green line) for each phalanx: a) DIP phalanx of index b) DIP phalanx of middle c) DIP phalanx of ring d) DIP phalanx of little e) PIP phalanx of index f) PIP phalanx of middle g) PIP phalanx of ring h) PIP phalanx of little I) MCP phalanx of index j) MCP phalanx of middle k) MCP phalanx of ring l) MCP phalanx of little finger (Color figure online)

Full size image
Fig. 7.
figure 7

Full telemanipulation system

Full size image

In the other experiment, the slow movement of each phalanx was explored. To find the desired trajectory of phalanges, the movements kinematic of all of them were analyzed during their tasks. Ten healthy subjects, seven males and three females, with different finger sizes, performed finger trials under the supervision of a physician [24]. They moved their phalanges (without robot) according to the physician instructions and an attached gyro sensor measured angle of rotation. The average of the collected data was found and fitted with a polynomial. Then, the experiments were done with the robot and different control algorithms. Figure 6 shows the results of the experiments with sliding mode controller and adaptive fuzzy SMC.

It can be understood from these experiments that the sliding mode controller improves the tracking performance, but there are some errors because of the chattering effects. The fuzzy controller reduces the chattering effects and makes the performance of the system better because it adjusts the output of the system according to the errors and disturbances. Adaptive fuzzy SMC decreases the error because this controller adapts the robot with different patients. According to the average data of the experiments, it is computed that using an adaptive fuzzy sliding mode controller (AFSMC) reduces the average errors in the wrist and phalanges about 80%.

6 Conclusion

In this paper, a novel mechanism for wrist and fingers is presented. In this system, the number of motors is reduced and the robot can rehabilitate all of the joints and wrist with only two motors. Still, each phalanx can be rehabilitated by this robot that makes rehabilitation very cost-efficient.

Furthermore, an AFSMC design method is proposed to control this robot. This controller can deal with unknown parameters and uncertainties and it enhances the system robustness. In this controller, the output of the fuzzy controller is calculated based on the error. Thus, the controller is more robust and independent of the system model. On the other hand, with different patients, there are different interaction forces between hand and robot and it is an important parameter that should be considered in the dynamic equation of the system. Therefore, there is a requirement for adapting the parameters, thus an adaptive controller beside the fuzzy SMC is designed to eliminate the effects of these forces. The effectiveness of the control system is examined with some trajectory tracking experiments. The experiments results show that the proposed AFSMC has much less error and as an average, the system performance improves by 80%.

For the future, following previous works like [4], a haptic system will be designed to make communication between the physician and the patient. This system can improve the efficiency of the rehabilitation procedure and has the potential not only to make the expert involvement more efficient but also to reduce the total duration of the rehabilitation due to only partially supervised offline-training capabilities (Fig. 7).