Abstract
Software that models business workflows is omnipresent in today’s society. These systems coordinate collaboration in hospitals, companies, and military institutions. Unfortunately, workflow systems may obfuscate the influence of current user actions on the desired end result. In order to make the right decision, users need to oversee the full process and all information available, both of which are usually buried in the system. We have developed a way to automatically generate next step hints for task oriented programs. Task oriented programming provides programmers with an abstraction over workflow software, while still being expressive enough to describe real world collaboration. By leveraging symbolic execution, we can calculate these hints without modification of the original program. To our knowledge, this is the first time that symbolic execution is used to automatically generate next step hints for end users. We prove the generated hints to be sound and complete, and also demonstrate that the symbolic execution semantics we employ is correct for sequential input. In addition, we have developed a Haskell implementation of our automatic next step hint generation system. By providing next step hints, the chance of human error is reduced, while still allowing end users to intervene if required. The overall performance is raised, since the quality of decisions will improve.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Software that supports people working together is used in most workplaces nowadays. Its aim is to automate business workflows, in order to simplify processes, to improve service, or to contain cost. In settings like hospitals, first responders and military operations, these systems could even prevent the loss of lives.
Automation and digitalisation of workflows and business processes comes at a cost. For end users it can be hard to see how an action influences their desired goal. They are unable to oversee the complete flow of the process and there might be an abundance of data that they are not fully aware of. End users might wonder if checking a box may prevent them, or someone else, from reaching their goal, or ask themselves if they have taken all information into consideration before making a decision.
To overcome these difficulties, we propose to integrate a next step hint system into workflow software. By combining previous research on symbolic execution for Task-Oriented Programming
[16] and end-user feedback systems for rule based problems
[15], we develop a next step hint end-user feedback system for the Task-Oriented Programming language TopHat (
 )
[20]. Our solution, which we call
)
[20]. Our solution, which we call
 , generates next step hints from existing code, and does not require extra work by the programmer. To our knowledge, this is the first work employing symbolic execution to automatically generate next-step hints for end users.
, generates next step hints from existing code, and does not require extra work by the programmer. To our knowledge, this is the first work employing symbolic execution to automatically generate next-step hints for end users.
Providing next step hints to end users will provide them with a quick insight in to their situation. It reduces the chance of human error, while still allowing the user to intervene if required. The quality of decisions will improve, raising the overall performance.
In this paper we will introduce Task-Oriented Programming and the
 language for readers unfamiliar with either of them, followed by some illustrative examples. Building further on this foundation we show how we use symbolic execution to automatically generate next step hints for end users. It is crucial that these hints are valid, meaning they allow users to reach the desired goal. Therefore we prove correctness of the automatic hint generation system. Our hint generation system relies on symbolic execution as presented in earlier work
[16]. There, we proved correctness for the symbolic semantics for single user inputs. Here, we prove the entire symbolic system to be correct, for any sequence of user inputs.
language for readers unfamiliar with either of them, followed by some illustrative examples. Building further on this foundation we show how we use symbolic execution to automatically generate next step hints for end users. It is crucial that these hints are valid, meaning they allow users to reach the desired goal. Therefore we prove correctness of the automatic hint generation system. Our hint generation system relies on symbolic execution as presented in earlier work
[16]. There, we proved correctness for the symbolic semantics for single user inputs. Here, we prove the entire symbolic system to be correct, for any sequence of user inputs.
1.1 Contributions
This paper makes the following contributions.
-
We describe an automatic end user next step feedback system for
 , called
, called
 , based on a previously presented symbolic semantics.
, based on a previously presented symbolic semantics. -
We prove the symbolic execution semantics of
 to be correct for sequential inputs.
to be correct for sequential inputs. -
We change the definition of simulation of
 programs to accommodate above proof.
programs to accommodate above proof. -
We prove soundness and completeness of next step hints generated by this system.
-
We present an implementation of the end user feedback system in Haskell.
1.2 Structure
Section 2 first introduces the Task-Oriented Programming (
 ) paradigm and the Task-Oriented Programming language
) paradigm and the Task-Oriented Programming language
 . Section 3 lists three example programs to illustrate how
. Section 3 lists three example programs to illustrate how
 works and to show what we like to achieve with
works and to show what we like to achieve with
 . In Sect. 4 we briefly introduce the symbolic execution semantics for
. In Sect. 4 we briefly introduce the symbolic execution semantics for
 , followed by a description of
, followed by a description of
 . In Sect. 5 soundness and completeness of the assistive system are shown. Section 6 gives an overview of related work, and finally Sect. 7 concludes.
. In Sect. 5 soundness and completeness of the assistive system are shown. Section 6 gives an overview of related work, and finally Sect. 7 concludes.
2 The TopHat Language
The Task-Oriented Programming (
 ) paradigm was first introduced by Plasmeijer et al.
[19]. It is created to improve the development and quality of software that coordinates collaboration between users.
) paradigm was first introduced by Plasmeijer et al.
[19]. It is created to improve the development and quality of software that coordinates collaboration between users.
 provides programmers with a high level of programming abstraction, while still being expressive enough to describe real world collaborations. It does so by using features from higher-order functional programming languages, combined with the notion of tasks. Tasks model units of work, which can be performed by a human or by a computer. From a task specification, a
provides programmers with a high level of programming abstraction, while still being expressive enough to describe real world collaborations. It does so by using features from higher-order functional programming languages, combined with the notion of tasks. Tasks model units of work, which can be performed by a human or by a computer. From a task specification, a
 implementation generates a distributive multi-user (web) application.
implementation generates a distributive multi-user (web) application.
Tasks have a couple of properties, listed below.
-
Tasks model collaboration.
Programmers describe what work needs to be done, by who and in what way.
-
Tasks are interactive.
Users can enter or update information into the system by using editors. They can progress to the next task, or choose between tasks.
-
Tasks can be observed.
Therefore, other users or the system itself can make decisions based on the observed progress of the task.
-
Tasks are modular.
They can be combined into bigger tasks by using combinators. The basic combinators are chosen in such a way, that they represent basic collaboration patterns. New combinators can be created by making use of basic combinators and the (higher order) facilities of the host language.
-
Tasks share information.
Information is passed along control flow, or, in order for tasks to exchange information, across control flow via references. In particular to share data between parallel tasks.
-
Tasks are typed.
This is not just to ensure safety at runtime, but also to automatically derive common program elements.
 systems automatically generate user interfaces and manage persistent storage of information.
systems automatically generate user interfaces and manage persistent storage of information.
Currently, there are three systems implementing the
 paradigm. The reference implementation is the
paradigm. The reference implementation is the
 framework
[19], which is an embedded domain specific language in the non-strict functional programming language Clean
[18].
framework
[19], which is an embedded domain specific language in the non-strict functional programming language Clean
[18].
 [13] is a
[13] is a
 implementation specifically designed for embedded systems. A formalisation of
implementation specifically designed for embedded systems. A formalisation of
 , called
, called
 (TopHat), has been created by Steenvoorden, Naus, and Klinik
[20].
(TopHat), has been created by Steenvoorden, Naus, and Klinik
[20].
 builds on
builds on
 and its symbolic counterpart
and its symbolic counterpart
 [16].
[16].
 implements
implements
 by embedding a task language in the simply typed lambda calculus with references, conditionals, and pairs. Note the omission of any fixed point language constructs, which make
by embedding a task language in the simply typed lambda calculus with references, conditionals, and pairs. Note the omission of any fixed point language constructs, which make
 a total language.
a total language.
 extends this with built in operators, lists, and most importantly symbols. References are used to model the shared data component of
extends this with built in operators, lists, and most importantly symbols. References are used to model the shared data component of
 . The complete syntax and semantics can be found in previous work
[20]. An overview can be found in the appendixFootnote 1. In the next subsections we describe the basic constructs of the
. The complete syntax and semantics can be found in previous work
[20]. An overview can be found in the appendixFootnote 1. In the next subsections we describe the basic constructs of the
 language. Section 4.1 details
language. Section 4.1 details
 .
.
2.1 Editors
Editors form the entry points for interaction and communication with the outside world. They are the most basic tasks and can be seen as an abstraction over widgets in a
 library or forms on a webpage. Users can change the value held by an editor, in the same way they can manipulate widgets in a
library or forms on a webpage. Users can change the value held by an editor, in the same way they can manipulate widgets in a
 .
.
When a
 implementation generates an application from a task specification, it derives user interfaces for the editors. The appearance of an editor depends on its type. For example, editors of type string can be represented by simple input fields, dates by calendars, and locations by pins on a map.
implementation generates an application from a task specification, it derives user interfaces for the editors. The appearance of an editor depends on its type. For example, editors of type string can be represented by simple input fields, dates by calendars, and locations by pins on a map.
There are three different editors in
 .
.
-
 Valued editor.
Valued editor.This editor holds a value v of a certain type. The user can replace the value by new values of the same type.
-
 Unvalued editor.
Unvalued editor.This editor holds no value, and can receive a value of type \(\tau \). When that happens, it turns into a valued editor.
-
 Shared editor.
Shared editor.This editor refers to a store location l. Its observable value is the value stored at that location. When it receives a new value, this value will be stored at location l.
2.2 Combinators
Editors can be combined into larger tasks using combinators. The order in which editors and tasks are executed is specified with combinators. Tasks can be performed in sequence, in parallel or a choice can be made between tasks. These combinators originate from basic collaboration patterns.
The following combinators are available in
 . Here, t stands for tasks and e for expressions.
. Here, t stands for tasks and e for expressions.
-
 Step.
Step.Users can work on task t. As soon as t has an observable value, as defined in the next section, that value is passed on to the right hand side e. The expression e is a function, taking the value as an argument, resulting in a new task.
-
 User Step.
User Step.Users can work on task t. When t has an observable value, the step becomes enabled. Then, users can send a continue event to the combinator. When that happens, the value of t is applied to the right hand side function e, with which it continues in the same way as normal steps do.
-
 Pair.
Pair.Users can work on tasks \(t_1\) and \(t_2\) in at the same time.
-
 Choice.
Choice.The system chooses between \(t_1\) or \(t_2\), based on which task first has an observable value. If both tasks have a value, the system chooses the left one. When neither of the two tasks has an observable value, users can continue to work on both tasks until one of them does.
-
 User choice.
User choice.A user has to make a choice between either the left or the right hand side. After picking a side, the user can work on that task.
In addition to editors and combinators,
 also contains the fail task (
also contains the fail task (
 ). Programmers can use this task to indicate that a task is not reachable or viable. When the right hand side of a step combinator evaluates to
). Programmers can use this task to indicate that a task is not reachable or viable. When the right hand side of a step combinator evaluates to
 , the step will not proceed to that task.
, the step will not proceed to that task.
2.3 Observations
Several observations can be made on tasks. These observations are used by the system to determine the progress of combinators, and to draw the user interface. They will also be used by
 to provide next step hints.
to provide next step hints.
Using the value function
 , the current value of a task can be determined. The value function is a partial function, since not all tasks have a value. For example empty editors do not have a value. The value of tasks composed of parallel and internal choice combinators, depends on the value of the subtasks. Parallel only has a value if both tasks have an observable value. Internal choice has a value if either of the two tasks has an observable value.
, the current value of a task can be determined. The value function is a partial function, since not all tasks have a value. For example empty editors do not have a value. The value of tasks composed of parallel and internal choice combinators, depends on the value of the subtasks. Parallel only has a value if both tasks have an observable value. Internal choice has a value if either of the two tasks has an observable value.
One can also observe whether or not a task is failing, by means of the failing function
 . A task is considered to be failing if, after normalisation, a user cannot interact with it. For example, the valued editor is not failing, since the user can update it with a new value. The task
. A task is considered to be failing if, after normalisation, a user cannot interact with it. For example, the valued editor is not failing, since the user can update it with a new value. The task
 is failing, as is a parallel combination of failing tasks
is failing, as is a parallel combination of failing tasks
 , since both the left and the right task cannot be interacted with. Both observation definitions can be found in Fig. 1.
, since both the left and the right task cannot be interacted with. Both observation definitions can be found in Fig. 1.
The step combinators make use of both functions in order to determine if they can step to the right hand side. First,
 determines if the left hand side produces a value. If that is the case,
determines if the left hand side produces a value. If that is the case,
 checks if stepping to the right hand side is successful.
checks if stepping to the right hand side is successful.
2.4 Input
Input events drive the evaluation of tasks. Because tasks are typed, input is typed as well. Editors only accept input of the correct type. For example, an editor can only be updated with a new value, if it has the same type as the old value. When the system receives a valid event, it applies this event to the current task, which evaluates to a new task. Everything in between two events is evaluated atomically with respect to inputs. This means that tasks are normalised up to the point where they await new user interactions.
Input events are synchronous, which means that the order of execution is completely determined by the order of the events. In particular, the order of input events determine the progression of parallel branches.
2.5 Semantics
The semantics of
 are defined in three layers. Figure 2 contains an overview of these semantics and their relations. The first layer consists of the standard big step semantics for the simply typed \(\lambda \)-calculus. We call this semantics evaluation (
are defined in three layers. Figure 2 contains an overview of these semantics and their relations. The first layer consists of the standard big step semantics for the simply typed \(\lambda \)-calculus. We call this semantics evaluation (
 ). All task specific language constructs, as described previously in Sects. 2.1 and 2.2, are normalised using a dedicated big step semantics (
). All task specific language constructs, as described previously in Sects. 2.1 and 2.2, are normalised using a dedicated big step semantics (
 ) in the second layer. Normalisation can be regarded as preparing tasks for user input. It makes use of a helper small step semantics called striding (
) in the second layer. Normalisation can be regarded as preparing tasks for user input. It makes use of a helper small step semantics called striding (
 ).
).
The above semantics are internal to the system and do not take any user interaction into account. On the third level, the small step interaction semantics (
 ) first handles any user input i using the handle semantics (
) first handles any user input i using the handle semantics (
 ) and then normalises the resulting task so it is ready to handle the next user input.
) and then normalises the resulting task so it is ready to handle the next user input.
The semantic rules can be found in the appendixFootnote 2. For a thorough explanation of all rules, we refer to previous work [20].
3 Examples
This section introduces three example
 programs. Each example illustrate different functionality of the
programs. Each example illustrate different functionality of the
 language. Section 3.1 demonstrates the step combinator, Sect. 3.2 includes the parallel and choice combinators, and finally Sect. 3.3 demonstrates the use of shares in order for tasks to communicate with each other. The examples will be used in Sect. 4 to demonstrate how
language. Section 3.1 demonstrates the step combinator, Sect. 3.2 includes the parallel and choice combinators, and finally Sect. 3.3 demonstrates the use of shares in order for tasks to communicate with each other. The examples will be used in Sect. 4 to demonstrate how
 works, and are included in the implementation.
works, and are included in the implementation.
3.1 Vending Machine
Using the editors and combinators described in Sect. 2, we can create a vending machine that dispenses a biscuit for one coin and a chocolate bar for two coins as follows:

This example demonstrates the usage of a user step guarded by a branching expression (Line 2) using the failure task (Line 4). The editor
 asks the user to enter an amount of money. It simulates a coin slot in a real machine that freely accepts and returns coins. There is a continue button, generated by the user step combinator
asks the user to enter an amount of money. It simulates a coin slot in a real machine that freely accepts and returns coins. There is a continue button, generated by the user step combinator
 . Only when the user has inserted exactly 1 or 2 coins will the continue button become enabled. Other cases will result in the failure task
. Only when the user has inserted exactly 1 or 2 coins will the continue button become enabled. Other cases will result in the failure task
 , and stepping to it is prohibited by definition. When the user presses the continue button, the machine dispenses either a biscuit or a chocolate bar, depending on the amount of money. Snacks are modelled using a custom type.
, and stepping to it is prohibited by definition. When the user presses the continue button, the machine dispenses either a biscuit or a chocolate bar, depending on the amount of money. Snacks are modelled using a custom type.
3.2 Tax Subsidy Request
The example program listed in this section is taken from our previous work on symbolic execution for
 [20]. It models a simplified tax subsidy application process for citizens who have installed solar panels. This was first described by Stutterheim et al.
[21], who worked on modelling a fictional but realistic law about solar panel subsidies.
[20]. It models a simplified tax subsidy application process for citizens who have installed solar panels. This was first described by Stutterheim et al.
[21], who worked on modelling a fictional but realistic law about solar panel subsidies.
A subsidy is only given under the following conditions.
-
The roofing company has confirmed that they installed solar panels for the citizen.
-
The tax officer has approved the request.
-
The tax officer can only approve the request if the roofing company has confirmed, and the request is filed within one year of the invoice date.
-
The amount of the granted subsidy is at most €600.

Listing 1.2 gives the
 code for this example. To enhance readability of the example, we omit type annotations and make use of pattern matching on tuples. The program works as follows.
code for this example. To enhance readability of the example, we omit type annotations and make use of pattern matching on tuples. The program works as follows.
In parallel, the citizen has to provide the invoice documents of the installed solar panels, while the roofing company has to confirm that they have actually installed solar panels at the citizen’s address (Line 6). Once the invoice and the confirmation are there, the tax officer has to approve the request (Line 7). The officer can always decline the request, but they can only approve it if the roofing company has confirmed and the application date is within one year of the invoice date (Line 5). The result of the program is the amount of the subsidy, together with all information needed to prove the required properties (Line 9).
In previous work, we have shown that this code indeed adheres to the requirements listed above. There we focussed on assisting the developer by proving the program correct. In this work we focus on supporting the end user that is requesting a subsidy. The end user wants the outcome of this program to be a subsidy amount larger than zero. In Sect. 4.4 we will show how to generate hints for the end user to reach this goal.
3.3 Dining Computer Scientists Problem
The dining philosophers problem is a classic concurrency problem in computer science. A number of philosophers sit at a round table with a meal in front of them. In between the plates lies a fork. In order to eat their meal, each philosopher has to acquire two forks. Only after eating his or her meal, is a philosopher allowed to place the two forks back on the table. This, of course, means that the philosophers cannot eat at the same time, since there are not enough forks. Deadlock can occur when all philosophers pick up the fork to their right (or left). Then, everybody has one fork. This means that each philosopher cannot start his or her meal. Next to that, is also not allowed to put his fork back on the table.
We look at dining computer scientists instead. Figure 3 shows a visual representation of the problem. Listing 1.3 lists an implementation in
 for this problem, with three computer scientists. The forks are represented by references containing Booleans (Lines 1 to 3). Using references allows tasks to communicate with each other across control flow. The value
for this problem, with three computer scientists. The forks are represented by references containing Booleans (Lines 1 to 3). Using references allows tasks to communicate with each other across control flow. The value
 indicates that the fork is available,
indicates that the fork is available,
 indicates that the fork is being used.
indicates that the fork is being used.
Picking up a fork is only possible when the fork is available, i.e. reading the reference results in
 (Line 5). This fork is then marked as being used (Line 6). Reading a reference l is denoted as !l, assigning a new value v to a reference l is written as \(l:=v\).
(Line 5). This fork is then marked as being used (Line 6). Reading a reference l is denoted as !l, assigning a new value v to a reference l is written as \(l:=v\).
The use of references ensures that the neighbouring scientist cannot pick up this fork: this choice will be disabled. After that, one can press continue if the second fork is also available (Line 7). For the sake of simplicity, one returns the first fork, rather than setting the second fork to
 , and then setting both to
, and then setting both to
 again.
again.
Each computer scientist takes as arguments a name and references to the two forks that he or she can reach (Line 9). They have a choice to take either the left or the right fork. This is represented with an user choice (
 , Line 10).). The last lines instantiate three computer scientists sitting next to each other (Lines 11 to 13). In
, Line 10).). The last lines instantiate three computer scientists sitting next to each other (Lines 11 to 13). In
 terms, this means they collaborate in parallel (
terms, this means they collaborate in parallel (
 ) while eating their dinner, sharing some resources, in this case \(\mathsf {fork0}\), \(\mathsf {fork1}\), and \(\mathsf {fork2}\).
) while eating their dinner, sharing some resources, in this case \(\mathsf {fork0}\), \(\mathsf {fork1}\), and \(\mathsf {fork2}\).
By design of
 , the events of picking up a fork are performed sequentially. That is, when one computer scientist decides to pick up his right fork, we will handle that event first. After that, we will handle the choices from the other scientists. So, the order of the events is explicitly determined by the scientists themselves.
, the events of picking up a fork are performed sequentially. That is, when one computer scientist decides to pick up his right fork, we will handle that event first. After that, we will handle the choices from the other scientists. So, the order of the events is explicitly determined by the scientists themselves.
In Sect. 4.5 we will analyse this example. Our goal is to provide each scientist with a hint on which choice to make, in order to reach the common goal of full bellies. When the scientists follow these hints, no deadlock will occur.

4 Generating Next Step Hints
This section introduces our
 system. The aim of
system. The aim of
 is to automatically provide next step hints. When users follow these hints, they can be sure that they will reach the goal they described beforehand. Users can, however, still decide to deviate from the given hints.
is to automatically provide next step hints. When users follow these hints, they can be sure that they will reach the goal they described beforehand. Users can, however, still decide to deviate from the given hints.
During the execution of
 programs, users are presented with input fields, choices and continue buttons. The way in which tasks progress and the resulting task value depend on these inputs. At any point during execution, we would like to present users with all possible inputs that leads users to the goal they have selected. These inputs are either concrete actions, like continue, pick the left task, pick the right task; or a restricted set of values to be entered into an editor. This set is restricted, since concrete values potentially influence the flow of the program. To give a concrete example, the user should enter an integer, but this integer must be larger than zero to reach the end goal.
programs, users are presented with input fields, choices and continue buttons. The way in which tasks progress and the resulting task value depend on these inputs. At any point during execution, we would like to present users with all possible inputs that leads users to the goal they have selected. These inputs are either concrete actions, like continue, pick the left task, pick the right task; or a restricted set of values to be entered into an editor. This set is restricted, since concrete values potentially influence the flow of the program. To give a concrete example, the user should enter an integer, but this integer must be larger than zero to reach the end goal.
To come to these concrete actions and restricted values, we make use of symbolic execution. In the next two sections, we briefly describe how symbolic execution for
 works and recap its symbolic semantics presented in earlier work
[16]. Thereafter, we show how to turn symbolic execution results into next step hints. In Sects. 4.4 and 4.5, we study what these automatically generated hints look like for the examples from Sect. 3.
works and recap its symbolic semantics presented in earlier work
[16]. Thereafter, we show how to turn symbolic execution results into next step hints. In Sects. 4.4 and 4.5, we study what these automatically generated hints look like for the examples from Sect. 3.
All examples have been tested in our implementation. We added
 to our existing implementation of
to our existing implementation of
 , which is written in Haskell.Footnote 3 It uses the
, which is written in Haskell.Footnote 3 It uses the
 solver under the hood. By defining the formal hints function directly on top of the symbolic execution semantics, we can leverage the already existing symbolic execution for
solver under the hood. By defining the formal hints function directly on top of the symbolic execution semantics, we can leverage the already existing symbolic execution for
 in the practical implementation.
in the practical implementation.
4.1 Symbolic Execution
A symbolic execution semantics [4, 12] aims to execute a program without knowing its input. Instead, symbols are fed into the program. During evaluation, the influence of values is recorded in the path condition. The resulting symbolic value together with the path conditions can be used to prove properties of the program.

Consider the tiny example in Listing 1.4. This program asks for two integer values. After the user has entered this information, the function to the right of the step combinator makes sure the result will be an editor containing a pair, where the second element is larger then the first. When we run this program symbolically, we have to create fresh symbols to be entered in either of the two editors, say \(s_0\) and \(s_1\). After entering both symbolic values and then normalising the task, there are two possible outcomes, namely
-
\(\langle s_1,s_0\rangle \), provided that the path condition \(\varphi _1 = s_0 > s_1\) holds; or
-
\(\langle s_0,s_1\rangle \), with path condition \(\varphi _2 = \lnot (s_0 > s_1)\).
Now, the property that we want to prove for this program is that no matter what the input is, the second element should always be larger than the first. We write this property as \(\psi (\langle a, b\rangle )= a \le b\). Looking at the two symbolic runs, we first need to verify that the symbolic runs are indeed viable. This is done by checking that both \(\varphi _1\) and \(\varphi _2\) are satisfiable, written
 and
and
 . Symbolic runs with a path condition that is not satisfiable are discarded. Finally, we check that both path conditions conform to the goal property \(\psi \), which is the case. Therefore, we can conclude that the property holds. When applying this technique to larger programs, it is a powerful tool to show that a program behaves as expected.
. Symbolic runs with a path condition that is not satisfiable are discarded. Finally, we check that both path conditions conform to the goal property \(\psi \), which is the case. Therefore, we can conclude that the property holds. When applying this technique to larger programs, it is a powerful tool to show that a program behaves as expected.
4.2 Symbolic Semantics
To support symbolic execution in
 , we extend our host language with symbols. In addition, we also need to modify the semantics described in Sect. 2.5, to accommodate symbolic execution. The observation functions from Sect. 2.3 are extended in a similar way. These new semantic relations operate on expressions which may contain symbols. Instead of stepping to one result, they lead to a set of possible symbolic results, accompanied with a path condition \(\varphi \).
, we extend our host language with symbols. In addition, we also need to modify the semantics described in Sect. 2.5, to accommodate symbolic execution. The observation functions from Sect. 2.3 are extended in a similar way. These new semantic relations operate on expressions which may contain symbols. Instead of stepping to one result, they lead to a set of possible symbolic results, accompanied with a path condition \(\varphi \).
We denote entities containing symbols with an additional tilde, and symbolic semantic relations with squiggly arrows instead of straight ones. So \(\tilde{t}\), \(\tilde{\sigma }\), and
 are respectively tasks, states, and inputs containing symbols. Table 1 gives an overview of the entities in the concrete world, and their symbolic counterparts. Concrete expressions are a subset of symbolic expressions. Therefore, symbolic semantic relations can be applied on concrete expressions, as well as symbolic expressions.
are respectively tasks, states, and inputs containing symbols. Table 1 gives an overview of the entities in the concrete world, and their symbolic counterparts. Concrete expressions are a subset of symbolic expressions. Therefore, symbolic semantic relations can be applied on concrete expressions, as well as symbolic expressions.
The symbolic interaction semantics (
 ) results in a set of symbolic runs, each of them just containing one symbolic input. In other words, the symbolic interaction semantics just looks ahead one symbolic interaction. To be able to reason about an end state after multiple symbolic interactions, we introduce the notion of simulation. Informally, simulation performs multiple symbolic interactions after each other, until the rewritten task has an observable value. I.e. if n is the number of interactions needed to be done,
) results in a set of symbolic runs, each of them just containing one symbolic input. In other words, the symbolic interaction semantics just looks ahead one symbolic interaction. To be able to reason about an end state after multiple symbolic interactions, we introduce the notion of simulation. Informally, simulation performs multiple symbolic interactions after each other, until the rewritten task has an observable value. I.e. if n is the number of interactions needed to be done,
 has a result for \(i = n\) but is undefined for all \(i < n\). Apart from this restriction, we want to permit only viable executions. This is enforced by validating the satisfiability (
has a result for \(i = n\) but is undefined for all \(i < n\). Apart from this restriction, we want to permit only viable executions. This is enforced by validating the satisfiability (
 ) of the conjunction of all sequential path conditions. More formally, simulating a task for multiple user inputs is defined as follows.
) of the conjunction of all sequential path conditions. More formally, simulating a task for multiple user inputs is defined as follows.
Definition 1
(Simulation (
 )). Let t and \(\sigma \) be a concrete task and concrete state. We define the simulation relation
)). Let t and \(\sigma \) be a concrete task and concrete state. We define the simulation relation

to be the set of results after performing symbolic interaction n times:

where:
-
the nth task has a value:
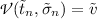 ;
; -
all tasks before do not have a value:
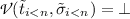 ;
; -
 is the concatenation of all symbolic inputs generated along the way;
is the concatenation of all symbolic inputs generated along the way; -
\(\Phi = \varphi _1 \wedge \cdots \wedge \varphi _n\), is the conjunction of all path conditions encountered.
Furthermore we require that:
-
the resulting predicate is satisfiable:
 .
.
The simulation definition used in this paper differs from the one in previous work [16]. Previously, infinite symbolic executions were filtered out by allowing two steps look-ahead in case of idempotent executions. The definition above only allows finite executions by definition.
4.3 Next Step Hints Observation
As we have seen in Definition 1, a symbolic task \(\tilde{t}\) is considered done as soon as it has an observable value \(\tilde{v}\). In order to calculate next step hints, one needs to formulate a goal over this resulting value. Only then, we can calculate next step hints for end users.
Hints are calculated by means of the
 function listed in Fig. 4. As input, it receives a concrete task t and concrete state \(\sigma \) together with a goal predicate g. The hints observation simulates t starting in \(\sigma \). This results in a set of symbolic values \(\tilde{v}\), together with a list of symbolic inputs \(\tilde{i}\cdot \tilde{I}\) and a condition \(\Phi \) to reach this path. We only want to use the symbolic executions that satisfy the goal g when applied to \(\tilde{v}\). Since \(\tilde{v}\) could contain symbols, it might be the case that \(g(\tilde{v})\) is symbolic and would clash with the path condition \(\Phi \). Therefore, we require that the conjunction of the path condition with the goal is satisfiable (
function listed in Fig. 4. As input, it receives a concrete task t and concrete state \(\sigma \) together with a goal predicate g. The hints observation simulates t starting in \(\sigma \). This results in a set of symbolic values \(\tilde{v}\), together with a list of symbolic inputs \(\tilde{i}\cdot \tilde{I}\) and a condition \(\Phi \) to reach this path. We only want to use the symbolic executions that satisfy the goal g when applied to \(\tilde{v}\). Since \(\tilde{v}\) could contain symbols, it might be the case that \(g(\tilde{v})\) is symbolic and would clash with the path condition \(\Phi \). Therefore, we require that the conjunction of the path condition with the goal is satisfiable (
 ). From the executions that fulfill this requirement, we return the first symbolic input
). From the executions that fulfill this requirement, we return the first symbolic input
 from the complete list of inputs
from the complete list of inputs
 , together with the full condition that must hold (\(\Phi \wedge g(\tilde{v})\)). The resulting set contains pairs of symbolic inputs guarded by this condition.
, together with the full condition that must hold (\(\Phi \wedge g(\tilde{v})\)). The resulting set contains pairs of symbolic inputs guarded by this condition.
To get a better understanding how
 works, we study it more concretely in the next subsections. Section 4.4 demonstrates on the basis of the tax example listed in Sect. 3.2, how the results of the symbolic execution are used to construct automatic next step hints. Section 4.5 shows how hints can be generated during the execution of the example
works, we study it more concretely in the next subsections. Section 4.4 demonstrates on the basis of the tax example listed in Sect. 3.2, how the results of the symbolic execution are used to construct automatic next step hints. Section 4.5 shows how hints can be generated during the execution of the example
 program listed in Sect. 3.3.
program listed in Sect. 3.3.
4.4 Tax Subsidy Request
Recall the Tax example program in
 from Sect. 3.2, which models the application for a solar panel tax refund. The user enters the invoice date and invoice amount, the installation company confirms, and finally the tax officer either approves or denies the request.
from Sect. 3.2, which models the application for a solar panel tax refund. The user enters the invoice date and invoice amount, the installation company confirms, and finally the tax officer either approves or denies the request.
In this section, we will demonstrate what symbolic execution looks like for this example, and how we generate next step hints from the symbolic execution results. First, we call the simulate function
 on the program, with an empty state. The resulting set of symbolic executions is listed in Table 2. Each line represents one symbolic execution. In the first column, the resulting symbolic value \(\tilde{v}\) is listed. The second column lists the symbolic input \(\tilde{I}\) that was produced to arrive at that value, followed by the path condition \(\Phi \) in the third column. The symbolic values that are produced are \(s_i\) for the invoice date and \(s_a\) for the invoice amount.
on the program, with an empty state. The resulting set of symbolic executions is listed in Table 2. Each line represents one symbolic execution. In the first column, the resulting symbolic value \(\tilde{v}\) is listed. The second column lists the symbolic input \(\tilde{I}\) that was produced to arrive at that value, followed by the path condition \(\Phi \) in the third column. The symbolic values that are produced are \(s_i\) for the invoice date and \(s_a\) for the invoice amount.
The definition of
 describes how these results should be used in order to calculate next step hints. First of all, we need a goal g to select the symbolic runs that we are interested in. The most straight forward goal would be that we want to end up in a situation where we get a subsidy amount larger than zero. This goal can be formulated as \(g(\langle v,\_,\_,\_,\_\rangle ) = v > 0\).
describes how these results should be used in order to calculate next step hints. First of all, we need a goal g to select the symbolic runs that we are interested in. The most straight forward goal would be that we want to end up in a situation where we get a subsidy amount larger than zero. This goal can be formulated as \(g(\langle v,\_,\_,\_,\_\rangle ) = v > 0\).
The first six symbolic runs listed in Table 2 fulfill this goal condition. From those runs, we then take the first symbolic input, together with the path condition conjugated with the goal. After removing duplicates and redundant information, the result of
 is as follows.
is as follows.

This means that, at this stage, users have three possible options.Footnote 4
-
1.
The applicant may enter an amount \(s_\mathrm {a}\) for which \(\min (600, s_{\mathrm {a}}/10) > 0\) should hold.
-
2.
The applicant may enter an invoice date \(s_\mathrm {i}\) for which \((\text {13 Feb 2020}-s_{\mathrm {i}}) < \text {365 days}\) should hold.
-
3.
The company should take the left choice (
 ) to confirm they installed the solar panels.
) to confirm they installed the solar panels.
4.5 Dining Computer Scientists
Recall the example program Dining Computer Scientists from Sect. 3.3. Three computer scientist sit at a table and have to coordinate their eating. We want to calculate all possible next steps that lead to the goal. The goal in this example is for all computer scientists to finish their meal. In terms of the resulting task value, this means that we want to reach the value “Full bellies”. Witten as a predicate, we get \(g(v) = v \equiv \text {``Full bellies''}\).
Let us assume that both Grace Hopper and Ada Lovelace have already picked up the forks to their left (\(\mathsf {fork2}\) and \(\mathsf {fork0}\) respectively). We then find ourselves in the situation shown in Fig. 5.
Calling
 will result in just one hint, namely
will result in just one hint, namely

This means that the only step towards goal g is for the second scientist,Footnote 5 which is Grace Hopper, to pick up the right fork. Although it is also possible for Alan Turing to pick up the fork to his left, this step is not a valid hint and performing this action will result in deadlock.
5 Properties
In this section, we want to validate our approach by proving correctness. For the hints function, which forms the heart of
 , we want to prove that its results are both sound and complete. Since the hints function relies on
, we want to prove that its results are both sound and complete. Since the hints function relies on
 , and more specifically, the updated definition of the simulate relation, we first prove correctness of simulate.
, and more specifically, the updated definition of the simulate relation, we first prove correctness of simulate.
5.1 Correctness of Simulate
The symbolic execution semantics is correct when all symbolic runs relate to a concrete run, and the other way around, when all concrete runs are contained in the set of all symbolic executions. These properties are, respectively, soundness and completeness.
The simulation applies symbolic interaction multiple times. In order to prove certain properties with respect to the concrete semantics, we need a concrete analog of simulation. Therefore, we define execution, which applies concrete interaction multiple times.
Definition 2
(Execution (
 )). Let t be a concrete task, \(\sigma \) a concrete state, and \(I = i_1 \cdots i_n\) a list of n concrete inputs. We define the execution relation
)). Let t be a concrete task, \(\sigma \) a concrete state, and \(I = i_1 \cdots i_n\) a list of n concrete inputs. We define the execution relation

to be the value of task t after performing concrete interaction for each input i in I:

where
-
v is the value of \(t_n\):
 ; and
; and -
all tasks before \(t_n\) do not have a value:
 .
.
Using execution, we can state soundness and completeness for simulation as follows.
Lemma 1
(Soundness of simulate). For all tasks t and states \(\sigma \) such that
 where
where
 , for each triple of results \(\langle \tilde{v},\tilde{I},\Phi \rangle \) there exists a concrete input I with the same length as the symbolic input \(\tilde{I}\) such that
, for each triple of results \(\langle \tilde{v},\tilde{I},\Phi \rangle \) there exists a concrete input I with the same length as the symbolic input \(\tilde{I}\) such that
 with \([s_i\mapsto c_i]\tilde{v}=v\) and \([s_i\mapsto c_i]\Phi \) where
with \([s_i\mapsto c_i]\tilde{v}=v\) and \([s_i\mapsto c_i]\Phi \) where
 and
and
 .
.
Lemma 2
(Completeness of simulate). For all tasks t, states \(\sigma \), and lists of input I such that
 , there exists a symbolic value \(\tilde{v}\) and a symbolic input \(\tilde{I}\) with the same length as I, such that
, there exists a symbolic value \(\tilde{v}\) and a symbolic input \(\tilde{I}\) with the same length as I, such that
 , with \(\tilde{i_i}\sim i_i\), \([s_i\mapsto c_i]\tilde{v}=v\) and \([s_i\mapsto c_i]\Phi \), where
, with \(\tilde{i_i}\sim i_i\), \([s_i\mapsto c_i]\tilde{v}=v\) and \([s_i\mapsto c_i]\Phi \), where
 and
and
 .
.
Where
 is defined as follows.
is defined as follows.
Definition 3
(Input simulation). A symbolic input
 simulates a concrete input i denoted as
simulates a concrete input i denoted as
 in the following cases.
in the following cases.
\(s\sim a\), where s is a symbol and a a concrete action.


And
 and
and
 are defined as follows.
are defined as follows.

Our strategy to prove these two lemma’s is outlined in Fig. 6. At the top, we start out with any task t and state \(\sigma \). The left side of the diagram is an overview of the evaluate function. Inputs \(i_1\) until \(i_n\) are sequentially applied, until the task has an observable value.
On the right side, symbolic execution is performed. One step of the symbolic interaction semantics is taken, which results in a symbolic task, state, input and a path condition. Provided that the path condition holds, interaction is executed sequentially until the symbolic task has an observable symbolic value.
Proving soundness and completeness of simulation now comes down to relating the left and right side of the diagram. From symbolic to concrete (right to left) is soundness, as stated in Lemma 1. From concrete to symbolic (left to right) is completeness, as stated in Lemma 2.
Since simulation and execution rely on the (symbolic) handling semantics, we prove soundness and completeness of those semantics first. Looking at Fig. 6, there are two different settings in which the (symbolic) handling semantics are applied. At the top, both symbolic and concrete execution start out with the same task and state. But further down, the task and state differ for both semantics. The task and state are related to each other however. The symbolic semantics introduces symbols, the concrete semantics handles concrete values. This relation is expressed by the consistence relation listed in Definition 5.
Definition 5
(Consistence relation
 ). A concrete task t and concrete state \(\sigma \) are considered to be consistent with a symbolic task \(\tilde{t}\), symbolic state \(\tilde{\sigma }\) and path condition \(\Phi \) under a certain mapping \(M=[s_1\mapsto c_1,\cdots ,s_n,\mapsto c_n]\), denoted as
). A concrete task t and concrete state \(\sigma \) are considered to be consistent with a symbolic task \(\tilde{t}\), symbolic state \(\tilde{\sigma }\) and path condition \(\Phi \) under a certain mapping \(M=[s_1\mapsto c_1,\cdots ,s_n,\mapsto c_n]\), denoted as
 if and only if \(M\tilde{t}=t\), \(M\tilde{\sigma }=\sigma \) and \(M\Phi \).
if and only if \(M\tilde{t}=t\), \(M\tilde{\sigma }=\sigma \) and \(M\Phi \).
Now Lemma 3 and Lemma 4 express soundness and completeness of interacting respectively.
Lemma 3
(Soundness of interacting). For all concrete tasks t, concrete states \(\sigma \), symbolic tasks \(\tilde{t}\), symbolic states \(\tilde{\sigma }\) path conditions \(\Phi \) and mappings M, we have that
 implies that for all pairs
implies that for all pairs
 in
in
 ,
,
 implies that there exists an input i such that
implies that there exists an input i such that
 ,
,
 and
and
 where
where
 and
and
 .
.
Lemma 4
(Completeness of interacting). For all concrete tasks t, concrete states \(\sigma \), symbolic tasks \(\tilde{t}\), symbolic states \(\tilde{\sigma }\) path conditions \(\Phi \) and mappings M, we have that
 implies that for all inputs i such that
implies that for all inputs i such that
 , there exists a symbolic input
, there exists a symbolic input
 ,
,
 such that
such that
 ,
,
 and
and
 where
where
 and
and
 .
.
In other words, if a symbolic and concrete task and state are related, they will still be related after (symbolic) handling. The top case, where both the symbolic and concrete semantics start out with the same task and state, can be seen as a special case of the consistence relation. Obviously a task and state are consistent with themselves, using the empty mapping and the path condition
 .
.
The full proof of all four lemma’s is listed in the appendix onlineFootnote 6.
5.2 Correctness of Hints
Now that soundness and completeness of simulate have been proven, we can prove that our hints function produces correct hints. Intuitively, for a next step hint to be correct, it should adhere to the following requirements:
-
it leads to concrete input users can actually insert; and
-
when users follow the hint, the end goal is still reachable.
Moreover, a set of next step hints is correct when:
-
each hint it contains is correct; and
-
it covers all possible inputs that lead to the end goal.
We separate these requirements into two lemma’s, namely soundness and completeness.
Theorem 1
(Soundness of hints). For all tasks t, states \(\sigma \), and goals g, for every next step hint
 in
in
 , there exists a sequence of concrete inputs I and a concrete input i such that
, there exists a sequence of concrete inputs I and a concrete input i such that
 ,
,
 ,
,
 and g(v).
and g(v).
Theorem 2
(Completeness of hints). For all tasks t, states \(\sigma \), lists of input \(i \cdot I\), and goals g, if
 and g(v), then there exists a symbolic input
and g(v), then there exists a symbolic input
 and path condition \(\Phi \) such that
and path condition \(\Phi \) such that
 with
with
 and
and
 with
with
 and
and
 .
.
The proofs of these two threorems are quite straight forward.
Proof
(Theorem 1). Theorem 1 follows from the definition of
 and Lemma 1 as follows.
and Lemma 1 as follows.
The definition of
 gives us that for every pair
gives us that for every pair
 produced by
produced by
 , there exists a triple
, there exists a triple
 with
with
 . Then by Lemma 1 we have that there exists a sequence of concrete inputs I such that
. Then by Lemma 1 we have that there exists a sequence of concrete inputs I such that
 and g(v).
and g(v).
Proof
(Theorem 2). In order to prove that i is contained in
 , we need to show that
, we need to show that
 , with
, with
 and
and
 , where
, where
 and \([c_0,\cdots ,c_n]\in i \cdot I\) and
and \([c_0,\cdots ,c_n]\in i \cdot I\) and
 .
.
By Lemma 2, we directly obtain that this indeed exists. Therefore we know that
 and \(\Phi \) exist.
and \(\Phi \) exist.
6 Related Work
In previous work, we have attempted to provide end users with next step hints by viewing workflows as rule based problems [15]. By abstracting over workflows, reasoning about them becomes simpler. A standard search algorithm can be run to find a path to the desired goal state. Two drawbacks of this approach however are that only very general hints can be given, that range over multiple steps, and that a programmer needs to augment existing workflows with extra information in order to convert it to a rule-based problem.
Stutterheim et al. [22] have developed Tonic, a task visualiser for iTasks with limited path prediction capabilities. The main goal is not to provide hints to end users, but the system is able to handle the complete task language, and visualise the effects of user input on the progression of tasks.
In order to overcome the problems of our own previous research and the limited use of Tonic for end user hints, we have combined symbolic execution, together with workflow modelling and next step hint generation. To our knowledge, this is the first work describing the combination of these techniques in this way. The different components coming together in this paper have been studied extensively. The following sections give an overview of the work done in those areas.
6.1 Symbolic Execution
Symbolic execution [4, 12] is typically being applied to imperative programming languages, but in recent years it has been used for functional programming languages as well. Ongoing work by Hallahan et al. [8, 9] aims to implement a symbolic execution engine for Haskell. Giantsios et al. [7] use symbolic execution for a mix of concrete and symbolic testing of Erlang programs. Their goal is to explore all execution paths up to a certain depth. Chang et al. [5] present a symbolic execution engine for a typed lambda calculus with mutable state where only some language constructs recognise symbolic values. They claim that their approach is easier to implement than full symbolic execution and simplifies the burden on the solver, while still considering all execution paths.
6.2 Workflow Modelling
Workflow modelling has been studied extensively from different viewpoints. Since many software exists that automates workflows, it is a research topic that potentially has a huge impact on society.
Workflow patterns are regarded as special design patterns in software engineering. Similar to the combinators in
 , they describe recurring patterns in workflow systems. Van der Aalst et al.
[3] identifies common patterns, and examines their availability in industry workflow frameworks.
, they describe recurring patterns in workflow systems. Van der Aalst et al.
[3] identifies common patterns, and examines their availability in industry workflow frameworks.
Workflow nets allow for the modelling an analysis of business processes [2]. Worflow Nets are a subclass of Petri nets, and are therefore graphical in nature. Research on workflow nets includes verification of models [1] and complexity analysis [14], just to name a few.
iTasks
[19] is an implementation of
 in the programming language Clean. It differs from the above mentioned modelling techniques, since it is not graphical in nature. iTasks supports higher order workflows, and leverages techniques from functional and generic programming.
in the programming language Clean. It differs from the above mentioned modelling techniques, since it is not graphical in nature. iTasks supports higher order workflows, and leverages techniques from functional and generic programming.
6.3 Automatic Hint Generation in Intelligent Tutoring Systems
The intelligent tutoring systems (
 ) research community is very elaborate. Work that is most relevant to our own is the research into automatic hint generation. More traditional
) research community is very elaborate. Work that is most relevant to our own is the research into automatic hint generation. More traditional
 rely heavily on experts to write dedicated hints for every specific case of an exercise. Automatic hint generation attempts to overcome this burden by calculating a hint rather than having every case specified.
rely heavily on experts to write dedicated hints for every specific case of an exercise. Automatic hint generation attempts to overcome this burden by calculating a hint rather than having every case specified.
Heeren et al.
[10] develop a framework for so called domain reasoners that allow for automatic hint generation. Feedback is calculated automatically from a high-level description of an exercise class. Their approach is applicable to domains like logic, mathematics and linear algebra. Paquette et al.
[17] present a different automatic next step hint
 , that is used to provide hints to students in a programming exercise.
, that is used to provide hints to students in a programming exercise.
Based on the work mentioned above by Heeren et al., an
 for Haskell exercises has been developed by Gerdes et al.
[6]. It tuns out that programming exercises is a popular area for automatic hint generation. Keuning et al.
[11] have written an excellent literature study of this research area.
for Haskell exercises has been developed by Gerdes et al.
[6]. It tuns out that programming exercises is a popular area for automatic hint generation. Keuning et al.
[11] have written an excellent literature study of this research area.
7 Conclusion
In this paper, we have demonstrated how to apply symbolic execution to automatically generate next step hints for
 programs. We have proven the symbolic execution to be sound and complete with regards to sequential inputs. Based on this property, we have also shown that the generated next step hints are correct. Furthermore, we have presented an implementation of the end user feedback system in Haskell.
programs. We have proven the symbolic execution to be sound and complete with regards to sequential inputs. Based on this property, we have also shown that the generated next step hints are correct. Furthermore, we have presented an implementation of the end user feedback system in Haskell.
7.1 Future Work
As future work, we are very interested in bringing the theory presented in this paper into practice. We feel that there are three possible angles to pursue this interest.
Presenting Hint Information. The information calculated by the current hints function cannot directly be presented to the end user. The set of calculated hints contains duplicates. This is due to the fact that there might be several different paths to the goal, that start out with the same symbolic input. Another source of redundant information is the path conditions. The path conditions contained in the hint tuple contains information about the complete execution, while the symbolic input is only concerned with the immediate next step. Therefore, the path condition may contain references to future inputs and constraints, which offer no information for the end user. In a future implementation of
 , we would like to filter out both sources of redundancy, in order to present the user with more concise information.
, we would like to filter out both sources of redundancy, in order to present the user with more concise information.
Hint Generation in iTasks. Since iTasks is currently the biggest
 framework, it would be the next logical step to integrate automatic hint generation into the framework. This would allow a wide range of applications to immediately benefit from automatic next step hint generation. The iTasks framework is shallowly embedded in the purely functional programming language Clean, which means that programmers can leverage the full power of the host language. This makes implementing symbolic execution non-trivial.
framework, it would be the next logical step to integrate automatic hint generation into the framework. This would allow a wide range of applications to immediately benefit from automatic next step hint generation. The iTasks framework is shallowly embedded in the purely functional programming language Clean, which means that programmers can leverage the full power of the host language. This makes implementing symbolic execution non-trivial.
Measuring Impact of Hints. Finally, we would like to test the impact of next step hints in workflow systems in an empirical study.
 research has been applied and studied in the field at the Royal Netherlands Sea Rescue Institution and the Royal Netherlands Navy, which would be ideal testing grounds for
research has been applied and studied in the field at the Royal Netherlands Sea Rescue Institution and the Royal Netherlands Navy, which would be ideal testing grounds for
 .
.
Notes
- 1.
- 2.
- 3.
- 4.
Note that the first branch, entering an amount, is denoted by
 ; the second branch, entering the invoice date, is denoted by
; the second branch, entering the invoice date, is denoted by
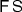 ; and the third branch, making a left/right choice, is denoted by
; and the third branch, making a left/right choice, is denoted by
 .
. - 5.
The second branch is denoted by
 . The action
. The action
 means pushing the continue button.
means pushing the continue button. - 6.
References
Aalst, W.M.P.: Verification of workflow nets. In: Azéma, P., Balbo, G. (eds.) ICATPN 1997. LNCS, vol. 1248, pp. 407–426. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63139-9_48
van der Aalst, W.M.P.: The application of petri nets to workflow management. J. Circuits Syst. Comput. 8(1), 21–66 (1998)
van der Aalst, W.M.P., ter Hofstede, A.H.M., Kiepuszewski, B., Barros, A.P.: Workflow patterns. Distrib. Parallel Databases 14(1), 5–51 (2003)
Boyer, R.S., Elspas, B., Levitt, K.N.: Select - a formal system for testing and debugging programs by symbolic execution. In: Proceedings of the International Conference on Reliable Software, pp. 234–245. ACM, New York (1975)
Chang, S., Knauth, A., Torlak, E.: Symbolic types for lenient symbolic execution. In: PACMPL 2(POPL), pp. 40:1–40:29 (2018)
Gerdes, A., Heeren, B., Jeuring, J., van Binsbergen, L.T.: Ask-Elle: an adaptable programming tutor for haskell giving automated feedback. Int. J. Artif. Intell. Educ. 27(1), 65–100 (2016). https://doi.org/10.1007/s40593-015-0080-x
Giantsios, A., Papaspyrou, N., Sagonas, K.: Concolic testing for functional languages. Sci. Comput. Program. 147, 109–134 (2017)
Hallahan, W.T., Xue, A., Bland, M.T., Jhala, R., Piskac, R.: Lazy counterfactual symbolic execution. In: McKinley, K.S., Fisher, K. (eds.) Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation, PLDI 2019, Phoenix, AZ, USA, 22–26 June 2019, pp. 411–424. ACM (2019)
Hallahan, W.T., Xue, A., Piskac., R.: Building a symbolic execution engine for haskell. In: Proceedings of TAPAS, vol. 17 (2017)
Heeren, B., Jeuring, J.: Feedback services for stepwise exercises. Sci. Comput. Program. 88, 110–129 (2014)
Keuning, H., Jeuring, J., Heeren, B.: A systematic literature review of automated feedback generation for programming exercises. TOCE 19(1), 3:1–3:43 (2019)
King, J.C.: A new approach to program testing. SIGPLAN Notices 10(6), 228–233 (1975)
Koopman, P., Lubbers, M., Plasmeijer, R.: A task-based DSL for microcomputers. In: Proceedings of the Real World Domain Specific Languages Workshop, RWDSL@CGO 2018, Vienna, Austria, 24–24 February 2018, pp. 4:1–4:11. ACM (2018)
Lassen, K.B., van der Aalst, W.M.P.: Complexity metrics for workflow nets. Inf. Softw. Technol. 51(3), 610–626 (2009)
Naus, N., Jeuring, J.: Building a generic feedback system for rule-based problems. In: Van Horn, D., Hughes, J. (eds.) TFP 2016. LNCS, vol. 10447, pp. 172–191. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-14805-8_10
Naus, N., Steenvoorden, T., Klinik, M.: A symbolic execution semantics for tophat. In: IFL 2019 (accepted for publication) (2019)
Paquette, L., Lebeau, J.-F., Beaulieu, G., Mayers, A.: Automating next-step hints generation using ASTUS. In: Cerri, S.A., Clancey, W.J., Papadourakis, G., Panourgia, K. (eds.) ITS 2012. LNCS, vol. 7315, pp. 201–211. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30950-2_26
Plasmeijer, R., van Eekelen, M., van Groningen, J.: Clean language report version 2.1 (2002)
Plasmeijer, R., Lijnse, B., Michels, S., Achten, P., Koopman, P.W.M.: Task-oriented programming in a pure functional language. In: Principles and Practice of Declarative Programming, PPDP 2012, Leuven, Belgium, 19–21 September 2012, pp. 195–206 (2012)
Steenvoorden, T., Naus, N., Klinik, M.: Tophat: a formal foundation for task-oriented programming. In: Proceedings of the 21st International Symposium on Principles and Practice of Programming Languages, PPDP 2019, Porto, Portugal, 7–9 October 2019, pp. 17:1–17:13 (2019)
Stutterheim, J., Achten, P., Plasmeijer, R.: Maintaining separation of concerns through task oriented software development. In: Wang, M., Owens, S. (eds.) TFP 2017. LNCS, vol. 10788, pp. 19–38. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89719-6_2
Stutterheim, J., Plasmeijer, R., Achten, P.: Tonic: an infrastructure to graphically represent the definition and behaviour of tasks. In: Hage, J., McCarthy, J. (eds.) TFP 2014. LNCS, vol. 8843, pp. 122–141. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-14675-1_8
Acknowledgements
This research is supported by the Dutch Technology Foundation STW, which is part of the Netherlands Organisation for Scientific Research (NWO), and which is partly funded by the Ministry of Economic Affairs.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Naus, N., Steenvoorden, T. (2020). Generating Next Step Hints for Task Oriented Programs Using Symbolic Execution. In: Byrski, A., Hughes, J. (eds) Trends in Functional Programming. TFP 2020. Lecture Notes in Computer Science(), vol 12222. Springer, Cham. https://doi.org/10.1007/978-3-030-57761-2_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-57761-2_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-57760-5
Online ISBN: 978-3-030-57761-2
eBook Packages: Computer ScienceComputer Science (R0)





 , called
, called
 , based on a previously presented symbolic semantics.
, based on a previously presented symbolic semantics. to be correct for sequential inputs.
to be correct for sequential inputs. programs to accommodate above proof.
programs to accommodate above proof. systems automatically generate user interfaces and manage persistent storage of information.
systems automatically generate user interfaces and manage persistent storage of information. Valued editor.
Valued editor. Unvalued editor.
Unvalued editor. Shared editor.
Shared editor. Step.
Step. User Step.
User Step. Pair.
Pair. Choice.
Choice. User choice.
User choice.
 gets the value of t,
gets the value of t,
 observes if it is unsafe to step to t. Note that
observes if it is unsafe to step to t. Note that
 is a partial function.
is a partial function.

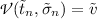 ;
;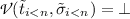 ;
; is the concatenation of all symbolic inputs generated along the way;
is the concatenation of all symbolic inputs generated along the way; .
.
 ) to confirm they installed the solar panels.
) to confirm they installed the solar panels.
 ; and
; and .
.
 ; the second branch, entering the invoice date, is denoted by
; the second branch, entering the invoice date, is denoted by
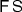 ; and the third branch, making a left/right choice, is denoted by
; and the third branch, making a left/right choice, is denoted by
 .
. . The action
. The action
 means pushing the continue button.
means pushing the continue button.