Forest Applications

Abstract

The application of polarimetric Synthetic Aperture Radar (SAR) to forest observation for mapping, classification and parameter estimation (especially biomass) has a relatively long history. The radar penetration through forest volume, and hence the multi-layer nature of scattering models, make fully polarimetric data the observation space enabling a robust and full inversion of such models. A critical advance came with the introduction of polarimetric SAR interferometry, where polarimetry provides the parameter diversity, while the interferometric baseline proves a user-defined entropy control as well as spatial separation of scattering components, together with their location in the third dimension (height). Finally, the availability of multiple baselines leads to the full 3-D imaging of forest volumes through TomoSAR, the quality of which is again greatly enhanced by the inclusion of polarimetry. The objective of this Chapter is to review applications of SAR polarimetry, polarimetric interferometry and tomography to forest mapping and classification, height estimation, 3-D structure characterization and biomass estimation. This review includes not only models and algorithms, but it also contains a large number of experimental results in different test sites and forest types, and from airborne and space borne SAR data at different frequencies.

2.1 Introduction

The application of radar polarimetry to forestry has a long history. Ever since the earliest days of airborne data trials with the JPL-AIRSAR system it was realized that forest scattering at microwave frequencies generates more linear cross-polarization (HV) than non-forest (especially at lower radar frequencies such as P- and L- bands). Since then, various groups have attempted to develop algorithms for the generation of imaging radar products based on forest mapping, classification and parameter estimation (especially biomass) requirements.

It was also quickly realized that improved products were obtained by using fully coherent scattering matrix or quad-pol PolSAR systems. These then allow the application of target decomposition and multivariate classification techniques accounting not only for backscatter amplitude and ratios, but also for phase and coherence statistics. The physics behind these techniques is based on the idea that there is significant forest penetration of microwave radiation, even to the surface layer under the forest, and hence multi-layer scattering theories are required to properly interpret the signatures. These multi-layer approaches in turn require multiple parameters for model based estimation and inversion and the use of quadpol data allows much more robust inversion of such models, providing as it does a wider set of observables than classical single or even dual-pol radars.

Still there remained a problem unique to forestry, namely high scattering entropy due to the complexity of the random media scattering environment generated by forests. This inevitably leads to lower accuracy and poorer resolution products. A significant advance therefore came with realization that lower entropy scattering could be obtained for forests by combining polarimetry with interferometry for PolInSAR. Here polarimetry provides again the parameter diversity, with the interferometric baseline now providing a user defined entropy control as well as spatial separation of scattering components.

This concept has also recently been extended to consider multiple baselines for multibaseline PolInSAR, which in the limit leads to 3-D imaging of forests through TomoSAR, while for limited baselines offers band-limited 3-D imaging, the quality of which is again greatly enhanced by the inclusion of polarimetry. This technology has now matured to the stage where several important products (especially forest height and vertical structure) can be accurately obtained at high spatial resolutions and with wide continuous coverage. Since 2006, with the launch of ALOS-PALSAR, such quad-pol capabilities have been available routinely from space imaging radars, enabling important developments in product maturity, as well as opening new possibilities by using time series analysis to capture dynamic changes in forests. A general classification of the applications is reported in Table 2.1.

Table 2.1 Remote sensing applications on forestry

2.2 Forest Classification

2.2.1 Land Cover Classification in Tropical Lands Using PolSAR

2.2.1.1 Introduction, Motivation and Literature Review

Recent radar space borne systems, like the C-band ENVISAT-ASAR, the C-band RADARSAT and the L-band ALOS-PALSAR systems, offer unique possibilities of mapping and monitoring the tropical forest, usually covered by clouds. Nevertheless it is still not clear which are the advantages of complex fully polarimetric systems over simple single or double polarized systems for certain applications. Also the specific use of frequencies and frequency combinations is still unclear: long radar wavelength like at L- and P- bands could add information to the short wavelengths at C- and X- bands due to the different scattering mechanisms involved in the wave interactions with the forest, the difference in canopy penetration, improving the classification of land cover classes or forest types.

Polarimetric radar classification simulations gave in the past insights into the accuracy of using certain band/polarization combination for land cover, forest type and biomass mapping (Hoekman and Quiñones 2000, 2002; Quiñones 2002). Nevertheless this information needed to be recreated on the frame of recent versatile, robust and computational efficient algorithms that can be applied over polarimetric and multi-frequency space borne data. In this Section, a pixel based unsupervised classification technique, developed in Hoekman et al. (2011), is used as a research tool to evaluate the NASA’s AIRSAR, C-, L- and P-band radar data acquired in 1993 over the Guaviare site in the Colombian Amazon. A polarimetric decomposition algorithm, that preserves the full polarimetric information content into six different radar intensities is used. Results give indication on the added valued of certain frequency and polarization combination in a tropical land. The robustness of the algorithm is further demonstrated by its applications to fine beam dual-pol (FBD) L-band HH/HV and wide beam (WB) L-band HH ALOS-PALSAR data in central Kalimantan.

2.2.1.2 Methodology

Classification accuracy results from unsupervised segmentations applied to different combinations of polarimetric C, L and P band data are used to evaluate the possible radar band combinations useful for tropical forest monitoring and mapping. Use is made of the unsupervised fully polarimetric SAR segmentation tool developed in Hoekman et al. (2011). The unsupervised approach consists of six processing steps extensively explained in Hoekman and Vissers (2003). The first step is a mathematical data transform which allows polarimetric data, without loss of any information, to be written in a form where classes are well approximated by multivariate normal distributions. This transform allows application of a wide class of mature image processing algorithms to polarimetric data, including unsupervised data clustering. The second step relates to unsupervised clustering encompassing a simple region-growing segmentation (incomplete and over-segmented), followed by model-based agglomerative clustering (Step 3), and expectation-maximization on the pixels of these segments (Step 4). Classification is achieved by Markov random field filtering on the original data (Step 5). The result is a series of segmented maps, which differ in the number of (unsupervised) classes.

For the analysis of the results three different accuracy percentages are used as indicators of the performance of a particular polarization/frequency combination in the classification of the four cover types. The first is the overall classification accuracy, calculated as the percentage of right and wrong classified pixels for all the classes, for a particular polarization/frequency combination. A Kappa statistic ($\hat{K}$) was computed to evaluate significant differences between any pair of classification results (Lillesand and Kiefer 1994). A test statistic $\Delta \hat{K}$ can be calculated as:

$$ \Delta \hat{K}=\frac{\left|{\hat{K}}_1-{\hat{K}}_2\right|}{\sqrt{{\hat{\sigma}}_{\infty}^2\left[{\hat{K}}_1\right]+{\hat{\sigma}}_{\infty}^2\left[{\hat{K}}_2\right]}} $$

(2.1)

where ${\hat{\sigma}}_{\infty}^2\left[\hat{K}\right]$ is the approximate large sample variance of $\hat{K}$. At the 95% confidence level two results may be considered significantly different if $\Delta \hat{K}>1.96$ (Benson and De Gloria 1985).

The second accuracy percentage is the users classification accuracy that indicates the percentages of pixels classified in a certain class given that the pixel was label into that class. This particular indicator is useful to evaluate the capacity of a certain combination to classify a class.

The third indicator is the percentage of confusion between two particular land cover types in the absence of other classes. This indicator is of particular interest for the evaluation of possible monitoring scenarios in a changing tropical forest. Monitoring scenarios are defined as the capacity to differentiate processes like deforestation, forest degradation and forest regeneration as explained in Hoekman and Quiñones (2000).

2.2.1.3 Experimental Results

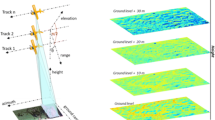
Test sites and corresponding radar and validation data sets selected for the generation of showcases on land cover classification in tropical lands are summarized in Table 2.2 and further described in Appendix A. Figure 2.1 shows an overview of the radar data.

Table 2.2 Test sites and corresponding radar and validation data selected for the generation of showcases on land cover classification

Fig. 2.1

Total power image of the P-, L- and C-band AIRSAR data, in the 45°–50° incidence angle range, over the Guaviare study site. Photographs illustrate the four vegetation cover types in this study. Polygons digitized over the visited field locations for all the four cover types are illustrated: (1) primary forest (red): 27 polygons (4983 pixels); (2) secondary forest (blue): 49 polygons (4004 pixels); (3) recently deforested areas (green): 30 polygons (2878 pixels); and (4) grasslands (white): 18 polygons (4046 pixels)

Fully polarimetric target properties for uniform distributed scatterers can be described by nine single-pol radar intensities as introduced in Hoekman and Vissers (2003). For the AIRSAR data the Stokes scattering operator matrix was set to zero for the four ‘asymmetric’ elements of the covariance matrix. For that reason it is assumed that the objects display azimuthal symmetry and that the asymmetrical information may be discarded. In this case the case of azimuthal symmetry (Freeman 1999) the covariance matrix simplifies to.

$$ {\mathbf{C}}_r=\left(\begin{array}{ccc}\left\langle {S}_{hh}{S}_{hh}^{\ast}\right\rangle & 0& \left\langle {S}_{hh}{S}_{vv}^{\ast}\right\rangle \\ {}0& \left\langle {S}_{hv}{S}_{hv}^{\ast}\right\rangle & 0\\ {}\left\langle {S}_{vv}{S}_{hh}^{\ast}\right\rangle & 0& \left\langle {S}_{vv}{S}_{vv}^{\ast}\right\rangle \end{array}\right) $$

(2.2)

In the intensity representation introduced in Hoekman and Vissers (2003) it is possible to find several sets of 5 independent intensity values containing this and only symmetrical information. At least one (non-redundant) possibility is needed to represent the polarimetric data. A selection of 6 intensities were made using the conjugated Real and Imaginary parts of the HH-VV phase differences as follows:

(2.3)

Intensity images created for the C-, L-, and P-band data are shown in Fig. 2.2.

Fig. 2.2

Intensity images derived from the C-, L-, and P-band AIRSAR polarimetric decompositions into intensity images. Horizontal (h), vertical (v), left circular (l), right circular (r), 45° linear (p) and −45° linear (m)

For each single frequency, comparisons were made between the combinations of dual-like polarizations (HH/VV), three linear polarizations (HH/VV/HV) and all 6 intensity polarizations (Pol-6i) containing the polarimetric information (HH/VV/HV/MR/PL/PM). For the comparison between multi-frequency data, combinations where made using two and three frequencies (C-L), (L-P), (C-L-P) with three linear polarizations (HH/VV/HV) and with all polarimetric data per frequency (HH/VV/HV/MR/PL/PM). Figure 2.3 shows the classification result from the unsupervised segmentation using different combinations. Table 2.3 shows all three accuracy percentages calculated for the studied frequency/polarizations combinations. Low overall classification accuracies and low users accuracy per class were found for all C-band combinations and for L- and P-band dual-pol (HH/VV)/single frequency combinations. High confusion between classes was also found for these channel combinations. For both L- and P-band the results by adding the HV channel to the dual-pol (HH/VV) were significantly higher (94.5% to 85.5%, for L-band and 93.5% to 61.2% for P-band, respectively) and improved both the users accuracy per class and the confusion between classes especially between primary and secondary forest and primary and recently cut areas in both cases. When these classes are confused the particular combination will not addressed the monitoring scenarios for detection of forest regeneration or deforestation processes, at least using only single-date data. The addition of HV polarization to the dual-pol (HH/VV) data, have significant impact on the classification accuracy for both L- and P-band data.

Fig. 2.3

A 400 × 400 pixels window, classification maps resulting from the unsupervised segmentation of images when using different frequency/polarization combinations. (1) primary forest (green); (2) secondary forest (yellow); (3) recently deforested areas (red); and (4) grasslands (blue). In the top left corner, a total power image is shown with some of the validation polygons that have been used as a reference to evaluate the results

Table 2.3 Accuracy classification results for different polarization combinations for all AIRSAR channels studied

The addition of polarimetric (Pol-6i) data to the three polarization (HH/VV/HV) combinations decreases the overall classification accuracy and in most of the cases increases the confusion between primary and secondary forest. In general the confusion between classes is below 10%, for all the land cover pairs, when using L- (HH/VV/HV) or P- (HH/VV/HV) and P- (Pol-6i) combinations. When comparing the results produced by the L- and the P-band combinations there are no significant differences in the results, meaning that both single L- or P- band data (HH/HV/VV) or (Pol-6i) are very good to assess the monitoring scenarios. All overall accuracies are above 90% for the frequency/polarizations combination. For the two frequencies combinations, the accuracy results of the C-L combination (91.5% and 91.7%) are significantly lower than the combinations of the L-P combinations (96.2% and 98%) for (HH/VV/HV) and (Pol-6i) respectively. Lower percentages when using C-band are explained by the relatively lower “user’s accuracy” classification results, for primary and secondary forest and the high confusion found between these same classes.

The combination of C-L-P (HH/VV/HV) and L-P (Pol-6i) were not significantly different from each other. These combinations also show high users accuracy for all the classes and low confusion percentages between all pairs of cover types, addressing all the monitoring scenarios.

2.2.1.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

Most of the classifications for the combinations involving C-band channels appear to be very irregular affecting the accuracy results. The low classification accuracies and the high confusion between classes, found when using the C-band single frequency combinations and the C-L multi-frequency combinations are obviously suffering from the effect of rough texture in the C-band images (high variance between neighboring pixels) due to the higher resolution of the C-band channels and also by the direct scattering occurring between the short C-band waves with the leaves and branches of the rough canopy of the primary forest and secondary vegetation. On the other hand, the results involving C-band channels are also affected by the nature of the classification algorithm and the application of the Markov random field filter to the segmentation procedure. When there is much variance between neighbors the classification of a pixel might be more affected by system filter parameters than for channels with less texture.

For combinations involving L- and P-band channels the classifications are smoother and borders are better defined. Classification accuracy results are higher, which might be explained by the physical interactions, mostly double bounces and volume scattering, occurring between the longer wavelengths and the larger scatterers in this land cover classes. These frequencies are more sensitive to contrasting vegetation structure as is the case by the cover types selected for this study.

The use of polarimetric data for both single frequency and multi frequency combinations, for the L- and P-band channels, did not add significant information compared to the (HH/VV/HV) combinations. For this contrasting vegetation structures polarimetric information is of no need, but might be of relevance for other applications like forest type mapping (Quiñones 2002).

In general, for addressing the monitoring scenarios in the tropical forest when using the land cover classes used in this study, the L- and P-band linear polarizations (HH/VV/HV) appear to be suitable, and there is no evidence that could show that any of this two frequencies should be preferred over the other.

What is certainly clear is that the use of only two like polarizations for the L and P band was not enough to differentiate this land cover classes and not good enough to address the monitoring scenarios in this study. The use of HV polarization significantly improved the overall classification accuracies and decreased the confusion between the cover classes. At that respect, the assessment of dual polarizations involving cross-polarized data (HV) is of interest for future studies.

With the launch of polarimetric space borne SAR systems like RADARSAT-2 (C-band) in December 2007 and ALOS-PALSAR (L-band) in January 2006, the need for simple, robust and accurate polarimetric classification and biophysical parameter estimation algorithms for monitoring applications and research is of great importance. Ideally, algorithms should be sufficiently versatile to handle multi-band, multi-polarization, multi-date and/or multi-sensor data sets. Moreover, it would be an important asset when algorithms could deal with situations were ground truth is sparse or incomplete. Combination of unsupervised with supervised approaches increases the accuracies of the classification as shown in Cao et al. (2010) so the possibility of using unsupervised segmentation algorithm as supervised segmentation procedure when classes are already being statistically described and labelled is very useful.

The current segmentation methodology applied for mapping and monitoring of tropical forest allows all the above mention possibilities. Until now, it is being extensively tested over images of the L-band WB and FBD-FBS ALOS-PALSAR, and C-band ENVISAT-ASAR and RADARSAT. Some issues surrounding the application of the current algorithm, to these space borne images, are related to speckle and image texture. The use of a Markov random field filter in the classification procedure helps to overcome partly the effect of speckle, nevertheless it is being demonstrated that filtering of radar images previous segmentation can help in the better statistical definition of classes and in the final classification results. In addition, the use of the current algorithms in the high resolution RADARSAT-2 and (X-band) TerraSAR-X images can create very blurry classifications and re-sampling of the data is necessary before getting reasonable results. Also regarding the legend development process, the field information is still necessary and the interpretation of the radar signatures can be of great complexity. Nevertheless several maps have been created using this algorithm (Hoekman et al. 2010). An example is a forest type map created for an ecologically complex area in Central Kalimantan. This map was created using a combination of space borne WB (HH) and FBD (HV/HH) polarizations for 2 years of ALOS-PALSAR acquisitions. The results are reported in Fig. 2.4. The overall classification accuracy calculated for the map is of 84% for 17 different vegetation cover types. This methodology has proven to be very robust to noise/outliers and overlapping clusters, is reasonably fast and is suitable for moderate to large images.

Fig. 2.4

Land cover Map (right|) created using a combination of WB and FBD- L-band ALOS-PALSAR data (left). Accuracy assessment was done using field photographs taken on the points over long transects in the study area (centre). Calculated accuracy 84% for 17 classes

2.2.2 Forest Mapping and Classification Using Polarimetric and Interferometric Data

2.2.2.1 Introduction, Motivation and Literature Review

Forest remote sensing from SAR data has been intensively studied during the last 15 years. Various types of SAR data (single-, dual- and quad-pol, single- or multi-frequency) acquired in multi-temporal, multi-angular or interferometric modes were used to retrieve geophysical property estimates. All these studies demonstrated that SAR quantities (intensity, phase, correlation, coherence…) show particular behaviors over forested areas and may be used for classification purposes. Forest classification may be split into two complementary applications requiring different levels of accuracy and processing complexity:

• forest area mapping, which consists in delimiting the extent of forested areas within a SAR image;

• discrimination of vegetation categories, which aims to separate pixels belonging to different types of vegetated media.

This Section proposes to gather complementary aspects of polarimetric and interferometric data processing techniques to improve forest mapping and classification performance. If SAR polarimetry is particularly well adapted to the analysis and description of scattering mechanisms, and hence may be used to discriminate different environments, it is well known that PolSAR parameters tend to saturate over volumetric media with highly random response, like dense forest observed at L band or at higher carrier frequency. Oppositely, interferometric SAR measurements permit to further investigate volumetric media properties but suffer from a lack of contrast over areas showing more polarimetrically deterministic responses like agricultural fields and open surfaces.

This Section proposes simple processing schemes, based on both SAR signal statistical properties and physical interpretations of wave scattering, that combine PolSAR and PolInSAR analysis techniques into hierarchical, supervised or unsupervised classification approaches. It is shown that forest mapping can be performed efficiently using PolSAR data processing and that refined segmentation results may be obtained by including POLinSAR information. Forest category identification is, in general, a significantly more complex task, since classical SAR indicators like reflectivity, or usual polarimetric parameters, can reveal highly misleading in the frame of forest classification, due to their saturation or high correlation with factors unrelated to the tree species under observation. As it is related hereafter, this serious limitation may be overcome by dealing with intrinsic PolInSAR parameters, that do not depend on forest radiometry and that are less affected by saturation effects.

Many studies report that SAR backscatter intensity value depends, up to a certain extent, on forest bio and geo-physical properties such as biomass, tree age (Lee et al. 2002). Nevertheless, high performance mapping or classification of forested areas can generally not be achieved by thresholding backscattered intensity due to the large variability of SAR image information. Single polarization data-based mapping techniques generally use additional modes of diversity, like texture (De Grandi et al. 2000; Wegmüller and Werner 1995), or time (seasonal variations, stability) (Grover et al. 1999; Lee et al. 1999; Paloscia et al. 1999). Partially or fully polarimetric SAR data may also be used to map forests, using cross-pol ratios or co-pol correlation (Hoekman and Quiñones 2000; Hoekman and Varekamp 2001) and combined with multi-frequency measurements (mainly P-, L- and C-bands) (Quegan et al. 2000; Ranson and Sun 1994; Ranson et al. 1995). However, the robustness of such supervised approaches has to be tempered by considering repeatability and generalization issues related to uncontrolled variations of polarimetric scattering patterns with time (year, season, month or even days) or depending on the geographical location or the investigated area (Ranson and Sun 1994; Le Toan et al. 2001; Cloude and Pottier 1997).

Unsupervised PolSAR approaches, related to the decomposition of polarimetric covariance matrices may be employed to determine the presence of forest from an interpretation of polarimetric scattering mechanisms (Le Toan et al. 2001; Cloude and Pottier 1997; Durden et al. 1989; Ferro-Famil et al. 2001, 2006). Such methods may meet some limitations over complex areas that cannot be separated from forests based on PolSAR information only (Ferro-Famil et al. 2003; Freeman and Durden 1998; Kurvonen and Hallikainen 1999). Single polarization interferometric coherence may be used to map forested areas (Askne et al. 1997; Dammert et al. 1999; Engdahl and Hyyppä 2003; Rignot et al. 1994a), but such techniques have to deal with exterior factors such as the spatial/temporal baselines compromises, forest density and topography that may affect the mapping accuracy and reliability. Finally, complementary aspects of both polarimetric and interferometric diversity modes may be combined in order to overcome intrinsic issues of each separate mode, and provide more reliable and accurate mapping results (Ferro-Famil et al. 2006).

An important number of studies have been led to discriminate different types of forest from single polarization SAR data (Dobson et al. 1996). Similarly to forest mapping applications, reasonable classification rates may be reached with supervised algorithms, particularly well adapted to one site or type of vegetation, but a systematic implementation may meet some problems of generalization, due to temporal variations and saturation of the basckscattered intensity (Lee et al. 2002; Hyypa et al. 1997; Mougin et al. 1999). The use of fully polarimetric and/or multifrequency data permit to further discriminate a large range of natural media (Hoekman and Quiñones 2000, 2002; Hoekman and Varekamp 2001; Ranson et al. 1995; Dobson et al. 1992) using supervised hierarchical classifiers, multi-frequency polarimetric acquisitions (Hoekman and Quiñones 2002; Dobson et al. 1992; Ferrazzoli et al. 1997; Hagberg et al. 1995), model-based approaches (Hoekman and Quiñones 2000; Hoekman and Varekamp 2001; Ranson and Sun 1994; Lombardo and Macrì Pellizzeri 2002), or directly based on polarimetric measurements (Ranson et al. 1995) or on pre-processed polarimetric indicators, such as polarimetric decompositions results (Ferro-Famil et al. 2001; Kurvonen and Hallikainen 1999). One has to note that parameter saturation over forested areas may affect polarimetric indicators too and may then limit the performance of all the classification approaches mentioned above. Radar interferometry is an efficient tool for forest observation (Grover et al. 1999) and may overcome limitations due to polarimetric scattering coefficient saturation. Interferometric classification approaches generally rely on the modeling of SAR measurement coherence and an interpretation of its relation to the observed media nature and geophysical characteristics (Askne et al. 1997, 2003; Eriksson et al. 2003a; Imhoff 1995a; Strozzi et al. 2000; Van Zyl 1993; Wegmüller and Werner 1997). Statistical segmentation procedures adapted to inSAR data sets have been developed as well (Dammert et al. 1999; Engdahl and Hyyppä 2003; Rignot et al. 1994a). Interferometry based classification meet limitations similar to those enounced in the case of forest mapping, mainly linked to temporal-spatial baselines, topography and to the lack of polarimetric diversity. Quad polarization interferometric data, Pol-In-SAR, based classification is a powerful alternative to multi-frequency data processing. The interpretation of this high-dimensional information by the way of optimisation procedures permits to isolate different kinds of forested areas and constitutes a good solution to forest classification (Ferro-Famil et al. 2006). The introduction of joint polarimetric and interferometric information in an unsupervised classification scheme has shown the complementarity of both data types permits to discriminate refined features that cannot be observed from separate analysis (Ferro-Famil et al. 2003). The use of polarimetric interferometric representation statistics, derived in Ferro-Famil and Neumann (2008), in the frame of already existing robust and powerful supervised/unsupervised classification algorithms (Ferro-Famil et al. 2006, 2003; Kurvonen and Hallikainen 1999), permit to reach higher levels of performance and robustness over a wide range of vegetation types (Ferro-Famil et al. 2006).

2.2.2.2 Methodology

The employed methodology for unsupervised forest mapping is illustrated in Fig. 2.5. The PolSAR image is first segmented using the Wishart $H/A/\overline{\alpha}$ statistical segmentation technique. An identification of basic scattering mechanisms is then run over each pixel of the image, from specific polarimetric indicators derived from the eigenvector decomposition of coherency matrices, as described in Ferro-Famil et al. (2003): according to the number of scattering mechanisms detected within pixel using the H and A parameters, specific procedures are run to assign the pixel under observation to the volume diffusion, single- or bouble-bounce class. In order to reduce the random aspect of the mapping and increase its robustness with respect to arbitrarily fixed decision boundaries, a global decision is taken over statistically compact clusters obtained from the Wishart $H/A/\overline{\alpha}$ segmentation using a winner-takes-all decision strategy. As mentioned earlier, such a mapping approach may lead to some false alarms over complex and dense volumetric areas, like urban environments observed at L-band, and PolInSAR coherence optimization may be used to refine the PolSAR map. Parameters built from the PolInSAR optimal coherence set are used to determine the number of coherent scattering mechanisms from which is derived an indicator of the level of volumetric scattering. This information is then combined with the PolSAR result in order to obtain a refined forest map (Ferro-Famil et al. 2003, 2006).

Fig. 2.5

Synopsis of the unsupervised forest mapping approach

Forest classification is performed here as a statistical supervised process which comprises two stages: a learning phase during which user-selected groups of data are used to learn the statistics of the different classes to be discriminated, and a classification phase which assigns a class label to each pixel on an image according to a statistical metric or to a specific decision rule whose parameters have been learned during the preceding phase. Here again, the random aspect of classification results may be reduced by taking global decisions over statistically compact clusters obtained from an unsupervised segmentation map.

This Section compares results obtained using the whole PolInSAR information, i.e. statistics of the (6 × 6) coherency matrix, or using reduced but more robust information consisting of the three optimal PolInSAR coherences.

2.2.2.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on forest mapping and classifications are summarized in Table 2.4 and further described in the Appendix.

Table 2.4 Test sites and corresponding radar and validation data selected for the generation of showcases on forest classification

The complexity of the SAR scene over the Traunstein forest may be appreciated from the Pauli color-coded image shown in Fig. 2.6. This site is composed of forested areas, pasture fields with scattered farms and isolated buildings and an urban area at the center left part of the image. The unsupervised Wishart classification given in Fig. 2.6 provides some useful indications on the PolSAR properties of this data set:

• the different types of environments cannot be separated using their PolSAR statistics since many classes are spread over the whole image;

• one may observe a clear distribution of the classes in the range direction, related to the dependency of the backscattered intensity on the incidence angle, and to the predominance of the span over other polarimetric indicators. This aspect may be highly limiting for discriminating media located at different range positions.

Fig. 2.6

Left: Pauli color-coded image of the Traustein site; right: result of the unsupervised PolSAR Wishart classification into 16 classes

Classification results shown in Figs. 2.6 and 2.7 indicate that PolInSAR data sets can be efficiently used in a supervised way to discriminate between different forest species and grow states or between different levels of biomass. The principal basic features of the ground information can be retrieved in the classification results whose spatial distribution is more heterogeneous than the provided reference map. This variability is mainly due to the fact that ground information is generally delivered under the highly simplified form of compact and homogeneous clusters, whereas forest stands are in general not homogeneous. A qualitative comparison between the ground information map and an aerial photograph revealed that some areas, considered as homogeneous in the ground maps, could indeed contain zones with varying tree densities, forest paths, clear cuts etc. On the other hand, some specific forest parcels belonging to slightly different types or having close biomasses may have very close PolInSAR responses that cannot be discriminated using statistical or hierarchical approaches. The overall performance of the biomass classification approach was evaluated over trusty locations, in terms of homogeneity, and a correct classification rate higher than 75% was found. The classification of forest type and growth states led to slightly lower rates.

Fig. 2.7

Left: simplified forest biomass map, where medium biomass (B) means 200 t/ha < B ≤ 310 t/ha; right: biomass classification result

As it has been mentioned earlier, single-pol techniques are mentioned in the literature for forest mapping and classification in the frame of marginal approaches, mainly based on texture and temporal analysis, in order to investigate the potential of existing spaceborne data sets for such applications. As reported in many studies, single polarization SAR data acquired at high frequency (L-band and higher) cannot be used in a robust way for mapping and classifying forested areas in general configurations, i.e. without a large amount of a priori information. The use of dual-pol data is not recommended either, due to the fact that the cross-pol HV channel is essential for accurately mapping and discriminating volumetric media with different physical features. Being this channel uncorrelated with other co-polarized measurements over the major part of natural environments, volumes and surfaces, a (2 × 2) co- and cross-pol covariance matrix would not bring sufficient information for applying the technique proposed here. A co-pol covariance matrix, e.g. built from the HH and VV channels, can be used for forest mapping through the analysis of its eigenvalues, but with a significant loss of performance and additional ambiguities compared with the fully polarimetric case. Such a configuration leads to a significant reduction of the contrast between the elements of the optimal PolInSAR coherence set involving a severe loss of performance for classifying different types of forested areas or different levels of biomass.

The following comparison aims to show that over forested areas, single image polarimetry, i.e. classical SAR polarimetry, can be highly misleading for characterizing dense volumetric environments at L-band. This fact is due to the saturation of the polarimetric response, i.e. the covariance matrix tends to be proportional to the identity matrix, which strongly limits the potential of analysis of polarimetry and to the high dependence of the backscattered energy, i.e. the polarimetric span, on the scene geometry in general and the local incidence angle in particular. As one may note in Fig. 2.8, classification results obtained from PolSAR only data are largely influenced by the spatial distribution of the backscattered intensity over the whole scene, which may be appreciated over the Pauli color-coded image displayed in Fig. 2.6. Due to its interferometric aspect, PolInSAR-based technique permits to overcome this saturation effect. Being based on the statistics of span-independent quantities, it presents greatly enhanced features, whose distribution is tightly linked to the kind of forest under observation and not the angular dependence of the span.

Fig. 2.8

Forest type classification results. Left: using the Wishart statistics of the PolSAR coherency matrix T; mid: reference map; right: using the proposed PolInSAR approach

Another illustration of this effect is given in Fig. 2.9 where classification results, obtained using the Wishart statistics of the full PolInSAR coherency matrix, are compared for various temporal and spatial baselines. The Wishart PolInSAR classifier output maps are quasi-insensitive to the level of interferometric correlation between the images. This observation shows that the volumetric analysis through interferometric coherence properties play a very little role during the classification, whereas the PolSAR part, saturated and strongly influenced by the span, predominates, leading to classification results poorly related to forest properties and perturbed by the scene topography or the acquisition geometry. Oppositely, the proposed approach, based on the statistics of the optimal coherence set, fully exploits the relative interferometric coherence information, and for a correct spatial and temporal configuration, provides results intrinsically related to forest properties and less affected by potential changes of incidence angle.

Fig. 2.9

Biomass classification using various temporal (B_t) and spatial (B_s) baseline configurations. Legend as in Fig. 2.7. Color coded images of the optimal Pol-inSAR coherence set are given (central panel). Results obtained using the statistics of the full PolInSAR coherency matrix are plotted in the top panel, and the ones obtained by using the statistics of the optimal PolInSAR coherence set are in the bottom panel

2.2.2.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

Polarimetry plays a key role for applications related to forest mapping or classification using SAR images. Despite the fact that single polarization intensity value depends, up to a certain extent, on forest geophysical properties such as biomass or tree age, high performance mapping or classification of forested areas can generally not be achieved by thresholding backscattered intensity due to the large variability of SAR image information, to the potentially important influence of factors related to the scene topography or to the acquisition geometry, and to the saturation of the relation relating intensity to biomass at L- or higher frequency bands.

SAR polarimetry offers the possibility to measure this saturation from indicators related to the number of effective scattering mechanisms estimated within each pixel. Media with a polarimetrically saturated responses are associated to complex volumes, hence to forests. Such an approach works well over most environments, but may lead to false alarms over highly heterogeneous zones, mainly urban areas. This problem may be overcome by further measuring the presence of dense volume using PolInSAR parameters. Here again, polarization plays an essential role as it permits to separate media whose interferometric coherence may vary depending on the chosen polarimetric channel.

Due to the saturation of the polarimetric response of an environment in the presence of volume, classical SAR polarimetry, i.e. based on a single PolSAR image, cannot be used to classify forested areas with a sufficient accuracy, and one has to use PolInSAR data sets. However, this showcase clearly demonstrates that using the whole PolInSAR information for classifying forested areas can be counter-productive, as a significant part of this information can be dominated by factors unrelated to the nature of biomass features of the observed forest. Instead, using a set of elaborated parameters that concentrates the relative part of the PolInSAR information provides interesting results and limits the effects of artefacts encountered with usual or direct approaches.

In conclusion, polarimetry represents a very useful and efficient mode of diversity for forest mapping and classification, and needs to be coupled to interferometric measurements for characterizing complex volumetric environments. Pre-processing steps, aiming to separate sources of potential perturbations, linked to the acquisition geometry or other parameters unrelated to forest from the useful part of the signal should be implemented.

2.2.3 Detection of Fire Scars

2.2.3.1 Introduction, Motivation and Literature Review

Canada is home to 10% of the world’s forests. Accounting of annual carbon emissions from forest fire events and monitoring changes in Canada’s forests are important activities at Natural Resources Canada (NRCan). In 2004, NRCan initiated a joint project between the Canadian Forest Service (CFS) and the Canada Centre for Remote Sensing (CCRS) to create a system, the Canadian Wildland Fire Information System (CWFIS), used to estimate direct carbon emissions from Canadian wildfires (Groot et al. 2007). Accurate knowledge of burned areas is required to produce burned area estimates at the national level for post fire mapping. Currently, optical remote sensors, like SPOT-VGT and Landsat, are used to map burned areas at low resolution (1 km) and high resolution (30 m) respectively. A final burned-area output is used as an input to the National Forest Carbon Monitoring, Accounting and Reporting System (NFCMARS) (Kurz and Apps 2006) to estimate national carbon emissions. However, for producing such burned area estimates, the earliest possible cloud-free satellite images are critical. Because of adverse weather, cloud and illumination conditions in the Canada North, the limitation of remote sensing images from these optical sensors is evident.

Advanced space-borne Synthetic Aperture Radar (SAR) systems, such as Japanese ALOS-PALSAR, the German TerraSAR-X, and the Canadian RADARSAT-2, can contribute specially to this estimation effort. Over previous sensors, these offer better spatial resolution, shorter revisiting times, availability of polarimetry, and all-weather data acquisition capability. Therefore, considerable polarimetric SAR research in forest applications has been conducted at CFS with support of the Canadian Space Agency (CSA) and NRCan. One of the motivations is to determine whether polarimetric SAR information can be used to detect fire scars effectively in forest lands and offer alternative to traditional sketch mapping methods and optical sensors.

Historic burned area estimates, created from sketch mapping from small planes, GPS mapping from helicopters, and photo interpretation (Fraser et al. 2000, 2004), are available from provincial and territorial forest fire agencies. Because the management and protection of these data resources fall under provincial and territorial jurisdiction, GIS wildfire polygon data varies in quality due to the limitations of the traditional GIS technologies available at the time. Several Canadian provinces maintain GIS wildfire polygon data for managed forests from the 1940s to the present day. Generally, the older the data the less reliable it becomes. Fire perimeters derived from these traditional methods often include unburned “islands” and may overestimate burned areas. Moreover, the distribution of remote wild fire events and environmental conditions make them a challenge to accurately map.

Research has been conducted in mapping forest fire scar using SAR, which can be used to provide measurements of post-fire ecosystem changes in forest structure, ground surface exposure and soil moisture patterns (Landry et al. 1995; Bourgeau-Chavez et al. 1997). In Bourgeau-Chavez’s studies based on radar backscatter analysis, he demonstrated that fire scars were detectable in a range of boreal ecosystems across the globe using C-band SAR and showed that the length of viewing time of fire scars with ERS or RADARSAT-1 data was between 3 and 7 years in Alaska and Canada (Bourgeau-Chavez et al. 2002).

In previous studies, it was discovered that, using the airborne Convair 580 C-band quad-pol data, it is possible to detect a historical fire scar, more than 50 years old, over our study site in Hinton, Alberta (Goodenough et al. 2006). Here, we focus on the detection of two roughly 9 years old fire scars, using ALOS-PALSAR L-band and RADARSAT-2 C-band quad-pol data data. The analysis includes data pre-processing, decomposition analysis and classification methodologies. The aim of the approach is to provide new fire-scar mapping methodologies from SAR quad-pol data in support of CWFIS and NFCMARS.

2.2.3.2 Methodology

Three techniques used to analyze space-borne quad-pol data for fire scar detection include polarimetric decomposition, scattering model, and classification. Decomposition approaches, such as the entropy-alpha decomposition (Cloude and Pottier 1997) and three component decomposition (Freeman and Durden 1998), provides various parameters showing different scattering characteristics of objects on the ground. Scattering model, such as the Oriented-Volume-over-Ground (OVOG) (Cloude 2009), estimates secondary parameters for volume and surface scattering components. The classification technique utilizes these scattering characteristics from the decomposition and modelling, performs image classification and extracts fire scars. Two latest classification methods employed here are a coherence-based geometrical detector described in Marino and Cloude (2010) and a data driven multi-dimensional clustering approach, i.e. the K-Nearest Neighbors (KNN) (Richardson et al. 2010).

Compact polarimetry (compact-pol) architecture is a new hybrid SAR mode and is proposed for the future Canadian RADARSAT Constellation Mission (RCM). The compact-pol mode transmits single circular polarization (left/right) and receives simultaneous coherent orthogonal linear polarizations. The advantages of this mode are wide-swath coherent polarimetric information, low data rate, and relatively simple transmitter architecture (Raney 2007). These advantages plus shorter satellite revisiting intervals are particularly attractive for forest applications. Therefore, it has become essential to quantitatively assess this new mode. RADARSAT-2 quad-pol data were used to simulate RCM compact-pol data and new compact-pol parameters using compact-pol decomposition theories were introduced (Cloude et al. 2012) to investigate whether the loss of information through the compact-pol projection affects the quality of detection of forest fire scars. A rule-based classifier based on the physical interpretation of the compact parameters was constructed. A detailed description of this classification approach is provided in Cloude et al. (2013).

2.2.3.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on fire scar detection are summarized in Table 2.5 and further described in the Appendix.

Table 2.5 Test sites and corresponding radar and validation data selected for the generation of showcases on fire scar detection

The L-band data set was first corrected for any Faraday rotation, a low frequency distortion arising from trans-ionospheric propagation from the satellite to the ground. Because all data sets provided were in single-look complex format, multi-looking in azimuth and range directions were performed to reduce speckle. Next, a box car filter was used to generate the 3 × 3 PolSAR coherency matrix. To further reduce topography relief effects on the polarimetric SAR data, polarization orientation shifts introduced by terrain slopes in the azimuth direction were detected and corrected to generate reflection symmetry in the coherency matrix of the polarimetric SAR data for the next stage of analysis.

The coherence-based geometrical detector was performed on the PALSAR quad-pol data over the Keg River site. Figure 2.10 is a Pauli RGB composite of the PALSAR scene. The variety of colours indicates the wide diversity of landcover types in this area. Figure 2.11 is the result of a fire scar coherence detector using a supervised approach, i.e. with training on a known fire scar region. Figure 2.12 is the result for an unsupervised fire scar detector, both of which showed good detection and low false alarm rates. Figure 2.13 illustrates the fire scar detection and clustering result from the KNN classification, using $H/A/\overline{\alpha}$ from the entropy-alpha decomposition as input. Both of the coherence-based detector and the KNN classifier showed very good fire scar results for the PALSAR L-band Keg River scene.

Fig. 2.10

Keg River, ALOS-PALSAR acquisition: Pauli RGB

Fig. 2.11

Keg River, ALOS-PALSAR acquisition: supervised coherence detector

Fig. 2.12

Keg River, ALOS-PALSAR acquisition: unsupervised coherence detector

Fig. 2.13

Keg River, ALOS-PALSAR acquisition: KNN (K = 55, 22 clusters)

A rule-based classifier was applied on simulated C-band compact-pol data with imagery dimension 29 km × 27 km, and the scene is shown in Fig.2.14. One issue was the temporal variability of the simulated compact data due to environmental changes. To avoid threshold values depending partly on the data set and meet the time-invariant classifier requirements, six simulated compact data sets in different seasons were combined to form a co-registered data stack. Each pixel was averaged in time across the whole stack to create a time averaged Stokes vector. Four decomposition parameters used for the rule-based classification were the compact minimum volume, the degree of polarization, the α-angle and the compact phase. Figure 2.15 is a pseudo colour classification map of the averaged compact data. The fire scars are dark grey areas and outlined by the GIS fire polygons (red). The output fire scars from the rule-based classification are shown in Fig. 2.16. In Bourgeau-Chavez et al. (2002), Bourgeau-Chavez showed that fire scars between 3 and 7 years in Alaska and Canada were detectable with ERS or RADARSAT-1 single polarization data. However, because their approach is a manual interpretation method based on the backscatter intensity, the accuracy of fire scar detection results were largely affected by human error, seasonal variations, topography effects, and environmental conditions.

Fig. 2.14

Keg River, RADARSAT-2 average acquisition: HH single-pol amplitude

Fig. 2.15

Keg River, RADARSAT-2 average acquisition: rule-based compact classification

Fig. 2.16

Keg River, RADARSAT-2 average acquisition: fire scar identification

In this Section, we demonstrated that the strong signature embedded in quad-pol SAR data provided much better capabilities for fire scar detection and monitoring. The fire scar detection results from quad-pol and simulated compact-pol data showed the improved mapping of historical fire scars in this age category. With such method, the fire scar detection now is much more reliant on polarization information, tolerant of topographic variations and robust to absolute changes in backscatter due to environmental conditions, which is complementary to optical remote sensing and current fire scar mapping techniques.

2.2.3.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

This Section focused on utilizing the phase information contained in polarimetric SAR data to increase the sensitivity of SAR measurement for scar identification. ALOS-PALSAR and RADARSAT-2 data were processed and analyzed over the study site in Keg River, Alberta. The results showed that it is feasible to clearly map historical fire scars of approximately 9 years of age with polarimetric SAR data from both sensors. The coherence-based geometrical detector and KNN classification results are encouraging, showing the potential and effectiveness of such methodology in segmenting and classifying polarimetric SAR data for fire scar detection.

Compact polarimetry provides a new wide-swath multi-channel coherent mode for radar imaging. However, the loss of information through projection and high entropy for vegetation scattering pose challenges for use in fire scar detection. Here, compact polarimetry decomposition and classification were employed. The degree of polarization, minimum-over-time-volume, and compact phase were very useful parameters for the rule-based classification, especially when supported by the α-angle. With carefully defined threshold values and the use of extended time series of simulated compact data, the historical fire scars in this study area were clearly detected. The false positives outside the fire scar region in simulated compact-pol data can be further reduced by using area filters. These results support the idea that, in absence of an operational quad-pol mode, the compact mode would be a good mode to use for wide area land-use monitoring and change detection.

2.3 Forest Height Estimation

2.3.1 Introduction, Motivation and Literature Review

Forest height is one of the most important parameters in forestry along with basal area and tree species or species composition. It provides information about stand development and/or site index and describes dynamic forest development, modeling and inventory. Forest height is an (standard) indicator for the site dependent timber production potential of a stand, and is closely related (through allometric relations) to forest biomass (see Sect. 2.5.1). Furthermore, accurate forest height measurements allow concluding on the successional state of the forest and can be used to constrain model estimates of above ground biomass and associated carbon flux components between the vegetation and the atmosphere. The distribution of forest heights within a stand can be further used to characterize the disturbance regime while high (spatial and temporal) resolution forest height maps can be used for detecting selective logging activities (Köhler and Huth 2010; Dubayah et al. 2010; Thomas et al. 2008; Hurtt et al. 2010).

When it comes to characterize dynamic forest processes the (accurate) estimation of forest height change is even more important than static forest height measurements. Forest height change can be directly used to characterize forest growth, mortality and deforestration and to conclude about the associated carbon fluxes without the need of assumptions (or knowledge) about the successional status (Köhler and Huth 2010; Dubayah et al. 2010).

Being a standard parameter in forest inventories, forest height is hard to be measured on the ground and typical estimation errors are around 10% accuracy, yet increasing with forest height and density. In terms of remote sensing techniques, lidar configurations have been today established as the reference (in terms of vertical and spatial resolution and/or accuracy) for measuring on local and regional scale vertical and horizontal distribution of vegetation structure components including vegetation height. Lidar estimation methodologies have been developed and validated through a variety of airborne and speceborne measurements and experiments (Lefsky 2010). However, the rather small footprints of spaceborne lidar configurations do not allow global forest height (and structure) monitoring with reasonable temporal resolution.

The introduction of polarimetric SAR interferometry (PolInSAR) at the end of the nineties was a decisive step towards developing remote sensing applications relevant to forest structure. The inherent sensitivity of the interferometric coherence to the vertical structure of volume scatterers combined with the potential of SAR polarimetry to interpret and characterise the individual scattering processes at different structural components allows a qualitative and quantitative determination of relevant (structure) parameters from SAR measurements. Today, PolInSAR is an established technique, allowing investigation of the 3-D structure of natural volume scatterers.

The fundamental interferometric measurement is the complex interferometric coherence, which comprises the interferometric correlation coefficient, as well as the interferometric phase. For a given spatial baseline (indicated by the vertical interferometric wavenumber k_z) and a given polarization (indicated by the unitary vector w (Cloude 2009; Marino and Cloude 2010)) the complex interferometric coherence is obtained by forming the (normalized) cross-correlation between the corresponding interferometric images S₁(w) and S₂(w):

$$ \gamma \left({k}_z,\mathbf{w}\right)=\frac{<{S}_1\left(\mathbf{w}\right){S}_2^{\ast}\left(\mathbf{w}\right)>}{\sqrt{<{S}_1\left(\mathbf{w}\right){S}_1^{\ast}\left(\mathbf{w}\right)><{S}_2\left(\mathbf{w}\right){S}_2^{\ast}\left(\mathbf{w}\right)>}}=\mid \gamma \left({k}_z,\mathbf{w}\right)\mid \exp \left( j\varphi \right). $$

(2.4)

The measured coherence depends on the system and imaging geometry, as well as on the dielectric and structural parameters of the scatterers within the scene. A detailed discussion of system induced coherence contributions can be found in Lefsky (2010). After calibration of system induced decorrelation contributions and compensation of spectral decorrelation in azimuth and range the estimated interferometric coherence can be decomposed into three main decorrelation processes (Zebker and Villasenor 1992; Bamler and Hartl 1998; Moreira et al. 2013):

$$ \gamma \left({k}_z,\mathbf{w}\right)={\gamma}_{\mathrm{Temp}}{{}\gamma}_{\mathrm{SNR}}{{}\gamma}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right) $$

(2.5)

• γ_SNR known as the Signal-to-Noise Ratio (SNR) decorrelation is introduced by the additive white noise contribution on the received signal;

• γ_Temp is the temporal decorrelation caused by dynamic changes in the scene occurring in the time between the two acquisitions. It depends on the structure and the temporal stability of the scatterer, the temporal baseline of the interferometric acquisition and the dynamic environmental processes occurring in the time between the acquisitions;

• The volume decorrelation γ_Vol(k_z, w) is the decorrelation caused by the different projection of the vertical component of the scatterer reflectivity spectrum into the two interferometric SAR images. It contains therefore information about the vertical structure of the scatterer (Cloude 2009; Bamler and Hartl 1998). Indeed, γ_Vol(k_z, w) is directly related to the vertical distribution of scatterers F(z, w) in the medium through a (normalized) Fourier transformation relationship (Bamler and Hartl 1998; Papathanassiou and Cloude 2001)

$$ {\gamma}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right)=\exp \left({jk}_z{z}_0\right)\frac{\underset{0}{\overset{h_V}{\int }}F\left({z}^{\prime },\mathbf{w}\right)\exp \left({jk}_z{z}^{\prime}\right)d{z}^{\prime }}{\underset{0}{\overset{h_V}{\int }}F\left({z}^{\prime },\mathbf{w}\right)d{z}^{\prime }} $$

(2.6)

where h_V indicates the height (or depth) of the volume. k_z = (m ⋅ 2π ⋅ Δθ)/[λ ⋅  sin (θ₀)] is the effective vertical (interferometric) wavenumber that depends on the imaging geometry (Δθ is the incidence angle difference between the two interferometric images induced by the baseline and θ₀ the local incidence angle) and the radar wavelength λ. z₀ is a reference height and φ₀ = k_zz₀ the associated interferometric phase. For monostatic acquisitions m = 2, while for bistatic acquisitions m = 1.

Accordingly, γ_Vol(k_z, w) contains the information about the vertical structure of the scatterers and allows to estimate F(z, w) (and/or associated structure parameters) from measurements of γ_Vol(k_z, w) (or γ(k_z, w)). Indeed, for the estimation of F(z, w) (and/or associated structure parameters) from γ_Vol(k_z, w) measurements at different polarisations, frequencies and/or (spatial) baselines two approaches have been explored in the literature:

• 1. The first one is to parameterise F(z, w) in terms of geometrical and scattering properties and to use then γ_Vol(k_z, w) measurements at different spatial baselines and/or different polarisations to estimate the individual model parameters. In this case, the scattering model is essential for the accuracy of the estimated parameters. On the one hand the model must contain enough physical structure to interpret the inreferometric measurements, while on the other hand it must be simple enough in terms of parameters in order to be determinable with the available (in general limited) number of observations (Cloude 2009; Papathanassiou and Cloude 2001; Cloude and Papathanassiou 2003).

• 2. The second approach to estimate F(z, w) is to approximate it by a (normalized) polynomial series or another orthogonal function basis P_n(z) (Cloude 2009; Cloude 2006):

$$ F\left(z,\mathbf{w}\right)=\sum \limits_n{a}_n\left(\mathbf{w}\right){P}_n(z) $$

(2.7)

and to use then γ_Vol(k_z, w) measurements to estimate the coefficients a_n(w) of the individual components. The advantage of this approach is that there is no assumption on the shape of F(z, w) required, allowing the reconstruction of arbitrary vertical scattering distributions (Cloude 2006).

2.3.2 Methodology

2.3.2.1 Random-Volume-Over-Ground Inversion

For vegetation applications two layer statistical models, consisting of a vertical distribution of scatterers F_V(z, w) that accounts for the vegetation scattering contribution, and a Dirac-like component m_G(w)δ(z − z₀) that accounts for the scattering contribution(s) with the underlying ground (i.e. direct surface and dihedral vegetation-surface contributions) have been proven to be sufficient in terms of robustness and performance especially at lower frequencies (Cloude 2009; Moreira et al. 2013; Papathanassiou and Cloude 2001):

$$ F\left(z,\mathbf{w}\right)={F}_V\left(z,\mathbf{w}\right)+{m}_G\left(\mathbf{w}\right)\delta \left(z-{z}_0\right) $$

(2.8)

where m_G(w) is the ground scattering amplitude. Substituting (2.8) into (2.6) leads to the model:

$$ {\tilde{\gamma}}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right)={e}^{j{\varphi}_0}\frac{{\tilde{\gamma}}_V\left({k}_z,\mathbf{w}\right)+\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)},{\tilde{\gamma}}_V\left({k}_z,\mathbf{w}\right)=\frac{\underset{0}{\overset{h_V}{\int }}{F}_V\left(z,\mathbf{w}\right)\exp \left({jk}_z{z}^{\prime}\right)d{z}^{\prime }}{\underset{0}{\overset{h_V}{\int }}{F}_V\left(z,\mathbf{w}\right)d{z}^{\prime }}. $$

(2.9)

The ratio $\mu \left(\mathbf{w}\right)={m}_G\left(\mathbf{w}\right)/{\int}_o^{h_V}{F}_V\left(z,\mathbf{w}\right) dz$ is the effective ground-to-volume amplitude ratio.

For modelling the vertical distribution of scatterers in the vegetation layer F_V(z, w), or equivalently ${\tilde{\gamma}}_V\left({k}_z,\mathbf{w}\right)$, different models can be used. A widely and very successfully used model for F_V(z, w) is an exponential distribution of scatterers (Moreira et al. 2013; Papathanassiou and Cloude 2001):

$$ {F}_V\left(z,\mathbf{w}\right)=\exp \left[2\sigma \left(\mathbf{w}\right)z/\cos \left({\theta}_0\right)\right] $$

(2.10)

where σ(w) is a mean extinction value for the vegetation layer that defines the attenuation rate of the profile. Besides the exponential profile, that appears to fit better higher frequencies, Gaussian, or Linear scattering distributions have been proposed especially at lower frequencies (Garestier and Le Toan 2010a, b; Kugler et al. 2009).

Equation (2.9) comprises four unknowns: the forest height h_V, the extinction σ(w), the ground topography phase φ₀, and the ground-to-volume amplitude ratio μ(w) and cannot be inverted by a single-channel (i.e. single polarisation) interferometric acquisition that provides only one (complex) γ_Vol(k_z, w) estimate. In order to invert (2.9), one has to increase the dimensionality of the observation space introducing:

• Baseline diversity: the dependency of γ_Vol(k_z, w) on the vertical wave number is essential as it allows to increase the observation space in an effective way (i.e. without increasing the number of unknown parameters) as F(z, w) does not change with k_z (Treuhaft and Siqueira 2000). At the same time, the choice of the vertical wave number allows to optimize the inversion performance (Krieger et al. 2005). However, the limitation of multibaseline inversion approaches arises when the acquisition of additional spatial baselines is associated with non-zero temporal decorrelations (i.e. when they are not acquired simultaneously).

• Polarimetric diversity: the variation of γ_Vol(k_z, w) with polarization is due to the polarization dependency of F(z, w). The fact that certain components of F(z, w) have a stronger polarised (scattering) behaviour than others allows to use the polarimetric dependency of γ_Vol(k_z, w) for the estimation of F(z, w) (Papathanassiou and Cloude 2001; Cloude and Papathanassiou 2003). Looking on the two layer model of (2.8), while the ground scattering component is strongly polarized and therefore has to be assumed to be polarization dependent, the volume scattering component can be both: in the case of oriented volumes (OV) the vertical distribution of scatterers in the volume is polarization dependent, while in the case of random volumes (RV), the vertical distribution of scatterers in the volume is the same for all polarisations, i.e. F_V(z, w) = F_V(z).

In forest applications random volumes have been established so that a single polarimetric baseline allows the inversion of the Random-Volume-over-Ground (RVoG) model (Cloude 2009). Oriented volumes are more expected to be important in agriculture applications where the scatterers within the agriculture vegetation layer are in many cases characterized by an orientation correlation introducing anisotropic propagation effects and differential extinction (Treuhaft and Cloude 1999; Ballester-Berman et al. 2005).

In the absence of temporal decorrelation (i.e. γ_Temp = 1) and assuming a sufficient high SNR (i.e. γ_SNR = 1), from (2.5) follows:

$$ \gamma \left({k}_z,\mathbf{w}\right)={\gamma}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right). $$

(2.11)

The inversion problem for the quad-pol single-baseline case is balanced with six unknowns (h_V, σ, μ_1 − 3, φ₀) and three measured complex coherences [γ(k_z, w₁) γ(k_z, w₂) γ(k_z, w₃)] each for any independent polarization channel

$$ \underset{h_V,\sigma, {\mu}_i,{\varphi}_0}{\min}\left\Vert \left[\begin{array}{c}\gamma \left({k}_z,{\mathbf{w}}_1\right)\\ {}\gamma \left({k}_z,{\mathbf{w}}_2\right)\\ {}\gamma \left({k}_z,{\mathbf{w}}_3\right)\end{array}\right]-\left[\begin{array}{c}{\tilde{\gamma}}_{Vol}\left({h}_V,\sigma, {\mu}_1|{k}_z\right)\\ {}{\tilde{\gamma}}_{Vol}\left({h}_V,\sigma, {\mu}_2|{k}_z\right)\\ {}{\tilde{\gamma}}_{Vol}\left({h}_V,\sigma, {\mu}_3|{k}_z\right)\end{array}\right]\begin{array}{c}\end{array}\right\Vert . $$

(2.12)

with ${\tilde{\gamma}}_{\mathrm{Vol}}\left({h}_V,\sigma, {\mu}_i|{k}_z\right)$ modelled as in (2.9) and under the RVoG assumption.

However, Eq. (2.12) does not have a unique solution for a single baseline. Uniqueness can be established in terms of a single baseline only by regularisation (Cloude 2009; Flynn et al. 2002). A very efficient regularisation approach is to assume no response from the ground in one polarization channel (i.e., μ₃ = 0) (Papathanassiou and Cloude 2001; Cloude and Papathanassiou 2003). This way, one obtains an inversion problem with five real unknowns (h_V, σ, μ_1 − 2, φ₀) and three measured complex coherences each for any independent polarization channel (Papathanassiou and Cloude 2001):

$$ \underset{h_V,\sigma, {\mu}_i,{\varphi}_0}{\min}\left\Vert \left[\begin{array}{c}\gamma \left({k}_z,{\mathbf{w}}_1\right)\\ {}\gamma \left({k}_z,{\mathbf{w}}_2\right)\\ {}\gamma \left({}_z,{\mathbf{w}}_3\right)\end{array}\right]-\left[\begin{array}{c}{\tilde{\gamma}}_{\mathrm{Vol}}\left({h}_V,\sigma, {\mu}_1|{k}_z\right)\\ {}{\tilde{\gamma}}_{\mathrm{Vol}}\left({h}_V,\sigma, {\mu}_2|{k}_z\right)\\ {}{\tilde{\gamma}}_{\mathrm{Vol}}\left({\left.{h}_V,\sigma, {\mu}_3=0\right|}_z\right)\end{array}\right]\begin{array}{c}\end{array}\right\Vert $$

(2.13)

Equation (2.13) has now a unique solution in terms of h_V and σ: each {h_V, σ} pair for a given baseline (i.e. vertical wavenumber κ_z) and φ₀ phase is mapped through (2.10) into a unique ${\tilde{\gamma}}_{\mathrm{Vol}}\left({k}_z\right)$ value. However, the validity of this assumption is not expected to be universal. Deviations of the real vertical structure from the modelled one degrade the inversion performance of (2.12) and (2.13). Two situations where such a reality/model mismatch becomes obvious are:

• 1. In low extinction forest scattering situations given in sparse forests the assumption that μ₃ = 0 is not valid, i.e. all polarizations are affected by a significant ground scattering contribution. Also underlying topographic variations within the scene can increase the ground scattering contribution in all polarization channels. The presence of a residual μ₃ in (2.13) biases the inversion results (usually causes an overestimation of forest height and/or an underestimation of the extinction coefficient). For a single-baseline inversion scenario, one way to still obtain a solution is to fix the extinction value. However, the relative strong variation of σ in forest environments limits the inversion performance obtained in many forest environments.

• 2. Inverse scattering distributions, i.e. cases where more effective scatterers are located in the lower forest layers than on the higher ones. This can be the case in sparse forest environments with more or less distinct understorey, or at lower frequencies when the effective scatterers become larger and therefore located lower within the forest architecture. In this case, the exponential decay of F_V(z) as assumed in (2.11) is no longer valid resulting in an underestimation of forest height and/or an overestimation of extinction.

However, quantitative model based estimation of forest height by means of (2.13) based on a single frequency, fully polarimetric, single baseline configuration has been successfully demonstrated at different frequencies, from P- up to X-band. Several space and airborne experiments demonstrated the potential of Pol-InSAR techniques to estimate with high accuracy forest height over a variety of natural and commercial; temperate, boreal and tropical sites characterized by different stand and terrain conditions (Lee et al. 2010, 2013; Lavalle et al. 2012).

2.3.2.2 Non-volumetric Decorrelation Contributions

Equation (2.9) accounts only for the volume decorrelation contribution while other non-volumetric decorrelation effects are ignored. Any decorrelation contribution reduces the interferometric coherence, and increases the variation of the interferometric phase. Furthermore, one has to distinguish between real and complex decorrelation contributions: while the expectation value of the interferometric phase remains invariant in the case of real decorrelation contributions, complex decorrelation biases the interferometric phase.

The most prominent decorrelation contribution in the case of non-simultaneous acquisitions (repeat pass system) is temporal decorrelation. It is caused by changes within the scene occurring in the time between (or even during) the two acquisitions. Such changes affect the location and/or the (scattering) properties of the scatterers within the scene inducing in the most general case a complex decorrelation (Lee et al. 2010, 2013; Lavalle et al. 2012).

In terms of the RVoG model (2.2), temporal decorrelation may affect both the volume component that represents the vegetation layer and the underlying ground layer and can be accounted for by introducing ${\gamma}_{\mathrm{Temp}}\left(\overrightarrow{w}\right)$ as complex temporal decorrelation coefficient in (2.11) (Lee et al. 2010):

$$ \gamma \left({k}_z,\mathbf{w}\right)={\gamma}_{\mathrm{Temp}}\left(\mathbf{w}\right){\gamma}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right)=\exp \left({jk}_z{z}_0\right){\gamma}_{\mathrm{Temp}}\left(\mathbf{w}\right)\frac{{\tilde{\gamma}}_V\left({k}_z\right)+\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)}. $$

(2.14)

It is expected that decorrelation processes within the volume layer differs from temporal decorrelation of the ground layer, to account for this γ_temp(w) needs to be split into a volume part and a ground part (Lee et al. 2010):

$$ \gamma \left({k}_z,\mathbf{w}\right)=\exp \left({jk}_z{z}_0\right)\frac{\gamma_{TV}\left(\mathbf{w}\right){\tilde{\gamma}}_V\left({k}_z\right)+{\gamma}_{TG}\left(\mathbf{w}\right)\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)}. $$

(2.15)

γ_TV(w) describes the temporal decorrelation of the volume layer and γ_TG(w) the temporal decorrelation of the underlying surface scatterer. Note that in general the decorrelation processes within the volume layer occur at much smaller time scales than the decorrelation processes on the ground (which includes both surface and dihedral scattering) (Lee et al. 2010, 2013). As indicated, both coefficients may be polarisation dependent and complex. For example, changes in the dielectric properties of the canopy or ground layer lead to (complex) polarisation dependent temporal decorrelation contributions γ_TV(w) and γ_TG(w) (Lee et al. 2010). Changes in the vertical distribution of scattererers lead to complex decorrelation contributions.

From the parameter inversion point of view now, the RVoG model (2.14) with general temporal decorrelation contributions cannot be solved under any (repeat-pass) observation configuration. Any additional measurement of γ(k_z, w) at a different spatial baseline and/or polarisation introduces the same number of unknowns (γ_TV and γ_TG) as observation parameters. However, even if the general temporal decorrelation scenario leads to an underdetermined problem, special temporal decorrelation events may be accounted under certain assumptions. The most common temporal decorrelation over forested terrain is wind-induced decorrelation due to the (wind-induced) movement of the scatterers (e.g. leaves and/or branches) within the canopy layer. In terms of the RVoG model, this corresponds to a change of the position of the scattering particles within the volume in the two acquisitions that introduces a non-volumetric decorrelation. However, in this case the scattering amplitudes as well as the propagation properties of the volume remain the same. Assuming further that the scattering properties of the ground do not change in the time between the two acquisitions (2.12) reduces to:

$$ {\tilde{\gamma}}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right)=\exp \left({jk}_z{z}_0\right)\frac{\gamma_{\mathrm{Temp}}{\tilde{\gamma}}_V\left({k}_z\right)+\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)} $$

(2.16)

γ_Temp describes the real temporal decorrelation of the volume scatterer. The inversion of PolInSAR coherences contaminated by temporal decorrelation using (2.13) leads to overestimated forest height as the RVoG model interprets the lower coherence by an increased forest height. Note that the estimation bias increases with increasing level of temporal decorrelation and is significantly larger for low(er) than for tall(er) forests stands. The effect of γ_Temp decreases with increasing spatial baseline (Lee et al. 2013).

As indicated by (2.5), γ(k_z, w) may include several non volumetric decorrelation contributions γ_Deco so that:

$$ \gamma \left({k}_z,\mathbf{w}\right)={\gamma}_{\mathrm{Deco}}{\gamma}_{\mathrm{Vol}}\left({k}_z,\mathbf{w}\right) $$

(2.17)

In this sense, Eq. (2.9) becomes:

$$ \gamma \left({k}_z,\mathbf{w}\right)=\exp \left(j{\varphi}_0\right){\gamma}_{\mathrm{Deco}}\frac{{\tilde{\gamma}}_V\left({k}_z\right)+\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)}. $$

(2.18)

The inversion of (2.18) requires apart from polarimetric also baseline diversity (Lee et al. 2010). Assuming γ_Deco to be polarisation independent, at least a second baseline is required for height inversion. Each baseline provides three measured coherences $\left[\gamma \left({\mathbf{w}}_1|{k}_{z,i}\right)\kern0.5em \gamma \left({\mathbf{w}}_2|{k}_{z,i}\right)\kern0.5em \gamma \left({\mathbf{w}}_3|{k}_{z,i}\right)\right]$:

$$ \gamma \left(\mathbf{w}|{k}_{z,i}\right)=\exp \left(j{\varphi}_{0,i}\right){\gamma}_{\mathrm{Deco},i}\frac{{\tilde{\gamma}}_V\left({k}_{z,i}\right)+\mu \left(\mathbf{w}\right)}{1+\mu \left(\mathbf{w}\right)} $$

(2.19)

where i = 1, 2 indicate the two spatial baselines. Assuming μ(w₃) = 0 the polarisation with the lowest ground contribution becomes:

$$ \gamma \left({\mathbf{w}}_3|{k}_{z,i}\right)=\exp \left(j{\varphi}_{0,i}\right){\gamma}_{\mathrm{Deco},i}{\tilde{\gamma}}_V\left({k}_{z,i}\right). $$

(2.20)

Equation (2.19) can be inverted in two steps. First, for each baseline all possible triplets {h_V, σ, γ_{Deco, i}} fulfilling (2.20) are estimated. Then the triplets with common height/extinction pairs {h_V, σ} are projected into each individual baseline and h_V, σ are estimated according to

$$ \underset{h_V,\sigma }{\min}\left\Vert \left[\begin{array}{c}\gamma \left({\mathbf{w}}_3|{k}_{z,1}\right)\\ {}\gamma \left({\mathbf{w}}_3|{k}_{z,2}\right)\end{array}\right]-\left[\begin{array}{c}{\gamma}_{\mathrm{Deco},1}{\tilde{\gamma}}_V\left({k}_{z,1}\right)\\ {}{\gamma}_{\mathrm{Deco},2}{\tilde{\gamma}}_V\left({k}_{z,2}\right)\end{array}\right]\right\Vert $$

(2.21)

The advantage of (2.18) is that it can be inverted in a multi-baseline sense without requiring absolute (i.e. residual geometric, ionospheric and/or atmospheric) phase corrections.

2.3.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on forest height estimation are summarized in Table 2.6 and further described in the Appendix.

Table 2.6 Test sites and corresponding radar and validation data selected for the generation of showcases on forest height estimation

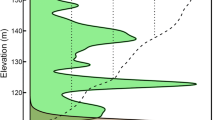
The results achieved at L-band over the temperate Traunstein site are presented in Fig. 2.17. The L-band HV intensity image of the Traunstein forest site is shown on the left. In the middle and on the right of Fig. 2.17 forest height maps derived from Pol-InSAR data acquired at L-band in 2003 (middle) and 2008 (right) are shown. Comparing the two forest height maps a number of changes within the forest become visible: the logging of individual tall trees as a result of a change in forest management between 2003 and 2008 (marked by the green box); the damage caused in January 2007 by the hurricane Kyrill which blew down large parts of the forest (marked by the orange box); and finally forest growth on the order of 3–5 m over young stands as seen within the area marked by the white circle. The validation plot against the lidar reference data, shown in Fig. 2.18, indicates correlation coefficient of 0.95 and a root mean square error (RMSE) below 2 m.

Fig. 2.17

E-SAR L-band HV intensity image of the Traunstein test site (left). Forest height map computed from PolInSAR data in 2003 (middle) and 2008 (right)

Fig. 2.18

Validation plot of forest height estimates at L-band over Traunstein (2008) against the lidar reference

The inversion results achieved at P-band over the tropical Mawas site are shown in Fig. 2.19. The HH amplitude image is shown on the top. The river crosses the left part of the image embedded in secondary riverine forest. The lidar strip is superimposed on the amplitude image. Forest height along the Lidar strip is constant within ±5 m around 27 m with lower heights in the parts close to the river and the disturbed forest areas. The PolInSAR forest height map is shown on the bottom. In the forested part the logging trails caused by logging activities 10–15 years ago appear clearly. On the top right the validation plot against the lidar reference data is shown characterized by a correlation coefficient of 0.94 and a RMSE of clearly below 2 m, indicating an estimation accuracy better than 10% of the mean forest height.

Fig. 2.19

Top: P-band HH intensity image of the Mawas test site. Bottom: Forest height map from PolInSAR data. Top right: associated validation plot against the lidar reference

2.3.4 Comparison with Single/Dual Polarimetric Data

The RVoG model, as given in (2.9) and assuming F_V(z, w) = F_V(z), can be inverted by means of a dual-polarimetric interferometric configuration that provides only two polarimetric channels w₁ and w₂. Assuming a zero ground-to-volume amplitude ratio for one polarization (i.e. μ(w₂) = 0) leads to a balanced inversion problem with unique solutions for four unknowns, i.e. the forest height h_V, the extinction σ, the ground topography phase φ₀ and the ground-to-volume amplitude ratio μ(w₁):

$$ \underset{h_V,\sigma, {\mu}_1,{\varphi}_0}{\min}\left\Vert \left[\begin{array}{c}\gamma \left({k}_z,{\mathbf{w}}_1\right)\\ {}\gamma \left({k}_z,{\mathbf{w}}_2\right)\end{array}\right]-\left[\begin{array}{c}{\tilde{\gamma}}_{\mathrm{Vol}}\left({h}_V,\sigma, \mu \left({\mathbf{w}}_1\right)|{k}_z\right)\\ {}{\tilde{\gamma}}_{\mathrm{Vol}}\left({h}_V,\sigma, \mu \left({\mathbf{w}}_2\right)=0|{k}_z\right)\end{array}\right]\begin{array}{c}\end{array}\right\Vert $$

(2.22)

Indeed, the inversion scheme of Eq. (2.22) has been used to invert airborne but also space borne dual-pol interferometric configurations (Cloude 2009; Kugler et al. 2014). Compared to the quad-pol case the performance of the dual-polarimetric inversion has a reduced performance in terms of:

• 1. Biased estimation results which are obtained when the assumption of a zero ground-to-volume amplitude ratio is violated, i.e. when the ground scattering contribution is significant in all polarisations. This can be the case at lower frequencies and/or sparse forest conditions. With respect to the zero ground-to-volume amplitude ratio assumption, conventional dual-polarimetric configurations acquiring a co- and a cross-polarised channel are in favour when compared to dual-polarimetric configurations acquiring the two co-polarised channels. However, even the cross-polarised channel can be affected by a significant ground scattering contribution especially in the presence of terrain slopes.

• 2. Larger variance of the obtained forest height estimates when compared to the inversion results achieved by using the full polarimetric information as only a polarimetric subspace is available for performing the inversion. This affects the conditioning of the inversion problem and the accuracy of the obtained estimates. For the Traunstein site the performance of two dual-polarimetric interferometric configurations, HH and HV as well as HH and VV has been evaluated and compared to the quad-polarimetric case. While the forest height estimates obtained from both dual-polarimetric configurations do not show any significant bias, their variance is significantly higher across all validation stands than the variance of the forest height estimates obtained from the quad-polarimetric configuration as indicated in Fig. 2.20.

• 3. Larger amount of (forest) points with no RVoG solution. This is, in most cases, also the result of a non-zero ground scattering contribution in the estimated γ_Vol(k_z, w) = γ_V(k_z) level that moves the γ_V(k_z) values out of the ${\tilde{\gamma}}_V\left({k}_z,{h}_V,\sigma \right)$ solution space. In the case of Traunstein, both dual-polarimetric inversion configurations have 15% more non-invertible forest points than the quad-polarimetric configuration where 95% of all forest points could have been inverted.

Fig. 2.20

Increase of forest height standard deviation (expressed in % of absolute forest height) for the dual-pol inversion case (blue: HH and HV, red: HH and VV) when compared to the quad-pol case for each validation stand of the Traunstein 2008 L-band

In the case of a single-polarimetric interferometric configuration that provides a single polarimetric channel w, the parameterisation of the measured interferometric coherence in terms of the RVoG model requires four parameters: forest height h_V, extinction σ, ground topography phase φ₀, and ground-to-volume amplitude ratio μ(w). Even neglecting the ground scattering contribution is not anymore sufficient to obtain a balanced inversion problem. In this case, the inversion relies on additional assumptions or external (a-priori) information on extinction or on ground topography. Fixing the extinction σ has been proved to compromise the inversion performance as it restricts the ability of the RVoG model to interpret the spatial variability of forest structure (Hajnsek et al. 2009).

A significant better performance is achieved by using an external digital terrain model (DTM) to estimate the ground topography phase exp(iφ₀) (Kurvonen and Hallikainen 1999; Dobson et al. 1996). In this case $\gamma \left({\kappa}_z,\overrightarrow{w}\right)$ can then be inverted for forest height h_V and extinction σ as.

$$ \underset{h_V,\sigma }{\min}\left\Vert \gamma \left({k}_z,\mathbf{w}\right)\exp \left(-j{\varphi}_0\right)-{\tilde{\gamma}}_V\Big({h}_V,\sigma, \mu =0|{k}_z\Big)\begin{array}{c}\end{array}\right\Vert $$

(2.23)

Figure 2.21 compares the two approaches using single- and dual-polarimetric TanDEM-X data sets acquired over Kryclan. The lidar-derived reference forest height map is shown on the top left. The corresponding single- and dual-pol forest height maps are on top middle and top right respectively. The associated validation plots are shown on bottom middle and bottom right. Compared to the single-pol inversion characterized by a correlation coefficient equal to 0.91 and a RMSE of about 1.6 m the dual-pol estimates is noisier, in particular for the taller forest stands, but the overall correlation coefficient equal 0.86 and a RMSE of 2.02 m remains convincing. On the bottom left, the single-pol forest height estimates are plotted against the dual-pol forest heights estimates. A correlation coefficient equal to 0.93 in combination with a RMSE of 1.44 m underlines the consistency of the results obtained by the two approaches.

Fig. 2.21

X-band single and dual-polarimetric inversion results. Top: Forest height maps. Lidar H100 map (left), single-pol forest height map (middle), dual-pol forest height map (right). Bottom: Validation plots: dual-pol (right), single-pol (middle), single- vs dual-pol (left)

2.3.5 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

Single-pol interferometric data at a single baseline do not provide enough measurables to invert forest height without a-priori information e.g. on terrain topography. A single-pol inversion is possible when multiple baselines are available, but the performance might be compromised by the presence of temporal decorrelation and the ratio of the spatial baselines. On the other hand, forest height inversion is possible with dual-pol interferometric data taking into account a reduced estimation performance when compared to the quad-pol case. The availability of quad-pol interferometric measurements, that allows the implementation of adaptive optimisation technique, is critical when algorithm robustness and performance matters.

Forest height estimation matured and developed in the last years from a pre-operational to an operational PolInSAR product that has been validated in the frame of several campaigns over a wide range of forest, terrain and environmental conditions. The overall obtained estimation accuracy is on the order of 10% or better. Uncompensated non-volumetric decorrelation contributions, such as temporal or additive noise decorrelation, are the most critical error sources. The limitations of the individual inversion approaches and the error propagation through them are today well understood as well as the options available to compensate for them.

2.4 Forest Vertical Structure Estimation Using Multi-baseline Polarimetric SAR Acquisitions

2.4.1 Polarimetric SAR Tomography

2.4.1.1 Introduction, Motivation and Literature Review

The vertical structure of forest is widely recognized to be an indicator of the above-ground biomass, whose knowledge is crucial for understanding the carbon cycle. Moreover, the knowledge of the vertical structure can reduce effects of saturation in the measurement of biomass by means of remote sensing systems. Through vertical structure it is possible to characterize the state of a forest ecosystem, for instance relatively to local/global climate change. Biodiversity in a forest environment depends on its vertical structure (Pretszch 2009).

Forest structure and biomass are still too poorly quantified across most part of the planet. For this reason, the estimation of forest vertical structure has become a very important research topic within the remote sensing community. Much work has been done in recent years in order to characterize the 3-D structure of the vegetation layer, as demonstrated on the one hand by the employment of lidar sensors, and on the other hand by the attention paid by different research groups to SAR systems. Especially the processing of SAR data results to be particularly appealing in forest observation. In fact, the unique ability of low frequency (P-/L-band) waves to penetrate into and through even dense vegetation and thus to interact with the different vegetation layers, provides sensitivity to vegetation structure. On the other hand, space borne SAR systems can acquire data continuously and provide the related products with high spatial and temporal resolution at a global scale.

A way to obtain the vertical structure of forests from SAR data consists in making use of SAR tomography (TomoSAR) techniques, which combine coherently (i.e. amplitude and phase) more than two acquisitions separated by horizontal and/or vertical displacements (baselines). The resulting cross-track baseline diversity allows to produce an aperture synthesis along the vertical plane to get full 3-D imaging through elevation beamforming for each given range-azimuth cell. The main result of this imaging process is a profile of the backscattered power as a function of the height. The size of the 3-D resolution cell is determined by pulse bandwidth along the slant range direction, and by the lengths of the synthetic apertures in the azimuth and cross-range directions. This concept is sketched in Fig. 2.22. It is worth noting that, provided a sufficient number of baselines, while polarimetric diversity per se is not required for obtaining forest profiles, polarimetric information is essential to characterize the individual scattering processes resolved in height. Such an enhanced representation results in the possibility to (1) extend from 2-D to 3-D all the classes of polarimetric estimation/decomposition techniques; (2) provide new estimation/decomposition techniques that are explicitly based on the joint exploitation of tomographic and polarimetric data.

Fig. 2.22

Left panel: pictorial view of a tomographic SAR system; right panel: cross range and slant range extent of the TomSAR resolution cell

The development of TomoSAR started with single-pol data. In parallel to the development of PolInSAR, TomoSAR for forest observation was demonstrated with an L-band airborne multibaseline (MB) experiment (Reigber and Moreira 2000) carried out by the DLR E-SAR platform over the Oberpfaffenhofen site. The possibility was shown to gain insights about the 3-D nature of the scattering mechanisms. However, two main limitations of SAR Tomography for forests were apparent since the beginning, namely the usually low number of images available for processing to avoid large acquisition times and the consequential temporal decorrelation, and the difficulty of obtaining ideal uniformly spaced parallel flight tracks due to navigation/orbital considerations. The baseline non-uniformity causes distortions in the imaging point-spread function along height, preventing from employing a simple Fourier-based focusing due to anomalous side and quasi-grating lobes.

In order to mitigate the effects of acquisition non-idealities, most of the subsequent research on (single-pol) TomoSAR investigated different imaging solutions. With particular reference to forest scenarios, a significant model-free advancement was reported in Lombardini and Reigber (2003), in which an adaptive beam forming technique based on the Capon spectral estimator was proposed and tested. The adaptive beam forming allows a reamarkable improvement in terms of both sidelobe level and resolution, and it has become a state-of-the-art technique in TomoSAR. Model-based alternatives were investigated as well, such as the multiple signal classification (MUSIC) (Nannini et al. 2009) and multi-baseline inversion approaches based on the covariance matching principle (Tebaldini 2010). These techniques have been extended in order to handle different polarimetric channels (Sauer et al. 2011; Huang et al. 2012; Ferro-Famil et al. 2012; Frey and Meier 2011). Many experiments carried out with real data have shown that the use of polarimetric information not only increments the number of observables, but it also improves the accuracy of height estimation of scatterers, increase height resolution, and allows to estimate a vector of complex coefficients describing the scattering mechanism at each height. Moreover, the combination of multibaseline polarimetric data can also be used to separate ground and canopy scattering, and to estimate their vertical structures by following a relatively simple algebraic approach based on the sum of Kronecker products (Tebaldini 2009) that extends with continuity the PolInSAR concept. Other authors have also shown the possibility to separate different contributions in the multibaseline PolInSAR coherences in order to estimate structural parameters associated e.g. to tree morphology (Neumann et al. 2010).

In this Section, the application of TomoSAR techniques to the estimation of the forest vertical structure is demonstrated with real data acquired in the framework of relevant (repeat-pass) airborne SAR campaigns. It is shown that the employed methodologies can separate different scattering layers and can estimate the distribution of the radar backscattered power along height, being such profile a proxy for a biomass distribution profile. Moreover, the role of polarimetry in improving and enriching the tomographic processing output will be emphasized and discussed.

2.4.1.2 Methodology

In order to estimate a vertical profile of the backscattered power, as already mentioned in Sect. 1.6, a plain Fourier-based 3-D focusing suffers from inflated sidelobes and poor height resolution (Lombardini and Reigber 2003). For this reason, in this Section the adaptive beam forming (from here on indicated with the acronym ABF for brevity) solution is considered. In this Section, we recall the ABF principle, while details can be found in Chap. 1.

In the classical single-pol TomoSAR, it is assumed to process data from an equivalent cross-track array of K phase centers, each of them corresponding to one of the K repeated flight tracks of the SAR sensor over the area of interest. As usual in SAR imaging and interferometry, after focusing in the range-azimuth plane, the images are assumed to be coregistered and properly compensated for the flat-earth phase. Moreover, N independent looks (here formed from multiple adjacent pixels) are used for processing. For each n-th look, the complex amplitudes of the pixels observed in the K SAR images at the same range-azimuth coordinate are collected in a number of K × 1 complex-valued vectors corresponding to the number of polarimetric channels (Sauer et al. 2011). If fully polarimetric data are available, without losing generality, they can be combined in the Pauli basis. The resulting MB data vectors can then be stacked one on top of the other in order to form the 3K-dimensional MB-polarimetric data vector y_P(n), which is statistically characterized by the MB-polarimetric covariance matrixR_P.

In forest scenarios, the scatterers at a given height z are characterized by a random polarimetric behaviour, and they are more properly described by means of a 3 × 3 polarimetric covariance matrix T(z) rather than by a deterministic (coherent) target vector (Ferro-Famil et al. 2012). In this way, the scattering mechanism at the generic z will contribute to R_P with T(z) ⊗ [a(z)a^T∗(z)], in which “⊗” denotes the Kronecker product and a(z) is the K × 1 MB steering vector. At the generic z, the ABF processor maximizes the total polarimetric power, and at the same time minimizes the interfering power contributions coming from heights different than z. By repeating this procedure for all the heights of interest, a stack of estimated polarimetric covariance matrices T(z) can be obtained. In this way, the polarimetric information can be exploited for a full 3-D characterization of the scattering, allowing for instance the use of incoherent polarimetric decompositions, as well as the application of physical scattering models for the 3-D identification of the single scattering components.

The Kronecker product representation discussed before can be specialized to express two-layer scattering models like the ones that are commonly used to describe model scenarios in the PolInSAR framework. A ground and a volume scattering layer will then contribute to R_P with 3 × 3 polarimetric covariance matrices T_G and T_V and with structure matrices (i.e. baseline-dependent only) R_G and R_V, respectively. As a consequence, under the RVoG assumption, the MB-polarimetric covariance matrix R_P can be modelled as a sum of Kronecker products as follows (Tebaldini 2009):

$$ {\mathbf{R}}_P={\mathbf{C}}_G\otimes {\mathbf{R}}_G+{\mathbf{C}}_V\otimes {\mathbf{R}}_V. $$

(2.24)

It is worth noting that if only one baseline is available, then Eq. (2.24) reduces to the classical PolInSAR model of (2.9), and therefore it constitutes its consistent multibaseline extension. The form of (2.24) allows to separate ground and volume scattering by means of algebraic techniques (Tebaldini 2009).

2.4.1.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on forest structure estimation are summarized in Table 2.7 and further described in the Appendix.

Table 2.7 Test sites and corresponding radar and validation data selected for the generation of showcases on forest structure estimation

To begin with, Fig. 2.23 shows a tomographic profile obtained in the range-height plane by processing both the L- and P-band Traunstein data with the full rank ABF at the same (fixed) azimuth coordinate. Polarimetric TomoSAR results have been derived from the selected data set by using a square multilook cell in the range-azimuth plane measuring around 25 m × 25 m. This cell corresponds to more than 100 independent looks, which is enough to guarantee a well-conditioned inversion of the MB-polarimetric covariance matrix. The slant range coordinate spans an interval of approximately 1.7 km, while the height varies in an interval of 160 m around 650 m above the sea level. The powers estimated in the three Pauli channel (i.e. the values on the diagonal of the estimated T(z)) have been RGB-coded, as usually done for polarimetric SAR images. Height resolution capabilities are apparent, allowing to distinguish different scatterers at different heights in the same cell, and do not worsen significantly from near to far range, being robust to the variation of the incidence angle. Bare ground areas can be distinguished from forested areas. Moreover, the ground scattering is located in correspondence of the lidar ground height, and it is more powerful at P-band than at L-band. In addition to height position, from the profiles of Fig. 2.23 a first insight of the occurring scattering mechanisms can be gained. For instance, in the forested areas, it is possible to distinguish mixed surface and double-bounce components at the ground level, as it is reasonable to expect from direct ground backscattering and tree trunk-ground interactions. Moreover, double-bounces are clearer at P-band, while at L-band their polarimetric signature looks more affected by the propagation through the canopy and/or the presence of understorey, although some estimation bias can have been induced by the volume due the limited height resolution and number of baselines. At the increase of the height, volumetric contributions (in green) start to appear at some range coordinates, sometime mixed to multiple (even or odd) bounce scattering contributions. They are always visible at L-band, while they are semi-transparent for many stands at P-band.

Fig. 2.23

Traunstein data set: tomographic slices obtained in the range-height plane at a fixed azimuth with the full-rank ABF. Estimated powers in the three Pauli channels are RGB-coded (Red: HH-VV, Green: 2 HV, Blue: HH + VV). Top panel: L-band; bottom panel: P-band

The following examples show how ground and volume scattering can be separated. One way to achieve this, is to exploit the ABF PolTomoSAR focusing. Using simple iterative MB-polarimetric techniques (Pardini and Papathanassiou 2013), the ground height has been retrieved from the data with an estimation accuracy of around 2 m at L-band and 1.5 m at P-band. Once the ground height is available, a simple separation between ground and volume can be performed. Figure 2.24 shows the Pauli RGB image of the ABF powers in correspondence of the estimated ground height at both L- and P-band. Double-bounce and direct surface scattering contributions are predominant, as expected, with a few contributions in the third Pauli channel due to residual understorey vegetation and possible orientation effects due to azimuth slopes. Notice that the ground scattering is more powerful at P-band than at L-band, as it is reasonable to expect. The availability of the polarimetric covariance matrix T_ABF(z) at each imaged height allows also to characterize the scattering by means of conventional incoherent decomposition tools developed in SAR polarimetry. A demonstration of this capability can be found in Fig. 2.25, in which the joint distribution of the entropy and $\overline{\alpha}$ angle are plotted in correspondence of the forested areas and for both ground and canopy contributions in isolation. The majority of the ground scattering (Fig. 2.25a, b) presents in general moderate entropy, with $\overline{\alpha}$ angles around 45°, as it typical for vegetated surface imaged after propagation through a forest canopy with relatively small baseline aperture, therefore with some volume-induced bias. Notice that the P-band ground scattering shows an increased number of low-entropy surface contributions with respect to L-band. Concerning the volume (Fig. 2.25c, d), an entropy/$\overline{\alpha}$ diagram characteristic of a random volume is obtained, although with entropy values lower at P-band than at L-band.

Fig. 2.24

Traunstein data set: Pauli images of the ground scattering isolated from the canopy (volume) scattering. Azimuth coordinate is on the horizontal axis. Color coding is as in Fig. 2.23. Left panel: L-band; right panel: P-band

Fig. 2.25

Traunstein data set: 2-D histograms of entropy and $\overline{\alpha}$ angle of forested areas for both ground and volume scattering in isolation after the ABF polarimetric TomoSAR processing. (a) Ground, L. (b) Ground, P. (c) Volume, L. (d) Volume, P

Ground and volume scattering can also be extracted by referring to model (2.24) and by using algebraic techniques. This possibility is shown experimentally here after processing the P-band Remningstorp and Krycklan data sets. With reference to the Remingstorp data set, the two profiles in the left panels of Fig. 2.26 were obtained by processing the HH (top left) and HV (bottom left) polarizations independently. The most apparent feature in these panels is that the strongest scattering contributions appear at the ground level, not only in HH polarization but in HV polarization as well. This observation was interpreted as a result of double bounce interactions between the vegetation and the terrain, which determined cross-pol contributions at the ground level. In this situation, the vertical resolution capabilities granted by TomoSAR do not suffice for the aim of separating ground and volume scattering, as both occur at the ground level. The results of the separation between ground and volume scattering are shown in the right panels of Fig. 2.26. In the profile relative to ground scattering the backscattered power is associated with the ground level only, as witnessed by the excellent agreement with lidar terrain height. The profile relative to volume scattering yields a much more uniform backscattered power distribution as compared to HV, and also provides an excellent agreement with lidar forest height.

Fig. 2.26

Remningstorp data set. Left panels: HH and HV profiles. Right panels: ground and volume Tomograms. All panels are normalized such that the sum along each column is one. The black and green lines are relative to terrain and forest height as estimated by lidar

The same procedure was applied to the aim of a large scale characterization of the forested area within the Krycklan river catchment. Figure 2.27 displays maps of the heights at which the estimated backscattered power for volume-only scattering undergoes a loss of 0 dB (i.e., no loss), 3 dB, 5 dB, and 7 dB with respect to the peak value (which corresponds by definition to the phase center height). Lidar heights are displayed in Fig. 2.27b to help the interpretation of the results. Forest height was assessed through a direct investigation of the shape of the backscattered power distribution. The estimation was found to be unbiased for forest height values larger than about 8 m. Standard deviation was assessed in about 3 m. Results are shown in Fig. 2.27c. Another effective way to characterize the forest vertical structure at large scale is to display the ground-to-volume backscattered power ratio at different polarizations, see Fig. 2.28. These maps are sensitive to both forest height and terrain topography, and may be used to assess the impact of multiple reflections on SAR images.

Fig. 2.27

Krycklan data set. (a) Tomographic heights relative to volume-only scattering. (b) lidar forest heights. (c) 2D histograms relative to TomSAR and lidar forest height estimates

Fig. 2.28

Krycklan data set: Ground-to-volume power patio [dB] at HH (left) and HV (right)

The analysis carried out up to now has assessed the quality and the information content of tomographic products. Moreover, some simple examples have been shown about the validity of the resulting polarimetric information for scattering interpretation. A further qualitative experiment can be carried out to understand if a correspondence exists between the ABF spectral components and the biomass components at different heights. For this validation, a few representative biomass profiles calculated from ground measurements have been selected, and the ABF full-rank profiles have been estimated in the same coordinates.

Figure 2.29a shows six different biomass profiles (first row) which refer to stands taller than 30 m. These profiles mainly present a biomass contribution close to the top (tree crown and stems) and an additional one close to the ground (tree trunk). Starting from the left, in the third and the last two profiles some understory vegetation can be noticed. In Fig. 2.29b the L-band ABF profiles are reported in the three Pauli channels. Qualitatively, it is apparent the agreement between the backscattered radar power and the biomass distributions already by processing a relatively low number of images (7) with a short total baseline (30 m), therefore resulting into a vertical Rayleigh resolution around 15 m for the profiles under analysis. It is worth noting that different polarimetric channels are sensitive to (slightly) different biomass components, as the profiles show variations from channel to channel. From this example, it is therefore possible to conclude that polarimetric diversity is crucial for a complete characterization of the mapping of biomass components into radar scattering components.

Fig. 2.29

Traunstein data set: reference biomass profiles and radar profiles estimated with the ABF processor from the L-band acquisitions. Profiles amplitudes are normalized with respect to the maximum. The ground is located at 0 m. The dashed horizontal lines indicate the Lidar stand height. (a) Biomas profiles estimated from ground measurements. (b) Polarimetric ABF profiles, Pauli basis, full-rank coherent processing. (c) ABF profiles, lexicographic basis, each channel processed independently. (d) Polarimetric ABF profiles, Pauli basis, each channel processed independently

2.4.1.4 Comparison with Single/Dual Polarization Data

The ABF profiles obtained by processing single polarization MB data in the lexicographic basis are plotted in Fig. 2.29c. It is apparent that one single power profile makes difficult the interpretation of the scattering from the different vegetation components. For instance, with this (realistic) baseline distribution it is not possible to discriminate the presence of understory vegetation without ambiguities. A way to circumvent this inconvenient could be to increase the number of baselines and at the same time to increase the height resolution in order to be able to separate many more power components. However, this may not be feasible depending on navigation/orbital considerations and temporal decorrelation problems. As a consequence, the polarimetric information, beyond the increased number of outputs, becomes crucial (1) to relax the acquisition requirements, and (2) to enhance profile interpretation by the application of physical scattering models.

A second comparison is in order. Supposing to have full polarization data available, one could also select a basis different from the lexicographic one and to process the new MB data independently from channel to channel. An example is shown (again in correspondence of the reference profiles) in Fig. 2.29d. Comparing them with the profiles in Fig. 2.29b, the polarization-coherent full-rank ABF can resolve slightly better different scattering components by keeping fixed the total baseline length. Clearly, the presence of volume scatterers reduces the contribution of polarimetry to any increase of vertical resolution, differently from e.g. urban scenarios. Not to be forgotten is of course the difference in the output. While a polarization-incoherent processing only outputs three real-valued profiles, the polarization-coherent approach outputs an entire polarimetric coherence matrix.

2.4.1.5 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

In this Section the application of PolTomoSAR algorithms has been demonstrated for the estimation of the vertical structure of forests. The scattering can therefore be described in 3-D by means of a stack of polarimetric covariance matrices estimated at each height of interest, or by focusing on certain layers. Experiments have been carried out with a P- and an L-band MB-fully polarimetric data sets acquired by the DLR E-SAR platform. Both data sets are characterized by a relatively low number of baselines and an height resolution in the order of magnitude of 10 m. The goodness of the extracted polarimetric signatures has been qualitatively assessed, and the estimated power distributions have been compared with the corresponding biomass profiles derived from ground measurements. A general agreement has been found.

To summarize, from the results of the experimental analysis, the crucial role of polarimetry in the coherent processing of MB data has been individuated in the following aspects:

• 1. Increased amount of structural-dependent information in output, allowing the physical interpretation of the estimated profile;

• 2. Enhanced possibility to separate scattering contributions at different heights beyond the height resolution limit imposed by both the total baseline length and the tomographic processor;

• 3. Higher height resolution in the profiles extracted in each channel of the polarimetric basis;

• 4. Higher accuracy in the estimation of vertical structure parameters.

Point (2), in turn, allows to relax constraints on the relative acquisition tracks displacements, and might be of help for forest vertical structure monitoring with non-optimal baseline distributions. Point (3) has been shown here also by comparing the coherent MB-polarimetric ABF with an adaptive processing incoherent in the polarization channels. Point (4) is out of the scope of this Section, but experimental examples can be found e.g. in Sauer et al. (2011) and Huang et al. (2012).

3-D (Pol)TomoSAR imaging requires additional efforts compared to traditional 2-D SAR products and PolInSAR, due to the need of gathering multiple viewpoints and to employ more sophisticated processing techniques. Also, compare to single-pol TomoSAR, a small disadvantage of TomoSAR is the need for a larger multilook cell in order to obtain a reliable and well-conditioned estimate of the MB-polarimetric covariance matrix. Nevertheless, this issue is mitigated in SAR sensors with very high range-azimuth resolution, for which a satisfactory multilook degree for a stable ABF inversion can be achieved without increasing dramatically the horizontal resolution cell of the output products. With reference to forest monitoring and applications, this has an impact on the resolution of forest structure products, and on the way in which they are able to describe (dynamic) phenomena that may occur at very different scales depending on the kind of forest.

Another limitation peculiar of forest scenarios is the temporal decorrelation of the scattering. This factor has limited until now the tomographic forest monitoring from space borne platforms due to the large revisit times. Very recently, the possibility to track scattering changes has been shown in the so-called differential tomographic framework, which combines in a synergic way spatial and temporal spectral analysis. However, although promising and extended in a polarimetric sense in Lombardini et al. (2010), these techniques are in a very early stage of experimentation. Nevertheless, space borne implementations of (Pol)TomoSAR will benefit from repeated single-pass (Pol)InSAR implementations, in which a temporal-decorrelation-free PolInSAR coherence is available for each satellite pass.

PolTomoSAR is quite well developed and mature from the signal processing point of view. Many alternative techniques are continuously being investigated and their performance characterized. In particular, the adaptive processing in general represents a state-of-the-art, model-free, yet well-performing algorithm. Modern techniques based on compressive sensing are being investigated as well. A still underdeveloped element is the physical interpretation of profiles. The link between the obtained profiles that depend in general on frequency, polarization and acquisition geometry and physical forest structure parameters is essential for establishing potential applications and is today not well understood, although intensively investigated.

2.4.2 Estimation of Vegetation Structure Parameters

2.4.2.1 Introduction, Motivation and Literature Review

Forest structure and biomass are important components in terrestrial ecosystem carbon and water cycles and provide significant controls on land–atmosphere interactions. The present estimate by IPCC (Intergovernmental Panel on Climate Change) is that deforestation amounts to between 10% and 30% of the total anthropogenic carbon flux. The range of uncertainty is large due to the lack of accurate measurement techniques. SAR observations can help to better quantify terrestrial carbon stocks and fluxes in forest biomass, providing several advantages over other techniques: independence of the time of the day (in comparison to optical remote sensing), cloud cover penetration (using selected low frequencies), large coverage (in comparison to lidar), and high resolution (in comparison to radiometers).

Early remote sensing attempts to estimate biomass were originally based on regression from microwave backscatter signal (possibly combining multiple frequencies and polarizations). However, methods based on radar backscatter signals are limited by saturation and loss of sensitivity to biomass for high biomass levels (maximum at about 80–200 tons/ha), depending on the wavelength, polarization, and incidence angle. In addition, the saturation is dependent on forest type, ground topography, and environmental conditions. Due to spatial and temporal forest variability and the signal dependence on instrument parameters, the regression approach poses difficulties to generalize over extended areas.

Recent advances in Lidar and InSAR enabled the estimation of vertical forest structure. To a large extent, forest biomass is determined by tree structure, which makes the vertical structure information a powerful indicator for biomass. Lidar illuminates the forest with laser rays and allows the reconstruction of vertical structure profile from the returned signal (waveform). Especially the recently developed small-footprint lidars provide unprecedented means for high-resolution structure estimation. However, lidar coverage is limited, disallowing global forest monitoring based on this technology alone.

On the other hand, the developments in InSAR, PolInSAR and TomoSAR enable large coverage and independence of cloud cover. Acquiring SAR signals from two (or more) slightly displaced flight trajectories (possibly using the same platform in a repeat pass configuration) and exploiting the effect of interference of coherent waves enables InSAR to estimate several phase centers inside of the forest, and thus the important parameters of forest structure extent. Polarimetry plays an important role by helping to decompose different scattering processes from the ground and the canopy. In order to further improve the accuracy of forest structure and biomass estimation, multibaseline (MB) approaches are considered. This showcase demonstrates the application of MB-PolInSAR to airborne SAR data over temperate and boreal forests estimating forest structure, biomass, tree morphology and ground scattering related parameters.

Interferometric decorrelation in volumetric media such as canopy, snow and ice has been modeled to measure vegetation depth and extinction for the first time in 1995–1996 (Hagberg et al. 1995; Treuhaft et al. 1996). The model resembles a simple sparse-medium water cloud model (Treuhaft et al. 1996). In 1997–1998 time frame, authors in Cloude and Papathanassiou (1998) and Papathanassiou and Cloude (2001) proposed to combine polarimetry with interferometry to discriminate ground scattering from volume scattering in the canopy. This enables to estimate forest height by differentiating the InSAR phase centers from different polarizations, or to invert the complex coherence model accounting for the extinction. PolInSAR coherence optimization in single- and multi-baseline configurations has also been used to reduce phase uncertainty and to determine the polarization with lowest/highest InSAR phase noise (Cloude and Papathanassiou 1998). Also extensive PolInSAR scattering models for random and oriented scattering in the canopy and single- and double-bounce scattering at the ground level were derived and evaluated in Treuhaft and Siqueira (2000). Since then, the PolInSAR approach to measure volumetric media properties has been extended and applied to other volumetric media (such as snow, ice, and agriculture (Lopez-Sanchez et al. 2007)) and to complex multi-scattering environments in urban areas. Polarimetry demonstrated to be a key factor in distinguishing physically different scattering centers inside individual resolution cells.

Alternative radar approaches to estimate forest structure are based on tomography (Reigber and Moreira 2000), multi-baseline InSAR estimation (Treuhaft et al. 2009), and polarization coherence tomography (Cloude 2006). The first aims to reconstruct the reflectivity profile of the volume by using conventional or adaptive beam forming techniques (see Sect. 2.4.1). The last two rely on structure models, which are fitted using coherences from different baselines, and which corresponds to probing the medium with different Fourier frequencies.

Another approach (Neumann et al. 2010), as presented in this Section, aims to further decompose the MB-PolInSAR data into ground and volume sources related to polarimetric scattering, vertical profile structure and temporal change. On the one hand, this improves the understanding of the involved processes, and on the other, providing e.g. tree morphology parameters would enhance tree species characterization and biomass estimation.

The limitations of PolInSAR are governed by the geometric configuration of the interferometer (structure sensitivity) and the ambiguities related to vertically non-homogeneous structure, spatial variability of the forest, temporal decorrelation in repeat pass acquisitions, and possibly other minor (but usually well understood) noise sources (thermal noise and other instrument/system induced effects) (Krieger et al. 2005).

Height sensitivity and accuracy is varying with environmental and acquisition configuration parameters. On one side, airborne acquisition geometry causes variation in height sensitivity along the swath, and on the other side, the optimal acquisition geometry depends on the actual forest height. One proposed approach was to combine height estimates from multiple single-baseline PolInSAR data sets, if they are available (Hajnsek et al. 2009).

Acquiring SAR data in repeat pass configuration leads to illuminating possibly changed targets. Recent airborne and ground-based studies confirmed several common sources of temporal change in PolInSAR observables, including wind, growth, and changes in soil and vegetation water content. Initially, temporal decorrelation has been modeled by a Gaussian process. Over a short temporal scale (sub-hour level), wind effects appear to be the dominating source of decorrelation. Therefore, in Askne et al. (1997), the authors incorporate change in the Gaussian motion with height, arguing that thinner branches (higher in the canopy) are stronger effected by the wind than thicker branches and the trunk (closer to the ground). Soil moisture effects have been observed to affect the interferometric coherence and phase. Diurnal variability of vegetation water content is as well expected to affect the temporal decorrelation, as recently observed in ground-based radar measurements (Hamadi et al. 2013).

Recent important contributions to PolInSAR statistical properties and estimation approaches promise further advances. Tests of common physical assumptions, such scattering symmetries and stationary behavior, were initially derived in Ferro-Famil and Neumann (2008). The singular value decomposition based “Sum of Kronecker Products” (SKP) provides an elegant way to decompose the MB-PolInSAR covariance matrix into a parametric form of independent contributions (Tebaldini 2009). This work was recently updated by deriving a maximum likelihood estimator for the linear structure of two independent layers, as presented in [R7].

2.4.2.2 Methodology

The MB-PolInSAR approach of this Section consists of combining a physical model–based polarimetric decomposition with the PolInSAR Random Volume over Ground (RVoG) coherence model for the vertical forest structure. The goal is to enhance vertical structure estimation and to permit the retrieval of morphological vegetation parameters as well as ground parameters under the vegetation. The temporal change is taken into account in order to compensate for the caused decorrelation.

The models used in PolInSAR are usually based on the two-layer model, where it is assumed that the signal can be decomposed into independent and distinctive layers, representing the ground and the volume. The “distinctiveness” can be based on three orthogonal principles: (1) polarimetric scattering, (2) vertical extent, and (3) temporal processes (compare Fig. 2.30). Though the layers are considered independent, they can affect each other. For instance, the volume layer attenuates the ground scattering, possibly modifying the ground scattering polarization by means of refraction. The double-bounce is caused by scattering in both layers, though structurally it is attributed to the ground layer.

Fig. 2.30

Information content of PolInSAR data, separated into polarimetric and interferometric sources in ground and volume layers

The modeled ground contribution consists of attenuated surface scattering from the soil, the double-bounce scattering between the soil and tree elements such as trunk and branches, and volumetric scattering from a low layer of understory. The volume layer is dominated by diffuse volume scattering from the canopy elements, including multiple scattering effects. Forest canopy is expected to be a sparse medium, attenuating the signal with the distorted Born approximation. The vertical profile is represented by an effective scattering profile F(z), which takes into account extinction and the distribution of the scattering elements. Different forms were proposed for F(z) in the literature, including a uniform attenuated, Gaussian, or represented by Fourier or Legendre series. In this example, to represent the temperate and boreal forests, F(z) is characterized by two parameters, extinction σ_x and the canopy-fill-ratio r_h, as outlined in Fig. 2.31.

Fig. 2.31

PolInSAR model and retrieval representation in the coherence plane

The polarimetric coherency matrix of the volume component is characterized by two parameters related to the polarization entropy in the canopy (called orientation randomness in Neumann et al. (2010), as it is more constrained than the generic entropy) and the effective scattering mechanism type. The particle anisotropy characterizes the effective shape of the average particle in the polarization plane in dependence of the particle and background permittivities The orientation randomness characterizes the width of the distribution of particle orientation angles in the polarization plane (Neumann et al. 2010). The polarimetry of the volume component can range from purely randomly oriented collection of scatterers with high polarization entropy to a less diffuse form with ordered branch structure.

Prior to parameter retrieval, data preparation consists of the following steps, starting with a stack of single-look complex (SLC) data sets for multiple acquisitions and polarizations: flat earth removal, range spectral filtering, polarimetric calibration, MB-PolInSAR covariance matrix estimation including pre-summing and speckle filtering, radiometric calibration, SNR compensation, polarimetric stationary calibration, local orientation angle compensation, ground topography phase shift, natural media (reflection symmetry) assumption, forest/non-forest pre-classification.

In the retrieval phase, most crucial is the estimation of the ground elevation phases and the linear ground-volume structure. Using one of the recently proposed least squares or maximum likelihood approaches (Tebaldini 2009) provides a parametric decomposition of the MB-PolInSAR covariance matrix. The determination of the decomposition parameters (which characterize the ground to volume ratio and the polarization responses at both layers) is based on a set of assumptions. Common assumptions are based on physical insights into the ground-volume distinctiveness and can include metrics on polarization entropy, scattering mechanism type, ranges for forest height and ground elevation, and temporal effects. The constrained optimization problem is solved in a least squares sense determining the decomposition of the MB-PolInSAR covariance matrix into two layers, providing the ground and volume PolSAR matrices, and a MB series of coherences for the ground and volume components. The physical structure indicators are extracted from the PolSAR matrices, such as canopy orientation randomness, scattering mechanism types, ground-to-volume ratio, etc. The final estimation of the vertical structure profile is performed in an additional step by fitting the coherence sets for the ground and volume to a model of the verticals structure distribution.

For the demonstration of biomass estimation, different regression frameworks (multiple linear regression (LR), support vector machines (SVM), and random forests (RF)) were evaluated by using field measurements of above-ground-biomass. Validation is performed using leave-one-out approach.

2.4.2.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on forest parameter estimation are summarized in Table 2.8 and further described in the Appendix.

Table 2.8 Test sites and corresponding radar and validation data selected for the generation of showcases on forest structure estimation

MB-PolInSAR modeling and inversion provide many retrievable parameters including: forest height, ground elevation topography, vertical structure characterizing parameters (attenuation, canopy-fill-factor, differential extinction), temporal decorrelation, ground-to-volume ratio, individual power contributions, ground and volume scattering mechanism types and orientation randomness. For the Traunstein 2003 data, only the forest height can be related to the validation data, as projected from the 1998 inventory. In the following, we will present several retrieved forest structure parameters from the Traunstein 2003 data as obtained in the study (Neumann et al. 2010). Estimates are plotted in Fig. 2.32.

• 1. Vertical forest structure: forest heights are estimated close to projected field measurements with an average stand-wise root mean square error (RMSE) of about 5 m and standard deviation of 4.3 m. The heights were underestimated by 1.5 m. However, in some stands, the forest heights vary continuously, indicating non-homogeneity inside of the stands. Figure 2.33a shows the forest heights and the individual canopy layer depths for the 20 evaluation stands. The red and green lines in this plot represent the field measured and PolInSAR estimated forest heights, respectively. The brown line delimits the canopy layer from the non-canopy layer above the ground and represents the canopy-fill-ratio, normalized to the total vegetation height. It is notable that the smallest error corresponds to the most homogeneous forest stand #2, which is largely dominated by a single species, Northern Spruce (bias: −0.3 cm; RMSE: 1.5 m). The highest errors correspond to stand #20: the heights are underestimated by 5 m with an RMSE of 7.6 m. However, examining the optical data, one can observe several clear cuts and roads inside of this forest stand, which we initially assumed to be homogenous. This indicates significant changes in the spatial structure of this forest stand between the forest inventory in 1998 and the date of radar acquisition in 2003.

• 2. Temporal decorrelation: using the full model inversion allows us to estimate the total amount of temporal decorrelation, which varied significantly with forest stand and baseline between 0.5 and 0.95, as presented in Fig. 2.33b. The temporal decorrelation of the volume at these time scales is mostly caused by wind, which is non-stationary, neither temporally nor spatially. These results indicate that the temporal decorrelation is more correlated with the forest height and the spatial baseline and less with the time separation at the given sub-hour level.

• 3. Orientation randomness: Fig. 2.32d shows the estimated degree of orientation randomness over the whole scene. The standard deviation of orientation randomness is low, and the distinctiveness is high, which permits discriminating between the different evaluation stands. As discussed in the theoretical part, this parameter depends mostly on the morphology of the tree structures and the incidence angle. The incidence angle dependence is clearly observable in the scatter plot in Fig. 2.33d. Forest species type effects on orientation randomness were well visible. While coniferous tree canopies caused lower orientation randomness, down to 0.65, the highest orientation randomness was observed for deciduous trees, and in particular for the maple dominated forest stand #3 in the center of the image.

• 4. Particle scattering anisotropy: The effective particle scattering mechanism type seems to be insensitive to the evaluation stand and the incidence angle. In contrast, the particle anisotropy phase has a large dynamic range of about 70 degrees over the different evaluation stands. These findings were surprising and still need to be confirmed by rigorous analysis.

• 5. Extinction and canopy fill factor: Extinction σ_x (average at 0.15 dB/m) and the canopy-fill-ratio (average at 0.6) provide additional degrees of freedom for the adaptation of the model to the given forest structure. However, these estimates were found to be partly correlated with each other, which indicates that the used forest structure model and inversion approach are still ambiguous and a better representation should be found.

• 6. Differential extinction and coherence: Based on the estimated structure (extinction) and the PolSAR covariance matrix, we estimated the differential extinction in the canopy between HH and VV polarizations to be up to 0.06 dB/m. This tree canopy orientation induced effect changes the PolInSAR coherence for the canopy. The induced effect on coherence magnitude and phase is at the order of 0.005° and 1°, respectively.

• 7. Ground level contributions: Next to ground topography elevation, PolInSAR allows to estimate the ground-to-volume ratio (estimated to be in average about 0.2) and the individual PolSAR covariance matrices for the ground and volume contributions. We observed noteworthy cross-polarized contributions (about 20%) at the ground level, but the major scattering power at the ground was observed in the Pauli HH-VV component (about 50%). Though HH-VV is dominant, these results suggest that a simple first-order models for the ground component are insufficient to reliably represent the ground scattering inside the forest.

Fig. 2.32

Traunstein test site: optical image, PolSAR image with delineated forest stands, estimated forest height, and orientation randomness

Fig. 2.33

Traunstein test site: Estimated forest structure, scatterplot of estimated height, temporal decorrelation, orientation randomness over incidence angle

Figures 2.34 and 2.35 represent the Krycklan catchment area and show forest structure parameters retrieved from MB-PolInSAR data: polarimetric image in Pauli matrix basis (2.34a), lidar top forest height (h100) (2.34b), forest height (2.34c), biomass using SVM regression (2.34d), ground and volume orientation randomness (2.35a, b) and ground and volume scattering mechanism types (2.35c, d). Investigating regression techniques using a combination of PolInSAR retrieved forest structure parameters allowed us to improve biomass estimation at both, L- and P-band frequencies. On the one hand, providing more structure-related input parameters naturally improves the regression. However, due to spatial and temporal forest variability this regression usually does not generalize over large forest areas. We evaluated three approaches (Multiple Linear Regression (LR), Support Vector Machines (SVM), and Random Forests (RF)) using up to 14 parameters, independently at both frequencies. Using “leave-one-out” cross-validation approach, the best biomass RMSE were 19.7 and 22.7 t/ha at L- and P-band, respectively, using either SVM or LR. For comparison, without providing any forest structure information, the best RMSE values were 27.3 and 28.5 t/ha at L- and P-bands (both using SVM).

Fig. 2.34

Krycklan catchment. From left: L-band PolSAR image, Lidar height (rh100), PolInSAR height and biomass estimates

Fig. 2.35

Krycklan catchment. From left: Ground and volume orientation randomness, and ground and volume scattering mechanism types

These were initial results on biomass regression from selected MB-PolInSAR forest structure estimates. It is to expect, that the results can be improved by more systematically evaluating the entire available parameter space and by performing a better regularization of the regression frameworks.

2.4.2.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

This Section demonstrated a MB-PolInSAR approach for forest structure and biomass estimation on two airborne data sets at L- and P-band frequencies. We presented a model to characterize polarimetric interferometric radar response from vegetation. For the volume component, a novel polarimetric model was used to allow varying degrees of orientation randomness and scattering anisotropy inside the canopy.

The forest height estimation performance has been evaluated on real airborne L–band SAR data over the Traunstein forest. Using three baselines, the forest height has been underestimated with an average bias of 1.51 m and RMSE of 4.97 m. In addition, polarimetric parameters and backscattered powers were estimated for both layers, the ground and the canopy. On the other hand, the estimations of the extinction and the canopy–fill–factor were not satisfactory, as there seems to rest a level of ambiguity and correlation between these two parameters. Furthermore, differential extinction and temporal decorrelation were estimated.

The same methodology was applied to boreal forest in the Krycklan Catchment to estimate forest structure parameters and to successively estimate biomass via regression. The combination of polarimetric canopy and ground indicators with estimated forest structure information (consisting of forest height and ground-to-volume ratio) improved the RMSE of biomass estimation up to 27% and 43% at L- and P-bands, respectively.

The limitations for the presented parameter retrieval framework are determined by model assumptions. Only a simplified vegetation structure is taken into account assuming vertically uniform and horizontally homogeneous layers. Next it is assumed, that the average effective particle shape is representative for all particles, and independent of height and polarization orientation. The variation of extinction with polarization is assumed to be insignificant for parameter retrieval. Also, a plane of reflection symmetry is assumed to exist for the illuminated vegetation area. The possibility to estimate the degree of temporal coherence over vegetation provides new opportunities for PolInSAR time series analysis, which might lead to competitive multi–temporal monitoring of ecosystem dynamics. However, further theoretical and experimental investigations need to be conducted to improve the understanding and to examine the possibilities and limits of radar remote sensing of the temporal behavior and the forest structure.

Interferometry and polarimetry provide complementary information on the illuminated forest and we only start to explore the potentials for forest monitoring using these techniques. Though, it is an actively developing field and over the last few years several important breakthroughs in information content understanding and processing were reported which should help making this technique operational.

2.5 Biomass Estimation

2.5.1 Biomass Estimation: A Review

2.5.1.1 Introduction, Motivation

Biomass is defined as the quantity of living organic matter per unit volume and is usually given as a mass, or a mass per unit area. Forest biomass refers to living and dead organic material of plants and trees in the forest including roots, stem, stump, branches, bark, seeds and foliage. Above ground forest biomass defines to the forest biomass above the soil (e.g. excluding the roots). About half of the forest biomass is carbon, so that biomass is often used as proxy for carbon and its spatial distribution characterises the distribution of carbon in the biosphere (Houghton et al. 2009; Houghton 2005; IPCC good practice guidance for land use, land use change and forestry2003). Dynamic variations in the biomass are therefore a direct measure of the exchange of carbon between the terrestrial ecosystem and the atmosphere (GCOS 2003, 2004; GOFC-GOLD 2016). In this context, biomass was identified by the UNFCCC as an Essential Climate variable (GCOS 2003), whose determination is of great importance to reduce the uncertainties in our knowledge of the climate system. The importance of biomass manifests itself not only due to its role as a carbon sink or carbon source (Canadell et al. 2007; DeFries et al. 2002), but also due to its relevance for characterising forest or ecosystem productivity (Keeling and Phillips 2007).

Biomass inventories and biomass dynamics in local, regional and global scales are essential, though, up to now, largely unknown initialisation parameters of current climate models. A precise determination (on the order of 20%) of the spatial distribution of forest biomass would be sufficient to match the inaccuracy of terrestrial carbon fluxes to the other components of the carbon cycle (IPCC good practice guidance for land use, land use change and forestry2003).

The significance of an accurate knowledge of biomass is further underlined by the increased importance of two other aspects: (1) the increasing use of biomass for generating energy and the resulting increase in the proportion of greenhouse gases emitted from biomass (Fargione et al. 2008), and (2) the increased interest in reducing greenhouse gases by preventing deforestation and forest damage (UNFCCC 2016; UN-REDD Programme 2008; Herold and Johns 2007).

Despite its importance, estimations of biomass at local, regional and global scales are today very inaccurate. One reason for this is the large effort required for a precise estimation of forest biomass. Direct biomass measurements are destructive and therefore costly in terms of resources, effort and time (Chave et al. 2003). Usually, biomass is estimated on a single tree basis from a number of measurements such as tree height and/or diameter and the use of appropriate allometric relationships (Chave et al. 2005). The stand biomass levels are then obtained by summing up the single tree biomass levels up. In heterogeneous forests, this procedure is very arduous and often inaccurate, meaning that ground measurements of biomass in natural forests are never better than 20% (Chave et al. 2003). Particularly in tropical forest ecosystems there are large deviations also induced by allometric deviations. On larger scales, apart from the uncertainties arising from forest complexity, the different definitions, measurement protocols and used generalisation methods introduce additional inconsistencies in regional and national inventories and data bases. Finally, the Intergovernmental Panel on Climate Change (IPCC) recognises the lack of exact spatial forest biomass data (the measurement errors often exceed the estimated mean value) as one of the largest uncertainties in the global carbon budget.

Figure 2.36 demonstrates the actual stand of uncertainty. It compares four biomass maps of the Brazilian Amazon basin: on top left the Saatchi et al. 2007 map (Saatchi et al. 2007a), top right the Saatchi et al. 2011 map (Saatchi et al. 2011a), bottom left the Nogueira et al. 2008 map (Nogueira et al. 2008) and bottom right the Baccini et al. 2012 map (Baccini et al. 2012). All four are generated by combining ground and remote sensing data. However, each of them is using a different set of remote sensing data, different approaches to interpolate ground and remote sensing data, and/or different allometric relations. It is quickly evident that the four maps deliver strongly deviating mean biomass values, spatial distribution patterns and spatial biomass trends.

Fig. 2.36

Four different biomass classification maps for the Brazilian Amazon. Top left: Saatchi et al. (2007a), top right: Saatchi et al. (2011a), bottom left: Nogueira et al. (2008), bottom right: Baccini et al. (2012)

Biomass is an integrative forest parameter that depends on multiple tree or stand attributes. Starting from a single tree, the above ground stem biomass AGB_T is given by the product of the stem volume V_T with the (species specific) wood density ρ_T:

$$ {\mathrm{AGB}}_T={V}_T{\rho}_T=\frac{1}{4}{H}_T{\mathrm{DBH}}_T^2{F}_T{\rho}_T $$

(2.25)

where H_T is the (top) tree height, DBH_T the diameter at breast height, F_T is a (species dependent) form-factor accounting for the deviation from a pure cylinder shape. The wood density ρ_T typically varies between 0.5 and 0.69 g/cm⁻³ (GOFC-GOLD 2016). The so-called biomass expansion factor (BEF) is used to account for the total above ground biomass including branches, understorey, etc. contributions (Canadell et al. 2007).

However, single-tree measurements are ineffective for large areas and global applications. In contrast, forest stand parameters are an option with great potential as remote sensing systems can measure them globally. In order to develop methodologies that use forest stand parameter to estimate aboveground biomass, new allometric relationships accounting for stand rather single tree parameters need to be derived and investigated. In this sense, moving from a single tree to a stand, the above ground stand biomass AGB is obtained by summing up the biomasses of the N individual trees in the stand

$$ \mathrm{AGB}=\sum \limits_{i=1}^N{\mathrm{AGB}}_{Ti}=\sum \limits_{i=1}^N{V}_{Ti}{\rho}_{Ti}=\sum \limits_{i=1}^N\frac{1}{4}{H}_{Ti}{\mathrm{DBH}}_{Ti}^2{F}_{Ti}{\rho}_{Ti} $$

(2.26)

Substituting in (2.26) the basal area BA, that describes the amount of the stand area occupied by tree stems, the mean top height H_M and a mean wood density ρ_M

$$ \mathrm{BA}=\frac{1}{4}\sum \limits_{i=1}^N{\mathrm{DBH}}_{Ti}^2,{H}_M=\frac{1}{N}\sum \limits_{i=1}^N{H}_{Ti},F=\frac{1}{N}\sum \limits_{i=1}^N{F}_{Ti},{\rho}_M=\frac{1}{N}\sum \limits_{i=1}^N{\rho}_{Ti} $$

(2.27)

follows

$$ \mathrm{AGB}={\mathrm{BAH}}_M{F}_M{\rho}_M. $$

(2.28)

Equation (2.28) makes clear that an accurate estimation of stand biomass relies on the knowledge of three key parameters: the tree height and density (expressed for example by the basal area in (2.28)) which both together define the woody volume of the stem and the wood density. Today there is no remote sensing configuration able to measure directly all three parameters.

Radar, and particular SAR remote sensing techniques for the estimation of above ground forest biomass, can be divided into three categories: (1) direct, (2) model-based, and (3) allometric techniques. Direct techniques use empirical or statistical relationships to relate directly the radar observables (primarily radar backscatter measurements at a single or different polarisations but also polarimetric or interferometric correlations) to above ground forest biomass values. Model based approaches rely on electromagnetic scattering models to interpret the SAR data and to establish the relationship to biomass. Finally, in allometric techniques, the radar observables are used for the estimation of one or more physical forest parameters, as for example forest height, and then these parameters are related to forest biomass through allometric relations. The different approaches and techniques will be reviewed in the following.

2.5.1.2 Methodology

2.5.1.2.1 Direct Biomass Estimation

The first approaches to estimate forest biomass directly from backscatter measurements at different frequencies and polarisations date back to the early days of SAR remote sensing, and are today still an active research area. The basis of these approaches is the fact that with increasing forest biomass the (measured) backscatter intensity increases. Accordingly the backscattered intensity from a young forest with low biomass is in general weaker than the backscattered intensity from an old taller forest with high biomass. This has been observed, investigated and reported in the frame of airborne SAR experiments (at different frequencies and polarisations) already back in the eighties – early nineties (Le Toan et al. 1992; Rignot et al. 1994b; Imhoff 1995b; Dobson et al. 1995; Kasischke et al. 1995; Rauste et al. 1994; Harrell et al. 1995) These early results initiated a big interest in exploring SAR measurements for forest biomass estimation. Following experiments and work focused on studying and establishing (empirical) relations between biomass and SAR intensity measurements at the conventional HV, VV and HV polarisations.

A number of experiments performed over different forests and at different frequencies, indicated that the HV polarised (back-) scattering coefficient is strongly correlated to biomass, that this is often the case also for the HH scattering coefficient, while the correlation between biomass and VV scattering coefficient is often weak. However, at lower frequencies and/or sparse forest conditions the HH scattering coefficient is contaminated by dihedral scattering contributions (characterised by a strong directional backscattering behaviour) and is therefore stronger affected by topographic variations. Accordingly, HV is identified as the best polarisation for biomass inversion because it is less affected by the disturbing ground scattering contributions. Figure 2.37 shows P-band HV backscattering coefficient plotted against aboveground biomass for four different sites. Calibration factors of 5 dB and −3 dB have been added to the datasets from La Selva and Remningstorp, respectively. The solid line is the regression curve derived from the combined data (Le Toan et al. 2011).

Fig. 2.37

P-band HV backscattering coefficient plotted against aboveground biomass for four different sites. (Le Toan et al. 2011)

However, even if the experimental results appear in many cases convincing the theoretical interpretation relationships used where rather weak and largely based on simple forest scattering models. Today is known that that there are three critical limitations common to these studies/approaches:

• 1. At every frequency (and polarisation) the sensitivity of the backscattered SAR intensity decreases with increasing biomass level. This effect is often referred as “saturation” and imposes a maximum limit for which a biomass estimation is possible within a given accuracy. The sensitivity and with it the saturation limit increases with increasing wavelength (decreasing frequency). Authors generally agree upon that L-Band saturates between 40 t/ha and 100 t/ha, and P-band between 120 t/ha and 200 t/ha. Longer wavelengths like VHF as provided by the Swedish VHF sensor CARABAS are sensitive to biomass levels beyond 200 t/ha.

• 2. The empirical and semi-empirical relationships between backscattered SAR intensity and biomass depend on site conditions, and forest type and structure.

• 3. The fact that the backscattered SAR intensity depends also on the acquisition geometry, terrain topography, seasonal and environmental (dielectric) conditions make the interpretation of the backscattered SAR intensity in terms of biomass levels ambiguous.

In order to overcome these limitations model-based approaches have been developed.

2.5.1.2.2 Model-Based Estimation

Model-based approaches use electromagnetic scattering models to establish the relation between SAR observables, primarily the (back-) scattering coefficients at one or more polarisations, and biomass. The main motivation behind their development was twofold: to better control the dependency of the biomass relation on the individual site characteristics by parameterising propagation and scattering processes and to reduce the distortion due to non-vegetation scattering contributions by decomposing the total scattering into elementary scattering contributions.

While they have been many approaches investigated and proposed addressing model based biomass estimation one can distinguish two different model families: The first family of models develop from the so called Water Cloud Model (Attema and Ulaby 1978), are in general two layer models (i.e. volume and ground layer) and are applicable primarily at higher frequencies where canopy attenuation is relevant (Henderson and Lewis 1998); The second one is derived by means of radiative transfer modelling, accounting in general up to three layers (i.e. grown, trunk and ground layer) and appears more suited for the lower frequency range (Saatchi and McDonnald 1997; Saatchi and Moghaddam 2000; Mitchard et al. 2011). Both approaches rely on the separation (or interpretation) of volume and ground (including surface and/or dihedral) scattering contributions either by means of polarimetric scattering coefficients or covariance matrices. This allows, depending on the implementation, to incorporate topographic corrections.

However, there are two critical points that constrain the applicability and/or performance of these models: the first one is the large number of model parameters required in relation to the low dimensionality of conventional SAR observation spaces. This results in a large number of parameters/coefficients that have to be a-priori known or estimated from forest biomass reference data. The second one is the rather poor integration of the effect of forest biomass into EM scattering models at relevant frequencies. This is primarily because of our inability to describe in a realistic way the complex scattering interactions occurring within a forest under different conditions and at different scales. The fact that forest biomass by itself depends on a number of forest parameters makes this task even more complex.

The advantage of using multitemporal SAR acquisitions to improve the performance of biomass estimators was already recognized at a very early stage (Kurvonen et al. 1999). The availability of multiple SAR acquisitions increases the sensitivity of the SAR backscattered intensity to biomass and allows an estimation even beyond the saturation point as recent studies demonstrated (Santoro et al. 2011, 2013). More than 100 acquisitions per year are used to derive biomass estimates from C-band radar backscatter. Averaging across large number of acquisitions, performed under slightly different incidence angles in different environmental (i.e. weather) and seasonal conditions allows to overcome the saturation appearing in single image relationships. The price to be paid is the low spatial resolution resulting from the large number of samples required to obtain robust estimates. This has been demonstrated in Santoro et al. (2011) with a stock volume map of the boreal zone from ENVISAT-ASAR data with a resolution of 1 km × 1 km. Up to 300 m³/ha (approx. 150 tons/ha) no saturation effect could be detected.

The introduction of SAR interferometry in the late nineties had a significant impact on forest applications by improving the performance of existing applications when introducing both interferometric coherences and/or interferometric phases or triggering the development of new ones.

The interferometric coherence has been explored in terms of its temporal as well as in terms of its volumetric contributions. As the temporal decorrelation contribution dominated the early C-band repeat-pass interferometric spaceborne data available the first attempts where based on empirically relating the amount of change (i.e. temporal decorrelation) estimated in the interferograms to the biomass (or the stock volume, or the height) of the individual stands (Koskinen et al. 2001; Pulliainen et al. 2003; Eriksson et al. 2003b). In Wagner et al. (2003) ERS interferometric coherence in combination with JERS backscattering was used with success to classify the biomass levels across Siberia. The availability of repeat-pass space borne interferometric acquisitions with smaller temporal baselines and/or at longer wavelengths (L-band) with weaker temporal decorrelation contributions allowed the development of more physical interpretation and inversion models for the interferometric coherence able to distinguish between temporal and volume decorrelation contributions. This helped to improve biomass estimation and to obtain more robust estimates, especially in boreal forests (Santoro et al. 2002; Askne and Santoro 2009; Askne et al. 2013).

Besides the interferometric coherence, interferometric phase measurements have been also used to support biomass estimation in cases where the coherence level was allowing meaningful phase reconstruction. The so-called scattering center height, i.e. the height of the interferometric phase center with respect to the underlying ground has been used as a proxy for forest height in different biomass estimation schemas (Solberg et al. 2010, 2013; Treuhaft et al. 2015). However, the dependency of the phase center location on the acquisition geometry and terrain topography as well as on seasonal and environmental variation constrains its robustness especially at lower frequencies.

2.5.1.2.3 Allometric Biomass Estimation

Accurate forest height measurements can be used as a proxy for aboveground biomass estimates, especially in high biomass regions (Mette et al. 2003, 2004a, b). Differently than the conventional biomass estimates at stand level obtained by multiplying stock volume with mean wood density, biomass estimates from forest height measurements rely on the use of allometric relationships (Mette et al. 2003). A first approach in this direction was introduced in Mette et al. (2003) where a simple power law allometric relationship was proposed

$$ \mathrm{AGB}={l}_a{(1.66H)}^b. $$

(2.29)

where AGB is the stand biomass (Mg/ha), H is the forest dominant (top) height or H100 (height of the 100 largest trees per hectare (Reigber and Moreira 2000)), b is the allometric exponent and l_a a scaling factor known as allometric level. The allometric level accounts primarily for differences in stand densities but also tree species and site conditions and decreases from climax tree species to pioneer tree species. For estimating AGB from height measurements in the context of (2.29) the allometric level needs to be known. On regional (i.e. landscape) scale a mean allometric level can be assumed (under the assumption of similar tree species composition, logging practices, management concepts and growth conditions).

Height-to-biomass allometric relationships proved to be robust and able to provide accurate AGB estimates from forest height in homogenous forest conditions. This has been demonstrated for a number of boreal, and temperate sites with different conditions. However, the approach meets its limitations in forest of heterogeneous structure and density. This is shown in Fig. 2.38 where the height (i.e. H100) to biomass relationship for four European forest test sites. The results have been achieved by using a common allometric exponent of 0.52 and site adapted values for the allometric level. The three more heterogeneous sites, namely Traunstein, Ebersberger Forst and the Nationalpark Bayrischer Wald, are characterised by a lower height–biomass correlations indicating the insufficiency of a fixed allometric level to represent the height to biomass relationship. On the other hand, the more homogeneous, in terms of horizontal and vertical structure, boreal forest in Krycklan is well described by a single allometric level. The correspondences obtained for the four test sites between the biomass estimated from ground measurements and using the height to biomass allometry are shown in Fig. 2.39. 

Fig. 2.38

Height to biomass allometry for four European forest test sites. Top left: Traunstein Site in Germany; top right: Ebersberger Forst in Germany; bottom left: Bayrischer Wald in Germany; bottom right: Krycklan in Sweden

The high correlation between forest height and biomass has been explored in Toraño-Caicoya et al. (2016a) to use forest height estimated from TanDEM-X interferometric data to estimate successfully biomass at boreal forests by means of (2.29).

In order to improve the performance of the conventional forest height to biomass allometry that degrades in structurally heterogeneous forests the direct or indirect use of forest structure information in (2.29) has been proposed and is currently investigated by several groups. The forest structure information can be obtained from inventory data or even more relevant from 3-D radar reflectivity reconstructed from tomographic measurements. One such example has been recently presented in Toraño-Caicoya et al. (2015) where the use of vertical structure information derived from 3-D radar reflectivity reconstructed at L-band by means of tomographic SAR techniques has been used to improve the performance of the height to biomass allometry. First the vertical reflectivity profile F(z) is expressed in terms of a Legendre polynomial series

$$ F(z)=\sum \limits_n{a}_n{P}_n(z)\kern0.5em \mathrm{where}\kern0.5em {a}_n=\frac{2n+1}{2}{\int}_{-1}^1F(z){P}_n(z) dz $$

(2.30)

where P_n(z) are the Legendre polynomials and a_n the associated Legendre coefficients. The first four Legendre coefficients (a₁, …a₄) are then used to define a structure ratio S_rat that allows to distinguish between different allometric levels

$$ {S}_{\mathrm{rat}}=\frac{\left|{a}_1\right|}{\left|{a}_2+{a}_3+{a}_4\right|}. $$

(2.31)

Fig. 2.39

Height and structure to biomass allometry for four European forest test sites. Top left: Traunstein Site in Germany; top right: Ebersberger Forst in Germany; bottom left: Bayrischer Wald in Germany; bottom right: Krycklan in Sweden

The lower frequency contribution, expressed by the first Legendre coefficient (a₁), is associated to the stem compartment while the higher frequency components, represented by the higher order coefficients a₂, a₃ and a₄ are associated to the crown/canopy compartment. Accordingly, the structure ratio S_rat S_rat may be used as a proxy to stand density to improve the allometric biomass estimation (Toraño-Caicoya et al. 2016b)

$$ \mathrm{AGB}=7{S}_{\mathrm{rat}}^{0.8}{H}^b. $$

(2.32)

Thus, for a constant height, if the numerator of the ratio increases (indicating a higher proportion of stem biomass), biomass increases, and if the denominator increases (indicating a higher proportion of crown biomass) biomass decreases. Figure 2.46 shows the improvement achieved by using (2.35) instead of (2.32). The high variance produced by the “height to biomass” allometric relation in (2.32) can be corrected with the inclusion of forest structure information.

2.5.1.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on biomass estimation are summarized in Table 2.9 and further described in the Appendix.

Table 2.9 Test sites and corresponding radar and validation data selected for the generation of showcases on biomass estimation with allometric relationships

Biomass maps have been obtained in the two selected test sites in two steps: first by estimating forest height from interferometric TanDEM-X and second by estimating biomass from height using following allometric relation provided by the Swedish National Forest Service Inventory (SLU)

$$ \mathrm{AGB}=0.3{H}^2. $$

(2.33)

Results are shown in Fig. 2.40.

Fig. 2.40

Biomass estimation using forest height-tobBiomass allometry. Left panel: Krycklan, TanDEM-X (27.02.2011), 13.5 × 18.8 km; right panel: Remningstorp, 9.3 × 11.3 km, 30.12.2011. From top to bottom: single look complex amplitude, coherence scaled from 0 (black) to 1 (white), forest height map scaled from 0 to 40 m, and biomass (classification) map. The 5 biomass classes are colored from light to dark green according to the mean biomass (center value) of each class

The accuracy of the estimated biomass depends on two error sources: the accuracy of the estimated height-to-biomass relationship (ΔAGB) and the accuracy of the forest height estimates (ΔH). ΔAGB is defined by the forest conditions and can only be improved when additional forest parameters (like forest density, structural parameters, etc.) are included in the allometric estimation process. Under the assumption of homogenous stand conditions across the boreal region, ΔAGB can be assumed constant and it is estimated from the bias observed in the height-to-biomass relationship applied to the reference data. ΔH depends on forest height estimation methodology and performance. Airborne lidar measurements provide height estimates with sub-meter accuracy and are therefore used as a reference.

For forest heights obtained from TanDEM-X data, ΔH depends, in general, on the acquisition mode (single-pol, dual-pol, dual-baseline) the number of available acquisitions (see Sect. 2.2) and on the associated range of spatial baseline.

Accordingly, the total biomass estimation sensitivity (ΔABG_tot) can be expressed as

$$ {\Delta \mathrm{AGB}}_{\mathrm{tot}}=\frac{\partial AGB}{\partial H}\Delta H+\Delta \mathrm{AGB}. $$

(2.34)

Using (2.33) in (2.34) it follows:

$$ {\Delta \mathrm{AGB}}_{\mathrm{tot}}=0.6H\Delta H+\Delta \mathrm{AGB}. $$

(2.35)

ΔH and ΔAGB determine the accuracy of biomass estimation. However, assuming the allometric error ΔAGB to be independent from H, the biomass estimation accuracy is driven by ΔH only.

Figure 2.41 shows classification performance obtained by means of (2.33) for a relative height error of 0% (top left) and 10% (top right), and 1 (bottom left) and 3 m (bottom right) absolute errors. The real biomass is plotted on the y-axis, the estimated biomass, for a 90% confidence interval, is plotted on the x-axis in 10 Mg/ha biomass steps. The blue dashed lines indicate the class boundaries, estimated at the point in which two biomass intervals do not overlap. Assuming an error free height measurement (ΔH = 0), up to 9 biomass classes can be obtained. This is the best performance that can be achieved, due to the residual error in ΔAGB. In case of a 10% height error five classes can be distinguished. For height errors larger than 20% only two biomass classes can be separated reducing the classification to a forest/non forest classification.

Fig. 2.41

Biomass estimation performance based on (2.36) for a 90% confidence interval for relative height errors on the top panel (0 left and 10% right) and absolute height errors on the bottom (1 m left and 3 m right) panel

The analysis above makes clear that the biomass estimation performance reacts very sensitive to height errors. Consequently, reliable and robust biomass estimates require accurate and robust height estimates which again strongly depend on the polarimetric configuration of the observation space. The performance shortcomings of dual-polarimetric observations in terms of:

• 1. biased estimation results due to the lack of appropriate observation dimensionality to account for ground depolarisation (especially at lower frequencies and/or sparse forest conditions);

• 2. larger amount of forest types/samples with model mismatch (due to the over constrained model);

• 3. larger variance of the obtained forest height estimates when compared to the inversion results achieved by using the full polarimetric information;

can be widely compensated by using quad-polarimetric observations.

2.5.1.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

Single-pol data interferometric data at a single baseline do not provide enough measurable to invert forest height from interferometric data without a-priori information on terrain topography. A single-pol inversion is possible when multiple baselines are available but the performance is compromised by the presence of temporal decorrelation and the ratio of the spatial baselines. On the other hand, forest height inversion is possible with dual-polarimetric interferometric data taking into account a reduced estimation performance when compared to the quad-polarimetric case. The availability of quad-polarimetric interferometric measurements - that allows the implementation of adaptive optimisation techniques - is critical when algorithm robustness and performance matters.

2.5.2 Biomass Estimation from Semi-empirical Relationships

2.5.2.1 Introduction, Motivation and Literature Review

Understanding the terrestrial carbon cycle and predicting future climate changes are important topics in climate research. One of the major uncertainties in the current carbon cycle models lies in terrestrial ecosystems, mainly forests (Solomon et al. 2007). Rather than estimating forest carbon directly, biomass can be used instead since about 50% of biomass is carbon. Furthermore, above-ground biomass B [t/ha] is often used as a proxy indicator which is estimated from remote sensing measurements, e.g. using P-band (ca 450 MHz) SAR as discussed in this Section. B is here defined as dry weight and includes stem, bark, branches, and needles/leaves, but excludes stump and roots.

Several studies of using P-band SAR for forest biomass retrieval have been performed in the past. The early studies (Ranson and Sun 1994; Imhoff 1995a; DeFries et al. 2002; Rauste et al. 1994; Beaudoin et al. 1994; Rignot et al. 1995) concluded that HV-polarized backscatter shows highest correlation with biomass. In later studies (Hoekman and Quiñones 2000; Rignot et al. 1995; Santos et al. 2003), retrieval models were extended to other polarisation channels, showing improved retrieval results. In Saatchi et al. (2007b, 2011b) and Sandberg et al. (2011), the need for topographic corrections was pointed out and models were improved. In Neumann et al. (2012), polarimetric and interferometric SAR observables were also used. Complementary approaches include polarimetric SAR interferometry (Cloude and Papathanassiou 1998; Papathanassiou and Cloude 2001; Cloude and Papathanassiou 2003; Neumann et al. 2010) or SAR tomography (Cloude 2006; Reigber and Moreira 2000; Tebaldini 2010). Although the models presented in the mentioned articles show promising results, the analysis were limited to a single test site and the diversity of the data was low. Therefore, the extrapolation capabilities of the models remain untested.

2.5.2.2 Methodology

Biomass retrieval using the following two polarimetric SAR models is analysed:

$$ {\displaystyle \begin{array}{l}\left(\mathrm{M}1\right)\ \ln B=3.280+0.138{\left[{\gamma}_{HV}^0\right]}_{dB}+0.049{\left[{\gamma}_{HH}^0\right]}_{dB}-0.113{\left[{\gamma}_{VV}^0\right]}_{dB}\\ {}\left(\mathrm{M}2\right)\ \ln B=3.129+0.093{\left[{\gamma}_{HV}^0\right]}_{dB}+\left(0.020+0.605u\right)\left({\left[{\gamma}_{HH}^0\right]}_{dB}-{\left[{\gamma}_{VV}^0\right]}_{dB}\right)\end{array}} $$

(2.36)

The coefficients were estimated by least squares using the 97 circular plots in Krycklan (for each plot, four data points representing each flight heading were used). The first model is a linear combination of the three like-pol backscatter channels. The second model is a model proposed in Soja et al. (2013), which includes HH/VV ratio (which was found to be less susceptible to temporal and topographic changes), and the ground-slope angle u, which introduces a first-order topographic correction. The models were tested in Solomon et al. (2007) for sensitivity to site, topography and temporal change. Furthermore, the models were evaluated using two sets of test data from two different test sites. The test sites are located 720 km apart and represent two different cases of boreal forest. Models fitted to data from one test site are evaluated on the other. In this manner, the model is validated independently of the training data set.

Biomass retrieval using a third model is also analysed, i.e. the single-pol model according to

$$ \left(\mathrm{R}1\right)\ \ln B={C}_0+{C}_1\left({\left[{\gamma}_{HV}^0\right]}_{dB}-0.766\right) $$

(2.37)

where C₀ = 3.8914 and C₁ = 0.1301 (Le Toan et al. 2011).

2.5.2.3 Experimental Results

Test sites and corresponding radar and validation data sets selected for the generation of showcases on direct biomass estimation with semi-empirical relationships are summarized in Table 2.10 and further described in the Appendix.

Table 2.10 Test sites and corresponding radar and validation data selected for the generation of showcases on biomass estimation

Averaged, stand-wise backscatter data were extracted from the geocoded SAR images for all stands and plots in both Remningstorp and Krycklan. A 50 × 50 m DEM was used for geocoding and normalisation. Although high-resolution lidar DEMs were also available for both test sites, they were not used because the evaluation scenario would be less realistic as comparable DEM resolutions are not available on global scale. All normalisation procedures were performed before averaging, that is on high-resolution SAR data. A buffer zone of 10 m was also added to avoid border effects.

Quantitative results for model M1 are shown in Fig. 2.42. Scatter plots for biomass for the 58 lidar stands and 10 field plots in Remningstorp are shown. Model parameters were extracted in Krycklan. As it can be seen in the figure, biomass is overestimated by 25–50 t/ha. Root mean square error (RMSE) for all data (all acquisitions at all headings and all dates) is measured to 39% of the mean biomass of 181 tons/ha (RMSE is estimated for field plots, for which biomass estimation error is a few per cent). For model M4, the corresponding results are shown in Fig. 2.44. RMSE is 25%, and bias is much lower than for model M1. It is thus concluded, that the inclusion of the HH/VV ratio and topography notably improves retrieval performance.

Fig. 2.42

Scatter plot for model M1. For each stand/plot, all available acquisitions are shown

Biomass maps for model M1 and M4 are shown in Figs. 2.43, 2.44, and 2.45. For M1, overestimation can be observed in many places in the maps. For M4, overestimation can be observed in some limited regions. This overestimation can been explained by physical scattering properties; see (Le Toan et al. 2011).

Fig. 2.43

Remningstorp: biomass maps for model M1. One single image for the 179-degree heading was used for each date to create SAR-based biomass maps (IDs: 0110, 0206, and 0412, March to May, respectively)

Fig. 2.44

Scatter plot for model M4. For each stand/plot, all available acquisitions are shown

Fig. 2.45

Remningstorp: biomass maps for model M4. One single image for the 179-degree heading was used for each date to create SAR-based biomass maps (IDs: 0110, 0206, and 0412, March to May, respectively)

In Figs. 2.46 and 2.47, quantitative results and biomass maps are shown for single-pol model R1. The model overestimates biomass gravely for almost all stands and is thus not suitable for across-site biomass retrieval.

Fig. 2.46

Scatter plot for model R1. For each stand/plot, all available acquisitions are shown

Fig. 2.47

Remningstorp:biomass maps for model R1. One single image for the 179-degree heading was used for each date to create SAR-based biomass maps (IDs: 0110, 0206, and 0412, March to May, respectively)

2.5.2.4 Discussion on the Role of Polarimetry, on the Maturity of the Application and Conclusions

The inclusion of polarimetry significantly improves biomass retrieval performance for regression-based models. Using the HH/VV-ratio, the geophysical variability common for both HH and VV is eliminated (for example, moisture, topography and structure). Using the slope angle u, the influence of topography is reduced.

2.6 Summary

Table 2.11 Summary of presented application, methods and preferred system configurations for forest monitoring