Abstract
This chapter critically summarizes the main theoretical aspects necessary for a correct processing and interpretation of the polarimetric information towards the development of applications of synthetic aperture radar (SAR) polarimetry. First of all, the basic principles of wave polarimetry (which deals with the representation and the understanding of the polarization state of an electromagnetic wave) and scattering polarimetry (which concerns inferring the properties of a target given the incident and the scattered polarized electromagnetic waves) are given. Then, concepts regarding the description of polarimetric data are reviewed, covering statistical and scattering aspects, the latter in terms of coherent and incoherent decomposition techniques. Finally, polarimetric SAR interferometry and tomography, two acquisition modes that enable the extraction of the 3-D scatterer position and separation, respectively, and their polarimetric characterization, are described.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
1.1 Theory of Radar Polarimetry
1.1.1 Wave Polarimetry
Polarimetry refers specifically to the vector nature of the electromagnetic waves, whereas radar polarimetry is the science of acquiring, processing and analysing the polarization state of an electromagnetic wave in radar applications. This section summarizes the main theoretical aspects necessary for a correct processing and interpretation of the polarimetric information. As a result, the first part presents the so-called wave polarimetry that deals with the representation and the understanding of the polarization state of an electromagnetic wave. The second part introduces the concept of scattering polarimetry. This concept collects the topic of inferring the properties of a given target, from a polarimetric point of view, given the incident and the scattered polarized electromagnetic waves.
1.1.1.1 Electromagnetic Waves and Wave Polarization Descriptors
The generation, the propagation and the interaction with matter of the electric and the magnetic waves are governed by Maxwell’s equations (Balanis 1989). For an electromagnetic wave that is propagating in the \( \hat{\mathbf{z}} \) direction, the real electric wave can be decomposed into two orthogonal components \( \hat{\mathbf{x}} \) and \( \hat{\mathbf{y}} \), admitting the following vector formulation:
which may be also considered in a complex form
where E0x and E0y are the amplitudes of the waves in each coordinate. The electric wave in (1.1) and (1.2) presents a harmonic time dependence of the type ejωt, where ω = 2πf is the angular frequency and f is the time frequency. The propagation direction of an electromagnetic wave is determined by the propagation vector \( \hat{\mathbf{k}} \) that in case of (1.1) and (1.2) is considered parallel to \( \hat{\mathbf{z}} \). The amplitude of the propagation vector is represented by k = 2π/λ, where λ is the wavelength. Finally, δx and δy represent the wave phases in each component. The magnetic wave \( \overrightarrow{\mathbf{H}}\left(z,t\right) \) can be also represented in the same form.
According to the IEEE Standard Definitions for Antennas (IEEE standard number 145 1983), the polarization of a radiated wave is defined as that property of the radiated electromagnetic wave describing a time-varying direction and relative magnitude of the electric wave vector, specifically the figure traced as a function of time by the extremity of the vector at a fixed location in space and the sense in which it is traced as observed along the direction of propagation. Hence, polarization is the curve traced out by the end point of the arrow representing the instantaneous electric wave.
Let us consider the geometric locus described by the electric wave, as a function of time, for a particular point in space, which can be assumed z = z0, without loss of generality. Under these hypotheses, the wave components Ex and Ey satisfy the following equation:
The previous equation describes an ellipse that is called polarization ellipse. As one may deduce from the previous equation, the electric wave, as a function of time, describes in the most general case an ellipse, whose shape does depend neither on time nor on space. The polarization ellipse, for some particular configurations, may reduce to a circle or to a line.
As it may be deduced from (1.3), the polarization state is completely characterized by three independent parameters: the wave amplitudes E0x and E0y and the phase difference δ = δy − δx. Figure 1.1 presents the polarization ellipse for a general polarization state. In addition to the previous three parameters, it is also possible to describe the polarization ellipse by a different set of parameters:
-
Orientation or tilt angle ϕ. This angle gives the orientation of the ellipse major axis with respect to the \( \hat{\mathbf{x}} \) axis in such a way that ϕ ∈ [−π/2, π/2]. This angle may be obtained as follows:
-
Ellipticity angle τ. This angle represents the ellipse aperture in such a way that τ ∈ [−π/4, π/4]. This angle may be obtained as follows:
-
The polarization sense or handedness. This determines the sense in which the polarization ellipse is described. This parameter is given by the sign of the ellipticity angle τ. Following the IEEE convention (IEEE standard number 145 1983), the polarization ellipse is right-handed if the electric vector tip rotates clockwise for a wave observed in the direction of propagation, given by \( \hat{\mathbf{k}} \). On the contrary, it is said to be left-handed. Therefore, for τ < 0 the polarization sense is right-handed, whereas for τ > 0 it is left-handed.
-
The polarization ellipse amplitude A. For a major and minor ellipse axes amplitudes a and b, respectively, \( A=\sqrt{a^2+{b}^2} \). This amplitude may be also obtained as
-
The absolute phase ζ. This phase represents the initial phase with respect to the phase origin for t = 0 in such a way that ζ ∈ [−π, π]. This term corresponds to the common phase in δx and δy. This absolute phase cannot be directly measured as it corresponds to the exit phase from the radar system at t = 0.
Considering the previous sets of parameters describing the polarization state of a wave, one can identify some important polarization states that can be considered as canonical polarization states:
-
Linear polarization state. Considering the expression for the real electric wave in (1.1), two canonical linear polarization states can be identified. Table 1.1 details the orientation and the ellipticity angles for these polarization states. These are the linear polarization states according to the \( \hat{\mathbf{x}} \) and to the \( \hat{\mathbf{y}} \) axes, respectively. The linear polarization states are characterized by presenting a phase difference of
As it may be seen, the linear nature of the polarization state is independent of the phase ζ.
-
Circular polarization state. In this particular case, also two canonical circular polarization states can be defined. Table 1.1 details the orientation and the ellipticity angles for these polarization states. When the ellipticity angle takes a value of −π/4, the circular polarization state is right-handed, whereas this value is equal to π/4 when it is left-handed. The circular polarization states are characterized by presenting a phase difference of
and equal amplitudes for the components of the electric wave E0 = E0x = E0y. Also for circular polarization states, the polarization state is independent of the absolute phase ζ.
-
Elliptical polarization state. When there are not restrictions on the orientation and ellipticity angle values, the electric wave is said to present an elliptical polarization state.
As observed, the polarization ellipse may be completely described by two equivalent sets of three independent parameters: the set of wave parameters {E0x, E0y, δ} or the set of ellipse parameters {ϕ, τ, A}. In addition to these, there exist additional equivalent descriptors that are detailed in the following.
Considering (1.1), the real electric wave vector can be directly obtained from the complex electric wave vector
where ℜ{⋅} denotes the real part. The time dependence has been removed from the wave description. This is possible as the polarization state of the wave does not change with time. In order to derive a simple and concise description of the polarization state, it is also possible to remove the space dependence of \( \overrightarrow{\underline {\mathbf{E}}}(z) \) by considering the polarization state in a particular point of the space. Without loss of generality, this point can be z = 0. Hence, \( \overrightarrow{\underline {\mathbf{E}}}(0) \) reduces to
The two-dimensional complex vector \( \underline {\mathbf{E}} \) is referred to as the Jones vector, and it is a concise representation of a monochromatic, uniform plane wave with a constant polarization (Jones 1941a; Jones 1941b; Jones 1941c).
In the rectangular coordinate system, the Jones vector can be written as a function of the parameters that describe the polarization ellipse (Huynen 1970):
The Jones vector, considering the unitary vectors \( \hat{\mathbf{x}} \) and \( \hat{\mathbf{y}} \), may be also expressed as
where the sub-index \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\} \) indicates that the Jones vector is expressed in the linear basis \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\} \). The Jones vector describes completely the polarization ellipse shape, as well as the rotation sense of the electric wave vector. On the contrary, handedness information cannot be included within the Jones vector as propagation information has been removed. The use of the Jones vector to describe the polarization state is of enormous importance as it allows to define a polarization algebra that makes possible to perform a mathematical treatment and analysis of the wave polarization. This treatment allows, for instance, the correct definition of orthogonal polarization states. Finally, Table 1.2 details the Jones vector, in the rectangular basis, i.e. \( {\underline {\mathbf{E}}}_{\left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\}} \), for some particular polarization states.
Another equivalent description of the wave polarization state is the so-called complex polarization ratio:
As in the case of the Jones vector, the complex polarization ratio is not able to determine the handedness of the polarization state as propagation information is removed.
The Jones vectors, as well as the complex polarization ratio, are complex quantities that describe the polarization state of a wave. Sir G. Stokes introduced a wave polarization and wave amplitude description based on four real quantities in polarization wave optics (Stokes 1852). The Stokes vector, in the rectangular coordinate system, is defined as (Stokes 1852)
where the elements of the vector \( \underline {\mathbf{g}} \) are simply called Stokes parameters. Consequently, the Stokes vector is a four-dimensional real vector. Since the Stokes vector describes the polarization state of an electromagnetic wave, it can be directly obtained from the geometrical parameters that describe the polarization ellipse, i.e. {ϕ, τ, A}:
The polarization state of an electromagnetic wave is completely characterized by means of three independent parameters. These statements also hold for the Stokes parameters, since, as it may be deduced from (1.15), the following relation applies
Table 1.3 details the Stokes vector, in the rectangular basis, i.e. \( {\mathbf{g}}_{\left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\}} \), for some particular polarization states.
1.1.1.2 Totally and Partially Polarized Waves
Single-frequency or monochromatic waves are completely polarized, that is, the tip of the electric wave vector describes an ellipse in the plane orthogonal to the propagation direction. The shape of this ellipse, neglecting attenuation propagation effects which affect only the overall power, does not change in time or space, and hence, the wave polarization is constant. Completely polarized waves appear when the different parameters of the wave ω, E0x, E0y, δx and δy are constant. Nevertheless, many waves present in the nature are characterized by the fact that the previous parameters depend on time or on space randomly. Hence, the tip of the electric wave vector no longer describes an ellipse. These waves are referred to as partially polarized waves. This loss of polarization is due to the randomness of the illuminated scene, to the presence of noise, etc.
The different parameters that characterize the electric wave, i.e. ω, E0x, E0y, δx and δy, may vary randomly. This type of variation makes the electric wave to be modulated and therefore to present a finite bandwidth, so waves can no longer be considered as being monochromatic, but polychromatic. Under this circumstance, it would be also desirable to have a complex representation of the electromagnetic wave as shown in (1.10). Nevertheless, in most of the applications, we are interested into electromagnetic waves that will only have appreciable values in a frequency range which is small compared to the mean frequency ω. Under this situation, waves are referred to as quasi-monochromatic waves. For such signals, the phase terms Θx(z, t) and Θy(z, t) change slowly when compared to the mean frequency. Then, one may represent the Jones vector of a quasi-monochromatic wave as
As one may see, the Jones vector of a quasi-monochromatic electric wave depends on time and on space; thus, this vector is no longer constant. When the time dependence of the Jones vector is deterministic, the polarimetric properties of the wave also change in a deterministic way through time. In this case, the description of the wave polarization is not problematic and may be performed considering the different descriptors detailed in Sect. 1.1.1.1. Nevertheless, if the time dependence is random, the analysis of the polarization state of the electromagnetic wave must be carefully addressed, as this description must take into account the stochastic nature of the electric wave.
As previously mentioned, the variation of the parameters E0x, E0y, δx and δy may be random, so the Jones vector will be also random. In order to characterize the polarization of the quasi-monochromatic electromagnetic wave expressed by the variable Jones vector in (1.17), it is necessary to address this characterization from a stochastic point of view. In the frame of radar remote sensing, the wave transmitted by the radar system may be considered monochromatic and hence totally polarized. Nevertheless, the scattered wave represented by the Jones vector in (1.17) results from the combination of many different waves originated by the different elementary scatterers that form the scattering media. The complex addition of these elementary waves resulting from the scattering process for one component of the electric wave can be represented as
where A represents the total wave and \( {a}_n{e}^{j{\theta}_n} \) is originated from the scattering from every elementary scatterer. Under the assumption of N, i.e. the total number of scattered waves, to be large enough and certain relations that may be established between the amplitude and the phase of the elementary waves (Chandrasekhar 1960; Goodman 1976), it is possible to demonstrate that the mean value of the electric wave and the Jones vector are zero. Consequently, the Jones vector cannot be employed to characterize the polarization state of a quasi-monochromatic wave. This characterization shall be performed considering higher statistical moments.
The second-order moments may be arranged in a vector form, giving rise to the so-called coherency vector of a quasi-monochromatic vector, which is defined in the following way:
where J stands for the temporal averaging, assuming the wave is stationary, ⊗ is the Kronecker product, (⋅)∗ represents complex conjugation and E{⋅} is the ensemble average. This vector is not zero for quasi-monochromatic waves. The arrangement of the second-order moments can be also done in a matrix, giving rise to the coherency matrix of the wave:
where the superscript (⋅)T denotes vector transposition.
In the previous section, it was mentioned that monochromatic waves are completely polarized. This is not the case for quasi-monochromatic waves. Indeed, completely polarized waves present a polarization state that can be considered as a limit in the sense that it is constant. The opposed extreme is a completely unpolarized wave for which the polarization state is completely random. Between both extremes, waves are said to present a partial polarization state. In order to characterize the degree of polarization, one may consider the degree of polarization defined as a function of the trace of matrix J as
1.1.1.3 Change of Polarization Basis
As seen in Sect. 1.1.1.1, an electromagnetic wave, considering the coordinate system \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}},, \hat{\mathbf{z}}\right\} \), that propagates in \( \hat{\mathbf{z}} \) may be decomposed as the sum of two orthogonal components. Separately, the electromagnetic wave of each component can be considered as linearly polarized. Therefore, it is possible to consider that the total electromagnetic wave results from the sum of two orthogonal linear polarized waves. Indeed, this representation must be extended in the sense that any electromagnetic wave propagating in an infinite, lossless, isotropic media can be decomposed as the sum of two orthogonal elliptically polarized waves. The advantage of this representation is that the electric wave is decomposed in a pair of orthogonal polarization states, so it is possible, through a deterministic transformation, to obtain the electric wave for any other pair of orthogonal polarization states. This process is referred to as change of polarization basis or polarization synthesis.
Given two vectors a and b, they are considered orthogonal if they verify
that is, the scalar (Hermitian) product of both vectors is zero. In case of two electromagnetic waves, expressed in terms of the corresponding Jones vectors, they are said to be orthogonal if the scalar product of the Jones vectors is zero, considering that both Jones vectors refer to waves propagating in the same direction and sense. The polarization ellipses corresponding to two orthogonal Jones vectors presents the same ellipticity angle, opposite polarization sense and mutually orthogonal polarization axis. That is, for a Jones vector representing a polarization state characterized by an orientation angle ϕ, an ellipticity angle τ and an absolute phase ζ, its orthogonal Jones vector presents an orientation angle of value ϕ + π, an ellipticity angle of value −τ and an absolute phase −ζ. In terms of (1.12), the corresponding orthogonal vector is
The symbol ⊥ denotes orthogonal Jones vector.
Considering what has been indicated, an electromagnetic wave propagating in an infinite, lossless, isotropic media may be described in the following way:
where the notation referring to the unitary vectors has been generalized. If (1.23) and (1.24) are considered, it may be seen that the unitary Jones vectors corresponding to the linear orthogonal polarization states \( \hat{\mathbf{x}} \) and \( \hat{\mathbf{y}} \) are transformed to the Jones vector of any polarization state and the corresponding orthogonal Jones vector through the transformation matrix U:
In the previous case, the matrix \( {\mathbf{U}}_{\left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\}} \) indicates the transformation matrix from the orthogonal basis \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\} \) to the arbitrary basis \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \). Considering (1.24), the electromagnetic wave expressed in the orthogonal basis \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \) takes the form
Therefore, the Jones vector in the new basis \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \), expressed in terms of the Jones vector in the basis \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}}\right\} \), is
The previous equation indicates that if an electromagnetic wave has been measured in the linear orthogonal basis, it is possible to calculate the same electromagnetic wave, but measured in a different polarization basis, just multiplying by the matrix \( {\mathbf{U}}_{\left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\}}^{-1} \). That is, it is possible to synthesize the electromagnetic wave for any arbitrary polarization basis just measuring it in a particular polarization basis.
Table 1.4 and Table 1.5 detail the polarization ellipse parameters, the Jones vector and the Stokes vector for different polarization states for the rotated and the linear polarization bases, respectively.
1.1.2 Scattering Polarimetry
The previous section was concerned with the characterization and the representation of the polarization state of an electromagnetic wave. Although this characterization is important when a radar system is considered, as it transmits and receives electromagnetic waves, nevertheless, the interest is on the scattering process itself. The radar system transmits an electromagnetic wave, with a given polarization state, that reaches the scatterer of interest. The energy of the incident wave interacts with the scatterer, and as a result part of this energy is reradiated to the space. The way this energy is reradiated depends on the properties of the incident wave, as well as on the scatterer itself. Consequently, it is possible to infer some information of the scatterer under consideration considering the properties of the scattered electromagnetic wave with respect to the incident wave, which is basically the transmitted wave by the radar. One possibility that can be studied to characterize distant targets is to consider the change of the polarization state that a scatterer may induce to an incident wave.
In order to analyse the scattering problem, it is worth to start describing the scattering process that occurs when an incident wave reaches a flat transition between two dielectric, infinite, lossless and homogeneous media in oblique incidence. This scattering situation is exemplified in Fig. 1.2. In this case, the incident wave that propagates in the first media reaches the transition between media where part of the incident energy is scattered in the same media and part of the energy is transmitted to the second media. In order to characterize the scattering process, it is necessary to introduce the concept of plane of scattering, which is defined as the plane generated by the propagating vectors of the incident and the scattered waves.
In order to examine specifically reflections at oblique angles of incidence for a general wave polarization, it is convenient to decompose the electric wave into its perpendicular and parallel components, relative to the plane of scattering. The total scattered and transmitted waves will be the vector sum from each of these two polarizations. When the wave is perpendicular to the plane of scattering, the polarization of the wave is referred to as perpendicular polarization or horizontal polarization as the electric wave is parallel to the interface. When the electromagnetic wave is parallel to the plane of scattering, the polarization is referred to as parallel polarization or vertical polarization as the electromagnetic wave is also perpendicular to the interface. As indicated in Fig. 1.2, the total incident wave \( {\overrightarrow{\underline {\mathbf{E}}}}^i \) can be decomposed into two orthogonal components in the plane orthogonal to the incident propagation vector \( {\hat{\mathbf{k}}}^i \). These are the parallel \( {\overrightarrow{\underset{\_}{\mathbf{E}}}}_{\parallel}^i \) and the perpendicular \( {\overrightarrow{\underline {\mathbf{E}}}}_{\perp}^i \) components, which can be written as
As observed, the incident wave has been defined with respect to the coordinate system \( \left\{{\hat{\mathbf{x}}}^{\prime },{\hat{\mathbf{y}}}^{\prime },{\hat{\mathbf{z}}}^{\prime}\right\} \) in such a way that \( {\hat{\mathbf{k}}}^i={\hat{\mathbf{z}}}^{\prime } \). It may be shown that the scattered wave components can be written similarly
but in this case according to \( \left\{{{\hat{\mathbf{x}}}^{\prime\prime }},{{\hat{\mathbf{y}}}^{\prime\prime }},{{\hat{\mathbf{z}}}^{\prime\prime}}\right\} \).
Considering the equations of the incident and the scattered wave, the question rising at this point is to determine whether it is possible or not to express mathematically the scattering process that occurs at the interface between both media. First of all, it is of crucial importance to take into consideration where, in the space, the expressions of the incident and scattered waves are valid. The expressions in (1.28), (1.29), (1.30) and (1.31) make reference to uniform plane waves. In the case of the incident wave on the scatterer, such a description for the wave, i.e. the wave originated at the transmitting antenna, is only valid if the scatter is in the far-field zone of the transmitting antenna. In the case of the scattered wave, this wave admits a uniform plane wave formulation if the point where the wave is considered is in the far field of the scatterer. In both cases, the waves in the far-field zone may be considered spherical waves, which locally may be considered as uniform plane waves. Considering a spherical coordinate system centred in the scatterer and under the previous assumptions, the incident wave on the scatter can be expressed vectorially, in the far-field zone, as
As observed, there are different points that need to be considered in the analysis of this problem. The first one is the use of different coordinate systems to characterize, in an unambiguous way, the polarization state of the different waves involved in the scattering process. The second aspect, coupled to the previous one, is to determine the way the scatterer under study changes the different components of the wave. This section has studied this entire problem considering the analytical expressions of the waves.
1.1.2.1 The Scattering Matrix
This section will address the generalization of the previous scattering problem, and it will introduce those concepts necessary to address it in a vector form. The first aspect that needs to be fixed is to determine the different coordinate systems necessary to characterize the scattering problem and the description of the incident and the reflected waves. In the scattering problem, three coordinate systems must be chosen. The first one is the coordinate system located at the centre of the scatterer under consideration and referred to as \( \left\{\hat{\mathbf{x}},, \hat{\mathbf{y}},, \hat{\mathbf{z}}\right\} \). This coordinate system may be considered as a kind of absolute or global coordinate system. In addition to it, it is necessary to define two additional local coordinate systems in order to determine, in an unambiguous way, the polarization states of the incident and the scattered or reflected waves, respectively. These two coordinate systems, associated with the waves, are defined in terms of the global coordinate system.
Let us consider an object illuminated by an electromagnetic plane wave which may be described as
where the unitary vectors \( {\hat{\mathbf{x}}}^{\prime } \) and \( {\hat{\mathbf{y}}}^{\prime } \) are arbitrarily defined. Hence, the propagation direction of the incident wave is conveniently selected to be \( {\hat{\mathbf{k}}}^i={\hat{\mathbf{z}}}^{\prime } \). The incident wave reaches the object of interest and induces currents on it, which in turn reradiates a wave. This reradiated wave, as shown, is referred to as the scattered wave. In the far-field zone, the scattered wave is an outgoing spherical wave that in the area occupied by the receiving antenna can be
The propagation direction of the scattered wave is therefore \( {\hat{\mathbf{k}}}^s={{\hat{\mathbf{z}}}^{\prime\prime }} \). The scattering process is finally analysed in terms of the plane of scattering, which is the plane that contains both the incident and the scattering propagating vectors. The concepts of perpendicular and parallel wave components, or horizontal and vertical wave components, are defined with respect to the plane of scattering. Consequently, and as indicated in (1.33), the perpendicular component of the wave admits to be considered as a horizontal component, i.e. \( {\hat{\mathbf{x}}}^{\prime }={\hat{\mathbf{h}}}_i \), whereas the parallel one admits to be considered as a vertical one, i.e. \( {\hat{\mathbf{y}}}^{\prime }={\hat{\mathbf{v}}}_i \). In the case of the scattered wave, the perpendicular component of the wave admits to be considered as a horizontal component, i.e. \( {{\hat{\mathbf{x}}}^{\prime\prime }}={\hat{\mathbf{h}}}_s \), whereas the parallel one admits to be considered as a vertical one, i.e. \( {{\hat{\mathbf{y}}}^{\prime\prime }}={\hat{\mathbf{v}}}_s \).
The incident and scattered waves in (1.33) and (1.34), respectively, may be also vectorially expressed by means of the Jones vectors:
In the definition of the previous two Jones vectors, the coordinate systems defined previously are assumed. By using this vector notation for the electromagnetic waves, it is possible to relate the scattered wave with the one of the incident wave by means of a 2 × 2 complex matrix:
Here, r is the distance between the scatterer and the receiving antenna, and k is the wavenumber of the illuminating wave. The coefficient 1/r represents the attenuation between the scatterer and the receiving antenna, which is produced by the spherical nature of the scattered wave. On the other hand, the phase factor represents the delay of the travel of the wave from the scatterer to the antenna. Equation (1.36) may be written as
The matrix S is referred to as scattering matrix, whereas its components are known as complex scattering amplitudes. The arrangement of the scattering matrix indicates how these complex scattering amplitudes are measured. The first column of S is measured by transmitting a horizontally polarized wave and employing two antennas horizontally and vertically polarized to record the scattered waves. The second column is measured in the same form, but transmitting a vertically polarized wave.
It is worth mentioning that the scattering matrix characterizes the target under observation for a fixed imaging geometry and frequency. In addition, the four elements must be measured at the same time, especially in those situations where the scatterer is not static or fixed. If they are not measured at the same time, the coherency between the elements may be lost as the different elements may refer to a different scatterer.
As indicated, the scattering matrix represents the scattering process for particular incident and scattering directions, i.e. \( {\hat{\mathbf{k}}}^i \) and \( {\hat{\mathbf{k}}}^s \), respectively. In addition to that, it is also necessary to provide the horizontal and vertical unitary vectors, for the incident and the scattered waves, as they are necessary to define the polarization states of the waves.
In the most general case, which occurs in bistatic configurations where the transmitter and receiver antennas are located in different positions, the scattering matrix contains up to seven independent parameters to characterize the scatterer under observation. These parameters are the four amplitudes and three relative phases; see (1.38). Indeed, any absolute phase in the scattering matrix can be neglected as it does not affect the received power:
As it was already highlighted previously, the scattering coefficients depend on the direction of the incident and the scattered waves. When considering the matrix S, the analysis of this dependence is of extreme importance since it also involves the definition of the polarization of the incident and the scattered waves. Since (1.37) considers the polarized electromagnetic waves themselves, it is mandatory to assume a frame in which the polarization is defined. There exist two principal conventions concerning the framework where the polarimetric scattering process is considered: Forward Scatter Alignment (FSA) and Backscatter Alignment (BSA); see Fig. 1.3. In both cases, the electric waves of the incident and the scattered waves are expressed in local coordinate systems centred on the transmitting and receiving antennas, respectively. All coordinate systems are defined in terms of a global coordinate system centred inside the target of interest.
The FSA convention (see Fig. 1.3), also called wave-oriented since it is defined relative to the propagating wave, is normally considered in bistatic problems, that is, in those configurations in which the transmitter and the receiver are not located at the same spatial position.
The bistatic BSA convention framework (see Fig. 1.3) is defined, on the contrary, with respect to the radar antennas in accordance with the IEEE standard. The advantage of the BSA convention is that for a monostatic configuration, also called backscattering configuration, that is, when the transmitting and receiving antennas are collocated, the coordinate systems of the two antennas coincide; see Fig. 1.4. This configuration is preferred in the radar polarimetry community. In the monostatic case, the scattering matrix in the FSA convention, SFSA, can be related to the same matrix referenced to the monostatic BSA convention SBSA as follows:
As it has been mentioned previously, in the radar polarimetry community, the monostatic BSA convention (backscattering) is considered as the framework to characterize the scattering process. The reason to select this configuration is due to the fact that the majority of the existing polarimetric radar systems operate with the same antenna for transmission and reception. One important property of this configuration, for reciprocal targets, is reciprocity, which states that
Then, the formalization of the scattering process given by (1.37), in the monostatic case under the BSA convention, reduces to
In the same sense, Eq. (1.38) takes the form
The main consequence of the previous equation is that in the backscattering direction, a given scatterer is no longer characterized by seven independent parameters, but by five. These are three amplitudes, two relative phases, and one additional absolute phase.
A central parameter when considering the scattering process occurring at a given scatterer consists of the scattered power. For single-polarization systems, the scattered power is determined by means of the radar cross section or the scattering coefficient. Nevertheless, a polarimetric radar has to be considered as a multichannel system. Consequently, in order to determine the scattered power, it is necessary to consider all the data channels, that is, all the elements of the scattering matrix. The total scattered power, in the case of a polarimetric radar system, is known as Span, being defined in the most general case as
In the backscattering case, due to the reciprocity theorem, the Span reduces to
The main property of the Span is that it is polarimetrically invariable, that is, it does not depend on the polarization basis employed to describe the polarization of the electromagnetic waves.
When the radar wave reaches a scatterer, part of the incident energy is reflected back to the system. If the incident wave is monochromatic, the target is unchanging and the radar-target aspect angle is constant, the scattered wave will be also monochromatic and completely polarized. Therefore, both the incident and the scattered waves can be characterized by their corresponding Jones vectors, and the scattering process can be characterized by the scattering matrix. These targets are referred to as point targets, single targets or deterministic targets, as when a radar images this type of scatterers, the scattered wave in the far-field zone appears to be originated by a single point. In other words, the target response is not contaminated by additional spurious, so it is possible to infer some information about the target from the single values of the scattering matrix. Table 1.6 shows the scattering matrix, expressed in the linear polarization basis, for some canonical bodies. These are referred to as canonical due to the simplicity of their scattering matrix.
1.1.2.2 Scattering Polarimetry Descriptors
The scattering matrix introduced in the previous section is indeed a scattering polarimetry descriptor that could be also included in this section. Nevertheless, it merits a separate section as this matrix represents the best vehicle to introduce the description of the scattering process when polarimetry is concerned, as the scattering matrix relates the Jones vectors of the involved electromagnetic waves. Section 1.1.1.1 introduced additional descriptors for the polarization state of an electromagnetic wave. As a consequence, some additional descriptors for the scattering process shall be introduced in the following.
The 2 × 2 complex scattering matrix, as indicated, describes the scattering matrix of a given target. Table 1.6 presented several examples for some simple or canonical scatterers. Nevertheless, a real target presents always a complex scattering response as a consequence of its complex geometrical structure and its reflectivity properties. Consequently, the interpretation of this response is obscure. As it shall be presented later on, a possible solution to interpret this response is to decompose the original scattering matrix into the response of canonical mechanisms. With this idea in mind, but also with the objective to introduce a new formulism to extract physical information, it is possible to transform the scattering matrix into a scattering vector that presents a clearer physical interpretation.
The construction of a target vector k is performed through the vectorization of the scattering matrix:
Ψ is a set of 2 × 2 complex basis matrices which are constructed as an orthonormal set under a Hermitian inner product. The interpretation of the target vector k depends on the selected basis Ψ. The most common matrix bases employed in the context of the radar polarimetry are the so-called lexicographic ordering basis and the Pauli basis. The lexicographic ordering basis consists of the straightforward lexicographic ordering of the elements of the scattering matrix:
The Pauli basis consists of the set of Pauli spin matrices usually employed in quantum mechanics:
Note that the multiplying factor in both bases is necessary in order to keep the total scattered power constant, i.e. trace(SS∗T).
The selection of the basis to vectorize the scattering matrix depends on the final purpose of the vectorization itself. When the objective is to study the statistical behaviour of the SAR data or the radar measurement, it is more convenient to consider the lexicographic basis due to its simplicity, as it shall be extended in the next sections. Nevertheless, when the objective is the physical interpretation of the scattering matrix, it is more convenient to consider the Pauli basis. Assuming the Pauli decomposition basis, an arbitrary 2 × 2 scattering matrix may be written in the following terms:
It is worth noting that the elements a, b, c and d are complex. If one considers the decomposition of the scattering matrix as performed in (1.49), it is possible to identify the four elements of the Pauli basis with some of the scattering matrices of canonical bodies presented in Table 1.6. Therefore, the elements a, b, c and d, i.e. the elements of the target vector k, represent the contribution of every canonical mechanism to the final scattering mechanism. Therefore, the following interpretation is possible:
-
a corresponds to the single scattering from a sphere or plane surface.
-
b corresponds to dihedral scattering.
-
c corresponds to dihedral scattering with a relative orientation of π/4 rad in the line of sight.
-
d corresponds to anti-symmetric, helix-type scattering mechanisms that transform the incident wave into its orthogonal circular polarization state (helix related).
All in all, what has been performed in (1.49) is a target decomposition. This concept shall be analysed in depth in the next. It is also worth to notice that the different components of the Pauli basis, or scattering components, are orthogonal. This means that from a practical point of view, the separation indicated in (1.49) is possible without ambiguities.
Finally, the explicit expressions of the target vector in the lexicographic and Pauli decomposition bases, considering the expression of the scattering matrix, in the most general case are:
In the backscattering case, under the BSA convention, the reciprocity property applies. Hence, the previous target vectors admit the following simplification:
The different 2 and \( \sqrt{2} \) factors that appear in the definition of the target vectors are necessary in order to maintain the total scattered power or Span. As it is evident, the Span must be constant and independent from the choice of the basis in which the scattering matrix is decomposed. This is known as total power invariance.
The concept of target vector, obtained as a vectorization of the scattering matrix, makes it possible to obtain a new formulation to describe the information contained in the scattering matrix by means of the outer product of the target vector with its conjugate transpose, or adjoint vector.
For a vectorization of the scattering matrix through the lexicographic basis, in the most general case, the outer product of the target vector with its transpose conjugate \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) leads to the matrix:
Due to a language abuse, the matrix \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) is sometimes referred to as covariance matrix and represented by C, but as it will be shown in Sect. 1.1.2.4, the covariance matrix presents a different definition. It is worth to observe that (1.52) is a 4 × 4, complex, Hermitian matrix. The construction of this matrix, through the outer product of the vector kl and its transpose conjugate, makes the matrix \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) have a rank equal to 1. Consequently, \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) presents exactly the same information as the scattering matrix, and hence it may have up to seven independent parameters. In the case of the backscattering direction under the BSA convention, and due to the fact that the reciprocity relation applies, \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) can be written, considering (1.51), as
As in the previous case, the \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) matrix presents a rank equal to 1 as it is obtained as the outer product of a vector and its transpose conjugate. Nevertheless, in this case, the covariance matrix may present up to five independent parameters, that is, the same number of independent parameters as the scattering matrix from which it derives.
A similar procedure can be applied when the scattering matrix is obtained considering the Pauli basis. In this case, the matrix is obtained from the outer product \( {\mathbf{k}}_p{\mathbf{k}}_p^{T\ast } \). Due to a language abuse, this matrix is sometimes referred to as coherency matrix and represented by T, but as it will be shown in Sect. 1.1.2.4, the coherency matrix presents a different definition. Under the most general imaging configuration, considering (1.65), the coherency matrix can be written as
As in the case of \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \), \( {\mathbf{k}}_p{\mathbf{k}}_p^{T\ast } \) presents a rank equal to 1, and therefore, it may present up to seven independent parameters. Finally, if the backscattering direction is considered under the BSA convention, the coherency matrix reduces to
Again, the previous matrix presents a rank equal to 1 and may have up to five independent parameters.
The lexicographic and the Pauli target vector are just a different transformation of the scattering matrix into a vector. Hence, the covariance and coherency matrices are related by the following unitary transformation in the most general configuration:
In the case of the backscattering direction under the BSA convention, the previous transformation reduces to
As it may be seen from all this section, the matrices \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) and \( {\mathbf{k}}_p{\mathbf{k}}_p^{T\ast } \) contain the same information as the scattering matrix, that is, they are rank 1 matrices. The necessity to introduce these matrices is that they will allow to define the covariance and coherency matrices.
The complex scattering matrix S is able to describe a single physical scattering process, as well as \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) and \( {\mathbf{k}}_p{\mathbf{k}}_p^{T\ast } \). All these descriptors are based on a wave representation of the data, which depend on the absolute phase from the scatterer. On the contrary, a power representation of the scattering process eliminates this dependence, as power parameters become incoherently additive parameters. In the most general case, assuming the BSA convention, one may define the 4 × 4 Kennaugh matrix as follows:
where
The Kennaugh matrix can be written in the following form:
where
In the previous definition, the sub-index ψ indicates that the different parameters are roll angle dependent, corresponding to the target rotation along the line of sight.
As detailed in Sect. 1.1.2.1, the scattering matrix relates the scattered wave to the incident Jones vector. The Kennaugh matrix is related to the associated Stokes vectors defined in Sect. 1.1.1.1. In the forward scattering case, where S is represented in the FSA coordinate formulation, this matrix is named the 4 × 4 Mueller matrix and is calculated by
The main difference of K and M, with respect to \( {\mathbf{k}}_l{\mathbf{k}}_l^{T\ast } \) and \( {\mathbf{k}}_p{\mathbf{k}}_p^{T\ast } \), is that the Kennaugh and the Mueller matrices are real matrices, whereas the covariance and coherency matrices are complex.
1.1.2.3 Partial Scattering Polarimetry
As indicated in Sect. 1.1.1.2, radar polarimetry is concerned with two types of waves. The first type is monochromatic, totally polarized electromagnetic waves where the polarization state is perfectly represented by the Jones vectors. Consequently, the scattering process can be completely represented by any of the scattering polarimetry descriptors detailed in the previous section, and especially the scattering matrix. This situation appears when the radar transmits a perfectly monochromatic wave and this wave reaches an unchanging scatterer, resulting in a perfectly polarized scattered wave. As mentioned, these targets are referred to as point targets or coherent targets. The most important point to be considered when coherent scattering is addressed is to determine the number of independent parameters necessary to represent the scattering process. That is, to determine the number of independent parameters necessary to represent the operator able to characterize the change of the polarization state of the scattered wave with respect to the incident wave that occurs in the scattering process. In a monostatic configuration, the scattering operator describing the scattering, i.e. any of the matrix operators indicated in Sections 1.1.2.1 and 1.1.2.2, may present up to five independent parameters. In the bistatic case, these descriptors may present up to seven independent parameters.
The situation changes when the scattering properties of the target being imaged by the radar system change in time, as it would be the case for a forest being affected by the wind conditions or, for instance, when the target presents more than one scattering centre (a point at which the incident wave can be considered to be reflected). Under this situation, although the radar system transmits a perfectly polarized wave, the wave scattered by the scatterer is partially polarized. A scatterer of this category is normally referred to as distributed scatterer, depolarizing scatterer or an incoherent scattering target. The change of the polarization state of the scattered wave makes not possible to use the scattering descriptors presented in Sects. 1.1.2.1 and 1.1.2.2 to describe the scattering process, as these descriptors are not able to describe the variation of the polarization state of the scattered wave.
In the case of partially polarized waves, the description of the polarization state must be addressed through polarization descriptors relying on the second-order moments of the electromagnetic wave. If a wave is decomposed into two orthogonal components in the plane perpendicular to the propagation direction, these second-order moments refer to the power of each orthogonal component and to the correlation between them. This information is perfectly represented by the vector and the wave coherency matrix or the Stokes vector. In the case of the description of the scattering process, this information can be perfectly represented by the covariance and coherency matrices as the mean values of these matrices are not zero.
1.1.2.4 Change of Polarization Basis
The scattering properties of a given scatterer, as demonstrated, are contained within the scattering matrix S, which, as shown previously, is measured in a particular polarization basis. Since there exist an infinite number of orthonormal polarization bases, the question rising at this point is whether it is possible or not to infer the polarimetric properties of the given target in any polarization basis from the response measured at a particular basis. This question presents an affirmative answer. The possibility to synthesize any polarimetric response of a given target from its measurement in a particular orthonormal basis represents the most important property of polarimetric systems in comparison with single-polarization systems. The most important consequence of this process is that the amount of information about a given scatterer can be increased, allowing a better characterization and study. This polarization synthesis process is based on the concept of change of polarization basis presented in Sect. 1.1.1.3.
Before describing the polarization synthesis process in the backscattering direction, it is necessary to analyse the scattering process given by (1.37) with respect to the direction of propagation of the incident and the scattered waves. It must be noticed that the incident wave propagates in the direction given by the unitary vector \( {\hat{\mathbf{k}}}^i \), whereas the scattered one propagates in the opposite direction, given by \( -{\hat{\mathbf{k}}}^i \). Consequently, this difference in the propagation direction must be taken into account when defining the polarization state of the wave. Given a Jones vector propagating in the direction \( \hat{\mathbf{k}} \), the Jones vector of a wave presenting the same polarization state but which propagates in the direction \( -\hat{\mathbf{k}} \) is obtained as
where, as mentioned previously, the BSA convention is considered. Under this assumption, the scattering matrix is referred to as the coordinate system centred in the transmitting/receiving system. Consider a polarimetric radar system which transmits the electromagnetic waves in the following orthonormal basis \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \). In this particular basis, the incident and scattered waves are related by the scattering matrix as follows:
As shown in Sect. 1.1.1.3, given the Jones vector measured in a particular basis, for instance, \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \), it is possible to derive it in any other polarization basis \( \left\{{\hat{\mathbf{u}}}^{\prime },{\hat{\mathbf{u}}}_{\perp}^{\prime}\right\} \), which may be rewritten as follows:
Then, the incident and the scattered waves transformed in the new basis may be considered:
In order to apply the transformation basis procedure to the scattered waves \( {\underline {\mathbf{E}}}_{\left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\}}^s \), we need to consider that it propagates in the opposite direction as the incident wave \( {\underline {\mathbf{E}}}_{\left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\}}^i \). The transformation indicated by (1.64) assumes that the incident and the scattered waves propagate in opposite directions, but (1.66) and (1.67) assume that both waves propagate in the same direction. Consequently it is necessary to consider the transformation indicated by (1.63) in (1.67). As a result, the transformation basis procedure applies to the scattered wave as follows:
where now the wave in (1.68) is assumed to propagate in opposite direction with respect to the incident wave in (1.66). Now, it is possible to introduce (1.66) and (1.68) in (1.64):
As the transformation matrix U is unitary, i.e. U−1 = U∗T,
from where it can be clearly identified the following identity
The transformation expressed in (1.71) receives the name of con-similarity transformation. This transformation allows to synthesize the scattering matrix in an arbitrary basis \( \left\{{\hat{\mathbf{u}}}^{\prime },{\hat{\mathbf{u}}}_{\perp}^{\prime}\right\} \) from its measure in the basis \( \left\{\hat{\mathbf{u}},{\hat{\mathbf{u}}}_{\perp}\right\} \).
1.1.2.5 Scatterers Characterization by Single, Dual, Compact and Full Polarimetry
The main objective behind the use of polarimetric diversity, also known as full polarimetry, when observing a particular scatterer is that this type of diversity allows a far more complete characterization of the scatterer than the characterization that could be obtained without polarimetric sensitivity, or simply single-polarization measurements. Although this improved characterization, if compared with single-polarization data, the use of polarimetric diversity comes at a price, as the average transmitted power must be doubled and the swath width halved. In addition, a fully polarimetric SAR is technologically more complex than a single-polarization SAR system. In order to understand the difference between these two philosophies and the improvement in the characterization of a scatterer provided by polarimetry, it is necessary to introduce two important concepts, since they will determine the way in which a target shall be characterized. It may happen the scatterer of interest to be smaller than the coverage of the radar system. In this situation, we consider the scatterer as an isolated scatterer, and from a point of view of power exchange, this target is characterized by the so-called radar cross section. Nevertheless, we can find situations in which the scatterer of interest is significantly larger than the coverage provided by the radar system. In these occasions, it is more convenient to characterize the target independently of its extent. Hence, in these situations, the target is described by the so-called scattering coefficient.
The most fundamental form to describe the interaction of an electromagnetic wave with a given scatterer is the so-called radar equation. This equation establishes the relation between the power the scatterer intercepts from the incident electromagnetic wave and the power reradiated by the same scatterer in the form of the scattered wave. The radar equation presents the following form:
where Pr represents the power detected at the receiving system. The term
is determined by the incident wave, and it consists of its power density expressed in terms of the properties of the transmitting system. The different terms in (1.73) are the transmitted power Pt, the antenna gain Gt and the distance between the system and the target rt. On the contrary, the term
contains the parameters concerning the receiving system: the effective aperture of the receiving antenna Ar and the distance between the target and the receiving system rr. The last term in (1.72), i.e. σ, determines the effects of the scatterer of interest on the balance of powers established by the radar equation. Since (1.73) is a power density, i.e. power per unit area, and (1.74) is dimensionless, the parameter σ has units of area. Consequently, σ consists of an effective area which characterizes the scatterer. This parameter determines which amount of power is intercepted from (1.73) by the scatterer and reradiated. This reradiated power is finally intercepted by the receiving system according to the distance rt. An important fact which arises at this point is the way the scatterer reradiates the intercepted power in a given direction of the space. In order to be independent of this property, the radar cross section shall be referenced to an idealized isotropic scatterer. Thus, the radar cross section of an object is the cross section of an equivalent isotropic scatterer that generates the same scattered power density as the object in the observed direction:
where \( {\left|\overrightarrow{\mathbf{E}}\right|}^2 \) represents the intensity of the electromagnetic wave and S is the complex scattering amplitude of the object. The final value of σ is a function of a large number of parameters which are difficult to consider individually: the wave frequency, the wave polarization, the imaging geometry or the geometrical structure and the dielectric properties of the scatterer. Then, the radar cross section σ is able to characterize the target being imaged for a particular frequency and imaging system configuration.
The radar equation, as given by (1.72), is valid for those cases in which the scatterer of interest is smaller than the radar coverage, that is, a point target or point scatterer. For those targets presenting an extent larger than the radar coverage, we need a different model to represent the scatterer. In these situations, a scatterer is represented as an infinite collection of statistically identical point scatterers. The resulting scattered wave \( {\overrightarrow{\mathbf{E}}}^s \) results from the coherent addition of the scattered waves from every one of the independent scatterers which model the extended scatterer. In order to express the scattering properties of the extended target independently of its area extent, we consider every elementary target as being described by a differential radar cross section dσ. In order to separate the effects of the target extent, we consider dσ as the product of the averaged radar cross section per unit area σ0 and the differential area occupied by the target ds. Then, the differential power received by the systems due to an elementary scatterer can be written as
Hence, to find the total power received from the extended target, we need to integrate over the illuminated area A0:
It must be noted that the radar equation at (1.72) represents a deterministic problem, whereas (1.77) considers a statistical problem. Eq. (1.77) represents the average power returned from the extended target. Hence, the radar cross section per unit area σ0, or simply scattering coefficient, is the ratio of the statistically averaged scattered power density to the average incident power density over the surface of the sphere of radius rr:
The scattering coefficient σ0 is a dimensionless parameter. As in the case of the radar cross section, the scattering coefficient is employed to characterize the scattered being imaged by the radar. This characterization is for a particular frequency f, polarization of the incident and scattered waves and incident and scattering directions.
As it has been shown, the characterization of a given scatterer by means of the radar cross section σ or the scattering coefficient σ0 depends also on the polarization of the incident wave \( {\overrightarrow{\mathbf{E}}}^i \). As one can observe in (1.75) and (1.78), these two coefficients are expressed as a function of the intensity of the incident and scattered waves. Consequently, σ and σ0 shall be only sensitive to the polarization of the incident waves through the effects the polarization has over the power of the related electromagnetic waves. Hence, if we denote by p the polarization of the incident wave and by q the polarization of the scattered wave, we can define the following polarization-dependent radar cross section and scattering coefficient, respectively:
As it has been shown, a given target of interest can be characterized by means of the radar cross section or the scattering coefficient depending on the nature of the scatterer itself; see (1.75) and (1.78). Additionally, in (1.79) and (1.80), it has been shown that these two coefficients depend also on the polarization of the incident and the scattered electromagnetic waves. A closer look to these expressions reveals that these two real coefficients depend on the polarization of the electromagnetic waves only through the power associated with them. Thus, they do not exploit, explicitly, the vectorial nature of polarized electromagnetic waves. A SAR system that measures σ or σ0 is usually referred to as single-polarization SAR systems as, normally, the same polarization is employed for transmission and for reception. In this case, the products delivered by the SAR system are real SAR images containing the information of σ or σ0.
In order to take advantage of the polarization of the electromagnetic waves, that is, their vectorial nature, the scattering process at the scatterer of interest must be considered as a function of the electromagnetic waves themselves. In Sect. 1.1.1.1, it was shown that the polarization of a plane, monochromatic, electric wave could be represented by the so-called Jones vector. Additionally, a set of two orthogonal Jones vectors form a polarization basis, in which any polarization state of a given electromagnetic wave can be expressed. Therefore, given the Jones vectors of the incident and the scattered waves, \( {\underline {\mathbf{E}}}^i \) and \( {\underline {\mathbf{E}}}^s \), respectively, the scattering process occurring at the target of interest is represented by the scattering matrix S. In contraposition to a single-polarization SAR system, a fully polarimetric SAR system measures the complete scattering matrix S. Therefore, the product delivered by this type of SAR systems corresponds to the 2 × 2 complex scattering matrix and not individual real SAR images.
As it can be observed, the polarimetric sensitivity of a measurement ranges from a complete absence of polarimetric sensitivity in the case of single-polarization SAR systems to a complete sensitivity in the case of fully polarimetric SAR systems. Polarimetric sensitivity comes to a price of a more complex system that implies, on the one hand, a heavier system and, on the other hand, the need to transmit a larger power. In addition, and due to the need to double the pulse repetition frequency to accommodate two polarizations in transmission, the radar swath is also reduced. Nevertheless, between both architectures, there exist other polarimetric radar configurations with may soften the previous limitations but at the cost of reducing the amount of acquired information.
A single-polarization or mono-polarization SAR system is composed of one transmission and one reception chain that operate at a fixed polarization. In most of the cases, both chains operate at the same polarization providing a co-pol or co-polarized channel. In the particular case of the linear polarization basis, these channels would correspond to σhh or \( {\sigma}_{hh}^0 \) and σvv or \( {\sigma}_{vv}^0 \) for the horizontal and the vertical polarization states, respectively. As indicated, these simple imaging radars deliver real SAR images, proportional to σ or σ0, as products. One possibility to increase the amount of information is to consider a dual-polarized radar by including a second reception chain in the system, in such a way that it transmits in one polarization, for instance, h, and it receives simultaneously on the same polarization h and also on the orthogonal one v, leading to one co-pol and the so-called co-polarized and the cross-polarized channels, respectively. A different alternative for a dual-polarized system is to consider a transmission chain that alternates between polarizations and a single reception chain. In all these cases, the polarimetric system provides images proportional to the radar brightness.
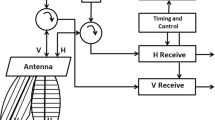
All the previous SAR systems present the limitation that the information that may be retrieved is restricted to the information that can be extracted from the real SAR images, proportional to σ or σ0, or their different combinations. Nevertheless, this limitation is overcome by allowing two simultaneous and coherent reception channels operating at orthogonal polarizations, making it possible to measure the relative phase between them. The coherent nature of the receiving channels allows measuring the different elements of the covariance or coherency matrix. The first option that may be considered is to assume a fixed polarization in transmission and orthogonal polarizations in reception. In the case of the transmission channel, the circular polarization and the 45° linear polarizations have been proposed, whereas for reception the horizontal and vertical linear polarizations are assumed. This type of systems are collectively known as compact polarized systems as, although they allow to measure some of the elements of the covariance and coherency matrix, they do not allow to measure the complete matrices. Finally, by allowing the system to transmit alternatively between orthogonal polarizations and to receive coherently at the same two orthogonal polarizations, a system like this is able to measure coherently the scattering matrix and to produce the covariance and coherency matrices. In the case of a bistatic configuration, without any type of assumption, these will be 4 × 4 complex matrices, whereas in the case of a monostatic configuration, these will be 3 × 3 complex matrices. Figure 1.5 details the complete hierarchy of polarimetric SAR systems.
1.2 SAR Data Statistical Description and Speckle Noise Filtering
Most of geophysical media, for instance, rough surfaces, vegetation, ice, snow, etc., have a very complex structure and composition. Consequently, the knowledge of the exact scattered electromagnetic wave, when illuminated by an incident wave, is only possible if a complete description of the scene was available. This type of description of the scatterers is unattainable for practical applications. The alternative, hence, is to describe them in a statistical form. Such scatters are named, consequently, as distributed or partial scatterers (Ulaby et al. 1986a, b).
SAR systems are mainly employed for natural scenes observation. Owing to the complexity of these scatterers, the scattered wave has also a complex behaviour. Hence, the scattering process itself needs to be analysed stochastically. Most of the techniques focused on solving the scattered wave problem trying to find, hence, the statistical moments of the scattered wave as a function of the incident wave properties, as well as the scatterer features.
In order to derive a stochastic model for the observed SAR images in the case of distributed scatterers, it is necessary to consider a model for the SAR imaging process, a model for the scattering process and a model for the distributed scatter being imaged.
The SAR imaging process is divided into two main processes. The former consists of the acquisition of the scattered data, as a result of the illuminating wave, whereas the latter comprises the focusing process. The second, which is in charge of collecting all the contributions of a particular scatterer focusing it as good as possible, tries to remove the effects of the acquisition process. The SAR impulse response, or SAR system model, embracing the acquisition, as well as the focusing processes, can be assumed to be a rectangular low-pass filter (Curlander and McDonough 1991):
In the previous equation, x and r indicate the azimuth and slant-range (simply called range in the following) dimensions of the SAR image, respectively, whereas δx and δr indicate the spatial resolutions in the same spatial dimensions. Finally, a SAR image, i.e. S(x, r), may be modelled as a two-dimensional low-pass filter, given by (1.81), applied to the scene’s complex reflectivity σs(x, r) (Curlander and McDonough 1991):
Since the spatial resolutions of the SAR impulse response, δx and δr, are not zero, it is possible to introduce the concept of resolution cell as the area given by δx × δr . Qualitatively, in the absence of signal re-sampling, the information contained by an image pixel is basically determined by the average complex reflectivity σs(x, r) within this resolution cell.
The resolution cell dimensions, δx and δr, are larger than the wavelength of the illuminating electromagnetic wave λ. As a consequence, the resulting scattered wave is due to an elaborated scattering process. In order to arrive to a tractable mathematical model of the SAR image S(x, r), it is convenient to find an approximation for the scattering process within the resolution cell. The most common simplification is the Born approximation or simple scattering approximation (Ulaby et al. 1986a). Under it, first, the distributed scatterer is considered to be composed of a set of discrete scatterers characterized by a deterministic response. This scatterer model might be reasonable for those cases in which the discrete scatterer description is valid, for instance, scattering from raindrops or vegetation-covered surfaces having leaves small compared with the wavelength. On the contrary, this assumption is not valid for continuous scatterers. In these cases, it is helpful to apply the concept of effective scattering centre (Ulaby et al. 1986a), in which the continuous scatterer is analysed in a discrete way, e.g. the facet model for surface scattering (Ulaby et al. 1986a; Beckmann and Spizzichino 1987). In a second step, the scattered wave from the resolution cell is supposed to be the linear coherent combination of the individual scattered waves of each one of the discrete scatters within the cell. The main limitation of the Born approximation is that it excludes attenuation or multiple scattering in the process.
Assuming the scattered wave from any distributed scatterer to be originated by a set of discrete sources, (1.82) can be considered in its discrete form:
where the sub-index k refers to each particular discrete scatterer in the resolution cell and N is the total number of these scatterers embraced by the response of the SAR system h(x, r). Equation (1.83) can be rewritten by using
as follows:
where \( {A}_k={h}_k\sqrt{\sigma_k} \). As observed in (1.87), the process to form a SAR image pixel consists of the complex coherent addition of the responses of each one of the discrete scatterers, which are not accessible individually. The sole available measure is the complex coherent addition itself. This coherent addition process receives the name of bi-dimensional random walk (McCrea and Whipple 1940; Doob et al. 1954).
At this point, it is necessary to consider certain assumptions about the elementary scattered waves \( {A}_k\exp \left(j{\theta}_{s_k}\right) \) in order to derive a stochastic model for the observed SAR image (Beckmann and Spizzichino 1987; Goodman 1985):
-
The amplitude Ak and the phase \( {\theta}_{s_k} \) of the k-th scattered wave are statistically independent of each other and from the amplitudes and phases of all other elementary waves. This fact states that the discrete scatterers are uncorrelated and that the strength of a given scattered wave bears no relation to its phase.
-
The phases of the elementary contributions \( {\theta}_{s_k} \) are equally likely to lie anywhere in the primary interval [−π, π).
Under these conditions, (1.87) may be seen as an interference process, in which the interference itself is determined by the phases \( {\theta}_{s_k} \). This interference can be constructive, as well as destructive. This effect can be clearly noticed in SAR images, as the amplitude or the intensity of (1.87) presents a salt and pepper or grainy aspect, as it may be observed in Fig. 1.6, which corresponds to |Shh| acquired with the RADARSAT-2 system over the city of San Francisco. Such a phenomenon is known as speckle (Goodman 1985; Lee 1981; Lopes et al. 1990; Raney 1983).
Speckle is a true electromagnetic measurement and has a complete deterministic nature, as shown in (1.87). Nevertheless, the information contained within speckle needs from two different analyses. In those cases in which there is a reduced number of discrete scatterers within the resolution cell, or its response is basically originated by a reduced set of dominant ones, speckle is said to be partially developed. Hence, the interference itself, i.e. the speckle, contains information about the scattering process. On the contrary, when there is a large number of discrete scatterers in the cell, without a dominant one, the interference process becomes so complex that it does contain almost no information about the scattering process itself (Oliver and Quegan 1998). This case is called fully developed speckle (Ulaby et al. 1986a), and the complexity of the interference process is overcome by analysing it by statistical means. Hence, speckle turns to be considered as a noise-like signal (Ulaby et al. 1986b; Lopes et al. 1990).
Summarizing, due to the lack of knowledge about the detailed structure of the distributed scatterer being imaged by the SAR system, it is necessary to discuss the properties of the scattered wave statistically. The statistics of concern are defined over an ensemble of objects, all with the same macroscopic properties, but differing in the internal structure. For a given SAR system imaging a particular scatterer, e.g. a rough surface, the exact value of each pixel cannot be predicted, but only the parameters of the distribution describing the pixel values. Therefore, for a SAR image, the actual information per pixel is very low as individual pixels are random samples from distributions characterized by a reduced set of parameters.
1.2.1 One-Dimensional Gaussian Distribution
Considering a SAR system to be described by a rectangular low-pass filter (see (1.81)) and the distributed scatterer to be modelled by a set of discrete deterministic scatterers, by means of the single or Born scattering approximation, a SAR image, S(x, r), can be described by the model presented in (1.87).
The main parameter in the SAR image model is the number of discrete scatterers within the resolution cell, i.e. N. Depending on the nature of this parameter, different SAR image statistical models can be derived. On the one hand, if N is considered as a constant value, provided that it is large enough, (1.87) leads to the complex, zero-mean, complex Gaussian pdf model, valid for homogeneous, non-textured SAR images (Beckmann and Spizzichino 1987; Goodman 1985; Papoulis 1984). On the other hand, to consider N as a random variable makes (1.87) to lead to pdf models valid for textured areas description. In the following, the zero-mean, complex Gaussian distribution model shall be considered, although possible extensions to textured image models shall be indicated.
When the number of discrete scatterers inside the resolution cell N is large, provided that Ak cos (jθk) and Ak sin (jθk) satisfy the central limit theorem (Oliver and Quegan 1998), the quantities ℜ{S} and ℑ{S} are Gaussian distributed, that is, they follow a zero-mean, Gaussian probability density function (pdf). The parameters of this pdf can be obtained on the basis of the discrete scatterers model. The mean values of ℜ{S} and ℑ{S} are equal to zero, and the variances are \( E\left\{{\Re}^2\left\{S\right\}\right\}=E\left\{{\Im}^2\left\{S\right\}\right\}=\frac{N}{2}E\left\{{A_k}^2\right\} \). Besides, the symmetry of the phase distribution of the discrete scatterers produces (Beckmann and Spizzichino 1987):
Under these conditions, ℜ{S} and ℑ{S}, denoted in the following by x and y, respectively, are described by means of zero-mean Gaussian pdfs:
where the variance is σ2 = (N/2)E{Ak2}. The pdfs px(x) and py(y) are denoted in the following as \( \mathcal{N}\left(0,{\sigma}^2\right) \). Consequently, a SAR image, S = x + jy = A exp (jθ), is described by a zero-mean, complex, Gaussian distribution, with uncorrelated real and imaginary parts, denoted next as \( \mathcal{N}\left(0,{\sigma}^2\right) \). From (1.89) and (1.90), it is straightforward to derive pA(A) and pθ(θ), where \( A=\sqrt{x^2+{y}^2} \) and θ = arctan (y/x), as:
The amplitude pdf, i.e. pA(A), is known as Rayleigh distribution. In addition, if intensity, i.e. I = A2, is considered, the Rayleigh pdf is transformed to an exponential pdf:
On the other hand, (1.93) shows that the SAR image phase has a uniform pdf. Consequently, this phase bears no information concerning the natural scene being imaged.
Given the SAR image amplitude pdf (1.92), the amplitude mean value is equal to \( \sigma \sqrt{\pi }/2 \), whereas the variance equals (1 − (π/4))σ2. If the coefficient of variation, defined as the standard deviation divided by the mean, is calculated, it equals \( \sqrt{\left(4/\pi \right)-1} \). For the intensity I, it has a value equal to 1 as the mean and the variance are equal to σ2. As a consequence, the intensity of a SAR image can be modelled as the product of two uncorrelated terms (Goodman 1985; Lee 1981; Lopes et al. 1990; Raney 1983), i.e.
The deterministic-like value is given by its mean, i.e. σ0, which corresponds to the mean incoherent power of the area under study (1.78). The random process n, with mean and variance equal to 1, is characterized by an exponential pdf and is defined as the speckle noise component. As it may be observed from the model (1.94) and (1.95), if the mean value of the intensity increases, the variance increases as well. Therefore, this model is known as the multiplicative speckle noise model. In other words, the signal to noise ratio of the image cannot be improved by increasing the transmitted power, as the variance of the data will increase proportionally.
The Gaussian model for SAR data, leading to (1.91) and (1.95), is able to characterize SAR data for homogeneous areas. In this case, useful information is described by a single degree of freedom, corresponding to the mean intensity. Nevertheless, for certain types of distributed scatterers, such a simple model cannot describe all the data variability. The reason behind this limitation is that this type of scatterers need from a more sophisticated model, with more than one degree of freedom, in order to be completely described. Collectively, these models are able to describe average intensity variations, which correspond to data texture (Oliver and Quegan 1998). A variety of two-degree of freedom pdf models have been proposed in the literature, for instance: K-distribution (Kong 1990), Weibull distribution or log-normal distribution (Oliver and Quegan 1998; Papoulis 1984; Kong 1990). All these models consist of assuming the number of scatterers N, within a resolution cell, no longer as a constant, but being described also by a certain distribution. Even so, there are situations in which these two-parameter models are not able to describe the scene. Hence, the solution goes into the direction of introducing more degrees of freedom, thus resulting in more elaborate image models (Oliver and Quegan 1998; Trunk and George 1970; Trunk 1972; Schleher 1975).
1.2.2 Multidimensional Gaussian Distribution
The previous section was concerned with the statistical description of one-dimensional complex data acquired by a complex SAR system, i.e. a single SAR image. As shown, despite the data’s complex nature, only the amplitude, or the intensity, contains useful information concerning the distributed target under analysis. The amount of information can be increased by acquiring more than one SAR image, if one or more imaging parameters, e.g. system position, acquisition time, frequency or polarization, are varied. What it is pursued, hence, is the study of the variation of the scatterer’s response to changes of the SAR system parameters. The volume of information is increased as more data channels are available but also because, if available, the multidimensional data correlation structure can be also exploited to extract information about the observed scatterer (Oliver and Quegan 1998; Cloude and Pottier 1996). The following list shows the most common multidimensional SAR configurations, as well as their main applications:
-
SAR Interferometry (InSAR) (Bamler and Hartl 1998): In this configuration, two SAR systems image the same scene from slightly different positions in space, leading to two-dimensional SAR data. In this way, the phase difference between the two acquisitions is proportional to the terrain’s topography. This configuration is extensively employed nowadays to obtain Digital Elevation Models (DEMs) of the terrain.
-
Differential SAR Interferometry (DInSAR) (Gabriel et al. 1989): This SAR configuration admits several variants. On the one hand, a differential interferogram can be obtained through the difference of two interferograms acquired with a zero spatial baseline, but at different times. Consequently, the “residual” differential interferogram can contain small topographic deformations or even atmospheric effects. On the other hand, the same effect can be observed if the topography of a given interferogram is compensated for by means of an external DEM.
-
SAR Polarimetry (PolSAR) (Ulaby and Elachi 1990): In this case, the parameters which vary between the different information channels are the polarization of the transmitted wave and the polarization with which the scattered wave by the terrain is collected. A set of two orthogonal polarization states are employed, being the most common the pair of horizontal and vertical polarizations. The most important property of polarimetry is that the polarimetric response to any polarization state of the incident wave of a given scatterer can be derived from the response to a pair of orthogonal polarization states. This SAR configuration exploits the fact that scatterers present different responses to different polarizations of the incident wave. For backscattering in which waves are transmitted and collected in the same position and by considering the reciprocity theorem, PolSAR leads to three-dimensional data. On the contrary, when scattered waves are collected in a different position with respect to the transmitted one, i.e. forward scattering, PolSAR data are four-dimensional data.
-
Polarimetric SAR Interferometry (PolInSAR) (Cloude and Papathanassiou 1998): This technique tries to combine both the advantages of InSAR and PolSAR. On the one hand, the introduction of interferometric diversity makes possible the data to be sensible to the structure of the target in the vertical dimension. On the other hand, the data are related to different scattering mechanisms in the same resolution cell, thanks to the polarimetric capabilities of the acquisition system. Hence, PolInSAR data are sensible to different scattering mechanisms in the same image pixel, located at different heights. The introduction of simple scattering models allows to extract relevant information about the scatterer under study. Among the possible applications of this technique, the most important is the extraction of parameters related to the vegetation cover which allow biomass estimation. In terms of data dimensionality, PolInSAR data consist of six-dimensional data if backscattering is considered, whereas they are eight-dimensional data for forward scattering.
-
SAR Tomography (TomoSAR) (Reigber and Moreira 2000): As shown in the previous point, PolInSAR represents a first step to resolve the vertical structure of the imaged scatterer. In this direction, SAR tomography is a technique directed to achieve a real three-dimensional reconstruction of the scene under observation. Both the SAR data acquisition and processing are based on the generation and processing of a synthetic aperture in the azimuth direction to reconstruct the object in this direction. In the same way, SAR tomography is based on the synthesis of an aperture in the dimension perpendicular to the plane formed by the azimuth and range dimensions, by acquiring several SAR images in the vertical dimension. Consequently, the phase information of these images can be employed to reconstruct, with enough spatial resolution, the vertical structure of the scatterer.
-
Multifrequency SAR (Sarabandi 1997; Lee et al. 1991): As shown in the literature, the response of a given scatterer depends on frequency. Consequently, in order to extract the maximum amount of information concerning the scatterer, several SAR images can be acquired at different frequencies. Therefore, the dimensionality of the data depends on the number of acquired images.
From a general point of view, a multidimensional SAR system acquires a set of SAR images, represented by the complex vector
where m represents the number of SAR images, i.e. the data dimensionality, according to the previous description. Each element of the vector k, i.e. Si for i = 1, 2, …, m, represents a single complex SAR image. In PolSAR, the k vector receives the name of scattering or target vector (in the straightforward lexicographic basis), and it represents a vectorization of the scattering matrix S as detailed in Sect. 1.1.2.2. The correlation structure of the vector k, provided that its m components \( {S}_i\sim \mathcal{N}\left(0,{\sigma}^2\right) \), is completely characterized by the Hermitian covariance matrix C, defined as follows:
In the particular case of PolSAR data, the data correlation structure can be also expressed by the Hermitian coherency matrix Τ (Cloude and Pottier 1996). Considering (1.97), one can see that the complex vector k is characterized by the following pdf (Lee et al. 1994; Tough et al. 1995):
Hence, (1.98) represents the data pdf model for a set of m correlated SAR images, which is denoted in the following as \( \mathcal{N}\left(\mathbf{0},\mathbf{C}\right) \). Since \( \mathbf{k}\sim \mathcal{N}\left(\mathbf{0},\mathbf{C}\right) \), it is completely characterized by the first and the second central moments, i.e. the mean target vector and the covariance matrix, respectively.
At this point, it is important to consider, as presented before, the issue that the mean value of the real and imaginary parts of k equals zero. The main consequence is that it prevents the possibility to extract useful information via an estimation of this mean value. For instance, this circumstance determines the way PolSAR data has to be considered when distributed scatterers are of concern. A PolSAR system measures the 2 × 2 complex scattering matrix S, which can be vectorized into the form presented by (1.96) (Cloude and Pottier 1996; Bebbington 1992); see also Sect. 1.1.2.2. On the one hand, when this scattering vector refers to a distributed scatterer, a given sample of it has almost no information concerning the scatterer itself, as k consists of a sample of the pdf given by (1.98) (Oliver and Quegan 1998). On the other hand, if the mean value of k is estimated, it turns out to be zero. Thus, as reported in the literature, when distributed scatterers are studied, the vector k, or the scattering matrix S in the particular case of PolSAR, cannot completely describe the properties of the distributed scatterer. Therefore, it is necessary to characterize these properties by means of higher-order moments, i.e. through an estimation of the covariance matrix C, or, additionally, the coherency matrix Τ. These two matrices are derived through the outer product of the target vectors kl and kp, respectively, as indicated in Sect. 1.1.2.2, so they are independent of the absolute phase of the scattering matrix S or the target vectors kl and kp. Hence, the expected value in (1.97) needs to be estimated. The process to estimate the covariance matrix C is also referred to as the polarimetric speckle noise removal process, as the objective is to remove the variability of the data making it possible to retrieve the C matrix.
In the rest, the complex, multidimensional Gaussian model, presented by (1.98), is taken as the multidimensional SAR imagery model. As for the one-dimensional model for a single SAR image, the complex, multidimensional Gaussian model can be considered valid for homogeneous areas, that is, areas in which the statistical properties of the data remain constant. The main reason of this choice has to be found in the fact that the simplicity of the complex, multidimensional Gaussian pdf, makes it possible the analytical analysis of the information which can be extracted from the data. In addition, many studies reported in the literature support this model.
The multidimensional, zero-mean, complex Gaussian pdf model is based on the following assumptions:
-
The distributed scatterer may be modelled as a collection of discrete or point scatterers, whereas the scattering process occurring at the surface, or within it, is considered under the Born or simple scattering approximation.
-
The properties of the distributed scatterer remain constant in space, hence leading to homogeneous SAR data.
Thus, whenever any of the previous two suppositions are not fulfilled, SAR data can no longer be assumed to be described by the complex, multidimensional Gaussian pdf model. These departures have been noticed in the literature at high resolutions or high frequencies, giving rise to data texture. As for one-dimensional SAR imagery, some of these departures can be explained by considering N, the total number of scatterers in the resolution cell, to be described by a certain pdf. If the mean number of scatterers contributing to the measurement at each pixel is large, then whatever the pdf of the number of discrete scatterers, the vector k can be represented by the product of two independent processes:
where T is a positive scalar texture and k′ is a complex, multidimensional Gaussian distributed vector, with the same covariance as k. When T is considered to be described by a square-root gamma pdf, the data k in (1.99) is described by the so-called K-distribution (Kong 1990). Although (1.99) gives rise to textured data, an important result is that any model based on the fluctuation of the number of discrete scatterers within the resolution cell gives rise to data that is multivariate Gaussian at each pixel. That is, despite the texture, the data’s correlation structure is still determined by the multidimensional Gaussian structure.
The main drawback of the model given by (1.99) is that, since the texture parameter T is a scalar, the texture information is the same of all the channels of the vector k. Nevertheless, recent results presented in the literature point out that, especially in the case of PolSAR data, the texture information could be different for every SAR data channel (Oliver and Quegan 1998; De Grandi et al. 2003). The physical reason that would explain this issue is that a scatterer presents different responses to different polarizations. Hence, these differences, of course considered in the covariance matrix C, could be also be present within the texture information.
As noticed, in order to extract the useful information concerning the distributed scatterer under analysis from multidimensional SAR data, it is necessary to estimate the covariance matrix C, or expressed in a different way, polarimetric speckle noise must be filtered out. The estimated value of the covariance matrix C, which generally receives the name of sample covariance matrix and is denoted by Z, is studied in detail in the following.
1.2.3 The Wishart Distribution
The nature of multidimensional SAR data, provided the zero-mean, multidimensional, complex Gaussian pdf to be the right data model, makes it necessary to study the distributed scatterer properties through the estimation of the covariance matrix C. The maximum likelihood estimation (MLE) of C (Oliver and Quegan 1998) corresponds to
If one considers the expectation of the MLE
it can be demonstrated that the MLE of the Hermitian covariance matrix is an unbiased estimator. In addition, it can be shown that the variance of the different matrix components of Z decreases with the number of samples n.
In SAR applications, the MLE of the covariance matrix receives often the name of covariance matrix multilook estimator (Sarabandi 1997), whereas Z is known as the sample covariance matrix (Kay 1993). Here, look refers to each one of the independent averaged samples. Hence, it can be concluded from (1.101) that the performance of the covariance matrix estimation Z, for homogeneous data, depends on the number of averaged samples or looks, in such a way that the larger the number of looks, the lower the variance and the better the estimation. As the Z matrix is estimated from random samples, this matrix is also a random matrix. Finally, the distribution of the sample covariance matrix Z corresponds to the Wishart distribution:
where etr(⋅) is the exponential of the matrix trace and the complex multivariate gamma function is defined as
The distribution presented in (1.102) is denoted by \( \mathbf{Z}\sim \mathcal{W}\left(n\mathbf{C},m\right) \). It can be observed from (1.102) that the Wishart distribution depends on three parameters: the number of data channels m, the number of averaged multidimensional data samples n and the true covariance matrix C. The expression of the Wishart distribution is only defined for n ≥ m in order to assure Z to be a full-rank matrix with a non-zero determinant.
As it has been highlighted, the Hermitian covariance matrix C represents the cornerstone in multidimensional SAR data processing, and especially in PolSAR, together with its counterpart, the coherency matrix T. The final objective of estimating these matrices is the possibility to extract physical information to characterize the distributed scatterers being imaged by the SAR system. This task is performed by a collection of algorithms and techniques, collectively known as inversion algorithms. The aim of these techniques is the establishment of relations between the physical properties of the distributed scatterer and the observed SAR data, hence making it possible the inversion of this process in order to extract physical information from observed multidimensional SAR data. Most of these techniques have the covariance matrix C, or certain information derived from it, as the main input of the inversion process. Since due to the intrinsic nature of SAR systems, direct access to the covariance matrix C is not possible, it must be estimated from the observed multidimensional SAR data.
As shown in Sect. 1.2.1, the estimation of incoherent power may be also understood as a filtering process. One alternative to define this filtering process is to assume a given noise model able to identify the information of interest and the noise sources that corrupt this information. In the case of single SAR images, this noise model corresponds to the multiplicative speckle noise model in (1.95). In the case of multidimensional SAR data, this model cannot be extended to the whole covariance matrix Z as it would imply uncorrelated SAR images. Nevertheless, the multiplicative speckle noise model can be extended to model the diagonal as well as the off-diagonal elements of Z (Lopez Martínez and Fabregas 2003). In this case, the nature of the speckle noise for a particular element of the covariance matrix depends on the correlation that characterizes this element. For low correlation, speckle noise presents an additive nature, whereas for high correlation, speckle noise is characterized by a multiplicative behaviour. Consequently, this model is referred to as the multiplicative-additive speckle noise model for multidimensional SAR data.
1.2.4 The Polarimetric Covariance and Coherency Matrix
As indicated in the previous section, the characterization of distributed scatterers must be performed through the covariance C or the coherency T matrices. In a bistatic configuration, and according to what has been presented in Sect. 1.1.2.2, these two matrices are defined as
and
respectively. In the case of a monostatic system configuration, the covariance and the coherency matrices are defined as
and
As demonstrated in the previous section, the maximum likelihood estimator of the expectation operator E{⋅} and therefore the maximum likelihood estimator of the covariance and coherency matrices correspond to the spatial averaging, referred to as multilook or boxcar filter. In this case, the estimated covariance and coherency matrices receive the names of sample covariance and sample coherency matrices, respectively.
Eqs. (1.106) and (1.107) represent the most general form of the covariance and coherency matrices, respectively, for a monostatic configuration. As these matrices are Hermitian, they contain up to nine independent parameters. Nevertheless, depending on the type of scatterer, the number of independent parameters can be lower leading to a particular form of the covariance C or the coherency T matrices. If the scatterer under study has reflection symmetry in a plane normal to the line of sight, then the covariance and the coherency matrices will have the following general forms:
that is, the cross-polar scattering coefficient will be uncorrelated with the co-polar terms. Under this hypothesis, the covariance C or the coherency T matrices present up to five independent parameters. In addition to reflection symmetry, a medium may also exhibit rotation symmetry. This type of symmetry is referred to as azimuthal symmetry, leading to a coherency matrix presenting the following form:
which has only two independent parameters α and β.
1.2.5 The Polarimetric Coherence
From the expressions of the covariance and coherency matrices that were introduced in Sect. 1.2.4, one may see that the elements of these matrices may be divided into two types: on the one hand, the diagonal elements containing the power information and, on the other hand, the off-diagonal elements that contain the correlation information between the different channels of information. This correlation information may be considered in an absolute way by considering just the off-diagonal elements of these matrices. Nevertheless, this correlation information may be also considered in a relative way through the so-called complex correlation parameter, defined as
This parameter contains the information of statistical resemblance between any two SAR images Sk and Sl. Indeed, these SAR images correspond to the different elements of the target vector k defined in Sect. 1.1.2.2. The amplitude of the complex correlation coefficient, normally referred to as correlation |ρ|, presents a value in the range [0,1]. If |ρ| = 0 it means that both SAR images are statistically independent, and the phase ϕx contains no information. For |ρ| = 1, both SAR images are statistically equal, and the phase information, free of noise, is a delta function containing information about the scattering process. For any other value, |ρ| establishes the correlation between both SAR images, and the phase information ϕx is contaminated by the effect of speckle noise.
In multidimensional SAR imagery, the complex correlation coefficient has been revealed as an important source of information. In particular, the correlation coefficient amplitude, named coherence, apart from depending on the SAR system characteristics, is also influenced by the physical properties of the area under study. The complex correlation coefficient is the most important observable for InSAR (Bamler and Hartl 1998). On the one hand, and considering the acquisition geometry, it has been demonstrated that its phase contains information about the Earth’s surface topography. Therefore, InSAR phase data are employed to derive Digital Elevation Models (DEMs) of the terrain. On the other hand, although there is not a complete understanding about the parameters and the physical processes affecting the interferometric coherence, it has been shown that this parameter may be successfully employed to characterize the properties and the dynamics of the Earth’s surface.
The coherence represents also an important source of information when PolSAR data are addressed. In particular, the complex correlation coefficient parameter derived from circularly polarized data has been employed to characterize rough surfaces (Mattia et al. 2003), to study the sea surface (Kasilingam et al. 2002) or to discriminate sea ice types (Wakabayashi et al. 2004). When obtained from linearly polarized data, the coherence has been also employed to characterize the forest cover in the Colombian Amazon (Hoekman and Quinones 2002). In conjunction with polarimetric techniques, i.e. polarimetric SAR interferometry (PolInSAR), the interferometric coherence is employed to retrieve the forest vegetation (Cloude and Papathanassiou 1998) or the crop plants heights (Ballester Berman et al. 2005).
All the techniques listed in the previous paragraph rely on a correct estimation of the coherence parameter. The estimated coherence values are overestimated, especially for low coherence values (Touzi et al. 1999). Under the homogeneity hypothesis, the coherence accuracy and bias depend on the extent of the averaging or estimation process, in such a way that the larger the number of averaged pixels, the higher the coherence accuracy and the lower the bias. Therefore, since coherence accuracy is achieved at the expense of spatial resolution and spatial details, this point represents a clear trade-off for coherence estimation. Coherence estimation techniques rely also on the hypothesis that all the signals involved in the estimation process are stationary and in particular locally stationary processes. When this is not the case, biased coherence values result (Touzi et al. 1999). Hence, a lack of signal stationarity can be considered as a second source of bias for coherence estimation. The departure of the stationarity condition may be induced by systematic phase variations mainly due to the terrain topography but also to atmospheric effects or to deformation gradients. The most reliable technique to eliminate this bias is to compensate for the topography by means of external DEMs. Nevertheless, the DEM may not be available for the scene under study, or its quality may be rather low for coherence estimation purposes. There exist alternative coherence estimation techniques aiming to solve these problems with different level of success.
1.2.6 Polarimetric Speckle Noise Filtering
As it has been explained previously, a PolSAR system measures the scattering matrix S for every pixel. In the case of deterministic or point scatterers, this matrix determines completely the scattering process, and it can be directly employed to retrieve physical information of the scatterer. Nevertheless, in the case of distributed scatterers, the scattering matrix S is no longer deterministic but random due to the complexity of the scattering process. As indicated, this random behaviour is referred to as speckle. Speckle is a true scattering measurement, but the complexity of the scattering process makes it necessary to consider it as a noise source. Consequently, the information of interest is no longer the scattering matrix, but the different stochastic moments necessary to specify completely the probability density function of the SAR data. These moments must be estimated from the measured data, or said in a different way, speckle noise must be filtered out or even eliminated to grant access to these statistical moments. In the case of PolSAR data, under the assumption of the vector k to be distributed according to the zero-mean, complex Gaussian distribution (1.98), these moments correspond to the covariance C or the coherency T matrices.
Section 1.2.3 already introduced the simplest approach to estimate the covariance or the coherency matrices, i.e. the multilook (1.100), which corresponds to an incoherent average or a spatial average. Although the multilook approach corresponds to the maximum likelihood estimator of the covariance or coherency matrices, it presents the drawback that the estimation of the data is obtained at the expense of degrading the spatial resolution and the spatial details of the data. Figure 1.7 shows an example of these effects.
Considering the limitations of the multilook filtering approach, it is necessary to define different filtering alternatives that improve the multilook approach in such a way that they are able to retain the spatial resolution and the spatial details of the image but also lead to a correct and unbiased estimation of the covariance and coherency matrices.
1.2.6.1 PolSAR Speckle Noise Filtering Principles
The objective of any PolSAR speckle noise filter to be defined is to estimate the covariance or the coherency matrix while retaining the spatial resolution and the spatial details of the data. From a general point of view, it would be necessary to determine the general principles a PolSAR filter should follow in order to perform a correct estimation of the information of interest. Different authors have addressed the necessity to specify the general principles of a PolSAR speckle filter and which are the potential limitations: Touzi et al. (Touzi and Lopes 1994), Lee et al. (Lee et al. 1999) and López-Martínez et al. (Lopez Martínez and Fabregas 2008).
In the previous three references, as the data is assumed to be characterized by the zero-mean, complex Gaussian pdf, the information to retrieve is on the second-order moments of the PolSAR data. In (Touzi and Lopes 1994), the authors propose the use of the Mueller matrix, although they also consider the covariance matrix. In (Lee et al. 1999; Lopez Martínez and Fabregas 2008), the filtering is performed on the covariance or on the coherency matrices. In any case, the use of the covariance, the coherency or the Mueller matrices to filter the data is equivalent as all these matrices contain the same information. For instance, as indicated previously in Sect. 1.1.2.2, the covariance and the coherency matrices are related by similarity transformations. Implicitly, the authors are considering that these matrices contain all the necessary information to characterize the PolSAR data. This assumption is only valid under the hypothesis of (1.98), which only applies in the case of stationary data. The presumption of more evolved stochastic data models that may take into account additional signal variability, for instance, texture, are always associated with the necessity to estimate additional stochastic moments associated with the texture information.
Another point in which all the previous three references are in agreement is the need to consider the estimation of the previous matrices locally, adapting to the stationarity or homogeneity of the PolSAR data. This requirement is justified from two different points of view. The first one refers, due to the stationarity of PolSAR data, to the need to maintaining the spatial resolution and the radiometric information in the case of point or deterministic scatterers, which may be extended to the idea of preserving the spatial resolution and the spatial details of the PolSAR data. The second refers to the fact that in the case of distributed scatterers, the covariance matrix must be estimated on stationary data, avoiding the mixture of different stationary areas. This idea implies that the PolSAR filter must adapt the filtering process to the morphology of the PolSAR data. The differences between the filtering principles for PolSAR data proposed by Touzi and Lopes (1994), Lee et al. (1999) and Lopez Martínez and Fabregas (2008) are on how to consider the information that may be provided by the off-diagonal elements of the covariance or coherency matrices and whether this information may be employed to optimize speckle noise reduction or not. The approaches proposed by Touzi and Lopes (1994) and Lee et al. (1999)) suggest an extension of the multiplicative speckle noise model that applies for the diagonal entries of the covariance matrix to the off-diagonal ones, although it is also admitted that this extension may not lead to an optimum filtering of the speckle noise component. In (Lee et al. 1999), the authors even propose that the use of the degree of statistical independence between elements must be avoided in order to avoid crosstalk and that all the elements of the covariance matrix must be filtered by the same amount. These principles were extended in (Lopez Martínez and Fabregas 2008), based on a more accurate PolSAR speckle noise model for the off-diagonal elements of the covariance matrix (Lopez Martínez and Fabregas 2003). This model predicts that for a given off-diagonal element of the covariance matrix, speckle presents a complex additive nature for low coherence values, whereas speckle tends to be multiplicative in the case of high coherences. Consequently, an optimum speckle noise reduction should adapt to the type of noise for the off-diagonal elements of the covariance matrix, that is, filtering must adapt to the level of coherence (Lopez Martínez and Fabregas 2008). As it may be concluded, a PolSAR filter needs also to be adapted to the polarimetric information content of the data. Consequently, in connection with what has been explained previously, the way a PolSAR filter adapts to the local information must consider all the information provided by the covariance or coherency matrices.
1.2.6.2 PolSAR Speckle Noise Filtering Alternatives
As indicated in Sect. 1.2.3, the first alternative to estimate the covariance or the coherency matrices is to consider their maximum likelihood estimator that corresponds to an incoherent spatial average as expressed in (1.101). In this case, the estimation of the information is obtained at the expense of the loss of spatial resolution and spatial details. Consequently, in order to avoid the previous drawbacks, the PolSAR data filters should adapt to the morphology of the SAR image to retain the spatial details while leading to a correct and unbiased estimation of the covariance or coherency matrices.
PolSAR images are inherently heterogeneous as they reflect the heterogeneity of the Earth surface. Consequently, a first alternative to adapt to this heterogeneity, in order to avoid the loss of spatial resolution and spatial details, is to adapt locally to the signal morphology. One option to achieve this local adaptation is to consider edge aligned windows, as proposed in (Lee et al. 1999). Previously to the PolSAR data filtering process, the algorithm in (Lee et al. 1999), known as refined Lee filter, proposed the use of directional masks, within the analysis window, to determine the most homogeneous part of the sliding window where the local statistics have to be estimated. This spatial adaptation permits to preserve relatively sharp edges and local details. Once the directional mask defines the homogeneous pixels that have to be employed to estimate the covariance or the coherency matrices, these are estimated by means of the Local Linear Minimum Mean Square Error (LLMMSE) approach, i.e.
where \( \hat{\mathbf{Z}} \) is the estimated value of the covariance matrix, \( \overline{\mathbf{Z}} \) is the local mean covariance matrix computed with the homogeneous pixels selected by the edge aligned window and Z corresponds to the covariance matrix of the central pixel. Finally, b is a weighting function having a value between 0 and 1 derived from the statistics of the Span image. Over homogeneous areas, b ≈ 0 so the estimated covariance matrix corresponds to the values of the local means as it would be expected in absence of spatial details. Nevertheless, in the case the central pixel of the analysis window corresponds to a deterministic scatterer, b ≈ 1 producing \( \hat{\mathbf{Z}} \) to be the covariance matrix of the central pixel. Consequently, the pixel is not filtered and the spatial resolution is preserved, as observed in Fig. 1.8. In relation with the filtering procedure proposed in (Lee et al. 1999), the authors proposed also a filtering alternative where the pixels to be averaged within the analysis window are those with the same scattering mechanism as the central pixel, obtained through the Freeman-Durden decomposition (Lee et al. 2006).
As it may be observed, the previous filtering approach adapts to the signal morphology through a family of edge aligned windows. Hence, the adaptation to the signal morphology is restricted to a finite family of aligned windows. In (Vasile et al. 2006), the authors extended the ideas presented in (Lee et al. 1999), but instead of considering edge aligned windows, the authors introduced the concept of region growing to define an adaptive set of homogeneous pixels surrounding the pixel under analysis in order to adapt to the local morphology of the data. As in the case of Lee et al. (1999)), the adaptation to the signal morphology is achieved through the Span image. The region growing process is based on comparing a given pixel against its neighbours to determine their similarity by considering their corresponding covariance and coherency matrices. Since a PolSAR system provides for every pixel only the scattering matrix, an initial process of regularization that assures full-rank covariance or coherency matrices is necessary. This regularization process could be performed with the multilook filter, but it would introduce a loss of spatial resolution and spatial details. In (Lee et al. 1999), the authors propose the use of the median filter. Nevertheless, this alternative introduces a bias in the estimated data, as in the case of non-symmetric distributions, such as the one of the amplitude or the intensity of a SAR image or the one of the Span, the median does not correspond to the mean.
All the previous filtering approaches adapt to the signal morphology locally under the assumption that the pixels surrounding the pixel of analysis present a high probability to be statistically similar. Hence, these filters assume that the data are locally stationary. Nevertheless, it has been recently demonstrated that this idea of local stationary could be relaxed under the assumption that similar pixels to the one of analysis are available not only on the neighbourhood of the pixel of analysis but on the complete image (Deledalle et al. 2010).
In order to increase the filtering effect, one option, as shown in (Vasile et al. 2006), is to increase the number of homogeneous pixels to be averaged that are similar to the pixel under consideration. In (Vasile et al. 2006), as well as in (Lee et al. 1999), the similarity is measured considering only the information contained in the diagonal elements of the covariance or coherency matrices. Therefore, these approaches neglect the information provided by the off-diagonal elements of these matrices. The way to take into account all the information provided by the covariance or the coherency matrices is to consider the concept of the distance in the space defined by the matrices themselves. This approach has been considered in (Deledalle et al. 2010) as well as in (Alonso Gonzalez et al. 2012). In (Alonso Gonzalez et al. 2012), the authors propose to introduce the concept of binary partition tree (BPT) as a hierarchical structure to exploit the relations that may be established between similar pixels. In essence, the filtering alternative proposed in (Alonso Gonzalez et al. 2012) produces first a binary partition tree that establishes the relations between similar pixels on the basis of a distance that takes into account all the polarimetric information. In a second step, the binary partition tree is pruned to find the largest homogeneous regions of the image. This filtering alternative allows to filter large homogeneous areas while maintaining the spatial details of the data as observed in Fig. 1.9.
The objective of all the previous filtering techniques is to obtain the best estimate of the covariance or coherency matrices by means of increasing the number of averaged samples. Nevertheless, if the number of available homogeneous pixels is not large enough, the way to improve the estimation of the covariance and coherency matrices must be addressed by considering a better exploitation of the Wishart distribution. As shown in (Lopez Martínez and Fabregas 2003), the Wishart distribution allows defining the multiplicative-additive speckle noise model for all the elements of the covariance or the coherency matrices. This model has been exploited for PolSAR data filtering in (Lopez Martínez and Fabregas 2008), where it is demonstrated that if the filtering process is adapted to the multiplicative or additive nature of speckle, depending on the correlation of a pair of SAR images, it may lead to an improved estimation of the different parametric parameters that characterize the covariance or coherency matrices.
Beyond all the PolSAR data filtering techniques presented in this section, there exist a wide variety of similar approaches in the related literature, where a comparison among some of them has been presented in (Foucher et al. 2012). Nevertheless, it may be concluded that reaching an optimal compromise of a joint preservation of the polarimetric and the spatial information, in the case of PolSAR data filtering, is still today a problem without an adequate solution. Consequently, the selection of a particular filtering alternative for PolSAR data must take into consideration the final application of the PolSAR data in order to determine the optimum filtering according to that application.
1.3 Polarimetric Scattering Decomposition Theorems
As shown in Sect. 1.1.2, the scattering matrix or the covariance and coherency matrices allow the characterization of a scatterer for a given frequency and a given imaging geometry. The information provided by these matrices, at a particular combination of transmitting and receiving polarization states, can be extended to any polarization state, thanks to the concept of polarization synthesis. Nevertheless, when facing real polarimetric SAR data, the interpretation of these matrices is not straightforward due to the complexity of the scattering process and the high variability of the scatterers. Polarimetric decomposition techniques appear as a solution to interpret the information provided by the scattering and the covariance and coherency matrices. These decomposition techniques must be divided into two main classes. The first one, referred to as coherent polarimetric decompositions, makes reference to those decomposition techniques applied to the scattering matrix. The validity of these decomposition techniques is restricted to point scatterers, that is, scatterers not affected by the speckle noise component. If applied to distributed scatterers, these decompositions would be random as they are not able to cope with the stochastic nature of the measurements. Distributed scatterers, on the contrary, can be analysed by the so-called incoherent polarimetric decompositions that base the analysis on the covariance or coherency matrices.
1.3.1 Coherent Scattering Decomposition Techniques
Section 1.1.2.1 introduced the 2 × 2 complex scattering matrix as a mathematical operator able to describe the scattering process that occurs when a wave reaches a given scatterer. As indicated, this matrix contains the necessary information to determine the far-field scattered wave by the scatterer as a function of the incident wave. Consequently, the scattering matrix characterizes the scatterer, for the employed imaging geometry and the working frequency. As indicated in Table 1.6, simple canonical scattering mechanisms may be recognized from the scattering matrix. Nevertheless, in real measurements, the scattering matrix usually presents a more complex structure that hinders the interpretation in physical terms. The objective behind coherent scattering decomposition techniques is to decompose the measured scattering matrix by the SAR system, i.e. S, as a combination of the scattering matrices corresponding to simpler scatterers:
In (1.157), the symbol Si corresponds to the response of every one of the simple or canonical scatterers, whereas the complex coefficients ci indicate the weight of Si in the combination leading to the measured S. As observed in (1.112), the term combination refers to the weighted addition of the k scattering matrices. In order to simplify the understanding of (1.112), but also with the objective to make possible the decomposition itself, it is desirable that the matrices Si present the property of independence among them to avoid a particular scattering behaviour to appear in more than one matrix Si. Often, the independence condition is substituted by the most restrictive property of orthogonality of the components Si. Orthogonality helps to eliminate possible ambiguities in the decomposition of the scattering matrix in those cases in which the elements Si are not orthogonal.
The scattering matrix S characterizes the scattering process produced by a given scatterer and therefore the scatterer itself. This is possible only in those cases in which both the incident and the scattered waves are completely polarized waves. Consequently, coherent scattering decompositions can be only employed to study the so-called coherent scatterers. These scatterers are also known as point or pure targets.
In a real situation, the measured scattering matrix by the radar S corresponds to a complex coherent scatterer. Only in some occasions, this matrix will correspond to a simpler or canonical object, in which a good example is, for instance, the trihedrals employed to calibrate SAR imagery. Other simple scattering mechanisms may be observed in Table 1.6. Nevertheless, in a general situation, a direct analysis of the matrix S, with the objective to infer the physical properties of the scatterer under study, is shown to be complex. Consequently, the physical properties of the target under study are extracted and interpreted through the analysis of the simpler responses Si and the corresponding complex coefficients ci in (1.112).
The decomposition exposed in (1.112) is not unique in the sense that it is possible to find a number of infinite sets {Si; i = 1, …, k} in which the matrix S can be decomposed. Nevertheless, only some of the sets {Si; i = 1, …, k} are convenient in order to interpret the information contained in S. Two examples of these decomposition bases have been already shown in Sect. 1.1.2.2. Other examples of coherent scattering decompositions are the Krogager (Krogager 1990) or the Cameron decompositions (Cameron and Leung 1990).
1.3.1.1 The Pauli Decomposition
The most relevant coherent scattering decomposition is the Pauli decomposition that was already introduced in Sect. 1.1.2.2. The Pauli decomposition expresses the measured scattering matrix S in the so-called Pauli basis. If we considered the conventional orthogonal linear basis \( \left\{\hat{\mathbf{h}},, \hat{\mathbf{v}}\right\} \), in a general case, the Pauli basis {Sa, Sb, Sc, Sd} is given by the following four 2 × 2 matrices:
As mentioned, it has been always considered that Shv = Svh, since reciprocity applies in a monostatic system configuration under the BSA convention. In this situation, the Pauli basis can be reduced to a basis composed by the matrices (1.113), (1.114) and (1.115), that is, {Sa, Sb, Sc}. Consequently, given a measured scattering matrix S, this matrix can be expressed as follows:
where the complex coefficients that determine the contribution of every component of the basis can be obtained as
From the previous equations, it can be shown that
The interpretation of the Pauli decomposition must be done according to the matrices {Sa, Sb, Sc} and their corresponding decomposition coefficients, i.e. {a, b, c}. In Sect. 1.1.2.1 it was seen that the matrices {Sa, Sb, Sc} correspond to the scattering behaviour of some canonical bodies.
The matrix Sa corresponds to the scattering matrix of a sphere, a plate or a trihedral; see Table 1.6. Generally, Sa is referred to as single- or odd-bounce scattering. Hence, the complex coefficient a represents the contribution of Sa to the final measured scattering matrix. In particular, the intensity of this coefficient, i.e. |a|2, determines the power scattered by scatterers characterized by single- or odd-bounce.
The second matrix Sb represents the scattering mechanism of a dihedral oriented at 0 degrees; see Table 1.6. In general, this component indicates a scattering mechanism characterized by double- or even-bounce, since the polarization of the returned wave is mirrored with respect to the one of the incident wave. Consequently, b stands for the complex coefficient of this scattering mechanism, and |b|2 represents the scattered power by this type of targets.
Finally, the third matrix Sc corresponds to the scattering mechanism of a diplane oriented at 45 degrees. As it can be observed in (1.115), and considering that this matrix is expressed in the linear orthogonal basis \( \left\{\hat{\mathbf{h}},, \hat{\mathbf{v}}\right\} \), the scatterer returns a wave with a polarization orthogonal to the one of the incident wave. From a qualitative point of view, the scattering mechanism represented by Sc is referred to those scatterers which are able to return the orthogonal polarization, from which one of the best examples is the volume scattering produced by the forest canopy. The complex scattering that occurs in the forest canopy, characterized by multiple reflections, makes possible to return energy on the orthogonal polarization, with respect to the polarization of the incident wave. Consequently, this third scattering mechanism is usually referred to as volume scattering. The coefficient c represents the contribution of Sc to S, whereas |c|2 stands for the scattered power by this type of scatters.
The Pauli decomposition of the scattering matrix is often employed to represent the polarimetric information in a single SAR image. The polarimetric information of S could be represented with the combination of the intensities |Shh|2, |Svv|2 and 2|Shv|2 in a single RGB image, i.e. each of the previous intensities coded as a colour channel. The main drawback of this approach is the physical interpretation of the resulting image in terms of |Shh|2, |Svv|2 and 2|Shv|2. Consequently, a RGB image can be created with the intensities |a|2, |b|2 and |c|2, which, as indicated previously, correspond to clear physical scattering mechanisms. Thus, the resulting colour image can be employed to interpret the physical information from a qualitative point of view. The most employed codification corresponds to
Then, the resulting colour of the RGB image is interpreted in terms of scattering mechanism as given in (1.113)–(1.115); see Fig. 1.10.
1.3.2 Incoherent Scattering Decompositions Techniques
As explained in the previous sections, the scattering matrix S is only able to characterize the point or deterministic scatterers. In this case, the scattering process is completely determined by the five independent parameters the matrix S may present. On the contrary, this matrix cannot be employed to characterize, from a polarimetric point of view, the distributed scatterers, as the five independent parameters of the S matrix are insufficient to characterize the scattering process. As detailed in Sect. 1.2, distributed scatterers can be only characterized statistically due to the presence of speckle noise by means of higher-order descriptors. Since speckle noise must be reduced, only second-order polarimetric representations can be employed to analyse distributed scatterers. In the case of monostatic scattering under the BSA convention, these second-order descriptors are the 3 × 3 Hermitian covariance C or coherency T matrices.
The complexity of the scattering process makes extremely difficult the physical study of a given scatterer through the direct analysis of C or T. Hence, the objective of the incoherent decompositions is to separate the C or T matrices as the combination of second-order descriptors corresponding to simpler or canonical objects, presenting an easier physical interpretation. These decomposition theorems can be expressed as
where the canonical responses are represented by Ci and Ti and pi and qi denote the coefficients of these components in C or T, respectively. As in the case of the coherent decompositions, it is desirable that these components present some properties. First of all, it is desirable that the components Ci and Ti correspond to pure scatterers in order to simplify the physical study. Nevertheless, this condition is not absolutely necessary, and Ci and Ti may also represent distributed scatterers. In addition, the components Ci and Ti should be independent or, in a more restrictive way, orthogonal.
1.3.2.1 Three-Component Freeman Decomposition
The Freeman decomposition, also known as Freeman-Durden decomposition (Freeman and Durden 1998), is the best exponent of the so-called model-based decompositions. In this type of decompositions, the canonical scattering mechanisms Ci and Ti in which the original matrices are decomposed into are fixed by the decomposition itself, i.e. the scattering mechanisms are imposed. In particular, the Freeman decomposition decomposes the original covariance or coherency matrices into the three following scattering mechanisms:
-
Volume scattering, where a canopy scatterer is modelled as a set of randomly oriented dipoles
-
Double-bounce scattering, modelled as a dihedral corner reflector
-
Surface or single-bounce scattering, modelled as a first-order Bragg surface scatterer
In the following, and without lack of generality, a formulation in terms of the covariance matrix C is considered.
The volume scattering component, mainly considered in forested areas, is modelled as the contribution from an ensemble of randomly oriented thin dipoles. If the set of randomly oriented dipoles are oriented according to a uniform phase distribution, the covariance matrix of the ensemble of thin dipoles corresponds to the following covariance matrix:
where fv corresponds to the contribution of the volume scattering. The covariance matrix Cv presents a rank equal to 3. Thus, the volume scattering cannot be characterized by a single scattering matrix of a pure scatterer. Finally, it is worth to indicate, as observed in (1.122), that the model assumed for forest scattering in the Freeman decomposition is fixed. In contrast, the other two scattering components of the decomposition, as it will be shown, admit a higher degree of flexibility.
The second component of the Freeman-Durden decomposition corresponds to double-bounce scattering. In this case, a generalized corner reflector is employed to model this scattering process. The diplane itself is not considered metallic. Hence, it is assumed that the vertical surface presents reflection coefficients Rth and Rtv for the horizontal and the vertical polarizations, respectively, whereas the horizontal surface presents the coefficients Rgh and Rgv for the same polarizations. Additionally, two phase components for the horizontal and the vertical polarizations are considered, i.e. \( {e}^{j2{\gamma}_h} \) and \( {e}^{j2{\gamma}_v} \), respectively. The complex phase constants γh and γh account for any attenuation or phase change effect. Hence, the covariance matrix of the double-bounce scattering component, after normalization with respect to the Svv component, can be written as follows:
where
and fd corresponds to the contribution of the double-bounce scattering to the |Svv|2component:
As it can be observed, in this case the covariance matrix Cd presents a rank equal to 1, and therefore it may be represented by a scattering matrix.
The third component of the Freeman-Durden decomposition consists of a first-order Bragg surface scattering modelling a surface rough scattering. Considering Rh and Rv the reflection coefficients for horizontally and vertically polarized waves, the covariance matrix corresponding to this scattering component is
where fs corresponds to the contribution of the double-bounce scattering to the |Svv|2 component:
and
As in the case for the double-bounce scattering mechanism, Cs presents a rank equal to 1.
Finally, it can be seen that the Freeman decomposition expresses the measured covariance matrix C as
that takes the expression
As one may deduce from (1.130), the Freeman decomposition presents five independent parameters {fv, fd, fs, α, β} but only four equations. Consequently, some hypothesis must be considered in order to find the values of {fv, fd, fs, α, β}. Considering that the Span of the covariance matrix may be expressed as a function of the power scattered by each component of the decomposition {Cv, Cd, Cs}, i.e.
the term Pv corresponds to the contribution of the volume scattering of the final covariance matrix C. Hence, the scattered power by this component may be written as
The power scattered by the double-bounce component is expressed as
whereas the power scattered by the surface component is
Consequently, the scattered power at each component {Pv, Pd, Ps} may be employed to generate a RGB image, similarly as in the case of the Pauli decomposition, to present all the colour-coded polarimetric information in a unique image; see Fig. 1.11.
1.3.2.2 Four-Component Yamaguchi Decomposition
As it may be observed in (1.130), the three-component Freeman decomposition is based on the assumption that the analysed scatterer presents reflection symmetry, that is, the correlation of the co-polar channels, either Shh or Svv, with the cross-polar one Shv is zero, that is, \( E\left\{{S}_{hh}{S}_{hv}^{\ast}\right\}=0 \) and \( E\left\{{S}_{hv}{S}_{vv}^{\ast}\right\}=0 \). This type of symmetry in the scattering process appears normally in the case of natural distributed scatterers such as forests or grassland areas. Nevertheless, in the case of more complex scattering scenarios, for instance, man-made scatterers, this assumption is no longer true. In addition to the previous limitation, the Freeman decomposition, as detailed in the previous section, considers only one type of volume scattering, as reflected in (1.122), where the scattering at the co-polar channels are supposed equal, i.e. E{|Shh|2} = E{|Svv|2}. The four-component Yamaguchi decomposition is proposed to overcome the previous two limitations of the Freeman decomposition (Yamaguchi et al. 2005).
If one considers the canonical scattering mechanisms presented in Table 1.6, it may be observed that only the rotated thin cylinder or the right- and left-handed helices are able to produce a covariance matrix such that \( E\left\{{S}_{hh}{S}_{hv}^{\ast}\right\}\ne 0 \) and \( E\left\{{S}_{hv}{S}_{vv}^{\ast}\right\}\ne 0 \) and therefore produce a covariance matrix without reflection symmetry. In the four-component Yamaguchi decomposition, the authors propose to take into account the absence of this type of symmetry by considering first the three scattering mechanisms considered by the Freeman decomposition, that is, volume, double-bounce and surface scattering, together with a fourth component composed by either the left- or the right-handed helix scattering (Krogager 1990). In particular, the helix scattering is characterized by generating a left-handed or a right-handed circular polarization for all incident linear polarizations, according to the scatterer helicity. The left-handed helix, whose scattering matrix is presented in Table 1.6, leads to the following covariance matrix:
whereas the right-handed helix results in the following covariance matrix:
where fc accounts for the contribution of the helix component. As it may be observed in the previous two matrices, the inclusion of the helix component allows to consider a scattering mechanism without reflection symmetry. The selection of the left- or the right-handed helix will be determined by the sign of the imaginary part of \( E\left\{{S}_{hh}{S}_{hv}^{\ast}\right\} \) or \( E\left\{{S}_{hv}{S}_{vv}^{\ast}\right\} \).
In order to model the volume scattering, the Freeman decomposition considered a set of randomly oriented dipoles, oriented according to a uniform phase distribution. Nevertheless, when confronted to a real forest, the effect of the trunk and the branches, especially at high frequencies, may lead to a scattering from a cloud of oriented dipoles but with a non-uniform distribution. In this case, depending on the main orientation of these thin dipoles, the power associated with E{|Shh|2} and E{|Svv|2} may be different if the dipoles are preferably oriented horizontally or vertically, respectively. As it may be seen, the volume model considered by the Freeman decomposition (1.122) cannot take into account this effect. In order to account for this preference in the orientation, instead of considering a uniform distribution for the orientation of the thin dipoles, it is proposed to consider the following distribution:
where θ is taken from the horizontal axis seen from the radar. When considering a cloud of randomly oriented, very thin horizontal dipoles, the volume scattering is represented by the following scattering matrix:
Otherwise, if the cloud of thin dipoles is considered to be composed of vertical dipoles, the covariance matrix representing the volume component is
In all the cases, fv corresponds to the contribution of the volume scattering.
Allowing the volume scattering to depend on the main orientation of the particles makes it necessary to introduce an additional step in the decomposition able to select the volume scattering most adapted to the data under observation. The four-component Yamaguchi decomposition proposes to select among (1.122), (1.138) and (1.139) according to the ratio χ = 10 log (E{|Svv|2}/E{|Shh|2}). Table 1.7 details the procedure to select the type of volume scattering proposed in (Yamaguchi et al. 2005).
Finally, the double-bounce and the surface scattering components of the four-component Yamaguchi decomposition are the same as the Freeman decomposition. Consequently, the Yamaguchi decomposition models the covariance matrix as
where the last matrix accounts for the volume scattering that has been selected according to Table 1.7. As one may deduce from (1.140), the four-component Yamaguchi decomposition presents six independent parameters {fv, fd, fs, fc, α, β}. Considering that the Span of the covariance matrix may be expressed as a function of the power scattered by each component of the decomposition {Cv, Cd, Cs, Clh/rh}, i.e.
the term Pv corresponds to the contribution of the volume scattering of the final covariance matrix C. Hence, the scattered power by this component may be written as
the power scattered by the double-bounce component is expressed as
the power scattered by the surface component is
whereas the power scattered by the helix component is
Consequently, the scattered power at each component {Pv, Pd, Ps, Pc} may be combined to generate a RGB image similarly as in the case of the Pauli decomposition, to present all the colour-coded polarimetric information in a unique image; see Fig. 1.12.
1.3.2.3 Non-negative Eigenvalue Decomposition
As indicated in the previous two sections, both the Freeman-Durden and the Yamaguchi decomposition work under the hypothesis that the measured covariance matrix may be decomposed as the sum of a set of scattering mechanisms. Whereas the first decomposition assumes reflection symmetry for the scattering medium, this limitation is addressed by the second one by considering a fourth scattering component represented by either the left- or the right-handed helix scattering. All the scattering mechanisms in which the measured covariance matrix is decomposed into are represented by their corresponding covariance matrices. As shown in (Van Zyl et al. 2011), these matrices should correspond to physical scattering mechanisms, so all their eigenvalues must be larger than or equal to zero; in other words, the power received by any combination of transmitting and receiving polarizations should never be negative.
A close analysis of the Freeman-Durden decomposition shows that the contribution of the volume scattering component is directly estimated from the cross-polarized term, that is, the decomposition assumes that neither the double-bounce nor the surface scattering components contribute to it. This assumption is very strict as, for instance, the rotation of the polarization basis of the scattering matrix due to terrain slopes in the along-track dimension (Lee et al. 2002) or even rough surfaces may lead to significant cross-polarized power (Hajnsek et al. 2003). Consequently, if these effects are not taken into account, they may produce an overestimation of the volume component. Once this volume component is estimated from the data, it is extracted from the measured covariance matrix to estimate the double-bounce and the surface components as
Consequently, if the volume component is not properly estimated, the previous subtraction may lead to a result in which the covariance matrix representing the double-bounce and the surface components Cd + s may present negative eigenvalues so it does not represent a physically possible scattering mechanism. The Yamaguchi decomposition also presents this drawback as the double-bounce and the surface like scattering components are estimated after the subtraction of the volume scattering component.
In order to correct the presence of negative eigenvalues when considering a decomposition based on (1.146), van Zyl et al. (Van Zyl et al. 2011) proposed the non-negative eigenvalue decomposition (NNED). The Freeman-Durden and the Yamaguchi decompositions assume that the measured covariance matrix results from the addition of a set of scattering mechanisms. Nevertheless, the NNED approach proposed to decompose the measured covariance matrix as
The matrix Cmodel represents the covariance matrix predicted by a theoretical model, for instance, the volume scattering component. The parameter a is introduced in (1.147) to assure that all the matrices in (1.147) represent physically realizable scattering mechanism. Finally, the second matrix Cremainder will contain whatever is in the measured matrix C that is not consistent with the model matrix Cmodel.
To find the value of a, (1.147) may be written as
Consequently, the value of a must assure that the eigenvalues of Cremainder must be positive. In the case of a scattering media with reflection symmetry, (1.147) may be written as
Therefore, the maximum value of a that assures that the eigenvalues of Cremainder are positive corresponds to
where \( Z=\left({\xi \zeta}_a+{\zeta \xi}_a\right)-{\rho \rho}_a^{\ast }-{\rho}^{\ast }{\rho}_a \). For the case of scattering media not presenting reflection symmetry, the process to derive the maximum value of a is similar, but results in more complex expressions.
The volume scattering model employed for the canopy scattering is based on a cosine-squared distribution raised to the nth power for the vegetation orientation (Arii et al. 2011). Considering that the basic scatterer in the canopy is a dipole, it was shown that the covariance matrix can be written as
where
and
In the previous equations, the parameter θ0 represents the mean orientation angle of the thin dipoles, whereas σ accounts for the randomness of the cloud of dipoles.
On the basis of the previous procedure to avoid the extraction of non-physical covariance matrices, Arii et al. (Arii et al. 2011) proposed an adaptive NNED decomposition theorem, where also the previous extended model for volume scattering is considered. According to the NNED decomposition, a covariance matrix for the volume scattering is first subtracted from the measured covariance matrix as follows:
As indicated previously, fv can be obtained analytically only under the assumption of reflection symmetry. In those cases in which the previous hypothesis does not apply, the maximum value of fv is obtained numerically by calculating the eigenvalues Cremainder at specific randomness σ and mean orientation angle θ0 by varying fv, and then, the maximum fv in which all three eigenvalues of Cremainder are nonnegative is selected. Once the volume component is extracted from the measured covariance matrix as specified in (1.157), the remainder matrix can be written as
where in this case Cd and Cs correspond to the double-bounce and surface scattering mechanisms already employed in the three-component Freeman-Durden decomposition. The parameters fd, fs and \( {\mathbf{C}}_{\mathrm{remainder}}^{\prime } \) are obtained through an eigenvalue decomposition. This procedure shows how to find the parameters in the decomposition for a specific pair of randomness σ and mean orientation angle θ0. To find the best fit decomposition, the power in the remainder matrix for all pairs of randomness and mean orientation angles is evaluated and then the set of parameters that minimize the power associated with \( {\mathbf{C}}_{\mathrm{remainder}}^{\prime } \) should be found.
Finally, the scattered power at each component {fv, fd, fs} may be combined to generate a RGB image similarly as in the case of the Pauli decomposition, to present all the colour-coded polarimetric information in a unique image; see Fig. 1.13.
1.3.2.4 Eigenvector-Eigenvalue-Based Decomposition
The previous incoherent decompositions were constructed on the assumption that the scattering of a given pixel was due to the combination of some predefined scattering mechanisms, hence assuming different properties of the scattering processes. These assumptions make these decompositions to be easy to interpret as the different scattering components present a clear physical interpretation. Nevertheless, as these decompositions consider only the predefined mechanisms, they are not able to identify additional scattering mechanisms when present. A way to circumvent this drawback is to decompose the covariance or coherency matrices based on their mathematical properties. Hence, contrary to the previous decompositions, the scattering mechanisms in which the original matrices are decomposed are not established a priori but given by the decomposition itself. The drawback of this approach is that the scattering mechanism found by the decomposition needs from a physical interpretation process.
The eigenvector-eigenvalue scattering decomposition, also known as Cloude-Pottier decomposition, is based on the eigendecomposition of the covariance C or coherency T matrices (Cloude and Pottier 1996). According to the eigendecomposition theorem, the 3 × 3 Hermitian matrix C may be decomposed as follows:
The 3 × 3, real, diagonal matrix Σ contains the eigenvalues of C:
such that ∞ > λ1 ≥ λ2 ≥ λ3 > 0. The 3 × 3 unitary matrix U contains the eigenvectors ui for i = 1, 2, 3 of C:
The eigenvectors ui for i = 1, 2, 3 of C can be reformulated, or parameterized, as
Considering (1.159), (1.160) and (1.161), the coherency matrix C may be written as
As (1.163) shows, the rank-3 matrix C can be decomposed as the combination of three rank 1 coherency matrices which can be related to the pure scattering mechanisms given in (1.162). Consequently, the eigendecomposition is not able to produce scattering mechanisms in which the original matrix is decomposed into with a rank larger than 1.
The eigenvalues (1.160) and the eigenvectors (1.161) of the decomposition are considered as the primary parameters of the eigendecomposition of C. In order to simplify the analysis of the physical information provided by this eigendecomposition, three secondary parameters are defined as a function of the eigenvalues and the eigenvectors of C:
-
Entropy:
where pi are known as the probabilities of the eigenvalue λi, respectively. These probabilities represent the relative importance of this eigenvalue with respect to the total scattered power, as
-
Anisotropy:
representing the relative importance of the second eigenvalue with respect to the third one:
-
Mean alpha angle:
As it shall be shown, this parameter allows the physical interpretation of the scattering mechanism found by the eigendecomposition.
The eigendecomposition of the coherency matrix is usually referred to as the \( H/A/\overline{\alpha} \)decomposition. An example of \( H/A/\overline{\alpha} \) decomposition is shown in Fig. 1.14. The interpretation of the information provided by the eigendecomposition of the coherency matrix must be performed in terms of the eigenvalues and eigenvectors of the decomposition or in terms of \( H/A/\overline{\alpha} \). Nevertheless, both interpretations have to be considered as complementary.
The interpretation of the scattering mechanisms given by the eigenvectors of the decomposition, ui for i = 1, 2, 3, is performed by means of a mean dominant mechanism which can be defined as follows:
where the remaining average angles \( \overline{\beta} \), \( \overline{\delta} \), \( \overline{\gamma} \) are defined in the same way as \( \overline{\alpha} \).
The study of the mechanism given in (1.168) is mainly performed through the interpretation of the mean alpha angle \( \overline{\alpha} \), since its value can be easily related to the physics behind the scattering process. The next list details the interpretation of \( \overline{\alpha} \):
-
\( \overline{\alpha}\to 0 \): the scattering corresponds to single-bounce scattering produced by a rough surface.
-
\( \overline{\alpha}\to \pi /4 \): the scattering mechanism corresponds to volume scattering.
-
\( \overline{\alpha}\to \pi /2 \): the scattering mechanism is due to double-bounce scattering.
The second part in the interpretation of the eigendecomposition is performed by studying the value of the eigenvalues of the decomposition. A given eigenvalue corresponds to the associated scattered power to the corresponding eigenvector. Consequently, the value of the eigenvalue gives the importance of the corresponding eigenvector or scattering mechanism. The ensemble of scattering mechanisms is studied by means of the entropy H and the anisotropy A. The Entropy H determines the degree of randomness of the scattering process, which can be also interpreted as the degree of statistical disorder. In this way
-
H → 0:
As observed, in this case, the covariance matrix C presents rank 1, and the scattering process corresponds to a pure scatterer.
-
H → 1:
In this situation, the covariance matrix C presents rank 3, that is, the scattering process is due to the combination of three pure targets. Consequently, C corresponds to the response of a distributed target. For instance, volume scattering for a forest canopy presents an entropy value very close to 1.
-
0 < H < 1: In this case, the final scattering mechanism given by C results from the combination of the three pure targets given by ui for i = 1, 2, 3, but weighted by the corresponding eigenvalue.
The anisotropy A, (1.166), is a parameter complementary to the entropy. The anisotropy measures the relative importance of the second and the third eigenvalues of the eigendecomposition. From a practical point of view, the anisotropy can be employed as a source of discrimination only when H > 0.7. The reason is that for lower entropies, the second and third eigenvalues are highly affected by the SAR system noise.
In relation with the previous parameters, the Shannon entropy (SE) was introduced in (Morio et al. 2007):
as the sum of two terms. The term SEI is the intensity contribution that depends on the total power
whereas SEP is the polarimetric contribution
As indicated in Sect. 1.1.2.5, for some particular configurations, a polarimetric SAR system may not measure the complete polarimetric information. In this simpler configuration of dual polarization, the radar transmits only a single polarization and receives, either coherently or incoherently, two orthogonal components of the scattered signal. In this configuration, the covariance C and coherency T matrices are 2 × 2 Hermitian matrices. As it has been demonstrated (Cloude 2007a), these reduced matrices can be decomposed also considering their eigendecompositions. The sole particularity is that in this situation the matrices present only two eigenvalues.
1.3.2.5 The Touzi Target Scattering Decompositions
The Touzi decomposition (Touzi 2007) was introduced as an extension of the Kennaugh-Huynen coherent target scattering decomposition (Huynen 1970; Kennaugh 1951), for the characterization of both coherent and partially coherent target scattering. To characterize partially coherent scattering, Huynen introduced a target decomposition theorem in which he decomposed an average Mueller matrix into the sum of a Mueller matrix for a single scatter presented in terms of the Kennaugh-Huynen decomposition parameters and a noise or the N-target Mueller matrix (Huynen 1970). In 1988, Cloude (Cloude 1988) showed that the Huynen N-target decomposition was not polarization independent and introduced the eigenvector decomposition for a unique and roll-invariant incoherent decomposition. Following that, both Huynen’s (N-target) incoherent decomposition and Huynen’s fork decomposition were abandoned. Recently, the Kennaugh-Huynen decomposition has been reconsidered and integrated in Cloude’s coherency eigenvector decomposition (Cloude 1988) for characterization of coherent and partially coherent scattering in terms of unique and polarization basis independent parameters (Touzi 2007).
The Kennaugh-Huynen decomposition, also named the Huynen fork, used to be the most popular method for decomposition of coherent target scattering (Touzi et al. 2004; Boerner et al. 1998). Huynen’s fork was abandoned because of the nonuniqueness of certain fork parameters, and in particular the skip angle (scattering type phase), due to nonuniqueness of the con-eigenvalue phases (Luneburg 2002). To solve these ambiguities, the Kennaugh-Huynen scattering matrix con-diagonalization was projected into the Pauli basis (Touzi 2007), and a new target scattering vector model, the TSVM, was introduced in terms of target parameters that are not affected by the con-eigenvalue phase ambiguities (Touzi 2007). A complex entity, named the symmetric scattering type, was introduced for an unambiguous description of target scattering type. The polar coordinates of the symmetric scattering type, αs and ϕαs, are expressed as a function of target scattering matrix polarization basis independent elements by (Touzi 2007)
where μ1 and μ2 are the con-eigenvalues of the target scattering matrix S. The scattering vector of a symmetric scatterer can be expressed on the Pauli trihedral-dihedral basis {Sa, Sb} as follows (Touzi 2007):
where the scattering type magnitude αs corresponds to the orientation angle of the symmetric scattering vector on the trihedral-dihedral {Sa, Sb} basis. ϕαs is the phase difference between the vector components in the trihedral-dihedral basis. The new scattering type phase entity introduced in (Touzi 2007) provides a measure of the phase offset between the trihedral and dihedral scattering components. The information provided by ϕαs as complementary to αs was shown to be essential for a better understanding of marsh wetland scattering variations between the spring run-off season and the fall using Convair 580 SAR data collected over the Mer Bleue wetland site (Touzi et al. 2007). The symmetric and asymmetric nature of target scattering was characterized using Huynen helicity τ (Touzi 2007). Notice that while the complex scattering parameters αs and ϕαs are independent of the basis of polarization (Touzi 2007; Paladini et al. 2012), Huynen’s helicity characterizes the symmetric nature of target scattering in the {h, v} polarization basis (Huynen 1970). Recently, a different expression of the helicity was derived at the circular polarization basis (Huynen 1970), and the complementary information it provides to the Huynen’s helicity was demonstrated (Paladini et al. 2012).
The projection of the Kennaugh-Huynen coherent target decomposition on the Pauli polarization basis can be represented as a function of the complex scattering αs and ϕαs and the Huynen maximum polarization parameters ψ and m as
where ψ, τ and m are the Huynen orientation, the helicity and the maximum return of the maximum polarization, respectively.
It is worth noting that for a symmetric scattering (τ = 0), αs and ϕαs are identical to the Touzi SSCM parameters η and φSb − φSa. αs and ϕαs are also identical to the Cloude-Pottier parameters (Cloude and Pottier 1996) α and δ = φ2 − φ1, respectively (Touzi 2007). For scatterers of locally asymmetric scattering, such as urban areas, treed wetlands and forests, large divergence between ϕαs and δ and αs and α have been noted (Cloude and Pottier 1996). Unlike Cloude-Pottier parameters (Trunk and George 1970), the TSVM characterizes target scattering type with the complex entity (αs and ϕαs), which only depends on the scattering matrix eigenvalues. This leads to a unique and unambiguous description of target scattering in terms of parameters, which are polarization basis independent, for both symmetric and asymmetric targets as discussed in (Touzi 2007).
For a unique characterization of coherent and partially coherent scattering, the TSVM (Touzi 2007) was integrated in Cloude’s coherency eigenvector decomposition (Touzi 2007). Like Wiener’s wave coherence characteristic decomposition (Wiener 1930), Cloude’s characteristic decomposition of the coherency matrix, T, permits the representation of T as the incoherent sum of coherency matrices that represent independent single scattering (Cloude 1988). Under the target reciprocity assumption, T is represented as the sum of up to three coherency matrices Ti, each of them being weighted by its appropriate positive real eigenvalue ηi:
In contrast to the Cloude-Pottier decomposition, the TSVM is used for the parameterization of each coherency eigenvector Ti (coherent single scattering) in terms of unique target parameters. In order to avoid any loss of information related to single scatterer parameters averaging, the target scattering decomposition is conducted through an in-depth analysis of each of the three single scattering eigenvectors ui, i = 1, 2, 3 represented by the coherency eigenvector matrix Ti of rank 1 and the normalized positive real eigenvalues λi = ηi/(η1 + η2 + η3). This leads to the representation of each single scattering ui in terms of five roll-invariant and independent target scattering parameters (αsi, ϕαsi, τi, mi, λi) and the Huynen orientation angle ψi.
1.4 Polarimetric SAR Interferometry
This section is devoted to the radar remote sensing technique called polarimetric interferometry (Cloude and Papathanassiou 1998). When used with synthetic aperture radar (SAR) systems, it is usually termed polarimetric interferometric SAR or PolInSAR for short (Papathanassiou and Cloude 2001). PolInSAR has important applications in the remote measurement of vegetation properties such as forest height (Papathanassiou et al. 2005a) and biomass (Mette et al. 2004), future applications (Williams and Cloude 2005), snow/ice thickness monitoring (Dall et al. 2003; Papathanassiou et al. 2005b) and urban height and structure applications (Schneider Zandona et al. 2005). As its name suggests, this technique combines two separate radar technologies, polarimetry and interferometry. The former, as detailed in the previous sections, involves switching the polarization state of transmit and receive channels to measure differences in backscatter due to orientation, shape and material composition (Cloude and Pottier 1996). This leads ultimately to measurement of the 2 × 2 complex scattering matrix S, from which we can synthesize the response of the image pixel to arbitrary polarization combinations. On the other hand, radar interferometry (Bamler and Hartl 1998) involves coherently combining signals from two separated spatial positions (defining the so-called baseline of the interferometer) to extract a phase difference or interferogram. In radar this can be achieved in two main configurations, so-called along-track interferometry, which involves time displacements between separated antennas along the flight direction of the platform leading to velocity estimation. Alternatively, we can perform across-track interferometry, involving lateral separation of antennas and leading to spatial information relating to the elevation of the scatterer above a reference ground position. In PolInSAR, interest centres mainly on across-track geometries, but in principle it can be applied to along-track configurations as well.
PolInSAR differs from conventional interferometry in that it allows generation of interferograms for arbitrary transmit and receive polarization pairs. It turns out that the phase of an interferogram changes with the choice of polarization and consequently we can extract important biophysical and geophysical parameters by interpreting this change in the right way. It shall be seen that consequently the combination of interferometry with polarimetry is greater than the sum of its parts and that PolInSAR allows us to overcome severe limitations of both techniques when taken alone. This is especially true in the important area of remote sensing of vegetated land surface, where polarimetry suffers from the inherent high entropy problem (Cloude and Pottier 1996), while standard interferometry remains underdetermined, i.e. the interferogram depends on many possible physical effects, no one of which can be identified from the data itself (Treuhaft et al. 1996).
1.4.1 SAR Interferometry
PolInSAR algorithms make use of interferometric coherence, or equivalently phase and local phase variance, rather than backscattered power (Bamler and Hartl 1998; Zebker and Villasenor 1992). For this reason, it is necessary to introduce and to study the problems associated with the estimation of coherence from radar data, especially in the case of interferometric data. A similar introduction for polarimetric data was already seen in Sect. 1.2.5. Starting with any two co-registered single-look complex (SLC) data channels S1 and S2, the interferometric coherence is formally defined as
where 0 ≤ |γ| ≤ 1. In practice, the sample coherence is frequently used as a coherence estimate of Eq. (1.178):
where k is the sample number and we have only a finite number n independent signal measurements available. Eq. (1.179) represents the maximum likelihood estimate of coherence and under some general statistical assumptions provides an estimate that is asymptotically unbiased (see Sect. 1.2.3). For jointly complex Gaussian processes S1 and S2, the pdf of \( \left|\hat{\gamma}\right| \) can then be derived as a function of the true coherence value |γ| and the number of samples n (Touzi et al. 1999). The estimated coherence value \( \left|\hat{\gamma}\right| \) is consistently biased towards higher values (Touzi et al. 1999); in the extreme of single-look estimation, the coherence estimate is equal to unity and so always overestimated and without information. However, the bias decreases with increasing number of independent samples n and with increasing underlying coherence |γ|. A second important parameter to estimate is the variance of the sample coherence magnitude. While the true estimated value would be desirable, often we assume zero bias, by using sufficient averaging, and estimate the variance by making use of simpler equations for speedier computations. In particular, the Cramér-Rao bounds provide lower limits on the variance for coherence and phase and have been derived in (Tabb and Carande 2001) to provide the simpler formulae:
As it can be deduced for phase-based processing, it is always better to operate at high coherence and avoid low coherences; the latter involves not only increased variance but also severe bias issues that can distort the phase information. It is a key limitation of polarimetry that scattering by vegetation leads to low coherences for all polarization channels because of so-called depolarization. This severely limits the ability to use polarimetric phase information over vegetated land surfaces. Interferometry on the other hand allows to partially control coherence via baseline selection. PolInSAR exploits this advantage to obtain high coherence in multiple polarization channels.
The above considerations for coherence estimation are important in PolInSAR, the major distinguishing feature of which is that we add an extra stage in the construction of the two SLC channels S1 and S2. In general, for a fully polarimetric data set, we take as input the three calibrated SLC images Shh, Shv and Svv and generate projections of these onto user-defined complex weight vectors w1 and w2 before calculating the coherence defined as
The weight vectors w1 and w2 define user-selected scattering mechanisms at ends 1 and 2 of the across-track baseline. In general, w1 and w2 can be different and both parameterized as complex unitary vectors of the form shown in (1.162) (Cloude and Pottier 1996). The weight vectors or scattering mechanisms in which the targets vectors could be projected could be the canonical mechanisms detailed in Table 1.6. However, it is a feature of PolInSAR algorithm development that use is often made of more general w vectors than those shown, derived, for example, as eigenvectors for coherence optimisation (Tabb and Carande 2001; Colin et al. 2003), or through prior model studies of scattering from vegetated terrain (Williams 1999). For this reason, we need to keep the more general notation of Eq. (1.162) so as to be able to consider arbitrary vectors in the formation of an interferogram. We now turn to consider such optimisation algorithms in more detail and to briefly assess their implications for coherence estimation and validation.
1.4.2 Algorithms for Optimum Interferogram Generation
Polarimetric interferometry is a special case of multichannel coherent radar processing (Reigber et al. 2000). Such problems are characterized by multidimensional covariance matrices (Lee et al. 1994, 2003). In PolSAR, for example, interest centres on the 3 × 3 Hermitian covariance matrix C, unitarily equivalent to the coherency matrix T as shown in Sect. 1.1.2.2. This is the basic building block in polarimetric interferometry, and so it can be designated as Λ1 to indicate how it relates to fully polarimetric measurements but made at only one spatial position. In single baseline PolInSAR, a second measurement at a displaced position 2 is added. This is now characterized by a 6 × 6 coherency matrix Λ2 as shown in (1.182). The 6 × 6 matrix can be naturally partitioned into three sub-matrices each of size 3 × 3. This formulation then scales in a natural way for multibaseline PolInSAR by expansion of the governing coherency matrix ΛN to a 3N × 3N complex system or 4N × 4N for bistatic multibaseline PolInSAR, where N is the number of baselines:
Returning now to the important case of Λ2, two of the sub-matrices T11 and T22 are Hermitian and relate to the polarimetry from positions 1 and 2, while the third Ω12 is a complex 3 × 3 matrix that contains information about the variation of interferometric coherence and phase for all possible weight vectors w1 and w2:
The previous relation leads to an important choice of approach to algorithm development in PolInSAR. In the first case, if the vectors w1 and w2 are known in advance, then the coherence can be directly estimated using (1.181) with the same InSAR fluctuation statistics and bias outlined in the previous section. However, often we wish to determine optimum weight vectors from the data themselves, and it follows from (1.183) that to do this we require estimates of the three 3 × 3 matrices, T11 and T22 and Ω12. This opens up a much wider discussion about the fluctuation statistics and bias arising from the fact that only estimates and not true matrix values can be used in (1.183). For example, to estimate the sub-matrices, we must first estimate the full 6 × 6 coherency matrix Λ2. This estimate Z is obtained by means of the multilook estimator.
One important application of (1.183) is the calculation of the optimum coherences in PolInSAR. The most general formulation of this was first presented in (Cloude and Papathanassiou 1998) and is summarized in (1.184). Here, we first state the problem mathematically, which is to choose w1 and w2 so as to maximize the coherence magnitude, defined from the complex coherence as a function of the three sub-matrices T11 and T22 and Ω12 as shown. This can be mathematically solved by using a Lagrange multiplier technique as shown and leads to the calculation of the required w vectors as eigenvectors of a pair of matrices, themselves defined as products of the composite matrices:
As it was noted in Sect. 1.4.1, the estimated value of the coherence magnitude is biased with respect to the true value in such a way that the larger the number of averaged samples and the higher the coherence magnitude, the lower the bias. The previous hypothesis was based on considering (1.181) where the vectors w1 and w2 are known in advance. Nevertheless, if (1.184) is considered to obtain the coherence magnitude, the vectors w1 and w2 must also be estimated from the data, leading to a larger coherence magnitude bias.
In order to obtain an optimization approach that has less bias for a given number of samples, it is necessary to reduce the effective dimensionality of the problem. Several authors have proposed adopting the a priori assumption w1 = w2, i.e. that the optimum coherence vector remains unknown but we assume that it doesn’t change with baseline (Colin et al. 2003; Sagues et al. 2000; Flynn et al. 2002). This idea is supported on physical grounds for short baselines in the absence of temporal decorrelation, i.e. for single-pass or low-frequency sensors where the scattering does not change significantly over the effective angular width of the baseline. This approach calls for a new mathematical formulation of the optimization process. One approach is based on a straightforward extension of the Lagrange multiplier technique to constrain w1 = w2. This leads by manipulation of (1.184) to a set of w vectors given as eigenvectors of the composite matrix:
One problem with the previous equation is that the eigenvalue is not the coherence, but its real part, and so the optimization is phase sensitive. For this reason, a second related approach based on maximization of the phase difference as a function of polarization vector w has been developed. In this case, the optimum vector is found by solving a phase-parameterized eigenvalue problem (Colin et al. 2003; Flynn et al. 2002):
This has been shown to be equivalent to calculating the numerical radius of the complex matrix A = T−1/2Ω12T−1/2. A proposed algorithm for finding this optimum state has been presented in (Colin et al. 2003; Colin et al. 2005). One drawback in this approach is that ϕ1 is a free parameter, and so either search or iterative methods must be used to secure the global optimum. This adds to the computational complexity for each pixel.
A third related approach has been proposed based on a sub-space Monte Carlo searching algorithm (Sagues et al. 2000). This limits the search for the optimum (again assuming w1 = w2) to the diagonal elements of Ω12, i.e. to co-polarized or cross-polarized combinations across the whole Poincaré sphere. This again acts to effectively limit the dimensionality of the problem and demonstrates less bias than the full Lagrange multiplier method. Finally, phase centre super-resolution techniques based on the ESPRIT algorithm have also been proposed to find the optimum w vectors (Yamada et al. 2001).
In all these cases, a sub-optimum solution is obtained compared to the unconstrained Lagrange multiplier method but often with better numerical stability. Given the general increased processing overhead of employing optimization, it is always of interest to investigate the potential benefits of employing an optimization approach over simple linear, Pauli and circular options.
1.4.3 Model-Based Polarimetric SAR Interferometry
The previous section considered an important optimisation problem in PolInSAR, namely, to investigate the maximum variation of coherence with polarization by solving an eigenvalue problem. This section will be focused on some canonical problems of interest in the remote sensing of land surfaces and try and use the mathematical solutions obtained to conclude as to the potential of optimisation versus standard coherence estimation in PolInSAR. We consider three important problems, scattering from non-vegetated surfaces, random volume scattering and finally a 2-layer surface+volume mixture which more closely matches the behaviour of natural vegetated land surfaces.
1.4.3.1 PolInSAR for Bare Surface Scattering
The starting point will be to consider the simplest case of non-vegetated terrain. Under the assumption of surface scattering only, the polarimetry can then be characterized as a reflection symmetric random media with a coherency matrix T of the form shown in (1.187) (Cloude and Pottier 1996; Cloude et al. 2004). The interferometry, following range spectral filtering and assuming no temporal or SNR decorrelation, is characterized by a single parameter, i.e. the ground phase ϕ:
From the previous equation, it follows that the optimum coherences are obtained as eigenvectors of the matrix K as shown. By multiplying terms we see that the matrix K is just the 3 × 3 identity matrix. This implies that all polarizations have the same interferometric coherence and PolInSAR plays no role in surface scattering problems. This is not quite true in practice for two important reasons: in practice there will be polarization-dependent SNR decorrelation. In fact, recently it has been suggested that such SNR coherence variations with polarimetry be used for quantitative InSAR surface parameter estimation. This formulation assumes that the scattering from the surface occurs within a thin layer. If there is significant penetration into the surface, then volume scattering effects can occur and this will lead to volume decorrelation effects. These effects have been observed for land ice (Treuhaft et al. 1996) and snow studies (Zebker and Villasenor 1992) where the surface is non-vegetated but covered by a low-loss scattering layer. Nonetheless, (1.187) demonstrates how for bare surface scattering PolInSAR plays only a secondary role. More interesting for application of natural land surfaces is to consider the presence of volume scattering due to vegetation cover.
1.4.3.2 PolInSAR for Random Volume Scattering
When considering scattering from a volume, interest centres on the special case of a random volume, i.e. one with macroscopic azimuthal symmetry (Cloude and Pottier 1996). In this case the polarimetric coherency matrix T is diagonal. However, more care is required over consideration of the interferometric phase in Ω12. In this case one must include the effects of volume decorrelation due to the random vertical distribution of scatterers (Treuhaft et al. 1996). In this case, the interferometry must include a complex integral I2 normalized by a real integral I1:
where
where the vegetation is characterized by a height hv and mean extinction rate σ and θ0 represents the mean incidence angle. In (1.188), it is also observed that K is proportional to the identity matrix, but this time the eigenvalues, all equal, are given by a ratio of integrals over the vertical distribution. This ratio is just the volume decorrelation displaying an increase in phase variance and a vegetation bias to the ground phase determined by hv and σ:
where
Here the vertical interferometric wavenumber kz (Bamler and Hartl 1998) appears as a function of the normal baseline Bn, the wavelength λ as well as the sensor height H. Δθ is the angular separation of the baseline end points from the surface pixel.
As it can be observed in (1.190), this coherence is independent of polarization, K has three degenerate eigenvalues and PolInSAR plays no role in the analysis of random volume scattering. This statement has to be modified in the presence of oriented volumes (Treuhaft and Cloude 1999), i.e. ones with a preferred orientation of scattering elements such as that occurring in some agricultural crops and even in forestry applications at low frequencies. In such cases PolInSAR does indeed play a role for volume scattering, with K developing three distinct eigenvalues. However, for the treatment of forestry applications at L-band and above, such orientation effects are small and the random volume assumption is justified (Papathanassiou et al. 2000).
In conclusion, both bare surfaces and random volumes lead to a degenerate eigenvalue spectrum for the matrix K. It is only when we combine these two effects together that we see the potential benefits of employing PolInSAR processing.
1.4.3.3 PolInSAR Two-Layer Combined Surface and Random Volume Scattering
In the general case when combined surface and volume scattering occurs, then PolInSAR coherence optimisation becomes useful as it is now demonstrated. In this two-layer case or Random-Volume-over-Ground (RVoG) model approach (Cloude and Papathanassiou 2003), the observed coherence is given by a mixture formula:
Here, the ground phase ϕ and complex volume coherence γv are combined with a new real parameter μ, the ratio of effective surface, i.e. all scattering contributions with a phase centre located at ϕ, to volume scattering. In effect, when μ = 0 the scattering reduces to the case of random volume scattering, while when μ tends to infinity, it reduces to the surface scattering case. Interest centres on the intermediate case because one has an unknown, but constant, complex contribution from the volume scattering combined with a polarization-dependent surface term. By isolating the polarization-dependent terms, the resulting coherence then lies along a straight line in the complex coherence plane as shown in (1.192).
This straight line model has been successfully tested on varied forest data sets and seems to be a good fit for L- and P-band PolInSAR forestry applications. It is interesting to note how the coherence varies as we adjust the single parameter μ along this line. Figure 1.15 illustrates three important cases. In all three we first note how the coherence starts for small μ at some value depending on the volume scattering contribution, 0.8 in the example. It then initially decreases with increasing surface contribution until reaching a turning point after which it increases with μ, always approaching unity as μ tends to infinity.
In Fig. 1.15 three important special cases of the eigenvalue spectrum of K for this scenario are also superimposed. The top left shows the case when μ is always small, i.e. when there is strong volume scattering with high extinction masking the surface contributions. As polarization w is adjusted, then μ will also change, and the optimizer has an incentive to select the minimum μ channel to maximize coherence. At the other extreme, when μ is large and surface scattering dominates, we see that the optimizer has an incentive instead to maximize μ in order to maximize coherence. A more interesting case, and one that occurs often in practice for L-band forestry applications, is the intermediate zone when the variation of μ (the μ spectrum) includes the turning point. In this case the coherence can be maximized by either increasing or decreasing μ depending on circumstances.
Two important conclusions can be made from this. Firstly, in the mixed two-layer scattering case, the coherence varies with polarization and so optimisation plays a role in PolInSAR analysis. Secondly, we see that we cannot simply associate the maximum coherence with, for example, the maximum value of μ. Both maxima and minima of μ can lead to the optimum coherence, depending on the circumstances. However, it follows that if we can estimate the μ spectrum for any problem, then we can compare the max/min with the values for the standard channel (linear, Pauli, etc.) to quantify the potential benefits of employing optimisation techniques.
The determination of the extreme points of the μ spectrum is related to a classical problem in radar polarimetry, namely, contrast optimisation (Novak and Burl 1990). The solution to this is obtained as the eigenvalues of the product of the inverse volume times the surface polarimetric coherency matrices:
Under the assumption of a random volume and reflection symmetric surface scattering component, the eigenvalues of this matrix can be determined analytically as
Equally importantly, the eigenvectors of this matrix indicate the w vectors that should be employed in PolInSAR to secure these extreme coherence values. We note from Eq. (1.194) that the optimum contrast solutions are not generally the simple HH, HV and VV channels. This supports the investigation of optimisation techniques based on fully polarimetric data acquisition for PolInSAR processing.
1.5 Polarimetric SAR Tomography
3-D SAR Tomography (TomoSAR) is an experimental multibaseline (MB) interferometric mode achieving full 3-D imaging in the range-azimuth-height space through elevation beam forming, i.e. spatial (baseline) spectral estimation (Reigber and Moreira 2000). Thanks to TomoSAR, the resolution of multiple scatterers is made possible in height in the same range-azimuth cell, overcoming a limitation of the conventional InSAR processing and complementing PolInSAR. TomoSAR can add more features for the analysis of complex scenarios, e.g. for the estimation of forest structure and biomass, sub-canopy topography, soil humidity and ice thickness monitoring and extraction of heights and reflectivities in layover urban areas. In order to retrieve information on the nature of the imaged scatterers, TomoSAR has also been extended to include the polarimetric information (briefly, PolTomoSAR) (Guillaso and Reigber 2005). It jointly exploits multibaseline SAR data acquired with different polarization channels to improve the accuracy of the estimation of the vertical position of the imaged scatterers and to estimate a set of normalized complex coefficients characterizing the corresponding polarimetric scattering mechanism.
The very first demonstration of the tomographic concept was carried out in 1995 by processing single-polarization data acquired in an anechoic chamber of a two-layer synthetic target (Pasquali et al. 1995). TomoSAR was then experimented from an airborne platform a few years later by acquiring L-band data by means of the DLR E-SAR platform over the Oberpfaffenhofen site (Reigber and Moreira 2000). Although this experiment was successful in demonstrating the 3-D imaging capabilities of forest volumes and man-made targets at L-band, two main limitations of TomoSAR were apparent, namely, (i) the usually low number of images available for processing to avoid large acquisition times and the consequent temporal decorrelation and (ii) the difficulty of obtaining ideal uniformly spaced parallel flight tracks due to navigation/orbital considerations.
In order to mitigate the effects of acquisition non-idealities, most of the subsequent research on (single-polarization) TomoSAR investigated different imaging solutions, model-based and not. Many experiments have shown that the use of polarimetric information not only increments the number of observables, but it also allows to enhance the accuracy of height estimation of scatterers, to increase height resolution and to estimate a vector of complex coefficients describing the scattering mechanism at each height (Guillaso and Reigber 2005). In forest scenarios, the combination of multibaseline polarimetric data can be used to separate ground and canopy scattering and to estimate their vertical structures by following a relatively simple algebraic approach (Tebaldini 2009).
1.5.1 TomoSAR and PolTomoSAR as Spectral Estimation Problems: Non-model-Based Adaptive Solutions
As usual in SAR imaging and interferometry, after focusing on the range-azimuth plane, the K SAR images available for processing are assumed to be co-registered and properly compensated for the flat-Earth phase. Moreover, N independent looks (here multiple adjacent pixels) are used for processing. For each n-th look, the complex amplitudes of the pixels observed in the K SAR images at the same range-azimuth coordinate are collected in the K × 1 complex-valued vector y(n) (Lombardini and Reigber 2003). y(n) is characterized by its covariance matrix. It can be demonstrated that the generic (l, m)-th element of R can be written as
where F(z) is the unknown vertical distribution of the backscattered power as a function of the height z and kz, m is the vertical wavenumber at the m-th track. From (1.195), it is apparent the Fourier relationship existing between the MB covariances and the profile of the backscattered power, and it justifies the use of spectral estimation as a processing tool to estimate F(z).
The inversion of (1.195) for the estimation of F(z) cannot be carried out through a plain Fourier-based 3-D focusing as it suffers from inflated sidelobes and poor height resolution. Among the investigated alternatives, a state-of-the-art solution is the adaptive beam forming (shortly, ABF), which is based on the Capon spectral estimator, and it has been demonstrated to have remarkable sidelobe rejection and resolution capabilities.
The single-polarization ABF spectral estimation problem can be equivalently stated as the problem of designing a complex-valued finite impulse response filter h of order K that leaves undistorted the multibaseline signal component at the height under test, say z, while rejecting possible other components from noise and other heights (Lombardini and Reigber 2003). In formulas
where a(z) is the so-called steering vector, with generic element [a(z)]k = exp { jkz, kz } for k = 1, …, K, and \( \hat{\mathbf{R}} \) is the sample covariance estimate. Notice that the resulting ABF filter h depends on \( \hat{\mathbf{R}} \), and it varies with z; In particular, the dependency on \( \hat{\mathbf{R}} \) results in a null-placing at proper heights in the filtering operation, thus increasing resolution and sidelobe suppression in the final estimate of F(z). The solution to the optimization problem (1.196) can be found in closed-form (Lombardini and Reigber 2003).
If fully polarimetric data are available, without losing generality, they can be combined in the Pauli basis. The resulting MB data vectors y1(n), y2(n) and y3(n) can then be stacked one on top of the other in order to form the 3K-dimensional multibaseline-polarimetric data vector yP(n). As a consequence, a MB-polarimetric sample covariance matrix \( {\hat{\mathbf{R}}}_P \) can be calculated from yP(n). Different from the single polarimetric case, the profile has now to be estimated also by considering the polarization state at the targeted height. In this sense, the definition of the steering vector can be extended to the polarimetric case by means of a three-dimensional target vector w whose elements are complex-valued coefficients describing the scattering mechanism in the Pauli basis, with ‖ w ‖2 = 1. In formulas, the polarimetric steering vector b(z, w) is given by
where
The ABF optimization problem (1.196) can be extended to the MB-polarimetric case as follows (Sauer et al. 2011):
where hP is the multibaseline-polarimetric ABF filter response. Now, hP is optimized in order to place proper nulls in height and in the polarimetric space generated by w. Notice that the dependence of w on z has been formally dropped for easiness of notation. From (1.199), the power of the filtered signal is
which is still a function of w. To estimate the vertical power distribution as a function of the only z, and the corresponding w, one can maximize (1.200) over w to finally obtain
where λmin{⋅} denotes the minimum eigenvalue operator. The resulting \( {\hat{\mathbf{w}}}_{ABF}(z) \) is the eigenvector associated with λmin. It is worth noting that the multibaseline-polarimetric ABF estimator (1.201) enhances the discrimination of particular scatterers or features. In other words, it is able to extract a rank 1 polarimetric information. This is generally the case of man-made targets like buildings in urban scenarios.
However, it can happen that the scatterers present at a given z are characterized by a random polarimetric behaviour, and they are more properly described by a 3 × 3 polarimetric covariance matrix T(z) rather than by a deterministic target vector (Ferro-Famil et al. 2012). This is generally the case in natural scenarios like forests. In this way, a scattering mechanism at the generic z will contribute to RP with T(z) ⊗ [a(z)aT∗(z)]. In light of this, the polarimetric ABF estimator from the rank 1 formulation (1.201) can be extended in a full-rank sense (Ferro-Famil et al. 2012). The derivation of such estimate is based on the definition of a full-rank objective function which uses the polarimetric span instead of the intensity associated with a given scattering mechanism. The full-rank ABF estimator then is
The availability of the polarimetric coherence matrix makes possible the full exploitation of the polarimetric information for the characterization of the scattering, allowing the 3-D calculation of parameters like, e.g. entropy and degree of polarization, as well as the application of polarimetric decompositions.
1.5.2 Model-Based PolTomoSAR
As mentioned in Sect. 1.6.1, the non-model-based ABF possess some intrinsic degree of super-resolution, i.e. it is able to separate scatterers with a height difference lower than the Rayleigh resolution limit, which in turn depends on the maximum available track separation. However, a higher super-resolution could be needed in some applications. For this reason, a solution is to resort to model-based tomographic processors, which generally exploit the statistical description of the received signal or equivalently of the scattering behaviours present in the observed scene.
Several methods have been proposed for single-polarization and then extended to full-polarization MB data sets. For instance, the MUSIC (multiple signal classification) is matched to point-like targets (Frey and Meier 2011), and it exploits the fact that the multibaseline response of each point-like scatterer (i.e. the steering vector) in the backscattered radiation is orthogonal to the noise subspace. As a consequence, closed-form solution of the MUSIC PolTomoSAR functional can be found that outputs the scattering mechanism of each scatterer (Sauer et al. 2011). Still in the category of the eigen-based processors, the weighted signal subspace fitting can cope with more complex statistical descriptions of distributed and coherent scatterers, although a multidimensional optimization is required (Huang et al. 2011).
Alternatively to the eigen-based PolTomoSAR, a solution adaptive to both coherent and distributed scatterers, but possibly leading to a lower computational time, is the so-called covariance matching estimator (COMET). If the multibaseline data are jointly Gaussian distributed, the knowledge of the MB-multipolarimetric covariance matrix RP is enough to perform a maximum likelihood (ML) estimation of the parameters describing the vertical distribution of the backscattered power. It can be demonstrated that the global ML problem can be decomposed by means of the extended invariance principle into a cascade of two ML problems (i.e. the estimation of RP and the estimation of the parameters of interest from \( {\hat{\mathbf{R}}}_P \)), leading to an asymptotically equivalent solution and with a non-negligible reduction of the computational complexity. Under the Gaussian hypothesis, the resulting COMET estimates can be obtained from the following minimization problem (Tebaldini and Rocca 2010):
where ρ is the vector containing the parameters that describe the multibaseline covariances. Equation (1.204) can be seen as the weighted Frobenius norm of the approximation error \( {\mathbf{R}}_P\left(\boldsymbol{\uprho} \right)-{\hat{\mathbf{R}}}_P \) with weight \( {\hat{\mathbf{R}}}_P^{-1} \). Worth of notice, the COMET estimator can be used also when data are not Gaussian, although it is not asymptotically optimal anymore.
1.5.3 Coherence Tomography
Besides the development of spectral estimation- and model-based PolTomoSAR, also the so-called (polarimetric) coherence tomography methods have been proposed which reconstruct the vertical distribution of scatterers from complex coherence measurements of volumetric scatterers. In a few words, the structure function is approximated through a weighted sum of a series of basis functions (Cloude 2007b). The individual parameterization has then to be inverted using a (limited) number of interferometric measurements at the same or different polarizations. In this class of “hybrid” algorithms, the different polarization channels can be used, e.g. to find a polarization state with lowest ground contribution.
References
Alonso Gonzalez A, Lopez Martinez C, Salembier P (2012) Filtering and segmentation of polarimetric SAR data based on binary partition trees. IEEE Trans Geosci Remote Sens 50:593–605
Arii M, Van Zyl JJ, Kim Y (2011) Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans Geosci Remote Sens 49:1104–1113
Balanis CA (1989) Advanced engineering electromagnetics. Wiley, New York
Ballester Berman JD, Lopez Sanchez JM, Fortuny Guasch J (2005) Retrieval of biophysical parameters of agricultural crops using polarimetric SAR interferometry. IEEE Trans Geosci Remote Sens 43:683–694
Bamler R, Hartl P (1998) Synthetic aperture radar interferometry. Inv Prob 14:R1–R54
Bebbington DHO (1992) Target vectors – spinorial concepts. In: Proc Second International Workshop on Radar Polarimetry
Beckmann P, Spizzichino A (1987) The scattering of electromagnetic waves from rough surfaces. Artech House, Norwood
Boerner WM et al (1998) Polarimetry in radar remote sensing: basic and applied concepts. In: Ryerson RA (ed) Manual of remote sensing: principles and applications of imaging radar, vol 3. Wiley, Hoboken, pp 271–356
Cameron WL, Leung LK (1990) Feature motivated polarization scattering matrix decomposition. In: Proceedings of IEEE 1990 International Radar Conference
Chandrasekhar S (1960) Radiative transfer. Dover, New York
Cloude SR (1988) Uniqueness of target decomposition theorems in radar polarimetry. In: Proceedings of NATO Adv. Res. Workshop on Direct Inverse Methods in Radar Polarimetry
Cloude SR (2007a) The dual polarization H/alpha decomposition: a PALSAR case study. Paper presented at 2007 international workshop on science and applications of SAR polarimetry and Polarimetric interferometry (POLinSAR)
Cloude SR (2007b) Dual-baseline coherence tomography. IEEE Geosci Remote Sens Lett 4:127–131
Cloude SR, Papathanassiou KP (1998) Polarimetric SAR interferometry. IEEE Trans Geosci Remote Sens 36:1551–1565
Cloude SR, Papathanassiou KP (2003) A 3-stage inversion process for polarimetric SAR interferometry. IEE Proc Radar Sonar Navigation 150:125–134
Cloude SR, Pottier E (1996) A review of target decomposition theorems in radar polarimetry. IEEE Trans Geosci Remote Sens 34:498–518
Cloude SR, Corr DG, Williams ML (2004) Target detection beneath foliage using polarimetric SAR interferometry. Waves Random Media 14:393–414
Colin E, Titin Schneider C, Tabbara W (2003) Investigation of different interferometric coherence optimisation methods. Paper presented at 2003 International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (POLinSAR)
Colin E, Titin Schneider C, Tabbara W (2005) Coherence optimization methods for scattering centre separation in polarimetric interferometry. J Electrom Waves App 19:1237–1250
Curlander JC, McDonough RN (1991) Synthetic aperture radar: systems and signal processing. John Wiley & Sons, New York
Dall J, Papathanassiou KP, Skriver H (2003) Polarimetric SAR interferometry applied to land ice: first results. In: Proceedings of IEEE 2003 International Geoscience and Remote Sensing Symposium (IGARSS)
De Grandi G, Lee JS, Schuler D, Nezry E (2003) Texture and speckle statistics in polarimetric SAR synthesized images. IEEE Trans Geosci Remote Sens 41:2070–2088
Deledalle CA, Tupin F, Denis L (2010) Polarimetric SAR estimation based on non-local means. In: Proceedings of IEEE 2010 International Geoscience and Remote Sensing Symposium (IGARSS)
Doob JL, Ornstein LS, Uhlenbeck GE, Rice SO, Kac M, Chandrasekhar S, Wax N (1954) Selected papers on noise and stochastic processes. Dover Publications, Mineola/New York
Ferro-Famil L, Huang Y, Reigber A (2012) High-resolution SAR tomography using full-rank polarimetric spectral estimators. In: Proceedings of IEEE 2012 International Geoscience and Remote Sensing Symposium (IGARSS)
Flynn T, Tabb M, Carande R (2002) Coherence region shape estimation for vegetation parameter estimation in POLINSAR. In: Proceedings of IEEE 2002 International Geoscience and Remote Sensing Symposium (IGARSS)
Foucher S, Landry T, Lopez Martinez C, Charbonneau F, Gagnon L (2012) An evaluation of PolSAR speckle filters on compact-pol images. In: Proceedings of IEEE 2012 International Geoscience and Remote Sensing Symposium (IGARSS)
Freeman A, Durden SL (1998) A three-component scattering model for polarimetric SAR data. IEEE Trans Geosci Remote Sens 36:963–973
Frey O, Meier E (2011) Analyzing tomographic SAR data of a forest with respect to frequency, polarization, and focusing technique. IEEE Trans Geosci Remote Sens 49:3648–3659
Gabriel AK, Goldstein RM, Zebker HA (1989) Mapping small elevation changes over large areas: differential radar interferometry. J Geo Res 94:9183–9191
Goodman JW (1976) Some fundamental properties of speckle. J Opt Soc Am 66:1145–1149
Goodman JW (1985) Statistical optics. John Wiley & Sons, New York
Guillaso S, Reigber A (2005) Scatterer characterisation using polarimetric SAR tomography. In: Proceedings of IEEE 2005 International Geoscience and Remote Sensing Symposium (IGARSS)
Hajnsek I, Pottier E, Cloude SR (2003) Inversion of surface parameters from polarimetric SAR. IEEE Trans Geosci Remote Sens 41:727–744
Hoekman DH, Quinones MJ (2002) Biophysical forest type characterization in the colombian amazon by airborne polarimetric SAR. IEEE Trans Geosci Remote Sens 40:1288–1300
Huang Y, Ferro-Famil L, Reigber A (2011) Under-foliage object imaging using SAR tomography and polarimetric spectral estimators. IEEE Trans Geosci Remote Sens 50:2213–2225
Huynen JR (1970) Phenomenological theory of radar targets. Ph.D. thesis, Technical University of Delft, The Netherlands
IEEE standard number 145 (1983) IEEE standard definitions of terms for antennas
Jones RC (1941a) A new calculus for the treatment of optical systems. I Descrip Discussion J Opt Soc Am 31:488–493
Jones RC (1941b) A new calculus for the treatment of optical systems. II Proof of the three general equivalence theorems. J Opt Soc Am 31:493–499
Jones RC (1941c) A new calculus for the treatment of optical systems. III: The Stokes theory of optical activity. J Opt Soc Am 31:500–503
Kasilingam D, Schuler D, Lee JS, Malhotra S (2002) Modulation of polarimetric coherence by ocean features. In: Proceedings of IEEE 2002 International Geoscience and Remote Sensing Symposium (IGARSS)
Kay SM (1993) Fundamentals of statistical signal processing. Estimation theory. Prentice-Hall, Englewood Cliffs
Kennaugh K (1951) Effects of type of polarization on echo characteristics, Technical report. Ohio State University
Kong JA (ed) (1990) Polarimetric remote sensing. Elsevier, New York
Krogager E (1990) New decomposition of the radar target scattering matrix. Electron Lett 26:1525–1527
Lee JS (1981) Speckle analysis and smoothing of synthetic aperture radar images. Comp Graphics Im Proc 17:24–32
Lee JS, Grunes MR, Mango SA (1991) Speckle reduction in multipolarization, multifrequency SAR imagery. IEEE Trans Geosci Remote Sens 29:535–544
Lee JS, Hoppel KW, Mango SA, Miller AR (1994) Intensity and phase statistics of multilook polarimetric and interferometric SAR imagery. IEEE Trans Geosci Remote Sens 32:1017–1028
Lee JS, Grunes MR, De Grandi G (1999) Polarimetric SAR speckle filtering and its implication for classification. IEEE Trans Geosci Remote Sens 37:2363–2373
Lee JS, Schuler DL, Ainsworth TL, Krogager E, Kasilingam D, Boerner WM (2002) On the estimation of radar polarization orientation shifts induced by terrain slopes. IEEE Trans Geosci Remote Sens 40:30–41
Lee JS, Cloude SR, Papathanassiou KP, Grunes MR, Woodhouse IH (2003) Speckle filtering and coherence estimation of PolInSAR data for forest applications. IEEE Trans Geosci Remote Sens 41:2254–2263
Lee JS, Grunes MR, Schuler DL, Pottier E, Ferro-Famil L (2006) Scattering-model-based speckle filtering of polarimetric SAR data. IEEE Trans Geosci Remote Sens 44:176–187
Lombardini F, Reigber A (2003) Adaptive spectral estimators for multibaseline SAR tomography with airborne L-band data. In: Proceedings of IEEE 2003 International Geoscience and Remote Sensing Symposium (IGARSS)
Lopes A, Touzi R, Nezry E (1990) Adaptive speckle filters and scene heterogeneity. IEEE Trans Geosci Remote Sens 28:992–1000
Lopez Martínez C, Fabregas X (2003) Polarimetric SAR speckle noise model. IEEE Trans Geosci Remote Sens 41:2232–2242
Lopez Martínez C, Fabregas X (2008) Model-based polarimetric SAR speckle filter. IEEE Trans Geosci Remote Sens 46:3894–3907
Luneburg E (2002) Aspects of radar polarimetry. Elektrik- Turkish J Electr Eng Comput Sci 10:219–243
Mattia F, le Toan T, Lee JS, Schuler DL (2003) On the sensitivity of polarimetric coherence to small and large scale surface roughness. In: Proceedings of IEEE 2003 International Geoscience and Remote Sensing Symposium (IGARSS)
McCrea WH, Whipple FJW (1940) Random paths in two and three dimensions. Proc R Soc Edinburgh 60:281–298
Mette T, Papathanassiou KP, Hajnsek I (2004) Biomass estimation from PolInSAR over heterogeneous terrain. In: Proc IEEE 2004 International Geoscience and Remote Sensing Symposium (IGARSS)
Morio J, Refregier P, Goudail F, Dubois Fernandez P, Dupuis X (2007) Application of information theory measures to polarimetric and interferometric SAR images. In: Proceedings of 2007 International Conference on Physics in Signal and Image Processing
Novak L, Burl MC (1990) Optimal speckle reduction in polarimetric SAR imagery. IEEE Trans Aerosp Electron Syst AES-26:293–305
Oliver C, Quegan S (1998) Understanding synthetic aperture radar images. Artech House, Boston
Paladini R, Ferro-Famil L, Pottier E, Martorella M, Berizzi F, Dalle Mese E (2012) Lossless and sufficient-invariant decomposition of random reciprocal target. IEEE Trans Geosci Remote Sens 50:3487–3501
Papathanassiou KP, Cloude SR (2001) Single baseline polarimetric SAR interferometry. IEEE Trans Geosci Remote Sens 39:2352–2363
Papathanassiou KP, Cloude SR, Reigber A (2000) Single and multi-baseline polarimetric SAR interferometry over forested terrain. In: Proceedings of 2000 European Conference on Synthetic Aperture Radar (EUSAR)
Papathanassiou KP, Cloude SR, Liseno A, Mette T, Pretzsch H (2005a) Forest height estimation by means of polarimetric SAR interferometry: actual status and perspectives. Paper presented at 2005 International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry (POLinSAR)
Papathanassiou KP, Hajnsek I, Nagler T, Rott H (2005b) Polarimetric SAR interferometry for snow cover parameter estimation. Paper presented at 2005 international workshop on science and applications of SAR polarimetry and polarimetric interferometry (POLinSAR)
Papoulis A (1984) Probability, random variables and stochastic processes. McGraw-Hill, New York
Pasquali P, Prati C, Rocca C, Seymour M, Fortuny J, Olmer E, Sieber AJ (1995) A 3D SAR experiment with EMSL data. In: Proceedings of IEEE 1995 International Geoscience and Remote Sensing Symposium (IGARSS)
Raney RK (1983) Transfer function for partially coherent SAR systems. IEEE Trans Aerosp Electron Syst AES-19:740–750
Reigber A, Moreira A (2000) First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans Geosci Remote Sens 38:2142–2152
Reigber A, Papathanassiou KP, Cloude SR, Moreira A (2000) SAR tomography and interferometry for the remote sensing of forested terrain. In: Proceedings of 2000 European Conference on Synthetic Aperture Radar (EUSAR)
Sagues L, Lopez Sanchez JM, Fortuny J, Fabregas X, Broquetas A, Sieber AJ (2000) Indoor experiments on polarimetric SAR interferometry. IEEE Trans Geosci Remote Sens 38:671–684
Sarabandi K (1997) Δk-radar equivalent of interferometric SAR’s: a theoretical study for determination of vegetation height. IEEE Trans Geosci Remote Sens 35:1267–1276
Sauer S, Ferro-Famil L, Reigber A, Pottier E (2011) Three-dimensional imaging and scattering mechanism estimation over urban scenes using dual-baseline polarimetric InSAR observations at L-band. IEEE Trans Geosci Remote Sens 49:4616–4629
Schleher DC (1975) Radar detection in log normal clutter. In: Proceedings of IEEE 1975 International Radar Conference
Schneider Zandona R, Papathanassiou K, Hajnsek I, Moreira A (2005) Polarimetric interferometry over urban areas: information extraction using coherent scatterers. In: Proc IEEE 2005 International Geoscience and Remote Sensing Symposium (IGARSS)
Stokes GG (1852) On the composition and resolution of streams of polarized light from different sources. Trans Cambridge Phil Soc 9:399–416
Tabb M, Carande R (2001) Robust inversion of vegetation structure parameters from low frequency polarimetric interferometric SAR. In: Proceedings of IEEE 2001 International Geoscience and Remote Sensing Symposium (IGARSS)
Tebaldini S (2009) Algebraic synthesis of forest scenarios from multibaseline PolInSAR data. IEEE Trans Geosci Remote Sens 47:4132–4142
Tebaldini S, Rocca F (2010) Single and multipolarimetric SAR tomography of forested areas: a parametric approach. IEEE Trans Geosci Remote Sens 48:2375–2387
Tough RJA, Blacknell D, Quegan S (1995) A statistical description of polarimetric and interferometric synthetic aperture radar data. Proc R Soc London 449:567–589
Touzi R (2007) Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans Geosci Remote Sens 45:73–84
Touzi R, Lopes A (1994) The principle of speckle filtering in polarimetric SAR imagery. IEEE Trans Geosci Remote Sens 32:1110–1114
Touzi R, Lopes A, Bruniquel J, Vachon PW (1999) Coherence estimation for SAR imagery. IEEE Trans Geosci Remote Sens 37:135–149
Touzi R, Boerner WM, Lee JS, Luneberg E (2004) A review of polarimetry in the context of synthetic aperture radar: concepts and information extraction. Can J Remote Sens 30:380–407
Touzi R, Deschamps A, Rother G (2007) Wetland characterization using polarimetric RADARSAT-2 capability. Can J Remote Sens 33:56–67
Treuhaft RN, Cloude SR (1999) The structure of oriented vegetation from polarimetric interferometry. IEEE Trans Geosci Remote Sens 37:2620–2624
Treuhaft RN, Madsen S, Moghaddam M, Van Zyl JJ (1996) Vegetation characteristics and underlying topography from interferometric data. Radio Sci 31:1449–1495
Trunk GV (1972) Radar properties of non-Rayleigh sea echo. IEEE Trans Aerosp Electron Syst AES-8:196–204
Trunk GV, George SF (1970) Detection of targets in non-gaussian sea clutter. IEEE Trans Aerosp Electron Syst AES-6:620–628
Ulaby FT, Elachi C (1990) Radar polarimetry for geoscience applications. Artech House, Norwood
Ulaby FT, Moore RK, Fung AK (1986a) Microwave remote sensing: active and passive, vol III. Artech House, Norwood
Ulaby FT, Moore RK, Fung AK (1986b) Microwave remote sensing: active and passive, vol II. Artech House, Norwood
Van Zyl JJ, Arii M, Kim Y (2011) Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans Geosci Remote Sens 49:3452–3459
Vasile G, Trouve E, Lee JS, Buzuloiu V (2006) Intensity-driven adaptive-neighbourhood technique for polarimetric and interferometric SAR parameters estimation. IEEE Trans Geosci Remote Sens 44:1609–1621
Wakabayashi H, Matsuoka T, Nakamura K, Nishio F (2004) Polarimetric characteristics of sea ice in the sea of Okhotsk observed by airborne L-band SAR. IEEE Trans Geosci Remote Sens 42:2412–2425
Wiener N (1930) Generalized harmonic analysis. Acta Mathematica 5:118–258
Williams ML (1999) Prediction and observation of SAR clutter from vegetation canopies. In: Proc IEEE 1999 International Geoscience and Remote Sensing Symposium (IGARSS)
Williams ML, Cloude SR (2005) Predictions of SAR polarimetry and InSAR coherence for a model wheat canopy. In: Proceedings of IEEE 2005 International Geoscience and Remote Sensing Symposium (IGARSS)
Yamada H, Yamaguchi Y, Rodriguez E, Kim Y, Boerner WM (2001) Polarimetric SAR interferometry for forest canopy analysis by using the super-resolution method. IEICE Trans Electron E84-C:1917–1924
Yamaguchi Y, Moriyama T, Ishido M, Yamada H (2005) Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans Geosci Remote Sens 43:1699–1706
Zebker HA, Villasenor J (1992) Decorrelation in interferometric radar echoes. IEEE Trans Geosci Remote Sens 30:950–959
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
López-Martínez, C., Pottier, E. (2021). Basic Principles of SAR Polarimetry. In: Hajnsek, I., Desnos, YL. (eds) Polarimetric Synthetic Aperture Radar. Remote Sensing and Digital Image Processing, vol 25. Springer, Cham. https://doi.org/10.1007/978-3-030-56504-6_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-56504-6_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56502-2
Online ISBN: 978-3-030-56504-6
eBook Packages: Earth and Environmental ScienceEarth and Environmental Science (R0)