Abstract
This chapter covers anisotropy in the context of probing microstructure of the human brain using single encoded diffusion MRI. We will start by illustrating how diffusion MRI is a perfectly adapted technique to measure anisotropy in the human brain using water motion, followed by a biological presentation of human brain. The non-invasive imaging technique based on water motions known as diffusion MRI will be further presented, along with the difficulties that come with it. Within this context, we will first review and discuss methods based on signal representation that enable us to get an insight into microstructure anisotropy. We will then outline methods based on modeling, which are state-of-the-art methods to get parameter estimations of the human brain tissue.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Accessing Brain Anisotropy Using Diffusion MRI
1.1 Introduction
Diffusion-weighted MR imaging is a non-invasive tool used to probe tissue microstructure. During a typical acquisition of tens of milliseconds in brain imaging, water molecules can displace up to tens of micrometers. Diffusion is therefore sensitive to a wide range of microstructural and physiological parameters in the tissue. The diffusing molecules get restricted by the boundaries of the underlying microstructure of tissues. Diffusion anisotropy corresponds to the hindrance of those molecules, otherwise free diffusing (i.e. isotropically). Changes in anisotropy have been related to brain diseases such as ischemia, multiple sclerosis, trauma, or brain tumors [2, 58]. Diffusion anisotropy is therefore considered as a potential biological marker for changes in tissue microstructure. A loss of anisotropy can also be the sign of an increasing isotropy, as neurons grow in size. Panagiotaki et al. [57] notably use this change to study the evolution of tumor cell size in response to a drug. An understanding of the origin of anisotropy change and a combined study of both anisotropy and isotropy can therefore lead to great discoveries on a tissue microstructure and its evolution.
An ultimate goal of a Magnetic Resonance (MR) diffusion theory is then to relate the microstructural and physiological parameters quantitatively to the diffusion-weighted signal. This task appears to be complicated as deducing those parameters constitutes a complex inverse problem requiring careful modeling of the diffusion signal over a wide range of diffusion time and diffusion weightings (diffusion weightings will be further explained in Sect. 2.2).
Regarding its cellular composition, brain can be decomposed in two main parts: white matter and grey matter. The former designates regions that contain mainly long-range myelinated axons, which cross the brain connecting different parts of grey matter, and relatively few cell bodies. A method to study those connections is called tractography and has been well explored during the past few years [28]. Grey matter contains mainly cell bodies, connected by neurites, and relatively few myelinated axons. Anisotropy exists in both white matter and grey matter and is due to the presence of cells with long cylindrical processes (axons in white matter and neurites in grey matter). Its presence, or its absence, will provide us with key information about the tissue structure at the cellular level.
Fick et al. dedicated a review on existing diffusion anisotropy metrics [14], which includes Fractional Anisotropy (FA) [3], Generalized Fractional Anisotropy (GFA) [60], Propagator Anisotropy (PA) [50], Orientation Dispersion Index (ODI) [67], and microscopic Fractional Anisotropy (µFA) [33]. We present here a complementary approach, which considers anisotropy as a probe for accessing microstructure, either through signal representations or tissue modeling.
1.2 Anisotropy as Reflected by Water Motion
Particles suspended in a fluid are constantly undergoing small random movements, which is known as Brownian motion [42]. The physical process of a steadily spread of a substance is called diffusion. Diffusion can therefore be considered a macroscopic manifestation of Brownian motion on the microscopic level. When no barrier impedes diffusion preferentially in one direction over another, molecular displacements are equal in all directions. This is known as isotropic diffusion. However, in brain, molecule movements are hindered by cell membranes. Diffusion is then not equal along all directions anymore and has become anisotropic. The distance traveled by a water molecule depends on its interactions. Certain geometric characteristics of the underlying structure at the microscopic level can therefore be inferred from the molecule movements [32]. The further a molecule travels during the time of an acquisition, the greater signal attenuation we get. The objective is to use this attenuation to deduce the structure of the medium where the water molecules are trapped in.
Depending on the diffusion time, i.e. the amount of time between two gradient pulses (see Sect. 2.1), the information we get about the structure will be different. If the diffusion time was extremely short, only the local intrinsic diffusivity of the fluid, i.e. the rate at which particles can spread, would be measured. The hindrance effects would only become apparent at longer times. The degree of anisotropy hence also depends on the diffusion time.
1.3 Structural Brain Anisotropy
Brain tissue is very anisotropic due to the cylindrical shapes of axons and processes. Water molecules within those fibers will on average move further along them than across them due to their small diameter. Typical axon diameter in humans is of the order of 1–10 µm [5]. Process diameters in grey matter lie between 0.1 and 15 µm.
The strong anisotropy in white matter due to the axons encouraged its wide study over the past decades. The more complex tissue structure and weaker anisotropy in grey matter make its study harder. The presence of isotropy in grey matter is partly due to the numerous somas whose shapes resemble spheres (see Sect. 4.1). Soma diameters range between 20 and 120 µm. White matter models need to be adapted to account for the presence of somas in order to be applied to grey matter [38, 53]. Myelin also appears to modulate the degree of diffusion anisotropy between axons and processes (and so between white matter and grey matter), but has a smaller role in anisotropy than membrane [6].
Note that anisotropy is not only a property of neural fibers. Anisotropy has also been observed in liquid crystals, muscles and other tissues, even in fruits and vegetables [5]. The degree of fractional anisotropy (see Sect. 3.1) is however higher in healthy neural fibers than in other tissues such as skeletal muscle, kidney, and myocardium [11, 18].
1.4 Measuring Anisotropy Using Diffusion MRI
Using Diffusion Magnetic Resonance Imaging (dMRI) as a non-invasive probe in human brain, we aim at getting information about its structure. The acquired diffusion signal is a sum of the diffusion signals coming from each compartment weighted by their relative volume fractions [56], and is therefore modulated by the geometry of the tissue microstructure. Relevant information to infer from it are soma diameters, soma and process densities, and diffusivities. Two complementary approaches have emerged for extracting these information about the tissue microstructure from the diffusion signal: signal representation and tissue modelling (denomination from Novikov et al. [48]).
Signal representations aim at quantifying parameters and are model-independent mathematical expressions. Their parameters do not carry any particular physical meaning. Representations can be used to store, compress or compare measurements. There is an infinite way to represent a continuous function. One chooses a representation according to the need of a particular neuroimaging study [44]. Although signal representations are suited for all kind of tissues, they lack specificity and provide only an indirect characterization of the microstructure.
Biophysical tissue models rely on a schematic geometry of the underlying tissue. They are pictures representing a physical reality relying on assumptions meant to simplify the complexity of a biological tissue. A good model only keeps relevant features which characterize the tissue and discards irrelevant degrees of freedom. The designed analytical expression is then fit to the diffusion data in order to estimate these relevant features of the microstructure. This advantage of providing greater specificity and interpretation of biologically-relevant parameters appears to be the weakness of the method. Indeed the initial geometric assumption must be chosen as to accurately capture all of the features of the tissue that effectively impact the diffusion signal in a given acquisition range [48], but we also must be able to mathematically solve this inverse problem. Model validations are important because a wrong model could lead to wrong interpretations of a physical phenomenon.
Techniques from these two approaches, signal representations and tissue modelling, will be reviewed respectively in Sects. 3 and 4.
2 Diffusion MRI: Introduction to a Non-Invasive Imaging Technique
Nuclear Magnetic Resonance Imaging allows to non-invasively study the brain in-vivo, and in particular brain anisotropy, induced by its microstructure.
2.1 Diffusion MRI Acquisition Sequence
Consider an MRI acquisition sequence. After slice selection, all the nuclei on this plane are precessing at the same frequency. To obtain a diffusion MR image, two gradient pulses are added to the acquisition sequence. The first applied pulse is going to make the particles go off phase. We then apply a second gradient with the same strength in the opposite direction, during the same amount of time. If molecules stayed still between those two gradients, they would have all come back to their original phase, the two gradients cancelling each other. However, after turning the first gradient on, molecules are moving randomly (Brownian motion). After a certain evolution time, if molecules are not at the same location, the second gradient causes destructive interference, which results in a loss of signal. The further a molecule travels from its initial position during the time between the two diffusion gradients along the gradient direction, the greater signal attenuation we get. The ratio between the signal obtained with diffusion gradients and the one without them quantifies the amount of ongoing diffusion. The objective is then to deduce the structure of the medium where the water molecules are trapped in from those signal losses.
2.2 Mathematical Foundations
Stejskal and Tanner invented in 1965 the Pulsed Gradient Spin Echo (PGSE) sequence [59] to measure diffusion in a specific direction. In this sequence, two opposite diffusion gradients are applied during a time \(\delta \), separated by a time interval \(\Delta \). The diffusion-weighting is globally encoded by the b-value [37], and reflects the strength and timing of the gradients used to generate the diffusion weighted images. This factor is computed as follow:
where \(\gamma \) ( MHzT\({}^{-1}\)) is the nuclear gyromagnetic ratio of the water proton \({}^1H\) and g is the strength of the diffusion gradient. In the following sections, g encodes the direction of the applied diffusion weighting in addition to its strength (\(g=||\mathbf {g}||\)), and \(\hat{\mathbf {g}}\) is the corresponding unit vector (\(\hat{\mathbf {g}} = \mathbf {g} / ||\mathbf {g}||\)).
The quantity \(E(b) = S(b)/S_0\) expresses, for each voxel, the attenuation of the diffusion-weighted signal along the selected gradient direction, \(S_0\) being the image acquired without diffusion gradients. In the absence of restrictions (free diffusion), the signal attenuation can be expressed as:
with D the diffusion coefficient.
If \(\delta \) is assumed to be infinitely narrow, i.e. the diffusion during that time is negligible, the signal attenuation can be related to the ensemble average propagator (EAP) \(P(\mathbf{r} , \tau )\) via a Fourier relationship under the q-space formalism [9, 59]:
where \(\mathbf{q} \) is the wave vector and \(\tau \) the diffusion time, which, for the PGSE sequence, are expressed as
The diffusion time \(\tau \) expresses the time interval during which spins are allowed to diffuse before measurement. By increasing the spatial frequency \(q = ||\mathbf{q} ||\) it is possible to achieve a higher spatial resolution of \(P(\mathbf{r} , \tau )\) in the displacement space described by r.
2.3 Acquisition Strategies
Experimental parameters, and especially q and \(\tau \), influence the diffusion signal attenuation along different gradient directions, and therefore the estimation of diffusion anisotropy. Ideally, many gradient directions, q-values and diffusion times would be required to completely characterize diffusion anisotropy in a tissue. In practice, the sampling strategy depends on the application and on the chosen signal representation. This way, only one shell of gradient directions and a single b-value are usually used in DTI (see Sect. 3.1). Also using only one shell at a higher b-value and more directions, are the High Angular Resolution Diffusion Imaging (HARDI) schemes, which aim at increasing the angular resolution of the diffusion signal with the intent of resolving crossing tissue configurations [61]. Different diffusion-weightings signal acquisitions are also needed for some signal representations. In that case, multi-shell acquisitions are set up using different q-shells with fixed diffusion time. Each shell then represents a collection of samples in the three-dimensional space with the same q-value. An optimal spatial coverage is important to measure the diffusion signal as efficiently as possible. Expansions have been proposed such that all the acquired samples lie on different non-collinear directions [10]. This multi-shell design can be extended to \(\tau \)-shells, called \(q\tau \) acquisitions [13] in order to exploit different values for both q and \(\tau \). In that case, a complete q-shell scheme is acquired for each desired diffusion time. Ning et al [44] reviews and compares 16 reconstruction algorithms (single and multi-shells) to help determine an appropriate acquisition protocol (number of b-values) and the analysis method to use for a particular neuroimaging study.
2.4 Difficulties
A main drawback to take into consideration is inherent to the dMRI acquisition process. Due to the acquisition device limitations and the mesoscopic size of neurons, one voxel, at the macroscopic scale, includes thousands of somas and processes. This means that the acquired signal is an average of the signal coming from all those cells. Several issues have then to be considered.
First, the acquired signal in a voxel will be an average of the signal of all the diffusing molecules within this voxel, which could correspond to not less than 3000 axons in white matter. Features that will then be computed from it, such as anisotropy, will be an average of all the components in the tissue. One needs to note that every tissue is made of several compartments and that the signals from each of these compartments where water molecules are present are averaged. Investigations using diffusion-weighted spectroscopy, an imaging technique with increased cellular specificity, are also led to try and target specific compartment(s) [38, 54]. This average problem leads to a second issue: a small change in anisotropy (or other features) can actually reflect greater pathological differences. It means that there needs to be a big change in the voxel to be able to detect it in the acquired diffusion signal. Third issue is that anisotropic cellular elements might be considered as isotropic due to the tree pattern of processes within grey matter [26] or to crossing fibers in white matter. At least, as expected from an acquisition, the signal is noisy. Low concentration of water molecules in some tissue (and thus long scan times) can lead to a poor signal-to-noise ratio.
In addition to those issues, we must recall that the spacing between axons, axon diameter, myelin thickness, etc are all also variables, even within the same tract, which adds to the complexity of the problem. The barriers to diffusion have also not a simple nor regular geometry. The correspondence between the biological features of the tissue and the non-invasive diffusion measure is therefore not straightforward.
3 Quantifying Anisotropy via Signal Representation
Signal representation is an indirect method that aims at describing the diffusion signal with no assumptions about the underlying structure. It can therefore be applied to healthy or diseased tissues. Several methods are described, with an emphasis made on the cumulant expansion, which is the most widespread signal representation.
3.1 Cumulant Expansion
Common signal representations are based on the cumulant expansion [39, 65], which corresponds to a development of the logarithm of the signal in polynomials up to a given order in b:
where D is the diffusion coefficient and K the kurtosis. This formula can also be written in the tensor form:
where \(C^{(l)}\) are the cumulant tensors, and g is the direction of the applied diffusion weighting (see Sect. 2.2). Note that Einstein’s convention of summation over repeated indices is used here.
An expansion in moments, which corresponds to a Taylor expansion of the signal, is also possible. While expansions in moments and in cumulants are mathematically equivalent, for a similar order truncation at some fixed (low) order, the cumulant series provides a more accurate estimation of the dMRI signal than a moment expansion. Moment expansion is more optimal for analytical treatments because contributions from different tissue compartments add up. A combinatorial relation exists between the two expansions [40, 65]. Computing the cumulant tensors and converting them into moments is promoted to be the most numerically stable methodology to adopt [49].
One of the most popular MRI techniques in brain research as well as in clinical practice is Diffusion Tensor Imaging (DTI) [3], based on the cumulant expansion up to the first order in b. This technique is valid for low diffusion weighting (\(b \ll (D K)^{-1}\)). Note that this technique does not assume that the medium is homogeneous with unrestricted diffusion (K \(=\) 0), which appears to be not true for most biological tissues, but that it follows a Gaussian law when \(b \ll (D K)^{-1}\).
Isotropic diffusion in somas can be modeled by a sphere (left). Anisotropic diffusion in neurites can be represented by an ellipsoid reflecting axial (\(\lambda _1\)) and radial (\(\lambda _2\) and \(\lambda _3\)) diffusion. This image has been inspired by the book chapter written by Christian Beaulieu [4]
Using tensor decomposition, three eigenvalues (\(\lambda _1, \lambda _2\) and \(\lambda _3\)) reflecting axial and radial diffusivity of molecules within fibers and in the extra-cellular space are computed (see Fig. 1). The difference between those two diffusivities enable to define variables such as Mean Diffusivity (MD) (the average of all the eigenvalues) or Fractional Anisotropy (FA), defined as follow:
Those two measures are complementary, as they bring different information to the comprehension of a tissue (Fig. 2). Hofstetter et al. [19] used MD to hypothesize the presence of bigger cells in the brain after a learning session. Beaulieu et al. also investigated anisotropy in the human brain grey matter using DTI [4].
Diffusion Kurtosis Imaging (DKI) goes beyond DTI and its first order expansion by also estimating the kurtosis of the diffusion probability distribution function [25]. The kurtosis quantifies the non-Gaussianity of a distribution. The information that it provides is complementary to DTI metrics. Fitting the kurtosis tensor significantly improves the accuracy of the diffusion tensor estimation [64]. In a same way, extending the series to the sixth order cumulant (in \(b^3\)) also increases the accuracy of the kurtosis estimation, albeit with a penalty on precision.
In order to estimate the six independent components of the diffusion tensor, the minimal required data is one b \(=\) 0 (unweighted) image and six non-collinear directions on a single diffusion weighting, or “shell”. The additional estimation of the 15 independent components of the kurtosis tensor requires a minimal acquisition of one b \(=\) 0 image and one or two nonzero shells with 15 non-collinear gradient directions, so that a total of 22 diffusion-weighted images are acquired [64]. The choice of the shell b-values is a trade-off between accuracy and precision. The b-values should be as low as possible to respect the validity of the cumulant expansion, but slightly higher values enable to limit the impact of noise [12]. Jelescu et al. [21] suggest a typical value around b \(=\) 1 ms µm\({}^{-2}\) for DTI and 2 ms µm\({}^{-2}\) for DKI in vivo. For further details on the optimization of acquisition parameters for precise measurement of diffusion in anisotropic systems, we invite the reader to have a look at the work of Jones et al. [31].
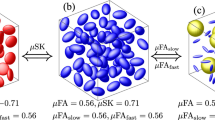
Mean diffusivity (MD) and fractional anisotropy (FA) are two complementary measures. Here are three examples of ellipses ranging from isotropic to anisotropic that have the same mean diffusivity (\(0.7 \times 10^{-3}~\mathrm {mm}^2 \mathrm {s}^{-1}\)). This image has been inspired by the book chapter written by Christian Beaulieu [4]
3.2 Other Representations
Yablonskiy et al. [66] hypothesize that the acquired diffusion signal is a sum of signals originating from many spin packets, present in different cell types, at different positions. Each spin packet having then different trajectories and facing different hindrances, they make the assumption that they all have a different apparent diffusion coefficient (ADC). Hence, they introduced a distribution of diffusion coefficients \(\rho (D)\), and expressed the diffusion signal as following:
Theoretically, the distribution of diffusion coefficients can be estimated using the inverse Laplace transform. In practice, some functional form needs to be assumed for \(\rho (D)\) due to the mathematical ill-conditioning of the inverse Laplace transform. In addition, a very strong diffusion weighted regime is needed for the estimated distribution to accurately reflect the tissue distribution of diffusion coefficients [34, 47].
Jian et al. [29] propose a statistical method to infer connectivity patterns based on the characterization of the water molecule diffusion by a continuous distribution of diffusion tensors. They described the MR signal attenuation as the Laplace transform of this probability distribution defined on the manifold of symmetric positive-definite tensors. Combined with a spherical deconvolution approach, displacement probability functions and distinct fiber orientations can be estimated in each voxel in a HARDI dataset.
The multi-shell Mean Apparent Propagator (MAP)-MRI method, as proposed by Özarslan et al. [50], expands the signal using harmonic oscillator basis functions. It indeed represents the diffusion-weighted signal by an anisotropic Gaussian modulated by a series of Hermite polynomials. This method allows the estimation of three-dimensional EAP, where both restricted (non-Gaussian) diffusion and crossing axons can be represented. However, according to [44], this method fails to estimate crossing angles correctly. The strength of the method resides on its capacity to accurately estimate diffusion properties such as return-to-origin probability, and mean-squared displacement. The propagator anisotropy (PA) metric was derived from this method, which is a measure of dissimilarity between the reconstructed EAP and its closest isotropic approximation EAP.
Hanyga et al. [17] proposed a new space-fractional diffusion model based on an anomalous anisotropic diffusion equation that preserves posivity. This method seems well-suited for applications to DTI [42].
Other representations exist, but have not been included in this chapter.
3.3 Limitations
The validity and therefore the usefulness of the cumulant expansion depends on its convergence towards the acquisition signal, characterized by the convergence radius \(b_c\) [35]. If \(b < b_c\), then the series can be approximated using a couple of low terms in Eq. 6, higher order terms being flooded by the noise, i.e. small contributions to the signal can not be decoupled from the noise in experimental data. The number of parameters to estimate is then reduced, but a good accuracy does not assure its validity. Otherwise, if \(b > b_c\), the series in Eq. 6 diverges which means that the model function cannot be reduced to a polynomial. A good quality fitting gives then more credit to the underlying model.
Hutchinson et al. [20] compare the DTI, DKI, MAP-MRI and NODDI (see Sect. 4.4.1) methods in different experimental conditions to study the influence of noise and sampling (among others) on parameter estimations. All methods proved to be influenced by the acquisition parameters such as the b-values, the resolution, the SNR and the diffusion time. The need of DKI to fit a higher order tensor explains its high sensitivity to noise.
Regional issues are also to be noted, related to crossing fibers, which can be detected as isotropic zones [1]. Indeed, several diffusion directions are possible in that case. The angular resolution needs to be high enough and the model designed to take this particular case into account.
4 Biophysical Modeling to Measure Anisotropy
This second approach is based on a biophysical model designed for a particular tissue geometry. This model is fit to the diffusion signal acquired, which allows the estimation of the relevant parameters of the microstructure. While it can provide a greater specificity of biological parameters, the design of the model remains difficult, as it needs to accurately capture all the features that effectively and substantially impact the diffusion signal in a given acquisition range (the coarse graining problem, see [46]).
Another big challenge of this approach comes from the number of unknowns to estimate after the definition of all effective parameters. To estimate them all we would need a lot of different b-values. This is unfeasible in clinical applications, because first the gradients used in clinical MRIs are not strong enough, and secondly it would require a patient to stay in the MRI device for a very long time. Some methods rely on constraint to bypass this problem, as presented in Sect. 4.4.
4.1 Multi-compartmental Model
Tissue in the brain can generally be decomposed into four compartments. The first one corresponds to the somas, which are the central part of the neurons, mainly present in grey matter. Glial cells are also comprised in this compartment, as done by Palombo et al. [54]. However, their possible high exchange rate with the extracellular space (ECS) is still a matter of discussion and this argument would argue in favor of their better modeling in the ECS compartment [15]. Somas can be modeled as spheres of different diameters. Neurites, the second compartment, connect those neurons together, either in short distances in grey matter (they are called dendrites), or long distance connections in white matter (axons). The diffusivity across the processes is considered zero due to the restriction implied by the fixed small diameter. Processes can therefore be modeled by cylinders with zero-radius (“sticks”) (see part Sect. 4.2 below). The orientation of a collection of processes within a voxel is characterized by an orientation distribution function (ODF) [60]. The third compartment corresponds to extra-cellular space (ECS) and is modeled as Gaussian anisotropic. The last one is the cerebrospinal fluid (CSF), which could contribute if a voxel contains part of a ventricle, and corresponds to free diffusing molecules. It is hence modeled as free diffusion.
The acquired water signal originates from these four compartments and are weighted according to their relative signal fraction f:
with \(f_{\mathrm {somas}} + f_{\mathrm {neurites}} + f_{\mathrm {ECS}} + f_{\mathrm {CSF}} = 1\). Remark that \(f_{\mathrm {somas}}\), \(f_{\mathrm {neurites}}\), \(f_{\mathrm {ECS}}\) and \(f_{\mathrm {CSF}}\) are not the relative volume fractions due to the T2 differences between the compartments. In the following models presented, a combination of those compartments is used to model particular tissues and keep only the relevant compartments. Note that a common assumption is made that the exchanges between the compartments can be neglected at the time scales of clinical dMRI, at least in white matter. The estimation of exchange rate in vivo is challenging and more investigations are needed to validate this hypothesis in white and gray matter.
4.2 Neurites as Sticks
Neurites have been modeled by zero-radius impermeable cylinders, characterized by their longitudinal diffusivity, the transverse diffusivity being considered zero. These neurites are called “sticks” and correspond to the most anisotropic Gaussian compartment possible [7, 26, 36].
The intra-neurite response function, i.e. the diffusion signal from water inside a stick of diffusivity \(D_a\) pointing in the unit direction \(\hat{\mathbf {n}}\), is defined as:
with \(\hat{\mathbf {g}}\) being the unit gradient direction of the measurement. It is determined by \(\cos \theta \equiv \hat{\mathbf {g}} \cdot \hat{\mathbf {n}}\), where \(\theta \) is the angle between \(\hat{\mathbf {n}}\) and \(\hat{\mathbf {g}}\).
The signal, after being isotropically averaged over multiple gradient directions \(\hat{\mathbf {g}}\), is the following [8, 24, 30]:
with \(\beta = \sqrt{\frac{\pi }{4}} \cdot {f_{\mathrm {neurites}}}/{(D_a^{||})^{1/2}}\).
In brain tissue, at sufficiently large b-values, the extra-axonal space signal is exponentially suppressed, its diffusivity being non-zero in any direction. The only remaining signal in white matter comes from the axons (\(S_{\mathrm {neurites}}\) in Eq. 9), and follows the power law from Eq. 11 [41, 62]. This equation captures the very anisotropy of white matter.
Veraart et al. [63] recently proved that the radius of the axons can be estimated for very high b-values, where the transverse diffusivity is not considered null anymore. The direction-averaged DWI signal then follows the following law:
Such law however does not hold in gray matter, which indicates that white matter and grey matter require different models in order to accurately capture their microstructure. Several hypothesis have been elaborated to explain the different behaviour of gray matter DWI signal. McKinnon et al. [41] and Veraart et al. [63] suggest that an increased permeability in cell membranes of neurites in gray matter might be the cause of an increased exponent, while Palombo et al. [52] advocate the abundance of cell body in gray matter. Özarslan et al. [51] suggest that curvy projections, along with longer pulse duration, lead to a disappearance of the \(b^{-1/2}\) decay.
4.3 Standard Model of Diffusion in Neural Tissue
The measured diffusion signal in brain white matter is a sum of anisotropic compartments. It can be modeled as a convolution between a response kernel \(\mathcal {K}\) from a perfectly aligned fascicle pointing in the direction \(\hat{\mathbf {n}}\) and the fiber orientation distribution (ODF) \(\mathcal {P}(\hat{\mathbf {n}})\) normalized to \(\int d \hat{\mathbf {n}} \mathcal {P}(\hat{\mathbf {n}}) \equiv 1\).
\(\hat{\mathbf {g}}\) being defined in Sect. 2.2.
In the case of white matter, the kernel can be written as:
with \(\xi =\hat{\mathbf {g}} \cdot \hat{\mathbf {n}}\). Those exponential contributions correspond to the intra-axonal space modeled by a stick compartment (Eq. 10), the extra-axonal space modeled by an axially symmetric Gaussian compartment with transverse and longitudinal diffusivities \(D_e^{\perp }\) and \(D_e^{||}\), and the cerebrospinal fluid (CSF) compartment. All those compartments are represented in Fig. 3. This decomposition has been widely used in white matter by the community. As a consequence, Novikov et al. suggested to call it the Standard Model (SM) [46]. For the sake of reference, we will also refer to it as the SM in this chapter.

This figure is reproduced from Novikov et al. [49]
Standard Model of diffusion in neuronal tissue. Two-compartment model (intra- and extra-neurite spaces) described by 4 independent parameters: f, \(D_a\), \(D_e^{\Vert }\) and \(D_e^{\perp }\) and a fiber orientation distribution \(\mathcal {P}(\hat{n})\).
4.4 Standard Model Parameter Estimation Using Constraints
In the previous sections we presented the SM of diffusion in neural tissue as a sum of anisotropic Gaussian compartments, as defined by Novikov et al. [46]. We will now introduce some methods based on the SM that rely on constraints to overcome the challenge of estimating many biological parameters of interest.
4.4.1 Neurite Orientation Dispersion and Density Imaging
In order to reduce the number of parameters that need to be estimated, Zhang et al. [67] proposed to impose restrictions on the intrinsic diffusivities. They introduced a method called Neurite Orientation Dispersion and Density Imaging (NODDI), which relies on a three-compartment SM (intra-axonal space, extra-axonal space and CSF), described by seven parameters: volume fractions \(f_{intra}\) and \(f_{iso}\), diffusivities \(D_a^{||}\), \(D_e^{||}\), \(D_e^{\perp }\) and \(D_{iso}\), and the orientation dispersion modeled by a Watson distribution of concentration parameter \(\kappa \). By fixing the diffusivities to the following values:
only the two volume fractions and the orientation dispersion need to be estimated.
Although this method allows to estimate the parameters, the validity of those constraints need to be questioned. To begin with, if we admit that the equalities are correct, they imply that a small deviation from the fixed values, as occurs in cerebral ischemia, will induce a non-negligible bias in the other parameters estimation, leading to false interpretations. However, studies using Diffusion weighted spectroscopy MR which can quantify the diffusion of specific metabolites (e.g. [55]), suggest, through the study of metabolites specifically found on different sections of the neurons and extra cellular tissue, that such diffusivity is not constant across the whole brain. Whether and how these findings can be used to shed light on water diffusion in the brain, is an open question.
Another drawback of this method is that it leads to indetermination, which means that NODDI returns one possible result among a multiplicity of mathematical solutions by fixing \(D_{a}^{\Vert } = D_{e}^{\Vert }\) [23, 49]. If we consider the case where all the parameter constraints are released and the CSF compartment neglected (called NODDIDA [22], which stands for NODDI with diffusivity assessment), two distinct solutions to the estimation problem exist: \(D_{a}^{\Vert } > D_{e}^{\Vert }\) and \(D_{a}^{\Vert } < D_{e}^{\Vert }\) (see Figs. 8 and 9 in Jelescu et al. [23]). Both solutions lie within biologically plausible ranges, and determining which solution is biologically correct is an active field of research, although most studies are suggesting \(D_{a}^{\Vert } > D_{e}^{\Vert }\). At least, the tortuosity approximation that relates \(D_e^{\perp }\) and \(D_e^{\Vert }\) has been invalidated in the case of tight packings of axons [45].
4.4.2 White Matter Tract Integrity Metrics
Another approach to estimate the relevant features of interest in a tissue proposes to relate the scalar parameters to the DKI components. Called White Matter Tract Integrity (WMTI) [16], it is a two-compartment SM that relies on the assumption that sticks are highly aligned within a voxel.
The tissue is described as a sum of two Gaussian compartments (intra- and extra-axonal space, Eq. 9 with \(f_{\mathrm {somas}} = 0\) and \(f_{\mathrm {CSF}} = 0\)), where axons are modeled as sticks embedded in a Gaussian anisotropic extra-axonal medium. Each compartment is characterized by a tensor (\(D_a\) and \(D_e\)) derived from the kurtosis tensors D and K. In any direction j:
We retrieve the two possible mathematical solutions mentioned before, as demonstrated by the square in Eq. 19. The solution chosen in this method is \(D_{a}^{\Vert } < D_{e}^{\Vert }\), which leads to:
Although WMTI enables to capture the changes of diffusivities, it has two main limitations. First, this approach is limited to regions of highly aligned single fiber bundles, which are only present in some white matter regions. Jespersen et al. suggested a method that alleviates this assumption by assuming a Watson distribution of the axons (like in NODDI) [27]. Second, as it relies on the DKI decomposition, this method is only restricted to the low b-value regime, which could lead to some bias.
4.5 Lemonade
As explained in Sect. 4, estimating both compartment diffusivities and orientation dispersion of neurites simultaneously is problematic and tends to be biased. Some methods suggest fixing some parameters such as NODDI or to limit its application to coherent fibers only as WMTI to work around these problems. Releasing these constraints necessitates to estimate a larger number of parameters.
A very recent method in white matter estimates the scalar parameters of a two-compartment kernel separately from the ODF without any constraints. The method developed by Novikov et al. [49] is based on the modeling of the diffusion signal as a convolution of the ODF and the response kernel from a perfectly aligned fiber segment, as presented in Sect. 4.3. It can be decomposed into two steps. A first step solves an algebraic system of equations that relates the kernel parameters to the signal moments for low b-values. This part was called LEMONADE, which stands for Linearly Estimated Moments provide Orientations of Neurites And their Diffusivities Exactly. It requires at least 3 non-zero b-shells inferior to 2.5 ms µm\({}^{-2}\) and returns estimates for \(f_{intra}\), \(D_a^\Vert \), \(D_e^\Vert \), \(D_e^\perp \) and \(p_{2}=\frac{3\left\langle (\cos \psi )^{2}\right\rangle - 1}{2}\), which gives an estimate of the orientation dispersion. In a second step, a rotationally invariant energy function of the system is minimized exploiting all available data and using the first estimates as initialization values.
This method emphasizes the existence of the two mathematical solutions as introduced before, and shows that, in principle, the degeneracy can be avoided using measurements up to the 3rd order of b-values. However, due to noise in the data, the solution selection remains difficult in practice and individual validation should be carried out.
The assumptions made in this approach are, as in the other methods previously presented, the existence of only two compartments, the uniformity of diffusivities across all axons in the voxel, and axial symmetry of the kernel. These assumptions are also the limitations of the model used. Validation in the case of pathological tissue also needs to be investigated.
We refer the reader to Jelescu and Budde’s review on the accuracy and validation of biophysical parameters of different diffusion models in white matter, which includes the ones presented before [21].
5 Summary and Above
We have shown two main approaches to describe microstructure anisotropy using diffusion MRI: signal representation and biophysical modeling. While the former are general and make no assumptions about the underlying tissue, models are designed for a particular tissue and therefore provide greater specificity and interpretation of the estimated biological parameters. The difficulties in modeling reside in accurately capturing the features that effectively and substantially impact the diffusion signal in a given acquisition range, and being able to correctly fit the model (inverse problem).
Anisotropy provides great insight into a tissue structure, and its evolution can enlighten the progression of certain pathologies. The presence of isotropy must not be neglected either, as it can be a great marker of other microstructures, such as in grey matter where it denotes the presence of somas.
Although great progresses have been made during the last decade, some questions remain unresolved. To cite a few, we can wonder to which extent we can consider compartments as non-exchanging. Diffusion time, brain region and myelination of the tissue will most likely impact the answer of this question. Can we also come up with methods less sensitive to the signal-to-noise ratio or a way to disentangle thermal noise and artifacts from the signal of interest?
References
Alexander, D.C., Seunarine, K.K.: Mathematics of Crossing Fibers. Diffusion MRI: Theory, Methods, and Application, pp. 451–464. Oxford (2010)
Assaf, Y., Pasternak, O.: Diffusion Tensor Imaging (DTI)-based white matter mapping in brain research: a review. J. Mol. Neurosci. 34(1), 51–61 (2008). https://doi.org/10.1007/s12031-007-0029-0
Basser, P., Mattiello, J., Lebihan, D.: Estimation of the effective self-diffusion tensor from the nmr spin echo. J. Magn. Reson. Ser. B 103(3), 247–254 (1994). https://doi.org/10.1006/jmrb.1994.1037, http://www.sciencedirect.com/science/article/pii/S1064186684710375
Beaulieu, C.: The basis of anisotropic water diffusion in the nervous system–a technical review. NMR Biomed. 15(7–8), 435–455 (2002). https://doi.org/10.1002/nbm.782
Beaulieu, C.: Chapter 8—the biological basis of diffusion anisotropy. In: Johansen-Berg, H., Behrens, T.E. (eds.) Diffusion MRI (Second Edition), 2nd edn., pp. 155 – 183. Academic Press, San Diego (2014). https://doi.org/10.1016/B978-0-12-396460-1.00008-1. http://www.sciencedirect.com/science/article/pii/B9780123964601000081
Beaulieu, C., Allen, P.S.: Determinants of anisotropic water diffusion in nerves. Magn. Reson. Med. 31(4), 394–400 (1994). https://doi.org/10.1002/mrm.1910310408
Behrens, T., Woolrich, M., Jenkinson, M., Johansen-Berg, H., Nunes, R., Clare, S., Matthews, P., Brady, J., Smith, S.: Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med. 50(5), 1077–1088 (2003). https://doi.org/10.1002/mrm.10609
Callaghan, P., Jolley, K., Lelievre, J.: Diffusion of water in the endosperm tissue of wheat grains as studied by pulsed field gradient nuclear magnetic resonance. Biophys. J. 28(1), 133–141 (1979). https://doi.org/10.1016/S0006-3495(79)85164-4
Callaghan, P.T., Coy, A., MacGowan, D., Packer, K.J., Zelaya, F.O.: Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature 351(6326), 467–469 (1991). https://doi.org/10.1038/351467a0
Caruyer, E., Lenglet, C., Sapiro, G., Deriche, R.: Design of multishell sampling schemes with uniform coverage in diffusion mri. Magn. Reson. Med. 69(6), 1534–1540 (2013). https://doi.org/10.1002/mrm.24736
Cleveland, G., Chang, D., Hazlewood, C., Rorschach, H.: Nuclear magnetic resonance measurement of skeletal muscle: anisotrophy of the diffusion coefficient of the intracellular water. Biophys. J. 16(9), 1043–1053 (1976). https://doi.org/10.1016/S0006-3495(76)85754-2
DK., J.: Precision and accuracy in diffusion tensor magnetic resonance imaging. Top Magn. Reson. Imaging 21, 87–99 (2010). https://doi.org/10.1097/RMR.0b013e31821e56ac
Fick, R.H.J., Petiet, A., Santin, M., Philippe, A.C., Lehericy, S., Deriche, R., Wassermann, D.: Multi-spherical diffusion mri: Exploring diffusion time using signal sparsity. In: Fuster, A., Ghosh, A., Kaden, E., Rathi, Y., Reisert, M. (eds.) Computational Diffusion MRI, pp. 71–83. Springer International Publishing, Cham (2017)
Fick, R.H.J., Pizzolato, M., Wassermann, D., Deriche, R.: Diffusion MRI anisotropy: modeling, analysis and interpretation. In: Schultz, T., Özarslan, E., Hotz, I. (eds.) Modeling, Analysis, and Visualization of Anisotropy, pp. 203–228. Springer International Publishing, Cham (2017). https://doi.org/10.1007/978-3-319-61358-1. Series Title: Mathematics and Visualization
Fields, R., Woo, D., Basser, P.: Glial regulation of the neuronal connectome through local and long-distant communication. Neuron 86(2), 374–386 (2015). https://doi.org/10.1016/j.neuron.2015.01.014, http://www.sciencedirect.com/science/article/pii/S0896627315000409
Fieremans, E., Jensen, J.H., Helpern, J.A.: White matter characterization with diffusional kurtosis imaging. NeuroImage 58(1), 177–188 (2011). https://doi.org/10.1016/j.neuroimage.2011.06.006, http://www.sciencedirect.com/science/article/pii/S1053811911006148
Hanyga, A., Magin, R.L.: A new anisotropic fractional model of diffusion suitable for applications of diffusion tensor imaging in biological tissues. Proc. R. Soc. Math. Phys. Eng. Sci. 470(2170), 20140319 (2014). https://doi.org/10.1098/rspa.2014.0319
Henkelman, R.M., Stanisz, G.J., Kim, J.K., Bronskill, M.J.: Anisotropy of nmr properties of tissues. Magn. Reson. Med. 32(5), 592–601 (1994). https://doi.org/10.1002/mrm.1910320508
Hofstetter, S., Tavor, I., Tzur Moryosef, S., Assaf, Y.: Short-term learning induces white matter plasticity in the fornix. J. Neurosci. 33(31), 12844–12850 (2013). https://doi.org/10.1523/JNEUROSCI.4520-12.2013, https://www.jneurosci.org/content/33/31/12844
Hutchinson, E.B., Avram, A.V., Irfanoglu, M.O., Koay, C.G., Barnett, A.S., Komlosh, M.E., Özarslan, E., Schwerin, S.C., Juliano, S.L., Pierpaoli, C.: Analysis of the effects of noise, dwi sampling, and value of assumed parameters in diffusion mri models. Magn. Reson. Med. 78(5), 1767–1780 (2017). https://doi.org/10.1002/mrm.26575
Jelescu, I.O., Budde, M.D.: Design and validation of diffusion MRI models of white matter. Front. Phys. 5, (2017). https://doi.org/10.3389/fphy.2017.00061
Jelescu, I.O., Veraart, J., Adisetiyo, V., Milla, S.S., Novikov, D.S., Fieremans, E.: One diffusion acquisition and different white matter models: how does microstructure change in human early development based on wmti and noddi? NeuroImage 107, 242–256 (2015). https://doi.org/10.1016/j.neuroimage.2014.12.009, http://www.sciencedirect.com/science/article/pii/S1053811914010015
Jelescu, I.O., Veraart, J., Fieremans, E., Novikov, D.S.: Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue: Degeneracy in Model Parameter Estimation of Diffusion in Neural Tissue. NMR Biomed. 29(1), 33–47 (2016). https://doi.org/10.1002/nbm.3450
Jensen, J.H., Glenn, G.R., Helpern, J.A.: Fiber ball imaging. NeuroImage 124, 824–833 (2016). https://doi.org/10.1016/j.neuroimage.2015.09.049, http://www.sciencedirect.com/science/article/pii/S105381191500871X
Jensen, J.H., Helpern, J.A., Ramani, A., Lu, H., Kaczynski, K.: Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Med. 53(6), 1432–1440 (2005). https://doi.org/10.1002/mrm.20508
Jespersen, S.N., Kroenke, C.D., Østergaard, L., Ackerman, J.J., Yablonskiy, D.A.: Modeling dendrite density from magnetic resonance diffusion measurements. NeuroImage 34(4), 1473–1486 (2007). https://doi.org/10.1016/j.neuroimage.2006.10.037, http://www.sciencedirect.com/science/article/pii/S1053811906010950
Jespersen, S.N., Olesen, J.L., Hansen, B., Shemesh, N.: Diffusion time dependence of microstructural parameters in fixed spinal cord. NeuroImage 182, 329–342 (2018). https://doi.org/10.1016/j.neuroimage.2017.08.039, http://www.sciencedirect.com/science/article/pii/S1053811917306869. Microstructural Imaging
Jeurissen, B., Descoteaux, M., Mori, S., Leemans, A.: Diffusion mri fiber tractography of the brain. NMR Biomed. 32(4), e3785 (2019). https://doi.org/10.1002/nbm.3785, https://onlinelibrary.wiley.com/doi/abs/10.1002/nbm.3785. E3785 NBM-17-0045.R2
Jian, B., Vemuri, B.C., Özarslan, E., Carney, P.R., Mareci, T.H.: A novel tensor distribution model for the diffusion-weighted mr signal. NeuroImage 37(1), 164–176 (2007). https://doi.org/10.1016/j.neuroimage.2007.03.074, http://www.sciencedirect.com/science/article/pii/S105381190700273X
Joabsson, F., Nydén, M., Linse, P., Söderman, O.: Pulsed field gradient nmr studies of translational diffusion in cylindrical surfactant aggregates. J. Phys. Chem. B 101(47), 9710–9716 (1997). https://doi.org/10.1021/jp971890g
Jones, D., Horsfield, M., Simmons, A.: Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magn. Reson. Med. 42(3), 515–525 (1999). https://doi.org/10.1002/(SICI)1522-2594(199909)42:3<515::AID-MRM14>3.0.CO;2-Q
Kac, M.: Can one hear the shape of a drum? Am. Math. Mon. 73(4P2), 1–23 (1966). https://doi.org/10.1080/00029890.1966.11970915
Kaden, E., Kruggel, F., Alexander, D.C.: Quantitative mapping of the per-axon diffusion coefficients in brain white matter. Magn. Reson. Med. 75(4), 1752–1763 (2016). https://doi.org/10.1002/mrm.25734
Kiselev, V.G.: Fundamentals of diffusion mri physics. NMR Biomed. 30(3), e3602 (2017). https://doi.org/10.1002/nbm.3602
Kiselev, V.G., Il’yasov, K.A.: Is the “biexponential diffusion” biexponential? Magn. Reson. Med. 57(3), 464–469 (2007). https://doi.org/10.1002/mrm.21164
Kroenke, C.D., Ackerman, J.J., Yablonskiy, D.A.: On the nature of the naa diffusion attenuated mr signal in the central nervous system. Magn. Reson. Med. 52(5), 1052–1059 (2004). https://doi.org/10.1002/mrm.20260
Le Bihan, D., Breton, E.: Imagerie de diffusion in-vivo par résonance magnétique nucléaire. Comptes-Rendus de l’Académie des Sciences 93(5), 27–34 (1985). https://hal.archives-ouvertes.fr/hal-00350090
Ligneul, C., Palombo, M., Hernández-Garzón, E., Carrillo-de Sauvage, M.A., Flament, J., Hantraye, P., Brouillet, E., Bonvento, G., Escartin, C., Valette, J.: Diffusion-weighted magnetic resonance spectroscopy enables cell-specific monitoring of astrocyte reactivity in vivo. NeuroImage 191, 457–469 (2019). https://doi.org/10.1016/j.neuroimage.2019.02.046, https://linkinghub.elsevier.com/retrieve/pii/S1053811919301429
Liu, C., Bammer, R., Acar, B., Moseley, M.E.: Characterizing non-gaussian diffusion by using generalized diffusion tensors. Magn. Reson. Med. 51(5), 924–937 (2004). https://doi.org/10.1002/mrm.20071
Mayer, J.E., Montroll, E.: Molecular distribution. J. Chem. Phys. 9(1), 2–16 (1941). https://doi.org/10.1063/1.1750822
McKinnon, E.T., Jensen, J.H., Glenn, G.R., Helpern, J.A.: Dependence on b-value of the direction-averaged diffusion-weighted imaging signal in brain. Magn. Reson. Imaging 36, 121–127 (2017). https://doi.org/10.1016/j.mri.2016.10.026, https://linkinghub.elsevier.com/retrieve/pii/S0730725X16301965
Meerschaert, M.M., Magin, R.L., Ye, A.Q.: Anisotropic fractional diffusion tensor imaging. J. Vib. Control 22(9), 2211–2221 (2016). https://doi.org/10.1177/1077546314568696. PMID: 27499605
M.R.S.E., R.B.F.H., V.P.L.S., R.A.: Xxvii. a brief account ofmicroscopicalobservations made in the months of june, july and august 1827, on theparticles contained in the pollen of plants; and on the general existence ofactive molecules in organic and inorganic bodies. Philoso. Mag. 4(21), 161–173 (1828). https://doi.org/10.1080/14786442808674769
Ning, L., Laun, F., Gur, Y., DiBella, E.V., Deslauriers-Gauthier, S., Megherbi, T., Ghosh, A., Zucchelli, M., Menegaz, G., Fick, R., St-Jean, S., Paquette, M., Aranda, R., Descoteaux, M., Deriche, R., O’Donnell, L., Rathi, Y.: Sparse reconstruction challenge for diffusion mri: validation on a physical phantom to determine which acquisition scheme and analysis method to use? Med. Image Anal. 26(1), 316–331 (2015). https://doi.org/10.1016/j.media.2015.10.012, http://www.sciencedirect.com/science/article/pii/S1361841515001541
Novikov, D.S., Fieremans, E.: Relating extracellular diffusivity to cell size distribution and packing density as applied to white matter. In: Proceedings of the 20th Annual Meeting of ISMRM, p. 1829 (2012)
Novikov, D.S., Fieremans, E., Jespersen, S.N., Kiselev, V.G.: Quantifying brain microstructure with diffusion MRI: theory and parameter estimation: brain microstructure with dMRI: theory and parameter estimation. NMR Biomed. e3998 (2018). https://doi.org/10.1002/nbm.3998, http://doi.wiley.com/10.1002/nbm.3998
Novikov, D.S., Kiselev, V.G.: Effective medium theory of a diffusion-weighted signal. NMR Biomed. 23(7), 682–697 (2010). https://doi.org/10.1002/nbm.1584
Novikov, D.S., Kiselev, V.G., Jespersen, S.N.: On modeling. Magn. Reson. Med. 79(6), 3172–3193 (2018). https://doi.org/10.1002/mrm.27101
Novikov, D.S., Veraart, J., Jelescu, I.O., Fieremans, E.: Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. NeuroImage 174, 518–538 (2018). https://doi.org/10.1016/j.neuroimage.2018.03.006, https://linkinghub.elsevier.com/retrieve/pii/S1053811918301915
Özarslan, E., Koay, C.G., Shepherd, T.M., Komlosh, M.E., İrfanoğlu, M.O., Pierpaoli, C., Basser, P.J.: Mean apparent propagator (map) mri: a novel diffusion imaging method for mapping tissue microstructure. NeuroImage 78, 16–32 (2013). https://doi.org/10.1016/j.neuroimage.2013.04.016, http://www.sciencedirect.com/science/article/pii/S1053811913003431
Özarslan, E., Yolcu, C., Herberthson, M., Knutsson, H., Westin, C.F.: Influence of the size and curvedness of neural projections on the orientationally averaged diffusion mr signal. Front. Phys. 6, 17 (2018). https://doi.org/10.3389/fphy.2018.00017
Palombo, M., Alexander, D.C., Zhang, H.: A generative model of realistic brain cells with application to numerical simulation of the diffusion-weighted MR signal. NeuroImage 188, 391–402 (2019). https://doi.org/10.1016/j.neuroimage.2018.12.025, https://linkinghub.elsevier.com/retrieve/pii/S1053811918321694
Palombo, M., Ianus, A., Guerreri, M., Nunes, D., Alexander, D.C., Shemesh, N., Zhang, H.: Sandi: A compartment-based model for non-invasive apparent soma and neurite imaging by diffusion mri. NeuroImage 215, 116835 (2020). https://doi.org/10.1016/j.neuroimage.2020.116835, http://www.sciencedirect.com/science/article/pii/S1053811920303220
Palombo, M., Ligneul, C., Najac, C., Le Douce, J., Flament, J., Escartin, C., Hantraye, P., Brouillet, E., Bonvento, G., Valette, J.: New paradigm to assess brain cell morphology by diffusion-weighted mr spectroscopy in vivo. Proc. Natl. Acad. Sci. 113(24), 6671–6676 (2016). https://doi.org/10.1073/pnas.1504327113, https://www.pnas.org/content/113/24/6671
Palombo, M., Ligneul, C., Valette, J.: Modeling diffusion of intracellular metabolites in the mouse brain up to very high diffusion-weighting: Diffusion in long fibers (almost) accounts for non-monoexponential attenuation: modeling diffusion of brain metabolites in vivo up to very high diffusion weighting. Magn. Reson. Med. 77(1), 343–350 (2017). https://doi.org/10.1002/mrm.26548
Panagiotaki, E., Schneider, T., Siow, B., Hall, M.G., Lythgoe, M.F., Alexander, D.C.: Compartment models of the diffusion mr signal in brain white matter: a taxonomy and comparison. NeuroImage 59(3), 2241–2254 (2012). https://doi.org/10.1016/j.neuroimage.2011.09.081, http://www.sciencedirect.com/science/article/pii/S1053811911011566
Panagiotaki, E., Walker-Samuel, S., Siow, B., Johnson, S.P., Rajkumar, V., Pedley, R.B., Lythgoe, M.F., Alexander, D.C.: Noninvasive quantification of solid tumor microstructure using verdict mri. Cancer Res. 74(7), 1902–1912 (2014). https://doi.org/10.1158/0008-5472.CAN-13-2511, https://cancerres.aacrjournals.org/content/74/7/1902
Soares, J., Marques, P., Alves, V., Sousa, N.: A hitchhiker’s guide to diffusion tensor imaging. Front. Neurosci. 7, 31 (2013). https://doi.org/10.3389/fnins.2013.00031
Tanner, J.E., Stejskal, E.O.: Restricted self-diffusion of protons in colloidal systems by the pulsed-gradient, spin-echo method. J. Chem. Phys. 49(4), 1768–1777 (1968). https://doi.org/10.1063/1.1670306
Tuch, D.S.: Q-ball imaging. Magn. Reson. Med. 52(6), 1358–1372 (2004). https://doi.org/10.1002/mrm.20279
Tuch, D.S., Reese, T.G., Wiegell, M.R., Makris, N., Belliveau, J.W., Wedeen, V.J.: High angular resolution diffusion imaging reveals intravoxel white matter fiber heterogeneity. Magn. Reson. Med. 48(4), 577–582 (2002). https://doi.org/10.1002/mrm.10268
Veraart, J., Fieremans, E., Novikov, D.S.: On the scaling behavior of water diffusion in human brain white matter. NeuroImage 185, 379–387 (2019). https://doi.org/10.1016/j.neuroimage.2018.09.075, https://linkinghub.elsevier.com/retrieve/pii/S1053811918319475
Veraart, J., Nunes, D., Rudrapatna, U., Fieremans, E., Jones, D.K., Novikov, D.S., Shemesh, N.: Noninvasive quantification of axon radii using diffusion mri. eLife 9, e49855 (2020). https://doi.org/10.7554/eLife.49855
Veraart, J., Poot, D.H.J., Van Hecke, W., Blockx, I., Van der Linden, A., Verhoye, M., Sijbers, J.: More accurate estimation of diffusion tensor parameters using diffusion kurtosis imaging. Magn. Reson. Med. 65(1), 138–145 (2011). https://doi.org/10.1002/mrm.22603
VG, K.: The cumulant expansion: an overarching mathematical framework for understanding diffusion nmr. In: DK, J. (ed.) Diffusion MRI: Theory, Methods, and Applications, pp. 152 – 68. Oxford University Press, Oxford (2010)
Yablonskiy, D.A., Bretthorst, G.L., Ackerman, J.J.: Statistical model for diffusion attenuated mr signal. Magn. Reson. Med. 50(4), 664–669 (2003). https://doi.org/10.1002/mrm.10578
Zhang, H., Schneider, T., Wheeler-Kingshott, C.A., Alexander, D.C.: NODDI: Practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage 61(4), 1000–1016 (2012). https://doi.org/10.1016/j.neuroimage.2012.03.072, https://linkinghub.elsevier.com/retrieve/pii/S1053811912003539
Acknowledgments
This work was supported by the ERC-StG NeuroLang and the ANR/NSF NeuroRef grants.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this paper
Cite this paper
Jallais, M., Wassermann, D. (2021). Single Encoding Diffusion MRI: A Probe to Brain Anisotropy. In: Özarslan, E., Schultz, T., Zhang, E., Fuster, A. (eds) Anisotropy Across Fields and Scales. Mathematics and Visualization. Springer, Cham. https://doi.org/10.1007/978-3-030-56215-1_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-56215-1_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-56214-4
Online ISBN: 978-3-030-56215-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)