Uncertainty in the DTI Visualization Pipeline

Abstract

Diffusion-Weighted Magnetic Resonance Imaging (DWI) enables the in-vivo visualization of fibrous tissues such as white matter in the brain. Diffusion-Tensor Imaging (DTI) specifically models the DWI diffusion measurements as a second order-tensor. The processing pipeline to visualize this data, from image acquisition to the final rendering, is rather complex. It involves a considerable amount of measurements, parameters and model assumptions, all of which generate uncertainties in the final result which typically are not shown to the analyst in the visualization. In recent years, there has been a considerable amount of work on the visualization of uncertainty in DWI, and specifically DTI. In this chapter, we primarily focus on DTI given its simplicity and applicability, however, several aspects presented are valid for DWI as a whole. We explore the various sources of uncertainties involved, approaches for modeling those uncertainties, and, finally, we survey different strategies to visually represent them. We also look at several related methods of uncertainty visualization that have been applied outside DTI and discuss how these techniques can be adopted to the DTI domain. We conclude our discussion with an overview of potential research directions.

1 Introduction

Recent advancements in magnetic resonance imaging (MRI) technology have led to the development of various remarkable techniques for the interpretation of brain anatomy. The most promising one is diffusion-weighted imaging  (DWI), the only non-invasive technique for the assessment of brain white matter connectivity. This approach relies on the measurement of anisotropic diffusion of water molecules. The imaging and the interpretation of the molecular diffusion have improved with the development of techniques like diffusion tensor imaging (DTI)  and high angular resolution diffusion imaging (HARDI). In this chapter, we will discuss the visualization pipeline of DTI, given its clinical applicability. However, several visualization strategies and sources of uncertainties associated are valid for more advanced models like HARDI models.

DTI allows direct in-vivo examination of the fibrous structure in the brain at a relatively low acquisition cost. By analyzing the three-dimensional shape of the diffusion tensor, it provides valuable information about the microstructure of brain tissues. Despite many advantages of this technique, some downsides limit its widespread use. The main reason is that the complexity in the data makes it notoriously difficult to infer and analyze.

The DTI visualization pipeline consists of four main stages, from data acquisition to the final visual representation of the results, as shown in Fig. 1. Each stage is based on assumptions, parameters, and estimations subject to considerable uncertainties. The uncertainties involved in each of the pipelines’ stage can lead to unpredictable variations in the final output.

Several state-of-the-art reports exist on DWI visualization [62, 92, 93, 99]. However, none of them give an overview of uncertainty, or they focus on some specific aspects. Most of the visualization literature about uncertainty in DTI focuses on issues related to the visual representation rather than sources of error involved in the pipeline [36, 47, 92]. In this chapter, we discuss the DTI visualization pipeline and analyze the sources of uncertainties present at each stage. We briefly cover the approaches used for quantification of uncertainties, which are often omitted in other studies [36, 47]. We review state-of-the-art strategies for uncertainty visualization in DTI and compare their main characteristics and drawbacks. We further investigate several methodologies for uncertainty visualization in other domains that have not been explored in DWI and discuss how these techniques can be adopted in this domain. DWI models beyond DTI share a similar pipeline as the one shown in Fig. 1. However, some parameters, error sources, and visual representations would differ from the tensor model. Specifically, diffusion modeling and fiber tracking would be based on different parameters and algorithms. In this chapter, we will indicate the methods from the DTI that are valid for the more general DWI pipeline.

In Sect. 2, we discuss the background and review the visualization techniques for DTI. In Sect. 3, we discuss the sources of uncertainties involved in the visualization pipeline and proceed with the uncertainty modeling techniques in Sect. 4. We review uncertainty visualization methods in Sect. 5 and conclude with open issues and research direction in Sect. 6.

2 Background

Diffusion refers to the constant rapid movement of microscopic particles due to the presence of thermal energy, i.e., ‘Brownian motion’. DWI deals with the diffusion of water molecules present in biological tissues where the diffusion is usually restricted due to the hindrance by many obstacles such as axonal membranes, macromolecules, and myelin. This kind of restricted diffusion is known as anisotropic diffusion. Stejskal and Tanner [94] observed the anisotropic diffusion of water molecules in tissues and investigated the related modeling of the diffusion effects for MRI. The clinical application of this technique was first presented by Bihan et al. [61] with the introduction of diffusion MRI along with the concept of apparent diffusion coefficient (ADC). In some neurological conditions, the amount of diffusion is disturbed in the affected area. Through studying these changes in diffusion, the abnormalities can be detected. In the following section, we will summarize how these measurements have been used to visualize white matter tracts in the brain.

Fig. 1

The DTI visualization pipeline with sources of uncertainties at each step

2.1 Diffusion Tensor

The pattern of diffusion anisotropy of white matter tracts in 3D space can be mathematically modeled by a second order tensor, called the diffusion tensor D, introduced by Basser et al. [5]. The tensor D is a symmetric, positive definite tensor represented by a 3$\,\times \,$3 matrix with six unique elements, denoted by $D_{ij}$ as follows:

$$\begin{aligned} D = \begin{pmatrix} D_{11} &{} D_{12} &{} D_{13} \\ D_{21} &{} D_{22} &{} D_{23} \\ D_{31} &{} D_{32} &{} D_{33} \end{pmatrix} \end{aligned}$$

(1)

The diagonal elements in the diffusion tensor D represent the diffusion coefficients along the principle axes x, y and z, while the off-diagonal elements represent the correlation of the diffusion between each pair of the principal direction. The diffusion tensor D is symmetric about the diagonal axis ($D_{ij} = D_{ji}$). By analysis of the eigenvectors and eigenvalues $\lambda _1$,$\lambda _2$,$\lambda _3$ of the diffusion matrix, the length and the direction of the principal axes of the diffusion tensor can be determined.  

Fig. 2

Barycentric space of diffusion tensor shapes

The six unique values in the tensor D provide the intervoxel diffusion information and the microstructure of a particular voxel. However, the six-dimensional diffusion tensor is hard to infer and present to a user. For this reason, several scalar quantities have been introduced to simplify the tensor to a single value. Fractional Anisotropy (FA), the most widely used scalar measure in diffusion tensor imaging [9] , represents the extent of the diffusion anisotropicity. A lower value of FA indicates that the diffusion is free (FA $=$ 0; isotropic), while a high value of FA implies that the diffusion is restricted to a single direction (FA $=$ 1; anisotropic). Another popular scalar measure in DTI is mean diffusivity (MD), which represents the overall amount of diffusion. Many other scalar measures have been proposed based on the more complex behaviour of molecular diffusion and are explained in detail in surveys by Novikov et al. [75], Rajagopalan et al. [83] and Vilanova et al. [99].

Visualization strategies: A Glyph is a general term for geometrically plotted specifier that represent multidimensional data values. Data information is mapped to glyph characteristics such as shape and color. Glyphs provide a way to represent the full six-dimensional information of a diffusion tensor by mapping the eigenvectors and eigenvalues to the orientation and shape of a geometric primitive. The most straight forward approach to visualize the diffusion tensor are ellipsoidal glyphs [82] as shown in Fig. 2a. The orientation of the ellipsoid represents the direction of the major eigenvector, while the length represents the corresponding eigenvalue. Westin et al. [104] introduced three metrics to measure linear ($\lambda _1$ > $\lambda _2$,$\lambda _3$), planar ($\lambda _1$=$\lambda _2$ > $\lambda _3$) and spherical diffusion ($\lambda _1$ $=$ $\lambda _2$ $=$ $\lambda _3$). Figure. 2 represents the barycentric space of diffusion tensor shapes in which the three extremes (linear, planar, and spherical) are at the corner of triangles. Among several other proposed techniques, the super quadratic glyph is considered state-of-the-art for glyph-based tensor visualization. Instead of interpolating between ellipsoidal shapes, Kindlmann [57] represents the diffusion by superquadrics with shape parameters defined by the barycentric coordinates,as shown in Fig. 2b.

Outside DTI, glyphs are also used to represent the orientation distribution function (ODF) of the molecular diffusion, which is commonly estimated by models that go beyond the diffusion tensor. ODF specifies the overall diffusion in a given direction, integrated over displacement magnitudes [103]. Spherical polar plots [98] parametrized surfaces [77], the HARDI glyph [81] and the HOME glyph [89] are some of the common glyph based visualization techniques for representing ODFs.

Fig. 3

Visualization techniques for deterministic tractography. Images are generated using vIST/e [1]

2.2 Fiber Tracking

The diffusion tensor provides per-voxel information about the orientation of the underlying neural tracts by analyzing the derived eigenvectors. By combining this information with other scalar measure, e.g. FA, one can estimate trajectories of white matter bundles in 3D space. The process of virtual reconstruction of the neural fiber tract on the basis of the diffusion tensor field is named Fiber Tracking or Tractography  [8, 71]. These techniques of generating brain anatomical connectivity from the diffusion information have been summarized in review articles [42, 72, 102]. Fiber tracking methods have found its way in many neurological applications [18, 31, 45, 73, 74].

The fiber tracking strategies can be mainly divided into deterministic, probabilistic, and global geometric techniques. Deterministic techniques always produce the same output with the same set of inputs. Probabilistic techniques, however, add randomness in the tracking process to incorporate the inherent uncertainty. We defer an extensive discussion of probabilistic methods to Sect. 4. Global geometric methods deduce connectivity in the white matter by globally optimizing a certain cost function based on the diffusion tensor information and are outside of the scope of this chapter.

Streamline tracing is the most commonly used algorithm for tractography. It is a deterministic technique that generates trajectories by integrating the vector field defined by the main eigenvector at each voxel position. The tracing process ends when the stopping criteria are met. Several constraints can be used as stopping criteria, such as maximum turning angle or FA, to limit tracts to the region where tensors realistically represent the fiber tracts.

Visualization strategies: Line-based approaches are the most straightforward technique to represent deterministic fiber tracts. Numerous strategies have been introduced for the visualization of the white matter tracts, such as thin polylines [70] illuminated streamlines [114] or cylindrical tubes [8]. Zhang et al. [112] introduced streamtubes to encode the local diffusion tensor information along the cross-section of the fiber tracts at each voxel. This technique has previously been used to represent the tensor field in fluid dynamics, where they were called Hyper-streamlines [25]. Figure 3 shows the most commonly used representations for deterministic tractography. 

So far, we have discussed the visualization pipeline methods used in DTI without the involvement of uncertainties. In the following sections, we will review the sources of uncertainty present in the pipeline, the modeling techniques and the strategies used to visualize them.

3 Sources of Uncertainty

Understanding the sources of uncertainties is essential to provide effective visualization. The DTI visualization pipeline involves complex stages of mathematical modeling, analysis, mapping, and rendering strategies, therefore, it is prone to uncertainty from various sources. Noise, patient movement, modeling residuals, and distortion from imaging artifacts produce uncertainty in the orientation of the diffusion tensor and are detrimental to fiber tracking algorithms. These uncertainties hamper the link between the data being measured and visualized. The sources of uncertainty involved at each stage of the DTI visualization pipeline are shown in Fig. 1. In this section, we will go through this pipeline and discuss the sources of error present at each stage. Even though we focus on the DTI modality, several of the sources of uncertainty are present in DWI pipelines that go beyond DTI.

3.1 Image Acquisition

MRI-based techniques usually suffer from various acquisition errors such as noise, motion artifacts, partial volume effects, etc. Signal to noise ratio in DWI sequences is relatively high given that signal attenuation is being measured. The effect of noise on the fiber tracking output has been widely studied in literature [3, 46, 59]. There has been a growing trend of increasing the gradient direction in DTI acquisition to improve the tractography quality. However, this further increases the acquisition time. In HARDI, the gradient directions for acquisition are much higher than that of DTI and, therefore, it needs more time. With higher acquisition time, it is more likely that the subject move during the scan, which in turn, introduces misalignment in the acquired image. These kinds of artifacts are known as motion artifacts. Providentially, these misalignments can be corrected during the registration process. Several automated techniques have been introduced to remove this artifact [113]. The finite resolution of the results also affects the output of the process. The resolution of a clinical DWI acquisition is typically in the order of millimeter (mm) in each direction, which is much lower than that of actual axons. Therefore, the signal values have to be averaged to be able to fit in a single image voxel. This loss of information is called the partial-volume effect (PVE). Several studies have been conducted in neurological literature to investigate the PVE in DTI [84, 85, 101]. Other sources of error during image acquisition involve magnetic distortion, scanner setting and others [14].

3.2 Diffusion Tensor Calculation

In DTI, the diffusion of a water molecule is mathematically represented by a second-order tensor, known as the diffusion tensor. Numerous measurements are performed along various gradient directions to determine the molecular diffusion at each voxel. The least-squares method is the most commonly used fitting technique to calculate the diffusion tensor, but other more accurate regression procedures can also be used [5, 6]. This fitting procedure introduces a fitting error and involves a model choice. Therefore it adds variation in the outcome of the DTI procedure. DTI technique can only estimate one dominant diffusion direction per voxel, and thus, is incapable of determining the structure where the multi-fiber direction is present and, therefore, results in unreliable outcomes. HARDI models emerge to overcome this limitation and able to model complex fibrous regions of the brain. It provides a way to estimate the multi-fiber populations that can then be used for robust tractography. HARDI models are more complex and usually introduce more parameters and choices to be determined than DTI.

3.3 Fiber Tracking

Fiber tracking involves the reconstruction of the fibrous structure of the brain white matter by gradually following the local fiber orientation estimated from the diffusion tensor. There are several parameters in fiber tracking to control the tracking process, however, these parameters add variability to the fiber tracking results. There are four major sources of uncertainties in the fiber tracking algorithm:

• 1. Region definition and filtering

• 2. Numerical approximation

• 3. Interpolation

• 4. Stopping criteria

Region definition and filtering: Regions are usually defined by the user to start, end, or control the fiber pathways. The seeding region refers to the starting point of the tracking process and defines the initial conditions for numerical integration. Regions are also used to extract a specific bundle of interest and filter out others to avoid visual clutter. The region definition in the fiber tracking process also adds variation in the outcome. Usually, these regions are defined manually, and therefore introduce an implicit user bias. A minor variation in the definition can result in largely different pathways. Recently, several techniques have been proposed to minimize the effect of seed region in the fiber tracking algorithms [21, 46, 102].

Numerical approximation: Different types of numerical approximation schemes can be implemented in the fiber tracking algorithm. Euler integration is the most straight forward technique [71] but it is a strong approximation. Higher-order methods, such as 2nd or 4th order Runge-Kutta methods [8], are typically less sensitive to noise and can be used for accurate fiber tracking. The integration step, or step size, further affect the quality of these integration schemes [97].

Interpolation: During the numerical approximation process, most of the time, the sample position after each integration step lies between volume grid points, hence, interpolation is needed to estimate values, based on the neighboring grid points. Several studies have been conducted to address the effect of interpolation in fiber tracking [32, 109]. Various kinds of interpolation schemes are present, each result in different pathways, and therefore, add variability in the results.

Stopping criteria: Different scalar measures, such as FA, MD, or curve angle, can be used as stopping criteria in the fiber tracking process. Fiber tracking algorithms are often highly sensitive to these values, meaning that a very small variation in the stopping criteria can lead to a very large change in the resulting fiber [97]. Brecheisen et al. [16] propose a visual exploration tool that allows users to investigate the behavior and sensitivity of DTI fiber tracking to stopping criteria.

In fiber tracking algorithms for HARDI models the principal directions are extracted from a multifiber representation which adds another layer of complexity to the algorithms.

3.4 Visualization

The visualization stage involves the mapping of the data into a geometric representation or visual primitives that are finally rendered on to the screen. This process can be another source the uncertainty. Various photo-realistic rendering techniques are used to simulate real world lighting as exact as possible, but this further complexity adds uncertainty in the outcome. Lighting models and shadows enhance the structural perception of the fibers and as such improve the recognition of the spatial relations between tracts; however, the controlling parameters can add further variability in the final results.

4 Uncertainty Modeling

As discussed in the previous section, many sources of uncertainties are present at each stage of the DTI visualization pipeline that affect the outcome of the process. These uncertainties propagate through the pipeline adding uncertainty in the derived quantities including diffusion tensor and fiber orientations. Estimating the error distribution of different sources is not a straight forward task. Different approaches have been used to model the uncertainty, however, each with pros and cons. We have classified the methods used for the uncertainty quantification into two categories:

• 1. Analytical methods

• 2. Stochastic methods

4.1 Analytical Methods

Analytical methods refer to approaches that provide an explicit mathematical formulation of the error distribution. These modeling techniques are based on the Bayes theorem [56] and were first introduced by Behrens et al. [12] in DWI. They estimated the probability distribution function (PDF) of the fiber orientation by a Bayesian model. The main disadvantage of this modeling technique is that they rely on the assumption of prior and noise present in the data. These techniques are computationally inexpensive, however, their dependence on the prior assumption limit their widespread use. Most of the Bayesian model-based techniques are often combined with random sampling methods, such as Markov Chain Monte Carlo (MCMC), to determine the distribution of model parameters [11, 12, 33]. The application of Bayesian model based methods in DTI and HARDI has been reported several times [48, 54, 64].

Shortest path algorithms are another useful approach for quantifying structural brain connectivity and were first introduced by O’Donnell et al. [78]. This approach relies on computing the connections between regions of interest rather than connections from a seed. Schober et al. [88] presented the distribution of the shortest path as a Gaussian process over the solution to an ordinary differential equation (ODE). This strategy offers novel ways to quantify and visualize uncertainty arising from the numerical computation and allow marginalization over a space of feasible solutions. Hauberg et al. [40] extended this work and incorporated data uncertainty in DTI by sub-sampling the diffusion gradients and solving the noisy ODE. Several other studies using the shortest path algorithms in fiber tracking can be found in the literature [39, 63].

4.2 Stochastic Methods

Describing the probability distribution analytically and propagating it through the visualization pipeline is extremely difficult and often not feasible. The alternative and the most straight forward way to estimate the probability distribution function is to repeat the acquisition multiple times, this approach is called the bootstrap method [27]. However, for robust estimation of the PDFs, hundreds of data sets are required, which is not practical in a clinical setting. Several stochastic techniques were proposed to overcome this limitation [20]. Among them, the most widely used techniques are residual bootstrapping and wild bootstrapping [106]. These techniques rely on a single scan and estimate the probability distribution from the residuals that remain after fitting diffusion tensor to the data. In residual bootstrapping [24], the distribution is estimated by randomly assigning the residuals among gradient directions. Another possibility is to resample the data based on randomly flipping the sign of the residuals by assuming symmetry in the distribution. The latter approach is called wild bootstrapping [23]. A detailed comparison of bootstrap methods has been presented by Chung et al. [20]. Stochastic bootstrapping has been widely used for DTI [50, 60, 79, 100]. These techniques generate multiple DTI volumes through stochastic simulations for estimating the probability distribution, however, they are computationally very expensive.

Various stochastic algorithms were introduced to incorporate uncertainty in tractography by adding randomness in the tracking process. These techniques are called probabilistic tractography [11, 87, 95]. These algorithms estimate the probability density function of the fiber orientation at each voxel and determine the propagation direction by drawing random samples from the distribution. Probabilistic fiber tracking is preferable in most cases as it takes uncertainty into account and can estimate the confidence interval for each reconstructed pathways, however, they are computationally expensive [12, 26]. Koch et al. [58] propose to use Monte Carlo random walks for the estimation of the fiber connectivity. The fiber tracking algorithm proceeds through each randomly selected neighboring voxel depending on the angle between the voxel’s main eigenvector and its connecting angle with the neighboring voxels. A similar approach has been used in other studies to establish a connectivity map in a probabilistic sense [10, 13, 34, 80]. Monte Carlo methods have also been used to generate fiber tracks based on random particle movement [38]. The PDF obtained from the analytical methods can be used to perform tractography with these stochastic techniques [33, 48]. These studies are based on DTI, however, the concept is extendable to HARDI as well, but they are not used much in this context [64].

5 Uncertainty Visualization

So far, we have discussed the sources of uncertainty present in the visualization pipeline and the methods used for their quantification. Visualization provides a way to communicate data effectively and efficiently, however, uncertainty is often omitted in the process. Visualizing uncertainty information in DWI can help assess the accuracy of the acquisition and modeling, which ultimately guide the users in making critical decisions. However, the visualization of complex data in itself is not straightforward, adding uncertainty representation to it further complicates the process. Issues of visual cluttering and loss of anatomical context are some of the few complications when visualizing uncertainties.

Table 1 Summary of uncertainty representation and visualization strategies

In this section, we will survey the strategies used for the visualization of the uncertainties in DTI and also discuss some related techniques used in the HARDI model. We also summarize these strategies in Table 1. The modeling column refers to the uncertainty quantification techniques, such as stochastic, bootstrapping, or analytical methods. Domain indicates the application area of the study and ensemble column categorizes the method into the local or global level. The representation specifies the measure used for the aggregations of the ensemble, and finally, the visualization column indicates the technique used to display the uncertainties. The visualization of uncertainty in DTI can roughly be divided into two categories.

• 1. Local uncertainty visualization 

• 2. Global uncertainty visualization 

Fig. 4

Glyphs with uncertainty encoding

5.1 Local Uncertainty Visualization

Local representations of the uncertainty depict variation per voxel inside the vector or tensor fields. Glyphs are typically used to depict the voxel-wise information of the data. Several glyph-based techniques have been proposed to visualize the inherent local uncertainty in DTI. Jones et al. [50] proposed a method to represent the confidence interval of the main fiber direction by rendering an uncertainty cone, as shown in Fig. 4a. Basser et al. [4] used a similar technique to represent the main eigenvector and their associated uncertainties. This visualization approach allows the representation of the main diffusion direction and the confidence interval concurrently, also described in Table 1. Schultz et al. [90] demonstrate a new glyph design, called HiFiVE, that provides a more detailed impression of the uncertainty. It represents the variation corresponding to the main eigenvector by rendering a double cone (blue color) and the density estimation of the uncertainty around it (represented as a gray surface), as shown in Fig. 4b.

Another way to represent the uncertainty in multivariate data is to estimate its covariance. It does not only express the variance in each coefficient but also indicates their linear dependencies. Since the diffusion tensor is a second-order tensor, its covariance is represented by a fourth-order tensor, however, the visualization of the fourth-order tensor is rather difficult in this context. Basser et al. [7] presented a novel technique for the spectral decomposition of the fourth-order covariance tensor and introduced the concept of tensorial normal distribution. They proposed a glyph representation, called radial glyphs , which depicts the overall variance and a composite glyph for representing the eigentensor of the fourth-order covariance. They visualized the expected mean tensor and its standard deviation as three isosurfaces. Abbasloo et al. [2] highlight that the radial glyph does not convey the correlation with the mean tensor and also suffers from high visual complexity in the tensor field. They proposed a more intuitive approach for the visualization of the covariance by using multiple levels of detail. Unlike Basser et al., Abbasloo et al. visualize the confidence interval at each eigenmode separately by glyph overlays and used animation to visualize the differences in each mode. Gerrits et al. [35] pointed out the shortcoming in both of these visualization techniques and proposed a generic approach that incorporates all the coefficients of the mean tensor and covariance in a single glyph.

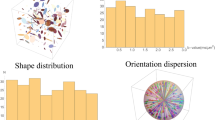
Various studies have been published concerning the representation of the tensor ensemble directly. Jones et al. [52] visualize the ensemble data simply by overlaying several glyphs. Although the superposition depicts the overall picture of the data, it adds visual clutter and occlusion during display. To remedy this, Zhang et al. [111] used transparency to minimize the occlusion. Abbasloo et al. [2] tried to minimize this problem by rendering the superimposed glyphs in complementary colors. Zhang et al. [110] proposed an approach to decompose the tensor data into three properties (i.e., scale, shape, and orientation), representing the structure of the underlying fibers, and measure the variation per property. A glyph based representation has been presented in this study to visualize the ensemble effectively. The variation in the ensemble is represented by Halo and texture over the surface as shown in Fig. 4c.

The orientation distribution function (ODF), associated with HARDI, specifies the overall amount of diffusion in a given direction. Unlike the diffusion tensor model, ODFs can have multiple maxima, and therefore are capable of modeling complex fibrous structure more accurately than DTI. However, this technique is computationally expensive. The representation of the ODF itself is a challenging task and adding uncertainty information only increases the complexity. Jiao et al. [49] proposed a technique to visualize uncertainty over polar ODF glyphs by using a volume rendering technique. They introduced shape inclusion probability (SIP) function to represent the orientation uncertainty of the tensor. Tournier et al. [96] presented a method to visualize uncertainties associated with ODFs by using semitransparent glyphs. They represent the mean ODF by the opaque surface and the mean + standard deviation by the transparent surface, as shown in Fig. 4d.

The visualization of uncertainty in a diffusion tensor is similar to the uncertainty representation in a vector field where orientation is considered important. Several glyph-based techniques exist in this scope. Wittenbrink et al. [108] presented a glyphs based representation of the uncertainty for atmospheric and oceanographic data. Likewise, Hlawatsch [43] and Lodha et al. [65] visualize the local uncertainty in a fluid flow field using glyphs. Zuk et al. [115] proposed a glyph design to provide uncertainty information in a bidirectional vector field. These techniques rely on the representation of the vector direction and magnitude with encoded uncertainties to depict the local uncertainty present in the field.

Fig. 5

Global uncertainty visualization strategies

5.2 Global Uncertainty Visualization

In contrast to the local strategies, global uncertainty visualization in DTI aims at providing information on how accurate fiber tract information is throughout the complete tensor field, and how the inherent uncertainties accumulate during the tracking process. In DWI independently of DTI or HARDI models being used, probabilistic tractography  is often used to incorporate these uncertainties. The most widely used approach to visualize fibers obtained through probabilistic tractography  is to superimpose the resulting fibers in a so-called spaghetti plot  [13, 22, 51], see Fig. 5a. This visualization technique, however, does not depict a clear view of the region-wise fiber connections and its uncertainty and suffers from strong cluttering. Color coding the fiber tracts according to their seed points [22] does not suffice to minimize the complexity of the visualization. Schober et al. [88] and Hauberg et al. [40] used wobbly spaghetti plot that emphasize the fact that the individual resulting paths cannot be considered as real fibers in the brain which is a common misinterpretation in spaghetti plot.  Instead, they are uncertain estimates of fibers.

To overcome the complexity and clutter caused by the multiple superimposed tracts, Enders et al. [29] presented a technique to group the fibers related to a certain nerve tract and generate a surface that wraps the resulting fibers. Similarly, Mehrof et al. [68] and Chen et al. [19] presented a method to cluster the fiber with a proximity-based algorithm and generate hulls encompassing the fiber bundles, as shown in Fig. 5b. The anatomical grouping helps the user to understand the underlying fibrous structure. Outside of DTI, Frest et al. [30] used a similar technique to visualize uncertainty in flow field ensembles. They performed principal component analysis to cluster the streamlines in a low dimensional space and determine the mean and confidence interval in an ensemble. These representations are visualized with a line enclosed by a transparent surface. The geometrical hulls and enclosed surfaces reduce clutter, however, they cannot resolve complex cluster shapes. To alleviate these problems, Illustrative techniques have been proposed to represent the confidence interval of the fiber bundle by creating silhouette, outline, and contours [15, 76], as shown in Fig. 5c.

To improve the understanding of ensembles of curves, it has been proposed to visualize the statistical information such as mean or confidence intervals rather than the direct ensemble visualization as spaghetti plot. Table 1 indicates the various representations used by the studies. These representations, e.g, mean and confidence interval, are the summarization of the raw samples. Unlike scalar values, the statistical measures are not well defined for curves, and therefore, several approaches have been proposed for the estimation of these terms. Brecheisen et al. [15] proposed to compute median and confidence intervals based on pre-selected distance measures between curves. In the field of fluid dynamics, a band-depth concept [66] has been introduced to analyze curve ensembles in two-dimensions [105] and three-dimensions [69]. This concept provides a way to determine centrality within the present curves and estimate the variations. Sanyal et al. [86] visualize the uncertainty in the wind trajectories by creating a ribbon along the ensemble mean. The width of a ribbon represents the variability at each point.

A widely used approach for the visualization of the global uncertainty is to represent and visualize measures derived from the probabilistic tractography. Voxel-wise fiber density computes the probability that a fiber tract traverses a voxel for a given seed region [17]. Voxel-wise fiber density [28, 38] helps to infer the anatomical connections. Another measure is the connectivity probability, which represents the probability of a fiber tract crossing a given voxel while connecting two fixed anatomical regions [91]. Von Kapri et al. [55] and McGraw et al. [67] used volume rendering for the visualization of density maps, as shown in Fig. 5d. The global visualization of the fiber tracts does not provide the local tensor information. To visualize the local uncertainty along with the probabilistic tracts, a stream tube technique has been proposed [53, 107], which maps the local uncertainty measure onto the cross-section of the tube.

A common problem with the three-dimensional approaches is that the geometrical representation often occludes the underlying information, hampering its interpretation. Various slice-based methods have been proposed for the visualization of probabilistic fibers [58, 80]. These techniques have been used in neuroscience as they provide a way to directly visualize the anatomical information, making it easy to interpret anatomical context. Goldou et al. [36, 37] presented a novel slice based approach for visualizing the probability by rendering fiber stipples. The number of stipples, present at a particular region depicts the fiber density. Hlawitschka et al. [44] proposes to use poisson-disk sampling for the generation of the fiber stipples.

Table 1 summarizes the survey indicating the domain, representation, and visualization strategies used to display the uncertainty. The table covers the approaches used for local and global uncertainty visualization in both the DWI and non-DWI domain.

6 Conclusion

Diffusion-weighted imaging relies on complex stages of signal acquisition, mathematical modeling, model assumptions, and hence, is exposed to many sources of uncertainty. Excluding this uncertainty from the visualization does not only affect the result but also cripples the user to make an effective decision. However, the efficient visualization of the uncertainty in DWI is nontrivial, as the data itself has high visual complexity and adding uncertainty to it only adds further complexity. In this chapter, we explored uncertainty in the various stages of the DTI visualization pipeline. Several of the problems and solutions discussed throughout this chapter are also valid for other models beyond Diffusion tensor, such as HARDI models. Even though we have not covered the technical background, where applicable, we have discussed the applicability of the strategies beyond DTI. Further, we have reviewed applicable uncertainty visualization techniques beyond the DWI domain.

DWI is still a growing field, considering the recent advancements and the frequent development of new techniques, this survey should not be considered complete, it rather should be enhanced in the future. Studies on uncertainty visualization so far are mostly focused on the research aspect, however, no uncertainty visualization solution exist to specifically support clinical tractography. Visual analytics, an emerging field in visualization, can be helpful in enabling detailed analysis of uncertainty present in DWI data, building on the top of the studies present in this survey. Most of the presented studies deal with uncertainty on the noise and modeling level, dealing with other sources of uncertainty and visualizing them as a whole part of the exploration is another open research direction.

We focus on the visualization pipeline and techniques mostly related to DTI, a study including other modeling techniques would be beneficial. In summary, even though the uncertainty visualization in DWI has evolved considerably in the last few years, we believe, a lot of work still needs to be done for the effective visualization and exploration of DWI data.