Abstract
The objective of this paper is to establish a new relationship between the Veronese sequence of analytic solutions of the Euclidean  sigma model in two dimensions and the orthogonal Krawtchouk polynomials. We show that such solutions of the
sigma model in two dimensions and the orthogonal Krawtchouk polynomials. We show that such solutions of the  model, defined on the Riemann sphere and having a finite action, can be explicitly parametrized in terms of these polynomials. We apply the obtained results to the analysis of surfaces associated with
model, defined on the Riemann sphere and having a finite action, can be explicitly parametrized in terms of these polynomials. We apply the obtained results to the analysis of surfaces associated with  sigma models, defined using the generalized Weierstrass formula for immersion. We show that these surfaces are spheres immersed in the 𝔰𝔲(2s + 1) Lie algebra, and express several other geometrical characteristics in terms of the Krawtchouk polynomials. Finally, a new connection between the 𝔰𝔲(2) spin-s representation and the
sigma models, defined using the generalized Weierstrass formula for immersion. We show that these surfaces are spheres immersed in the 𝔰𝔲(2s + 1) Lie algebra, and express several other geometrical characteristics in terms of the Krawtchouk polynomials. Finally, a new connection between the 𝔰𝔲(2) spin-s representation and the  model is explored in detail. It is shown that for any given holomorphic vector function in
model is explored in detail. It is shown that for any given holomorphic vector function in  written as a Veronese sequence, it is possible to derive a sequence of analytic solutions of the
written as a Veronese sequence, it is possible to derive a sequence of analytic solutions of the  model through algebraic recurrence relations which turn out to be simpler than the analytic relations known in the literature.
model through algebraic recurrence relations which turn out to be simpler than the analytic relations known in the literature.
In honour of Decio Levi (University of Roma Tre)
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
W.J. Zakrzewski, Low Dimensional Sigma Models (Hilger, Bristol, 1989)
P.P. Goldstein, A.M. Grundland, Invariant recurrence relations for
 models. J. Phys. A Math. Theor. 43(265206), 1–18 (2010)
models. J. Phys. A Math. Theor. 43(265206), 1–18 (2010)P.P. Goldstein, A.M. Grundland, S. Post, Soliton surfaces associated with sigma models: differential and algebraic aspects. J. Phys. A Math. Theor. 45(395208), 1–19 (2012)
P.P. Goldstein, A.M. Grundland, On a stack of surfaces obtained from the
 sigma model. J. Phys. A Math. Theor. 51(095201), 1–13 (2018)
sigma model. J. Phys. A Math. Theor. 51(095201), 1–13 (2018)J. Bolton, G.R. Jensen, M. Rigoli, L.M. Woodward, On conformal minimal immersion of S 2 into
 . Math. Ann. 279, 599–620 (1988)
. Math. Ann. 279, 599–620 (1988)N. Crampé, A.M. Grundland,
 sigma models described through hypergeometric orthogonal polynomials. Ann. Henri Poincaré 20(10), 1–23 (2019)
sigma models described through hypergeometric orthogonal polynomials. Ann. Henri Poincaré 20(10), 1–23 (2019)P.P. Goldstein, A.M. Grundland, Analysis of
 sigma models via soliton surfaces, in A Volume in Honour of V. Hussin, ed. by S. Kuru, et al. CRM series in Math. Phys. (Springer, New York, 2019), pp. 341–358
sigma models via soliton surfaces, in A Volume in Honour of V. Hussin, ed. by S. Kuru, et al. CRM series in Math. Phys. (Springer, New York, 2019), pp. 341–358E. Merzbacher, Quantum Mechanics (Wiley, New York, 1998)
T. Koornwinder, Krawtchouk polynomials, a unification of two different group theoretic interpretation. SIAM J. Math. Anal. 13, 10111023 (1982)
Y.I. Granovski, A. Zhedanov, Orthogonal polynomials in the Lie algebras. Sov. Phys. J. 29, 387393 (1986)
A.M. Grundland, I. Yurdusen, On analytic descriptions of two-dimensional surfaces associated with the
 model. J. Phys. A Math. Theor. 42(172001), 1–5 (2009)
model. J. Phys. A Math. Theor. 42(172001), 1–5 (2009)
Acknowledgements
This research was supported by the NSERC operating grant of one of the authors (A.M.G.). N.C. is indebted to the Centre de Recherches Mathématiques (CRM), Université de Montréal for the opportunity to hold a CRM-Simons professorship.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Crampé, N., Grundland, A.M. (2021). The Veronese Sequence of Analytic Solutions of the  Sigma Model Equations Described via Krawtchouk Polynomials.
In: Paranjape, M.B., MacKenzie, R., Thomova, Z., Winternitz, P., Witczak-Krempa, W. (eds) Quantum Theory and Symmetries. CRM Series in Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-030-55777-5_5
Sigma Model Equations Described via Krawtchouk Polynomials.
In: Paranjape, M.B., MacKenzie, R., Thomova, Z., Winternitz, P., Witczak-Krempa, W. (eds) Quantum Theory and Symmetries. CRM Series in Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-030-55777-5_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-55777-5_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-55776-8
Online ISBN: 978-3-030-55777-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)




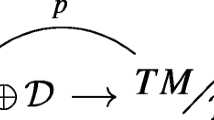
 models. J. Phys. A Math. Theor. 43(265206), 1–18 (2010)
models. J. Phys. A Math. Theor. 43(265206), 1–18 (2010) sigma model. J. Phys. A Math. Theor. 51(095201), 1–13 (2018)
sigma model. J. Phys. A Math. Theor. 51(095201), 1–13 (2018) . Math. Ann. 279, 599–620 (1988)
. Math. Ann. 279, 599–620 (1988) sigma models described through hypergeometric orthogonal polynomials. Ann. Henri Poincaré 20(10), 1–23 (2019)
sigma models described through hypergeometric orthogonal polynomials. Ann. Henri Poincaré 20(10), 1–23 (2019) sigma models via soliton surfaces, in A Volume in Honour of V. Hussin, ed. by S. Kuru, et al. CRM series in Math. Phys. (Springer, New York, 2019), pp. 341–358
sigma models via soliton surfaces, in A Volume in Honour of V. Hussin, ed. by S. Kuru, et al. CRM series in Math. Phys. (Springer, New York, 2019), pp. 341–358 model. J. Phys. A Math. Theor. 42(172001), 1–5 (2009)
model. J. Phys. A Math. Theor. 42(172001), 1–5 (2009)