Abstract
Monopole operators are topological disorder operators in 2 + 1 dimensional compact gauge field theories appearing notably in quantum magnets with fractionalized excitations. For example, their proliferation in a spin-1/2 kagome Heisenberg antiferromagnet triggers a quantum phase transition from a Dirac spin liquid phase to an antiferromagnet. The quantum critical point (QCP) for this transition is described by a conformal field theory: Compact quantum electrodynamics (QED3) with a fermionic self-interaction, a type of QED3-Gross–Neveu model. We obtain the scaling dimensions of monopole operators at the QCP using a state-operator correspondence and a large-N f expansion, where 2N f is the number of fermion flavors. We characterize the hierarchy of monopole operators at this \( \operatorname {\mathrm {SU}}(2) \times \operatorname {\mathrm {SU}}(N_f)\) symmetric QCP.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In vector notation using spherical coordinates on Euclidean spacetime
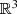 , it would be written as \(A^q_\mu = q(1-\cos \theta )/(r \sin \theta ) \delta _\mu ^{\phi }\).
, it would be written as \(A^q_\mu = q(1-\cos \theta )/(r \sin \theta ) \delta _\mu ^{\phi }\). - 2.
Divergences in the gap equation are treated with a Zeta regularization.
- 3.
Divergences in the scaling dimension and the related gap equation are treated with a zeta function regularization. It is important to keep the same regularization scheme that was used to determine the critical effective action in the non-compact theory (7).
- 4.
Note that contrary to other transitions described in Sect. 1, here the symmetric mass generates a Chern–Simons term which prevents monopole proliferation.
References
A.M. Polyakov, Compact gauge fields and the infrared catastrophe. Phys. Lett. B 59, 82–84 (1975)
A.M. Polyakov, Quark confinement and topology of gauge theories. Nuclear Phys. B 120, 429–458 (1977)
V. Borokhov, A. Kapustin, X. Wu, Topological disorder operators in three-dimensional conformal field theory. J. High Energy Phys. 2002, 049 (2002)
M.A. Metlitski, M. Hermele, T. Senthil, M.P.A. Fisher, Monopoles in
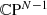 model via the state-operator correspondence. Phys. Rev. B 78, 214418 (2008)
model via the state-operator correspondence. Phys. Rev. B 78, 214418 (2008)Y. Ran, M. Hermele, P.A. Lee, X.-G. Wen, Projected-wave-function study of the spin-1∕2 heisenberg model on the kagome lattice. Phys. Rev. Lett. 98, 117205 (2007)
P. Sindzingre, C. Lhuillier, Low-energy excitations of the kagome antiferromagnet and the spin-gap issue. Europhys. Lett. 88, 27009 (2009)
Y. Iqbal, F. Becca, S. Sorella, D. Poilblanc, Gapless spin-liquid phase in the kagome spin-1∕2 Heisenberg antiferromagnet. Phys. Rev. B 87, 060405 (2013)
Y. Iqbal, D. Poilblanc, F. Becca, Spin-1∕2 Heisenberg J 1−J 2 antiferromagnet on the kagome lattice. Phys. Rev. B 91, 020402 (2015)
Y.-C. He, M.P. Zaletel, M. Oshikawa, F. Pollmann, Signatures of Dirac Cones in a DMRG study of the Kagome Heisenberg model. Phys. Rev. X 7, 031020 (2017)
W. Zhu, X. Chen, Y.-C. He, W. Witczak-Krempa, Entanglement signatures of emergent Dirac fermions: Kagome spin liquid and quantum criticality. Sci. Adv. 4(11), eaat5535 (2018)
S.S. Pufu, Anomalous dimensions of monopole operators in three-dimensional quantum electrodynamics. Phys. Rev. D 89, 065016 (2014)
X.Y. Xu, Y. Qi, L. Zhang, F.F. Assaad, C. Xu, Z.Y. Meng, Monte Carlo study of lattice compact quantum electrodynamics with fermionic matter: the parent state of quantum phases. Phys. Rev. X 9, 021022 (2019)
X.-Y. Song, C. Wang, A. Vishwanath, Y.-C. He, Unifying description of competing orders in two-dimensional quantum magnets. Nat. Commun. 10(1), 4254 (2019)
M.F. Atiyah, I.M. Singer, The index of elliptic operators on compact manifolds. Bull. Amer. Math. Soc. 69(3), 422–433 (1963)
M. Hermele, Y. Ran, P.A. Lee, X.-G. Wen, Properties of an algebraic spin liquid on the kagome lattice. Phys. Rev. B 77, 224413 (2008)
Y.-M. Lu, G.Y. Cho, A. Vishwanath, Unification of bosonic and fermionic theories of spin liquids on the kagome lattice. Phys. Rev. B 96, 205150 (2017)
T.T. Wu, C.N. Yang, Dirac monopole without strings: monopole harmonics. Nuclear Phys. B 107(3), 365–380 (1976)
É. Dupuis, M.B. Paranjape, W. Witczak-Krempa, Transition from a Dirac spin liquid to an antiferromagnet: monopoles in a QED3-Gross-Neveu theory. Phys. Rev. B 100, 094443 (2019)
S.M. Chester, L.V. Iliesiu, M. Mezei, S.S. Pufu, Monopole operators in U(1) Chern-Simons-matter theories. J. High Energy Phys. 2018, 157 (2018)
C. Wang, A. Nahum, M.A. Metlitski, C. Xu, T. Senthil, Deconfined quantum critical points: symmetries and dualities. Phys. Rev. X 7, 031051 (2017)
C. Itzykson, M. Nauenberg, Unitary groups: representations and decompositions. Rev. Mod. Phys. 38, 95 (1966)
Acknowledgements
We thank Tarun Grover, Joseph Maciejko, David Poland, Zi Yang Meng and Chong Wang for the interesting discussions and useful observations on our work during the symposium. We also thank Jaume Gomis and Sergueï Tchoumakov for useful discussions. É.D. was funded by an Alexander Graham Bell CGS from NSERC. M.B.P. was funded by a Discovery Grant from NSERC. W.W.-K. was funded by a Discovery Grant from NSERC, a Canada Research Chair, a grant from the Fondation Courtois, and a “Établissement de nouveaux chercheurs et de nouvelles chercheuses universitaires” grant from FRQNT.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Dupuis, É., Paranjape, M.B., Witczak-Krempa, W. (2021). Monopole Operators and Their Symmetries in QED3-Gross–Neveu Models. In: Paranjape, M.B., MacKenzie, R., Thomova, Z., Winternitz, P., Witczak-Krempa, W. (eds) Quantum Theory and Symmetries. CRM Series in Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-030-55777-5_31
Download citation
DOI: https://doi.org/10.1007/978-3-030-55777-5_31
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-55776-8
Online ISBN: 978-3-030-55777-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


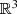 , it would be written as
, it would be written as 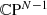 model via the state-operator correspondence. Phys. Rev. B 78, 214418 (2008)
model via the state-operator correspondence. Phys. Rev. B 78, 214418 (2008)