Abstract
We consider a one-dimensional Anderson model where the potential decays in average like n −α, α > 0. This simple model is known to display a rich phase diagram with different kinds of spectrum arising as the decay rate α varies.
We review an article of Kiselev, Last and Simon where the authors show a.c. spectrum in the super-critical case \(\alpha >\frac 12\), a transition from singular continuous to pure point spectrum in the critical case \(\alpha =\frac 12\), and dense pure point spectrum in the sub-critical case \(\alpha <\frac 12\). We present complete proofs of the cases \(\alpha \ge \frac 12\) and simplify some arguments along the way. We complement the above result by discussing the dynamical aspects of the model. We give a simple argument showing that, despite of the spectral transition, transport occurs for all energies for \(\alpha =\frac 12\). Finally, we discuss a theorem of Simon on dynamical localization in the sub-critical region \(\alpha <\frac 12\). This implies, in particular, that the spectrum is pure point in this regime.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
M. Aizenman, S. Molchanov, Localization at large disorder and at extreme energies: an elementary derivations, Comm. Math. Phy. 157, 245–278 (1993)
M. Aizenman, S. Warzel, Random Operators: Disordered effects on Quantum Spectra and Dynamics. Graduate Studies in Mathematics, vol 168 (American Mathematical Society, Providence, 2016)
M. Aizenman, R. Sims, S. Warzel, Stability of the absolutely continuous spectrum of random Schrödinger operators on tree graphs. Probab. Theory Related Fields 136, 363–394 (2006)
K. Azuma, Weighted sums of certain dependent random variables. Tôhoku Math. J. 19(3), 357–367 (1967)
J. Bourgain, On random Schrödinger operators on
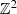 . Discret Contin. Dyn. Syst. 8, 1–15 (2002)
. Discret Contin. Dyn. Syst. 8, 1–15 (2002)J. Bourgain, Random lattice schrödinger operators with decaying potential: some higher dimensional phenomena, in Geometric Aspects of Functional Analysis. Lectures Notes in Mathematics, vol. 1807 (Springer, Berlin, 2003), pp. 70–98
O. Bourget, G. Moreno, A. Taarabt, Dynamical localization for the one-dimensional continuum Anderson model in a decaying random potential. Ann. Henri Poincaré, 21(8), (2020)
O. Bourget, G. Moreno, A. Taarabt, One-dimensional discrete dirac operators in a decaying random potential I: Spectrum and dynamics. Math. Phys. Anal. Geom. 23(20), (2020).
R. Carmona, Exponential localization in one dimensional disordered systems. Duke Math. J. 49, 191–213 (1982)
R. Carmona, A. Klein, F. Martinelli, Anderson localization for bernoulli and other singular potentials. Commun. Math. Phys. 108, 41–66 (1987)
H.L. Cycon, R.G. Froese, W. Kirsch, B. Simon, Schrödinger Operators with Applications to Quantum Mechanics and Global Geometry. Texts and Monographs in Physics, Springer Study Edition (Springer, Berlin, 1987)
D. Damanik, A. Gorodetski, An extension of the Kunz-Souillard approach to localization in one dimension and applications to almost-periodic Schrödinger operators. Adv. Math. 297, 149–173 (2016)
D. Damanik, G. Stolz, A continuum version of the Kunz–Souillard approach to localization in one dimension. J. Für die reine und Angewandte Math. (Crelles J.) 660, 99–130 (2011)
R. Del Rio, S. Jitomirskaya, Y. Last, B. Simon, What is localization? Phys. Rev. Lett. 75, 117–119 (1995)
R. Del Rio, S. Jitomirskaya, Y. Last, B. Simon, Operators with singular continuous spectrum IV: Hausdorff dimensions, rank one perturbations and localization. J. Anal. Math. 69, 153–200 (1996)
F. Delyon, Appearance of a purely singular continuous spectrum in a class of random Schrödinger operators. J. Statist. Phys. 40, 621–630 (1985)
F. Delyon, B. Simon, B. Souillard, From power pure point to continuous spectrum in disordered systems. Ann. Henri Poincaré, 42(6), 283–309 (1985)
R. Durrett, Probability: Theory and Examples. Cambridge Series in Statistical and Probabilistic Mathematics, 4th edn. (Cambridge University Press, New York, 2010)
A. Figotin, F. Germinet, A. Klein, P. Müller, Persistence of Anderson localization in Schrödinger operators with decaying random potentials. Ark. Mat. 45. 15–30 (2007)
R. Froese, D. Hasler, W. Spitzer, Absolutely continuous spectrum for the Anderson model on a tree: a geometric proof of Klein’s theorem. Comm. Math. Phys. 269, 239–257 (2007)
L. Ge, X. Zhao, Exponential dynamical localization in expectation foe one dimensional Anderson model. J. Spect. Theory
F. Germinet, A. Klein, Bootstrap multiscale analysis and localization in random media. Commun. Math. Phys. 222, 415–448 (2001)
F. Germinet, A. Taarabt, Spectral properties of dynamical localization for Schrödinger operators. Rev. Math. Phys. 25(9), 1350016 (2013)
F. Germinet, A. Kiselev, S. Tcheremchantsev, Transfer matrices and transport for Schrödinger operators. Ann. Inst. Fourier 54, 787–830 (2004)
F. Germinet, A. Klein, J. Schenker, Dynamical delocalization in random Landau Hamiltonians. Ann. Math. 166, 215–244 (2007)
I. Goldsheid, S. Molchanov, L. Pastur, A pure point spectrum of the stochastic one-dimensional Schrödinger equation. Funct. Anal. Appl. 11, 1–10 (1977)
V. Jaks̆ić, Y. Last, Spectral structure of Anderson type Hamiltonians. Inven. Math. 141, 561–577 (2000)
S. Jitomirskaya, X. Zhu, Large deviations of the Lyapunov exponent and localization for the 1D Anderson model. Comm. Phys. Math. 370, 311–324 (2019)
A. Klein, Extended states in the anderson model on the bethe lattice. Adv. Math. 133, 163–184 (1998)
W. Kirsch, M. Krishna, J. Obermeit, Anderson model with decaying randomness: mobility edge. Math. Z. 235, 421–433 (2000)
A. Kisselev, Y. Last, B. Simon, Modified Prüfer and EFGP transforms and the spectral analysis of one-dimensional schrödinger operators. Comm. Math. Phys. 194, 1–45 (1998)
S. Kotani, N. Ushiroya, One-dimensional Schrödinger operators with random decaying potentials. Comm. Math. Phys. 115, 247–266 (1988)
M. Krishna, Anderson model with decaying randomness: existence of extended states. Proc. Indian Acad. Sci. (Math. Sci.) 100, 285–294 (1990)
H. Kunz, B. Souillard, Sur le spectre des opérateurs aux différences finies aléatoires. Comm. Math. Phys. 78, 201–246 (1980)
Y. Last, B. Simon, Eigenfunctions, transfer matrices, and absolutely continuous spectrum of one-dimensional Schrödinger operators. Invent. Math. 135, 329–367 (1999)
B. Simon, Some Jacobi matrices with decaying potential and dense point spectrum. Comm. Math. Phys. 87, 253–258 (1982)
B. Simon, Spectral Analysis of Rank One Perturbations and Applications. CRM Lectures Notes, vol. 8 (American Mathematical Society, Providence, 1995), pp. 109–149
Acknowledgements
O. Bourget is partially supported by Fondecyt grant 1161732. G. Moreno Flores is partially supported by Fondecyt grant 1171257, Núcleo Milenio ‘Modelos Estocásticos de Sistemas Complejos y Desordenados’ and MATH Amsud ‘Random Structures and Processes in Statistical Mechanics’. A. Taarabt is partially supported by Fondecyt grant 11190084.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix A: Some Technical Lemmas
Appendix A: Some Technical Lemmas
1.1 A.1 Two Results on Unimodular Matrices
We say that a matrix is unimodular if it has determinant equal to 1. The following lemma is used to compare the asymptotics of the transfer matrix with those of the sequence (R n)n.
Lemma A.1
Let A be an unimodular matrix and let \(\hat \theta = (\cos \theta ,\, \sin \theta )\). Then, for all pair of angles \(|\theta _1-\theta _2|\leq \frac {\pi }{2}\),
Proof
First, there exists angles θ 0 and σ 0 such that \(A^* \hat \sigma _0 = \| A \| \hat \theta _0\). Then, for any angle θ,
This way, for any pair of angles, we obtain
To conclude, just note that for all |γ|≤ π∕2, the minimum of the function \(x\mapsto \max \{|\cos {}(x)|, \) \( |\cos {}(x+\gamma )|\}\) is attained at π∕2 − γ∕2 and is equal to \(|\cos {}(\pi /2-\gamma /2)|=|\sin {}(\gamma /2)|\). □
The following lemma is used to find eigenfunctions with the proper decay.
Lemma A.2
For a unimodular matrix with ∥A∥ > 1, define 𝜗 = 𝜗(A) as the unique angle \(\vartheta \in (-\frac {\pi }{2},\frac {\pi }{2}]\) such that \(\| A \hat \vartheta \| = \| A \|{ }^{-1}\). We also define r(A) = ∥A(1, 0)T∥∕∥A(0, 1)T∥.
Let (A n)n be a sequence of unimodular matrices with ∥A n∥ > 1 and write 𝜗 n = 𝜗(A ) and r n = r(A n). Assume that
-
(i)
limn→∞∥A n∥ = ∞,
-
(ii)
\(\displaystyle \lim _{n\to \infty } \frac {\| A_{n+1}A_n^{-1}\|}{\| A_n \| \, \| A_{n+1}\|}=0\).
Then,
-
1.
(𝜗 n)n has a limit 𝜗 ∞∈ (−π∕2, π∕2) if and only if (r n)n has a limit r ∞∈ [0, ∞). If 𝜗 n →±π∕2, then r n →∞ but, if r n →∞, we can only conclude that |𝜗 n|→ π∕2.
-
2.
Suppose (𝜗 n)n has a limit \(\vartheta _{\infty }\neq 0,\, \frac {\pi }{2}\). Then,
$$\displaystyle \begin{aligned} \begin{array}{rcl}{} \lim_{n\to\infty} \frac{\log \| A_n \hat\vartheta_{\infty}\|}{\log \| A_n \|} = -1 \quad \mathit{\text{if and only if}} \quad \limsup_n \frac{\log |r_n - r_{\infty}|}{\log \| A_n \|} \leq -2.\qquad \quad \end{array} \end{aligned} $$(A.2)
Proof
Recall 𝜗 n denotes the unique angle in (−π∕2, π∕2] such that \(\| A_n \hat \vartheta _n\| = \| A_n \|{ }^{-1}\). Let \(\vartheta _n^{\prime } \in (\vartheta _n-\pi /2, \vartheta _n+\pi /2]\) be the unique angle such that \(\| A_n \hat \vartheta _n^{\prime }\| = \| A_n \|\) and let \(\vartheta _n^\perp \) be either 𝜗 n − π∕2 or 𝜗 n + π∕2 and such that \(\vartheta _n^{\prime }\) lies between 𝜗 n and \(\vartheta _n^{\perp }\).
Let \(\displaystyle v_0 = \begin {pmatrix} 1 \\0 \end {pmatrix}\), \(\displaystyle w_0 = \begin {pmatrix} 0\\1 \end {pmatrix}\), v n = A nv 0 and w n = A nw 0. Then,
and applying A n on both sides,
as ∥A n∥→∞. Hence,
This shows that, if 𝜗 n → 𝜗 ∞, then \(r_n\to |\tan \vartheta _\infty |\in [0,\infty ]\). On the other hand, if r n → r ∞∈ [0, ∞], then \(|\vartheta _n| \to \arctan (\rho _{\infty })\), with the convention \(\arctan (\infty )=\pi /2\). If ρ ∞ = ∞, we only get that |𝜗 n|→ π∕2. Otherwise, it is enough to prove that 𝜗 n − 𝜗 n−1 → 0 to show the convergence of 𝜗 n. For this, we use the decomposition
Applied to 𝜗 n+1, this yields
and
Hence,
In the last step, we used that the A n’s are unimodular to switch from \(\| A_n A_{n+1}^{-1}\|\) to \(\| A_{n+1}^{-1} A_n \|\). By condition (ii), it is enough to show that \(\|A_n\hat \vartheta _n^\perp \| \gtrsim \|A_n\|\). For this, decompose
for some coefficients such that α 2 + β 2 = 1. Note that, by construction, |α n| > |β n| and hence |α n|≥ 1∕2. Therefore,
This finishes the proof Part 1.
To prove Part 2, assume 𝜗 n → 𝜗 ∞∈ (0, π∕2) and apply (A.6) to 𝜗 = 𝜗 ∞ to obtain
Recalling that ∥A n∥→∞, 𝜗 n − 𝜗 ∞→ 0 and \(\|A_n \hat \vartheta _n^\perp \| \asymp \|A_n\|\),
Hence, the left condition in (A.2) is satisfied if and only if
But, disregarding multiplicative constants which will disappear in the limit,
□
We apply this with A n = T ω,n to prove Proposition 5.5. Define
and let \(R^{(i)}_n,\, \theta ^{(i)}_n,\, n\geq 1\), i = 1, 2 be the corresponding Prüfer radii and phases. We let \(r_n=R^{(1)}_n/R^{(2)}_n\) and 𝜗 n be as in Lemma A.2. Then it follows from (3.5) and some elementary trigonometry that
where \(\bar {\theta }^{(i)}_n = nk -\theta ^{(i)}_n\). On the other hand,
This, together with the convergence
gives
Remember the decomposition (5.10). We have to estimate the difference of the expansions for \(\log R^{(1)}_n\) and \(\log R^{(2)}_n\). By (A.19), \(|\sin {}(\bar \theta ^{(2)}_n-\bar \theta ^{(1)}_n)| \lesssim n^{-\beta +\epsilon }\), for any 𝜖 > 0. Hence, there exists random sequences  and
and  such that \(\bar \theta ^{(1)}_n-\bar \theta ^{(2)}_n=m_n\pi + \Delta _n\) and \(|\Delta _n|\lesssim n^{-\beta +\epsilon }\). Therefore,
such that \(\bar \theta ^{(1)}_n-\bar \theta ^{(2)}_n=m_n\pi + \Delta _n\) and \(|\Delta _n|\lesssim n^{-\beta +\epsilon }\). Therefore,
This shows that
by a similar argument. Hence,
where the first sum is a convergent martingale by Lemma 5.3 with \(\gamma =\frac 12 + 2\beta -\epsilon \) and the second one is absolutely convergent as A j = O(j −1−2β+𝜖). This shows that r n → r ∞∈ (0, ∞) almost surely which implies that 𝜗 n has a limit 𝜗 ∞≠ 0, π∕2 by the first part of Lemma A.2.
The equivalence (A.2) in our context corresponds to
Let us denote by \(\log r_n = M_n + S_n\) the decomposition (A.21) and \(\log r_{\infty }=M_{\infty }+S_{\infty }\) where M ∞ and S ∞ are the almost sure limits of M n and S n respectively. Then,
by the last statement of Lemma 5.3 with \(\gamma = \frac 12 + 2\beta - \epsilon \). This finishes the proof of Proposition 5.5.
1.2 A.2 Analysis of the Prüfer Phases
We begin with a simple observation: from (3.6),
for n large enough. Hence, for n large enough, |θ n+1 − θ n| < π∕2 and
This can be written in the equivalent form
for some c 0 > 0, which will be more suitable for our purposes.
The next lemma provides the control of the Prüfer phases needed to complete the proof of Proposition 5.2.
Lemma A.3
Let \(0<\alpha \leq \frac 12\). Let E ∈ (−2, 2) corresponding to values of k different from \(\frac {\pi }{4}\), \(\frac {\pi }{2}\) and \(\frac {3\pi }{4}\). Then,

Proof
The key to the proof is [31, Lemma 8.5] which states: suppose that  is not in
is not in  . Then, there exists a sequence of integers q
l →∞ such that
. Then, there exists a sequence of integers q
l →∞ such that
for all  .
.
We will treat the term with \(\cos {}(4\bar {\theta }_j)\) as the other one is similar. We will take y = 4k above. Let n be large enough so that it can be written as n = n 0 + Kq l with \(n_0\ge q_l^2\) and \(4c_0 n_0^{-\alpha }\le q_l^{-2} \) (where c 0 is the constant from (A.27)). Then,
By (A.29),
Now, by (A.27),

Thus,
for some finite c 1 > 0. To estimate B, we use that
for some finite c 2 > 0 which shows that
where we used \(q_l^2 n_0^{-1}\leq 1\). This last sum can be estimated as above. Summarizing,
for some finite c 3 > 0. This finishes the proof. □
Rights and permissions
Copyright information
© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Bourget, O., Flores, G.R.M., Taarabt, A. (2020). One-dimensional Discrete Anderson Model in a Decaying Random Potential: from A.C. Spectrum to Dynamical Localization. In: Miranda, P., Popoff, N., Raikov, G. (eds) Spectral Theory and Mathematical Physics. Latin American Mathematics Series(). Springer, Cham. https://doi.org/10.1007/978-3-030-55556-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-55556-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-55555-9
Online ISBN: 978-3-030-55556-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


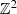 . Discret Contin. Dyn. Syst. 8, 1–15 (2002)
. Discret Contin. Dyn. Syst. 8, 1–15 (2002)