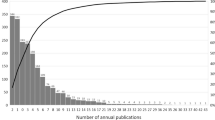
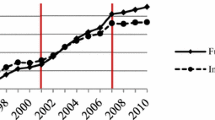
Abstract
This paper models scientific productivity and reward, as well as the emergence and dynamics of new scientific fields. The crucial features are the individual reward that depends in addition on own abilities and the collective knowledge of a field. The overall knowledge about a field leads to increasing, at low levels (i.e., at the beginning) and at high level to decreasing. This set up renders individual as well as collective decisions, planned or as a market outcome, non-trivial. We suggest, formulate (and partly solve) problems about individual and collective behavior of scientists and study the conditions that a field emerges.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
The field can correspond, for example, to the (first) letter in the JEL classifications in economics and similar in other sciences. A subfield is then identified by the following two numbers of the JEL-code. The only crucial point is that we assume that a subfield can be invented by a researcher (but rarely a larger area which we call field) and generate several publications by one or many persons.
- 2.
This is only used as a metaphor. Both, mining and research, are looking for useful elements that are mixed with things useless. The analogy is in growing skills to find a mine (or research subfield) and in lowering the probability to find something useful after some time of exploitation. Both processes can be described by similar mathematical models.
- 3.
He was treacherously committed to an asylum by his colleague where died 14 days later after being beaten by the guards.
- 4.
Scientists are among the most vain people as Carl Djerassi, the discoverer of the anti-baby pill observed. Richard Blair wrote under the pseudonym George Orwell, but the idea that Einstein had published his general theory of relativity under a pseudonym is absurd. Sir Isaac Newton is another example in his fight against Gotthold Ephraim Leibniz about priority over calculus.
- 5.
In physics, when we move to the height h above the sea level, the density of atmosphere declines exponentially. This is also an example of a deterministic outcome for the law of large numbers, due to very large number of particles. The similar deterministic equivalence of random outcome is assumed here in “research mining,” but it is less justifiable and is assumed for simplicity.
- 6.
Scientific reward is not directly linked to productivity due to the so-called Matthew effect (“For to everyone who has will more be given, and he will have abundance; but from him who has not, even what he has will be taken away,” Matthew 25:29). This point was first addressed by the sociologist Merton [19], in order to explain why eminent scientists get disproportionately credit for their contributions, while relatively unknowns get disproportionately little. Therefore, a person with many written, maybe partially unpublished, papers gets lower reward per written paper compared to a famous scientist, even after accounting for quality.
- 7.
G corresponds to both output and time. G can be calibrated as typical life cycle of a subfield, for example, 100 years. If the unit of time (t = 1) is, for example, 40 years then G = 2.5. If the maximal productivity in this subfield is G2/4, it can be measured by maximal intensity of total publications per unit of time (here 40 years). If G2/4 = 2.52/4 = 3.125 in this example, while in reality is 312 papers, then a unit of publication is 100 papers.
- 8.
For example, the authors of this paper have presumably missed the transition to experiments.
- 9.
Here X is the mass (quantity) of researchers. It is normalized in such a way that maximal productivity is for \(X=G/2\). Both can be calibrated. For example, we know that maximal productivity, \(G^{2}/4\), is for 10 researchers in subfield. Then \(X=G/2\) corresponds to 10 researchers. A researcher lives between t and \(t+1\), so that q is measured in the units of lifetime salary, and G can be defined correspondingly.
- 10.
With the first isocline coinciding with the stable path.
- 11.
This also often happens with interdisciplinary papers.
- 12.
And they also have low incentives to do that.
References
Diamond Jr, A. M. (2008). Economics of science. The New Palgrave Dictionary of Economics, 7, 328.
Lotka, A. (1926). The frequency distribution of scientific productivity. Journal of the Washington Academy of Sciences, 16(12), 317–323.
Merton, R. K. (1988). The Matthew effect in science, II: Cumulative advantage and the symbolism of intellectual property. isis, 79(4), 606–623.
Merton, R. K., Barber, E. (2004). The travels and adventures of serendipity: A study in sociological semantics and the sociology of science. Princeton: Princeton University Press.
Kuhn, T. (1962). The structure of scientific revolutions. University of Chicago Press.
Skiba, A. K. (1978). Optimal growth with a convex-concave production function. Econometrica, 46, 527–539.
Sethi, S. P. (1979). Optimal advertising policy with the contagion model. Journal of Optimization Theory and Applications, 29(4), 615–627.
Dechert, D. W., Nishimura, K. (1983). Complete characterization of optimal growth paths in an aggregative model with a non-concave production function, Journal of Economic Theory, 31, 332–354.
Brock, W. A. (1983). Pricing, predation and entry barriers in regulated industries. In D. S. Evans (Ed.), Breaking Up Bell (pp. 191–229). Amsterdam, North Holland.
Brock, W. A., Davis, W. D. (1985). Dynamic ramsey pricing. International Economic Review, 26, 569–591.
Mäler Karl Göran. (2000). Development, ecological resources and their management: A study of complex dynamic systems, Joseph Schumpeter lecture. European Economic Review, 44, 645–665.
Romer, P. (1986). Increasing returns and long-run growth. Journal of Political Economy, 94(5), 1002–1037.
Arthur, W. B. (1994). Increasing returns and path dependence in the economy, p. 201. University of Michigan Press.
Arthur, W. (1989). Brian, competing technologies, increasing returns, and lock-in by historical events. Economic Journal, 99, 116–131.
Arthur, W. B. (1990). Positive feedbacks in the economy. Scientific American.
Arthur, W. B. (1996). Increasing returns and the new world of business, Harvard Business Review, 100.
Franz, Wirl, & Feichtinger, G. (2005). History dependence in concave economies. Journal of Economic Behavior and Organization, 57, 390–407.
Stephan, P. E. (1996). The economics of science. Journal of Economic literature, 34(3), 1199–1235.
Merton, R. K. (1968). The matthew effect in science: The reward and communication systems of science are considered. Science, 159(3810), 56–63.
Daron, Acemoglu, Aghion, Philippe, Bursztyn, Leonardo, & Hemous, David. (2012). The environment and directed technical change. The American Economic Review, 102, 131–166.
Pierre, Azoulay. (2011). Gustavo manso and Joshua Graff Zivin, incentives and creativity: Evidence from the academic life sciences. RAND Journal of Economics, 42(3), 527–554.
Popper K. R. (1935). Logik der Forschung, Springer-Verlag Wien.
Krugman, P. (1991). History versus expectations. The Quarterly Journal of Economics, 106(2), 651–667.
Mascarilla-i-Miro, O., Yegorov, Y. (2005). Modelling functional area and commuting flows. Cuadernos de economia, 28, 39-56.
Yegorov, Y. (2009). The dynamics of research schools and the demand for teaching. In Proceedings of INTED 2009 (p. 12). Valencia, Spain; ISBN 978-84-612-7578-6.
Franz, Wirl. (2016). Indeterminacy and history dependence of strategically interacting players. Economics Letters, 145, 19–24.
Franz, Wirl. (2011). Conditions for indeterminacy and thresholds in neoclassical growth models. Journal of Economics, 102, 193–215.
Franz, Wirl, & Feichtinger, G. (2007). Social interactions within a dynamic competitive economy. Journal of Optimization Theory and Applications, 133, 385–400.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Yegorov, Y., Wirl, F. (2021). On Scientific Innovations and Constraints: A Dynamic Analysis. In: Haunschmied, J.L., Kovacevic, R.M., Semmler, W., Veliov, V.M. (eds) Dynamic Economic Problems with Regime Switches. Dynamic Modeling and Econometrics in Economics and Finance, vol 25. Springer, Cham. https://doi.org/10.1007/978-3-030-54576-5_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-54576-5_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-54575-8
Online ISBN: 978-3-030-54576-5
eBook Packages: Economics and FinanceEconomics and Finance (R0)