Abstract
Here we start with two more variants of normality. There is the perfect normality, which turns out to be a conjunction of the classical perfectness (which is slightly different in the point-free context due to the different behaviour of sublocales and subspaces) and normality; in a way it can be viewed as a weaker form of metrizability. Next we deal with the technically important collectionwise normality. Then, in the penultimate section we prove and discuss the Katětov–Tong insertion theorem, using (to advantage) the techniques of the point-free real line. We finish with a certain duality between normality and extremal disconnectedness that allows to translate several results concerning normality to facts about extremal disconnected frames.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
- 3.
The σ-frame ϱL consists precisely of all countable joins of regular elements of L since any finite meet of regular elements is regular by (4) in A.2.1.1.
- 4.
Two subsets U and V of X are separable if there is a continuous map
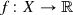 such that f[U] = {1} and f[V ] = {0}; of course, this is only possible if the closures of U and V are disjoint.
such that f[U] = {1} and f[V ] = {0}; of course, this is only possible if the closures of U and V are disjoint. - 5.
Originally announced by Tong in 1948 (the proof was, however, not published until 1952 [273]), Katětov shares the name of the theorem because of his independent version of 1951, with a simpler proof [177]. Such results have roots in Baire (1905, [8]), Hahn (1917, [134]) and Dieudonné (1944, [78]) who proved it for the real line, metrizable spaces and paracompact spaces, respectively.
- 6.
Katětov relations appear in the literature under various other names such as, e.g. quasi-proximities or subordinations. They share some of the defining properties of the so-called strong relations that describe the compactifications of a frame [27].
- 7.
T. Kubiak was the first to notice that several pairs of results in classical topology characterizing the concepts of normality and extremal disconnectedness show a “remarkable duality” [187] between the two concepts: each pair is identical in structure but prove facts about normal spaces on one side of the pair and about extremally disconnected spaces on the other [185]. The point-free study of this duality was undertaken in [131].
- 8.
F-frames are the frames in which the open quotient of any (dense) cozero element is a C ∗-quotient.
References
R. Baire. Leçons sur les fonctions discontinues, professées au collège de France. Gauthier-Villars, Paris, 1905.
R. N. Ball, J. Walters-Wayland. C- and C ∗-quotients in pointfree topology. Dissertationes Mathematicae (Rozprawy Mat.) 412 (2002) 1–62.
B. Banaschewski. σ-frames. Unpublished manuscript, 1980.
B. Banaschewski. Compactifications of frames. Math. Nachr. 149 (1990) 105–115.
B. Banaschewski. The Real Numbers in Pointfree Topology. Textos de Matemática, vol. 12. University of Coimbra, 1997.
B. Banaschewski, T. Dube, C. R. A. Gilmour, J. Walters-Wayland. Oz in pointfree topology. Quaestiones Math. 32 (2009) 215–227.
B. Banaschewski, C. R. A. Gilmour. Oz revisited. In: Proceedings of the Conference Categorical Methods in Algebra and Topology (ed. by H. Herrlich, H.-E. Porst), pp. 19–23. Math. Arbeitspapiere Nr. 54, Universität Bremen, 2000.
M. C. Charalambous. Dimension theory for σ-frames. J. London Math. Soc. 8 (1974) 149–160.
J. Dieudonné. Une généralisation des espaces compacts. J. de Math. Pures et Appl. 23 (1944) 65–76.
C. H. Dowker, D. Papert. On Urysohn’s lemma. In: General Topology and its Relations to Modern Analysis and Algebra, II, pp. 111–114. Proc. Second Prague Topological Sympos., 1966. Academia, Prague, 1967.
T. Dube, O. Ighedo. More on locales in which every open sublocale is z-embedded. Topology Appl. 201 (2016) 110–123.
C. R. A. Gilmour. Realcompact Alexandroff spaces and regular σ-frames. Mathematical Monographs of the University of Cape Town, vol. 3. University of Cape Town, Department of Mathematics, 1985.
J. Gutiérrez García, T. Kubiak, J. Picado. Lower and upper regularizations of frame semicontinuous real functions. Algebra Universalis 60 (2009) 169–184.
J. Gutiérrez García, T. Kubiak, J. Picado. Localic real-valued functions: a general setting. J. Pure Appl. Algebra 213 (2009) 1064–1074.
J. Gutiérrez García, T. Kubiak, J. Picado. Perfectness in locales. Quaestiones Math. 40 (2017) 507–518.
J. Gutiérrez García, T. Kubiak, J. Picado. Perfect locales and localic real functions. Algebra Universalis 81 (2020) Art. 32, 18 pp.
J. Gutiérrez García, I. Mozo Carollo, J. Picado, J. Walters-Wayland. Hedgehog frames and a cardinal extension of normality. J. Pure Appl. Algebra 223 (2019) 2345–2370.
J. Gutiérrez García, J. Picado. On the algebraic representation of semicontinuity. J. Pure Appl. Algebra 210 (2007) 299–306.
J. Gutiérrez García, J. Picado. On the parallel between normality and extremal disconnectedness. J. Pure Appl. Algebra 218 (2014) 784–803.
H. Hahn. Über halbstetige und unstetige Funktionen. Sitzungsberichte Akad. Wien Abt. IIa 126 (1917) 91–110.
R. W. Heath, E. A. Michael. A property of the Sorgenfrey line. Compositio Math. 23 (1971) 185–188.
O. Ighedo, M. Mugochi. On some parallelism between complete regularity and zero-dimensionality. Quaestiones Math. 41 (2018) 423–435.
M. Katětov. On real-valued functions in topological spaces. Fund. Math. 38 (1951) 85–91; errata ibid. 40 (1953) 203–205.
T. Kubiak. On Fuzzy Topologies. Doctoral Dissertation, Uniwersytet im. Adama Mickiewicza, Poznań, 1985.
T. Kubiak. Second open question. In: Applications of category theory to fuzzy subsets (ed. by S. E. Rodabaugh, E. P. Klement, U. Höhle), pp. 349. Kluwer, Dordrecht, 1992.
T. Kubiak. Separation axioms: extension of mappings and embedding of spaces. In: Mathematics of Fuzzy Sets: Logic, Topology and Measure Theory (ed. by U. Höhle, S. E. Rodabaugh), pp. 433–479. The Handbooks of Fuzzy Sets Series, vol.3. Kluwer, Dordrecht, 1999.
Y.-M. Li, Z.-H. Li. Constructive insertion theorems and extension theorems on extremally disconnected frames. Algebra Universalis 44 (2000) 271–281.
J. Picado. A new look at localic interpolation theorems. Topology Appl. 153 (2006) 3203–3218.
J. Picado, A. Pultr. Frames and Locales: Topology without points. Frontiers in Mathematics, vol. 28, Springer, Basel, 2012.
J. Picado, A. Pultr. A Boolean extension of a frame and a representation of discontinuity. Quaestiones Math. 40 (2017) 1111–1125.
T. Plewe. Sublocale lattices. J. Pure Appl. Algebra 168 (2002) 309–326.
A. Pultr. Remarks on metrizable locales. Rend. Circ. Mat. Palermo (2) 6 (1984) 247–258.
E. V. Schepin. Real-valued functions, and spaces close to normal. Sib. Math. J. 13 (1972) 1182–1196.
M. Singal, A. Singal. Mildly normal spaces. Kyungpook Math. J. 13 (1973) 27–31.
M. H. Stone. Boundedness properties in function-lattices. Canad. J. Math. 1 (1949) 176–186.
H. Tietze. Über Funktionen, die auf einer abgeschlossenen menge stetig sind. J. Reine Angew. Math. 145 (1915) 9–14.
H. Tong. Some characterizations of normal and perfectly normal spaces. Duke Math. J. 19 (1952) 289–292.
P. S. Urysohn. Über die Mächtigkeit der zusammen hängenden Mengen. Math. Ann. 94 (1925) 262–295.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Picado, J., Pultr, A. (2021). More on Normality and Related Properties. In: Separation in Point-Free Topology. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-53479-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-030-53479-0_8
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-53478-3
Online ISBN: 978-3-030-53479-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


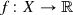 such that f[U] = {1} and f[V ] = {0}; of course, this is only possible if the closures of U and V are disjoint.
such that f[U] = {1} and f[V ] = {0}; of course, this is only possible if the closures of U and V are disjoint.