Abstract
SRL is a reversible programming language conceived as a restriction of imperative programming languages. Each SRL program that mentions n registers defines a bijection on n-tuples of integers. Despite its simplicity, SRL is strong enough to grasp a wide class of computable bijections and to rise non-trivial programming issues. We advance in the study of its expressivity. We show how to choose among alternative program-branches by checking if a given value is positive or negative. So, we answer some longstanding questions that the literature poses. In particular, we prove that SRL is primitive recursive complete and that its program equivalence is undecidable.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Reversible programming languages
- Imperative programming languages
- Primitive recursive functions
- Decidability
1 Introduction
Reversible computing is an unconventional form of computing that identifies an interesting restriction of the classical digital computing model which, perhaps surprisingly, still is Turing-complete [3]. Classical computation is deterministic in a forward manner, i.e. each state is followed by a unique state. The reversible computation is a classic computation which is also required to be backward-deterministic: every state has a unique predecessor state.
The research interest for reversible computing is emerged in a plethora of situations (see [25] for a survey). Inside the classical computing, often we come across this subject inadvertently and accidentally. Think about lossless compression, cryptographic procedures, view-update problem, and so on. However, the interest for the reversible paradigm in the classical computing is far broader than that, because it is linked to the ubiquitous backtracking mechanism. Albeit specific researches on these classic arguments have been developed, the quest for an overall theory of reversible computing has been initially motivated from a different search: the interest for thermodynamic issues of the computation. This research goal can potentially contribute to decrease energy consumption, systems overheat and, battery stockpiling in portable systems. Furthermore, we like to remind that the reversible computation is intimately linked to emerging computing models, like, for example, the quantum computing paradigm.
The literature proposes several reversible languages (see [25] for a survey). We focus our attention on SRL and its variants, namely a family of total reversible programming languages introduced in [10]. These languages have been conceived as a restriction of the LOOP language defined in [14, 15]. The LOOP language identifies a sub-class of programs that exist inside WHILE programming languages and which correspond the class of primitive recursive functions, crucial in recursion theory. The distinguishing difference between SRL languages and LOOP, or WHILE ones, is that their registers store both positive and negative integers (like standard programming languages) and not only natural numbers. The three instructions common to every variant of SRL are the increment (viz. \(\mathsf{inc\,}{\textsc {r}}\)), the decrement (viz. \(\mathsf{dec\,}{\textsc {r}}\)) and the iteration (viz. \(\mathsf{for\,}\textsc {r}(P)\), where P is a subprogram that cannot modify the content of register \(\textsc {r}\)). Registers contain values in \(\mathbb {Z}\) and a program that mentions n registers defines a bijection \(\mathbb {Z}^n\rightarrow \mathbb {Z}^n\).
For each program P of SRL, we can build the program \(P^{-1}\) that reverses the behavior of P in an effective way. I.e., executing \(P^{-1}\) just after P is equivalent to the identity. Patently, increment and decrement are mutual inverses. On the other hand, \(\mathsf{for\,}\textsc {r}(P)\) iterates n times the execution of P, whenever \(n\ge 0\), and iterates n times the execution of the inverse of P whenever \(n\le 0\); so, it can be used to invert itself.
Despite the instruction set of SRL is quite limited, its operational semantics is unexpectedly complex. The literature [10, 12, 13, 18, 21] leaves many questions open, mainly concerning the relation between SRL and the class of computable bijectionsFootnote 1, which form a core of computable functions [10, 19, 20, 22,23,24].
We aim at answering some of those questions.
-
1.
Is the program equivalence of SRL decidable?
-
2.
Is it decidable if a program of SRL behaves as the identity?
-
3.
Is it possible to decide whether a given program is an inverse of a second one?
-
4.
Is SRL primitive-recursive complete?
-
5.
Is SRL sufficiently expressive to represent RPP [21] or RPRF [18, 20]?
Patently, these questions are correlated in many ways. Quite trivially 1, 2 and 3 are equivalent. Also 4 and 5 are because RPP and RPRF are primitive-recursive correct and complete. A positive answer to 4 would imply a positive answer to 5 and a negative one to 1 because the equivalence between primitive-recursive functions is undecidable [26, Ch. 3].
In this work we answer to all of them by solving the open problem in [21]: “It is an open problem if the conditional instruction of RPP can be implemented in SRL.” Encoding a conditional behavior as a program of SRL allows to compile programs of RPP and RPRF in SRL, so answering question 5. Since RPP is primitive-recursive complete [21], then SRL is, answering question 4. So, the program equivalence for SRL is undecidable because that one of primitive recursive functions is [26, Ch.3]. This answers questions 1, 2 and 3.
Contents. Section 2 introduces SRL and some useful notations. Section 3 introduces the representation of truth values. Section 4 shows how to test numbers and zero. Section 5 shows how RPP can be represented in SRL. Conclusions are in Sect. 6.
2 The Language SRL
SRL is a reversible programming language [10, 11, 25] that Armando Matos distills from a variant of Meyer and Ritchie’s LOOP language [14, 15]. Specifically, SRL restricts a FOR language that, in its turn, is a total restriction of any WHILE programming language (a.k.a. IMP) [5, 9, 26]. A FOR language is in [17] which revisits results in [14, 15] about the relation between programming and primitive recursive functions.
The choice of letting SRL-languages to operate on all integers eases the design of a reversible language because \(\mathbb {Z}\), endowed with sum, is a group while \(\mathbb {N}\) is not. Therefore, the registers that a program of SRL uses store values of \(\mathbb {Z}\). Each program P defines a bijection \(\mathbb {Z}^n\rightarrow \mathbb {Z}^n\), where \(n\ge 1\) is an upper bound to the number of registers that occur in P. As a terminology, we take “mentioned” and “used” as synonymous of “occur” in a sentence like “registers that occur in P”. The inverse of P is \({P}^{-1}\), i.e. the inverse bijection that P represents. We shall explain how to get \({P}^{-1}\) from P in a few.
The minimal dialect of SRL languages we focus on is as follows:
Definition 1
Let \( \textsc {r}\) be a meta-variable denoting register names that we range over by lowercase letters, possibly with subscripts and superscripts. Valid SRL-programs are the programs generated by the following grammar:
that, additionally, satisfy the following linear constraint: \(\mathsf{for\,}r(P)\) is part of a valid program iff r is not used in P as argument of \(\mathsf{inc\,}{}\) or \(\mathsf{dec\,}{}\).
The operational semantics of SRL says that (i) \(\mathsf{inc\,}{x}\) increments the content of the register x by 1; (ii) \(\mathsf{dec\,}{x}\) decrements the content of the register x by 1; (iii) \(P_0; P_1\) is the sequential composition of 2 programs that we execute from left to right; and, (iv) if \(n\in \mathbb {Z}\) is the initial content of the register r then, \(\mathsf{for\,}r(P)\) executes, either \(\underbrace{P;\dots ;P}_n\) whenever \(n\ge 0\), or \(\underbrace{{P}^{-1};\dots ;{P}^{-1}}_{|n|}\) whenever \(n\le 0\), where |n| is the absolute value of n. We notice that executing \(\mathsf{for\,}r(P)\) cannot alter the value in r because of the linear constraint on the syntax.
The inverse of an SRL-program is obtained by transforming \(\mathsf{inc\,}{x}\), \(\mathsf{dec\,}{x}\), \(P_0; P_1\) and \(\mathsf{for\,}r(P)\) in \(\mathsf{dec\,}{x}\), \(\mathsf{inc\,}{x}\), \({P_1}^{-1}; {P_0}^{-1}\) and \(\mathsf{for\,}r({P}^{-1})\), respectively. More on SRL, its extensions, as well as results about it, is in [10, 11, 21, 25].
For the sake of simplicity, the following notation concisely and formally allows to see SRL programs as bijective functions.
Notation 1
(Register names). Without loss of generality, we shall only consider SRL-programs whose registers’ names are a single letter, typically r, indexed by means of different natural numbers. Also, we assume that, if a program mentions \(n\in \mathbb {N}\) registers, then \(r_0, \ldots , r_{n-1}\) are their names.
We use vectors of integers to denote the contents of all registers as a whole, both for input and output. If a vector contains n integers then, we say that n is its size and we index such integers from 0 to \(n-1\). The idea is that the content of the register \(r_i\) is in position i of the vector. As for quantum computing [16], we represent such vectors as column arrays written downwards.
Notation 2
Let P be a SRL program that respects Notation 1. Let \(n\in \mathbb {N}\) be an upper bound of the indexes of the registers that P uses. Let \(\,| v_{in} \rangle \,\) and \(\,| v_{out} \rangle \,\) denote (column) vectors of size n. Then, \(\,| v_{in} \rangle \, P \,| v_{out} \rangle \,\) denotes that P sets the content of its register with the values in \(\,| v_{out} \rangle \,\), starting from registers set to the values in \(\,| v_{in} \rangle \,\). Slightly abusing our notation:
is the computation of \(P_1; \ldots ; P_n\) applied to \( \,| v_{1} \rangle \, \) with the value of the registers’ intermediate contents made explicitly.
We conclude with simple examples of SRL programs that use ancillary registers. Specifically, a register is said to be a “zero-ancilla” whenever we assume that its initial value is 0; when its initial value is different, we are just not interested in the behaviour of the program.
Lemma 1 (Integer-Negation)
If \(r_1\) is used as a zero-ancilla then:
inverts the sign of the value in \(r_0\).
Proof
Let \(a\in \mathbb {Z}\). It is easy to see that:

\(\square \)
We remark that (2) resets the zero-ancilla to zero, so that it can be reused for as many applications of (2) as we need. So, we can use the macro \(\textsf {neg\,}{r_i}\) as a name of (2), hiding an additional zero-initialized ancillary register.
Lemma 2 (Swap)
If \(r_2\) is used as a zero-ancilla then:
swaps the content of \(r_0\) and \(r_1\), and leaves the zero-ancilla clean.
Proof
Let \(a,b\in \mathbb {Z}\). It is easy to see that:

\(\square \)
We shall use the macro:
as a name of (3) which mentions two distinct registers \( r_i \) and \( r_j \) and which hides an additional zero-initialized ancillary register. Remarkably, that unique silent zero-ancilla can be used by all swaps and negations that possibly occur in a program. For completeness, we recall that swap and negation, analogous to the ones here above, are taken as primitive operations in variants of SRL [10, 11].
3 Representing Truth Values
In order to represent truth values in SRL, we conventionally use a pair of registers.
Definition 2
(Truth values). A pair of registers is called truth-pair whenever one register contains 0 and the other contains 1. If 1 is in the first register, then the truth-pair encodes true. Otherwise, 1 is in the second register and the truth-pair encodes false.
Definition 2 recalls the representation of qbits in quantum computing [16] and, indeed, it has been inspired by the quantum programming languages designed in [22, 23]. Definition 2 relies on some observations:
-
1.
“\(\mathsf{for\,}\)”, natively included in SRL, works as a basic conditional operator. If r contains 1, then \(\mathsf{for\,}r(P)\) executes P once. Furthermore, the program:
$$\mathsf{for\,}r_0(P); \mathsf{for\,}r_1(Q)$$simulates an “if-then-else” whenever \(r_0, r_1\) is a truth-pair which drives the mutually exclusive selection between P and Q.
-
2.
It is easy to negate a truth-value by means of \(\mathsf{swap}(r_i,r_j)\), as defined in (3), which, we recall, uses a silent additional ancilla.
A first application of truth-pairs is to check the parity of a register’s content.
Lemma 3 (isEven)
Given the truth-pair \(r_1,r_2\) set to true, \( \mathsf{for\,}r_0( \mathsf{swap}(r_1,r_2))\) decides the parity of the number in \(r_0\). It leaves \(r_1,r_2\) set true iff the content of \(r_0\) is even.
Proof
Let \(n\in \mathbb {Z}\). Then:

where both \(b_{\textit{even}}\) is 1 (\(b_{\textit{odd}}\) is zero) if and only if n is even and \(b_{\textit{odd}}\) is 1 (\(b_{\textit{even}}\) is zero) if and only if n is odd. \(\square \)
We observe that a truth-pair can drive \(\mathsf{for\,}r_1(P);\mathsf{for\,}r_2(Q)\) to simulate an “if-then-else” that chooses between P and Q. Once chosen, we can set the truth-pair back to its initial content by applying the inverse of (5), i.e. Bennet’s trick [1,2,3], in accordance with programming strategy widely used in [21]. In principle, Bennet’s trick allows to reuse the truth-pair for a further parity test.
Lemma 3 justifies the use of the macro \(\textsf {isEven}(r_i,r_j,r_k)\) as a name for (5), provided that \(r_i,r_j,r_k\) are distinct registers and that \(r_j,r_k\) form a truth-pair. If the content of \(r_i\) is even the truth-value contained in \(r_j,r_k\) is not changed, otherwise it is logically negated. We also note that the inverse of (5) is \(\mathsf{for\,}r_i( \mathsf{swap}(r_j,r_k)) \), because the swap is commutative on its arguments.
An Euclidean division by 2 on positive numbers, relying on Lemma 3, divides the dividend, an integer, by the divisor, yielding a quotient and a remainder smaller than the divisor.
Lemma 4 (Halve)
Let \(r_1,r_2\) be a truth-pair initialized to true. Let \(r_3\) be a zero-ancilla. Then:
halves the content of \(r_0\), leaves the quotient of the integer division by 2, which is decremented by one in the case \(r_0\) contains a negative odd number, in \(r_3\) and, finally, lives the remainder in \(r_2\).
Proof
Let \(n\ge 0\). Then:

where \(b_{\textit{even}}\) and \(b_{\textit{odd}}\) flag the parity of the value in \(r_0\) in accordance with Lemma 3. In particular, \(r_1, r_2\) contain 1, 0, respectively, iff the remainder of the division is zero. Otherwise, \(r_1, r_2\) contain 0, 1, respectively. If \(n< 0\), then:

where \(b_{\textit{even}}\) and \(b_{\textit{odd}}\) flag the parity of the value in \(r_0\) in accordance with Lemma 3. \(\square \)
Lemma 4 justifies the use of the macro \(\mathsf{halve}(r_i)(r_j)(r_k)(r_h)\) as a name for (6) in order to halve the value in \(r_i\), whenever \( r_i, r_j, r_k \) and \(r_h\) are pairwise distinct. Clearly, \(\mathsf{halve}\) silently assumes the use of an additional zero-ancilla.
4 Testing SRL-Registers
We here discuss how to check if an integer number is smaller than \( -1 \) in order to leave the answer in a truth-pair. The test is crucial to answer longstanding questions about the expressivity of SRL, firstly posed in [10] and reiterated in other papers [12, 13, 18, 20, 21].
The Fundamental Theorem of Arithmetic is the starting point [4, p. 23]:
“... Any integer not zero can be expressed as a unit \((\pm 1)\) times a product of positive primes. This expression is unique except for the order on which the primes factors occur. ...”
Technically, every integer \(n\ne 0\) has prime-decomposition \((\pm 1) 2^k p_1p_2\cdots p_m\), unique up to the order of its factors. For every \(k, m\ge 0\) and \(1\le i \le m\), the factor \(p_i\) is a prime, positive and odd number not smaller than 3. The odd-core of n, decomposed as \((\pm 1) 2^k p_1p_2\cdots p_m\), is \((\pm 1) p_1p_2\cdots p_m\). For instance, 21 is prime-decomposed as either \((1) \cdot 2^0 \cdot 3\cdot 7\) or \((1) \cdot 2^0 \cdot 7\cdot 3\) with odd-core 21, and \(-90\) is prime-decomposed in \((-1)\cdot 2^1\cdot 3\cdot 3\cdot 5\) with odd-core \(-45\).
Proposition 1
Let \(n\ne 0\) be an integer and let \((\pm 1) 2^k p_1p_2\cdots p_m\) be the prime-decomposition of n, for some \(k,m\ge 0\).
-
1.
\(k \le |n|\), where |n| is the absolute value of n.
-
2.
For each \(h\le k\), the division of n by \(2^h\) returns \((\pm 1) 2^{k-h} p_1p_2\cdots p_m\) as quotient and 0 as remainder.
-
3.
The division of n by \(2^{k}\) returns an odd number. So, dividing n by \(2^{k+1}\) has 1 as its remainder.
Proof
Trivial. \(\square \)
Crucially, for each \(j\in \mathbb {N}\), if we divide 0 by \(2^{j}\), then 0 is both remainder and quotient. Therefore, given an integer N and an integer M greater than N, we can show that a program of SRL exists which iteratively divides N by 2 for M times. If N is 0, the only reminder we can obtain is 0. Otherwise, a remainder equal to 1 necessarily shows up.
Theorem 3 here below defines the program. It assumes the existence of two occurrences of N. One is the dividend, the other drives the iteration. We remark that producing a copy of a given N costs just a single zero-ancilla more.
Theorem 3
(isLessThanOne). Let \(r_2,r_3\) and \(r_5,r_6\) be truth-pairs initialized to true and let \(r_4\) be a zero-ancilla. Let both \(r_0\) and \(r_1\) contain the value N. Then:

leaves true in the truth-pair \(r_5,r_6\) if and only if N is strictly lower than 1.
Proof
Both \(r_0,r_1\) contain N because \(r_0\) iterates as many times as required, and \(r_1\) is the dividend. Some remarks are worth doing.
-
The comments /* \( \mathtt{SP}0 \) */... name the part of program to their left that begins with “\(\mathsf{for\,}\)”.
-
We can think of \(r_1\), \(r_2\), \(r_3\), \(r_4\) as the arguments of \(\mathsf{halve}\), i.e. we could rewrite \(\mathtt{SP}0\) as \(\mathsf{for\,}r_5( \;\mathsf{halve}(r_1,r_2,r_3,r_4) \; )\). So, Lemma 4, implies that \(\mathtt{SP}0\) halves \(r_1\), leaving the quotient in \(r_4\) and the remainder in \(r_3\).
-
Only swap-operations modify truth pairs.
-
It would be sufficient to initialize \(r_0\) with any number greater than the exponent of 2 in the prime-decomposition of N.
-
Making explicit the statement requirements,

sums up the input for SRL program (7).
The behaviour of the SRL program (7) can described by considering three cases: \(N=0\), \(N>0\) and \(N<0\).
-
Let \(N=0\). Then (7) does nothing and result is immediate. We remark that the result does not change if we arbitrarily modify the value in \(r_0\).
-
Let \(N \ge 1\). The outermost “\(\mathsf{for\,}{r_0}\)” iterates its body as many times as N and the computation proceeds as discussed in the following.
-
1.
Let us consider \(\mathtt{SP}0\). If the truth-pair \(r_5,r_6\) contains true, the program (7) executes \(\mathsf{halve}(r_1,r_2,r_3,r_4)\) once. Lemma 4 implies that the value of \(r_1\) does not change, that the remainder is stored in the truth-pair \(r_2,r_3\) and that the result of dividing \(r_1\) by 2 is in \(r_4\). Otherwise, the truth-pair \(r_5,r_6\) contains false and nothing is done.
-
2.
Let us consider \(\mathtt{SP}1\). We observe that only \(\mathtt{SP}1\) can modify \(r_5,r_6\). If the truth-pair \(r_2,r_3\) contains true, i.e. \(r_1\) has even value in it, then nothing is done. Otherwise, the truth-pair \(r_2,r_3\) contains false, i.e. \(r_1\) contains an odd number. Then, \(\mathtt{SP}1\) yields the global result by setting the truth-pair \(r_5,r_6\) to false.
-
3.
Let us consider \(\mathtt{SP}2\) which, we remark, is crucial that the program (7) executes at most once. Let the truth-pair \(r_5,r_6\) contain true. We both subtract from \(r_1\) half of its value, which is in \(r_4\) after we execute \(\mathtt{SP}0\), and we reset \(r_4\) to zero. This sets \(r_1\), \(r_2\), \(r_3\) and \(r_4\) for the next halve-iteration. If the truth-pair \(r_5,r_6\) contains false, then nothing is done.
-
4.
Let us consider \(\mathtt{SP}3\). If the truth-pair \(r_5,r_6\) contains true, then nothing is done. Globally, this means that the body of \(\mathtt{SP}3\) cannot run until \(r_1\) is possibly set with an odd value. If the truth-pair \(r_5,r_6\) contains false, then we must consider two cases in order to ensure that \(\mathtt{SP}3\) leaves the value false in the truth-pair \(r_2,r_3\).
-
Let \(r_1\) contain an odd value n after executing \(\mathtt{SP}1\), which sets \(r_5,r_6\) to false, and which is followed by \(\mathtt{SP}2\) that, doing nothing, leaves register’s contents unchanged. Since \(\mathsf{for\,}r_1( \mathsf{for\,}r_2( \mathsf{dec\,}{r_4}); \mathsf{swap}(r_2,r_3))\) is the inverse of \(\mathsf{halve}(r_1,r_2,r_3,r_4)\), then:
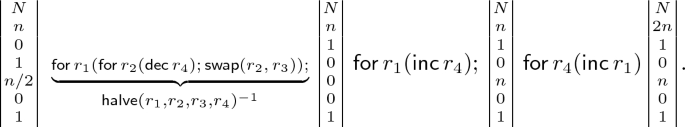
To sum up, (i) the truth-pair \(r_2,r_3\) is restored to true, (ii) the contents of \(r_1\) and \(r_4\) are now both even. Specifically, \(r_1\) contains an even value and \(r_4\) doubles that value.
-
Let \(r_1\) contain an even value n. This sub-case can only occur when the preceding sub-case, with \( r_1 \) initially set to an odd value n, has already occurred once. Moreover, both \(\mathtt{SP}0, \mathtt{SP}1\) and \(\mathtt{SP}2\) cannot not change the content of the registers anymore, because \(r_5,r_6\) contain the false and \(r_1\) is doubled by every iteration in order to permanently maintain true in the pair \(r_2,r_3\). Then:
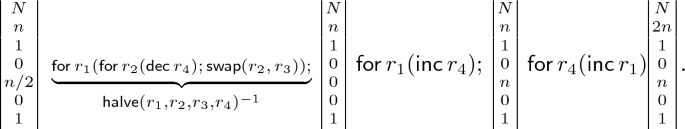
To sum up, (i) the truth-pair \(r_2,r_3\) remains true, (ii) the contents of \(r_1\) and \(r_4\) are both even. Specifically, \(r_1\) contains an even value and \(r_4\) doubles that value.
-
-
1.
-
Let \(N \le -1\). By definition, \(\mathsf{for\,}r_0(P)\) executes \({P}^{-1}\) as many times as \(n_0\) if \(n_0\) is the value of \(r_0\). We have to check that (7) doubles the content of \(r_1\) before checking its parity. Hence, \(r_1\) can never be read off with an odd number in it. Thus, (7) simply checks the parity of \(r_1\) and doubles \(r_1\), at every of its iterations, according to the following details:
-
Let us consider \(\mathtt{SP}3\). The body of the outermost “\(\mathsf{for\,}\)” of \(\mathtt{SP}3\) never executes, for the truth-pair \(r_5,r_6\) contains true all along the execution.
-
Let us call \(B_{\mathtt{SP}2}\) the body \(\mathsf{for\,}r_4( \mathsf{dec\,}{r_1});\; \mathsf{for\,}r_1( \mathsf{dec\,}{r_4})\) of \(\mathtt{SP}2\). Then, every iteration of (7) executes \(B_{\mathtt{SP}2}\). Since N is negative and \(r_5\) contains 1, we have to consider \(B_{\mathtt{SP}2}^{-1}\), i.e. \( \mathsf{for\,}r_1( \mathsf{inc\,}{r_4});\;\mathsf{for\,}r_4( \mathsf{inc\,}{r_1})\). Moreover, since \(r_1\) contains a negative number, we remark that the outermost occurrence of “\(\mathsf{for\,}\)” in \(B_{\mathtt{SP}2}^{-1}\) further inverts its body. Since \(N \le -1\), we consider a generic negative number n. Thus:
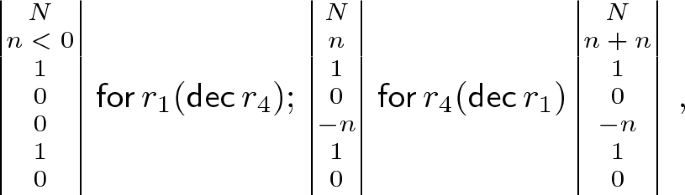
where both n and \(n+n\) are negative, so \(-n\) is positive.
-
Let us consider \(\mathtt{SP}1\). Since the truth-pair \(r_2,r_3\) is never changed from its initial value true, the body of the outermost occurrence of “\(\mathsf{for\,}\)” in \(\mathtt{SP}1\) is always skipped.
-
Let us consider \(\mathtt{SP}0\) and let name \( \mathsf{for\,}r_5( \mathsf{for\,}r_1(\, \mathsf{swap}(r_2,r_3); \mathsf{for\,}r_2( \mathsf{inc\,}{r_4}) \, ))\), i.e. the body of \(\mathtt{SP}0\), as \(B_{\mathtt{SP}0}\). Every iteration of (7) executes \(B_{\mathtt{SP}0}\) because the initial true value in the truth-pair \(r_5,r_6\) never changes. Since N is negative, we consider \(B_{\mathtt{SP}0}^{-1}\), i.e. \( \mathsf{for\,}r_5( \mathsf{for\,}r_1(\, \mathsf{for\,}r_2( \mathsf{dec\,}{r_4});\; \mathsf{swap}(r_2,r_3);))\). Nevertheless, also \(r_1\) contains a negative number, thus the body of \(\mathsf{for\,}(r_1)\) is subject to a further inversion that annihilates the first one. Since \(N \le -1\), we consider a generic negative number n. Thus:

Summing up, in the case \(N \le -1\) each iteration executes two steps: (i) \(\mathtt{SP}2\) copies the content of \(r_1\) in \(r_4\) and doubles \(r_1\); (ii) \(\mathtt{SP}0\) resets \(r_4\) to zero and leaves all other registers unchanged. \(\square \)
-
Concluding observations and remarks on (7) follow.
We can drop the constraint that both \(r_0\) and \(r_1\) contain the same value by letting \(r_1\) be a zero-ancilla and starting (7) with \(\mathsf{for\,}r_0(\mathsf{inc\,}{r_1})\), to recover the current assumptions of Theorem 3. Therefore:
can be a name for the program (7) that we assume to apply to distinct registers such that: (i) \(r_{j_2},r_{j_3}\) and \(r_{j_5},r_{j_6}\) are truth-pairs with initial value set true, and (ii) \(r_{j_1},r_{j_4}\) are variables with initial value set 0. Under these assumptions, after executing \(\textsf {isLessThanOne}(r_{j_0},r_{j_1}, r_{j_2},r_{j_3},r_{j_4},r_{j_5},r_{j_6})\), the truth-pair \(r_{j_5},r_{j_6}\) still contains true if and only if \(r_{j_0}\) was containing either zero or a negative integer.
Using one more additional zero-ancilla would allow to further simplify (7) in the minimal version of SRL that we program with in this work: all the explicit uses of the swap-macros would disappear. In accordance with Theorem 3, \(\textsf {isLessThanOne}\) always returns the content of \(r_{j_0}\) unchanged. Yet, in accordance with Theorem 3, \(\textsf {isLessThanOne}\) always returns the truth-pair \(r_{j_2},r_{j_3}\) clean. Therefore, w.l.o.g., it is possible to use it silently. On the other hand, the truth-pair \(r_{j_5},r_{j_6}\) is used for the result and so it cannot be used silently. Worst, the registers \(r_{j_1},r_{j_4}\) are left “dirty”, i.e. containing useless values for our goal. It is an open question if a program, equivalent to (7), exists that stops with all ancillary variables, but the truth-pair \(r_5,r_6\) that contains the result, clean, i.e. with their starting values in them.
The program (7) of Theorem 3 and its sub-procedures, have been checked by using the Haskell meta-interpreter in [11, page 86]. The main drawback of \(\textsf {isLessThanOne}\) is that the value of \(r_1\) grows exponentially. More precisely, let N be an integer different from zero and \((\pm 1) 2^k p_1p_2\cdots p_m\) its prime-decomposition with odd-core \(d=p_1p_2\cdots p_m\). If N is positive, then the above program leaves the value \(d*2^{N-k}\) in \(r_1\). If N is negative, then value is \(N*2^N\). We leave the problem of eliminating the exponential blow up as open.
5 Expressivity
We here prove that SRL can represent all Primitive Recursive functions (PR). We begin by recalling what Reversible Primitive Permutations (RPP) are. Second, we show that SRL can represent every element of RPP. Since RPP can express all PR [21], then SRL enjoys the same property.
By analogy with PR, we build \( \mathsf{RPP} \) by means of composition schemes that we apply to base functions. \(\mathsf{RPP} \) contains total reversible endofunctions on tuples of integers, i.e. elements of \(\mathbb {Z}^n\) for some \(n\in \mathbb {N}\).
Definition 3
(Reversible Primitive Permutations [21]). Reversible Primitive Permutations (\( \mathsf{RPP} \)) is a sub-class of endofunctions on \(\mathbb {Z}^n\) for some \(n\in \mathbb {N}\). In order to identify the endofunctions of \(\mathsf{RPP} \) specifically defined on \(\mathbb {Z}^k\), for some given k, we write \(\mathsf{RPP} ^k\) with the following meaning:
-
\(\mathsf{RPP} ^1\) includes the identity function \( \mathsf {I}\), the successor function \(\mathsf {S}\) that increments an integer, the predecessor function \(\mathsf {P}\) that decrements an integer, the negation function \( \mathsf {N}\) that inverts the sign of an integer;
-
\(\mathsf{RPP} ^2\) includes the transposition \(\chi \) that exchanges two integers;
-
If \( f, g\in \mathsf{RPP} ^k\) then, their series-composition
 belongs to \( \mathsf{RPP} ^k\). It is the function that sequentially applies f and g to the k-tuple of integers provided as input (i.e., it is the programming composition that applies functions from left to right);
belongs to \( \mathsf{RPP} ^k\). It is the function that sequentially applies f and g to the k-tuple of integers provided as input (i.e., it is the programming composition that applies functions from left to right); -
If \( f\in \mathsf{RPP} ^j\) and \( g\in \mathsf{RPP} ^k\), for some \( j, k \in \mathbb {N}\), then the parallel composition \( ( f\parallel g)\) belongs to \( \mathsf{RPP} ^{j+k}\). It is the function that applies f on the first j arguments and, in parallel, applies g on the other ones;
-
If \( f\in \mathsf{RPP} ^{k}\), then the finite iteration \( {\mathsf {It}^{}_{}\left[ f \right] } \) belongs to \(\mathsf{RPP} ^{k+1}\) and it is the function defined as:

-
Let \( f, g, h\in \mathsf{RPP} ^{k}\). The selection \( \mathsf {If}^{}_{}\left[ f,g,h\right] \) belongs to \(\mathsf{RPP} ^{k+1}\) and it is the function defined as:
$$\begin{aligned} \mathsf {If}^{}_{}\left[ f,g,h\right] \, ( \langle x_1, \ldots , x_k , z)&:= {\left\{ \begin{array}{ll} ( f\parallel \mathsf {I})\, ( \langle x_1, \ldots , x_k , z) &{} \text { if } z > 0\ ,\\ ( g\parallel \mathsf {I})\, ( \langle x_1, \ldots , x_k , z) &{} \text { if } z = 0\ ,\\ ( h\parallel \mathsf {I})\, ( \langle x_1, \ldots , x_k , z) &{} \text { if } z < 0\ . \end{array}\right. } \end{aligned}$$
Summing up, \(\mathsf{RPP} \) [21] is a quite simple language that simplifies the reversible language presented in [18]. We recall from [21] that no reversible programming language can represent all and only the total reversible functions and that an algorithm exists, which is linear both in time and space, able to generate the inverse of every element in \(\mathsf{RPP} \).
Many notions of definability exist. Good references are [17, 20, 21], for example. Typically, they deal with classes of functions that yield single value as result. However, \(\mathsf{SRL} \)-programs and \(\mathsf{RPP} \) functions return tuples. In order to relate \(\mathsf{SRL} \) and \(\mathsf{RPP} \) to classes of single-value return functions we introduce what definability means in our context:
Definition 4
(Definability). Let f be an endofunction on \(\mathbb {Z}^k\). The function f is definable whenever there is a program \( P \) that involves \(k+h\) registers, for some \(h\in \mathbb {N}\), such that: if the first k registers are initialized to \(v_0, \ldots , v_{k-1}\) and the others are initialized to zero, then the application of \( P \) sets the first k registers to \(f(v_0, \ldots , v_{k-1})\). Moreover, f is r-definable whenever P ends by also resetting the last h registers to zero.
Clearly, a reversible programming language like SRL can r-define reversible functions only. Also, from the definition here above, it follows that the definition of SRL and \( \mathsf{RPP} \) can be strengthened to explicitly construct the inverse of any of their elements. We mean that, if P is a program of SRL, for example, it is easy to see that \( P \) r-defines f iff \( P ^{-1}\) r-defines \(f^{-1}\).
Theorem 4
(RPP-definability). If \(f\in \mathsf{RPP} \), then there is an SRL-program \( P \) that r-defines it.
Proof
By induction, if \(f\in \mathsf{RPP} ^k\), then we prove that there is a program
 that r-defines f and uses \(k+h\) registers, for some \(h\in \mathbb {N}\).
that r-defines f and uses \(k+h\) registers, for some \(h\in \mathbb {N}\).
-
If f is either an identity, a successor or a predecessor, then it can be easily r-defined with no additional register. If f is a negation, then it can be r-defined by using the procedure of Lemma 1, by using one additional register. If f is a transposition, then it can be r-defined by using the procedure of Lemma 2 with a one additional register.
-
Let
 . By induction, there is \(P_i\) that r-defines \(f_i\) by using the registers \(r_0, \ldots , r_{k+h_i-1}\) (\(1\le i \le 2\)). Then \(P_1;P_2\) r-defines f by using \(h=\max \{h_1,h_2\}\) additional registers (reset to zero by both \(P_1\) and \(P_2\)).
. By induction, there is \(P_i\) that r-defines \(f_i\) by using the registers \(r_0, \ldots , r_{k+h_i-1}\) (\(1\le i \le 2\)). Then \(P_1;P_2\) r-defines f by using \(h=\max \{h_1,h_2\}\) additional registers (reset to zero by both \(P_1\) and \(P_2\)). -
Let \(f=( f_1\parallel f_2)\) such that \(f_i\in \mathsf{RPP} ^{k_i}\) (\(1\le i \le 2\)) and \(k_1+k_2=k\). By induction, there is \(P_i\) that r-defines \(f_i\) by using the registers \(r_0, \ldots , r_{k_i+h_i-1}\). Let \(P_1^*\) be the program \(P_1\) where \(r_{k_1}, \ldots , r_{k_1+h_1-1}\) (viz. its h additional registers) are simultaneously renamed \(r_{k}, \ldots , r_{k+h_1-1}\). Let \(P_2^*\) be the program \(P_2\) where \(r_{0}, \ldots , r_{k_2+h_2-1}\) are simultaneously renamed \(r_{k_1}, \ldots , r_{k_1+k_2+h_2-1}\). Then f is r-defined by \(P_1^*; P_2^*\) with \(\max \{h_1,h_2\}\) additional registers.
-
Let \(f= {\mathsf {It}^{}_{}\left[ f' \right] } \) where \(f'\in \mathsf{RPP} ^{k'}\) (\(k=k'+1\)). By induction, there is \(P'\) using the registers \(r_0,\ldots , r_{k'-1}, \ldots , r_{k'+h'-1}\) that r-defines \(f'\) with \(h'\) additional registers. The register \(r_k\) is expected to drive the execution of \( {\mathsf {It}^{}_{}\left[ f \right] } \), thus we denote \(P^*\) the program \(P'\) where each register with index \(r_i\) (\(i\ge k\)) are renamed \(r_{i+1}\).
We use \(\textsf {isLessThanOne}\) in (8) in order to check the content of \(r_k\) using \(8+1\) registers, the distinguished one being a zero-ancilla that occurrences of \( \mathsf{swap} \) in (4) relies on. In this work we do not focus on minimizing the number of additional variables. We are looking for a program that receives the input in the first k registers and it uses \(h'+8+1\) additional zero-ancillae. Thus \(r_1, \ldots , r_{k'+h'}\) (except \(r_k\)) are used by \( P ^*\), while \(r_k, r_{k+h'+1}, \ldots , r_{k+h'+7}\) are the eight registers that supply the input of \(\textsf {isLessThanOne}\) and \( r_{k+h'+8}\) is sometimes used to reverse a procedure.
We r-define \( {\mathsf {It}^{}_{}\left[ f' \right] } \) by means of the following program (named \(P_{{\mathsf {It}^{}_{}\left[ f' \right] }}\)):
$$\begin{aligned}&\mathsf{inc\,}{r}_{k+h'+1}; \mathsf{inc\,}{r}_{k+h'+5};\end{aligned}$$(9)$$\begin{aligned}&\mathsf{inc\,}{r}_k; \textsf {isLessThanOne}(r_k,r_{k+h'+1}, \ldots , r_{k+h'+6});\mathsf{dec\,}{r}_k;\end{aligned}$$(10)$$\begin{aligned}&\mathsf{for\,}r_{k+h'+6}(\mathsf{for\,}r_{k}( P ^*));\end{aligned}$$(11)$$\begin{aligned}&\mathsf{for\,}r_{k+h'+5}(\mathsf{dec\,}{r_{k+h'+8}} ; \mathsf{for\,}r_{k+h'+8}(\mathsf{for\,}r_{k}( P ^*)); \mathsf{inc\,}{r_{k+h'+8}} )\end{aligned}$$(12)$$\begin{aligned}&\mathsf{inc\,}{r}_k; \big (\textsf {isLessThanOne}(r_k,r_{k+h'+1}, \ldots , r_{k+h'+6}) \big )^{-1};\mathsf{dec\,}{r}_k;\end{aligned}$$(13)$$\begin{aligned}&\mathsf{dec\,}{r}_{k+h'+5}; \mathsf{dec\,}{r}_{k+h'+1}; \end{aligned}$$(14)Line (9) initializes the truth-pairs \(r_{k+h'+2},r_{k+h'+3}\) and \(r_{k+h'+5},r_{k+h'+6}\) to true. I.e., it prepares the execution of \(\textsf {isLessThanOne}\) in accordance with the requirements of Theorem 3. Line (10) increments the content of \(r_k\) before testing it. It results that the truth-pair \(r_{k+h'+5},r_{k+h'+6}\) is left to true if and only if the content of \(r_k\) is strictly less than zero. Finally, it restores \(r_k\) to its initial value. Let n be the content of \(r_k\). Line (11), if n is positive, then \(r_{k+h'+5},r_{k+h'+6}\) is false and \( P ^*\) is executed n times. Otherwise, \(r_{k+h'+6}\) contains 0 and nothing is done. Line (12), if n is strictly negative, then \(r_{k+h'+5}\) contains 1 and \( P ^*\) is executed |n| times because \(r_{k+h'+8}\) is set to \(-1\) so that \(\mathsf{for\,}r_{k+h'+8}\) ensures the inversion of the application of \( P ^*\), which, in its turn, was inverted by the negative value n. Lines (13) and (14) reset all additional registers to zero, implementing Bennet’s trick locally to this procedure.
Albeit the execution of \({\mathsf {It}^{}_{}\left[ f' \right] } \) amounts to a non predetermined number of sequential compositions of \(f'\), we emphasize that the number of ancillae that the translation \(P_{{\mathsf {It}^{}_{}\left[ f' \right] }}\) requires is bounded because (i) the number of ancillae that \(P'\) contain is, in its turn, bounded (by induction), and (ii) \(P'\) r-defines \(f'\), meaning that \(P'\) leaves its ancillae clean at the end of each iteration, whatever number of compositions are involved.
-
Let \(f= \mathsf {If}^{}_{}\left[ f_1,f_0,f_2\right] \) such that \( f_1, f_0, f_2\in \mathsf{RPP} ^{k}\). This case is simpler than the preceding one. We need to adapt the construction in Theorem 3’s proof in order to write two programs that check if the given argument is bigger, or lesser, than one and that leave their answer in a truth-pair. We notice that two nested \(\mathsf{for\,}\) are necessary to trigger the application of g, because we have to check that the value driving the selection is neither bigger, nor lesser than one. \(\square \)
Since all primitive recursive functions are definable in RPP by [21, Th. 5], Theorem 4 immediately implies that SRL can express every element of PR. Therefore, we answer the open questions that we recall in the introduction.
6 Conclusions
Many essential reversible programming languages appear in the literature. A survey is in [25], albeit we should add many recent proposals as, for instance, R-WHILE [6], R-CORE [7], RPRF [18], RPP [21], RFUN [8]. Some comparative discussion is useful to frame the relevance of the presented result.
SRL has been conceived by distilling the reversible core of the language LOOP [14, 15]. For this reason SRL enjoys two main characterizing features, up to some details. First, it allows to program total procedures only. Second, it is also a (reversible) core of a standard imperative programming language.
Almost all reversible programming languages are conceived to be Turing-complete, so the first feature distinguishes SRL from them. We do not consider this feature, that it shares with RPRF and RPP, as a limitation. The relevance of studying classes of total functions only is unquestionable, since results about Primitive Recursive Functions (see [17] as instance) like Kleene Normalization Theorem, Grzegorczyk Hierarchies, and so on. Turing-complete languages are not immediately suitable for such kinds of investigations until the identification of a minimal total core of programs/functions in them. Thanks to its conciseness and expressive power, that we studied in this paper, we consider SRL as the best candidate for theoretical investigations in analogy with that done on primitive recursive functions.
Let us consider the second feature. Janus has been the first reversible programming language distilled from an imperative structured programming language. Many interesting extensions and paradigmatic languages stem from it, in particular the recent R-WHILE and R-CORE. Their primitives are based on iterators that may not terminate (roughly while-iterators) and which are somewhat stretched to behave reversibly, by incorporating some form of “assertion”. Quite interestingly, the introduction of R-CORE relies on the observation that a possibly non terminating iterator of R-WHILE can encode the conditional. However, these languages neglect the very standard imperative total iterator \(\mathsf{for\,}\). It is worth to emphasize that modifying the semantics of “\(\mathsf{for\,}\)” (in SRL) by not inverting its body when applied to negative numbers, in analogy with the iterator in RPP, we obtain a version of SRL straightforwardly included in the core of standard imperative programming languages. Furthermore, our expressivity results still hold for such a variant of SRL. On the other hand, we wonder if all the reversible while-iterators have to be extended with some exiting-test, that are not standard in classical languages. We leave this as a further open question.
Notes
- 1.
We remark that, traditionally, computable bijections are studied on natural numbers, while in this setting, studies extend them, w.l.o.g., to the whole set of integers.
References
Axelsen, H.B., Glück, R.: What do reversible programs compute? In: Hofmann, M. (ed.) Foundations of Software Science and Computational Structures, pp. 42–56. Springer, Heidelberg (2011). https://doi.org/10.1007/s00236-015-0253-y
Axelsen, H.B., Glück, R.: On reversible turing machines and their functionuniversality. Acta Informatica 53(5), 509–543 (2016). https://doi.org/10.1007/s00236-015-0253-y
Bennett, C.H.: Logical reversibility of computation. IBM J. Res. Dev. 17(6), 525–532 (1973). https://doi.org/10.1147/rd.176.0525
Birkhoff, G., Mac Lane, S.: A Survey of Modern Algebra, 4th edn. Macmillan, New York (1977)
Calude, C.: Theories of Computational Complexity. Elsevier (1988), annals of Discrete Mathematics - Monograph 35
Glück, R., Yokoyama, T.: A linear-time self-interpreter of a reversible imperative language. Comput. Softw. 33(3), 108–128 (2016). https://doi.org/10.11309/jssst.33.3_108
Glück, R., Kaarsgaard, R.: A categorical foundation for structured reversible flowchart languages: Soundness and adequacy. Log. Methods Comput. Sci. 14(3) Sepember 2018. https://doi.org/10.23638/LMCS-14(3:16)2018, https://lmcs.episciences.org/4802
Jacobsen, P.A.H., Kaarsgaard, R., Thomsen, M.K.: CoreFun: A typed functional reversible core language. In: Kari, J., Ulidowski, I. (eds.) Reversible Computation. pp. 304–321. Springer (2018)
Kristiansen, L., Niggl, K.H.: On the computational complexity of imperative programming languages. Theoret. Comput. Sci. 318(1–2), 139–161 (2004). https://doi.org/10.1016/j.tcs.2003.10.016
Matos, A.B.: Linear programs in a simple reversible language. Theoret. Comput. Sci. 290(3), 2063–2074 (2003). https://doi.org/10.1016/S0304-3975(02)00486-3
Matos, A.B.: Register reversible languages (work in progress). Technical report, LIACC (2014). https://www.dcc.fc.up.pt/~acm/questionsv.pdf
Matos, A.B., Paolini, L., Roversi, L.: The fixed point problem for general and for linear SRL programs is undecidable. In: Aldini, A., Bernardo, M. (eds.) Proceedings of the 19th Italian Conference on Theoretical Computer Science, Urbino, Italy, 18–20 September 2018. CEUR Workshop Proceedings, vol. 2243, pp. 128–139. CEUR-WS.org (2018). http://ceur-ws.org/Vol-2243/paper12.pdf
Matos, A.B., Paolini, L., Roversi, L.: The Fixed Point Problem of aSimple Reversible Language. Theor. Comput. Sci. 813, 143–154 (2020). https://doi.org/10.1016/j.tcs.2019.10.005. http://www.sciencedirect.com/science/article/pii/S0304397519306280
Meyer, A.R., Ritchie, D.M.: Computational complexity and program structure. Technical report. RC 1817, IBM (1967)
Meyer, A.R., Ritchie, D.M.: The complexity of loop programs. In: Proceedings of the 22nd National Conference of the ACM, pp. 465–469. ACM, New York (1967). https://doi.org/10.1145/800196.806014
Nielsen, M.A., Chuang, I.L.: Quantum Computation and Quantum Information: 10th Anniversary Edition, 10th edn. Cambridge University Press, New York (2011)
Odifreddi, P.: Classical Recursion Theory - The Theory of Functions and Sets of Natural Numbers, vol. I. Studies in Logic and the Foundations of Mathematics, Elsevier North Holland (1989)
Paolini, L., Piccolo, M., Roversi, L.: A class of reversible primitive recursive functions. Electron. Notes Theor. Comput. Sci. 322(18605), 227–242 (2016). https://doi.org/10.1016/j.entcs.2016.03.016
Paolini, L., Piccolo, M., Roversi, L.: A Certified Study of a Reversible Programming Language. In: Uustalu, T. (ed.) 21st International Conference on Types for Proofs and Programs (TYPES 2015). Leibniz International Proceedings in Informatics (LIPIcs), vol. 69, pp. 7:1–7:21. Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik, Germany (2018). https://doi.org/10.4230/LIPIcs.TYPES.2015.7
Paolini, L., Piccolo, M., Roversi, L.: On a class of reversible primitive recursive functions and its turing-complete extensions. New Gener. Comput. 36(3), 233–256 (2018). https://doi.org/10.1007/s00354-018-0039-1
Paolini, L., Piccolo, M., Roversi, L.: A class of Recursive Permutations which is Primitive Recursive complete. Theor. Comput. Sci. 813, 218–233 (2020). https://doi.org/10.1016/j.tcs.2019.11.029. Submitted to the journal in 2016
Paolini, L., Piccolo, M., Zorzi, M.: QPCF: higher-order languages and quantum circuits. J. Autom. Reasoning 63(4), 941–966 (2019). https://doi.org/10.1007/s10817-019-09518-y
Paolini, L., Roversi, L., Zorzi, M.: Quantum programming made easy. In: Ehrhard, T., Fernández, M., Paiva, V.d., Tortora de Falco, L. (eds.) Proceedings Joint International Workshop on Linearity & Trends in Linear Logic and Applications. Electronic Proceedings in Theoretical Computer Science, Oxford, UK, 7–8 July 2018, vol. 292, pp. 133–147. Open Publishing Association (2019). https://doi.org/10.4204/EPTCS.292.8
Paolini, L., Zorzi, M.: \(\sf qPCF\): a language for quantum circuit computations. In: Gopal, T.V., Jäger, G., Steila, S. (eds.) TAMC 2017. LNCS, vol. 10185, pp. 455–469. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-55911-7_33
Perumalla, K.: Introduction to Reversible Computing. CRC Press, Boca Raton (2014)
Schoning, U.: Gems of Theoretical Computer Science. Springer, Heidelberg (1998)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Matos, A.B., Paolini, L., Roversi, L. (2020). On the Expressivity of Total Reversible Programming Languages. In: Lanese, I., Rawski, M. (eds) Reversible Computation. RC 2020. Lecture Notes in Computer Science(), vol 12227. Springer, Cham. https://doi.org/10.1007/978-3-030-52482-1_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-52482-1_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-52481-4
Online ISBN: 978-3-030-52482-1
eBook Packages: Computer ScienceComputer Science (R0)






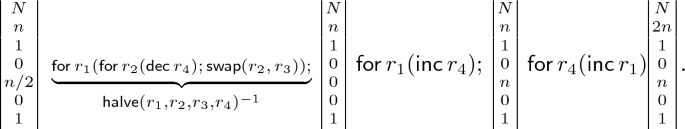
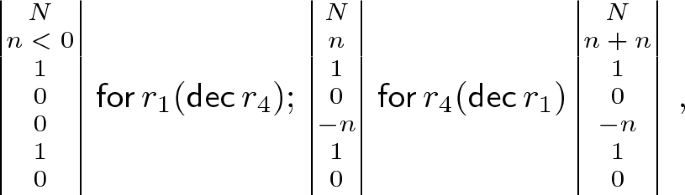

 belongs to
belongs to 
 . By induction, there is
. By induction, there is