Keywords

1 Introduction

Texture wears the basic characteristic that appears in each natural surface, which gives a hardness to determine a specific definition by the scientific community [15]. Texture analysis is omnipresent as one of the most arduous and defying issue in computer founded pattern recognition, due to their similarity in spectral features between the various surfaces. However, until now, it has been considered as the only powerful manner that can present a fundamental discriminate based on various methods of feature extraction used in image processing and recognition. In texture image processing, several applications such as: face recognition [14], object detection [13], image matching [5] segmentation [1] and texture classification [9]. In the literature, there exists four main approaches for texture analysis: statistical methods [11], model-based method [2], structural-based approach [8] and spectral-based or filter-based methods [7].

In order to allow an efficient classification of the texture, two main steps are required. The texture representation phase and the classification phase. These make it possible to generate a model using compact and discriminating characteristics extracted from the first phase. To extract features, several approaches have been developed. Specifically, the Local Binary Patterns (LBP) descriptor introduced by [11] has obtained important attention caused by their robustness and performance in front of illumination and scale variation with minimum algorithmic complexity. Based on LBP, many extensions have been defined and studied such as: ILBP [6], DLBP [1], CLBC [17], LDP [16], MRELBP [10] and SSLBP [4].

Recently, GAN-based Minkowski maps proposed by [12] have been employed for texture analysis as a powerful technique that has already proved its effectiveness on gray tone and color images in a local, adaptive and multi-scale way. In [3] this method is applied in combination with LBP descriptors to classify skin lesions. More precisely, the geometrical GAN-based features of each pixel are extracted from the texture images, then the LBP are computed to characterize them. The GAN processes the image locally.

In this work, to obtain better details of the image, we present a new LBP method based on the impact of homogeneous tolerance used in General Adaptive Neighborhood [3, 12] named Homogeneous Local Binary Pattern HLBP. This one allows to overcome the shortcoming of the initial approach by using a thresholding based on a selected criterion such as luminance, contrast, thickness, etc. Pixel criterion values fit within a specified range of homogeneity tolerance which allow to better take into consideration the relationships between the neighboring pixels. Therefore, the neighborhoods of the pixels correspond more to the underlying spatial structures. Consequently, HLBP descriptor obtains more intrinsic characteristics of the image. The proposed descriptor offers robust and powerful discriminative features in low dimension which are used as input of the support vector machine (SVM) classifier. The classical database Outex of texture images is employed to evaluate the method. According to the experimental results, the proposed HLBP gives the best performance in term of classification accuracy.

The following paper is organized as follows: a depth explanation of the specified methods and tools including the new approach of LBP is presented after the introduction. Thereafter, the performance of the descriptor is evaluated using the outex texture image dataset in Sect. 3, followed by discussion and conclusion in the last section.

2 Background

2.1 Local Binary Pattern LBP

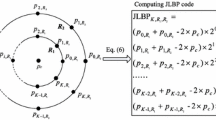
LBP is one of the effective approaches to represent the texture characteristics which generate binary code for each pixel by thresholding the neighboring pixels with the central pixel value [11]. For the neighbors that have a value strictly negative from the center value pixel are encoded with 0; otherwise, they are encoded with 1. A concatenation of these binary values presents a binary number that is multiplied with corresponding weights to generate the LBP code as a decimal value employed for labeling the given pixel. This code is computed as follows:

$$\begin{aligned} LBP_{P,R}(x,y) =\sum _{i=0}^{P-1} s(g_i - g_c)2^i, s(g_i,g_c)= \left\{ \begin{array}{rcr} 1 &{} g_i\ge g_c \\ 0 &{} g_i<g_c \end{array} \right. \end{aligned}$$
(1)

Where P is the number of neighbor pixels and R is the radius, \(g_c\) and \(g_i\) are respectively pixel center and pixels neighbors of position \(i^{th}\). The basic LBP is extending to a circular symmetric area [11], due to the limitation that can provide from LBP using square neighbors front of rotating invariant features. The following equations illustrate the rotation invariant uniform LBP \((LBP^{riu2}_{P ; R})\)

$$\begin{aligned} LBP^{riu2}_{P,R} = \left\{ \begin{array}{rcr} \mathop {\sum }\nolimits _{i=0}^{P-1} s(g_i - g_c)2^i,&{} if U(LBP_{P,R}) \ge 2\\ P+1 &{} otherwise \end{array} \right. \end{aligned}$$
(2)

where the uniform LBP is given by:

$$\begin{aligned} U(LBP_{P,R}) = |s(g_{P-1} - g_{c})-s(g_{0} - g_{c})|+ |s(g_{i} - g_{c}) - s(g_{i-1} - g_{c})|. \end{aligned}$$
(3)

3 Proposed Approach

In this section, we will describe in details our new proposed approach HLBP, in order to improve LBP and obtain more intrinsic image characteristics.

3.1 Homogeneous Local Binary Pattern Method

First of all, we observe that the GAN approach is provides homogeneous spatial regions using m tolerance with a specific criterion function (luminance, contrast ...) that make him robust compared to other methods for analyzing gray tone and color images. Therefore, based on this observation, we propose the HLBP descriptor that aims to improve LBP by using the condition of criterion homogeneity of its pixels \(g_i\) close to the one of the center \(g_c\). Formally, the \(HLBP_{P,R}\) is defined as:

$$\begin{aligned} HLBP_{P,R,m}(x,y) =\sum _{i=0}^{P-1} s(g_i - g_c)2^i, \end{aligned}$$
(4)
$$\begin{aligned} s(g_i,g_c)= \left\{ \begin{array}{rcr} 1 &{} \{|h(g_i)-h(g_c)| \le m \}\\ 0 &{} otherwise \\ \end{array} \right. \end{aligned}$$
(5)

With the same notations as LBP, \(g_c\) is the center of the pixel, \(g_i\) denotes the pixel neighbors at the \(i^{th}\) position, P the number of samples and R the radius. s() represents the sign function with a new additional parameter for HLBP: the homogeneity tolerance \(m \in \mathrm{I\!R}^+ \) with respect to the criterion (luminance, contrast, ....) h which helps to threshold all the neighbor pixels in a specific interval.

To get the HLBP code we need to follow this steps:

  1. 1.

    Firstly, we need to specify the size of the window by choosing the radius R and the sample number of neighbor pixels P.

  2. 2.

    Secondly, we must precise homogeneity tolerance m by considering in our approach the luminance criterion \( h\equiv f\) (f is pixel intensity) to get pixels that are adjacent to \(g_c\) in relation to the criterion mapping.

  3. 3.

    Finally, calculating the code of homogeneous Local Binary Pattern. In this step, the value of the center is substituted with binary code of the neighbors which are thresholded in relation with the center pixel \(|f(g_i)-f(g_c)| \le m \). Precisely, each pixel is sill by homogeneity tolerance m with its neighbors by subtracting the center pixel value. The resulting that is respect threshold values are encoded with 1, otherwise are encoded with 0. Then, all binary numbers are concatenated to obtain decimal code which label the pixel.

To clarify the proposed approach, in figure “Fig. 1” we illustrate the complete procedure with specific parameters of R and P (8,1). We have an example of local pattern with the center \(g_c=190\) we substitute all neighbors \(|g_c-g_i|\) then we compare it with homogeneity tolerance that we choose as \(m=15\) to compose binary code “10001101”.

Fig. 1.
figure 1

Example of HLBP of (P = 8, R = 1) and m = 15.

Full size image

4 Experimental Results

The objective of this section is to figure out the effectiveness of our proposed method in texture classification.

4.1 Texture Dataset

The experiment is realized using one of the most popular databases in texture analysis “Outex TC 0010”. This database is composed of 24 classes of rich surface texture (random motifs, irregular patterns, texture regularity, various granularity, ect), each class contains 180 images with size 128*128. In the total, 4320 texture images are provided, with a variety of angle orientation (0.5, 10, 15, 30, 45, 60, 75 and 90). Some samples of each class are illustrated in figure “Fig. 2”.

Fig. 2.
figure 2

Example of Outex TC 0010 database.

Full size image

4.2 Experimental Procedure

In order to test our proposed method, we use the support vector machine SVM as one of the powerful classifiers in literature where 10 cross validation is employed.

In the proposed method, we use variation of two parameters radius R = 1, 2, 3, 4, 5, 6 and homogeneity tolerance m = 5, 10, 15, 20, 30. This variation allows to extract multiscale HLBP. In order to reduce the feature dimension and computational time in this paper, we fix P to 8 neighbors for all R. With the aim to evaluate the performance of our descriptor, we use Outex_TC_00010. Table 1 illustrates the results of the proposed experiments.

Experiment 1

In experiment 1, we compare our method with the texture descriptor based on LBP “General Adaptive Neighborhood-Minkowski Local Binary Pattern Descriptor” presented in [3].

It is clearly remarkable that our proposed descriptor gives the best classification accuracy compared with GANLBP for \(m=15\) we have 92.48%, 98.40% and 98,17% for R = 1, 2 and 3 respectively. Furthermore, they achieve also good results: 98.17%, 98.66% and 97.87% with different parameters of homogeneity tolerance \(m=15, m=20\) and \(m=30\) respectively. “Fig. 3” illustrates examples of HLBP using different homogeneity tolerances m and radius R. Generally, our approach HLBP gives better performance by capturing more intrinsic characteristics of the image due to the use of sill of homogeneity tolerance m allowing to better take into account the relationships between neighboring pixels.

Fig. 3.
figure 3

Example of images HLBP employing different parameter.

Full size image
Table 1. Classification accuracy (%) of the HLBP and HLBP+LBP descriptor for different values of radius R on the Outex-TC-10 dataset.
Full size table

Experiment 2

In Table 1 for homogeneity tolerance \(m=15\) our approach outperforms LBP for most of radius. However, we did not stop here since we want to increase robustness of HLBP to surpass LBP precisely, in all multiscale variation (radius and homogeneity tolerance), therefore, we proposed the second experiment. The idea is to combine the histograms of HLBP and LBP.

As expected the performance of other descriptors such as GANLBP+LBP and LBP drops for this dataset owing to loose the structural information compared to HLBP+LBP which keep their performance in front of other methods through a margin that shows its robustness with the homogeneity criterion m. For \(m=15\) we have 98.59% 99.54% 99.70% 99.54% 98.91% 99.14% in R = (1, 2, 3, 4, 5 and 6) respectively.

5 Conclusion

In this work we have proposed a new texture classification descriptor HLBP that helps to get a robust discriminative information from an image based on the tolerance threshold m which take into consideration the relationship between neighboring pixels. Therefore, the neighborhoods of pixels much more correspond to the underlying spatial structures. Different experiments are carried out using one of the publicly available texture databases Outex_TC_0010 showing the performance and robustness of our approach.