Petri Nets Validation of Markovian Models of Emergency Department Arrivals

Abstract

Modeling of hospital’s Emergency Departments (ED) is vital for optimisation of health services offered to patients that shows up at an ED requiring treatments with different level of emergency. In this paper we present a modeling study whose contribution is twofold: first, based on a dataset relative to the ED of an Italian hospital, we derive different kinds of Markovian models capable to reproduce, at different extents, the statistical character of dataset arrivals; second, we validate the derived arrivals model by interfacing it with a Petri net model of the services an ED patient undergoes. The empirical assessment of a few key performance indicators allowed us to validate some of the derived arrival process model, thus confirming that they can be used for predicting the performance of an ED.

1 Introduction

Optimisation of hospital’s Emergency Departments (ED) is concerned with maximising the efficiency of health services offered to patients that shows up at an ED requiring treatments with different level of emergency. In this respect the ability to build formal models that faithfully reproduce the behaviour of an ED and to analyse their performances is vital. A faithful model of an ED must consist of at least two components: a model of the patients arrival and a model of the ED services (the various activities that an ED patient may undergo throughout his permanence at the ED). The composition of these two models must be such that the model of patients arrival is used to feed in the services model and the analysis of the performances of the composed model, through meaningful key performance indicators (KPIs), may yield essential indications as to where intervene so to improve the overall efficiency of the ED.

Contribution. In this paper we focus on the problem of deriving a stochastic model of the patient arrivals that is capable of correctly reproducing the statistical character of a given arrivals dataset. To this aim we considered a real dataset relative to the activity of the ED of an hospital of the city of Cantù in northern Italy and which contains different data including the complete set of timestamps of the arrival of each patients over one year (i.e. the year 2015). Based on the statistical analysis of the dataset we derived different instances of Markovian models belonging to different classes (i.e. Markov renewal processes, Markov arrival processes, hidden Markov models) and we showed that only one model instance, amongst those derived, is capable of fully reproducing the statistical character of the dataset, including the periodicity of patients arrivals exhibited by the dataset. To further validate the derived models we developed a formal encoding in terms of stochastic Petri nets. This allowed us to compare the performances of each arrival models, coupled with a model of ED services, through assessment of a KPI formally encoded and accurately assessed through a statistical model checking tool. The obtained results evidenced that one amongst the derived arrival models faithfully match the dataset behaviour hence it can reliably be used for analysing the performances of different ED services.

Paper Organisation. The paper is organised as follows: In Sect. 2 we present the statistical analysis of the dataset and discuss the main statistical characteristics of the patient’s arrival process by considering different perspectives. In Sect. 3 we describe the derivation of different kinds of Markovian models of the patient arrival’s process, specifically we discuss the class of renewal Markov processes given in terms of continuous phase type (CPH) distributions, in Sect. 3.1, the class of Markov arrival process (MAP), in Sect. 3.2 and finally the class of hidden Markov models (HMM), in Sect. 3.3. In Sect. 4 we give the formal encoding of each of the derived models in terms of stochastic Petri nets. Finally in Sect. 5 we present the results of some experiments aimed at assessing a KPI against the model given by the composition of patient arrival models and a simple model of the ED services. Conclusive remarks wrap up the paper in Sect. 6.

Related Work. Literature on modeling of hospital EDs is very wide, faces different kinds of problems and cannot be reviewed in brief. We mention only some works to position ourselves in the literature and point out differences. Many works, such as [2, 3, 12, 14, 21, 24], deal with forecasting the number of patients arrivals but do not experiment with Markovian models. The models proposed in this paper can also be applied to forecasting but we cannot elaborate on this issue due to space limits. Several works, e.g., [20, 22], build a queuing model of ED but do not deal with data driven modeling of the arrival process. Few works, e.g., [31], are concerned with the data-driven development of stochastic models capturing both the patient arrival as well as the services received at the ED. Our paper falls in this category but with respect to other we experiment with a wide range of Markovian processes to model patient arrivals and provide also their Petri net counterpart which can be derived in an automatic manner.

2 Statistical Analysis of the Cantù Hospital Dataset

One way of representing the patient arrival flow is to register the time elapsed between consecutive show ups. To this end let $X_i, i=1,2,3,...$ denote the ith inter-arrival time. Another possibility is to count the number of patients that arrive in an interval of a certain length. We will use intervals whose length is one hour, one day or one week. The associated series are $Y_{\mathcal{H},i}, Y_{\mathcal{D},i}$ and $Y_{\mathcal{W},i}$ with $i=1,2,3,...$ which denote the number of patient arrivals in the ith hour, day and week, respectively. Clearly, the second approach keeps less information with respect to the first but it has the advantage that it relates easily to the periodic nature of the patient arrival process. For example, the series $Y_{\mathcal{H},3+24j}$ with $j=0,1,2,...$ provides the number of arrivals between 2am and 3am during the 1st, the 2nd, the 3rd day, and so on.

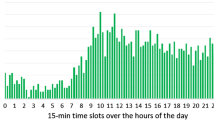
We start off by analyzing the patient arrival pattern inside a day by considering the average and the variance of the number of patient arrivals during the ith hour of the day. I.e., we calculate $E_{\mathcal{H},i}=E\left[ \{Y_{\mathcal{H},i+k}|k=0,24,48,...\}\right]$ and $Var_{\mathcal{H}, i}=Var\left[ \{Y_{\mathcal{H},i+k}|k=0,24,48,...\}\right]$ with $i=1,2,...,24$. In Fig. 1, $E_{\mathcal{H}, i}$ and $Var_{\mathcal{H}, i}$ are depicted as a function of i. The highest number of patient arrivals is registered between 9am and 10am with about 5.9 patients on average. Between 5am and 6am the average number of patients is instead less than 1. As expected, the time of the day has a strong impact on the number of patient arrivals. The variance, $Var_{\mathcal{H}, i}$, has very similar values to those of the mean $E_{\mathcal{H}, i}$, which is compatible with a well-known characteristic of the Poisson process, hence suggesting that the patient arrival process may be adequately modelled through a Poisson process with time inhomogeneous intensity. To further investigate this issue, we calculate the distribution of the number of arrivals during a given hour of the day and compare it the Poisson distribution with the same mean. The resulting probability mass function (pmf) is depicted in Fig. 2 for the interval 1pm-2pm and 5am-6am. The interval 1pm-2pm is the hour of the day where the Poisson distribution differs most from the actual distribution of the number of arrivals (the difference is calculated as the sum of absolute differences in the pmf) while the interval 5am-6am is the hour where the Poisson distribution is most similar to the experimental distribution.

Fig. 1.

Average and variance of number of arrivals in the ith hour of the day.

Fig. 2.

Pmf of number of arrivals between 1pm and 2pm (left) and between 5am and 6am (right) and pmf of the Poisson distribution with equal mean.

The hourly autocorrelation function (acf) is defined as

$$ R_{\mathcal{H},n}=\frac{E[(Y_{\mathcal{H},i}-E[Y_{\mathcal{H},i}])(Y_{\mathcal{H},i+n}-E[Y_{\mathcal{H},i}])]}{Var[Y_{\mathcal{H},i}]} \quad \text{ with } n=1,2,3,... $$

and it is depicted in Fig. 3. The oscillation present in the autocorrelation is due to the changing patient arrival intensity during the day (Fig. 1) and it remains unaltered even for very large values of n.

We study now $Y_{\mathcal{D},i}$ in order to determine if there is a pattern in the patient arrivals during a week. In Fig. 4 we depict $E_{\mathcal{D}, i}=E\left[ \{Y_{\mathcal{D},i+k}|k=0,7,14,...\}\right]$ and $Var_{\mathcal{D}, i}=Var\left[ \{Y_{\mathcal{D},i+k}|k=0,7,14,...\}\right]$ with $i=1,2,...,7$ and observe that there are not large differences between days of the week. The variance differs to a large extent from the average on most days of the week. We calculated also the acf of $Y_{\mathcal{D},i}$ and saw that there is only a very mild correlation between number of arrivals of consecutive days. For this reason we do not aim to model daily correlation with our models.

Fig. 3.

$R_{\mathcal{H}, n}$, i.e., acf of the sequence $Y_{\mathcal{H},i}$ as function of n.

Fig. 4.

Average and variance of number of arrivals in the ith day of the week.

Finally, we look at the series containing the inter-arrival times themselves, $X_i$ with $i=1,2,3...$. The average inter-arrival time is 19.43 and its variance is 483.18. The largest value in the series is 337 min. In Fig. 5 we provide the front and the tail of the probability density function (pdf) of the inter-arrival times, respectively. The autocorrelation present in $X_i$ is depicted in Fig. 6 where there is oscillation due to the fact that a period with high arrival intensity (8am-22pm) are followed by a period with low arrival intensity (22pm-8am). This oscillation however is less easy to interpret than that in Fig. 3 and fades away as n grows because for large values of n there is no deterministic connection between the time of the day of the ith and the $(i+n)$th arrival.

Fig. 5.

Front (left) and tail (right) of the pdf of the inter-arrival times.

Fig. 6.

Acf in the inter-arrival times series.

3 Markovian Models of Patient Arrivals and Their Application to the Cantù Dataset

3.1 Markovian Renewal Process Approximation

The simplest arrival models are renewal processes, i.e., processes in which consecutive inter-arrival times are independent and share the same distribution. To have a Markovian renewal process, we can approximate the observed inter-arrival time distribution by phase type (PH) distributions. A degree-n PH distributions is given by the distribution of time to absorption in a Markov chain (MC) with n transient states (the phases) and one absorbing state [25]. A PH distribution is continuous if a continuous time MC (CTMC) is used and it is discrete if a discrete time MC (DTMC) is applied. In this work we apply continuous PH (CPH) distributions.

In order to understand basic concepts about CPH models, consider the degree-3 CPH distribution depicted in Fig. 7 where numbers inside a state indicate the initial probability of the state and numbers on the arcs are transition intensities. The gray state is the absorbing one. A CPH distribution is conveniently described by the vector of initial probabilities of the transient states denoted by $\alpha$ (we assume in this work that the initial probability of the absorbing state is 0) and the matrix, denoted by Q, containing the transition intensities among the transient states and the opposite of the sum of the intensities of the outgoing transitions in the diagonal (this allows to determine the transition intensities toward the absorbing state). For the CPH in Fig. 7 we have

$$\begin{aligned} \begin{aligned} \alpha =(0.2,~0.8,~0),\\ Q=\left( \begin{array}{ccc} -3 &{} 2 &{} 0 \\ 2 &{} -3 &{} 1 \\ 0 &{} 2 &{} -8 \end{array} \right) \end{aligned} \end{aligned}$$

(1)

Fig. 7.

Graphical representation of the degree-3 PH distribution used as example (left) and its pdf (right).

The pdf of a CPH distribution can be obtained based on basic properties of CTMCs as $f(x)=\alpha e^{Qx}(-Q)\mathrm{1I}$ where $\mathrm{1I}$ is the column vector of 1s. From the previous the moments can be derived and have the form $m_i=i! \alpha (-Q)^{-i}\mathrm{1I}$. We depicted the pdf of the above example in Fig. 7. Several well-known distributions are contained in the family of CPH distributions. The exponential distribution is a degree-1 CPH distribution. Also hyper-exponential and Erlang distributions are simple to represent as CPH distributions.

Our aim is to find $\alpha$ and Q such that the pdf of the associated CPH distribution is a good approximation of the pdf of the patient inter-arrival times. There are two families of approaches to face this problem. The first is based on the maximum likelihood principle, i.e., having set the degree n to a given value, $\alpha$ and Q are searched for such that it is most likely to reproduce the empirical value at hand. Techniques based on this approach suffers from two drawbacks: first, the number of parameters in $\alpha$ and Q grows quadratically with n; second, the vector-matrix representation provided by $\alpha$ and Q is redundant and this gives rise to difficult optimization problems. One of the first methods in this line is described in [9] and an associated tool is presented in [17]. The second family of approaches is based on matching a set of statistical parameters of the available data. The set usually includes only moments [5, 18] but can refer also to characteristics of the pdf [4] or the cumulative distribution function at some points [15]. We apply here moment matching techniques which require much less computational effort, result in good fit of the inter-arrival distribution under study and have the advantage of considering a non-redundant representation (based on the moments every entry of $\alpha$ and Q is determined directly).

It is known that a degree-n CPH distribution is determined by $2n-1$ moments (see, e.g., [11]). Not any valid $2n-1$ moments can be realized however by a degree-n CPH distribution. The approaches proposed in [5, 18] construct a degree-n CPH distribution matching $2n-1$ moments if the moments can be realized by a degree-n CPH distribution. The methods are implemented in the BuTools package (http://webspn.hit.bme.hu/~butools/) and we applied them with $n=1,2$ and 3. In the following we report the initial probabilities and the transition intensities of the resulting CPH distributions:

• $n=1$ (one moment matched): $\alpha =(1)$ and $Q=(-0.051453)$

• $n=2$ (three moments matched): $\alpha =(0.0409229,~0.959077)$ and

  $$ Q=\left( \begin{array}{cc} -0.0213213 &{} 0.0213213 \\ 0 &{} -0.0570911 \end{array} \right) $$

• $n=3$ (five moments matched): $\alpha =(0.0284672,0.881506,0.0900266)$ and

  $$ Q=\left( \begin{array}{ccc} -0.699657 &{} 0 &{} 0 \\ 0.0667986 &{} -0.0667986 &{} 0 \\ 0 &{} 0.0260063 &{} -0.0260063 \end{array} \right) $$

The pdf of the above CPH approximations is depicted in Fig. 8. With $n=1$, the resulting exponential distribution, which captures only the first moment, is a bad approximation both of the front and of the tail. With $n=2$ the tail is approximated well but the shape of the front is rather different. With $n=3$ both the front and the tail are captured to a satisfactory extent.

Fig. 8.

Front (left) and tail (right) of pdf of CPH distribution approximations of the inter-arrival time distribution based on moment matching.

It is evident that, even if the inter-arrival time distribution is well approximated, a renewal process is significantly different from the data set under study because it cannot exhibit correlation and periodicity. Nevertheless, as we will show in Sect. 5, the renewal process with a proper PH distribution can give good approximation of some performance indices. In the following we propose models in which there is correlation in the inter-arrival time sequence.

3.2 Markovian Arrival Processes

Continuous time Markovian arrival processes (MAP), introduced in [26], are a wide class of point processes in which the events (arrivals) are governed by a background CTMC and they can be seen as the generalization of the Poisson process allowing for non-exponential and correlated inter-arrival times. We provide here a brief introduction to MAPs.

The infinitesimal generator matrix of the underlying CTMC of an n-state MAP will be denoted by the $n\times n$ matrix D. Arrivals can be generated in two ways. First, in each state i of the CTMC a Poisson process with intensity $\lambda _i$ is active and can give rise to arrivals during a sojourn in the state. Second, when in the CTMC a transition from state i to j occurs an arrival is generated with probability $p_{i,j}$. A convenient and compact notation to describe a MAP is obtained by collecting all intensities in two matrices, $D^{(0)}$ and $D^{(1)}$, in such a way that $D^{(0)}$ contains the transition intensities that do not generate an event and $D^{(1)}$ those that give rise to one, including the intensities of the Poisson processes in the diagonal of $D^{(1)}$. Moreover, the diagonal entries of $D^{(0)}$ are set in such a way that we have $D^{(0)}+D^{(1)}=D$. Accordingly, the entries of $D^{(0)}$ and $D^{(1)}$ are

$$\begin{aligned} \forall i,j,i\not =j&:\quad D^{(0)}_{i,j}=(1-p_{i,j})D_{i,j},\quad D^{(1)}_{i,j}=p_{i,j}D_{i,j} \\ \forall i&:\quad D^{(0)}_{i,i}=-\sum _{\forall j, j\not = i} D_{i,j}-\lambda _i, ~~ D^{(1)}_{i,i}=\lambda _i \end{aligned}$$

In most of the literature, the vector of steady state probabilities of the background chain, denoted by $\gamma =(\gamma _1,...,\gamma _n)$, is used as initial probability vector of the model¹. In this paper we will do the same. As an example, consider the 2-state MAP described by

$$\begin{aligned} D^{(0)}=\left( \begin{array}{ll} -3 &{} 1 \\ 0 &{} -7 \end{array} \right) \quad D^{(1)}=\left( \begin{array}{ll} 0 &{} 2 \\ 2 &{} 5 \end{array} \right) \quad D=\left( \begin{array}{ll} -3 &{} 3 \\ 2 &{} -2 \end{array} \right) \end{aligned}$$

(2)

which implies that during a sojourn in state 1 no arrivals are generated while during a sojourn in state 2 a Poisson process with intensity equal to 5 is active. Moreover, a transition from state 1 to state 2 generates an arrival with probability 2/3 while transitions from state 2 to 1 are always associated with an arrival. The steady state probabilities of the background chain are $\gamma =(0.4,0.6)$.

The well-known Poisson process is a MAP with a single state ($n=1$). The renewal process used in Sect. 3.1 can be expressed in terms of a MAP by setting $D^{(0)}=Q,~~D^{(1)}=(-Q)\mathrm{1I}\alpha$. The Markov modulated Poisson process, in which a Poisson process is active in every state of a background CTMC, is a MAP whose $D^{(1)}$ matrix contains non-zero entries only in its diagonal.

As for CPH distributions, two families of parameter estimation methods have been developed in the literature: the first based on the maximum-likelihood principle ([13, 27, 29]) and the second based on matching a few statistical parameters of the arrival process. The representation given by $D^{(0)}$ and $D^{(1)}$ contains $2n^2-n$ parameters (in every row of $D=D^{(0)}+D^{(1)}$ the sum of the entries must be zero) and it is redundant as an n-state MAP is determined by $n^2+2n-1$ parameters ($2n-1$ moments of the inter-arrival times and $n^2$ joint moments of consecutive inter-arrival times; see [30] for details). Maximum-likelihood based methods suffers from the same drawbacks described before in case of CPH distributions. In this paper we experiment with methods that belong to the second family of approaches.

A 2-state MAP is determined by 3 moments of the inter-arrival times and the lag-1 auto-correlation of the inter-arrival time sequence [10, 30]. Our sequence has however such a lag-1 auto-correlation that cannot be realized with only 2 states. In [19] a method was proposed that creates a MAP with any 3 inter-arrival time moments and lag-1 auto-correlation. This method, implemented in the BuTools package, provides the following 6-state MAP:

$$\begin{aligned} D^{(0)}=\left( \begin{array}{c cc c c c} -0.0293 &{} 0.0293 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} -0.1883 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -0.0103 &{} 0.0103 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -0.0989 &{} 0.0989 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -0.0989 &{} 0.0989 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -0.0989 \end{array} \right) \end{aligned}$$

(3)

$$\begin{aligned} D^{(1)}=\left( \begin{array}{cccccc} 0. &{} 0. &{} 0. &{} 0. &{} 0. &{} 0. \\ 0.023 &{} 0.1288 &{} 0.0002 &{} 0.0362 &{} 0. &{} 0. \\ 0. &{} 0. &{} 0. &{} 0. &{} 0. &{} 0. \\ 0. &{} 0. &{} 0. &{} 0. &{} 0. &{} 0. \\ 0. &{} 0. &{} 0. &{} 0. &{} 0. &{} 0. \\ 0.0037 &{} 0.0207 &{} 0.0004 &{} 0.074 &{} 0. &{} 0. \end{array} \right) \end{aligned}$$

(4)

with which the steady state probability vector of the background Markov chain is $\gamma =(0.149503, 0.153343, 0.0126432, 0.22817, 0.22817,0.22817)$.

As opposed to the approach used in Sect. 3.1, in the arrival process generated by a MAP there can be correlation between subsequent inter-arrival times. In Fig. 9 we depict the acf in the inter-arrival time sequence generated by the above 6-state MAP and that computed on the available dataset. As guaranteed by the applied method for $n=1$ the auto-correlation is matched exactly but then it fails to follow the auto-correlation of the data. The acf of the sequence counting the number of arrival per hour generated by the same MAP is given instead in Fig. 10 which is very different from the that of the dataset. In the number of patients per day sequence the auto-correlation of the 6-state MAP with $n=1$ is 0.00469433, i.e., it is negligible, as opposed to that in the data where it is 0.22.

Fig. 9.

Acf of the inter-arrival time sequence of the original data and of the MAP given in (3-4).

Fig. 10.

Acf of the number of arrivals per hour sequence of the original data and of the MAP given in (3-4).

As seen above, 6 states are necessary to match three moments and just the lag-1 autocorrelation of the inter-arrival times. This indicates that a MAP with large number of states is necessary to capture the peculiar statistical features of the patient arrival process. General purpose MAP fitting techniques are not applicable however with such large number of states.

3.3 Hidden Markov Processes

A Hidden Markov model (HMM) [28] can be thought of as a generalisation of a DTMC for which an external observer cannot directly see the states but only observe some output whose probability to be emitted depends on the state. In practice an HMM is characterised by: i) a set of states $\mathcal{S}=\{s_1,\ldots ,s_n\}$; ii) a set of possible observations $\mathcal{O}=\{o_1,\ldots ,o_m\}$; iii) a $n \times n$ state-transition probability matrix $A=\{a_{ij}\}$ with $a_{ij}$ being the probability of transitioning from state $s_i$ to $s_j$; iv) a $n \times m$ state-observation probability matrix $B=\{b_{ij}\}$ where $b_{ij}$ is the probability of observing $o_j$ when the chain enters state $s_i$; v) an initial distribution over the set of states S denoted by $\alpha$. Accordingly, an HMM is completely determined by the triple $(\alpha ,A,B)$.

There exist three classical problems for HMM, all of which requiring a sequence of observations $O=(o_1, \ldots o_k)$. The first one is the evaluation problem: given an HMM by $(\alpha ,A,B)$ and a sequence O, calculate the probability that the HMM produces O. The second, called decoding problem, consists of determining the most probable state sequence given a HMM and a sequence O. The third one, the learning problem, has only O as input and is about finding such triple $(\alpha ,A,B)$ with which observing O is most probable.

In this paper we focus on the third type of problem and in particular we develop and study two HMMs aimed at reproducing the statistical characteristics of the patients’ arrival dataset (described in Sect. 2). We start off with a rather coarse-grained (only 3-state) but general HMM, which reveals to be capable of reproducing only marginally the auto-correlation characteristics of the patients arrivals data. Then we propose a HMM with particular underlying DTMC that shows good agreement with the dataset from a statistical point of view.

A 3 States HMM. Here we consider a 3 state HMM in which every time slot corresponds to one hour and the possible observations are $\mathcal{O}=\{0,1,...,14\}$ interpreted as the number of patient arrivals per hour². This means that the sequence generated by the HMM has to be post-processed if we need to specify the exact arrival instance for each patient. This post-processing will consist of distributing the arrivals in uniform manner inside the hour.

There are 2 free parameters in $\pi$, $3 \times 2=6$ in A and $3\times 14=42$ in B (because $\pi$ must be normalized and also the rows both in A and B must be normalized). We applied the Baum-Welch algorithm [8] to determine the optimal parameters starting from several initial parameter sets chosen randomly. With this relatively small model, the final optimal parameters obtained by the Baum-Welch algorithm are independent of the initial values (apart from permutations of the states). The obtained HMM is with $\pi =(0,1,0)$ and

$$\begin{aligned} \nonumber A&=\left( \begin{array}{ccc } 0.865 &{} 0.135 &{} 0 \\ 0 &{} 0.835 &{} 0.165 \\ 0.134 &{} 0 &{} 0.866 \end{array}\right) \quad B=\left( \begin{array}{cccccc} 0.0007 &{} 0.0227 &{} 0.0807 &{} 0.1569 &{} 0.1756 &{} 0.1731 \\ 0.024 &{} 0.1103 &{} 0.2237 &{} 0.2249 &{} 0.19 &{} 0.1323 \\ 0.3533 &{} 0.3752 &{} 0.1989 &{} 0.0583 &{} 0.0116 &{} 0.0025 \end{array} \right. \\&\left. \begin{array}{ccccccccc} 0.1652 &{} 0.0991 &{} 0.0625 &{} 0.0292 &{} 0.0177 &{} 0.009 &{} 0.0058 &{} 0.0006 &{} 0.0006 \\ 0.0544 &{} 0.0303 &{} 0.0052 &{} 0.0025 &{} 0 &{} 0 &{} 0.0004 &{} 0 &{} 0\\ 0&{}0&{} 0&{} 0&{} 0&{} 0&{} 0&{} 0 &{} 0 \end{array} \right) \end{aligned}$$

(5)

The mean number of arrivals per hour with the above HMM is 3.0862 and its variance is 5.67669 while in the data trace the mean and the variance are 3.08676 and 5.69061, respectively.

In Fig. 11 (left) we depict the autocorrelation of the number of arrivals per hour. As one can expect, the 3-state HMM is not able to reproduce the sustained oscillation present in the data shown in Fig. 3 (autocorrelation is negligible for $n\ge 10$) but does much better than the 6-state MAP given in (3-4) (see Fig. 10).

A 24 States HMM. In order to have a model that is able to exhibit oscillation in the autocorrelation function of the number of arrivals per hour, we define a 24-state HMM in which each state corresponds to an hour of the day and the transition probabilities are such that the process deterministically cycles through the 24 states. Accordingly, A is $24\times 24$ and its entry in position (i, j) is 1 in $j=(i+1)\pmod {24}$ and it is 0 otherwise. The initial probability vector is set to $\pi =(1,0,...,0)$. As before, the possible observations are $\mathcal{O}=\{0,1,...,14\}$.

The Baum-Welch algorithm is such that parameters set to 0 initially remain 0. Consequently, the algorithm does not change the matrix A and the vector $\pi$ and has an effect only on the entries of B. The number of parameters is larger, it is $24\times 14=336$, but thanks to the deterministic behavior of the underlying DTMC the Baum-Welch algorithm determines the parameters in a single iteration. With the resulting HMM the mean number of arrivals per hour is 3.08619 while the variance is 5.67465. The hourly autocorrelation is shown in Fig. 11 (center). This model provides very similar hourly autocorrelation to that of the data set.

Fig. 11.

Comparing the autocorrelation function (acf) of the dataset with that of the 3-state HMM (left), the 24-state HMM with deterministic (center) and non-deterministic (right) underlying Markov chain.

We experimented also with a 24-state HMM letting the Baum-Welch algorithm to change any entry of the matrix A (i.e., the initial entries of A are random strictly greater than 0 and strictly smaller than 1). This way the number of free parameters is $24\times 23+24\times 14=888$. With this large number of parameters the Baum-Welch algorithm performs 4798 iterations and requires about 3 min of computation time on a standard portable computer. The resulting HMM has mean and variance equal to 3.08539 and 5.67468, respectively. The matrix A has a similar structure to the one before but the probabilities of going to the next state is not 1 but a value between 0.6 and 0.99. The resulting autocorrelation structure is depicted in 11 (right). With the non-deterministic underlying Markov chain the autocorrelation cannot exhibit sustained oscillation and the autocorrelation vanishes after about 150 hours (i.e., 6–7 days).

4 Petri Nets Model of the Patients Arrival Process

In order to assess the validity of the patients arrivals models presented in Sects. 3.1–3.3, we define a formal encoding of, respectively, the renewal Markov arrival model, the MAP and the HMM models, in terms of a superset of the Generalised Stochastic Petri Net (GSPN) [23] formalism, that we refer to as extended GSPN (eGSPN). Specifically, eGSPN is a class of stochastic Petri nets that, like GSPN, allows for combining immediate and stochastic timed transitions, but that, differently from the original GSPN, is not constrained to exponentially distributed timed transitions. We will use the eGSPN models described in this section to run a validation through the assessment of a number of key performance indicators (KPIs, see Sect. 5). For the sake of space we only give the syntactic elements necessary for characterizing an eGSPN, while we omit the formal semantics. We remark that if it is well known that the semantics of a GSPN can be reduced (by elimination of vanishing markings) to a CTMC process, equivalently it can be shown that the semantics of an eGSPN model corresponds to a generalised semi-Markov process (GSMP) [16], i.e. a larger class of stochastic processes that subsumes CTMCs.

Definition 1

An eGSPN is defined by a 8-tuple (P, T, I, O, H, del, W, pol) where:

• P: set of places,

• T: set of transitions,

• $I,O,H: T \rightarrow Bag(P)$: are the input (I), output (O) and inhibition (H) arc functions (where Bag(P) is the set of multi-sets built on P),

• $del: T \rightarrow dist(\mathbb {R}_{\ge 0})$: is a function that associates transitions with delay distributions (where $dist(\mathbb {R}_{\ge 0})$ is the set of probability distributions with non-negative real support),

• $W:T\rightarrow \mathbb {R}^+$: is the weight function that maps transitions onto positive real numbers,

• $pol: T\rightarrow \{\textit{single}, \textit{infinite}\}$ associates each transition with a semantics which, in this paper, is either single server or infinite server.

I, O and H give the multiplicities of arcs of connecting places of P with transitions of T. The function del allows to associate a generic probability distribution with the delay of firing of an enabled transition. Observe that since we put no restriction on the nature of the delay distributions, identical schedules for different transitions may have a positive probability (in case of non-continuous delay distributions): in this case the weight W is used to chose in a probabilistic manner the next transition to fire. In this paper, we will use four kinds of delay in del. Immediate transitions are associated with constant zero firing time. Exponential transitions fire after a delay described by the exponential distribution. Deterministic transitions are associated with fixed positive delay. Finally, uniform transitions have a firing time according to the uniform distribution. For what concerns pol, single server and infinite server semantics are as usual [23].

4.1 Petri Net Encoding of Markov Renewal Arrival Models

In the following we define a Petri net that represents the patient arrival process in which inter-arrival times follow a degree-n PH distribution given by the vector-matrix pair, $(\alpha , Q)$ (as described in Sect. 3.1).

The set of places is $P=\{P_0,P_1,...,P_n,P_{n+1},Arrs\}$ where $P_0$ will be used to start the process according to $\alpha$ after each arrivals, $P_1,...,P_n$ correspond to the transient states of the PH distribution, $P_{n+1}$ corresponds to the absorbing state and Arrs is the place where patient arrivals are accumulated. The set of immediate transitions is $T_\mathcal{I}=\{t_{arr} \cup \{t_{0,i}: 1\le i \le n, \alpha _i > 0\} \}$ where the weight of transition $t_{arr}$ is 1 and the weight associated with transitions $t_i,1\le i \le n, \alpha _i > 0$ is $\alpha _i$. Firing of $t_{arr}$ will generate an arrival while firing of a transition $t_i$ will imply that phase i is chosen as initial state in the MC associated with the PH distribution. Exponential transitions are used to model the transitions among the phases. Their set is $T_\mathcal{E}=\{\{t_{i,j}:1 \le i,j\le n, Q_{i,j} > 0\}\cup \{t_{i,n+1}:1 \le i \le n, \sum _{j=1}^n Q_{i,j}<0\}\}$ where the first set in the union contains transitions among the transient states while the second those to the absorbing state. Accordingly, the rate associated with these transitions is $Q_{i,j}$ for transition $t_{i,j}$ if $1 \le i,j \le n$ and it is $-\sum _{j=1}^n Q_{i,j}$ for transition $t_{i,n+1}$ with $1\le i \le n$. The set of transitions is $T=T_\mathcal{I}\cup T_\mathcal{E}$. Transition $t_{i,j}, 0 \le i,j \le n+1$, if present, is with input bag $\{P_i\}$ and output bag $\{P_j\}$. Input bag of transition $t_{arr}$ is $\{P_{n+1}\}$ and its output bag is $\{P_0,Arrs\}$. In Fig. 12 we depict the PN representation of the arrival process in which inter-arrival times are PH according to the example proposed in Sect. 3.1. For immediate transitions (black bars) we specify the weight while for exponential ones (white rectangles) the rate.

4.2 Petri Net Encoding of Markov Arrival Models

Now we turn our attention to MAPs defined by the pair of matrices $D^{(0)}$ and $D^{(1)}$ as described in Sect. 3.2.

In case of an n-state MAP, the set of places is $P=\{P_0,P_1,...,P_n, Arrs\}$ where $P_0$ is used to start to model, places $P_0,...,P_n$ correspond to the states of the MAP and place Arrs is where the patients are gathered. A set of immediate transitions is used to start the process according to the steady state probabilities, $\gamma$. This set is $T_\mathcal{I}=\{t_{0,i}: 1\le i \le n, \gamma _i > 0\}$ in which each transition $t_{0,i}$ is associated with weight $\gamma _i$. In the set of exponential transitions, a transition is associated with each positive entry of the matrices $D^{(0)}$ and $D^{(1)}$. Accordingly, the set is $T_\mathcal{E}=\{\{t_{i,j}:1 \le i,j\le n, {D^{(0)}}_{i,j}> 0\}\cup \{t^*_{i,j}:1 \le i,j \le n, {D^{(1)}}_{i,j}> 0\}\}$ where the second set in the union is the set of transitions that generate arrival. The rates of transitions $t_{i,j}$ and $t^*_{i,j}$ are ${D^{(0)}}_{i,j}$ and ${D^{(1)}}_{i,j}$, respectively. The set of transitions is $T=T_\mathcal{I}\cup T_\mathcal{E}$. Transition $t_{i,j}, 0 \le i,j \le n$, if present, is with input bag $\{P_i\}$ and output bag $\{P_j\}$. Transition $t^*_{i,j}, 0 \le i,j \le n$, if present, is with input bag $\{P_i\}$ and output bag $\{P_j,Arrs\}$. Figure 13 shows the eGSPN encoding of the arrival process using the MAP specified in (2).

Fig. 12.

eGSPN encoding of PH arrival model with PH specified in (1) in Sect. 3.1

Fig. 13.

eGSPN encoding of MAP arrival model with MAP given in (2) in Sect. 3.2

4.3 Petri Net Encoding of HMM Arrival Models

In the following we provide the PN encoding of an n-state HMM given by the triple $(\pi ,A,B)$, assuming that the observations are interpreted as number of arrivals in an hour and distributing the arrivals within the hour in a uniform manner.

The set of places is $P=\{P_0,P_1,...,P_n, O_1,...,O_n,W,Arrs\}$ where $P_0$ is used to start the model according to the initial probabilities given in $\pi$, places $P_1,...,P_n$ correspond to the states of the background chain, places $O_i,1\le i \le n$ are used to emit the observation when the background chain enters state i, place W collect arrivals that has to be distributed in a given hour, and place Arrs gathers all arrivals. A set of immediate transitions, $T_{\mathcal{I},1}=\{t_{0,i}: 1\le i \le n, \pi _i > 0\}$, is used to start the process according to $\pi$. A set of deterministic transitions models the background Markov chain: $T_\mathcal{D}=\{t_{i,j}:1 \le i,j\le n, {A}_{i,j}> 0\}$ in which all transitions are associated with fixed delay of one time unit and $t_{i,j}$, if present, is with weight $A_{i,j}$. Another set of immediate transitions, $T_{\mathcal{I},2}=\{t^{(o)}_{i,j}:1 \le i \le n, 1\le j \le m, {B}_{i,j}> 0\}$ in which $t^{(o)}_{i,j}$ is with weight $B_{i,j}$, is used to emit observations. In order to distribute the arrivals inside an hour a uniform transition is used $t_{dist}$ whose minimal firing time is 0 and maximal firing time is 1. The overall set of transitions is $T=T_{\mathcal{I},1} \cup T_{\mathcal{I},2} \cup T_\mathcal{D} \cup \{t_{dist}\}$. Input bag and output bag of transition $t_{0,i}$ is $\{P_0\}$ and $\{P_i,O_i\}$, respectively. Input bag and output bag of transition $t_{i,j}$ is $\{P_i\}$ and $\{P_j,O_j\}$, respectively. Input bag of transition $t^{(o)}_{i,j}$ is $\{O_i\}$ while its output bag contains $j-1$ times place W in order to generate the right number of arrivals. Input bag and output bag of transition $t_{dist}$ is $\{W\}$ and $\{Arrs\}$, respectively. Transition $t_{dist}$ is the only one associated with infinite server policy.

Fig. 14.

Part of Petri net encoding of the 3-state HMM model given in (5).

In Fig. 14 we show a part of the PN that represents the 3-state HMM given in (5). Deterministic transitions are drawn as gray rectangles and are provided with their weight. The single uniform transition is drawn as a black rectangle and labeled with its firing interval. Number of occurrences of a place in a bag is written as a label to the corresponding arc if it is different from 1. In the figure we omitted transitions $t^{(o)}_{i,\bullet }$ with $i=1,2$ and connecting arcs.

5 Validation Through KPI Assessment

In order to validate the different models of patients arrival process we have coupled each of them with an elementary model of the ED services a patient may go through during his permanence at the ED and assessed meaningful KPI on the coupled models. For the sake of simplicity we assumed the ED patient flow consisting of a simple pipeline of 3 services: triage, visit and discharge for each of which we considered exponentially distributed service time with the following settings³: triage$\sim$Exp(12), the visit$\sim$Exp(6) and discharge$\sim$Exp(60) (i.e. visit is assumed to be the slowest while discharge the fastest service). Figure 15 shows the eGSPN encoding of the ED service model: notice that place $Arrs$ is shared with the eGSPN models of the patient arrivals (representing the composition of the two models). To validate each arrival model we compared their performance with that resulting by the simulation of the ED service model (Fig. 15) with the actual arrivals of the dataset (for this we generated an eGSPN encoding of the dataset arrivals).

Fig. 15.

A simple eGSPN model of ED services consisting of 3 pipelined services (to be composed by overlapping of place $Arrs$ with an eGSPN model of the patients arrivals).

One relevant KPI that we considered for comparing the performances of the different patient arrival models coupled with the ED services model is:

$\phi _1\equiv ~pmf~of~the~number~of~patients~in~the~ED~during~a~periodic~time-window.$

We formally specified $\phi _1$ by means of the Hybrid Automata Specification Language (HASL) [7] and assessed it through the statistical model checking platform Cosmos [1, 6]. HASL model checking is a procedure that takes a stochastic model (in terms of an eGSPN) as input as well as a linear hybrid automaton (LHA) together with a list of quantities $Z_i$ to be estimated. The procedure uses the LHA as a monitor (i.e., a filter) to select trajectories which are automatically sampled from the eGSPN. The statistics, which are stored in the LHA variables, are collected on the trajectories and used to obtain a confidence interval for each quantity $Z_i$ associated with the LHA monitor (we refer the reader to [7] for more details).

Figure 16 depicts the HASL specification for $\phi _1$. The LHA consists of 4 states ($l_0$,$l_{ on }$,$l_{ off }$,$l_{ end }$), 1 clock variable (t), 2 stopwatches ($t_a$, $t_p$), $M+1$ real valued variables $x_i$ ($0\le i\le M$, whose final value is the probability that i patients have been observed in the ED during the periodic time windows), plus a number of auxiliary variables and parameters.

Fig. 16.

Automaton for measuring the pmf of the number of patients in the ED.

The LHA is designed so that measuring, along a trajectory, is periodically switched ON/OFF (parameter $TP$ being the ON period duration) and stops as soon as the $NP$-th period has occurred. In the initial state $l_0$ the occurrence of any transition is ignored ($l_0\xrightarrow {\text {ALL}, \textit{t} < \textit{initT}, \emptyset }l_0$) for an initial transient of duration initT (initT being a parameter of the LHA) at the end of which the LHA moves to $l_{ on }$ ($l_0\xrightarrow {\sharp ,\textit{t} \ge \textit{initT}, \emptyset }l_{ on }$). In $l_{ on }$ the LHA reacts to the occurrence of patients arrival as well as patients discharge events. When a patient arrives (resp. is discharged) while i patients are in the ED ($l_{ on }\xrightarrow [\{n\mathrel {+}=1, x_{i}\mathrel {+}=t_a, t_a=0\}]{\{\textit{tarr}\}, n=i\wedge \textit{tp}< TP \wedge \textit{tp}< TP \wedge \textit{np} < NP }l_{ on }$, resp. $l_{ on }\xrightarrow [\{n\mathrel {-}=1, x_{i}\mathrel {+}=t_a, t_a=0\}] {\{\textit{discharge}\}, n=i\wedge \textit{np} < NP }l_{ on }$) the patients counter n is incremented (resp. decremented), the duration of the last time interval on which the ED contained i patients is added up to $x_i$, and the arrival stopwatch $t_a$ is reset. Any event different from a patient’s arrival/discharge is ignored in $l_{ on }$ ($l_{ on }\xrightarrow [\textit{tp}< TP \wedge np< \textit{NP},\textit{t}_p < \textit{TP}, \emptyset ]{ \text {ALL}\setminus \{tarr,discharge\}}l_{ on }$). As soon as the ON-period expires ($t_p= TP$) the LHA moves from $l_{ on }$ to $l_{ off }$ where it suspends registering the duration of different number of patients in the ED. In that respect observe that if the end of an ON-period corresponds with i patients being in the ED, the variable $x_i$ (which accumulates the durations of i patients being in the ED) is added up with the time elapsed since the arrival of the last patient ($l_{ on }\xrightarrow [np\mathrel {+}=1, x_{i}\mathrel {+}=t_a, t_p=0\}]{\sharp , np< NP \wedge tp= TP \wedge n=i}l_{ off }$), hence the end of the ON-period is made corresponding with the end of the duration of having i patients in the ED. In $l_{ off }$ the automata ignores any event ($l_{ off }\xrightarrow {\text {ALL},\textit{tp}< 24- TP , \emptyset }l_{ off }$) while it switches back to $l_{ on }$ as soon as the reciprocal (w.r.t. 24 hours) of the ON-period duration elapsed ($l_{ off }\xrightarrow {\sharp ,\textit{tp}= 24- TP , \{t_a=0\}}l_{ on }$) and in so doing the timer $t_a$ (which stores the duration of the occupation at i patients since the last arrival/departure) is reset so that it can correctly be used in the freshly started ON-period. Finally, the LHA stops monitoring as soon as $NP$ ON-periods have been observed along the monitored trajectory: at that moment each $x_i$ is normalised w.r.t. the sum of all $x_i$, hence on ending the monitoring of trajectory $x_i$ is assigned with the probability that the i patients have been observed in the ED during NP observed periods ($l_{ on }\xrightarrow {\sharp ,\textit{np}= NP ,\{x_0=\frac{x_0}{\sum _{i=\!0}^{M} x_i},\ldots , x_{M}=\frac{x_{M}}{\sum _{i=0}^{M} x_i}\}}l_{ end }$). Observe that such an LHA can also be used for “non-periodic” measures: it suffices to set $TP =0$. The HASL specification for $\phi _1$ is completed by the list of HASL expressions $AVG (last(x_i))$ which indicate that a confidence interval for average of the last value that $x_i$ has at the end of an accepted trajectory is computed by COSMOS.

Fig. 17.

Pmf of the num. of patients in the ED computed through 3-phases PH renewal model, 6-state MAP, 3-state HMM and 24-state HMM versus dataset model over the whole day (left), during a low-arrival hour (center) and high-arrivals hour (right).

Figure 17 depicts plots computed with the COSMOS tool and resulting from assessing specification $\phi _1$ (i.e., the pmf of the number of patients in the ED) against the eGSPN models of the patient arrivals coupled with the 3-services model of the ED (Fig. 15). Plotted results refer to a 1-year (365 days) observation window and have been computed as 99.99% confidence interval of $10^{-3}$ width. The plot on the left refers to the pmf measured without taking into account any specific time-window over the day (continuous measuring over 24 h for 365 days), while the plots in the center and on the right refer to periodic measuring over a 1-hour period, at low arrival intensity (from 2am to 3am, center picture) and at high arrival intensity (from 11am to 12pm, right picture), respectively. The obtained results witness the clear advantage of the HMM24 model over the rest: if when no specific hour of the day is considered the pmf of the 3-phases renewal model and of the 6-states MAP provide an acceptable approximation of the pmf computed w.r.t. to dataset (red dashed plot) and the pmf of the HMM3 and HMM24 are essentially indistinguishable, this is no longer the case when the pmf is computed on a specific time window as shown in the center and right plots. Only the pmf of the HMM24 matches that of the dataset during a low-arrivals [2am,3am] window and a high-arrival [11am,12pm] window: the pmf of the renewal and map models instead are essentially identical to those measured continuously while that for the HMM3 exhibits a slight tendency towards matching the pmf of the dataset at low-arrivals but completely fails to do so when arrivals become intense.

6 Conclusion

In this paper we have considered the problem of deriving stochastic models that are capable to accurately reproduce the statistical nature of patients arrivals process observed on a real dataset of the ED of an Italian hospital. Starting from the statistical analysis of the dataset we figured out relevant characteristics of the patients arrival process, e.g., the hour of the day with highest/lowest number of arrivals, the moments, the variance and, most importantly, the periodic nature of number of arrivals-per-hour, the latter shown by auto-correlation function estimated on the dataset. In quest for a model capable of capturing all of these aspects we have considered different classes of Markovian models namely, renewal Markov processes, Markov arrival processes and hidden Markov models. Based on the considered dataset, we derived for each class a few model instances (1, 2 and 3-phase PH renewal process, a 6-state MAP, a 3-state and a 24-state HMM). We assessed the quality of each model by comparing their basic statistical characteristics (i.e., moments, auto-correlation) with those assessed initially on the dataset. To complete the validation process we then considered the coupling of patient’s arrival model with a simple Petri net model of the ED services. To this aim we gave a formal encoding of the different kind of patients arrival Markov models in form of stochastic Petri nets. We then evaluated each model by estimation of the pmf of the number of patients in the ED during a given period of the day which we formally encoded and accurately assessed through HASL statistical model checking. The obtained results showed that the 24-states HMM is the only model, amongst those considered, capable of reproducing the statistical characteristics of the dataset, including the hourly periodicity of the arrivals. Therefore such a model could be validly used for predicting the performances of a realistic ED design once coupled with a more realistic model of the internal ED services.