A Categorical Semantics for Guarded Petri Nets

Abstract

We build on the correspondence between Petri nets and free symmetric strict monoidal categories already investigated in the literature, and present a categorical semantics for Petri nets with guards. This comes in two flavors: Deterministic and with side-effects. Using the Grothendieck construction, we show how the guard semantics can be internalized in the net itself.

1 Introduction

Category theory has been used to study Petri nets at least since the beginning of the nineties [6]. Throughout this time, the main effort in this direction of research consisted in showing how Petri nets can be thought of as presenting various flavors of free monoidal categories [2, 5, 6, 8] This idea has been very influential, successfully modeling the individual-token philosophy via process semantics.

On the other hand, shortly after Petri’s first publications about the nets that carry his name [7] researchers started investigating what happens when nets are enriched with new features. One of the most successful extensions of Petri nets is guarded (or coloured) nets [3]. Modulo different flavors of modeling what boils down to be the same concept, a guarded net is a Petri net with the following extra properties:

• To each token is attached some “attribute”. The kind of attributes we can attach to tokens depends on the place the token is in;

• Each arc is decorated with an expression, which modifies tokens’ attributes as they flow through the net;

• Each transition is decorated with a predicate and only fires on tokens whose attributes satisfy the predicate.

At a fist glance, guarded nets allow for a more expressive form of modeling with respect to their unguarded counterparts, but as we will see shortly, this is not necessarily the case. Indeed, depending on the underlying theory from which properties, expressions, and predicates are drawn the gain in expressive power with respect to undecorated nets may be nil: With a wise choice of underlying theory, coloured nets amount to be nothing more than syntactic sugar for standard nets, though of course the availability of such syntactic sugar can greatly simplify the modeling of complex processes using the Petri net formalism.

Recently there has been renewed interest in employing Petri nets as the basis for a programming language [10]. In this setting, the categorical correspondence between nets and symmetric monoidal categories has been of the utmost importance, single-token philosophy being considered necessary to make the programming language usable [9]. Clearly, extending nets with new features such as guards or timings is desirable to make the language more expressive.

In this work we try to unify these two longstanding directions of research – the categorical approach to Petri nets and the study of guarded nets – by showing how guarded nets can be modeled as ordinary Petri nets with a particular flavor of semantics in the style of [1].

Importantly, we are able to define both a deterministic semantics and a non-deterministic semantics in our formalism. The first models the traditional notion of guards deterministically modifying data attached to tokens, while the second describes a setting where token data is modified depending on side effects.

Using the Grothendieck construction, we show how the guard semantics can be internalized in the net itself, providing a categorical proof that in our model, guarded nets do not increase expressivity, as compared to traditional nets. This is a desired feature, since it means that many nice properties of nets such as termination or decidability of the reachability relation are preserved. It also shows that the core mathematical abstraction in computer implementations of Petri nets need not be modified when offering users the flexibility of guarded nets.

We save all proofs for the appendix, which starts on page 14.

2 Guarded Nets

Having given an intuitive version of what a guarded net is, we now start modeling the concept formally. We will use the formalism developed in [1], of which we recall some core concepts.

We denote by $\mathfrak {F}\left( N\right)$ the free symmetric strict monoidal category associated to a Petri net N, and with $\mathfrak {U}\left( \mathcal {C}\right)$ the Petri net associated to the free symmetric strict monoidal category $\mathcal {C}$. We denote composition in diagrammatic order; i.e. given $f:c\rightarrow d$ and $g:d\rightarrow e$, we denote their composite by .

Definition 1

Given a strict monoidal category $\mathcal {S}$, a Petri net with $\mathcal {S}$ -semantics is a pair $\left( N, {N}^\sharp \right)$, consisting of a Petri net N and a strict monoidal functor

$$\begin{aligned} {N}^\sharp : \mathfrak {F}\left( N\right) \rightarrow \mathcal {S}. \end{aligned}$$

A morphism $F: \left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ is just a strict monoidal functor $F: \mathfrak {F}\left( M\right) \rightarrow \mathfrak {F}\left( N\right)$ such that .

Nets equipped with $\mathcal {S}$-semantics and their morphisms form a monoidal category denoted $\mathbf{Petri} ^{\mathcal {S}}$, with the monoidal structure arising from the product in $\mathbf{Cat}$.

Definition 2

We denote by $\mathbf{Set _{*}}$ the category of sets and partial functions, and by $\mathbf{Span}$ the 1-category of sets and spans, where isomorphic spans are identified. Both these categories are symmetric monoidal. From now on, we will work with the strictified version of $\mathbf{Set _{*}}$ and $\mathbf{Span}$, respectively.

Example 1

Let $\mathbf 1$ denote the terminal symmetric monoidal category. A Petri net with $\mathbf 1$-semantics is just a Petri net. Petri nets are in bijective correspondence with free symmetric strict monoidal categories, so $\mathbf{Petri} ^\mathbf{1 }$ denotes the usual category of free symmetric strict monoidal categories and strict monoidal functors between them.

Notation 1

Recall that a morphism $A\rightarrow B$ in $\mathbf{Span}$ consists of a set S and a pair of functions $A\leftarrow S\rightarrow B$. When we need to notationally extract this data from f, we write

$$\begin{aligned} A\xleftarrow {f_1}S_f\xrightarrow {f_2}B \end{aligned}$$

We sometimes consider the span as a function $f:S_f\rightarrow A\times B$, thus we may write $f(s)=(a,b)$ for $s\in S_f$ with $f_1(s)=a$ and $f_2(s)=b$.

Perhaps unsurprisingly, $\mathbf{Set _{*}}$ and $\mathbf{Span}$ will be the target semantics corresponding to two different flavors for our guards, with $\mathbf{Span}$ allowing for some form of nondeterminism – expressed as the action of side-effects – whereas $\mathbf{Set _{*}}$ models a purely deterministic semantics. Expressing things formally:

Definition 3

A guarded net is an object of $\mathbf{Petri} ^{\mathbf{Set _{*}}}$. A guarded net with side effects is an object of $\mathbf{Petri} ^\mathbf{Span }$. A morphism of guarded nets (with side effects) is a morphism in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ (resp. in $\mathbf{Petri} ^\mathbf{Span }$).

Remark 1

Although it doesn’t affect our formalism by any means, in practice the choice of semantics, both for $\mathbf{Set _{*}}$ and $\mathbf{Span}$, is limited by computational requirements: the places in a net are usually sent to finite sets, while transitions are usually sent to computable functions and spans¹, respectively. Such restrictions are necessary to make sure the net is executable and to keep model checking decidable.

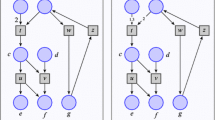
Let us unroll the cryptic Definition 3, starting from the case $\mathbf{Petri} ^{\mathbf{Set _{*}}}$. An object in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ is a net N together with a strict monoidal functor ${N}^\sharp :\mathfrak {F}\left( N\right) \rightarrow \mathbf{Set _{*}}$. It assigns to each place p of N – corresponding to a generating object of $\mathfrak {F}\left( N\right)$ – a set ${N}^\sharp (p)$, representing all the possible colours a token in p can assume. A transition $f:p\rightarrow p'$ – corresponding to a generating morphism of $\mathfrak {F}\left( N\right)$ – gets sent to a partial function ${N}^\sharp (f):{N}^\sharp (p)\rightarrow {N}^\sharp (p')$, representing how token colours are transformed during firing. Importantly, the fact that the functions in the semantics are partial means that a transition may not be defined for tokens of certain colors. An example of this is the net in Fig. 1a, which is shown together with its semantics. Although reachability in the base net seems quite straightforward, we see that a token in the leftmost place will never reach the rightmost place, since the rightmost transition is not defined on the tokens output by the leftmost one.

Fig. 1.

The same net (below), equipped with a partial function and span semantics, respectively (above).

In the case of $\mathbf{Petri} ^\mathbf{Span }$ the intuition is similar. Objects are sent to sets, exactly as in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$, but transitions are mapped to spans. Spans can be understood as relations with witnesses, provided by elements in the apex of the span. Practically, this means that each path from the span domain to its codomain is indexed by some element of the span apex, as it is shown in Fig. 1b. The presence of witnesses allows to consider different paths between the same elements. Moreover, an element in the domain can be sent to different elements in the codomain via different paths. We interpret this as non-determinism: The firing of the transition is not only a matter of the tokens input and output, it also includes the path chosen, which we interpret as having side-effects that are interpreted outside of our model. As one can see, in both Figs. 1a and 1b the composition of paths is the empty function (resp. span). Seeing things from a reachability point of view, the process given by firing the left transition and then the right will never occur. Let us make this intuition precise:

Definition 4

Given a guarded Petri net (with side effects) $\left( N, {N}^\sharp \right)$, a marking for $\left( N, {N}^\sharp \right)$ is a pair (X, x) where X is an object of $\mathfrak {F}\left( N\right)$ and $x \in {N}^\sharp X$. We say that a marking (Y, y) is reachable from (X, x) if there is a morphism $f: X \rightarrow Y$ in $\mathfrak {F}\left( N\right)$ such that ${N}^\sharp f(x) = y$.

The goal we will pursue in the next section will be to internalize the guard semantics in the free category $\mathfrak {F}\left( N\right)$ associated to a net.

3 Internalizing Guards

By “internalizing the semantics of a guarded net N in $\mathfrak {F}\left( N\right)$” we mean obtaining an unguarded net M such that $\mathfrak {F}\left( M\right)$ represents all the possible runs of N. For readers familiars with coloured Petri nets, this corresponds to the claim that reachability in a coloured net is equivalent to reachability in a suitably constructed “standard” net [3].

Since our point of view is process-theoretic, and we are working with symmetric strict monoidal categories and functors, such internalization must be built categorically. The main tool we will use is the Grothendieck construction [4], which in our context we will specialize to functors to $\mathbf{Set _{*}}$ and $\mathbf{Span}$, respectively.

Definition 5

Let $\left( M, {M}^\sharp \right) \in \mathbf{Petri} ^{\mathbf{Set _{*}}}$ be a guarded net. We define its internalization, denoted $\textstyle \int {{M}^\sharp }$, as the following category:

• The objects of $\textstyle \int {{M}^\sharp }$ are pairs (X, x), where X is an object of $\mathfrak {F}\left( M\right)$ and x is an element of ${M}^\sharp X$. Concisely:

  $$\begin{aligned} {\text {Obj}} \, \textstyle \int {{M}^\sharp } := \left\{ (X,x) \, \mid \vert \, (X \in {\text {Obj}} \, \mathfrak {F}\left( M\right) ) \wedge (x \in {M}^\sharp X)\right\} . \end{aligned}$$

• A morphism from (X, x) to (Y, y) in $\textstyle \int {{M}^\sharp }$ is a morphism $f:X \rightarrow Y$ in $\mathfrak {F}\left( M\right)$ such that x is sent to y via ${M}^\sharp f$. Concisely:

  $$\begin{aligned} {\text {Hom}}_{\,\textstyle \int {{M}^\sharp }}\left[ (X,x),(Y,y)\right] := \left\{ f \, \mid \vert \, (f \in {\text {Hom}}_{\,\mathfrak {F}\left( M\right) }\left[ X,Y\right] ) \wedge ({M}^\sharp f(x) = y)\right\} . \end{aligned}$$

It is worth giving some intuition of what the Grothendieck construction does in our context. It basically makes a place for each element of the set we send a place to, and makes a transition for each path between these elements, as shown below:

An equivalent definition exists when the semantics is taken to be in $\mathbf{Span}$, which is the following:

Definition 6

Let $\left( M, {M}^\sharp \right) \in \mathbf{Petri} ^\mathbf{Span }$ be a guarded net with side effects. We define the internalization of $\left( M, {M}^\sharp \right)$, denoted with $\textstyle \int {{M}^\sharp }$, as the following category:

• The objects of $\textstyle \int {{M}^\sharp }$ are pairs (X, x), where X is an object of $\mathfrak {F}\left( M\right)$ and x is an element of ${M}^\sharp X$. Concisely:

  $$\begin{aligned} {\text {Obj}} \, \textstyle \int {{M}^\sharp } := \left\{ (X,x) \, \mid \vert \, (X \in {\text {Obj}} \, \mathfrak {F}\left( M\right) ) \wedge (x \in {M}^\sharp X)\right\} . \end{aligned}$$

• A morphism from (X, x) to (Y, y) in $\textstyle \int {{M}^\sharp }$ is a pair (f, s) where $f:X \rightarrow Y$ in $\mathfrak {F}\left( M\right)$ and $s\in S_{{M}^\sharp f}$ in the apex of the corresponding span connects x to y. Concisely:

  $$\begin{aligned}&{\text {Hom}}_{\,\textstyle \int {{M}^\sharp }}\left[ (X,x),(Y,y)\right] :=\\&\qquad :=\left\{ (f,s) \, \mid \vert \, (f \in {\text {Hom}}_{\,\mathfrak {F}\left( M\right) }\left[ X,Y\right] ) \wedge (s\in S_{{M}^\sharp f})\wedge ({M}^\sharp f(s) = (x,y))\right\} . \end{aligned}$$

The intuition in the span case is exactly as for partial functions, and we don’t deem it useful to draw the same picture again. Looking at the example, though, a couple of things become clear. The first is that to justify the idea of the Grothendieck construction turning an assignment of semantics into a net we have to prove that the resulting category is symmetric strict monoidal and free. The second is that the net thus built is fibered over the base net, and there should be an opposite construction sending $\textstyle \int {{M}^\sharp }$ to M. Both of these claims are true, as we now prove:

Lemma 1

In the case of both $\mathbf{Set _{*}}$ and $\mathbf{Span}$, the category $\textstyle \int {{M}^\sharp }$ has a strict symmetric monoidal structure.

Theorem 1

In both the case of $\mathbf{Set _{*}}$ and of $\mathbf{Span}$ the strict symmetric monoidal category $\textstyle \int {{M}^\sharp }$ is free.

Counterexample 1

(Relations). Theorem 1 does not hold – the Grothendieck construction does not yield a free symmetric strict monoidal category – if we replace $\mathbf{Set _{*}}$ or $\mathbf{Span}$ with $\mathbf{Rel}$. To see this, consider $\textstyle \int {{M}^\sharp }$ in the case that ${M}^\sharp :\mathfrak {F}\left( M\right) \rightarrow \mathbf{Rel}$. Let M be the Petri net consisting of three places X, Y, Z and two transitions $f:X \rightarrow Y$ and $g:Y \rightarrow Z$. Let ${M}^\sharp$ send X to $\{x\}$, Y to $\{y_1, y_2\}$, and Z to $\{z\}$. On morphisms, let ${M}^\sharp$ send f to the maximal relation on $\{x\} \times \{y_1, y_2\}$ and g to the maximal relation on $\{y_1, y_2\} \times \{z\}$. Then we have the following four generating morphisms in $\textstyle \int {{M}^\sharp }$:

$$\begin{aligned}&f_1:(X,x) \rightarrow (Y,y_1) \qquad f_2:(X,x) \rightarrow (Y,y_2) \\&g_1:(Y,y_1) \rightarrow (Z, z) \qquad g_2:(Y,y_2) \rightarrow (Z,z) \end{aligned}$$

There is an equality as morphisms $(X,x) \rightarrow (Z,z)$ in $\textstyle \int {{M}^\sharp }$, proving $\textstyle \int {{M}^\sharp }$ is not free.

The reason that Theorem 1 holds in the span case is that spans keep track of different paths between elements, whereas relations do not. To see this, consider the span composition:

It is clear that in this composition the two paths from x to z are considered as separated in the $\mathbf{Span}$ case, and witnessed by $y_1,y_2$ respectively, while in the case of $\mathbf{Rel}$ they would have been conflated to one. The result is that these paths correspond to the same morphism in the relational case of $\textstyle \int {{M}^\sharp }$, introducing new equations and breaking freeness, while they stay separated in the span case.

Lemma 2

In the case of both $\mathbf{Set _{*}}$ and $\mathbf{Span}$, there is a strict monoidal functor $\pi _M:\textstyle \int {{M}^\sharp } \rightarrow \mathfrak {F}\left( M\right)$ sending (X, x) to X and $f:(X,x) \rightarrow (Y,y)$ to $f:X \rightarrow Y$ (resp. $(f,s):(X,x) \rightarrow (Y,y)$ to $f:X \rightarrow Y$).

Remark 2

In general, $\pi _M$ is not an opfibration. This is because our target categories $\mathbf{Set _{*}}$ and $\mathbf{Span}$ allow for partial functions. Indeed, if $f:X\rightarrow Y$ in M is sent by ${M}^\sharp$ to a partial function that is not defined on $x\in {M}^\sharp X$, then there is no coCartesian lift emanating from (X, x) for the morphism f.

We conclude this section by proving that the reachability semantics of a guarded net coincides with the reachability semantics of its internalization.

Theorem 2

Let $\left( N, {N}^\sharp \right)$ be a guarded Petri net (with side effects). (Y, y) is reachable from (X, x) if and only if (Y, y) is reachable from (X, x) in the net $\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right)$.

4 Properties of Internalizations

The Grothendieck construction provides a way to internalize partial function and span semantics to nets. As such, it acts on objects of the categories $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ and $\mathbf{Petri} ^\mathbf{Span }$, respectively. It is thus worth asking what happens to morphisms in these categories. The answer is, luckily, easy to find:

Lemma 3

Let $F:\left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ be a morphism in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ (resp. in $\mathbf{Petri} ^\mathbf{Span }$). Then it lifts to strict monoidal functor (resp. $\widehat{F}:\textstyle \int {{M}^\sharp } \rightarrow \textstyle \int {{N}^\sharp }$), such that the following diagram on the left (resp. on the right) commutes:

Notation 2

The notation for the liftings in Lemma 3 is easy to remember: The arrow over looks like a stylized function, while the hat over $\widehat{F}$ looks like a sylized span.

The lifting of Lemma 3 is quite well-behaved. First of all, it is worth stressing how it preserves some relevant categorical properties:

Lemma 4

For any map $F:(M,{M}^\sharp )\rightarrow (N,{N}^\sharp )$ in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ (respectively in $\mathbf{Petri} ^\mathbf{Span }$), the functor F is faithful if and only if is faithful (resp. $\widehat{F}$ is faithful). If F is full, then so is (resp. $\widehat{F}$).

Having ascertained that “basic” categorical properties are preserved, it is worth asking what happens to particular classes of functors in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ and $\mathbf{Petri} ^\mathbf{Span }$, respectively.

Following [1], there are three relevant kinds of morphisms in a category of Petri nets with semantics. On one hand there are transition-preserving functors, which represent morphisms of free monoidal categories arising purely from the topological structure of their underlying net. On the other there are functors representing glueings of nets, which are themselves divided into synchronizations (defined in terms of addition and erasing of generators, that is, double pushouts) and identifications (defined in terms of pushouts). Let us investigate which ones of these properties are preserved.

Definition 7

A strict symmetric monoidal functor F between FSSMCs $\mathcal {C}$, $\mathcal {D}$ is said to be transition-preserving when each generating morphism f of $\mathcal {C}$ is mapped to for some generating morphism g of $\mathcal {D}$ and symmetries $\sigma , \sigma '$.

Lemma 5

If F is transition-preserving, so are and $\widehat{F}$.

Lemma 6

If F is injective on objects, so are and $\widehat{F}$.

Another interesting class of morphisms is identifications:

Definition 8

A Petri net $\left( N, {N}^\sharp \right)$ is said to be an identification of $\left( M, {M}^\sharp \right)$ if there is a morphism $F: \left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ such that:

• There is a Petri net O, and a pair of transition-preserving functors $l,r: \mathfrak {F}\left( O\right) \rightarrow \mathfrak {F}\left( M\right)$;

• ; and

• F is the coequalizer of l and r.

Identifications are also preserved. The ultimate reason for this is that identifications are defined purely in terms of coequalizers of transition-preserving functors, which are preserved by the Grothendieck construction.

Lemma 7

If $\left( N, {N}^\sharp \right)$ is an identification of $\left( M, {M}^\sharp \right)$ via F and witnesses O, l, r, then $\textstyle \int {{N}^\sharp }$ is an identification of $\textstyle \int {{M}^\sharp }$ via and witnesses . The span case is analogous.

Preservation of identifications also entails that addition of generators for a net are preserved by internalizations.

Definition 9

A net $\left( M, {M}^\sharp \right)$ is an addition of generating morphisms to $\left( K, {K}^\sharp \right)$ via W, w if:

• There is a net W together with a strict monoidal functor $w: \mathfrak {F}\left( W\right) \rightarrow \mathfrak {F}\left( K\right)$ which sends generating objects to generating objects, is injective on objects and faithful;

• $\mathfrak {F}\left( M\right)$ is the pushout of $\mathfrak {F}\left( \overline{W}\right) \hookrightarrow \mathfrak {F}\left( W\right) \xrightarrow {w} \mathfrak {F}\left( K\right)$ and $\mathfrak {F}\left( \overline{W}\right) \hookrightarrow \mathfrak {F}\left( W\right)$, where $\overline{W}$ denotes the net with the same places of W and no transitions; and

• ${M}^\sharp$ arises from the universal property of the pushout.

Lemma 8

Let $\left( M, {M}^\sharp \right)$ be an addition of generating morphisms to $\left( K, {K}^\sharp \right)$ via W, w. Then $\textstyle \int {{M}^\sharp }$ is an addition of generating morphisms to $\textstyle \int {{K}^\sharp }$ via . The span case is analogous.

Finally, we investigate what happens when considering erasings of generators from a net. To do this, we first follow [1] to define subnets:

Definition 10

Given Petri nets $N, N_w$, we say that $N_w$ is a subnet of N if its places and transitions are a subset of places and transitions of N, and input and output functions on $N_w$ are restrictions of the input and output functions on N. If $N_w$ is a subnet of N, then there is an obvious identity on objects, identity on morphisms strict monoidal functor, $\iota : \mathfrak {F}\left( N_w\right) \hookrightarrow \mathfrak {F}\left( N\right)$ between their associated free symmetric strict monoidal categories. From this, we say that a net $(N_w, {N_w}^\sharp )$ is a subnet of $\left( N, {N}^\sharp \right)$ if $N_w$ is a subnet of N and .

This enables us to define erasings of generators:

Definition 11

Let $(N_w, {(N_w)}^\sharp )$ be a subnet of $\left( N, {N}^\sharp \right)$. An erasing of generators of $\left( N, {N}^\sharp \right)$ via $N_w$ is a net $\left( K, {K}^\sharp \right)$ such that:

• $\left( K, {K}^\sharp \right)$ is a subnet of $\left( N, {N}^\sharp \right)$;

• $\left( \overline{N_w}, {\overline{N_w}}^\sharp \right)$, where $\overline{N_w}$ denotes the net with the same places of $N_w$ and no transitions, is a subnet of $\left( K, {K}^\sharp \right)$; and

• $\mathfrak {F}\left( N\right)$ is the pushout of $\mathfrak {F}\left( \overline{N_w}\right) \hookrightarrow \mathfrak {F}\left( N_w\right)$; and $\mathfrak {F}\left( \overline{N_w}\right) \hookrightarrow \mathfrak {F}\left( K\right)$.

Indeed, erasings of generators are preserved as well by our internalization:

Lemma 9

Let $\left( K, {K}^\sharp \right)$ be an erasing of generating morphisms from $\left( N, {N}^\sharp \right)$ via a subnet $N_w$. Then $\textstyle \int {{K}^\sharp }$ is an erasing of generators from $\textstyle \int {{N}^\sharp }$ via . The span case is analogous.

Surprisingly, even if erasing and addition of generators are preserved by internalizations, synchronizations are not. Indeed, following [1], $\left( M, {M}^\sharp \right)$ is a synchronization of $\left( N, {N}^\sharp \right)$ via W, w when $\mathfrak {F}\left( M\right)$ is defined to be the result of applying the following double pushout rewrite rule to $\mathfrak {F}\left( N\right)$:

Here, we require that w factorizes through $w'$. In internalizing this construction the pushouts are preserved, but the rewrite rule is not! This becomes evident by lifting the definition of synchronization altogether, where in the following diagram we are sticking to the notation developed in [1]:

The black arrows are just the definition of synchronization. The dotted arrows denote the pushout arrows, while the dashed arrows arise from the universal property of the pushout. The maroon arrows and objects represent the Grothendieck construction and the lifting of the functors obtained from Lemma 3, while the $\pi$s stand for the functors obtained in Lemma 2, where we omitted subscripts to avoid clutter.

As one can see the pushout squares are both preserved, but $\textstyle \int {{M}^\sharp }$ is not a synchronization of $\textstyle \int {{N}^\sharp }$ via since

In other words, is too big of a subcategory of $\textstyle \int {{N}^\sharp }$ to make $\textstyle \int {{M}^\sharp }$ into a synchronization. An analogous observation holds for spans.

Counterexample 2

(Synchronizations not preserved). We provide a practical counterexample of why synchronizations are not preserved by internalizations. Consider the following nets, where we are borrowing the graphical notation developed in [1], decorating net elements with their images in $\mathbf{Set _{*}}$.

At the base level we have two nets, M on the left and N on the right. Eliding the functor ${N}^\sharp$, the places of N are mapped to sets:

While transitions are mapped to partial functions $f:X \rightarrow Y$ and $g:Y \rightarrow Z$, defined as follows:

$$\begin{aligned} f(x) = y_1 \qquad g(y_1) = g(y_2) = z \end{aligned}$$

M is clearly a synchronization of N via F: The generators f and g have been erased and a generator corresponding to has been added. Taking the Grothendieck construction on M and N (top left and top right in the figure, respectively), we see how the erasing of generators is problematic: The morphism g in N branches into $g(y_1)$ and $g(y_2)$ in $\textstyle \int {{N}^\sharp }$, of which only $g(y_1)$ forms a path with f(x). In lifting the synchronization M to $\textstyle \int {{M}^\sharp }$, we would expect $g(y_1)$ and f(x) to be erased and conflated into , whereas $g(y_2)$ stays. But this is not the case, since in M the generator g has already been erased “before being allowed to branch”, taking $g(y_2)$ with it when we take $\textstyle \int {{M}^\sharp }$!

As we said before, this ultimately depends on the fact that the internalization of the subnet provided by the synchronization witness contains too many morphisms, and ends up erasing more generators than we would like it to.

5 Internalization as a Functor

In this final section, we put together some of the properties we have proved so far about internalizations, and prove that internalization is a functor. The intuitive argument behind the results that are about to follow is this: If $\textstyle \int {{N}^\sharp }$ internalizes the semantics of $\left( N, {N}^\sharp \right)$, in either the case ${N}^\sharp :N\rightarrow \mathbf{Set _{*}}$ or ${N}^\sharp :N\rightarrow \mathbf{Span}$, then $\textstyle \int {{N}^\sharp }$ should be considered as “just a ne”, that is, an object of $\mathbf{Petri} ^\mathbf{1 }$; see Example 1.

Putting together results about lifting of functors obtained in the previous section, we are indeed able to prove this.

Theorem 3

Denote with $\mathbf 1$ the terminal category, together with the trivial symmetric monoidal structure on it. There is a faithful, strong monoidal functor $\texttt {emb}_\mathbf{Set _{*}}:\mathbf{Petri} ^{\mathbf{Set _{*}}}\rightarrow \mathbf{Petri} ^\mathbf{1 }$ defined as follows:

• On objects, it sends $\left( M, {M}^\sharp \right)$ to $\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right)$.

• On morphisms, we send the functor $F:\left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ to the functor²

  $$\begin{aligned} \hat{F}:\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right) \rightarrow \left( \mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) }^\sharp \right) \end{aligned}$$

Similarly, there is a faithful, strong monoidal functor $\texttt {emb}_\mathbf{Span} :\mathbf{Petri} ^\mathbf{Span }\rightarrow \mathbf{Petri} ^\mathbf{1 }$ defined as follows:

• On objects, it sends $\left( M, {M}^\sharp \right)$ to $\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right)$.

• On morphisms, we send the functor $F:\left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ to the functor³

  $$\begin{aligned} \hat{F}:\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right) \rightarrow \left( \mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) }^\sharp \right) \end{aligned}$$

Finally, it is worth nothing that for each choice of semantics $\mathcal {S}$ there is another obvious functor from $\mathbf{Petri} ^{\mathcal {S}}$ to $\mathbf{Petri} ^\mathbf{1 }$, which just forgets the semantics altogether. It is worth asking how this functor and the ones provided in Theorem 3 are related.

Proposition 1

Denote with

$$\begin{aligned} \texttt {for}_\mathbf{Set _{*}}:\mathbf{Petri} ^{\mathbf{Set _{*}}}\rightarrow \mathbf{Petri} ^\mathbf{1 }\qquad \texttt {for}_\mathbf{Span} :\mathbf{Petri} ^\mathbf{Span }\rightarrow \mathbf{Petri} ^\mathbf{1 }\end{aligned}$$

the “forgetful” functors defined by sending each Petri net $\left( M, {M}^\sharp \right)$ to $\left( M, {M}^\sharp \right)$. Then there are natural transformations:

6 Conclusion and Future Work

In this work, we described guarded Petri nets as Petri nets endowed with a functorial semantics. We provided two different styles of semantics: a deterministic one, realized using the category of sets and partial functions, and a non-deterministic one that allows for side effects, realized using the category of partial functions and that of spans.

We moreover showed how, using the Grothendieck construction, the guards can be internalized, obtaining a Petri net whose reachability relation is equivalent to the one of the guarded one. We proved that internalizations have nice properties, and the internalization construction is functorial in the choice of the guarded net we start from.

Regarding directions of future work, a pretty straightforward thing to do would be to figure out which semantics, other than $\mathbf{Set _{*}}$ and $\mathbf{Span}$, are internalizable. That is, if $F:\mathfrak {F}\left( N\right) \rightarrow \mathcal {S}$ is a symmetric monoidal functor, which properties do $\mathcal {S}$ and F need to have so that $\textstyle \int {F}$ is a free symmetric strict monoidal category.

Appendix – Proofs

Lemma 1. In the case of both ${\varvec{Set}}_{*}$ and ${\varvec{Span}}$, the category $\textstyle \int {{M}^\sharp }$ has a strict symmetric monoidal structure.

Proof

We start with the case of $\mathbf{Set _{*}}$. Since ${M}^\sharp$ is strict monoidal, ${M}^\sharp (X\otimes Y)={M}^\sharp X\times {M}^\sharp Y$. Thus on objects, we can set . On morphisms, we just use the monoidal product $f \otimes g$ from $\mathfrak {F}\left( M\right)$. The monoidal unit is $(I, *)$, where I is the monoidal unit of $\mathfrak {F}\left( M\right)$ and $*$ is the unique element of the monoidal unit $\{*\}$ of $\mathbf{Set _{*}}$. The rest of the proof is a straightforward check.

Now we consider the case of $\mathbf{Span}$. On objects, we set again . On morphisms, we set , where $f\otimes g$ is as in $\mathfrak {F}\left( M\right)$ and (s, t) is the pair of span-apex elements:

The monoidal unit is $(I, *)$, where I is the monoidal unit of $\mathfrak {F}\left( M\right)$ and $*$ is the unique element of the monoidal unit $\{*\}$ of $\mathbf{Span}$.

The remainder of the proof is as in the previous case.   $\square$

Theorem 1. In both the case of ${\varvec{Set}}_{*}$ and of ${\varvec{Span}}$ the strict symmetric monoidal category $\textstyle \int {{M}^\sharp }$ is free.

Proof

We start with the case of $\mathbf{Set _{*}}$. Consider the free symmetric strict monoidal category $\hat{M}$ generated as follows:

• Object generators are pairs (X, x), with X object generator in $\mathfrak {F}\left( M\right)$ and $x \in {M}^\sharp X$;

• A morphism generator $(X,x) \rightarrow (Y,y)$ is a morphism generator $f:X \rightarrow Y$ of $\mathfrak {F}\left( M\right)$ such that ${M}^\sharp f(x) = y$.

We want to prove that $\hat{M}$ and $\textstyle \int {{M}^\sharp }$ are isomorphic.

First, let (X, x) be an object in $\textstyle \int {{M}^\sharp }$. Then X is an object of $\mathfrak {F}\left( M\right)$, which is free, and hence we have $X = X_1 \otimes \dots \otimes X_n$ for generating objects $X_1 \dots X_n$ in $\mathfrak {F}\left( M\right)$. By definition, we have $x \in {M}^\sharp X$. Being ${M}^\sharp$ strict, this means:

$$\begin{aligned} x \in {M}^\sharp X&\Leftrightarrow x \in {M}^\sharp (X_1 \otimes \dots \otimes X_n)\\&\Leftrightarrow x \in {M}^\sharp X_1 \times \dots \times {M}^\sharp X_n\\&\Leftrightarrow \exists !(x_1 \in {M}^\sharp X_1), \dots ,\exists ! (x_n \in {M}^\sharp X_n). ( x = (x_1, \dots , x_n)) \end{aligned}$$

Hence (X, x) = $(X_1, x_1) \otimes \dots \otimes (X_n, x_n)$, and the object generators of $\textstyle \int {{M}^\sharp }$ are the pairs (X, x) with X object generator in $\mathfrak {F}\left( M\right)$ and $x \in {M}^\sharp X$. This means that there is a bijection on objects of $\hat{M}$ and $\textstyle \int {{M}^\sharp }$:

$$\begin{aligned} (X_1, x_1) \otimes \dots \otimes (X_n, x_n) \mapsto (X_1 \otimes \dots \otimes X_n, (x_1, \dots , x_n)) \end{aligned}$$

We can then define a symmetric monoidal functor $T:\hat{M} \rightarrow \textstyle \int {{M}^\sharp }$ that is bijective on objects, and sends a generating morphism $f:(X,x) \rightarrow (Y,y)$ of $\hat{M}$ to the morphism $f:(X,x) \rightarrow (Y,y)$ in $\textstyle \int {{M}^\sharp }$.

We want to prove that T is full and faithful. Faithfulness is obvious; given $f_1, f_2:(X,x) \rightarrow (Y,y)$ in $\hat{M}$, if $T(f_1)=T(f_2)$ then in particular $f_1=f_2$ in $\mathfrak {F}\left( M\right)$. It follows from the fact that ${M}^\sharp$ is at most single-valued – i.e. ${M}^\sharp g(x)=x'$ and ${M}^\sharp g(x)=x''$ imply $x'=x''$ – that $f_1=f_2$ also in $\hat{M}$. For fullness, take a morphism $f:(X,x) \rightarrow (Z,z)$ in $\textstyle \int {{M}^\sharp }$, and notice the following:

• If $f:(X,x) \rightarrow (Z,z)$ is equal to , where $f_1:X \rightarrow Y$ and $f_2: Y \rightarrow Z$, then we have:

  

  So there is a $y \in {M}^\sharp Y$ such that ${M}^\sharp f_1(x) = y$ and ${M}^\sharp f_2(y) = z$. This means that $f_1:(X,x) \rightarrow (Y,y)$ and $f_2:(Y,y) \rightarrow (Z,z)$ are morphisms in $\textstyle \int {{M}^\sharp }$;

• If $f:(X_1 \otimes X_2,(x_1, x_2)) \rightarrow (Y_1 \otimes Y_2, (y_1, y_2))$ is equal to $f_1 \otimes f_2$, where $f_1:X_1 \rightarrow Y_1$ and $f_2: X_2 \rightarrow Y_2$, then we have:

  $$\begin{aligned} (y_1,y_2)= {M}^\sharp f (x_1, x_2) = {M}^\sharp (f_1 \otimes f_2) (x_1, x_2) = ({M}^\sharp f_1 \times {M}^\sharp f_2)(x_1, x_2) \end{aligned}$$

  This means that ${M}^\sharp f_1(x_1) = y_1$ and ${M}^\sharp f_2(x_2) = y_2$, and hence that $f_1:(X_1,x_1) \rightarrow (Y_1,y_1)$ and $f_2:(X_2,x_2) \rightarrow (Y_2,y_2)$ are morphisms in $\textstyle \int {{M}^\sharp }$.

By definition, since $\mathfrak {F}\left( M\right)$ is free, any morphism $f:X\rightarrow Z$ can be decomposed into a composition of monoidal products of morphism generators, symmetries and identities. The points above prove that $f:(X,x)\rightarrow (Z,z)$ can be decomposed in the same way, and hence is in the image of T; thus it is full.

Our correspondence is bijective on objects and fully faithful, proving that $\hat{M}$ and $\textstyle \int {{M}^\sharp }$ are isomorphic as categories. Since $\hat{M}$ is free so is $\textstyle \int {{M}^\sharp }$, completing the proof.

We now consider the case of $\mathbf{Span}$. The structure of the proof is similar. Consider the free symmetric strict monoidal category $\hat{M}$ generated as follows:

• Object generators are pairs (X, x), with X object generator in $\mathfrak {F}\left( M\right)$ and $x \in {M}^\sharp X$;

• For each morphism generator $f:X \rightarrow Y$ and $s \in S$ such that ${M}^\sharp f(s) = (x,y)$, there is a morphism generator $(f,s):(X,x) \rightarrow (Y,y)$.

We want to prove that $\hat{M}$ and $\textstyle \int {{M}^\sharp }$ are isomorphic.

On objects, the proof of bijectivity is as in the previous case. We can then define a symmetric monoidal functor $\hat{M} \rightarrow \textstyle \int {{M}^\sharp }$ that is bijective on objects, and sends a generating morphism $(f,s):(X,x) \rightarrow (Y,y)$ of $\hat{M}$ to the morphism $(f,s):(X,x) \rightarrow (Y,y)$ in $\textstyle \int {{M}^\sharp }$.

We want to prove that this functor is full and faithful. Faithfulness is again straightforward. Suppose given $(f_1,s_1), (f_2,s_2):(X,x) \rightarrow (Y,y)$ in $\hat{M}$. By construction, $(f_1,s_1) = (f_2, s_2)$ in $\textstyle \int {{M}^\sharp }$ if and only if $f_1 = f_2$ in $\mathfrak {F}\left( M\right)$ and $s_1 = s_2$. But this means that $(f_1,s_1) = (f_2,s_2)$ also in $\hat{M}$.

For fullness, take a morphism $(f,s):(X,x) \rightarrow (Z,z)$ in $\textstyle \int {{M}^\sharp }$, and notice the following:

• Each morphism (f, s) such that f is a generator, an identity or a symmetry in $\mathfrak {F}\left( M\right)$ is also in $\hat{M}$;

• If $(f,s):(X,x) \rightarrow (Z,z)$ is such that , where $g:X \rightarrow Y$ and $h:Y \rightarrow Z$, then by definition of composition in $\mathbf{Span}$, we have $s = (t,u)$ for some t, u with ${M}^\sharp g(t)=(x,y)$ and ${M}^\sharp h(u)=(y,z)$. This means that $(g,t):(X,x) \rightarrow (Y,y)$ and $(h,u):(Y,y) \rightarrow (Z,z)$ are morphisms in $\textstyle \int {{M}^\sharp }$;

• If $(f,s):(X_1 \otimes X_2,(x_1, x_2)) \rightarrow (Y_1 \otimes Y_2, (y_1, y_2))$ is such that $f=f_1 \otimes f_2$, where $f_1:X_1 \rightarrow Y_1$ and $f_2:X_2 \rightarrow Y_2$, then $s = (s_1,s_2)$ for some $s_1, s_2$, and we have:

  $$\begin{aligned} ((x_1,x_2),(y_1,y_2))= {M}^\sharp f (s) = {M}^\sharp (f_1 \otimes f_2) (s_1, s_2) = ({M}^\sharp f_1 \times {M}^\sharp f_2)(s_1, s_2) \end{aligned}$$

  This means that ${M}^\sharp f_1(s_1) = (x_1,y_1)$ and ${M}^\sharp f_2(s_2) = (x_2,y_2)$, and hence that $(f_1,s_1):(X_1,x_1) \rightarrow (Y_1,y_1)$ and $(f_2, s_2):(X_2,x_2) \rightarrow (Y_2,y_2)$ are morphisms in $\textstyle \int {{M}^\sharp }$.

By definition, since $\mathfrak {F}\left( M\right)$ is free, any morphism f can be decomposed into a composition of monoidal products of morphism generators, symmetries and identities. The points above prove that each of such morphisms is also in $\textstyle \int {{M}^\sharp }$, and hence in $\hat{M}$. So f in $\textstyle \int {{M}^\sharp }$ is the image of f in $\hat{M}$, and the functor is full.

Since our correspondence is bijective on objects and fully faithful, this proves that $\hat{M}$ and $\textstyle \int {{M}^\sharp }$ are isomorphic as categories. Since $\hat{M}$ is free so is $\textstyle \int {{M}^\sharp }$, completing the proof.   $\square$

Theorem 2. Let $\left( N, {N}^\sharp \right)$ be a guarded Petri net (with side effects). (Y, y) is reachable from (X, x) if and only if (Y, y) is reachable from (X, x) in the net $\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right)$.

Proof

By definition (Y, y) is reachable from (X, x) if and only if there is a morphism $f:X \rightarrow Y$ in $\mathfrak {F}\left( N\right)$ such that ${N}^\sharp f(x) = y$ (resp. ${N}^\sharp f(s) = (x,y)$ for some $s \in S_f$). Again by definition, this means that $f:(X,x) \rightarrow (Y,y)$ (resp. $f_s:(X,x) \rightarrow (Y,y)$) is a morphism of $\textstyle \int {{N}^\sharp }$. Since $\textstyle \int {{N}^\sharp }$ is free, f (resp. $f_s$) can be decomposed as a composition of monoidal products of generating morphisms. But every generating morphism of $\textstyle \int {{N}^\sharp }$ corresponds to a transition of $\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right)$, from which the thesis follows.    $\square$

Lemma 5. If F is transition-preserving, so are and $\widehat{F}$.

Proof

The proof is obvious considering that, by construction, $f:(X,x) \rightarrow (Y,y)$ is a generator (resp. a symmetry) in $\textstyle \int {{N}^\sharp }$ if and only if it is a generator (resp. a symmetry) in $\mathfrak {F}\left( N\right)$.

An analogous argument holds for $\widehat{F}$.    $\square$

Theorem 3. Denote with ${\varvec{1}}$ the terminal category, together with the trivial symmetric monoidal structure on it. There is a faithful, strong monoidal functor defined as follows:

• On objects, it sends $\left( M, {M}^\sharp \right)$ to $\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right)$.

• On morphisms, we send the functor $F:\left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ to the functor⁴

  

Similarly, there is a faithful, strong monoidal functor defined as follows:

• On objects, it sends $\left( M, {M}^\sharp \right)$ to $\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right)$.

• On morphisms, we send the functor $F:\left( M, {M}^\sharp \right) \rightarrow \left( N, {N}^\sharp \right)$ to the functor⁵

  $$\begin{aligned} \widehat{F}: \left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right) \rightarrow \left( \mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) }^\sharp \right) . \end{aligned}$$

Proof

The proofs for $\mathbf{Set _{*}}$ and $\mathbf{Span}$ are very similar, so we just provide the one for $\mathbf{Set _{*}}$. Clearly if F is the identity functor $\left( M, {M}^\sharp \right) \rightarrow \left( M, {M}^\sharp \right)$ then so is . For composition, consider $F:\left( M, {M}^\sharp \right) \rightarrow \left( M, {M}^\sharp \right) {{N}^\sharp }$ and $G:\left( N, {N}^\sharp \right) \rightarrow \left( P, {P}^\sharp \right)$. We have to prove that . On objects, sends (X, x) in $\textstyle \int {{M}^\sharp }$ to in $\textstyle \int {{P}^\sharp }$, so it coincides with . Now consider a morphism $f:(X,x) \rightarrow (Y,y)$ in $\textstyle \int {{M}^\sharp }$. This is sent by to $Ff:(FX,x) \rightarrow (FY,y)$, and applying to it one gets $G(Ff):(G(FX),x) \rightarrow (G(FY), y)$. Since $G(F(\_))$ is , we are done. This proves that $\texttt {emb}_\mathbf{Set _{*}}$ is a functor. Faithfulness is trivial.

Now we focus on monoidality. First of all we have to prove that

$$\begin{aligned} \texttt {emb}_\mathbf{Set _{*}}\left( \left( M, {M}^\sharp \right) \otimes \left( N, {N}^\sharp \right) \right) \simeq \texttt {emb}_\mathbf{Set _{*}}\left( M, {M}^\sharp \right) \otimes \texttt {emb}_\mathbf{Set _{*}}\left( N, {N}^\sharp \right) \end{aligned}$$

Remembering from Definition 1 that for each choice of semantics $\mathcal {S}$ the monoidal structure on $\mathbf{Petri} ^{\mathcal {S}}$ is defined in terms of coproduct of symmetric monoidal categories, and hence from the coproduct of the underlying nets, this means that:

$$\begin{aligned}&\left( \mathfrak {U}\left( \textstyle \int {[{M}^\sharp ,{N}^\sharp ]}\right) , {\mathfrak {U}\left( \textstyle \int {[{M}^\sharp ,{N}^\sharp ]}\right) }^\sharp \right) =\\&\qquad \qquad \qquad \qquad \qquad = \texttt {emb}_\mathbf{Set _{*}}(M + N, [{M}^\sharp ,{N}^\sharp ])\\&\qquad \qquad \qquad \qquad \qquad = \texttt {emb}_\mathbf{Set _{*}}(\left( M, {M}^\sharp \right) \otimes \left( N, {N}^\sharp \right) )\\&\qquad \qquad \qquad \qquad \qquad \simeq \texttt {emb}_\mathbf{Set _{*}}\left( M, {M}^\sharp \right) \otimes \texttt {emb}_\mathbf{Set _{*}}\left( N, {N}^\sharp \right) \\&\qquad \qquad \qquad \qquad \qquad = \left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right) \otimes \left( \mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) }^\sharp \right) \\&\qquad \qquad \qquad \qquad \qquad = \left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) + \mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) , \left[ {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp , {\mathfrak {U}\left( \textstyle \int {{N}^\sharp }\right) }^\sharp \right] \right) \end{aligned}$$

Since $\mathfrak {U}\left( \_\right)$ preserves isomorphisms and coproducts, it is sufficient to prove:

$$\begin{aligned} \textstyle \int {[{M}^\sharp ,{N}^\sharp ]} \simeq \textstyle \int {{M}^\sharp } + \textstyle \int {{N}^\sharp } \end{aligned}$$

• By definition, objects of $\textstyle \int {[{M}^\sharp ,{N}^\sharp ]}$ are pairs (X, x) with $X \in \mathfrak {F}\left( M+N\right) \simeq \mathfrak {F}\left( M\right) + \mathfrak {F}\left( N\right)$ and $x \in [{M}^\sharp ,{N}^\sharp ]X$. This is clearly isomorphic to ${\text {Obj}} \, \textstyle \int {{M}^\sharp } \sqcup {\text {Obj}} \, \textstyle \int {{N}^\sharp }$.

• Again by definition, we have

  $$\begin{aligned}&{\text {Hom}}_{\,\textstyle \int {[{M}^\sharp ,{N}^\sharp ]}}\left[ (X,x),(Y,y)\right] :=\\&\qquad := \left\{ f \in {\text {Hom}}_{\,\mathfrak {F}\left( M\right) +\mathfrak {F}\left( N\right) }\left[ X,Y\right] \, \mid \vert \, [{M}^\sharp ,{N}^\sharp ]f(x) = y\right\} \end{aligned}$$

  This follows noting that by definition the set of morphisms of $\mathfrak {F}\left( M\right) + \mathfrak {F}\left( N\right)$ is the disjoint union of the sets of morphisms of $\mathfrak {F}\left( M\right)$ and $\mathfrak {F}\left( N\right)$.

Then we have to prove that $\texttt {emb}_\mathbf{Set _{*}}(F \otimes G) = \texttt {emb}_\mathbf{Set _{*}}F \otimes \texttt {emb}_\mathbf{Set _{*}}G$. Unrolling definitions this amounts to prove that , which is obvious.

Finally, we need to prove that $\texttt {emb}_\mathbf{Set _{*}}$ preserves the monoidal unit. Notice that for each choice of semantics $\mathcal {S}$ the monoidal unit in $\mathbf{Petri} ^{\mathcal {S}}$ is taken to be $(\emptyset , {\emptyset }^\sharp {\mathcal {S}})$. $\mathfrak {F}\left( \emptyset \right)$ is the free category consisting of only the monoidal unit I, and ${\emptyset }^\sharp {\mathcal {S}}: \mathfrak {F}\left( \emptyset \right) \rightarrow \mathcal {S}$ sends the monoidal unit to the monoidal unit and its identity to itself. In our case, the monoidal unit of $\mathbf{Petri} ^{\mathbf{Set _{*}}}$ is $(\emptyset , {\emptyset }^\sharp )$, with ${\emptyset }^\sharp$ sending the monoidal unit of $\mathfrak {F}\left( \emptyset \right)$ to the singleton set $\{*\}$ in $\mathbf{Set _{*}}$. In particular, this means that $\textstyle \int {{\emptyset }^\sharp } \simeq \mathfrak {F}\left( \emptyset \right)$, proving that

$$\begin{aligned} \texttt {emb}_\mathbf{Set _{*}}\left( \emptyset , {\emptyset }^\sharp \right) = \left( \mathfrak {U}\left( \textstyle \int {{\emptyset }^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{\emptyset }^\sharp }\right) }^\sharp \right) \simeq \left( \mathfrak {U}\left( \mathfrak {F}\left( \emptyset \right) \right) , {\mathfrak {U}\left( \mathfrak {F}\left( \emptyset \right) \right) }^\sharp \right) \simeq \left( \emptyset , {\emptyset }^\sharp \right) \end{aligned}$$

   $\square$

Proposition 1. Denote with

the functors defined by sending each Petri net $\left( M, {M}^\sharp \right)$ to $\left( M, {M}^\sharp \right)$. Then there are natural transformations:

Proof

For each object $\left( M, {M}^\sharp \right)$ in $\mathbf{Petri} ^{\mathbf{Set _{*}}}$, we set

$$\begin{aligned} \pi _{\left( M, {M}^\sharp \right) }: \left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) , {\mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) }^\sharp \right) \rightarrow \left( M, {M}^\sharp \right) \end{aligned}$$

to be the functor $\mathfrak {F}\left( \mathfrak {U}\left( \textstyle \int {{M}^\sharp }\right) \right) \simeq \textstyle \int {{M}^\sharp } \xrightarrow {\pi _M} \mathfrak {F}\left( M\right)$, where $\pi _M$ is defined as in Lemma 3. The naturality condition follows from Lemma 3 as well. The span case is analogous.    $\square$