Abstract
In this paper, we discuss the mechanisation of some fundamental propositional modal model theory. The focus on models is novel: previous work in mechanisations of modal logic have centered on proof systems and applications in model-checking. We have mechanised a number of fundamental results from the first two chapters of a standard textbook (Blackburn et al. [1]). Among others, one important result, the Van Benthem characterisation theorem, characterises the connection between modal logic and first order logic. This latter captures the desired saturation property of ultraproduct models on countably incomplete ultrafilters.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The theory of modal logic has long been a fruitful area when it comes to mechanisation. The proof systems are appealing, and the applications in model-checking are of clear real-world interest. It helps also that the subject domain (proof calculi and automata) are well-suited to “standard” theorem-proving technology (rule inductions and interesting data types).
There has been much less work on the model theory behind modal logic; indeed even in first order logic, most developments concern themselves only with model theory inasmuch as it is required to show completeness of an accompanying proof system. As our experience demonstrates, it is also clear that modern theorem-proving systems are not necessarily so well-suited to the mathematics behind model theory. Harrison [5] complained in 1998 that the very notion of validity is awkward to capture in HOL, and our own work shows up further failings in simple type theory.
Nonetheless, there is much interesting mathematics to be found even in the early chapters of a standard text such as Blackburn et al. [1]. The fact that mechanising only as far as [1, Chapter 2] requires what we believe to be the first mechanisation of the notion of ultraproduct (ultimately leading to Łoś’s theorems and other results), is a strong suggestion that we are exploring novel mathematical ground for interactive theorem-proving systems.
Contributions. This paper presents the first mechanised proofs of a number of basic results from the first two chapters of Blackburn et al. [1] (e.g., bounded morphisms, bisimulations and the finite model property via selection), as well as
-
Two versions of Łoś’s theorem on the saturation of ultraproduct models;
-
modal equivalence as bisimilarity between ultrafilter extensions; and
-
a close approximation of Van Benthem’s Characterisation Theorem.
We also discuss where HOL’s simple type theory lets us down: some standard results (including the best possible statement of Van Benthem’s Characterisation Theorem) seem impossible to prove in our setting.
HOL4 Notation. All of our theorems have been pretty-printed to
 from the HOL theory files. We hope that most of the basic syntax is easy to follow. In a few places we use
from the HOL theory files. We hope that most of the basic syntax is easy to follow. In a few places we use
 to denote the arbitrary choice of an element from set
to denote the arbitrary choice of an element from set
 (appealing to the Axiom of Choice). The power-set of a set
(appealing to the Axiom of Choice). The power-set of a set
 is written
is written
 . In a number of places, we use HOL’s “itself” type to allow us to explicitly mention a type via a term. The type
. In a number of places, we use HOL’s “itself” type to allow us to explicitly mention a type via a term. The type
 has just one value inhabiting it for any given choice of
has just one value inhabiting it for any given choice of
 ; that value is written
; that value is written
 .
.
Source Availability. Our HOL4 sources are available from GitHub at https://github.com/u5943321/Modal-Logic
The sources build under HOL4 commit with SHA 03829d8986f.
2 Syntax, Semantics and the Standard Translation
In our mechanisation, we consider the basic modal language, in which the only primitive modal operator is the ‘\(\Diamond \)’. A modal formula is either of form
 , where p is of type
, where p is of type
 , enumerating all the possible variable symbols, a disjunction
, enumerating all the possible variable symbols, a disjunction
 (pretty-printed to
(pretty-printed to
 in most places), the falsity
in most places), the falsity
 , a negation
, a negation
 , or, finally, of the form
, or, finally, of the form
 . We define a data type called
. We define a data type called
 to represent the formulas of this modal language.
to represent the formulas of this modal language.
Definition 1
[1, Definition 1.9]

If we wanted to consider modal operators with any arity, we should change the last constructor of modal formulas so it takes two parameters: a natural number indexing the modal operator, and a list of modal formulas. This would in turn require a well-formedness predicate to be defined over formulas to make sure that modalities were applied to the right number of arguments.
A model where these formulas can be interpreted consists of a frame and a valuation, where a
 is a
is a
 -set with a relation on it, and a model adds valuations for the variables present at each world:
-set with a relation on it, and a model adds valuations for the variables present at each world:
Definition 2
[1, Definition 1.19]

In the rest of the paper, the field
 \(.\mathsf valt\) of a model
\(.\mathsf valt\) of a model
 will be called the valuation, and
will be called the valuation, and
 ,
,
 and
and
 are used to denote the world set, the relation, and the valuation of
are used to denote the world set, the relation, and the valuation of
 respectively. The interpretation of modal formulas on a model is given by the predicate satisfaction. We read ‘
respectively. The interpretation of modal formulas on a model is given by the predicate satisfaction. We read ‘
 ’ as ‘\(\phi \) is satisfied at the world w in
’ as ‘\(\phi \) is satisfied at the world w in
 ’.
’.
Definition 3
[1, Definition 1.20]

By requiring
 in various clauses above, we ensure that models’ world sets must be non-empty if they are to satisfy any formulas.
in various clauses above, we ensure that models’ world sets must be non-empty if they are to satisfy any formulas.
Two worlds
 and
and
 are modal equivalent (written
are modal equivalent (written
 ) if they satisfy the same set of modal formulas. If
) if they satisfy the same set of modal formulas. If
 are modal formulas, we say they are equivalent over
are modal formulas, we say they are equivalent over
 models (written
models (written
 ) if they are satisfied in the same worlds in every model:
) if they are satisfied in the same worlds in every model:
Definition 4 (Notions of equivalence)

We cannot omit the type parameter
 in the definition, as there would otherwise be a type, namely the type of the underlying set of the models we are talking about, that only appears on the right-hand side but not on the left-hand side of the definition. HOL forbids such definitions for soundness reasons. Also, HOL does not permit quantification over types, so it is impossible to write
in the definition, as there would otherwise be a type, namely the type of the underlying set of the models we are talking about, that only appears on the right-hand side but not on the left-hand side of the definition. HOL forbids such definitions for soundness reasons. Also, HOL does not permit quantification over types, so it is impossible to write
 , with \(\mu \) a type. Therefore, this definition is not exactly encoding the equivalence in the usual sense: when we mention equivalence of formulas in usual mathematical language, we are implicitly referring to the class of all models, but the constraint here bans us from talking about all models of all possible types at once.
, with \(\mu \) a type. Therefore, this definition is not exactly encoding the equivalence in the usual sense: when we mention equivalence of formulas in usual mathematical language, we are implicitly referring to the class of all models, but the constraint here bans us from talking about all models of all possible types at once.
A modal formula can be translated into a first-order formula via the standard translation. To mechanise this translation, we build on Harrison’s construction of first-order logic [5]. The first-order connectives are decorated with an \(\mathsf f\). A first order model
 is a set
is a set
 with interpretation of function symbols
with interpretation of function symbols
 and predicate symbols
and predicate symbols
 . A valuation
. A valuation
 of
of
 is a function that maps all the natural numbers into the domain of
is a function that maps all the natural numbers into the domain of
 . If a first-order formula
. If a first-order formula
 is satisfied in a first-order model
is satisfied in a first-order model
 with
with
 a valuation assigning free variables of
a valuation assigning free variables of
 elements in the domain of
elements in the domain of
 , we write
, we write
 .
.
For a modal formula
 ,
,
 is the standard translation of
is the standard translation of
 using
using
 as the only free variable that may occur:
as the only free variable that may occur:
Definition 5
[1, Definition 2.45 (Standard Translation)]

As one would expect, we translate
 into an existential formula. To ensure we use a fresh variable, we use \(x+1\) as our new variable symbol in this clause. The standard translation gives a first-order reformulation of satisfaction of modal formulas:
into an existential formula. To ensure we use a fresh variable, we use \(x+1\) as our new variable symbol in this clause. The standard translation gives a first-order reformulation of satisfaction of modal formulas:
Proposition 1
[1, Theorem 2.47 (i)]

Here
 is the function that turns a modal model into a first-order model, defined as:
is the function that turns a modal model into a first-order model, defined as:

That is, the model obtained by converting a modal model
 has domain
has domain
 , maps every term
, maps every term
 into an arbitrary world, maps each propositional letter to distinct predicates on worlds, and uses one binary predicate (the “0th predicate”) to encode the frame relation.
into an arbitrary world, maps each propositional letter to distinct predicates on worlds, and uses one binary predicate (the “0th predicate”) to encode the frame relation.
3 Basic Results
We discuss some highlights of mechanised results from Blackburn et al. [1, §2.1–§2.3] below.
3.1 Tree-Like Property
A tree-like model is a model whose underlying frame is a tree. If
 , a frame, is also a tree with root r, we write
, a frame, is also a tree with root r, we write
 :
:
Definition 6
[1, Definition 1.7]

The tree-like property says each satisfiable modal formula can be satisfied in a tree-like model:
Proposition 2
[1, Proposition 2.15]

The world set of the tree-like model constructed from
 is a set of lists of worlds in
is a set of lists of worlds in
 (such lists are effectively paths from the root to various positions within the tree). Thus, passing to a tree-like model does not preserve the model type. The tree-like lemma is used to prove the finite model property via selection afterwards.
(such lists are effectively paths from the root to various positions within the tree). Thus, passing to a tree-like model does not preserve the model type. The tree-like lemma is used to prove the finite model property via selection afterwards.
3.2 Bisimulation
Though apparently verbose, the definition of bisimulation in HOL is straightforward.
Definition 7
[1, Definition 2.16 (Bisimulations)]

It is trivial to prove by induction that bisimilar worlds are modal equivalent. As the most significant theorem on the basic theory of bisimulations, we proved the Hennessy-Milner theorem, which states that modal equivalence and bisimulation on image-finite models are the same thing. An image-finite model is a model where every world can only be related to finitely many worlds. In HOL, we get:
Theorem 1
[1, Theorem 2.24 (Hennessy-Milner Theorem)]

Bisimulation is an interesting topic in modal logic. Three other significant theorems on bisimulations (including an approximation of Van Benthem Characterisation theorem) are discussed later.
3.3 Finite Model Property
There are two classical approaches to constructing finite models using model theory, namely via selection and via filtration. The complicated one is the former: Given
 , where \(\phi \) has degree k, we can construct
, where \(\phi \) has degree k, we can construct
 ,
,
 and
and
 consecutively, such that
consecutively, such that
 is the finite model we want, where:
is the finite model we want, where:
-
 is the tree-like model obtained from Proposition 2 with root
is the tree-like model obtained from Proposition 2 with root
 such that
such that
 .
. -
 is the restriction of
is the restriction of
 to height k.
to height k. -
 is obtained from
is obtained from
 by modifying the valuation into
by modifying the valuation into
 where
where
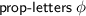 is the set of all propositional letters used by
is the set of all propositional letters used by
 .
.
The construction of
 requires a lemma:
requires a lemma:
Lemma 1
[1, Proposition 2.29]

The proof of Lemma 1 further relies on the following fact: Given a set
 of modal-formulas that is finite up to equivalence, if we combine the elements of
of modal-formulas that is finite up to equivalence, if we combine the elements of
 using only connectives other than
using only connectives other than
 , then we get only finitely many non-equivalent formulas. To show this, we prove that there is an injection from the set of equivalence classes of such combinations to a finite set. For the antecedent of Lemma 1, we require the assumption that the universe of \(\beta \) is infinite since we rely on the fact that two modal formulas
, then we get only finitely many non-equivalent formulas. To show this, we prove that there is an injection from the set of equivalence classes of such combinations to a finite set. For the antecedent of Lemma 1, we require the assumption that the universe of \(\beta \) is infinite since we rely on the fact that two modal formulas
 and
and
 are equivalent if and only if
are equivalent if and only if
 and
and
 are equivalent. This would be easy to prove in set theory. However, in simple type theory, the proof of
are equivalent. This would be easy to prove in set theory. However, in simple type theory, the proof of
 iff
iff
 requires us (in the right-to-left direction) to be able to construct a model with a new world inserted, something only sure to be possible if the
requires us (in the right-to-left direction) to be able to construct a model with a new world inserted, something only sure to be possible if the
 universe is infinite. As the construction used Proposition 2, we change the type of the model by passing to a finite model via selection:
universe is infinite. As the construction used Proposition 2, we change the type of the model by passing to a finite model via selection:
Theorem 2
[1, Theorem 2.34 (Finite model property, via selection)]

We also mechanised the filtration approach, but omit the details for lack of space. The advantage of filtration is that the resulting finite model is over worlds of the same type as in the starting model.
All the results proved above can be captured using
 models everywhere. If one takes
models everywhere. If one takes
 to be
to be
 (or any infinite type) in Theorem 2, one can also exploit the fact that numbers and lists of numbers have the same cardinality to derive a finite model result that preserves the “input type”.
(or any infinite type) in Theorem 2, one can also exploit the fact that numbers and lists of numbers have the same cardinality to derive a finite model result that preserves the “input type”.
4 Mechanising Ultrafilters and Ultraproducts
A number of results in Blackburn et al. [1, §2.5–§2.7] rely on theorems about ultrafilters and ultraproducts.
4.1 Ultrafilters
Given a non-empty set J, a set
 is a filter if it contains J itself, is closed under binary intersection, and is closed upward.
is a filter if it contains J itself, is closed under binary intersection, and is closed upward.
Definition 8
[1, Definition A.12 (Filters)]

We call L a proper filter if L is not the whole power set. An ultrafilter is a filter U such that for every \(X\subseteq J\), exactly one of X or \(J\setminus X\) is in U. Intuitively, subsets
 in an ultrafilter
in an ultrafilter
 are considered as ‘large’ subsets of
are considered as ‘large’ subsets of
 .
.
The ultrafilter theorem states that every proper filter is contained in an ultrafilter:
Theorem 3
[1, Fact A.14, first half]

(The proof uses Zorn’s Lemma.)
A subset A of the power set on J has finite intersection property if once we take the intersection of a finite, nonempty family in A, the resultant set is nonempty.
Definition 9
[1, Definition A.13 (Finite Intersection Property)]

As a corollary of ultrafilter theorem, a set with finite intersection property is contained in an ultrafilter.
4.2 Ultraproducts
The notion of ultraproducts is defined for sets, modal models, and first-order models.
Ultraproduct of Sets. A family of sets indexed by
 is a function
is a function
 in HOL. For
in HOL. For
 ,
,
 is the set indexed by
is the set indexed by
 . Given a family
. Given a family
 indexed by a non-empty set
indexed by a non-empty set
 such that each
such that each
 is non-empty, the ultraproduct of
is non-empty, the ultraproduct of
 is defined as a quotient of the cartesian product of the family.
is defined as a quotient of the cartesian product of the family.
Definition 10
[1, Page 495 (Cartesian product)]

If U is an ultrafilter on J, for two functions f, g in the Cartesian product
 , we say f and g are U-equivalent (notation:
, we say f and g are U-equivalent (notation:
 ) if the set
) if the set
 (where the values of f and g agree) is in U. The ultraproduct of
(where the values of f and g agree) is in U. The ultraproduct of
 modulo U is the quotient of
modulo U is the quotient of
 by
by
 .
.
Definition 11
[1, Definition 2.69 (Ultraproduct of Sets)]

We write
 to denote the equivalence class that f belongs to. In the case where
to denote the equivalence class that f belongs to. In the case where
 for all \(j\in J\), the ultraproduct is called the ultrapower of
for all \(j\in J\), the ultraproduct is called the ultrapower of
 modulo U.
modulo U.
Ultraproduct for Modal Models. Given a family
 of modal models indexed by J and an ultrafilter U on J, the ultraproduct model of
of modal models indexed by J and an ultrafilter U on J, the ultraproduct model of
 modulo U (notation:
modulo U (notation:
 ) is described as follows:
) is described as follows:
-
The world set is the ultraproduct of world sets of
 modulo U.
modulo U. -
Two equivalence classes \(f_U,g_U\) of functions are related in
 iff there exist \(f_0\in f_U,g_0\in g_U\), such that
iff there exist \(f_0\in f_U,g_0\in g_U\), such that
 is in U.
is in U. -
A propositional letter p is satisfied at \(f_U\) in
 iff there exists \(f_0\in f_U\) such that
iff there exists \(f_0\in f_U\) such that
 is in U.
is in U.
Definition 12
[1, Definition 2.70 (Ultraproduct of Modal Models)]

As
 is an equivalence relation, if one element in an equivalence class satisfies the required condition, then all the elements in the equivalence class will satisfy the condition. Therefore, if we replace all the existential quantifiers with universal quantifiers in the above definition, the construction is still valid, and will give the same model as the current definition.
is an equivalence relation, if one element in an equivalence class satisfies the required condition, then all the elements in the equivalence class will satisfy the condition. Therefore, if we replace all the existential quantifiers with universal quantifiers in the above definition, the construction is still valid, and will give the same model as the current definition.
The critical result we need about ultraproducts of modal models is a modal version of the fundamental theorem of ultraproducts, also known as Łoś’s theorem.
Theorem 4 (Łoś’s theorem, Modal version)

According to our intuition about ultrafilters, we can gloss this theorem to mean that the ultraproduct of a family of modal models satisfies a modal formula if and only if ‘most of’ the models in the family satisfy the formula. Though it is possible to derive this result from Łoś’s theorem of first-order models using the standard translation, our proof is direct, by structural induction on
 .
.
Ultraproducts for First-Order Models. Given a family
 of first-order models indexed by J and an ultrafilter U on J, the ultraproduct model of
of first-order models indexed by J and an ultrafilter U on J, the ultraproduct model of
 modulo U (notation:
modulo U (notation:
 ) is given by:
) is given by:
-
The domain is the ultraproduct of the domains of
 over U on J.
over U on J. -
A function named by symbol (natural number) n sends a list
 of equivalence classes to the equivalence class of a function that sends \(j\in J\) to
of equivalence classes to the equivalence class of a function that sends \(j\in J\) to
 , where the k-th member of the list l is a representative of the k-th member (which is an equivalence class) of
, where the k-th member of the list l is a representative of the k-th member (which is an equivalence class) of
 .
. -
A predicate named by symbol p will hold for a list
 of equivalence classes if and only if when we have a list
of equivalence classes if and only if when we have a list
 , where k-th member is a representative of the k-th member of zs, the set of elements
, where k-th member is a representative of the k-th member of zs, the set of elements
 such that
such that
 is in U.
is in U.
Definition 13
[1, Definition A.18 (Ultraproduct of First-Order Models)]

Here we fix the representative of each equivalence class
 to be
to be
 . Therefore, as described above, the functions
. Therefore, as described above, the functions
 and
and
 are:
are:

The semantic behavior of ultraproduct models is characterised by Łoś’s theorem: for the ultraproduct of a family
 of first-order models over an ultrafilter
of first-order models over an ultrafilter
 on J, a formula
on J, a formula
 is satisfied under a valuation
is satisfied under a valuation
 if and only if the set indexing the models
if and only if the set indexing the models
 in the family where
in the family where
 is true under the valuation
is true under the valuation
 is in the ultrafilter U.
is in the ultrafilter U.
Theorem 5
[1, Theorem A.19 (Łoś’s theorem)]

where
 means the functions of
means the functions of
 never map a list out of the domain of
never map a list out of the domain of
 .
.
5 Ultrafilter Extensions
The first application of the theory of ultrafilters above is to construct the ultrafilter extension of a model, which has the nice property of being modally saturated (m-saturated hereafter). To define m-saturation, we give the following three definitions (the first two are called finitely satisfiable, satisfiable) consecutively:
Definition 14
[1, Definition 2.53]

For m-saturated models, bisimulation and modal equivalence coincide:
Proposition 3
[1, Proposition 2.54]

Given a model
 and a set
and a set
 of worlds of
of worlds of
 , the set of worlds that ‘can see’ X (notation:
, the set of worlds that ‘can see’ X (notation:
 ) is the set of worlds
) is the set of worlds
 of
of
 such that there exists some
such that there exists some
 such that
such that
 . We define the ultrafilter extension
. We define the ultrafilter extension
 of
of
 as:
as:
-
The world set is the set of all ultrafilters on
 .
. -
Two ultrafilters
 ,
,
 on
on
 are related in the ultrafilter extension of
are related in the ultrafilter extension of
 if for every
if for every
 , the set of worlds that can see
, the set of worlds that can see
 is in
is in
 .
. -
A propositional letter p to be satisfied at an ultrafilter v if and only if the set of worlds in
 which satisfies p is in v.
which satisfies p is in v.
In HOL:
Definition 15
[1, Definition 2.57 (Ultrafilter Extension)]

Using the ultrafilter theorem and some basic properties about ultrafilters, we derive:
Proposition 4
[1, Proposition 2.59 (i)]

In particular, every world
 is embedded as the principal filter
is embedded as the principal filter
 on
on
 generated by
generated by
 in the ultrafilter extension or
in the ultrafilter extension or
 . Also, the above leads to the proof of the fact that the ultrafilter extension of every model is m-saturated. The m-saturatedness of ultrafilter extensions together with Proposition 3 immediately gives the central result about ultrafilter extension: bisimilarity of worlds in a model
. Also, the above leads to the proof of the fact that the ultrafilter extension of every model is m-saturated. The m-saturatedness of ultrafilter extensions together with Proposition 3 immediately gives the central result about ultrafilter extension: bisimilarity of worlds in a model
 can be characterised as bisimilarity in
can be characterised as bisimilarity in
 .
.
Theorem 6
[1, Proposition 2.62]

6 Countable Saturatedness of Ultrapower Models
Given a first-order model
 with no information about interpretation of its function symbols, we can expand the model
with no information about interpretation of its function symbols, we can expand the model
 by adding an interpretation of some function symbols. For our purpose, we are only interested in adding the interpretation of finitely many nullary function symbols, also called constants. We write
by adding an interpretation of some function symbols. For our purpose, we are only interested in adding the interpretation of finitely many nullary function symbols, also called constants. We write
 to denote the model that is the result of adding each element in A to
to denote the model that is the result of adding each element in A to
 as a new constant. Further, the function f is a bijection between \(\{0,\cdots ,n-1\}\) and A, which is assumed to be finite, so that each nullary function symbol c will be interpreted as
as a new constant. Further, the function f is a bijection between \(\{0,\cdots ,n-1\}\) and A, which is assumed to be finite, so that each nullary function symbol c will be interpreted as
 in
in
 .
.
Definition 16
[1, Definition A.9 (Expansion)]

As is apparent from the definition, the only difference between a model and its expansion is the interpretation of function symbols.
A set
 of first-order formulas is called consistent with a model
of first-order formulas is called consistent with a model
 if for every finite subset
if for every finite subset
 , there exists a valuation of
, there exists a valuation of
 such that all elements of
such that all elements of
 are satisfied, in this case, we write
are satisfied, in this case, we write
 . A set
. A set
 of first-order formula is an x-type if for each formula in
of first-order formula is an x-type if for each formula in
 , the only free variable that may contain is x. In this case, we write ‘
, the only free variable that may contain is x. In this case, we write ‘
 ’ in HOL. If
’ in HOL. If
 is an x-type, when evaluating formulas in
is an x-type, when evaluating formulas in
 , the valuations will only control where the only free variable x goes to. We say
, the valuations will only control where the only free variable x goes to. We say
 is realised in
is realised in
 if there is an element w in the domain of
if there is an element w in the domain of
 such that
such that
 for all
for all
 . In this case, we write ‘
. In this case, we write ‘
 ’ in HOL. Let
’ in HOL. Let
 be a model and
be a model and
 be a natural number. If for every
be a natural number. If for every
 with \(|A|<n\) and every \(f:{\mathbb N}\rightarrow \)
with \(|A|<n\) and every \(f:{\mathbb N}\rightarrow \)
 , the model
, the model
 realises every x-type
realises every x-type
 that is consistent with
that is consistent with
 , then we say
, then we say
 is n-saturated. In HOL:
is n-saturated. In HOL:
Definition 17
[1, Definition 2.63 (n-Saturated)]

We say
 is countably saturated if
is countably saturated if
 is n-saturated for every natural number n. The ultimate goal is to prove a lemma to be used in the proof of Van Benthem characterisation theorem: For a family of non-empty models, their ultraproduct on a countably incomplete ultrafilter is countably saturated.
is n-saturated for every natural number n. The ultimate goal is to prove a lemma to be used in the proof of Van Benthem characterisation theorem: For a family of non-empty models, their ultraproduct on a countably incomplete ultrafilter is countably saturated.
Lemma 2
[1, Lemma 2.73]

Here a countably incomplete ultrafilter is an ultrafilter that contains a countably infinite family that intersects to the empty set. We prove in HOL that such ultrafilters do exist using Theorem 3. The above theorem is not simply a direct consequence of Łoś’s theorem: that result is about ultraproducts of first-order models, and it says nothing about expansion. But to prove Lemma 2, we must prove a statement for an expanded first-order model, and this first order model is itself obtained by converting a ultraproduct of modal models.
To deal with this issue, the key observation is that constants are nothing more than forcing some symbols to be sent to some points in a model under every valuation, hence rather than use nullary function symbols, we fix a set of variable letters, each corresponding to a function symbol, and only consider the valuations that send these variable letters to certain fixed points. With this idea, we can remove all the constants in a formula, and hence change our scope from an expanded model back to the unexpanded model. To get rid of the constants \(\{0,\cdots , n-1\}\), we replace every
 with
with
 , and replace every constant
, and replace every constant
 by
by
 . This operation is done by the function
. This operation is done by the function
 which takes a natural number (the number of constants we want to remove), and a first-order formula (where the only function symbols may appear are the constants \(0,\cdots , n-1\)). Since \(0,\cdots ,n-1\) in a shifted formula are now designed to be sent to fixed places \(f \ 0,\cdots ,f \ (n-1)\), it does not make sense to assign these variable symbols anywhere else. Therefore, to talk about evaluation of shifted formula, the first thing is to make sure that the valuations we are considering send the variables which actually denote constants to the right place. Hence we shift the valuations accordingly, and then prove that a formula is satisfied on an expanded model is satisfied under a valuation if and only if the shifted formula is satisfied under the shifted valuation. Also, we prove that ‘taking the ultraproduct first-order model commutes with the convertion from modal to a first-order model on certain formulas’, in the sense that the resulting models satisfies the same first-order formulas without function symbols. By putting these two results together, we prove Lemma 2 using the proof in Chang and Keisler [3].
which takes a natural number (the number of constants we want to remove), and a first-order formula (where the only function symbols may appear are the constants \(0,\cdots , n-1\)). Since \(0,\cdots ,n-1\) in a shifted formula are now designed to be sent to fixed places \(f \ 0,\cdots ,f \ (n-1)\), it does not make sense to assign these variable symbols anywhere else. Therefore, to talk about evaluation of shifted formula, the first thing is to make sure that the valuations we are considering send the variables which actually denote constants to the right place. Hence we shift the valuations accordingly, and then prove that a formula is satisfied on an expanded model is satisfied under a valuation if and only if the shifted formula is satisfied under the shifted valuation. Also, we prove that ‘taking the ultraproduct first-order model commutes with the convertion from modal to a first-order model on certain formulas’, in the sense that the resulting models satisfies the same first-order formulas without function symbols. By putting these two results together, we prove Lemma 2 using the proof in Chang and Keisler [3].
7 Van Benthem’s Characterisation Theorem
Note that the standard translation of any modal formula can only contain unary predicate symbols which correspond to propositional letters, one binary predicate symbol which corresponds to the relation, and no function symbols. A first-order formula which only uses these symbols is called an \({\mathcal L}_{\tau }^1\)-formula. An \({\mathcal L}_{\tau }^1\)-formula which contains only one free variable is called invariant under bisimulation if for all models
 and
and
 with
with
 and
and
 , if there exists a bisimulation relation between
, if there exists a bisimulation relation between
 and
and
 relating w and v, then \(\phi \) holds at
relating w and v, then \(\phi \) holds at
 if and only if it holds at
if and only if it holds at
 when both
when both
 and
and
 are viewed as first-order models.
are viewed as first-order models.
Definition 18
[1, Definition 2.67 (Invariant for Bisimulations)]

Because of the same problem we met when defining equivalence of formulas, the type parameters are necessary here. However, although it is possible to prove theorems for different types \(\alpha \) and \(\beta \) in the above definition, in the theorems to come, we will only consider the case where \(\alpha \) and \(\beta \) are the same.
The Van Benthem characterisation theorem says an \(\mathcal L_{\tau }^1\) formula with at most one free variable x is invariant under bisimulation precisely when it is equivalent to the standard translation of some modal formula at x. It is immediate from Proposition 1 that every such formula which is equivalent to a standard translation is invariant for bisimulation. We cannot prove it as an ‘if and only if’ statement, since according to the proofs in [1], we can only prove the two directions separately as:
Proposition 5
[1, Theorem 2.68, as two separate directions]

which cannot be put together into a double implication. To see the reason: given an \(\mathcal L_{\tau }^1\)-formula \(\phi \) with no more then one free variable, by the second theorem above, if
 is invariant under bisimulation for models with
is invariant under bisimulation for models with
 -worlds, then \(\phi \) is equivalent to a standard translation on a model with \(\alpha \)-worlds. However, if we want to prove the converse of this statement, we need to start with the assumption that \(\phi \) is equivalent to a standard translation on models with \(\alpha \)-worlds, and prove that \(\phi \) is invariant for bisimulation for models with
-worlds, then \(\phi \) is equivalent to a standard translation on a model with \(\alpha \)-worlds. However, if we want to prove the converse of this statement, we need to start with the assumption that \(\phi \) is equivalent to a standard translation on models with \(\alpha \)-worlds, and prove that \(\phi \) is invariant for bisimulation for models with
 -worlds. But by the first theorem above, we can only conclude \(\phi \) is invariant for bisimulation for models of type \(\alpha \). The point is that it is not the fact that all our desired operations can be taken within a type. In particular, we cannot take ultraproducts of models and preserve cardinalities. The cardinality of the type universe of
-worlds. But by the first theorem above, we can only conclude \(\phi \) is invariant for bisimulation for models of type \(\alpha \). The point is that it is not the fact that all our desired operations can be taken within a type. In particular, we cannot take ultraproducts of models and preserve cardinalities. The cardinality of the type universe of
 is too large to be embedded into \(\alpha \), so we cannot just fix the ‘base type’ to be
is too large to be embedded into \(\alpha \), so we cannot just fix the ‘base type’ to be
 and get an ‘if and only if’ statement-we cannot derive \(\phi \) is invariant for bisimulation for models with
and get an ‘if and only if’ statement-we cannot derive \(\phi \) is invariant for bisimulation for models with
 -worlds from the fact that \(\phi \) is invariant for bisimulation for models with \(\alpha \)-worlds. If we could quantify over types (as we could in a theorem prover based on dependent type theory), then we can could define ‘invariant under bisimulation for models of every type’, and hence prove the original statement of Van Benthem characterisation theorem.
-worlds from the fact that \(\phi \) is invariant for bisimulation for models with \(\alpha \)-worlds. If we could quantify over types (as we could in a theorem prover based on dependent type theory), then we can could define ‘invariant under bisimulation for models of every type’, and hence prove the original statement of Van Benthem characterisation theorem.
For the proof of the two theorems above, the first one is immediate from Proposition 1, and the second one requires another critical lemma saying ‘modal equivalence between two worlds implies bisimilarity of the two worlds when embedded in some other models’. More precisely, if two worlds
 and
and
 are modal equivalent, then we can find an ultrafilter U on J such that in ultrapower models of
are modal equivalent, then we can find an ultrafilter U on J such that in ultrapower models of
 and
and
 on U respectively, there is a bisimulation between the worlds corresponding to
on U respectively, there is a bisimulation between the worlds corresponding to
 and
and
 .
.
Theorem 7
[1, Theorem 2.74, one direction]

The proof of the above relies on Lemma 2.
8 Conclusion
To summarise, we have mechanised all of the results (appearing as propositions, lemmas and theorems) in the first two chapters in Blackburn et al. [1] that can be captured by the HOL logic, and which are about the basic modal language. The exceptions are:
-
The result in Sect. 2.6 about ‘definability’, which requires a definition of the ‘models closed under taking ultraproducts’. Simple type theory cannot capture such large sets.
-
The result about ‘safety’ in Sect. 2.7 is a result about the PDL language, which has infinitely many modal operators. For the moment, we have restricted our attention to the basic modal language, with only \(\Diamond \) (and the derived \(\Box \)).
The two characterisation theorems from Blackburn et al. [1], namely Theorem 2.68 (Van Benthem’s Characterisation Theorem) and Theorem 2.78, are the only two mechanised theorem such that translating the ‘if and only if’ statements from set theory into simple theory does not yield an ‘if and only if’ statement. Blackburn et al.’s proof of Theorem 2.78 has the same pattern as Van Benthem’s Characterisation Theorem (discussed earlier), and is less complicated.
For each of the mechanised definitions and results, we write the statement in HOL to be as close as possible to the original statement in [1]. We believe that this makes it as easy as possible for people who are interested in mechanising other results in [1] to continue with our work as a starting point. The work on ultraproducts up to Łoś’s theorem is independent of our work on modal model theory, and should be generally useful in other model-theoretic applications.
8.1 Related Work
We believe that we are the first to mechanise the bulk of the results in this paper. Of course, much work has been done in this and similar areas. For example, de Wind’s thesis [7] is a notable early mechanisation of modal logic, mainly focusing on proving the validity of modal formulas via natural deduction. Of similar vintage is Harrison’s mechanisation of foundational results about first order model theory [5], in particular compactness. We used this mechanisation directly in our own work. A great deal of work has also been done in the mechanisation of first order proof theory, such as the recent pearl by Blanchette et al. [2], showing completeness in elegant fashion.
The connections between modal logic and process algebra are well-understood and there has been a great deal of mechanised work on the operational theory of such (co-)algebraic systems, starting at least as far back as Nesi [6]. Our proof of the Hennessy-Milner theorem (Theorem 1) is a gesture in this direction, but Van Benthem’s theorem is much deeper and uses bisimulations as a tool to understanding the connection between modal and first order logics, rather than as a connection to process algebras.
Mechanised work with ultrafilters began with Fleuriot’s use of them to mechanise non-standard analysis [4]. We are unaware of any previous mechanised use of ultraproducts or ultrapowers.
References
Blackburn, P., de Rijke, M., Venema, Y.: Modal Logic. Cambridge University Press, Cambridge (2001)
Blanchette, J.C., Popescu, A., Traytel, D.: Unified classical logic completeness. In: Demri, S., Kapur, D., Weidenbach, C. (eds.) IJCAR 2014. LNCS (LNAI), vol. 8562, pp. 46–60. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08587-6_4
Chang, C.C., Keisler, H.J.: Model Theory. North Holland, Amsterdam (1990)
Fleuriot, J.: A Combination of Geometry Theorem Proving and Nonstandard Analysis with Application to Newton’s Principia. Springer, London (2001). https://doi.org/10.1007/978-0-85729-329-9
Harrison, J.: Formalizing basic first order model theory. In: Grundy, J., Newey, M. (eds.) TPHOLs 1998. LNCS, vol. 1479, pp. 153–170. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055135
Nesi, M.: Mechanising a modal logic for value-passing agents in HOL. Electron. Notes Theor. Comput. Sci. 5, 31–46 (1996). https://doi.org/10.1016/S1571-0661(05)80682-6
de Wind, P.: Modal Logic in Coq. Master’s thesis, Vrije Universiteit (2001)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Xu, Y., Norrish, M. (2020). Mechanised Modal Model Theory. In: Peltier, N., Sofronie-Stokkermans, V. (eds) Automated Reasoning. IJCAR 2020. Lecture Notes in Computer Science(), vol 12166. Springer, Cham. https://doi.org/10.1007/978-3-030-51074-9_30
Download citation
DOI: https://doi.org/10.1007/978-3-030-51074-9_30
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-51073-2
Online ISBN: 978-3-030-51074-9
eBook Packages: Computer ScienceComputer Science (R0)





 is the tree-like model obtained from Proposition
is the tree-like model obtained from Proposition  such that
such that
 .
. is the restriction of
is the restriction of
 to height k.
to height k. is obtained from
is obtained from
 by modifying the valuation into
by modifying the valuation into
 where
where
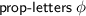 is the set of all propositional letters used by
is the set of all propositional letters used by
 .
. modulo U.
modulo U. iff there exist
iff there exist  is in U.
is in U. iff there exists
iff there exists  is in U.
is in U. over U on J.
over U on J. of equivalence classes to the equivalence class of a function that sends
of equivalence classes to the equivalence class of a function that sends  , where the k-th member of the list l is a representative of the k-th member (which is an equivalence class) of
, where the k-th member of the list l is a representative of the k-th member (which is an equivalence class) of
 .
. of equivalence classes if and only if when we have a list
of equivalence classes if and only if when we have a list
 , where k-th member is a representative of the k-th member of zs, the set of elements
, where k-th member is a representative of the k-th member of zs, the set of elements
 such that
such that
 is in U.
is in U. .
. ,
,
 on
on
 are related in the ultrafilter extension of
are related in the ultrafilter extension of
 if for every
if for every
 , the set of worlds that can see
, the set of worlds that can see
 is in
is in
 .
. which satisfies p is in v.
which satisfies p is in v.