Abstract
This paper introduces a new cross-platform programming framework for developing quantum-accelerated scientific computing applications and executing them on most of today’s cloud-based quantum computers and simulators. It makes use of C++ template meta-programming techniques to implement quantum algorithms as generic, platform-independent expressions, which get automatically synthesized into device-specific compute kernels upon execution. Our software framework supports concurrent and asynchronous execution of multiple quantum kernels via a CUDA-inspired stream concept.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The development of practically usable quantum computing technologies is in full swing involving global players like Alibaba, Atos, Google, IBM, and Microsoft and specialists in this field such as Rigetti Computing and D-Wave. These parties compete for technology lead and, finally, simply the raw number of qubits they can provide through their quantum processing units (QPUs), which can be either hardware quantum computers or quantum computer simulators running on classical high-performance computing hardware. This situation resembles the very early days of GPU-accelerated computing when the first generation of general-purpose programmable graphics cards became available but their productive use in scientific applications was largely hindered by the non-availability of software development kits (SDKs) and easy-to-use domain-specific software libraries and, even more severe, the lack of standardized non-proprietary development environments that would lower the dependence on a particular GPU vendor.
Today’s quantum software landscape can be grouped into three main categories: quantum SDKs [1, 6, 15, 19, 22], stand-alone quantum simulators [5, 11, 13], and quantum assembly (QASM) [2, 3, 12] or instruction languages (QUIL) [21]. A recent overview and comparison of gate-based quantum software platforms by LaRosa [14] shows that the field is highly fragmented making it impossible to perform a fair quantitative performance comparison. Moreover, the tools focus on quantum computing experts who are mainly interested in the development of stand-alone quantum algorithms rather than their use as computational building blocks within a possibly hybrid classical-quantum solution procedure.
In our opinion, practical quantum computing has the highest chances to become a game-changer for the computational sciences if it is positioned as special-purpose accelerator technology that will become available in future heterogeneous compute platforms equipped with GPUs, QPUs and other emerging accelerators like field-programmable gate arrays (FPGAs). Researchers and scientific application developers will then have the free choice between, say, running the HHL-algorithm [9] on a QPU accelerator and adopting one of the many classical numerical methods for solving linear systems of equations on CPUs, GPUs or FPAGs depending on problem sizes and matrix characteristics. In [17] we have outlined a conceptual framework for QPU-accelerated automated design optimization that builds on the HHL-solver as main computational driver.
We believe that end-users from the community of computational science and engineering would be interested in giving QPU-accelerated computing a try with the right software tools at hand. With this vision in mind, we created the  -project [16] (pronounced Lib-Ket), which is a cross-platform programming framework that aims at making QPU-accelerated computing as easily accessible for the masses as GPU computing is today through frameworks like CUDA [18].
-project [16] (pronounced Lib-Ket), which is a cross-platform programming framework that aims at making QPU-accelerated computing as easily accessible for the masses as GPU computing is today through frameworks like CUDA [18].
The remainder of this paper is structured as follows: Sect. 2 discusses the design principles underlying the  framework, which is introduced in Sect. 3. Implementation details are discussed in Sect. 4 followed by a brief demonstration of
framework, which is introduced in Sect. 3. Implementation details are discussed in Sect. 4 followed by a brief demonstration of  ’s capabilities in Sect. 5. Section 6 completes the paper with a conclusion and an outlook on functionality planned for future releases.
’s capabilities in Sect. 5. Section 6 completes the paper with a conclusion and an outlook on functionality planned for future releases.
2 Design Principles
To achieve our set-out vision,  is designed based on the following principles:
is designed based on the following principles:
-
QPU-accelerated computing: Quantum computers are used as special-purpose accelerator devices within a heterogeneous computer system that can host multiple accelerator technologies (GPUs, FPGAs, ...) side by side.
-
Concurrent task offloading: Quantum algorithms are implemented as compute kernels describing concurrent tasks launched on QPU devices.
-
Single-source quantum-classical programming: Classical and quantum code is implemented in a single source file, which is compiled into one hybrid binary executable executed on the host computer, who offloads certain parts of the computation to the accelerator devices.
-
Write once run anywhere: Quantum algorithms are implemented once and for all as generic expressions, which can be executed on current and future QPU-device types. Support for a particular type is realized by a small set of conversion functions between
 ’s unified interface layer and the device-specific low-level application programming interface (API).
’s unified interface layer and the device-specific low-level application programming interface (API). -
Standing on the shoulders of giants:
 is developed on top of existing vendor-specific tools and libraries to exploit their full optimization potential.
is developed on top of existing vendor-specific tools and libraries to exploit their full optimization potential. -
Seamless integration into status quo:
 does not create new standards that need to be implemented by others but utilizes the available tools.
does not create new standards that need to be implemented by others but utilizes the available tools.
The first three principles suggest a conceptual design in the spirit of CUDA [18] or OpenCL [23], which are de-facto standards for GPU computing. To underline the postulated similarity between QPU- and GPU-accelerated computing and to make quantum computing more accessible to experts in classical accelerator technologies, we will utilize a GPU-inspired terminology such as host (the CPU and its memory) and device (the QPU and its memory), kernels and streams, as well as asynchronous execution and synchronization throughout this paper.
The write-once-run-anywhere principle has led us to adopt template meta-programming techniques to implement quantum algorithms as generic expressions, whose evaluation for a particular QPU type is delayed until the program flow has reached the point, where its actual value is really needed. This approach is also known as lazy evaluation or call-by-need principle in programming language theory and is used successfully in linear algebra libraries [4, 7, 8, 10, 20, 24].
The last two principles are mainly based on pragmatic considerations. Firstly, introducing yet another approach to quantum programming incompatible to the existing ones would escalate the fragmentation of the quantum software landscape instead of improving the situation for the potential end-users. Moreover, the chosen approach allows for exploiting the expertise and manpower of scientists worldwide working on different aspects of quantum computing and their expert knowledge of non-disclosed technical details of QPU devices to create an open software ecosystem that immediately benefits from any improvement in one of the underling core components. Finally, most human beings are more open to emerging technologies if they come as evolutionary increments of the status quo instead of radical paradigm shifts that call for dumping all previous work.
3 The 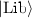 Programming Framework
Programming Framework
The open-source, cross-platform  programming framework is designed as header-only C++14
programming framework is designed as header-only C++14  Footnote 1 with minimal external dependencies, namely, an embedded Python interpreter and, possibly, header and/or library files from the respective quantum backends. It can be downloaded free-of-charge from the GitLab repository https://gitlab.com/mmoelle1/LibKet, which provides documentation in form of a wiki and an API documentation and several tutorial examples to get started. In addition to the primary C++ API, C and Python APIs are being implemented, which adopt just-in-time compilation techniques to exploit the full potential of C++ template meta-programming internally and expose
Footnote 1 with minimal external dependencies, namely, an embedded Python interpreter and, possibly, header and/or library files from the respective quantum backends. It can be downloaded free-of-charge from the GitLab repository https://gitlab.com/mmoelle1/LibKet, which provides documentation in form of a wiki and an API documentation and several tutorial examples to get started. In addition to the primary C++ API, C and Python APIs are being implemented, which adopt just-in-time compilation techniques to exploit the full potential of C++ template meta-programming internally and expose  ’s functionality in C and Python-style to the outside.
’s functionality in C and Python-style to the outside.
A comprehensive overview of the  programming framework is given in Fig. 1. It consists of three layers that provide components for application programmers (high-level (HL) API), quantum algorithm developers (mid-level (ML) API), and QPU providers (low-level (LL) API), respectively.
programming framework is given in Fig. 1. It consists of three layers that provide components for application programmers (high-level (HL) API), quantum algorithm developers (mid-level (ML) API), and QPU providers (low-level (LL) API), respectively.
Before we describe the different software layers in more detail we give a short example on  ’s general usage. Consider the C++ code snippet given in Listing 1 which puts the first and third qubit of a quantum register into the maximally entangled first Bell state, where A is qubit 1 and B is qubit 3:
’s general usage. Consider the C++ code snippet given in Listing 1 which puts the first and third qubit of a quantum register into the maximally entangled first Bell state, where A is qubit 1 and B is qubit 3:

The easiest way to achieve this is to start from the computational basis  and apply a Hadamard gate to one qubit followed by a controlled-NOT (CNOT) gate
and apply a Hadamard gate to one qubit followed by a controlled-NOT (CNOT) gate

This is realized by the quantum expression that is constructed in lines 8–9 of the code snippet, thereby demonstrating two of  ’s most essential components, namely, Quantum Filters and Quantum Gates, which are implemented in the namespaces LibKet::filters and LibKet::gates, respectively.
’s most essential components, namely, Quantum Filters and Quantum Gates, which are implemented in the namespaces LibKet::filters and LibKet::gates, respectively.
As the name suggests, filters select a subset of the quantum register; see Sect. 4.1 for more details. Here, sel\(<1>\)() selects the first qubit for applying the Hadamard gate. This sub-expression serves as first argument, the control, to the binary CNOT gate, whose action is applied to the third qubit (
 ). The
). The
 gate puts all qubits of the quantum register into the computational basis
gate puts all qubits of the quantum register into the computational basis  . More information on gates is given in Sect. 4.2. It should be noted that the resulting quantum expression is generic, that is, object expr holds an abstract syntax tree (AST) representation of the Bell state creation algorithm that can be synthesized to any of
. More information on gates is given in Sect. 4.2. It should be noted that the resulting quantum expression is generic, that is, object expr holds an abstract syntax tree (AST) representation of the Bell state creation algorithm that can be synthesized to any of  ’s quantum backends. For the cloud-based Quantum-Inspire (QI) platformFootnote 2, this is accomplished by lines 15 and 18. In short, line 15 creates a deviceobject that holds 6 qubits and specializes the generic quantum expression exprinto common QASM code v1.0 [12], the programming language for the QI backend. The internally stored quantum kernel code as well as the quantum expression exprcan be printed as illustrated in lines 21 and 12, respectively; see Listing 2. The probability amplitudes resulting from 1024 runs of the quantum algorithm are presented in the same diagram.
’s quantum backends. For the cloud-based Quantum-Inspire (QI) platformFootnote 2, this is accomplished by lines 15 and 18. In short, line 15 creates a deviceobject that holds 6 qubits and specializes the generic quantum expression exprinto common QASM code v1.0 [12], the programming language for the QI backend. The internally stored quantum kernel code as well as the quantum expression exprcan be printed as illustrated in lines 21 and 12, respectively; see Listing 2. The probability amplitudes resulting from 1024 runs of the quantum algorithm are presented in the same diagram.

The actual execution of the quantum kernel is triggered in line 24, which starts an embedded Python interpreter as sub-process to communicate with the cloud-based quantum simulator platform via the vendor-specific QI-SDKFootnote 3. This call performs blocking execution and returns a JSON object upon successful completion, from which the result can be retrieved. More details on how to customize the execution process, run multiple quantum kernels concurrently and perform non-blocking asynchronous kernel execution are given in Sect. 4.5.

4 Implementation Details
In what follows, we address the individual  components and shed some light on their internal realization and ways to extend them to support new backends.
components and shed some light on their internal realization and ways to extend them to support new backends.
4.1 Quantum Filter Chains
As stated before,  ’s quantum filters are meant to select subsets of qubits from the global quantum register to which the following quantum operation is being applied, which is comparable to matrix views in the Eigen library [8].
’s quantum filters are meant to select subsets of qubits from the global quantum register to which the following quantum operation is being applied, which is comparable to matrix views in the Eigen library [8].
Since today’s and near-future quantum processors have a very limited number of qubits, typically, between 5–50, we consider the assumption of a single global quantum register and the absence of dynamic memory (de)allocation capabilities most practical. Moreover, quantum computing follows the in-memory computing paradigm, that is, data is stored and manipulated at fixed locations in memory. This is in contrast to the classical von-Neuman computer architecture, where data is transported between the randomly accessible main memory (RAM) and the central processing unit (CPU), the latter performing the computations.
 ’s quantum filters.
’s quantum filters.Table 1 lists all quantum filters supported by  . All filtering operations are applied relative to the given input, which makes it possible combine multiple filters to so-called filter chains. Consider, for instance, the filter chain qubit \(2\) (shift \(2\) (range \(2,5\) ())), which selects the 6-th qubit from the global register, more precisely, the pre-selected set of qubits passed as input.
. All filtering operations are applied relative to the given input, which makes it possible combine multiple filters to so-called filter chains. Consider, for instance, the filter chain qubit \(2\) (shift \(2\) (range \(2,5\) ())), which selects the 6-th qubit from the global register, more precisely, the pre-selected set of qubits passed as input.
Thanks to the use of C++ template meta-programming techniques, quantum filters are evaluated at compile time and, hence, even complex filter chains cause no overhead costs at run time. With the aid of gototag<Tag>() it is possible to restore a previously stored filter configuration that has been tagged by the tag<Tag>() function. It is generally recommended to safeguard quantum expressions that should be used as building blocks in larger algorithms by tag-gototagpairs to prevent side effects from internal manipulation of the qubit selection.
All components listed in Table 1 come in two flavours, a class whose instantiated objects span the abstract syntax tree (AST) of the expression and a creator function that returns an object of the respective type. Classes are required to implement the
 for all expressions that should be supported; see Listing 3 for an example. Here and below the universal-reference variant, i.e.
for all expressions that should be supported; see Listing 3 for an example. Here and below the universal-reference variant, i.e.
 is omitted due to space limitations but it is implemented for all types to support C++11 move semantics.
is omitted due to space limitations but it is implemented for all types to support C++11 move semantics.
Though not foreseen in the current implementation, the just described quantum filter mechanism can be easily extended to support rudimentary stack memory based on a reserved region of the global quantum register. Together with  ’s just-in-time (JIT) capabilities (see below) even dynamic memory (de)allocation would be possible with the adopted concept once a sufficiently large number of qubits and circuit depths are reliably supported in quantum hardware to make this feature relevant for practical applications.
’s just-in-time (JIT) capabilities (see below) even dynamic memory (de)allocation would be possible with the adopted concept once a sufficiently large number of qubits and circuit depths are reliably supported in quantum hardware to make this feature relevant for practical applications.
4.2 Quantum Gates
 ’s implementation of quantum gates follows the same programming paradigm (class with overloaded
’s implementation of quantum gates follows the same programming paradigm (class with overloaded
 and gate-creator function) as described above. Additionally, the class provides an overloaded apply(QData \(...\) & data)method, which is specialized for each supported backend type. Listing 4 illustrates how the application of the Hadamard gate appends QASM code to the data’s internal quantum kernel for the cQASMv1backend; see lines 4–13. The static range()method is one of several filter utility functions that returns the actual list of selected qubits based on data’s concrete register size at compile time.
and gate-creator function) as described above. Additionally, the class provides an overloaded apply(QData \(...\) & data)method, which is specialized for each supported backend type. Listing 4 illustrates how the application of the Hadamard gate appends QASM code to the data’s internal quantum kernel for the cQASMv1backend; see lines 4–13. The static range()method is one of several filter utility functions that returns the actual list of selected qubits based on data’s concrete register size at compile time.
Invoking the Hadamard function (lines 16–19) returns a UnaryQGateobject (see below) that stores the current sub-expression, the gate to be applied next, and the filter selection internally. The specialized overload in lines 21–25 ensures that the immediate double-application of the Hadamard gate gets eliminated.  makes extensive use of this type of rule-based optimization to eliminate gate-level expressions of the form t(tdag(...))as well as entire quantum circuits followed immediately by their inverse, e.g., qft(qftdag(...)).
makes extensive use of this type of rule-based optimization to eliminate gate-level expressions of the form t(tdag(...))as well as entire quantum circuits followed immediately by their inverse, e.g., qft(qftdag(...)).

To orchestrate the interplay of expressions, filters and gates,  implements unary, binary, and ternary gate containers that hold the aforementioned information as types except for the actual sub-expression which is stored by-value. Instantiations of these nearly stateless classes span the quantum expression’s AST (see Listing 2 (left)), whereby an overloaded
implements unary, binary, and ternary gate containers that hold the aforementioned information as types except for the actual sub-expression which is stored by-value. Instantiations of these nearly stateless classes span the quantum expression’s AST (see Listing 2 (left)), whereby an overloaded
 method dispatches between the different variants to apply quantum gates to expressions.
method dispatches between the different variants to apply quantum gates to expressions.
Next to the set of quantum gates that are typically supported by most QPU backends,  comes with a special hook-gate that can be used to implement common quantum building blocks, e.g., the first Bell state from Listing 1
comes with a special hook-gate that can be used to implement common quantum building blocks, e.g., the first Bell state from Listing 1

4.3 Quantum Circuit
The main advantage of  ’s generic quantum-expression approach becomes visible for circuits, which represent compile-time parametrizable algorithms like the well-known Quantum Fourier transform, invoked via the qft()function. The implementation follows the same programming paradigms (class with overloaded
’s generic quantum-expression approach becomes visible for circuits, which represent compile-time parametrizable algorithms like the well-known Quantum Fourier transform, invoked via the qft()function. The implementation follows the same programming paradigms (class with overloaded
 and corresponding creator function with rule-based optimization) but, typically, with a generic apply() method, whose synthetization to device-specific instructions is handled by the gates. Our approach makes it, however, possible to also specialize full circuits for selected QPU backends, e.g., to use Qiskit’s [1] internal realization of the HHL-solver [9] for the IBM Q platform.
and corresponding creator function with rule-based optimization) but, typically, with a generic apply() method, whose synthetization to device-specific instructions is handled by the gates. Our approach makes it, however, possible to also specialize full circuits for selected QPU backends, e.g., to use Qiskit’s [1] internal realization of the HHL-solver [9] for the IBM Q platform.

To ease the development of generic quantum circuits,  implements a static for-loop that accepts the body as functor being passed as template argument together with loop bounds and step size as illustrated in Listing 5.
implements a static for-loop that accepts the body as functor being passed as template argument together with loop bounds and step size as illustrated in Listing 5.
Moreover,  comes with just-in-time (JIT) compilation capabilities making it possible to generate quantum expressions dynamically from user input. Quantum expressions that are given in string format are JIT compiled into dynamically loaded libraries that are cached across multiple program runs.
comes with just-in-time (JIT) compilation capabilities making it possible to generate quantum expressions dynamically from user input. Quantum expressions that are given in string format are JIT compiled into dynamically loaded libraries that are cached across multiple program runs.

4.4 Quantum Devices
The synthetization of generic quantum expressions into device-dependent quantum instructions that can be executed on a specific QPU is realized by the many specializations of the QDevice class, which brings together a particular backend type with device-specific details, such as credentials and parameters for connecting to cloud-based services, the maximum number of qubits, the native gate set, and the lattice structure, which might require internal optimization passes.
Lines 15 and 18 of Listing 1 create a device instance for running the quantum algorithm remotely on the Quantum-Inspire simulator platform and populate its internal quantum kernel with the expression given by Eq. (1) for creating the first Bell state, respectively. Next to providing methods for executing the kernel as described in the next section, some device types support extra functionality such as the transpilation of the generic quantum circuit into device-optimized quantum instructions and the export of the resulting circuit to  . The quantum circuits depicted in Fig. 2 were produced by the following code snippet
. The quantum circuits depicted in Fig. 2 were produced by the following code snippet

We consider this functionality helpful for getting a better understanding of the actual circuit – possibly with extra swap gates added to enable two-qubit operations on non-neighboring qubits – that is executed on the device rather than its idealized textbook version. The transpilation step can be bypassed by choosing generic simulators such as ibmq_qasm_simulator and cirq_simulator.
Quantum circuits for producing the first Bell state, cf. Eq. (1), optimized for (a) IBM’s 5-qubit London chip and (b) Google’s 22-qubit Foxtail chip.
4.5 Quantum Kernel Execution
Once the generic expression has been synthesized into device-dependent instructions it can be executed on the respective QPU device. As explained before, our aim is to ease the transition from GPU programming to QPU-accelerated computing.  therefore adopts a CUDA-inspired stream-based execution model, which enables concurrent quantum kernel execution on multiple QPU devices.
therefore adopts a CUDA-inspired stream-based execution model, which enables concurrent quantum kernel execution on multiple QPU devices.
The device’s eval()method called in line 24 of Listing 1 accepts a so-called QStream<QJobType::Python> object as optional parameter and so do the methods execute()and execute_async()as shown in the following code snippet

While the eval()method waits until the execution has finished and returns the result as JSON object or throws an exception upon failure, the execute()method returns a pointer to a job object QJob<QJobType::Python> that supports query(),wait() and get() operations. Its non-blocking counterpart execute_async() can be used to hide the latency stemming from the execution of the quantum kernel on remote QPUs and the overhead costs due to invoking the embedded Python interpreter with other computations on the CPU or other accelerator devices. It is even possible to execute multiple quantum algorithms concurrently on multiple QPUs by launching their kernels in different streams.
Use of an embedded Python interpreter as interface between classical host code and quantum kernels has the advantage that the full potential of vendor-specific SDKs can be exploited to perform circuit optimization and other pre- and post-processing tasks including possible validity checks on the host side before communicating the quantum kernel to the remote QPU device for execution.
The three unused parameters in line 2 of the above code snippet can be used to inject user-defined code preceding the import of Python modules and right before and after the execution of the quantum circuit, respectively. A possible application of this feature is the internal post-processing of measurement results with the functionality provided by a particular SDKFootnote 4, e.g., to visualize the measurement outcome as histogram and write it to a graphics file

While retrieving the outcome of a quantum experiment as JSON object is most flexible it requires backend-specific post-processing steps to extract the desired information. For widely used data such as job identifier and duration, histogram of results, and the state with highest likelihood, each QDevice class specialization provides functionality to extract information from the JSON object and convert it into  -specific or intrinsic C++ types, e.g.
-specific or intrinsic C++ types, e.g.

Let us finally remark that  also supports the native execution of quantum kernels written in C++, e.g., for quantum simulators like QX [13] and QuEST [11], using the multithreading capabilities that come with C++ 11.
also supports the native execution of quantum kernels written in C++, e.g., for quantum simulators like QX [13] and QuEST [11], using the multithreading capabilities that come with C++ 11.
5 Demonstration
 is a rather young project that is under continuous development. The correct functioning of the core framework described in this paper has been verified by extensive unit tests. A comprehensive presentation of computational examples is beyond the scope of this paper and not possible within the given page limit. We therefore restrict ourselves to a single test case, namely, the quantum expression qft(init()) and apply it to a quantum register consisting of 1–12 qubits as a first benchmark to measure the performance of different QPU backends.
is a rather young project that is under continuous development. The correct functioning of the core framework described in this paper has been verified by extensive unit tests. A comprehensive presentation of computational examples is beyond the scope of this paper and not possible within the given page limit. We therefore restrict ourselves to a single test case, namely, the quantum expression qft(init()) and apply it to a quantum register consisting of 1–12 qubits as a first benchmark to measure the performance of different QPU backends.
Figure 3 depicts the run times measured for the following QPU backends: Cirq [6] (v0.7.0, generic simulator), pyQuil [21] (v2.19.0, 9q-square-simulator), QI [13] (v1.1.0), Qiskit [1] (v.0.17.0, qasm-simulator), and QuEST [11] (v3.1.1, CPU-OpenMP simulator). All runs were performed with 1024 shots on a dual-socket Intel Xeon E5-2687W Sandy Bridge EP system with 2 \(\times \) 8 cores running at 3.1 GHz with 128 GB of DDR3-1600 memory except for the QI runs, which were executed on a remote system with unknown hardware specification.
For some backends, such as pyQuil and Qiskit, increasing the number of qubits and the circuit depth results in significantly longer run times, while others are less sensitive to these parameters. It should be noted that the run times measured for the pyQuil backend include the transformation of the quantum circuit into executable code by the Quil Compiler, which might explain the higher values. The QuEST backend does not allow repeated evaluation of the circuit so that the measured run time might be dominated by overhead costs.
We would like to stress that the presented results are preliminary and should not be considered a comprehensive performance analysis of the QPU backends under consideration. Systematic benchmarking of many more simulator and hardware backends for quantum circuits of different depth and level of entanglement is underway and will be presented in a forthcoming publication.
6 Conclusion
In this paper we have introduced our novel cross-platform programming framework  , which aims at facilitating the use of quantum computers (and their simulators) for accelerating the solution of scientific problems. Primarily addressing today’s GPU programmers as early adopters, our framework is largely inspired by Nvidia’s CUDA toolkit and offers a similar programming model based on quantum kernels that can be executed concurrently using multiple streams. As a unique feature,
, which aims at facilitating the use of quantum computers (and their simulators) for accelerating the solution of scientific problems. Primarily addressing today’s GPU programmers as early adopters, our framework is largely inspired by Nvidia’s CUDA toolkit and offers a similar programming model based on quantum kernels that can be executed concurrently using multiple streams. As a unique feature,  does not focus on one particular QPU backend but adopts C++ template meta-programming techniques to enable the development of quantum algorithms as generic expressions that can be synthesized to various QPU-backend types, following the write-once-run-anywhere principle.
does not focus on one particular QPU backend but adopts C++ template meta-programming techniques to enable the development of quantum algorithms as generic expressions that can be synthesized to various QPU-backend types, following the write-once-run-anywhere principle.
Ongoing developments focus on the extension of the algorithm library (mid-level API; cf. Fig. 1), especially, variants of the HHL-solver [9] and its computational ingredients such as eigenvalue estimation. Another line of research work addresses the implementation of basic arithmetic routines, which are also used inside the HHL-algorithm to invert eigenvalues. Finally, the extension of the low-level API to support additional QPU backends and to reduce the computational overhead incurred by the use of the embedded Python interpreter and the conversion from JSON objects to C++ types is a permanent quest.
Despite the early development stage of the  framework, we would like to encourage the scientific computing community to report their experience with it and express feature requests for forthcoming releases to the authors.
framework, we would like to encourage the scientific computing community to report their experience with it and express feature requests for forthcoming releases to the authors.
Notes
- 1.
In the Dutch language, the word quantum is spelled kwantum. Hence, the name
 (pronounced Lib-Ket) is an allusion to the bra-ket notation introduced in 1939 by Paul Dirac that is widely used for expressing quantum algorithms.
(pronounced Lib-Ket) is an allusion to the bra-ket notation introduced in 1939 by Paul Dirac that is widely used for expressing quantum algorithms. - 2.
https://www.quantum-inspire.com designed and built by the Dutch research center for Quantum Computing and Quantum Internet QuTech (https://qutech.nl). The basic user account only allows utilization of the 26-qubit version of the QI simulator.
- 3.
- 4.
Generation of the history plot by the ibmq device requires the packages qiskit and matplotlib to be installed and accessible by the embedded Python interpreter.
References
Abraham, H., et al.: Qiskit: an open-source framework for quantum computing (2019). https://doi.org/10.5281/zenodo.2562110
Atos: Atos QLM software stack (2019)
Cross, A.W., et al.: Open quantum assembly language (2017)
Demidov, D., et al.: Programming CUDA and OpenCL: a case study using modern C++ libraries. SIAM J. Sci. Comput. 35(5), C453–C472 (2013)
Gidney, C.: Quirk: a drag-and-drop quantum circuit simulator that runs in your browser (2019). https://github.com/Strilanc/Quirk
Gidney, C., et al.: Cirq: a Python framework for creating, editing, and invoking noisy intermediate scale quantum (NISQ) circuits (2019). https://github.com/quantumlib/Cirq
Gottschling, P., et al.: Generic compressed sparse matrix insertion: algorithms and implementations in MTL4 and FEniCS. In: Proceedings of the 8th Workshop on Parallel/High-Performance Object-Oriented Scientific Computing, POOSC 09, pp. 2:1–2:8. ACM, New York (2009)
Guennebaud, G., et al.: Eigen v3 (2010). http://eigen.tuxfamily.org
Harrow, A.W., et al.: Quantum algorithm for linear systems of equations. Phys. Rev. Lett. 103, 150502 (2009)
Iglberger, K.: Blaze C++ linear algebra library (2012). https://bitbucket.org/blaze-lib
Jones, T., et al.: Quest and high performance simulation of quantum computers. Sci. rep. 9(1), 10736 (2019). https://doi.org/10.1038/s41598-019-47174-9
Khammassi, N., et al.: cQASM v1.0: towards a common quantum assembly language (2018)
Khammassi, N., et al.: QX: a high-performance quantum computer simulation platform. In: Proceedings of the 2017 Design, Automation & Test in Europe Conference & Exhibition (DATE), pp. 464–469. IEEE, United States (2017)
LaRose, R.: Overview and comparison of gate level quantum software platforms. Quantum 3, 130 (2019)
Microsoft: Quantum development kit (2019). https://www.microsoft.com/en-us/quantum/development-kit
Möller, M., et al.: LibKet: the quantum expression template library (2019). https://gitlab.com/mmoelle1/LibKet
Möller, M., et al.: A conceptual framework for quantum accelerated automated design optimization. Microprocess. Microsyst. 66, 67–71 (2019)
Nickolls, J., et al.: Scalable parallel programming with CUDA. Queue 6(2), 40–53 (2008)
Rigetti Computing: PyQuil: a Python library for quantum programming using Quil (2019). https://github.com/rigetti/pyquil
Rupp, K., et al.: ViennaCL – linear algebra library for multi- and many-core architectures. SIAM J. Sci. Comput. 38(5), S412–S439 (2016)
Smith, R.S., et al.: A practical quantum instruction set architecture (2016)
Steiger, D.S., et al.: ProjectQ: an open source software framework for quantum computing. Quantum 2, 49 (2018)
Stone, J.E., et al.: OpenCL: a parallel programming standard for heterogeneous computing systems. Comput. Sci. Eng. 12(3), 66–73 (2010)
Yalamanchili, P., et al.: ArrayFire - a high performance software library for parallel computing with an easy-to-use API (2015). https://github.com/arrayfire/arrayfire
Acknowledgments
The authors would like to thank Kelvin Loh and Richard Versluis from TNO for fruitful discussions and financial support of the second author. Moreover, financial support by the 4TU. Centre for Engineering Education is acknowledged. We finally thank the anonymous reviewers for their constructive feedback.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Möller, M., Schalkers, M. (2020).  : A Cross-Platform Programming Framework for Quantum-Accelerated Scientific Computing.
In: Krzhizhanovskaya, V., et al. Computational Science – ICCS 2020. ICCS 2020. Lecture Notes in Computer Science(), vol 12142. Springer, Cham. https://doi.org/10.1007/978-3-030-50433-5_35
: A Cross-Platform Programming Framework for Quantum-Accelerated Scientific Computing.
In: Krzhizhanovskaya, V., et al. Computational Science – ICCS 2020. ICCS 2020. Lecture Notes in Computer Science(), vol 12142. Springer, Cham. https://doi.org/10.1007/978-3-030-50433-5_35
Download citation
DOI: https://doi.org/10.1007/978-3-030-50433-5_35
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-50432-8
Online ISBN: 978-3-030-50433-5
eBook Packages: Computer ScienceComputer Science (R0)


 ’s unified interface layer and the device-specific low-level application programming interface (API).
’s unified interface layer and the device-specific low-level application programming interface (API). is developed on top of existing vendor-specific tools and libraries to exploit their full optimization potential.
is developed on top of existing vendor-specific tools and libraries to exploit their full optimization potential. does not create new standards that need to be implemented by others but utilizes the available tools.
does not create new standards that need to be implemented by others but utilizes the available tools.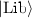 Programming Framework
Programming Framework
 programming framework.
programming framework.

 (pronounced Lib-Ket) is an allusion to the bra-ket notation introduced in 1939 by Paul Dirac that is widely used for expressing quantum algorithms.
(pronounced Lib-Ket) is an allusion to the bra-ket notation introduced in 1939 by Paul Dirac that is widely used for expressing quantum algorithms.