Keywords

1 Introduction

Radial basis functions (RBFs) are a powerful mathematical tool introduced by Hardy [1] in the late sixties for the interpolation of scattered data in the field of surveying and mapping. A review of the multiquadric (MQ) approach was published by Hardy himself [2] twenty years later; here the author explains that the MQ is bi-harmonic for 3D problems. Since their inception, RBF where adopted in many different fields and their mathematical framework developed [3] by exploring a variety of RBF kernels; among them the compact supported ones were introduced by Wendland [4].

An RBF interpolation at a generic point \( \varvec{x} \) (see Eq. 1) consists in the weighted summation of inter-distance interactions of the point \( \varvec{x} \) with a set of given points, defined sources \( \varvec{x}_{{\varvec{s}i}} \), where the inter-distance interaction consists in the Euclidean distance transformed by the radial function \( \varphi \left( {\text{r}} \right) \). The weights \( \gamma_{i} \) are computed so that the RBF gets at the sources the known input values to be interpolated.

$$ s\left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i} \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{\varvec{s}i}} } \right\|} \right)} $$
(1)

RBF are nowadays adopted in several engineering applications [5] and are well accepted as one of the most powerful and versatile mathematical approach to manage mesh morphing. The RBF allows creating a scalar field that interpolates a function defined on a set of source points: in the case of 3d mesh morphing a vector field is defined by individually interpolating the three components of the displacement known at source points. The RBF vector field is a point function independent from the mesh itself, all the points in the space receiving the field are called targets. A typical mesh morphing problem that can be faced using RBF consists in a three-dimensional mesh to be adapted according to a known displacement of the surface; surface nodes are extracted from the surface mesh as sources and all the nodes of the volume mesh receive the morphing field as targets.

Computer Aided Engineering (CAE) is more and more demanding for advanced methods capable to generate and adapt computational grids for multi-physics models. High fidelity models are widely employed, for instance, in computational fluid dynamics (CFD) and computational structural mechanics (CSM). The size of the grids daily adopted for CFD according to industrial best practices can be comprised of many millions of cells and, in some situation, close to one billion [6]; structured meshes of hexahedrons, hybrid meshes of tetrahedrons with prisms layers at the wall and meshes of Cartesian polyhedrons with inflation of prisms at surfaces are common adopted options for CFD. For CSM applications the mesh size is about one-two order lower than CFD ranging from hundred thousand up to some million of nodes for the most complex cases [7]; parabolic tetrahedrons are in this case widely adopted and the extra complexity of mid-side nodes management is added. In view of mesh morphing we have to consider that to the complexity of the mesh typology (i.e. linear/parabolic, tetra/hexa/poly) we have to add special cases for management of interfaces: moving/rotating parts are common in CFD, contact connections are common in CSM.

Mesh morphing for CAE applications is required as a companion/replacement of meshing when multiple shape variations of the same component/system are required. This is typical of design optimization which requires the automatic update of the CAE grid onto new design configurations to be explored: the baseline mesh is updated onto the new configuration instead of generating a new mesh onto the updated geometry [8, 9]. Morphing becomes very useful for optimization where the new shape is not known in advance but predicted by automatic sculpting methods as the adjoint based [10, 11] and the biological growth method [12]. Mesh morphing can furthermore help the solver itself as a tool to support the shape evolution (ice/snow deposition, erosion) [27], to enable fluid structure interaction (1-way, 2-way, structural modes embedding) [13, 14] and to move the CAE model onto “as built” configurations surveyed. Mesh morphing is also a key enabler toward the creation of reduced order models (ROM) that are adopted for the creation of digital twins [15].

Whatever is the need for mesh morphing, there are common requirements to fulfill to set-up an effective mesh morphing approach. Among these there are the ability to:

  • manage different element typology (linear/parabolic, tetra/hexa/poly);

  • go across interfaces (contact/rotating parts) and across partitions (distributed meshes for parallel calculations);

  • adapt the mesh with the minimum distortion (stretching/compression);

  • preserve the aspect ratio of cells at the boundary so that the ability to capture stress raisers/boundary layers is preserved;

  • adapt the mesh in a reasonable time even for very large models.

RBF mesh morphing satisfactorily fits above mentioned requirements because it comes with two distinctive advantages that makes it very flexible: it is mesh independent and it allows a node wise precision. Its meshless nature is due to the fact that once the RBF field is defined, the mesh deformation becomes a point function; nodal positions are updated regardless the attached mesh elements, and interfaces (contact/partitions boundaries) are implicitly preserved as the same field is received on coincident locations. The meshless nature is a distinctive feature of another widely adopted mesh morphing method: the free form deformation (FFD) [16]. One of the major drawbacks of FFD is that a point-wise precision cannot be achieved. Mesh based methods, as for instance the use of an auxiliary FEM solution [17, 18], allow the user to have pointwise control; despite this benefit their mesh based nature makes complex the management of arbitrary elements typology and interfaces.

Considering the great advantages of RBF, it is clear why a large research effort has been invested over the last decades toward their effective implementation. There are however two major drawbacks to be handled: numerical complexity and deformed mesh quality.

RBFs require the solution of large linear systems whose size is equal to the number of source points. The source points count grows fast especially if a node-wise control is needed because large portions of the nodes on the surface mesh are used as sources. Most of the implementations that are considered for research purposes exploits direct linear solvers because a great flexibility is possible and different radial function kernels can be seamlessly adopted. Unfortunately the numerical complexity scales up in this case with a cubic law so the maximum size of the RBF problem (number of sources) is limited to about 10 000 points. To overtake such limit there are different strategies: replace the original cloud with a smaller one (point decimation) fine enough to guarantee the desired precision [19], adopt iterative [20] solvers, use of the partition of unity [21] and use of fast multipole expansion [22]. The best “recipe” for a fast and effective RBF solver is still an open issue and the acceleration extent is strictly related to the adopted kernel.

The quality of the morphed mesh is of paramount importance and the effectiveness of deformation depends on the radial kernel adopted. The distortion (stretching/compression) of the mesh should be limited as much as possible because the validity of the numerical solution is maintained only within a certain range (which is solver related) of the element/cellFootnote 1 quality (skeweness, aspect ratio, …). Keeping a good quality usually is not enough; a proper spacing of the cells close to the surfaces is required, as example, for CFD meshes in order to preserve the capability to correctly solve the boundary layer. The same spacing is expected in the deformed mesh. This means that while the shape of the surface is changed, the deformation orthogonal to the surface itself has to be minimum so that the boundary layers are solved keeping a similar overall thickness and spacing.

The aim of this paper is to provide useful insights on two specific kernels that are widely adopted for mesh morphing: the bi-harmonic spline (BHS) and the Wendland C2 (WC2). The BHS minimizes the mesh distortion and it is known to have the feature of “smoothest interpolant” for the three-dimensional case; it is computationally expensive because of the full support of the radial function and so a dense linear system has to be solved. The WC2 is compactly supported and so a sparse system has to be solved; however it may lack in smoothness and the behavior close to the surfaces is strongly dependent on the radius of the support.

An overview of the studied problem is given in the first section (this introduction), a refresh of the math of RBF, including first derivatives calculation, is provided in the second section; the third section demonstrates how various RBFs perform for a square plate with a central circular hole, the fourth section deals with an aeronautical example faced with an industrial software and, finally, the fifth section wraps the study with the concluding remarks.

2 Radial Basis Functions Mesh Morphing

2.1 Radial Basis Functions Background

The RBF interpolation of a generic scalar field can be adopted to represent a variety of quantities. A generic component of a displacement field can be interpolated as

$$ \delta \left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{\delta } \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{\varvec{s}i}} } \right\|} \right)} $$
(2)

In this study we consider the case where the quantity to be interpolated \( \varvec{\delta}_{\varvec{s}} \) is given at the source point locations

$$ \delta \left( {\varvec{x}_{{\varvec{s}i}} } \right) = \delta_{si} , 1 \le i \le N $$
(3)

The unknown coefficient vector \( \varvec{\gamma}^{\varvec{\delta}} \) can be computed by solving the linear system

$$ \varvec{M\gamma }^{\varvec{\delta}} =\varvec{\delta}_{\varvec{s}} $$
(4)

Where the interpolation matrix \( \varvec{M} \) is

$$ M_{ij} = \varphi \left( {\left\| {\varvec{x}_{{\varvec{s}i}} - \varvec{x}_{{{\text{s}}j}} } \right\|} \right),1 \le i \le N,1 \le j \le N $$
(5)

Different radial functions can be adopted. In this study we focus on the splines and on the Wendland, summarized in Table 1. In the case of three-dimensional spaces the interpolated function can be rewritten as

Table 1. Radial functions for RBF interpolation
Full size table
$$ \delta \left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{\delta } \varphi \left( {\sqrt {\left( {x - x_{{si_{\text{x}} }} } \right)^{2} + \left( {y - x_{{si_{\text{y}} }} } \right)^{2} + \left( {z - x_{{si_{\text{z}} }} } \right)^{2} } } \right) } $$
(6)

And can be differentiated, for instance, with respect to \( x \)

$$ \frac{{\partial \delta \left( \varvec{x} \right)}}{\partial x} = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{\delta } \frac{{{\text{d}}\varphi \left( {\text{r}} \right)}}{\text{dr}}\frac{1 }{{2\sqrt {\left( {x - x_{{{\text{s}}i_{\text{x}} }} } \right)^{2} + \left( {y - x_{{{\text{s}}i_{\text{y}} }} } \right)^{2} + \left( {z - x_{{{\text{s}}i_{\text{z}} }} } \right)^{2} } }}2\left( {x - x_{{{\text{s}}i_{\text{x}} }} } \right)} $$
(7)

The full gradient of the interpolated function can be computed accordingly

$$ \nabla \delta \left( \varvec{x} \right) = \left( {\begin{array}{*{20}c} {\frac{{\partial \delta \left( \varvec{x} \right)}}{\partial x}} \\ {\frac{{\partial \delta \left( \varvec{x} \right)}}{\partial y}} \\ {\frac{{\partial \delta \left( \varvec{x} \right)}}{\partial z}} \\ \end{array} } \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{\delta } \frac{{\frac{{\partial \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{{\text{s}}i}} } \right\|} \right)}}{{\partial {\text{r}}}}}}{{\left\| {\varvec{x} - \varvec{x}_{{{\text{s}}i}} } \right\|}}\left( {\begin{array}{*{20}c} {x - x_{{{\text{s}}i_{\text{x}} }} } \\ {y - x_{{{\text{s}}i_{\text{y}} }} } \\ {z - x_{{{\text{s}}i_{\text{z}} }} } \\ \end{array} } \right)} $$
(8)

2.2 RBF Mesh Morphing

When RBFs are used for mesh morphing, the three components of a displacement field (Eq. 9), that is typically assigned at a cloud of control points here defined as RBF centers or source points, are interpolated in the space and used to update the nodal positions of the mesh nodes to be morphed.

$$ \left\{ {\begin{array}{*{20}c} {u\left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{u} \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{\varvec{s}i}} } \right\|} \right)} } \\ {v\left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{v} \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{\varvec{s}i}} } \right\|} \right)} } \\ {w\left( \varvec{x} \right) = \sum\nolimits_{i = 1}^{N} {\gamma_{i}^{w} \varphi \left( {\left\| {\varvec{x} - \varvec{x}_{{\varvec{s}i}} } \right\|} \right)} } \\ \end{array} } \right. $$
(9)

The field is applied to process all the nodal positions to be updated.

$$ \varvec{x}_{{\varvec{node}\_\varvec{new}}} = \varvec{x}_{{\varvec{node}}} + \left[ {\begin{array}{*{20}c} {u\left( {\varvec{x}_{{\varvec{node}}} } \right)} \\ {v\left( {\varvec{x}_{{\varvec{node}}} } \right)} \\ {w\left( {\varvec{x}_{{\varvec{node}}} } \right)} \\ \end{array} } \right] $$
(10)

The local deformation due to the morphing field can be inspected by computing the derivatives of the three components of displacement thus obtaining the strains as follows

$$ \varepsilon_{x} = \frac{\partial u}{\partial x} \;\varepsilon_{y} = \frac{\partial v}{\partial y} \;\varepsilon_{z} = \frac{\partial w}{\partial z}\; \varepsilon_{xy} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\;\varepsilon_{yz} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}\;\varepsilon_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x} $$
(11)

The definition of the RBF problem, i.e. the arrangement of the cloud of RBF sources and their input values, is the key enabler for RBF based mesh morphing and, considering its meshless nature and the great flexibility offered by the RBF mathematics, there are a variety of options to impose a desired morphing action. An overview of RBF mesh morphing strategies is given in [23, 24], while a deeper presentation about the use of RBF mesh morphing in industrial applications can be found in [25]. Among such a variety of mesh morphing paradigms the simpler one, which is the easiest to be automated, consists in the usage of all the nodes (or a subset) onto the surfaces as sources [26]. For sake of simplicity the study herein presented is based on such approach. The example of Fig. 1 demonstrates how the mesh of a notched bar can be updated controlling the radius of the notch. In this case the new CAD representation allows the user to define the positions of the RBF sources. An uniform spacing is imposed to all curves of the original geometry. The deformed positions of sources are then computed onto the updated CAD by keeping the same parametric distribution along the curve. The RBF field produced by source points is then used to update all the nodes of the mesh.

Fig. 1.
figure 1

The notched bar is reshaped adopting RBF mesh morphing. The nodes on all the curves are updated onto the new geometrical model keeping the same parametric spacing along the curves.

Full size image

3 A Square Plate with a Circular Hole

The first application faced to understand how the different radial functions are capable to handle mesh morphing consists in a simple geometry: the square plate (1.0 m side) with a circular hole (0.2 m radius) represented in Fig. 2.

Fig. 2.
figure 2

Square plate with a circular hole: the nodes on the curves are used to define the RBF sources, the nodes of the mesh are the morphing targets. FEM mesh on the left, FEM nodes in original and morphed position on the right.

Full size image

The implementation of this RBF mesh morphing demonstrator is divided in two parts. The mesh morphing set-up is performed using a pre-processor for FEA applications, the NX Femap in this case. The mesh is exported in a readable ASCII format (Nastran data deck in this example) so that the full mesh (nodes and elements) together with boundary conditions (constrained nodes with prescribed displacements) can be translated. The second part is a Mathcad application that implements basic RBF according to [5] and provides a fast bench to play around with the math and with obtainable morphed mesh. This implementation is good for investigate the method thanks to great flexibility provided, but it is not intended to be used for the assessment of numerical performances.

3.1 Changing the Diameter of the Hole

All the nodes belonging to the curves on the boundary are in this case used as RBF sources. The ones along the square perimeter are kept fixed while the ones on the hole are moved radially of 0.1 m so that the radius is changed from 0.2 m to 0.3 m. The effect of the radial functions is firstly investigated by generating a uniform map of points in the square (100 × 100 samples). The surface plot of the \( \varepsilon_{y} \) strain is then generated for all the points with the exception of the ones inside the circle for which a zero value is imposed. All surface plots of Fig. 3 (top BHS and THS, bottom WC2 with support radius 0.2 m and 0.1 m) have the same scale (−2, 1). We can clearly notice that, as expected, the maximum strain is 0.5 for all the situations: it is the hoop strain imposed at the circle and it occurs along the x direction. As far as the minimum strain, this is related to the compression of the cell required to accommodate morphing, and it has a peak along the y direction (pure radial on the circle). The minimum value represents the severity of element compression due to morphing. It clearly grows moving form BHS to THS and becomes more and more severe with WC2, especially if a small support radius is selected.

Fig. 3.
figure 3

Map of the \( \varepsilon_{y} \) strain for the BHS (top left), THS (top right) and WC2 with support radius 0.2 m (bottom left) and 0.1 m (bottom right)

Full size image

A better insight can be gained by plotting the \( \varepsilon_{y} \) strain along the vertical segment that starts from the midpoint of the bottom side of the square and ends at the intersection with the circle (Fig. 4). In this comparison also the WC0 and WC4 functions are included. The value of the \( \varepsilon_{y} \) strain at the intersection with the circle for BHS, THS is respectively: 0.04, 0.109; its values with support radius 0.1 m for WC0, WC2, WC4 are respectively: 0.276, −0.242, −0.244; its values with support radius 0.2 m for WC0, WC2, WC4 are respectively: −0.093, −0.235, −0.238.

Fig. 4.
figure 4

Chart of \( \varepsilon_{y} \) along the path highlighted in the figure for BHS, THS, WC0, WC2 and WC4 (support radii 0.1 m and 0.2 m).

Full size image

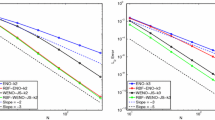
The ability of the RBF to succesfully adapt the mesh is investigated by plotting the minimum quality of the triangles (i.e. the ratio between the inner circle and the outer circle for each triangle) as a function of the deformation intensity (Fig. 5). The chart for BHS and THS is very similar so only BHS is plotted. The WC2 with radius 0.2 m is at the limit whilst the case of WC2 with radius 0.1 m (Fig. 6 right) produces negative quality at an half of the intensity.

Fig. 5.
figure 5

Chart of minimum mesh quality as a function of the deformation intensity for the BHS (left) and for the WC2 with support radius 0.2 m (right)

Full size image
Fig. 6.
figure 6

Chart of minimum mesh quality as a function of the deformation intensity for the WC2 with support radius 0.4 m (left) and for the WC2 with support radius 0.1 m (right)

Full size image

To better understand the effect of the support radius for the WC2 a larger value of 0.4 m has been considered. Figure 6 (right) shows that in this case a valid mesh can be achieved for the full interval. The case of 0.1 m is plotted as well to show how the quality is strictly related to the support radius. It is worth to notice that such large support radius allows to add the long distance interactions; the benefit of generating sparse system will be in this case reduced or lost.

4 Industrial Example

The application shown in this section was tackled adopting an industrial software implementation: the RBF Morph module for the ANSYS Fluent CFD solver [25]. RBF Morph allows to set-up the RBF mesh morphing problems with a variety of methods including the simple ones relevant for this study. The software features a fast RBF solver that comes with specific acceleration for the BHS. A library of Wendland functions is available as well.

4.1 Ice Profile on an Aircraft Wing Airfoil

The study presented in this section refers to the problem studied in [27, 28]. Mesh morphing is adopted to simulate the growth of ice; advanced CFD simulations coupled with icing models allow to compute the distribution of ice thickness onto the surfaces. The ice profile has an aerodynamic impact which cannot be neglected if the shape change is relevant. In the icing workflow the mesh is adapted onto the new “as iced” shape after a certain number of iterations. The CFD model of the 2D geometry is meshed in 3D as a single layer of hexahedrons; the mesh is represented in Fig. 7 where a detail of the mesh around the airfoil profile is shown. The chord length of the wing is 1 m and the thickness is 0.12 m. It is worth to notice that, as anticipated in the introduction, the spacing of the cells close to the wall is defined to solve the boundary layer. A key feature of the mesh adapted onto new shapes is to preserve such spacing similar to the one of the baseline mesh.

Fig. 7.
figure 7

Lateral view of the CFD mesh (left) with a detail of the mesh around the airfoil profile (right). Mesh vertexes at the walls are used as RBF sources (red points). (Color figure online)

Full size image

The mesh morphing set-up can be appreciated in Fig. 7 and in the detail of Fig. 8 where the shape of the ice profile is shown.

Fig. 8.
figure 8

Detail of the controlled sources that define the ice nose profile.

Full size image

The mesh morphing behavior depends on the radial function. In Fig. 9 the BHS is compared with the WC2 with support radius 0.1 m. The figure clearly shows the local nature of the compact supported RBF. It comes with lighter computational efforts, especially if a sparse solver is adopted. Remote points on the inlet outlet walls could in this case be deleted as there is no interaction. Instead, the BHS allows to distribute the deformation over the full domain at the cost of full long distance interactions and a dense interpolation matrix.

Fig. 9.
figure 9

Morphed mesh around the ice nose for the BHS (left) and the WC2 with support radius 0.1 m (right).

Full size image

The effect of the radial function can be visually inspected in Fig. 10 where a detail of the deformed mesh is represented in overlay with the baseline one. To have a quantitative metric of mesh distortion close to the wall, the distance from the surface of the fifth layer of cells is measured along the horizontal direction starting from the nose of the leading edge. Such distance on the baseline mesh is 21.7 mm and, after morphing, it becomes 22.3 mm for the BHS, 28.9 mm for the WC2 with radius 0.5 mm, 27.5 mm for the radius 0.3 mm, 17.5 mm for the radius 0.1 mm. Adopting a radius of 0.15 mm the distance becomes 22.7 mm.

Fig. 10.
figure 10

Detail of the morphed mesh for the BHS (top left) and the WC2 with support radius 0.5 m (top right), 0.3 m (bottom left) and 0.1 m (bottom right).

Full size image

5 Conclusions

In this paper a brief introduction about RBF mesh morphing is given with a special focus on the selection of the radial function. Among the many available options two of the most adopted ones have been considered in detail: the BHS and the WC2. The first example examined is a very simple mesh constituted of triangular elements representing a square plate with a circular hole. The deformation fields are in this case examined in details for BHS, WC2 with various support radii and for THS, WC0, WC4 as well. The study clearly shows that the radial function has an important effect on how deformations are distributed and on their peaks. A successful morphing is obtained with BHS and THS whilst the success of the WC2 depends from the radius. If too small values are adopted the morphed mesh results to have reversed cells. With increased radii (0.1 m, 0.2 m, 0.4 m) the filling ratio of the matrix increases (4.0%, 7.9%, 23.7%) together with the linear system solving effort.

An industrial aeronautical application is also faced. In this case the morphing action is applied to the nose of an airfoil to adapt its shape to the shape of the ice computed by an ice accretion grow code. Inspected radial functions (BHS and WC2) allow to get a successful morphing with all the examined combinations of parameters. Also for this application the deformation intensity is strongly dependent on the radial function. A qualitative comparison between global supported BHS and compact supported WC2 with support radius 0.1 m is firstly given showing the differences between the global and local morphing. The effect of the support radius is then investigated by examining how the spacing of first five layers of cells close to the leading edge evolves after morphing. The BHS allows to preserve such a spacing with a variation (small increment) that is smaller than 3%. As far as the WC2 is concerned, such variation is strongly affected by the radius. The smaller radius considered (0.1 m) results in a reduction of such distance of about 20%. The larger one produces an opposite effect with an increment of about 33%. A proper tuning of the radius (0.15 m) allows to almost preserve the distance with an increment lower than 5%.

The numerical tests presented in this paper support what is well known from practical experience in industrial applications of mesh morphing. BHS, if compared to WC2, allows to get less distortion, a better overall quality and a good preservation of mesh spacing close to the boundaries. When adopting WC2 the results are strongly affected by the support radius. The BHS, on the other hand, produces a full populated linear system and requires far source points to limit the morphing field not needed with the WC2 that, thanks to the compact support, produces a decaying morphing field.