Model-Based Sensitivity Analysis of Nondestructive Testing Systems Using Machine Learning Algorithms

Abstract

Model-based sensitivity analysis is crucial in quantifying which input variability parameter is important for nondestructive testing (NDT) systems. In this work, neural networks (NN) and convolutional NN (CNN) are shown to be computationally efficient at making model prediction for NDT systems, when compared to models such as polynomial chaos expansions, Kriging and polynomial chaos Kriging (PC-Kriging). Three different ultrasonic benchmark cases are considered. NN outperform these three models for all the cases, while CNN outperformed these three models for two of the three cases. For the third case, it performed as well as PC-Kriging. NN required 48, 56 and 35 high-fidelity model evaluations, respectively, for the three cases to reach within $1\%$ accuracy of the physics model. CNN required 35, 56 and 56 high-fidelity model evaluations, respectively, for the same three cases.

1 Introduction

The process of testing, inspecting or evaluating assemblies or components for discontinuities or damages without affecting the serviceability of the part is known as nondestructive testing (NDT) [1]. Various NDT methods, such as electromagnetic testing [2] and ultrasonic testing (UT) [3], have been developed and used in different engineering fields such as automobile manufacturing, in-service inspection of aircraft and wind turbines.

To quantify the effect of the different variability parameters on the model responses from NDT systems, sensitivity analysis (SA) [4] can be utilized. SA can be local [5] or global [6]. Local SA focuses on quantifying the effects of small perturbations near an input space value on the model response. Global SA is used to quantify the effects of the input variability on the output responses. For this study, global SA based on Sobol’ indices [7] is used.

Traditional NDT measurements have relied heavily on experimental methods. These methods, however, are time-consuming and costly. To speed up this process, various physics-based NDT models, such as finite element methods [8] and boundary element methods [9], have been developed. Unfortunately, for SA, a large number of model evaluations are required in order to propagate the random input uncertainties to the model responses. This results in high computational cost, which renders SA for NDT systems challenging to complete within a required time frame.

To overcome the computational burden, metamodeling methods [10] can be used. These models replace the time-consuming, but accurate high-fidelity physics-based models with a computationally efficient one. Metamodeling methods can be broadly categorized in two classes: data-fit methods [11] and multifidelity methods [12]. In data-fit methods, a response surface is fit through the evaluated model responses at sampled high-fidelity data points. Multifidelity metamodeling reduces the computational burden by using information from two or more fidelities. Low-fidelity data can be used to provide the cost function trend to high-fidelity data.

In this work, two data-fit methods, namely neural networks (NN) [13] and convolutional NN (CNN) [14] are used as a part of model-based SA for three UT benchmark cases. The results from this case is compared to Kriging [15], least-angle regression (LARS) [16] based polynomial chaos expansions (PCE) [17] and polynomial chaos-based Kriging (PC-Kriging) [18]. Model-based SA can be used as a precursor to experimental testing, as it would provide important information on which input variability parameters are most crucial for NDT. This would result in a reduction of the total number of physical experiments that need to be performed, hence saving time and cost.

The paper is organised as follows. The next section introduces the method used to construct the NN and CNN as well perform SA. These algorithms are then applied to the three UT benchmark cases in the following section. The final section concludes the paper and provides suggestions for future work.

2 Methods

This section details the construction of the NN and CNN as well as the SA. The Keras [19] wrapper with Tensorflow [20] is used in this study to construct the NN and CNN. The following subsections describe the workflow, the sampling plan, the NN and CNN architectures, as well as SA using Sobol’ indices.

2.1 Workflow

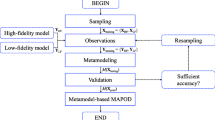
The model-based SA flowchart is shown in Fig. 1. The process starts by sampling for the training data. At these sample points, the high-fidelity physics-based model responses are observed from which the metamodel is constructed. This metamodel is then validated using a separate testing set. If the required accuracy is not met, resampling is done with a higher number of training points. Once the required accuracy is met, the model-based SA is performed. The following subsections describe each step of the algorithm in Fig. 1.

2.2 Sampling Plan

The first step in the model-based SA involves sampling. In order to capture the trend of the model responses, sampling needs to be performed at a fixed combinations of the input variability parameters. The training data in this study is generated using Latin Hypercube sampling (LHS) [10], while the testing data is generated using Monte Carlo sampling (MCS) [21]. The training data is first generated using ten data points, which is increased during resampling until the required accuracy is met. The testing data is fixed to 1,000 points.

Fig. 1.

Flowchart for the model-based sensitivity analysis

2.3 Neural Networks

Figure 2 depicts a NN [13] with an input layer with three inputs, one hidden layer with “n” neurons, and an output layer. A NN is constructed through linear combination of inputs followed by nonlinear transformations through activation functions. Each neuron has an activation function given by

$$\begin{aligned} {z_j} = a\Big (\sum \nolimits _{i=1}^{3} \omega _{ij} x_i\Big ), \end{aligned}$$

(1)

where a is the activation function and $\omega _{ij}$ is the weight between the $i^{th}$ input layer and $j^{th}$ neuron in the hidden layer. Here, the maximum value of i is three as there are three inputs to the NN. x and z are the input values and outputs of the neurons respectively. The NN output prediction is given by

$$\begin{aligned} {\hat{y}} = \sum \nolimits _{i=1}^{n} \eta _{i} z_i, \end{aligned}$$

(2)

where $\eta _{i}$ is the weight between the $i^{th}$ neuron in the hidden layer and the output layer. To obtain the weights, a minimization problem is solved with a gradient-based algorithm. The cost function used is the mean squared error (MSE), given by

$$\begin{aligned} {MSE} = \sum \nolimits _{i=1}^{N_{t}} (\hat{y}^{(i)} - y^{(i)})^2 / N_{t}, \end{aligned}$$

(3)

where the physics-based model observation are given by y. $N_t$ is the total number of testing data points. For this study, the following hyperparameters are used: hyperbolic tangent activation function, 50 neurons in the hidden layer and total number of epochs (iterations) of 10,000. The Nesterov-accelerated Adaptive Moment Estimation [22] stochastic gradient descent algorithm with a batch size of 20, learning rate of 0.01 and momentum rate of 0.99 are also used. Details of these terms can be found in Goodfellow et al. [13]. In general, there is no rule-of-thumb on how to setup the NN architecture and its hyperparameters. This was done using trial and error in this work.

Fig. 2.

Depiction of the neural network structure

2.4 Convolutional Neural Networks

Figure 3 shows the CNN architecture used this in study. The input layer has been replaced by an input grid of size $3\times 1$. CNN was originally developed to work on images [14], where each grid location contains the pixel value. For this study, the pixel values used are the variability parameters values, scaled to have values between zero and one. A kernel of size $1\times 1$ passes over this grid from top to bottom. During this process the convolutional operation is preformed. The convolutional operation here is the product of the input and the value of the kernel. The resulting value in the convolutional feature map layer is given by

$$\begin{aligned} {c_i} = a\Big ( \epsilon x_i\Big ), \end{aligned}$$

(4)

where c is the value in the feature map, a is the activation function, $\epsilon$ is the value of the kernel and x is the input value. This layer is then connected to the hidden layer, which is similar to that of the standard NN. The output of the hidden layer is given by

$$\begin{aligned} {z_j} = a\Big (\sum \nolimits _{i=1}^{3} \omega _{ij} c_i\Big ). \end{aligned}$$

(5)

The weight between the $i^{th}$ grid location of the convolutional feature maps layer and $j^{th}$ neuron in the hidden layer is $\omega _{ij}$. The CNN output prediction $\hat{y}$ is same as (2). The hyperparameters used for this study, in the case of CNN, are the same as those of the NN, except for the batch size and the number of neurons in the hidden layer. These values are set to 10 and 100, respectively.

Fig. 3.

Flowchart for the model-based sensitivity analysis

2.5 Validation

The root mean squared error (RMSE), given by

$$\begin{aligned} {RMSE} = \sqrt{MSE}, \end{aligned}$$

(6)

and the normalized RMSE (NRMSE), given by

$$\begin{aligned} {NRMSE} = {RMSE} / ({max}(\mathbf{y} ) - {min}(\mathbf{y} )), \end{aligned}$$

(7)

are used to validate the metamodel in this work. The maximum and minimum model observation of the testing points are given by max($\mathbf{y}$) and min ($\mathbf{y}$), respectively. An RMSE less than or equal to $1\%\sigma _{{testing}}$ (standard deviation of testing points) is taken as the acceptable global accuracy criterion in this work.

2.6 Model-Based Sensitivity Analysis

Variance-based Sobol’ indices [6] are used in this work. To determine by how much each variability parameter affects the model response. In this work, MCS is used to estimate these indices.

Given a black-box model,

$$\begin{aligned} M(\mathbf{X} ) = f(\mathbf{X} ), \end{aligned}$$

(8)

where $\mathbf{X}$ is the input vector of m random variables. This equation can be decomposed as

$$\begin{aligned} M(\mathbf{X} ) = f_0 + \sum _{i=1}^{m}f_i(X_i) + \sum _{i<j}^{m}f_{i,j}(X_i, X_j) + ... + f_{1,2,..., m}(X_1, X_2, ..., X_{m}), \end{aligned}$$

(9)

where $f_0$ is a constant, and $f_i$ is a function of $X_i$. The functional decomposition terms are orthogonal, which can then be decomposed in terms of conditional expected values

$$\begin{aligned} f_0 = {{{\,\mathrm{\mathbb {E}}\,}}}(M(\mathbf{X} )), \end{aligned}$$

(10)

$$\begin{aligned} f_i(X_i) = {{{\,\mathrm{\mathbb {E}}\,}}}(M(\mathbf{X} )|X_i) - f_0, \end{aligned}$$

(11)

$$\begin{aligned} f_{i,j}(X_i, X_j) = {{{\,\mathrm{\mathbb {E}}\,}}}(M|X_i, X_j) - f_0 - f_i({X_i}) - f_j({X_j}), \end{aligned}$$

(12)

and so on. The variance of (9) is then

$$\begin{aligned} {{{\,\mathrm{\mathbb {V}}\,}}}{ar}(M(\mathbf{X} )) = \sum _{i=1}^{m}V_i + \sum _{i<j}^{m}V_{i,j} + ... + V_{1,2,...,m}, \end{aligned}$$

(13)

where

$$\begin{aligned} V_i = {{{\,\mathrm{\mathbb {V}}\,}}}{ar}_{X_i}({{{\,\mathrm{\mathbb {E}}\,}}}_\mathbf{X _{\sim i}}(M(\mathbf{X} )|X_i)), \end{aligned}$$

(14)

$$\begin{aligned} V_{i,j} = {{{\,\mathrm{\mathbb {V}}\,}}}{ar}_{X_{i,j}}({{{\,\mathrm{\mathbb {E}}\,}}}_\mathbf{X _{\sim i,j}}(M(\mathbf{X} )|X_i, X_j)) - V_i - V_j, \end{aligned}$$

(15)

and so on, where $\mathbf{X} _{\sim i}$ notation denotes the set of all variables except $X_i$.

The main effect indices, given by the first-order Sobol’ indices are

$$\begin{aligned} S_i = \frac{V_i}{{{{\,\mathrm{\mathbb {V}}\,}}}{ar}(M(\mathbf{X} ))}. \end{aligned}$$

(16)

The total-order indices, given by the total-effect Sobol’ indices are

$$\begin{aligned} S_{T_i} = \frac{{{{\,\mathrm{\mathbb {E}}\,}}}_\mathbf{X _{\sim i}}({{{\,\mathrm{\mathbb {V}}\,}}}{ar}_{X_i}(M(\mathbf{X} )|\mathbf{X} _{\sim i}))}{{{{\,\mathrm{\mathbb {V}}\,}}}{ar}(M(\mathbf{X} ))} = 1 - \frac{{{{\,\mathrm{\mathbb {V}}\,}}}{ar}_\mathbf{X _{\sim i}}({{{\,\mathrm{\mathbb {E}}\,}}}_{X_i}(M(\mathbf{X} )|\mathbf{X} _{\sim i}))}{{{{\,\mathrm{\mathbb {V}}\,}}}{ar}(M(\mathbf{X} ))}. \end{aligned}$$

(17)

3 Numerical Examples

The model-based SA using NN and CNN used in this paper are demonstrated on three UT benchmark cases. These metamodels are compared to PCE, Kriging and PC-Kriging. The computational cost is computed as the total number of training samples required to reach the desired accuracy.

3.1 Problem Setup

Three benchmark cases developed by the World Federal Nondestructive Evaluation Center [23] are used in this work. The three cases are the spherically-void-defect case under focused transducer (Case 1), spherically-void-defect cases under planar transducer (Case 2), and the spherically-inclusion-defect case under focused transducer (Case 3).

Fig. 4.

Setup of the ultrasonic testing system for the benchmark cases

Table 1. The variability parameters used in the numerical examples

The setup of the UT system is shown in Fig. 4. The variability parameters for Cases 1 and 3 are the probe angle ($\theta$), the x location of the probe ($x_p$) and the F-number (F). The F-number is the focal length divided by the diameter of the transducer. For Case 2, the F-number is replaced with the y location of the probe ($y_p$). For all the cases $\theta$ and $x_p$ have the normal distribution N(0 deg, $0.5^2$ deg$^2$) and uniform distribution U(0 mm, 1 mm), respectively. F has a U(13,15) and U(8,10) for Case 1 and 3, respectively. $y_p$ has a distribution U(0 mm, 1mm). A summary of the variability parameter is given in Table 1.

The Thomspon Grey model [24] is used to predict the voltage wave forms at the receiver, while the multi-Gaussian beam model [25] evaluates the velocity diffraction coefficient. Separation of variables [26] is then used to calculate the scattering amplitude, which results in a closed-form expression. For this study, the transducer has a center frequency of 5 MHz. The fused quartz block has a density of 2,000 kg/m$^3$, a longitudinal wave speed of 5,969.4 m/s and a shear wave speed of 3,774.1 m/s. For more information about the models, refer to Du et al. [27].

Fig. 5.

Case 1 setup and model validation: (a) RMSE ($a = 0.5\,\text {mm}$), (b) NRMSE with respect to defect size

3.2 Results

The NN and CNN model used in this study are compared to the PCE [17], Kriging [15] and PC-Kriging [18] metamodels. To measure the global accuracy, RMSE and NRMSE metrics are used. This is done at the defect size (a) of 0.5 mm. The number of training points used to generate the metamodel is increased until the desired accuracy of $1\%\sigma _{{testing}}$ is reached. Once this accuracy is reached, the model is retrained on data for different defect size and the accuracies measured again. Note that the same number of training points are used to measure accuracy at different defect sizes.

Figures 5(a), 6(a) and 7(a) show the RMSE for all the metamodels for an increasing number of training points, for Cases 1, 2 and 3, respectively. In Case 1, both NN and CNN outperform the remaining metamodels. CNN, however, required only 35 training points, compared to 48 for NN (Table 2). For Case 2, both CNN and NN require the same number of training data to reach the desired accuracy and outperform all the other metamodels (Table 3). Table 4, shows that NN outperforms all the other training models, however, CNN performs as well as the PC-Kriging model. Figures 5(b), 6(b) and 7(b) show that all the metamodels fall within the desired accuracy for the NRMSE for all the defect sizes and all the cases.

Fig. 6.

Case 2 setup and model validation: (a) RMSE ($a = 0.5\,\text {mm}$), (b) NRMSE with respect to defect size

Fig. 7.

Case 3 setup and model validation: (a) RMSE ($a = 0.5\,\text {mm}$), (b) NRMSE with respect to defect size

Table 2. Case 1 computational cost

Table 3. Case 2 computational cost

Table 4. Case 3 computational cost

Fig. 8.

Case 1 sensitivity analysis: (a) 1st-order Sobol’ indices, (b) Total-order Sobol’ indices

Fig. 9.

Case 2 sensitivity analysis: (a) 1st-order Sobol’ indices, (b) Total-order Sobol’ indices

SA plots for the three cases are shown in Figs. 8, 9 and 10. 75,000 MCS were used to perform the physics-based model evaluations to obtain the sensitivity information for each of the three cases. This serves as the baseline to compare the metamodeling results. In the case of the PCE metamodel, its coefficients can be used to provide the $1^{st}$ and total order Sobol’ indices [27]. For the remaining metamodels, 75,000 MCS points were used to provide satisfactory results for the SA for each of the cases. Figures 8 and 10 show that the F-number has negligible effect on the model response and can be neglected while setting up the NDT experiments. For Case 2, $y_p$ is small enough to be ignored, as shown in Fig. 9.

Fig. 10.

Case 3 sensitivity analysis: (a) 1st-order Sobol’ indices; (b) Total-order Sobol’ indices

4 Conclusion

In this work, NN and CNN are used to perform model-based SA for three different UT benchmark cases. These metamodels are compared to other data-fit metamodels, namely, PCE, Kriging and PC-Kriging. NN is shown to outperform these three metamodeling methods for all the UT benchmark cases in terms of number of training points required to reach an accuracy of $1\%\sigma _{{testing}}$. CNN outperforms NN for Case 1, performs equally well for Case 2 as NN, and performs similarly to PC-Kriging for Case 3.

The SA shows that NN and CNN match the physics-based model results well. The F-number and $y_p$ are shown to be of no importance while measuring the model response and can be neglected for experimental NDT. The remaining two parameters, $x_p$ and $\theta$, are important and cannot be ignored during experimental measurements. This study shows how machine learning algorithms, such as NN and CNN, can be used to perform accurate and fast SA for NDT systems. This help decide which variable parameters should be used for NDT using experimental methods, resulting in time and cost savings. Future work will include problems with high number of variability parameters, which require significantly more data to reach the desired accuracy.