Abstract
There are numerous words across languages expressing similarity or indistinguishability. In this paper, three types of similarity expressions in German and English are compared—ähnlich/similar, so/such, and gleich/same. They differ in a number of respects, one of them being gradability: While ähnlich/similar are gradable, so/such as well as gleich/same are not. The analysis in this paper starts from the analysis of German so as a demonstrative expressing similarity (instead of identity) to its demonstration target (Umbach and Gust 2014). It is suggested that the meaning of the three types of similarity expressions is based on a common similarity relation, while differences in meaning are provided by constraints referring to the selection of dimensions of comparison and preconditions of usage. The focus of the paper is on gradability and on the question of what it means for a pair of items to be more similar than another pair. An analysis in the spirit of Klein (1980) is presented accounting for the fact that ähnlich/similar are gradable while neither so/such nor gleich/same are. The formal framework makes use of representations based on attribute spaces and classifiers, where representations may be of different granularity.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
There are numerous words across languages expressing that items are similar or indistinguishable in some sense, for example in German and English ähnlich/similar, so/such, and gleich/same. It seems reasonable to assume that the common core of the meaning of these words is a relation of similarity, which is considered in Cognitive Science as “… an organizing principle by which individuals classify objects, form concepts, and make generalizations” (Tversky 1977, p. 327). Still, there are significant differences between similarity expressions, one of them being gradability: While ähnlich and similar are gradable, so and such as well as gleich and same are not, see (1)–(3).Footnote 1

The starting point of this paper is the analysis of the German demonstrative so in Umbach and Gust (2014) arguing that German so as well as, e.g., Polish tak and English such are similarity demonstratives, that is, demonstratives expressing similarity (instead of identity) to the target of the demonstration (see Sect. 2). The similarity analysis is spelled out with the help of multi-dimensional attribute spaces defining similarity as indistinguishability with respect to, basically, a set of dimensions of comparison.
German ähnlich and English similar express similarity, too. But while so and such are demonstratives, ähnlich and similar are two-place predicates, and while similarity as denoted by so and such is reflexive,Footnote 2 it will be shown that this is not the case for ähnlich and similar. The most challenging difference, however, is gradability , which will be in focus in this paper.
Considering their scale structure, ähnlich and similar are clearly not open scale—increase of similarity is not open-ended. But at the same time they resist common tests for being upper-closed (see Kennedy and McNally 2005). For example, combination with vollkommen/completely yields heavily marked results. Intuitively, however, there is a maximum for ähnlich and similar which is expressed by the adjectives gleich and same, see (4).

In this paper, we start from the idea that the meaning of the three types of similarity expressions—so/such, ähnlich/similar, and gleich/same—is based on a single similarity relation. Differences in meaning are characterized in terms of additional constraints. The research questions addressed in this paper will be

In this paper, we will consider only nominal phrases (ignoring e.g., ähnlich aussehen/look similar and also ähneln/resemble; for resemble see Meier 2009) and we will only consider anaphoric/deictic uses (ignoring reciprocal constructions like Anna and Berta are similar, see footnote 11 in Sect. 3). Since the German and English expressions under consideration are close in meaning and distribution they will be analyzed in parallel.
This paper is organized as follows: In Sect. 2, the similarity analysis for so/such will be outlined as far as required in the subsequent sections. In Sect. 3, differences in distribution and meaning between the three types of similarity expressions will be explored. In Sect. 4, an analysis will be suggested accounting for the gradability of ähnlich/similar which is inspired by Klein (1980). Formal details are provided in the Appendix.
2 Similarity Demonstratives
There is a class of demonstratives found across languages modifying verbal, nominal and/or degree expressions, for example German so/solch, English such, Polish tak and Turkish böyle (see König and Umbach 2018). Some of them are uniform across categories, like German so and Polish tak; others are restricted to particular syntactic categories, like English such. In (5), German so and English such modify a noun.

In Umbach and Gust (2014), demonstratives like so/such are called similarity demonstratives and are analyzed in a framework spelling out similarity as indistinguishability with respect to given dimensions of comparison. This section provides a summary of the analysis and a brief overview of the formal framework. Details are provided in the Appendix.
The analysis starts from the common idea that the target of the demonstration is an individual or event. But while standard demonstratives like this denote identity between the demonstration target and the referent (as is in-built in Kaplan’s 1989 system), similarity demonstratives denote similarity rather than identity. Accordingly, so/such include a deictic component and a similarity component which jointly create sets of items similar to the target of demonstration. For example, so ein Tisch/such a table in (5) denote a set of tables similar to the table pointed at. This analysis entails that so/such are directly referential in the sense of Kaplan, which will be one key point in distinguishing so/such from ähnlich/similar and gleich/same in Sect. 3.
Similarity depends on dimensions of comparison.Footnote 3 The selection of the relevant dimensions is another key point in comparing the three varieties of similarity
expressions. In the formal framework (Gust and Umbach 2015, Gust and Umbach to appear), dimensions of comparison
define multidimensional attribute spaces and are equipped with measure functions mapping individuals to points in those spaces. Dimensions and measure functions are two components of what is called a representation. The third component is a set of classifiers, which are predicates on points in attribute spaces. They can be seen as defining a “grid”Footnote 4 where points within a cell are indistinguishable. Classifiers derived from basic ones by logical operations provide coarser (by disjunction) or finer granularity (by conjunction), which will be essential in devising a gradable notion of similarity
in Sect. 4.2. Slightly simplifying, a representation \( {\mathcal{F}} \) is defined as a quadruple including a domain D, an attribute space F, a measure function μ: D
 F and a set of classifiers P*, \( {\mathcal{F}} = \, \left\langle { F,\mu, P^{*}, D } \right\rangle\) (see Appendix, Definition 2).
F and a set of classifiers P*, \( {\mathcal{F}} = \, \left\langle { F,\mu, P^{*}, D } \right\rangle\) (see Appendix, Definition 2).
Similarity is defined as a three-place relation combining two individuals to be compared and a representation, sim(x, y, \( {\mathcal{F}} \)), such that two individuals are similar relative to a representation if and only if the points in the attribute space they are mapped to are indistinguishable relative to the given set of classifiers (Appendix, Definitions 3 and 4). Similarity defined in this way is an equivalence relation.Footnote 5
Consider, for example, the phrases so einen Tisch/such a table in (5). The semantic interpretation is shown in (6). Let us assume, for the sake of the example, that relevant dimensions of comparison are height, material, legs, and extras, and that tables are “measured” by the function in (7). Now suppose that the table the speaker points at is mapped to 〈55 cm, metal, 4, {}〉 and the set of classifiers is such that points within a range of height:40–60; material:{metal, plastics}; legs:2–4; extras:{} cannot be distinguished. Then (5) is true iff Anna’s table is mapped to a point within this range.Footnote 6,Footnote 7,Footnote 8

According to the similarity analysis, demonstratives like so/such create classes of similar items, e.g. similar tables. There is some evidence that in the nominal and verbal case (though not in the adjectival case) these similarity classes constitute ad-hoc kinds (see Umbach and Gust 2014). Anderson and Morzycki (2015) present an alternative analysis claiming that demonstratives like German so, English such and Polish tak are pro-kind expressions, adapting Carlson’s (1980) kind-referring analysis of such. The final results of the two accounts are fairly close (in the case of nominal and verbal phrases). However, Umbach and Gust not just postulate that there are kinds denoted by so phrases, but in addition show how these kinds emerge, namely by similarity. Moreover, by referring to a common similarity relation, this framework offers a basis to compare different types of similarity expressions, which is the topic in this paper.
Finally, it is important to note that the notion of similarity in this framework is qualitative (property-based), unlike that in Gärdenfors’ (2000) conceptual spaces which is quantitative (distance-based) (see Sect. 4.2).Footnote 9,Footnote 10 Even more importantly, unlike Gärdenfors’ conceptual spaces, multi-dimensional attribute spaces in the Umbach and Gust framework are integrated into referential semantics by means of generalized measure functions mapping referents to points in multi-dimensional attribute spaces . Note that this is just a generalization of degree semantics (e.g. Kennedy 1999) from the one-dimensional to the multi-dimensional case.
3 Three Types of Similarity Expressions
In this section the three types of similarity expressions—so/such, ähnlich/similar and gleich/same—will be compared focusing on semantic characteristics (for lexical and distributional data see Umbach 2014). First, ähnlich/similar as well as gleich/same are relational adjectives comparing two individuals. The second argument may be explicit (Ann’s car is similar to Berta’s car) or anaphoric (Ann’s car is similar).Footnote 11 In contrast, so/such are demonstratives (to be used deictically as well as anaphorically). Even though the target of the demonstration (or antecedent) is not identical to the referent of the phrase—the referent of such a table is not (necessarily) identical to the table pointed to—it would be misleading to think of so/such as expressions relating two distinct individuals. This is obvious when considering reciprocal readings which are licensed by ähnlich/similar (as well as gleich/same), but not by so/such (Anna and Berta have similar cars/*have such cars). Instead, these demonstratives create an ad-hoc set of items similar to the target—a set of tables similar to the table pointed to—which is then used to introduce a novel discourse referent (note that so/such are incompatible with definite determiners, *so der Tisch/*such the table).
Furthermore, while ähnlich/similar as well as gleich/same are predicates denoting pairs of individuals and may vary across indices, so/such are demonstratives. They refer directly to the target pointed at and block indexical shift (Kaplan 1989). This is shown in (8): (8a) is clearly true. But even though Adam and Ben both drive a Porsche, (8b) is false because the counterfactual index is irrelevant to the target of the demonstration—the speaker is still pointing to the old VW. In contrast, ähnlich/similar (as well as gleich/same) are evaluated at the counterfactual index, and thus (8c) is true.Footnote 12

Another difference between the three types of similarity expressions is given by the selection of the dimensions of comparison. In the case of so/such, dimensions are first of all determined by the lexical meaning of the noun—dimensions to be considered for something to be a table or be a bike. Other dimensions can be relevant as long as they relate to properties suited to create a subkind of the kind corresponding to the noun. Take the noun bike. For something to be such a bike it has to be similar to the bike pointed at in relevant bike dimensions. There may be additional dimensions which are not specific for bikes, surfacing in properties like rusty or dented. But properties like bought last year from her neighbor or fantastic would not qualify for comparison. This is why the namely continuations in (9a) and (b) are unmarked whereas in (c) and (d) they are clearly bad. In the case of so/such, dimensions of comparison are not restricted to those determined by the lexical meaning of the noun, but they must not relate to indexical (in a broad sense) or evaluative properties, because indexical and evaluative properties are unsuited to create subkinds (experimental evidence is described in Umbach and Stolterfoht in prep., see also König and Umbach 2018, Sect. 5).

Selection of dimensions is different in the case of ähnlich/similar. Consider the example in (10). First, while so/such phrases are perfect as kind-denoting terms in generic sentences, ähnlich/similar phrases are not, see (10a, b). Secondly, changing the (unacceptable) generic sentences in (10b) into the episodic sentence in (10c) reveals a clear difference in meaning: so ein Geschenk/such a present is something rare and valuable which can reasonably be considered as showing appreciation for the guest. A Panda bear serves this purpose, but an old manuscript or painting would do as well. In contrast, ein ähnliches Geschenk/a similar present need not be valuable, but it has to be similar to a Panda bear. When asked, what a similar present could be, informants mention tigers, rhinos, crocodiles etc. This is strong evidence that the ähnlich/similar version of similarity selects dimensions made salient by the antecedent.

In the case of gleich/same, there is a type and a token interpretation (Nunberg 1984). (11) may mean that Anna and Berta drive cars of the same type, or that Anna and Berta share a car (token).Footnote 13 The token interpretation yields referential identity, x = y, but the type interpretation is, first of all, just similarity —being indistinguishable with respect to dimensions given by the lexical meaning of the noun. Different from so/such and ähnlich/similar, additional dimensions are blocked for gleich/same. Suppose that Anna drives a Ford Fiesta. Then the same car on a type interpretation has to be a Ford Fiesta. But even if Anna’s car is rusty and dented, the same car could be spotless. Obviously, non-car-specific dimensions like conditions of usage are irrelevant. Moreover, while such a car may deviate from the values of the antecedent in some dimensions—e.g. by having two instead of four doors—the same car has to be exactly like the antecedent in every car dimension.

We will assume that for every noun there is a lexically associated canonical set of dimensions (called N-related dimensions). They are provided by criteria of application—what it means to be a table—and are not to be mistaken for criteria of identity.Footnote 14 Our hypothesis on the selection of dimensions of comparison is thisFootnote 15:

Let us finally consider reflexivity. In the example in (13) so eine Feuerwehr/such a fire brigade in (a) is anaphorically related to the previously mentioned team of fire fighters, which is the team the mayor intends to praise. So the referent of the so/such phrase is identical to the antecedent. When so/such is substituted by ähnlich/similar, as in (b), the mayor seems to praise a fire brigade different from the successful team, which appears strange in this context. A similar effect is found with gleich/same—(c) again gives the impression that there is another fire brigade (for (d) see below).

(13a) clearly shows that in the case of so/such similarity is reflexive. (13b) shows that in the case of ähnlich/similar reflexive pairs are excluded. But we started out from the idea that the three varieties of similarity expressions are based on one common similarity relation—it would be unintuitive to have an irreflexive similarity relation sim’ in addition to the ‘regular’ reflexive one. More importantly, (13c) shows the same effect as in (13b): there seem to be two distinct fire brigades. It would be absurd, however, to claim that gleich/same are not reflexive. We will therefore postulate distinctiveness as a precondition of usage (due to the two-place character of the lexical items).Footnote 16
Postulating distinctiveness as a precondition yields the required result for ähnlich/similar. Note, however, that in the case of gleich/same the distinctiveness effect is slightly different from what was found for ähnlich/similar. (13c) is strange only of there is no different description of the fire brigade available. But if the mayor earlier in his speech mentioned the fire brigade the community had 10 years ago, he could refer to the actual one by “the same fire brigade [as 10 years ago]” in the sense of token identity (suppose the group of fire fighters did not change), see (13d). So gleich/same do not require distinct referents but instead distinct senses—Arten des Gegebenseins—as in Frege’s distinction between sense and reference. The sentence The morning star is the same star as the morning star is decidedly odd whereas The morning star is the same star as the evening star is fine, which led Frege to distinguish sense and reference (Frege 1892). Accordingly, (13d) is fine because although the fire brigade referent is identical to the one 10 years ago (on the token reading) there are two different senses—fire brigade now, fire brigade 10 years ago.
Therefore, while ähnlich/similar presuppose distinctiveness of referents, gleich/same—on the token reading!—require distinctiveness of descriptions, or ways of identification. The type reading of gleich/same, on the other hand, requires that referents are distinct, which is trivial because otherwise it would not be a type reading.
Summing up, all of the three variants of similarity expressions can be analyzed as being based on a single similarity relation, sim(x, y, \( {\mathcal{F}})\). Their differences are due to differences in selecting dimensions of comparison and in different preconditions of usage.

Two remarks: First, we do not touch upon the issue of constraints on determiners due to reasons of space, (see Umbach 2014). Secondly, the precondition of usage in (b) may be formulated as a presupposition. This is not possible in (c) because way of identification is an intensional notion, which is not (yet) available in the similarity framework (see Appendix).
4 Gradability of ähnlich/similar
This section focuses, first, on the question of how ähnlich/similar compares to other gradable predicates, and what it means for two items to be more similar than some other two items. In the second part of this section, cognitive models of similarity are considered from the point of view of gradability, and the basic ideas of the model suggested in this paper are introduced (technical details are given in the Appendix). Finally, we will give a tentative answer to the question of why ähnlich/similar are gradable but neither so/such nor gleich/same are.
4.1 What Does It Mean to Be More Similar?
For relative gradable adjectives, the truth of the positive form depends on the relevant comparison class—Anna is tall may be true when comparing Anna to her classmates and false when comparing her to her basketball teammates. Absolute gradable adjectives do not require comparison classes because they make use of minimal or maximal degrees of the gradable property—The door is closed is true only if it is maximally closed, and false if it is ajar (cf. Kennedy and McNally 2005). So unlike relative adjectives, absolute ones include a lower or upper bound (or both).
Neither ähnlich nor similar admit reference to overt comparison classes, see (15a). The examples improve slightly when referring to a relativizing state of affairs, see (15b). Examples are unmarked when referring to dimensions of comparison (15c), which is no surprise since similarity generally requires dimensions.

Maxima can be linguistically indicated with the help of degree modifiers like vollständig and completely. As noted earlier, neither ähnlich nor similar admit these modifiers.Footnote 17 In fact, the combinations vollständig ähnlich and completely similar appear inconsistent, see (16a). Intuitively, if two items are similar, they do not fully agree in their properties, and if agreement is complete, the items are no longer called ähnlich/similar but instead gleich/same. So there is an upper bound, a maximum at which two items cannot possibly be more similar than they are. But this maximum is denoted by gleich/same, on either a token or a type reading, see (16b).Footnote 18

The intuition that gleich/same denote maximal similarity is based on the idea that the more features two items share, the more similar they are.Footnote 19 It is important to note, however, that this is one of two opposite perspectives. If there is a fixed set of features, then two items are more similar than two other items if they share more of these features.Footnote 20 If, on the other hand, the set of features is variable, then two items may be similar w.r.t. a reduced feature set, even if they were not similar in the original set. Take lens resolution in a camera, which is responsible for the details that can be distinguished. If lens resolution is given, similarity can only be increased by changing the facts in the world. But if lens resolution is decreased similarity is increased in the sense that two items may be similar even if they were not similar in the original resolution (while facts in the world did not change). The second perspective is the one taken in the next section.
Considering gleich/same from this perspective, both the token and the type reading entail maximal discriminating capacity in the following sense: The type reading implies similarity, i.e. indistinguishability, in any representation spanned by N-related dimensions regardless how fine-grained it might be, and the token reading implies similarity in any representation at all (i.e. including accidental properties).
4.2 Gradability and Granularity
In Cognitive Science, models of similarity are either distance-based or feature-based. Distance-based models, for example Gärdenfors’ (2000) Conceptual Spaces, start out from distances between points in a geometrical space representing objects of the domain in question. Similarity is determined by distance—the closer the points are (in a given metric) the more similar are the corresponding objects. Similarity is an intrinsic component of geometric representations and is exploited, e.g., in defining convexity.
In a distance-based model the notion of distance provides a “degree” of similarity. In degree-based accounts of gradability the meaning of the comparative, say, taller, is given by comparing degrees—a is taller than b iff a’s height exceeds b’s height. The positive, tall, is defined on top of the comparative by making use of a threshold provided by a comparison class (e.g. Bierwisch 1987; Kennedy 1999)—a is tall iff a’s height exceeds the threshold of the relevant comparison class.Footnote 21
The comparative of ähnlich/similar can be straightforwardly defined in distance-based models via the notion of distance (see, e.g., the comparative semantics for resemble in Meier 2009). The problem would be the positive. It is hard to imagine a way to define a predicate similar on the basis of the comparative, because there is no principled way to determine the threshold—what would be a plausible distance for two tables to count as similar?
The other type of Cognitive Science models of similarity are feature-based ones, most prominently Tversky’s (1977) contrast model. Tversky argued that there are empirical findings in conflict with the basic axioms of metric distance functionsFootnote 22: (a) minimality is problematic in view of results concerning the identification probability for identical stimuli, (b) symmetry is apparently false—the judged similarity of North Korea to Red China exceeds the judged similarity of Red China to North Korea—and (c) triangle inequality is hardly compelling—Jamaica is similar to Cuba (geographical proximity) and Cuba is similar to Russia (political affinity) but Jamaica and Russia are not similar at all.Footnote 23
In view of these issues Tversky claimed that “… the assessment of similarity between stimuli may better be described as comparison of features rather than as the computation of metric distance between points” (p. 328). He proposed a model in which similarity between two objects is computed on the basis of common and distinctive features: Similarity of two objects increases with an increase of common features and/or a decrease of distinctive ones.Footnote 24 This idea is modelled by a function S taking weighted sums of the feature sets A and B of objects a and b to an interval scale such that sim(a, b) ≤ sim(c, d) iff S(a, b) ≤ S(c, d), where S(a, b) = θf(A ∩ B) − αf(A − B) − βf(B − A).Footnote 25
As before in distance-based models, the notion of similarity in Tversky’s feature-based model corresponds to a “degree” of similarity, thereby facilitating comparative statements. And as before, it is hard to imagine a way to define a predicate similar on the basis of the comparative because there is no principled way to determine the threshold.
The account of similarity proposed in this paper is feature-based. But instead of summing up common and distinctive features it makes use of dimensions and of classifiers determining whether values on these dimensions count as distinct. Similarity is defined in this account as indistinguishability with respect to given dimensions and classifiers: Two objects are similar if relative to the relevant dimensions and classifiers they are indistinguishable (see Appendix). In this account, the positive form similar is given, and the comparative form, more-similar, has to be defined on the basis of the positive.
In addition to degree-based accounts, there are so-called vague-predicate accounts of gradability, most prominently Klein (1980). In the latter, the comparative is defined on the basis of the positive form by making use of different interpretation contexts, i.e. (tripartite) partitions of the domain determining the extension of predicates. For example, a is taller than b is true if there is an interpretation context such that a counts as tall while b does not. The pros and cons of the two approaches have been the topic of a longstanding debate. One core issue is that degree semantics presupposes degrees, which are natural with adjectives like tall and old, since these adjectives are associated with units of measurement. But what would be degrees in the case of multidimensional adjectives like skillful and good and ähnlich/similar? If you think of multidimensional adjectives as spanning a multidimensional space, points in this space may be considered as degrees. But since points in a multidimensional space lack a natural order, some extra order has to be imposed (as, e.g., in Sassoon 2013, see footnote 10). This seems to suggest that in the case of multidimensional adjectives, vague-predicate approaches are more natural.
We adapt the idea of vague-predicate approaches by making use of representations of different granularity. Less granular representations have less discriminating capacity (pace dimensions and classifiers), and the lower the discriminating capacity of a representation is, the more items are similar, i.e. indistinguishable. Since the basic predicate similar is defined relative to a representation, the comparative will also be relative to a representation. We define the comparative in the following way:
Two items a and b are more similar than two items c and d in a representation \( {\mathcal{F}} \) if and only if there is a less granular representation \( {\mathcal{F}}^{{\prime }} \) such that a and b are similar in \( {\mathcal{F}}^{{\prime }} \) while c and d are not (Appendix, Definition 6, see also the remark on lens resolution at the end of Sect. 4.1).
Comparing this account to the Kleinian vague-predicate account, there are two points to be noted: First, one major characteristic of the Kleinian account is the elimination of degrees. However, the representations employed in defining a comparative of the similarity predicate include points in attribute spaces, which are in some sense analogous to degrees, thereby raising the question of why, in the similarity-based account, degree-like entities still play a role.Footnote 26 The answer is straightforward: Klein assumes predicates denoted by the positive forms, e.g. tall, to be given. The similar relation, in contrast, is not assumed to be given, but instead defined via representations. So points in attribute spaces are already required when defining the predicate denoted by the positive forms ähnlich/similar, independent of the definition of the comparative.
On a related issue, while Klein’s account presupposes a natural order on the items in the domain, e.g., w.r.t height, there is no natural order of similarity—being similar is in general relative to a representation. The requirement for Kleinian interpretation contexts to be consistent with the order on the domain can be seen as a grounding requirement: Interpretations must comply with the given structure of the world. Representations are the counterpart to interpretation contexts, raising the question of whether there is a grounding requirement for representations. In fact, there is such a requirement built into the similarity framework by means of a consistency constraint: Classifiers have to be consistent with the results of the predicates they correspond to (Appendix, Definition 2).
So from a broader perspective, both representations and Kleinian interpretation contexts are grounded in factual matters. The Kleinian account directly refers to orderings in the domain—this is why interpretation contexts need not themselves be ordered. In the similarity account, representations have to be ordered, thereby lifting the Kleinian order requirement to the level of representations.
Let us finally come to the question why the ähnlich/similar variety of similarity expressions is gradable while neither so/such nor gleich/same are. It turns out that the explanation is straightforward, in both cases referring to the need of a less granular representation in defining the comparative.
In the case of so/such, representations other than the actual one are inaccessible because so/such are demonstratives instead of content words and thus have to be evaluated in the actual context. Since representations are clearly part of the context, they are part of what cannot be shifted in the case of demonstratives.
In the case of gleich/same, maximal discriminative capacity is required—type identity entails indistinguishability in any representation spanned by the N-related dimensions, token identity entails indistinguishability in any representation whatsoever. In either case, defining a comparative making use of less granular representations is ruled out.
5 Conclusion
In this paper, three types of expressions were compared that express similarity in some sense—so/such, ähnlich/similar and gleich/same—starting from the observation that ähnlich/similar are gradable but neither so/such nor gleich/same are. Their semantics was compared on the basis of a common similarity relation revealing differences in, e.g., the selection of dimensions of comparison and the status of reflexive pairs. The similarity relation is spelled out as indistinguishability in a mathematically precise framework of representations combining multi-dimensional attribute spaces with classification functions. A predicate more-similar was defined in a Kleinian style making use of representations of varying granularity. The definition predicts gradability of ähnlich/similar but not of so/such and gleich/same.
The paper provides a semantic analysis of three closely related types of expressions which have, if at all, been considered only in isolation. Moreover, it can be seen as a contribution to a long-standing debate on sameness and indistinguishability in natural language (see, e.g., Nunberg 1984, 2004; Lasersohn 2000; Barker 2010).
Future research will extend the analysis to include demonstratives like dieser/this, the notorious contrast between German derselbe and der gleiche and the contrast between English same and identical, and also include expressions of difference.
Notes
- 1.
There is mehr so (‘more so’) in the sense of eher so (‘rather so’) which is, however, a hedging construction instead of a comparative, as is evident from the fact that the standard parameter is wie instead of als: Anna hat mehr/eher so einen Haarschnitt wie Claire/*als Claire (‘Anna has more such a haircut as/than Claire.’).
- 2.
For similarity expressed by so and such it holds that ∀x∈D.sim(x,x).
- 3.
Without taking dimensions of comparison into account, similarity runs the risk of being trivial, which is nicely demonstrated in Goodman (1972).
- 4.
The term “grid” is not to be misunderstood as implying a distance-based notion of similarity.
- 5.
- 6.
Note that this approach does not classify objects as tables but instead creates subsets of similar tables.
- 7.
Regarding ex. (6), there are two options to interpret adnominal so/such: Either so/such are considered as modifiers of the indefinite determiner, or they are considered as modifiers of the nominal (and have been moved into the prenominal position). The first option yields the interpretation in (a) and the second the one in (b). Since the resulting quantifiers are identical and in German the prenominal position is licensed for solch (‘such’)—ein solcher Tisch ‘a such table’—we will analyze so/such in this paper as nominal modifiers, as in (b) and (6). This option facilitates comparison with ähnlich/similar and gleich/same because they occur as nominal modifiers, too.
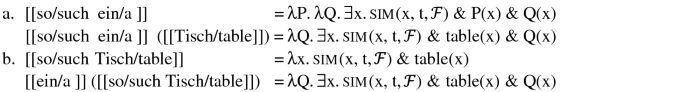
- 8.
On a related note, in ex. (6), German so, but not English such, may modify verbal and adjectival expressions:
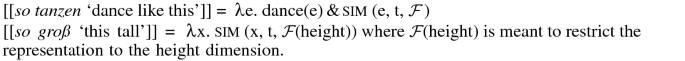
- 9.
Voroni tesselations are restricted to distance-based accounts with prototypes.
- 10.
Sassoon (2013) investigates the meaning of multidimensional adjectives such as healthy and sick. She suggests a classification by the way dimensions are combined presupposing that for each dimension there is some standard. Conjunctive adjectives require entities to reach the standard in all of their dimensions while disjunctive adjectives require the same for some dimensions. Comparatives are analyzed by means of counting dimensions. Sassoon’s account is directed at the issue of dimension integration. Questions of similarity and indistinguishability do not play a role in her account.
- 11.
We ignore reciprocal and NP-dependent occurrences, as in Anna has similar dogs./Anna and Berta have similar dogs, see Beck (2000) on the meaning of different.
- 12.
Regarding ex. (8b), it could be objected that, in German, an equative construction would yield a true proposition—Wenn Adam vor dem Tor parken würde, hätte Ben auch so ein Auto wie das vor dem Tor. (‘If Adam were parked in front of the gate, Ben would have a car like the one in front of the gate.’). This effect is due to the fact that so in equatives is not a demonstrative but instead a correlative and does not refer at all.
- 13.
There are prescriptive efforts to restrict German gleich to type readings and require token readings to be expressed by selb, but German speakers don’t follow this rule. That does not imply, however, that there is no differences between gleich and selb, just that the rule is not descriptively correct, see Umbach (2019). Moreover, there are reasons to assume that the parallelism between German gleich and English same breaks down when it comes to type identity, in that same is closer to selb than to gleich.
- 14.
Gupta (1980) postulates that nouns provide criteria of identity determining the way objects are counted (in addition to criteria of application). His famous example is
(a) Easyjet served 10 million passengers last year.
(b) Easyjet served 10 million people last year.
(a) can be true and (b) false at the same time because one person may count as two passengers on two different flights. Barker (2010) argues against this idea, attributing the effect to the fact that deverbal nominals like passenger may (but need not) give rise to a per-event reading in addition to the regular per-individual reading. The slightly absurd dialog below confirms Barker’s position:
On a flight to Bilbao in June 2017.
Flight attendant A: Look at seat 12a. This is the same passenger that flew to Barcelona in April 2016.
Flight attendant B: No, it is the same person but not the same passenger.
- 15.
Regarding ex. (12iii). Type identity of gleich may in addition be limited to mass produced entities and clones (Stephanie Solt p.c.).
- 16.
In Umbach (2014) ähnlich was said to carry a distinctiveness constraint, thereby explaining that additive particles appear redundant with ähnlich but not with so (… Berta has such a car, too./?? a similar car, too). But distinctiveness was wrongly conflated with irreflexivity in that paper.
- 17.
Corpus research for completely similar in COCA (more than 500 million words) returned three tokens; vollständig ähnlich in DEWAC (more than 1 billion words) returned only one token. A few more were found for vollkommen ähnlich und völlig ähnlich, the latter including a famous subtitle of a drawing showing Leibniz in Park Herrenhausen saying
Leibniz behauptet, daß nicht zwei Blätter einander völlig ähnlich seien.
Leibniz claims that no two leaves are completely similar.
- 18.
As one reviewer noted, this behavior is analogous to open intervals since the margin is not contained but we can come arbitrarily close.
- 19.
We use an informal notion of ‘feature’ here, like ‘property’, or ‘dimension + value’.
- 20.
This is the perspective in Tversky (1977).
- 21.
For a degree-based account of similar/different see also Alrenga (2007).
- 22.
A metric distance function δ has to comply with
-
(i)
minimality (δ(a, b) ≥ δ(a, a) = 0),
-
(ii)
symmetry (δ(a, b) = δ(b, a)) and
-
(iii)
triangle inequality (δ(a, b) + δ(b, c) ≥ δ(a, c)).
-
(i)
- 23.
It has to be mentioned though that these results are highly controversial. Before dismissing transitivity on the basis of the Jamaica/Cuba/Russia example, one should consider the role of switching features within the two comparison steps. On symmetry, there is a detailed study by Gleitman et al. (1996) showing that the alleged asymmetry hinges on the way of presentation. In Tversky’s original studies presentation was directional (North Korea is similar to Red China.). As soon as presentation is non-directional (North Korea and Red China are similar) similarity is found to be symmetric (which was already suggested by Tversky himself). For reflexivity, see the discussion in Sect. 3.
- 24.
When speaking of features, Tversky refers to what we would call dimension + value pairs, that is properties.
- 25.
α, β, θ denote weighting functions and f denotes a nonnegative scale.
- 26.
Many thanks to the reviewer who pointed out this question.
- 27.
- 28.
More precisely: p* ◦ μ approximates p.
- 29.
This includes all points in the convex closure of the images of the positive exemplars. For convex closure operators see Korte et al. (1991). For the concept of convexity in conceptual structures see (Gärdenfors 2000). Intuitively, the convex closure of a subset X of F is the smallest convex subset of F containing X.
- 30.
where {true, false}F is the set of characteristic functions in F. Additionally we expect that classification functions come with algorithmic methods to compute these functions.
References
Alrenga, P. (2007). Dimensions in the semantics of comparatives. Dissertation, University of California, Santa Cruz.
Anderson, C., & Morzycki, M. (2015). Degrees as kinds. Natural Language & Linguistic Theory, 33–3, 791–821.
Barker, C. (2010). Nominals don’t provide criteria of identity. In M. Rathert & A. Alexiadou (Eds.), The semantics of nominalizations across languages and frameworks (pp. 9–24). de Gruyter Berlin.
Beck, S. (2000). The semantics of different. Comparison operator and relational adjective. Linguistics & Philosophy, 23(2), 101–139.
Bierwisch, M. (1987). Semantik der Graduierung. In M. Bierwisch & E. Lang (Eds.), Grammatische und konzeptuelle Aspekte von Dimensionsadjektiven (pp. 91–286). Berlin: Akademie Verlag.
Carlson, G. N. (1980). Reference to kinds in English. Garland, New York & London.
Carpenter, B. (1992). The logic of typed feature structures. Cambridge Tracts in Theoretical Computer Science, Cambridge University Press.
Frege, G. (1892). Über Sinn und Bedeutung. Zeitschrift f. Philosophie u. phil. Kritik, NF 100, S.25–50).
Gärdenfors, P. (2000). Conceptual spaces. MIT Press.
Gleitman, L., Gleitman, H., Miller, C., & Ostrin, R. (1996). Similar, and similar concepts. Cognition, 58, 321–376.
Goodman, N. (1972). Seven strictures on similarity. In N. Goodman (Ed.), Problems and Projects (pp. 437–447). Indianapolis and New York: The Bobbs Merrill Company.
Gupta, A. (1980). The logic of common nouns: an investigation of quantified modal logic. New Haven, CT: Yale University Press.
Gust, H., & Umbach, C. (2015). Making use of similarity in referential semantics. In H. Christiansen, I. Stojanovic, G. Papadopoulos (Eds.), Proceedings of the 9th conference on modeling and using context. Context 2015. LNCS, Springer.
Gust, H., & Umbach, C. (to appear) A qualitative similarity framework for the interpretation of natural language similarity expressions. In L. Bechberger, K. -U. Kühnberger, & M. Liu (Eds.), Concepts in action - representation, learning and application. Language, cognition, and mind. Springer.
Kaplan, D. (1989). Demonstratives. In J. Almog, J. Perry, & H. Wittstein (Eds.), Themes from Kaplan (pp. 481–563). Oxford University Press.
Kennedy, C. (1999). Projecting the adjective. New York: Garland Press.
Kennedy, C., & McNally, L. (2005). Scale structure, degree modification, and the semantics of gradable predicates. Language, 81, 345–381.
Klein, E. (1980). A semantics for positive and comparative adjectives. Linguistics and Philosophy, 4(1), 1–45.
König, E., & Umbach, C. (2018). Demonstratives of manner, of quality and of degree: A neglected subclass. In M. Coniglio, E. Schlachter, & T. Veenstra (Eds.), Atypical demonstratives: Syntax, semantics and typology. Berlin: de Gruyter Mouton.
Korte, B., Lovász, L., & Schrader, R. (1991). Greedoids. Springer.
Lasersohn, P. (2000). Same, models and representation. In Proceedings of semantics and linguistic theory (Vol. 10).
Meier, C. (2009). A comparative analysis for resemblance. In L. Kálmán (Ed.), Proceedings of the 10th Symposium on Logic and Language, Hungarian Academy of Sciences, pp. 141–148.
Minsky, M. L. (1975). A framework for representing knowledge. In P. H. Winston (Ed.), The psychology of computer vision. New York.
Nunberg, G. (1984). Individuation in context. In Proceedings of the West Coast conference on formal linguistics (pp. 203–217). Stanford University.
Nunberg, G. (2004). Indexical descriptions and descriptive indexicals. In M. Reimer & A. Bezuidenhout (Eds.), Descriptions and beyond. Oxford University Press.
Pawlak, Z. (1998). Granularity of knowledge, indiscernibility and rough sets. In Proceedings of the IEEE international conference on fuzzy systems (pp. 106–110).
Sassoon, G. (2013). A typology of multidimensional adjectives. Journal of Semantics, 30, 335–380.
Tversky, A. (1977). Features of similarity. Psychological Review, 84, 327–352.
Umbach, C., & Gust, H. (2014). Similarity demonstratives. Lingua, 149, 74–93.
Umbach, C. (2014). Expressing similarity: On some differences between adjectives and demonstratives. In Proceedings of IATL 2013, MIT working papers in linguistics.
Umbach, C. (2019) Dasselbe oder das gleiche? - warum wir dann doch dieselbe Pizza bestellen können wie der Gast nebenan. Jahrbuch 2018 des Zentrums Allgemeine Sprachwissenschaft (ZAS), Berlin.
Umbach, C., & Stolterfoht, B. (in prep.). Ad-hoc kind formation by similarity.
Acknowledgements
We would like to thank two reviewers for their detailed and very helpful reviews. We would also like to thank the audience of the Cognitive Structures conference (Düsseldorf, 2016) and of the ZAS workshop “Records, Frames and Attribute Spaces” (Berlin, 2018), and in particular Robin Cooper, Louise McNally, Wiebke Petersen and Stephanie Solt for their valuable comments. Finally, we like to express our gratitude to the editors of this volume for their patience and support. The first author acknowledges financial support by the German Research Foundation (Deutsche Forschungsgemeinschaft), UM 100/1-3.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Granularity in Multi-dimensional Attribute Spaces
Appendix: Granularity in Multi-dimensional Attribute Spaces
In the Appendix, the basic mathematical ideas and definitions of the similarity framework are presented. For more details see Gust and Umbach (to appear).
1.1 Domains and Representations
The core of the appendix are sets of representations equipped with a preorder structure. This preorder implements a concept of granularity and will be used to construct a predicate more_similar based on a similarity relation. We start with defining a domain as a subset of the universe together with a set of predicates and non-overlapping sets of positive and negative examples for each predicate.
Definition 1 Domain
A domain
 is a quadruple 〈D, _+, _−, P〉 with:
is a quadruple 〈D, _+, _−, P〉 with:
-
D a set of individuals/entities (called the carrier of the domain),
-
P = {p1, … pn} a set of predicates over D, (a subset of the powerset of D)
-
_+: P
 (D) a function which assigns (a finite set of) positive examples to each predicate,
(D) a function which assigns (a finite set of) positive examples to each predicate,for _+(p) we write p+
-
_−: P
 (D) a function which assigns (a finite set of) negative examples to each predicate,
(D) a function which assigns (a finite set of) negative examples to each predicate,for _−(p) we write p−
-
\( \forall {\text{p}} \in {\text{P}}:{\text{p}}^{ + } \cap {\text{p}}^{ - } = \emptyset \)
We view the elements of D as entities to which we have only indirect access via a (generalized) measure function μ which constructs representations of the entities in D in an attribute space F much like observables in physics. Attribute spaces are common structures for representation.Footnote 27 They generalize vector space approaches in allowing heterogeneous dimensions equipped with value sets of different scales (nominal, ordinal, interval, ratio etc.), where value sets may themselves be attribute spaces.
An attribute space F is given by a set of attributes A = {a1…an}, such that for each ai in A there is a set of possible values \(V_{\varvec{ai}} \) of ai. Elements of D are mapped to points in \(V_{\varvec{a1}} \)× … × \(V_{\varvec{an}} \), the carrier of the attribute space F.
A representation includes an attribute space F, a (generalized) measure function μ mapping elements of a domain into the attribute space, and a set of classification functions p* talking about points in the attribute space. These classification functions (short classifiers) serve as approximationsFootnote 28 of the predicates in P. Moreover, the extensions of the classifiers will be assumed to be convex. This means that F comes with a convex closure operator cl and p* must be true on cl(μ(p+)).Footnote 29 Intuitively, using the n-dimensional Euclidean space as an example, this means that the extensions of the classifiers must not have holes, notches or coves in the representation space F.
Definition 2 Representation
A representation
 = 〈〈F, cl 〉, μ, _*,
= 〈〈F, cl 〉, μ, _*,
 〉 of a domain
〉 of a domain
 = 〈D, _+, _−, P〉 is given by
= 〈D, _+, _−, P〉 is given by
-
an attribute space F, with a closure operator cl
(we will write F for 〈F, cl〉 if we are not interested in the closure operator cl)
-
a measure function μ: D
 F,
F, -
a function _*: P
 {true, false}F (again we write p* for _*(p) and call them classifiers)Footnote 30
{true, false}F (again we write p* for _*(p) and call them classifiers)Footnote 30
together with the consistency conditions
-
∀p∈P the extension of p* must be convex in 〈F, cl〉
-
∀p∈P ∀x∈p+: p*(μ(x)) = true
-
∀p∈P ∀x∈p−: p*(μ(x)) = false
From this we get μ(p +i ) ∩ μ(p −i ) = ∅.
As mentioned above, attribute spaces are familiar methods of representation. What distinguishes attribute spaces and the representations proposed in this paper is the idea of classifiers on attribute spaces. On the worldy side, a domain includes a set of relevant predicates p∈P. On the representation side these predicates have counterparts, namely classifiers p*∈P*. By P* we denote the set of all (basic) classifiers: P* = {p* | p∈P}. These classification functions are required to be consistent with their corresponding predicates over D; more precisely, they have to agree in truth value on the set of positive/negative exemplars known for the original predicate (see Definition 2).
While attribute spaces can provide highly structured representations, classifiers provide binary features (attributes with possible values in {true, false}). Given a set of basic classifiers we assume the possibility to construct derived classifiers by logical operations: For the logical conjunction this works fine (convex sets are closed under intersection). For the logical disjunction we have to apply the convex closure operator cl to the result. For negation this does not work at all. So we do not allow to define complex classifiers by applying negation to elementary ones. We name the set of derived classifiers \( \tilde{P}^{*} \) (Fig. 1).
1.2 Indiscernibility
Given a system of predicates P we can ask, which elements in a domain D can be distinguished. There are two reasons why we may not be able to distinguish between two elements of D:
-
Two elements may lead to the same value of the function μ. Then there is no way to discriminate between the two elements.
-
The two elements disagree on μ (so we see them as different), but they agree on all classification functions in \( \tilde{P}^{*}. \)
For the second case we borrow the term indiscernible from Rough Set Theory (Pawlak 1998):
Definition 3 Indiscernible
Given a representation

we define:
\(\hfill {\text{For}}\,{\text{x}},{\text{y}} \in {\text{F}}:\quad {\text{x}}\sim_{\mathcal{F}} {\text{y}} \equiv \forall {\text{q}} \in \tilde{\text{P}}^{*} ,{\text{q}}({\text{x}}) \leftrightarrow {\text{q}}({\text{y}})\hfill \)
where \( \tilde{P}^{*} \) is the set of all derived classifiers.
This relation talks about points in F. However, the similarity relation we are interested in talks about elements of the domain D. So we have to apply the measure function first:
Definition 4 Similar
\(\hfill \forall {\text{x}}, {\text{y}} \in {\text{D}}:\text{sim} ({\text{x}},{\text{y}},{\mathcal{F}}) \equiv\upmu({\text{x}})\sim_{{\mathcal{F}}}\upmu({\text{y}}) \hfill \)
Obviously, Definition 4 defines an equivalence relation on D.
The indiscernibility relation provides attribute spaces with a level of granularity, facilitating comparison of attribute spaces of distinct granularity which are identical otherwise.
1.3 Granularity and Gradability
For two representations \( {\mathcal{F}} \) and \( {\mathcal{F}}^{{\prime }} \) we can ask whether one is more fine-grained than the other, that is, whether there are entities that can be distinguished in one representation but not in the other. Since indiscernability of entities in a representation depends on the set of dimensions of the corresponding F and of the corresponding predicates P given in \( {\mathcal{F}} \), granularity of representations depends on these parameters, too. Maybe there are more constraints we would like to impose on systems of representations to make such a system coherent in some sense. But we will not go into details here.
On representations we can define a reflexive and transitive relation (a preorder), which relates granularity levels:
Definition 5 Coarser representation
Given two representations

we define:

This means that what is indiscernible in the finer representation cannot be discriminated in the coarser representation. The strict version < is used such that \( {\mathcal{F}} \) is finer than \( {\mathcal{F}}^{{\prime }} \), or \( {\mathcal{F}}^{{\prime }} \) is coarser than \( {\mathcal{F}} \), if \( {\mathcal{F}} \) < \( {\mathcal{F}}^{{\prime }} \) (in a preorder: x < y if x ≤ y but not y ≤ x).
Based on our similarity relation sim and the preorder on representations we define a general relation more_sim(a, b, c, d, \( {\mathcal{F}} \)), which is intended to be true if a is more similar to b than c is to d, with respect to a representation \( {\mathcal{F}} \).
Definition 6 More similar
Given a representation \( {\mathcal{F}} \) we define

The widely used 3-place version more_sim(x, y, z, \( {\mathcal{F}} \)) in the sense that x is more similar to z than y can be defined straightforwardly by:

This approach shows how to model different similarity situations by selecting suitable sets of representations.
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2021 The Author(s)
About this chapter
Cite this chapter
Umbach, C., Gust, H. (2021). Grading Similarity. In: Löbner, S., Gamerschlag, T., Kalenscher, T., Schrenk, M., Zeevat, H. (eds) Concepts, Frames and Cascades in Semantics, Cognition and Ontology. Language, Cognition, and Mind, vol 7. Springer, Cham. https://doi.org/10.1007/978-3-030-50200-3_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-50200-3_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-50199-0
Online ISBN: 978-3-030-50200-3
eBook Packages: Religion and PhilosophyPhilosophy and Religion (R0)





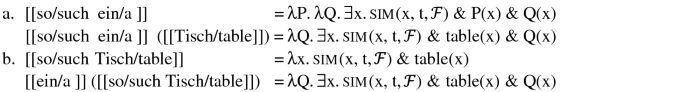
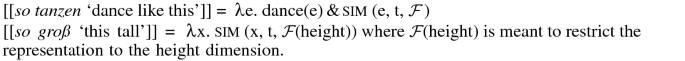
 (D) a function which assigns (a finite set of) positive examples to each predicate,
(D) a function which assigns (a finite set of) positive examples to each predicate, (D) a function which assigns (a finite set of) negative examples to each predicate,
(D) a function which assigns (a finite set of) negative examples to each predicate, F,
F, {true, false}F (again we write p* for _*(p) and call them classifiers)
{true, false}F (again we write p* for _*(p) and call them classifiers)