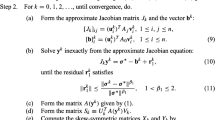Abstract
In this work, we develop efficient solvers for linear inverse problems based on randomized singular value decomposition (RSVD). This is achieved by combining RSVD with classical regularization methods, e.g., truncated singular value decomposition, Tikhonov regularization, and general Tikhonov regularization with a smoothness penalty. One distinct feature of the proposed approach is that it explicitly preserves the structure of the regularized solution in the sense that it always lies in the range of a certain adjoint operator. We provide error estimates between the approximation and the exact solution under canonical source condition, and interpret the approach in the lens of convex duality. Extensive numerical experiments are provided to illustrate the efficiency and accuracy of the approach.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Boutsidis, C., Magdon-Ismail, M.: Faster SVD-truncated regularized least-squares. In: 2014 IEEE International Symposium on Information Theory, pp. 1321–1325 (2014). https://doi.org/10.1109/ISIT.2014.6875047
Chen, S., Liu, Y., Lyu, M.R., King, I., Zhang, S.: Fast relative-error approximation algorithm for ridge regression. In: Proceedings of the 31st Conference on Uncertainty in Artificial Intelligence, pp. 201–210 (2015)
Ekeland, I., Témam, R.: Convex Analysis and Variational Problems. SIAM, Philadelphia, PA (1999). https://doi.org/10.1137/1.9781611971088
Eldén, L.: A weighted pseudoinverse, generalized singular values, and constrained least squares problems. BIT 22(4), 487–502 (1982). https://doi.org/10.1007/BF01934412
Engl, H.W., Hanke, M., Neubauer, A.: Regularization of Inverse Problems. Kluwer, Dordrecht (1996). https://doi.org/10.1007/978-94-009-1740-8
Frieze, A., Kannan, R., Vempala, S.: Fast Monte-Carlo algorithms for finding low-rank approximations. J. ACM 51(6), 1025–1041 (2004). https://doi.org/10.1145/1039488.1039494
Gehre, M., Jin, B., Lu, X.: An analysis of finite element approximation in electrical impedance tomography. Inverse Prob. 30(4), 045,013,24 (2014). https://doi.org/10.1088/0266-5611/30/4/045013
Golub, G.H., Van Loan, C.F.: Matrix Computations, 3rd edn. Johns Hopkins University Press, Baltimore, MD (1996)
Griebel, M., Li, G.: On the decay rate of the singular values of bivariate functions. SIAM J. Numer. Anal. 56(2), 974–993 (2018). https://doi.org/10.1137/17M1117550
Gu, M.: Subspace iteration randomization and singular value problems. SIAM J. Sci. Comput. 37(3), A1139–A1173 (2015). https://doi.org/10.1137/130938700
Halko, N., Martinsson, P.G., Tropp, J.A.: Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53(2), 217–288 (2011). https://doi.org/10.1137/090771806
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, Cambridge (1985). https://doi.org/10.1017/CBO9780511810817
Ito, K., Jin, B.: Inverse Problems: Tikhonov Theory and Algorithms. World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ (2015)
Jia, Z., Yang, Y.: Modified truncated randomized singular value decomposition (MTRSVD) algorithms for large scale discrete ill-posed problems with general-form regularization. Inverse Prob. 34(5), 055,013,28 (2018). https://doi.org/10.1088/1361-6420/aab92d
Jin, B., Xu, Y., Zou, J.: A convergent adaptive finite element method for electrical impedance tomography. IMA J. Numer. Anal. 37(3), 1520–1550 (2017). https://doi.org/10.1093/imanum/drw045
Kluth, T., Jin, B.: Enhanced reconstruction in magnetic particle imaging by whitening and randomized SVD approximation. Phys. Med. Biol. 64(12), 125,026,21 (2019). https://doi.org/10.1088/1361-6560/ab1a4f
Kluth, T., Jin, B., Li, G.: On the degree of ill-posedness of multi-dimensional magnetic particle imaging. Inverse Prob. 34(9), 095,006,26 (2018). https://doi.org/10.1088/1361-6420/aad015
Maass, P.: The x-ray transform: singular value decomposition and resolution. Inverse Prob. 3(4), 729–741 (1987). http://stacks.iop.org/0266-5611/3/729
Maass, P., Rieder, A.: Wavelet-accelerated Tikhonov-Phillips regularization with applications. In: Inverse Problems in Medical Imaging and Nondestructive Testing (Oberwolfach, 1996), pp. 134–158. Springer, Vienna (1997)
Musco, C., Musco, C.: Randomized block Krylov methods for stronger and faster approximate singular value decomposition. In: NIPS 2015 (2015)
Neubauer, A.: An a posteriori parameter choice for Tikhonov regularization in the presence of modeling error. Appl. Numer. Math. 4(6), 507–519 (1988). https://doi.org/10.1016/0168-9274(88)90013-X
Pilanci, M., Wainwright, M.J.: Iterative Hessian sketch: fast and accurate solution approximation for constrained least-squares. J. Mach. Learn. Res. 17, 38 (2016)
Sarlos, T.: Improved approximation algorithms for large matrices via random projections. In: Foundations of Computer Science, 2006. FOCS ’06. 47th Annual IEEE Symposium on (2006). https://doi.org/10.1109/FOCS.2006.37
Somersalo, E., Cheney, M., Isaacson, D.: Existence and uniqueness for electrode models for electric current computed tomography. SIAM J. Appl. Math. 52(4), 1023–1040 (1992). https://doi.org/10.1137/0152060
Stewart, G.W.: On the perturbation of pseudo-inverses, projections and linear least squares problems. SIAM Rev. 19(4), 634–662 (1977). https://doi.org/10.1137/1019104
Szlam, A., Tulloch, A., Tygert, M.: Accurate low-rank approximations via a few iterations of alternating least squares. SIAM J. Matrix Anal. Appl. 38(2), 425–433 (2017). https://doi.org/10.1137/16M1064556
Tao, T.: Topics in Random Matrix Theory. AMS, Providence, RI (2012). https://doi.org/10.1090/gsm/132
Tautenhahn, U.: Regularization of linear ill-posed problems with noisy right hand side and noisy operator. J. Inverse Ill-Posed Probl. 16(5), 507–523 (2008). https://doi.org/10.1515/JIIP.2008.027
Wang, J., Lee, J.D., Mahdavi, M., Kolar, M., Srebro, N.: Sketching meets random projection in the dual: a provable recovery algorithm for big and high-dimensional data. Electron. J. Stat. 11(2), 4896–4944 (2017). https://doi.org/10.1214/17-EJS1334SI
Wei, Y., Xie, P., Zhang, L.: Tikhonov regularization and randomized GSVD. SIAM J. Matrix Anal. Appl. 37(2), 649–675 (2016). https://doi.org/10.1137/15M1030200
Witten, R., Candès, E.: Randomized algorithms for low-rank matrix factorizations: sharp performance bounds. Algorithmica 72(1), 264–281 (2015). https://doi.org/10.1007/s00453-014-9891-7
Xiang, H., Zou, J.: Regularization with randomized SVD for large-scale discrete inverse problems. Inverse Prob. 29(8), 085,008,23 (2013). https://doi.org/10.1088/0266-5611/29/8/085008
Xiang, H., Zou, J.: Randomized algorithms for large-scale inverse problems with general Tikhonov regularizations. Inverse Prob. 31(8), 085,008,24 (2015). https://doi.org/10.1088/0266-5611/31/8/085008
Zhang, L., Mahdavi, M., Jin, R., Yang, T., Zhu, S.: Random projections for classification: a recovery approach. IEEE Trans. Inform. Theory 60(11), 7300–7316 (2014). https://doi.org/10.1109/TIT.2014.2359204
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix A: Iterative refinement
Appendix A: Iterative refinement
Proposition 1 enables iteratively refining the inverse solution when RSVD is not sufficiently accurate. This idea was proposed in [29, 34] for standard Tikhonov regularization, and we describe the procedure in a slightly more general context. Suppose \(\mathscr {N}(L)=\{0\}\). Given a current iterate \(x^j\), we define a functional \(J_\alpha ^j(\delta x)\) for the increment \(\delta x\) by
Thus the optimal correction \(\delta x_\alpha \) satisfies
i.e.,
with \(B=AL^\dag \). However, its direct solution is expensive. We employ RSVD for a low-dimensional space \(\tilde{V}_k\) (corresponding to B), parameterize the increment \(L\delta x\) by \(L\delta x=\tilde{V}_k^*z\) and update z only. That is, we minimize the following functional in z
Since \(k\ll m\), the problem can be solved efficiently. More precisely, given the current estimate \(x^j\), the optimal z solves
It is the Galerkin projection of (20) for \(\delta x_\alpha \) onto the subspace \(\tilde{V}_k\). Then we update the dual \(\xi \) and the primal x by the duality relation in Sect. 6:
Summarizing the steps gives Algorithm 3. Note that the duality relation (17) enables A and \(A^*\) to enter into the play, thereby allowing progressively improving the accuracy. The main extra cost lies in matrix-vector products by A and \(A^*\).
The iterative refinement is a linear fixed-point iteration, with the solution \(x_\alpha \) being a fixed point and the iteration matrix being independent of the iterate. Hence, if the first iteration is contractive, i.e., \(\Vert x^1-x_\alpha \Vert \le c\Vert x^0-x_\alpha \Vert \), for some \(c\in (0,1)\), then Algorithm 3 converges linearly to \(x_\alpha \). It can be satisfied if the RSVD approximation \((\tilde{U}_k,\tilde{\varSigma }_k,\tilde{V}_k)\) is reasonably accurate to B.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Ito, K., Jin, B. (2020). Regularized Linear Inversion with Randomized Singular Value Decomposition. In: Beilina, L., Bergounioux, M., Cristofol, M., Da Silva, A., Litman, A. (eds) Mathematical and Numerical Approaches for Multi-Wave Inverse Problems. CIRM 2019. Springer Proceedings in Mathematics & Statistics, vol 328. Springer, Cham. https://doi.org/10.1007/978-3-030-48634-1_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-48634-1_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-48633-4
Online ISBN: 978-3-030-48634-1
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)