Abstract
This paper examines several measures of space complexity on variants of stack automata: non-erasing stack automata and checking stack automata. These measures capture the minimum stack size required to accept any word in a language (weak measure), the maximum stack size used in any accepting computation on any accepted word (accept measure), and the maximum stack size used in any computation (strong measure). We give a detailed characterization of the accept and strong space complexity measures for checking stack automata. Exactly one of three cases can occur: the complexity is either bounded by a constant, behaves (up to small technicalities explained in the paper) like a linear function, or it grows arbitrarily larger than the length of the input word. However, this result does not hold for non-erasing stack automata; we provide an example when the space complexity grows with the square root of the input length. Furthermore, an investigation is done regarding the best complexity of any machine accepting a given language, and on decidability of space complexity properties.
The research of I. McQuillan and L. Prigioniero was supported, in part, by Natural Sciences and Engineering Research Council of Canada Grant 2016-06172.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
When studying different machine models, it is common to study both time and space complexity of a machine or an algorithm. In particular, the study of complexity of Turing machines gave way to the area of computational complexity, which has been one of the most well-studied areas of theoretical computer science for the past 40 years [7]. The field of automata theory specializes in different machine models, often with more restricted types of data stores and operations. Various models of automata differ in the languages that can be accepted by the model, in the size of the machine (e.g. the number of states), in the algorithms to decide various properties of a machine, and in the complexity of these algorithms. Some of the well-studied automata models with more restricted power than Turing machines are finite automata [5, 9], pushdown automata [5, 9], stack automata [4], checking stack automata [4], visibly pushdown automata [1], and many others.
For Turing machines, several different space complexity measures have been studied. Some of these complexity measures are the following [13]:
-
weak measure: for an input word w, the smallest tape size required for some accepting computation on w;
-
accept measure: for an input word w, the largest tape size required for any accepting computation on w;
-
strong measure: for an input word w, the largest tape size required for any computation on w.
For any of these measures, the space complexity of a machine can be defined as a function of an integer n as the maximum tape size required for any input word of length n under these conditions. Finally, given a language, one can examine the space complexity of different machines accepting this language. For many of the more restricted automata models, some of these three complexity measures have not been studied as extensively as for Turing machinesFootnote 1. This paper aims to fill the gaps for several machine models.
We study the above complexity measures for machines and languages of one-way stack automata, non-erasing stack automata, and checking stack automata. One-way stack automata are, intuitively, pushdown automata with the additional ability to read letters from inside the stack; but still only push to and pop from the top of the stack. Non-erasing stack automata are stack automata without the ability to erase (pop) letters from the stack. Finally, checking stack automata are further restricted so that as soon as they read from inside of the stack, they can no longer push new letters on the stack.
It is known that checking stack languages form a proper subset of non-erasing stack languages, which form a proper subset of stack languages [4], and those in turn form a proper subset of context-sensitive languages [8]. In terms of space complexity, it is possible to study the three space complexity measures (weak, accept, and strong) as the maximum stack size required for any input of length n. It is already known that every stack language can be accepted by some stack automaton which operates in linear space using the weak measure [8, 12]. However, this does not imply that every stack automaton has this property. We prove here that every checking stack automaton has this property. Further results are known relating one-way and two-way versions of these machines to other models, and to space complexity classes of Turing machines, e.g. [3, 10, 12].
For checking stack automata, we give a complete characterization of the possible accept and strong space measures. For both measures, exactly one of the following three cases must occur for every checking stack automaton:
-
1.
The complexity is \(O(1)\). Then the automaton accepts a regular language.
-
2.
There is some word (accepted word for the accept measure) u which has computations (accepting computations, respectively) that use arbitrarily large stack space on u, and so the complexity is not \(O(f(n))\) for any integer function f. The language accepted can be regular or not.
-
3.
The complexity is \(O(n)\), but it is not \(o(n)\). The language accepted can be regular or not.
The third case is essentially saying that the complexity is \(\varTheta (n)\), except for some minor technicalities that will be discussed further in the paper. Therefore, there is a “gap” in the possible asymptotical behaviors of space complexity. No checking stack machine can have a space complexity between \(\varTheta (1)\) and \(\varTheta (n)\); or complexity above \(\varTheta (n)\) (as long as there is some function which bounds the space). The lower bound proof uses a method involving store languages of stack automata (the language of all words occurring on the stack of an accepting computation). We have not seen this technique used previously in the literature. Indeed, store languages are used in multiple proofs of this paper.
For non-erasing stack automata, there are differences with checking stack automata, as the complexity can be in \(o(n)\), though not constant. We present an automaton with a weak and accept space complexity in \(\varTheta (\sqrt{n})\).
We also consider the following problem: Given a language (accepted by one of the stack automaton models) and one of the space complexity measures, what are the space complexities of the machines accepting it? We show that there is a checking stack language such that with the strong measure, every machine accepting it can use arbitrarily larger stack space than the input size, and therefore it is not O(f(n)) for any function f. Lastly, decidability questions on space complexity are addressed. It is shown that it is undecidable whether a checking stack automaton operates in constant space using the weak measure, however for both the strong and accept measures, it is decidable even for arbitrary stack automata.
2 Preliminaries
This section introduces basic notation used in this paper, and defines the three models of stack automata that we shall consider.
We assume that the reader is familiar with basics of formal language and automata theory. Please see [9] for an introduction. An alphabet is a finite set of letters. A word over an alphabet \(\varSigma = \{a_1, \ldots , a_k\}\) is a finite sequence of letters from \(\varSigma \). The set of all words over \(\varSigma \) is denoted by \(\varSigma ^*\), which includes the empty word, denoted by \(\lambda \). A language L (over \(\varSigma \)) is any set of words \(L \subseteq \varSigma ^*\). The complement of L over \(\varSigma \), denoted by \(\overline{L}\) is equal to \(\varSigma ^* \setminus L\). Given a word \(w\in \varSigma ^*\), the length of w is denoted by |w|, and the number of occurrences of a letter \(a_i\) in w by \(|w|_{a_i}\). The Parikh image of w is the vector \(\psi (w) = (|w|_{a_1},\ldots , |w|_{a_k})\), which is extended to a language L as \(\psi (L) = \{{\psi (w)}\mid {w \in L}\}\). We do not define the concept of semilinearity formally here, but it is known that a language L is semilinear if and only if there is a regular language \(L'\) with \(\psi (L) = \psi (L')\) [5]. Given two words \(w,u \in \varSigma ^*\), we say that u is a prefix of w if \(w = uv\) for some \(v \in \varSigma ^*\). The prefix closure of a language L, \(\text {pref}(L)\), is the set of all prefixes of all words in L. It is known that if L is a regular language, then \(\text {pref}(L)\) is also regular.
2.1 Automata Models
Next, we define the three types of stack automata models discussed in this paper.
Definition 1
A one-way nondeterministic stack automaton (SA for short) is a 6-tuple \(M = (Q, \varSigma , \varGamma , \delta , q_0, F)\), where:
-
Q is the finite set of states.
-
\(\varSigma \) and \(\varGamma \) are the input and stack alphabets, respectively.
-
\(\varGamma \) contains symbols \({\triangleright \,}\) and \({\,\triangleleft }\), which represent the bottom and top of the stack. We denote by \(\varGamma _0\) the alphabet \(\varGamma \setminus \{ {\triangleright \,}, {\,\triangleleft }\}\).
-
\(q_0 \in Q\) and \(F\subseteq Q\) are the initial state and the set of final states, respectively.
-
\(\delta \) is the nondeterministic transition function from \(Q \times (\varSigma \cup \{ \lambda \} ) \times \varGamma \) into subsets of
 . We use the notation \((q,a,y) \rightarrow (p,\iota )\) to denote that \((p, \iota ) \in \delta (q,a,y)\).
. We use the notation \((q,a,y) \rightarrow (p,\iota )\) to denote that \((p, \iota ) \in \delta (q,a,y)\).
A configuration c of an SA is a triple \(c=(q, w, \gamma )\), where \(q \in Q\) is the current state, \(w \in \varSigma ^*\) is the remaining input to be read, and \(\gamma \) is the current stack tape. The word \(\gamma \) either has to be of the form  , or of the form
, or of the form  . The symbol denotes the position of the stack head, which is currently scanning the symbol directly preceding it. We shall occasionally refer to the “pure” stack content, that is, the word \(\gamma \) without the end markers and the head symbol. We denote this word by \(\hat{\gamma }\). The stack size of c is \({\Vert {c}\Vert }_{\varGamma } = |{\hat{\gamma }}| = |{\gamma }| -3\).
. The symbol denotes the position of the stack head, which is currently scanning the symbol directly preceding it. We shall occasionally refer to the “pure” stack content, that is, the word \(\gamma \) without the end markers and the head symbol. We denote this word by \(\hat{\gamma }\). The stack size of c is \({\Vert {c}\Vert }_{\varGamma } = |{\hat{\gamma }}| = |{\gamma }| -3\).
We use two relations between configurations:
-
The write relation: If \((q, a, y) \rightarrow (p, \iota )\), where \(q, p \in Q\), \(a \in \varSigma \cup \{\lambda \}\), \(y \in \varGamma _0 \cup \{ {\triangleright \,}\}\), and
 ; then for \(u \in \varSigma ^*\), \(\gamma \in \varGamma ^*\), with \(\gamma y \in {\triangleright \,}\varGamma _0^*\):
; then for \(u \in \varSigma ^*\), \(\gamma \in \varGamma ^*\), with \(\gamma y \in {\triangleright \,}\varGamma _0^*\):-
 if \(\iota = \mathtt {stay}\),
if \(\iota = \mathtt {stay}\), -
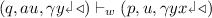 if \(\iota = \mathtt {push(}x\mathtt {)}\),
if \(\iota = \mathtt {push(}x\mathtt {)}\), -
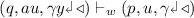 if \(\iota = \mathtt {pop}\) and \(y \ne {\triangleright \,}\).
if \(\iota = \mathtt {pop}\) and \(y \ne {\triangleright \,}\).
Notice that the write relation is defined only if
 , and \(\mathtt {pop}\) transitions are performed when the stack head is scanning the topmost symbol of the stack. If one of these operations is executed when the stack head is not on the top of the stack, the machine halts and rejects.
, and \(\mathtt {pop}\) transitions are performed when the stack head is scanning the topmost symbol of the stack. If one of these operations is executed when the stack head is not on the top of the stack, the machine halts and rejects. -
-
The read relation: If \((q, a, y) \rightarrow (p, \iota )\), where \(q, p \in Q\), \(a \in \varSigma \cup \{\lambda \}\), \(y \in \varGamma \), and \(\iota \in \{ -1,0,1 \}\); then for \(u \in \varSigma ^*\), \(\gamma _1, \gamma _2 \in \varGamma ^*\), with \(\gamma _1 y \gamma _2 \in {\triangleright \,}\varGamma _0^* {\,\triangleleft }\):
-
 if \(\iota = -1\) and \(y \ne {\triangleright \,}\),
if \(\iota = -1\) and \(y \ne {\triangleright \,}\), -
 if \(\iota = 0\),
if \(\iota = 0\), -
 if \(\iota = +1, \gamma _2 = x \gamma _2'\) and \(x \in \varGamma \).
if \(\iota = +1, \gamma _2 = x \gamma _2'\) and \(x \in \varGamma \).
-
The union of \(\vdash _w\) and \(\vdash _r\) is denoted by \(\vdash \). The transitive closures of \(\vdash _w\), \(\vdash _r\), and \(\vdash \) are denoted by \(\vdash _w^+\), \(\vdash _r^+\), and \(\vdash ^+\); and their transitive and reflexive closures by \(\vdash _w^*\), \(\vdash _r^*\), and \(\vdash ^*\), respectively.
A partial computation of the automaton M on an input word u is a sequence of configurations
where  . If also \(u_n = \lambda \), we say that this is a computation; and furthermore, if also \(p_n \in F\) then it is an accepting computation. The stack size of the (partial) computation \(\mathcal {C}\), denoted by \({\Vert \mathcal{{C}}\Vert }_{\varGamma }\), is defined as \(\max \{{{\Vert {c_j}\Vert }_{\varGamma }}\mid {0 \le j \le n}\}\).
. If also \(u_n = \lambda \), we say that this is a computation; and furthermore, if also \(p_n \in F\) then it is an accepting computation. The stack size of the (partial) computation \(\mathcal {C}\), denoted by \({\Vert \mathcal{{C}}\Vert }_{\varGamma }\), is defined as \(\max \{{{\Vert {c_j}\Vert }_{\varGamma }}\mid {0 \le j \le n}\}\).
The language accepted by an SA M, denoted by \(L(M)\), is the set of words w for which M has an accepting computation on w. The store language of M, \(S(M)\), is the set of state and stack contents that can appear in an accepting computation: \(S(M) = \{{q \gamma }\mid {(q, u, \gamma ) \text { is a configuration in some accepting}}\}{\text {computation of } M}\). Notice that these words contain both the state and the stack head position. It is known that for every SA M, \(S(M)\) is a regular language [2, 11].
The accepting computation in Eq. (1) can be written uniquely as
We call a sequence of transitions \(c_i \vdash _w^*d_{i+1}\) a write phase, and a sequence of transitions \(d_i \vdash _r^*c_i\) a read phase. By this definition, a computation always starts with a write phase and ends with a read phase. For the purpose of this paper, we can assume without loss of generality that both the first write phase and last read phase are non-empty, by altering the machine to always start by writing with a \(\mathtt {stay}\) instruction, and to always read with a 0 instruction before finishing.
Furthermore, for any such SA \(M = (Q,\varSigma ,\varGamma ,\delta , q_0, F)\) (with a non-empty initial read phase and final write phase), we can construct an SA \(M' = ( Q_w \cup Q_r, \varSigma , \varGamma , \delta ', {{q_0}_w}, F')\); where \(Q_w\) and \(Q_r\) are two distinct copies of the state set Q of M, with the copied states denoted by the \({}_w\) and \({}_r\) subscripts, \(F' = \{{q_r}\mid {q \in F}\}\), and where \(\delta '\) is a union of two transition functions:
-
\(\delta _w\), which contains transitions \(( q_w, a, y ) \rightarrow (p_w, \iota )\) and \(( q_w, a, y ) \rightarrow (p_r, \iota )\); where \((q, a, y) \rightarrow (p, \iota )\) in \(\delta \), and
 ; and
; and -
\(\delta _r\), which contains transitions \(( q_r, a, y ) \rightarrow (p_w, \iota )\) and \(( q_r, a, y ) \rightarrow (p_r, \iota )\); where \((q, a, y) \rightarrow (p, \iota )\) in \(\delta \), and \(\iota \in \{-1, 0, 1\}\).
We call transitions in \(\delta _w\) write transitions, and transitions in \(\delta _r\) read transitions. Similarly, we call states in \(Q_w\) (resp. \(Q_r\)) write states (resp. read states). Observe that the language accepted by \(M'\) is the same as the one accepted by M.
Any stack machine that has states that can be partitioned into write and read ones, such that write transitions can only be applied from write states, and read transitions can only be applied from read states, is said to have partitioned states. In such a machine, the current state in every configuration dictates whether the next transition to be taken is a write or a read transition.
A stack automaton is called non-erasing (NESA) if it contains no transitions to an element of \(Q \times \{ \mathtt {pop}\}\). A non-erasing stack automaton is called a checking stack automaton (CSA) if it has partitioned states and it contains no transitions from a read state to a write state. Every accepting computation of a checking stack automaton therefore has a single write phase followed by a single read phase.
We denote by \(\mathcal{L}(\textsf {SA}), \mathcal{L}(\textsf {NESA})\), and \(\mathcal{L}(\textsf {CSA})\) the families of languages accepted by the three types of devices.
3 Complexity Measures on Stack Automata
For an \(\textsf {SA}\) \(M = (Q, \varSigma ,\varGamma ,\delta , q_0, F)\), one can consider three different space complexity measures defined similarly as for Turing machines [13]. Consider an input word \(u \in \varSigma ^*\) to M.
-
weak measure:
$$ \sigma ^\mathrm{w}_M(u) = {\left\{ \begin{array}{ll} \min \left\{ {\Vert \mathcal {C}\Vert }_{\varGamma } \mid \mathcal {C} \text{ an } \text{ accepting } \text{ computation } \text{ on } u\right\} , &{} \text{ if } u\in L(M),\\ 0, &{} \text{ otherwise. } \end{array}\right. } $$ -
accept measure:
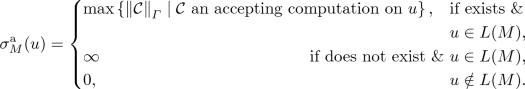
-
strong measure:
$$ \sigma ^\mathrm{s}_M(u) = {\left\{ \begin{array}{ll} \max \left\{ {\Vert \mathcal {C}\Vert }_{\varGamma } \mid \mathcal {C} \text{ is } \text{ a } \text{ partial } \text{ computation } \text{ on } u\right\} &{} \text{ if } \text{ it } \text{ exists },\\ \infty &{} \text{ otherwise. } \end{array}\right. } $$
Next, we are interested in studying stack sizes as a function of the length of the input. Thus, for each \(z \in \{\mathrm{w},\mathrm{a},\mathrm{s}\}\), we define the functions,
The latter essentially forces the space complexity to be a non-decreasing function. We leave off M if it is clear based on the context.
Using this notation, we can now write \(\sigma ^z(n) \in O(f(n))\), o(f(n)), \(\varOmega (f(n))\), etc., for some function f(n) from \(\mathbb {N}_0\) to \(\mathbb {N}_0\), in the usual fashion.
Note that, if there is any single word u with \(\sigma ^z(u) =\infty \), with \(z \in \{\mathrm{a}, \mathrm{s}\}\) (this occurs if there are infinitely many accepting computations of the word u of arbitrarily large stack sizes), then \(\sigma ^z(n) = \infty \) for \(n = |u|\), and \(\sigma ^z(n)\) cannot be in O(f(n)) for any integer function f. If there is such a word u, then we say that M is z-unlimited, and z-limited otherwise.
Example 2
Consider the language
This contains for example \(a^3 b^6\) because 3 divides 9. It contains \(ab^4\) because 1 divides 5, but there are no other words accepted of length 5 since 5 is prime.
An obvious \(\textsf {CSA}\) M accepting L copies \(a^m\) to the stack, then verifies that m divides k by going back and forth on the checking stack while reading from the input and checking that both the stack and input reach the ends of their tape at the same time.
Here are some properties of M:
-
1.
\(\sigma ^\mathrm{s}(n), \sigma ^\mathrm{a}(n), \sigma ^\mathrm{w}(n)\) are all O(n).
-
2.
For every even n, \(\sigma ^\mathrm{a}(a^{n/2}b^{n/2}) = n/2\), and thus \(\sigma ^\mathrm{a}(n) \ge n/2\). Therefore, \(\sigma ^\mathrm{a}(n)\) is not o(n).
-
3.
Also \(\acute{\sigma }^\mathrm{a}(n)\) is \(\varOmega (f(n))\) since \(\acute{\sigma }^\mathrm{a}(n)\) is non-decreasing.
-
4.
For every prime number n, \(\sigma ^\mathrm{a}(n) = 1\). Thus, \(\sigma ^\mathrm{a}(n)\) is not \(\varOmega (n)\). Further, \(\sigma ^\mathrm{a}(n)\) is not \(\varOmega (f(n))\) for any f(n) in \(\omega (1)\) (i.e. f(n) is \(\omega (1)\) if for any positive constant c, there exists a constant k such that \(0 \le c < f(n)\) for all \(n \ge k\)). So, if we use the function \(\sigma ^\mathrm{a}\) instead of the non-decreasing function \(\acute{\sigma }^\mathrm{a}\), then it is no longer at least linear.
4 Space Complexities of Stack Automata
In [8] it was shown that for every stack automaton M, there exists another stack automaton \(M'\) such that \(L(M) = L(M')\) and \(\sigma ^\mathrm{w}_{M'}(n)\) is O(n). Here we show the stronger statement that for any checking checking stack automaton M, \(\sigma ^\mathrm{w}_M(n)\) is in O(n) (i.e. it is true for M without converting to \(M'\)). Furthermore, it is also true for the accept (and strong) measures as well as long as they are \(\mathrm{a}\)-limited (\(\mathrm{s}\)-limited).
The basic idea of the proof for the weak measure is the following: consider some accepting computation \(\mathcal {C}\) on some string \(u \in L(M)\). Consider the stack at the end of this computation. We shall look for maximal sections of the write phase whereby, from the start of pushing this section until the end of pushing this section, only \(\lambda \)-transitions are applied; and then in later read phases, this section of the stack is also only read on \(\lambda \)-transitions. Therefore, the behavior of the automaton in this section of the stack does not depend on the input string. We shall show that if this section of the stack is too large (larger than some constant \(z'\)), then we can find some smaller word that we can replace it with, without altering this behavior. This means that for every accepted string u, we can find an accepting computation in which each of these sections is at most \(z'\) letters long. Since each of these sections of the stack are surrounded by cells of the stack in which the automaton reads some input symbol, there can be at most \((|u|+2) z'\) letters on the stack in this new computation. A similar argument can be used for the accept and strong measures.
Proposition 3
Let M be a CSA. The following are true:
-
\(\sigma ^\mathrm{w}_M(n)\) is in O(n);
-
if \(\sigma ^\mathrm{a}_M(n)\) is \(\mathrm{a}\)-limited, then \(\sigma ^\mathrm{a}(n)\) is O(n);
-
if \(\sigma ^\mathrm{s}_M(n)\) is \(\mathrm{s}\)-limited, then \(\sigma ^\mathrm{s}(n)\) is O(n).
Whether or not the result above holds for \(\textsf {NESA}\) and \(\textsf {SA}\) generally is an open problem.
Notice that in the proposition above, it is not true that every \(\textsf {CSA}\) machine M has \(\sigma ^\mathrm{a}(n)\) in O(n), because of the following more general fact:
Remark 4
Consider a \(\textsf {CSA}\) machine M accepting \(\varSigma ^*\) that nondeterministically pushes any string onto the stack using \(\lambda \)-transitions, and then reads any input and accepts. Here, M is not \(\mathrm{a}\)-limited or \(\mathrm{s}\)-limited and \(\sigma ^\mathrm{a}(n)\) is not O(f(n)) for any function f.
Lower bounds on the space complexity functions can also be studied similarly to upper bounds. The next proof starts with an accepting computation using some stack word, and then finds a new accepting computation on some possibly different input word that is roughly linear in the size of the stack. It then uses the regularity of the store languages of stack automata in order to determine that for every increase in some constant c, there’s at least one more input word of that length that has a stack that is linear in the size of the input. That is enough to show that the accept and strong space complexities cannot be o(n), and if the non-decreasing function \(\acute{\sigma }^z\) is used, then it is at least linear.
Lemma 5
Let \(z \in \{\mathrm{a}, \mathrm{s}\}\). Let M be a CSA such that \(\sigma ^z(n) \notin O(1)\) and M is z-limited. The following are true:
-
there exist c, d, e such that, for every \(n \in \mathbb {N}_0\), there is some input \(u \in \varSigma ^*\) (with \(u \in L(M)\) if \(z = \mathrm{a}\)) where \(n \le |u| \le n+c\) and \(d |u| \le \sigma ^z(u) \le e |u|\),
-
\(\sigma ^z(n)\) cannot be o(n),
-
\(\acute{\sigma }^z(n) \in \varOmega (n)\).
Lemma 5 is the “best possible result” in that it is not always the case that \(\sigma ^\mathrm{a}(n) \in \varOmega (n)\) since the space complexity can periodically go below linear infinitely often as demonstrated with Example 2. But what this lemma says is that it returns to at least linear infinitely often as well. Furthermore, there is a constant c such that it must return to at least linear for every increase of c in the length of the input. Putting together all results for \(\textsf {CSA}\) so far, we get the following complete characterization:
Theorem 6
Let M be a CSA. For \(z \in \{\mathrm{a}, \mathrm{s}\}\), exactly one of the following must occur.
-
1.
M is z-unlimited, and so there is no f such that \(\sigma ^z(n) \in O(f(n))\) (and L(M) can be either regular or not);
-
2.
M is z-limited, \(\sigma ^z(n) \in O(1)\), and L(M) is regular;
-
3.
M is z-limited, \(\sigma ^z(n) \in O(n), \sigma ^z\notin o(n)\), and \(\acute{\sigma }^z(n) \in \varTheta (n)\) (and L(M) can be either regular or not).
Proof
Consider the case \(z = \mathrm{a}\). Either M is \(\mathrm{a}\)-limited, or not. If it is not, then L(M) can be either regular or not. Moreover, both are possible, as one can take an arbitrary \(\textsf {CSA}\) \(M'\) (which can either be regular or not), and modify it to \(M''\) by starting by pushing an arbitrary word over a new stack letter x on \(\lambda \)-transitions, then simulating \(M'\). Thus, \(L(M') = L(M'')\), and \(M''\) is \(\mathrm{a}\)-unlimited.
Assume that M is \(\mathrm{a}\)-limited. And, assume that \(\sigma ^\mathrm{a}(n)\) is O(1). Then only a bounded amount of the stack is used, and M can therefore be simulated by an \(\textsf {NFA}\), and hence L(M) is regular.
Assume \(\sigma ^\mathrm{a}(n)\) is not O(1). Then Lemma 5 applies, and the statement follows. Also, it is possible for it to be non-regular (Example 2), or regular (by taking a \(\textsf {DFA}\) and simulating it with a \(\textsf {CSA}\) that copies the input to the stack while simulating the \(\textsf {DFA}\)). \(\square \)
The question arises next of whether the lower bound is also true for \(\textsf {NESA}\) and \(\textsf {SA}\). We see that this is not true.
Proposition 7
There exists a NESA (and a SA) M that accepts a non-regular language such that \(\sigma ^\mathrm{a}(n)\) and \(\sigma ^\mathrm{w}(n)\) are in \(\varTheta (\sqrt{n})\), and \(\sigma ^\mathrm{s}(n) \in O(\sqrt{n})\).
Proof
Consider the language \(L = \{a^{1} b a^{2} b \cdots a^{r}b \mid r \ge 1 \}\), and let \(L_0 = \text {pref}(L)\), which is not regular. Then \(L_0\) can be accepted as follows. Consider the input \(a^{l_1} b a^{l_2} b \cdots a^{l_r}b a^l, r,l \ge 0\). M starts by reading and pushing a, then it repeats the following: It reads b and pushes one a on the stack, moves to the left end of the stack and matches the a’s on the stack to the next block of a’s of the input. These steps are repeated until the end of the last section, that can be (the only one) shorter than the word stored in the stack.
On an input of size n, there is one word accepted of this length and the stack \(\gamma \) satisfies \(1/2 \sqrt{n} \le |\gamma | \le \sqrt{n}\). Thus, \(\sigma ^\mathrm{a}(n)\) and \(\sigma ^\mathrm{w}(n)\) are in \(\varTheta (\sqrt{n})\). For the strong measure, the stack is at most \(\sqrt{n}\) in size. \(\square \)
It is possible to observe that there exists a \(\textsf {NESA}\) M that accepts a regular language such that \(\sigma ^\mathrm{a}(n) \in \varTheta (\sqrt{n})\) and \(\sigma ^\mathrm{s}(n) \in O(\sqrt{n})\). Let us consider \(L_0 \cup \{a,b\}^* = \{a,b\}^*\). A machine \(M'\) can be built that either simulates M described in the proof of Proposition 7, or it reads the input and accepts without using the stack. Thus, \(\sigma ^\mathrm{a}_M(n) = \sigma ^\mathrm{a}_{M'}(n)\) and \(\sigma ^\mathrm{s}_M(n) = \sigma ^\mathrm{s}_{M'}(n)\).
In conclusion, \(\sqrt{n} \in o(n)\), and thus Lemma 5 cannot be generalized to \(\textsf {NESA}\) or \(\textsf {SA}\). Therefore, unlike \(\textsf {CSA}\), there is not a complete gap between \(\varTheta (1)\) and \(\varTheta (n)\), and the exact functions possible between them (besides \(\sqrt{n})\) remains open.
5 Space Complexities of Languages Accepted by Stack Automata
Just as the space complexity of stack machines can be studied, it is also possible to ask the question, given a language \(L \in \mathcal{L}(\textsf {CSA})\), what are the space complexities of the machines in \(\textsf {CSA}\) accepting L? (and similarly for \(\textsf {NESA}, \textsf {SA}\)). It follows from Proposition 3 that for every \(L \in \mathcal{L}(\textsf {CSA})\), there exists a machine \(M \in \textsf {CSA}\) such that \(\sigma ^\mathrm{w}(n)\) is O(n). A similar result is also known to be true for \(\textsf {SA}\) generally [8, 12].
For the strong measure, we will see that there are languages where all the machines that accept them are more complicated.
Example 8
Consider the language
Certainly, there is an \(M \in \textsf {CSA}\) that accepts L as follows: on input \(u' \$ u'' \# v' \$ v''\), M guesses two words u and v in advance on \(\lambda \)-transitions, and pushes \(u \# v\) on the stack; then M verifies that \(u = u' = u''\), and \(v = v' = v''\).
For the accept measure, \(\sigma ^\mathrm{a}_M(n) \in O(n)\), as all computations that accept have a stack that is linear in the input. However, for the strong measure, because the machine M starts by guessing and pushing both u and v on \(\lambda \)-transitions, M could guess u and v that are substantially longer (arbitrarily longer) than \(u'\) and \(v'\). This machine M is therefore \(\mathrm{s}\)-unlimited.
The question arises as to whether every machine that accepts \(L_\mathrm{copy}\) is \(\mathrm{s}\)-unlimited. We will see that this is indeed the case. To show this, we first prove the following lemma, which again uses store languages
Lemma 9
Let \(M=(Q,\varSigma ,\varGamma ,\delta ,q_0,F)\) be a CSA with partitioned states \(Q_w\) and \(Q_r\). The language

composed of all the input words scanned by M during the (complete) write phase of each accepting computation, is a regular language.
This is useful towards the following proposition.
Proposition 10
For the language \(L_\mathrm{copy} \in \mathcal{L}(\textsf {CSA})\) from Example 8, for all M accepting \(L_\mathrm{copy}\), M is \(\mathrm{s}\)-unlimited. Thus, for each such M accepting \(L_\mathrm{copy}\), there is no function f such that \(\sigma ^\mathrm{s}_M(n)\) is O(f(n)).
Proof
We show that for every \(\textsf {CSA}\) M accepting \(L_\mathrm{copy}\), M can perform an arbitrarily long sequence of \(\lambda \)-transitions that write (either push or stay) where the size of the stack can grow arbitrarily without reading input letters. If there is some sequence of \(\lambda \)-transitions that writes (that can be reached from the initial configuration) that is bigger than the number of states of the machine multiplied by the stack alphabet, then M has a cycle in which only write \(\lambda \)-transitions occur. Then as long as this cycle has at least one push transition in it, the stack can grow arbitrarily. Hence, there exist infinitely many (possibly rejecting) computations during which arbitrarily many letters are pushed on the stack making the machine \(\mathrm{s}\)-unlimited.
Let \(M = (Q, \varSigma , \varGamma ,\delta , q_0, F)\) be an arbitrary \(\textsf {CSA}\) accepting \(L_\mathrm{copy}\). Assume, by contradiction, that \(L_\mathrm{copy}\) is \(\mathrm{s}\)-limited. Consider the language \(L_{w,M}\) from Lemma 9, which is a regular language. Furthermore, let \(W = \text {pref}(L_{w,M})\cap \{a,b\}^*\$\{a,b\}^*\sharp \), which must also be regular. Assume that W is infinite. Thus, there exist infinitely many words in W that have an accepting computation that does not enter the read phase until after \(\#\). But as W is regular, and only contains words of the form \(u\$ u \#\), there must be some infinite subset of \(\{u \$ u \# \mid u \in \{a,b\}^*\}\) that is regular, a contradiction, by the pumping lemma. Thus, W must be finite.
Let u be some word such that \(u\$u\# \notin W\). Thus, for all accepting computations on any word in \(L_\mathrm{copy} = \{u\$ u \sharp v' \$ v'' \mid v', v'' \in \{a,b\}^*\}\), it must enter the read phase before reaching the \(\#\) symbol. Also, there must exist a constant c such that for all of these accepting computations, the stack must grow to at most \(c|u |\), otherwise M could enter an infinite cycle on \(\lambda \)-transitions that push in the write phase, and it would be \(\mathrm{s}\)-unlimited. Consider some word \(u\$u \# v \$ v \in L_\mathrm{copy}\) where \(|v| > |Q| \cdot c \cdot |u|\), and consider some accepting computation (where it must enter the read phase before hitting \(\#\)). When scanning the second v, there must be two configurations reached where M reaches the same state and stack position, and at least one letter of \(\varSigma \) was read between them. Hence, \(u\$u\# v \$ v'\) is also accepted, \(v \ne v'\), a contradiction. Hence, M is \(\mathrm{s}\)-unlimited. \(\square \)
For the accept measure, the situation is more complicated, and it is left open. However, we have the following conjecture. Consider the language
This language can be accepted by a \(\textsf {CSA}\) machine that, for every 1 read, pushes a nondeterministically guessed word over \(\{0,1\}^*\) on the stack so that its contents is \(u_1\# \cdots \# u_k\). Then, for each \(v_i\) on the input, it guesses some \(u_j\) on the stack and verifies that they are equal. However, this machine does not keep track of whether each \(u_j\) on the stack was matched to some \(v_i\) (and it seems to have no way of keeping track of this), and \(u_j\) could be arbitrarily long. We conjecture that every \(M \in \textsf {CSA}\) accepting L is \(\mathrm{a}\)-unlimited. In fact, we conjecture that this is true for every \(M \in \textsf {SA}\).
6 Decidability Properties Regarding Space Complexity of Stack Machines
It is an easy observation that when the space used by a checking stack automaton is constant, the device is no more powerful than a finite automaton. Nevertheless, given a checking stack automaton M, it is not possible to decide whether or not it accepts by using a constant amount of space with the weak measure. This result can be derived by adapting the argument used in [14] for proving that, when the weak measure is considered, it is not decidable whether or not a nondeterministic pushdown automaton accepts by using a constant amount of pushdown store. In that case, the authors used a technique introduced in [6], based on suitable encodings of single-tape Turing machine computations and reducing the proof of the decidability to the halting problem; this can be done here as well.
Proposition 11
It is undecidable whether a CSA M accepts in space \(\sigma ^\mathrm{w}(n)\in O(1)\) or not.
On the other hand, although it may seem counterintuitive, the same problem is decidable for the accept and strong measures, even for stack automata.
Proposition 12
For \(z \in \{ \mathrm{a}, \mathrm{s} \}\), it is decidable whether an SA M satisfies \(\sigma ^z(M) \in O(1)\) or not.
Proof
For the accept measure, first, we construct a finite automaton \(M'\) accepting the store language of M. We can then decide finiteness of \(L(M')\) since it is regular, which is finite if and only if M operates in constant space.
For the strong measure, we can take M, and change it so that all states are final, then calculate the store language, and decide finiteness. \(\square \)
7 Conclusions and Future Directions
In this paper, we defined and studied the weak, accept, and strong space complexity measures for variants of stack automata. For checking stack automata with the accept or strong measures, there is “gap”, and no function is possible between constant and linear, or above linear. For non-erasing stack automata, there are machines with complexity between constant and linear. Then, it is shown that for the strong measure, there is a checking stack language such that every machine accepting it is \(\mathrm{s}\)-unlimited (there is no function bounding the strong space complexity). Lastly, it is shown that it is undecidable whether a checking stack automaton has constant space complexity with the weak measure. But, this is decidable for both the accept and strong measures even for stack automata.
Many open problems remain. It is desirable to know whether there are any gaps between constant and linear space for the weak space complexity measure for checking stacks. Also, it is open whether all stack automata have linear weak space complexity (it is known that every language has some machine that operates in linear space complexity). The exact accept and strong space complexity functions possible for non-erasing and stack automata (besides constant, square root, and linear) still need to be determined. It is also open whether there is some stack language (or non-erasing stack language) such that every machine accepting it is \(\mathrm{s}\)-unlimited. Furthermore, for the accept measure, we conjecture that there is a \(\textsf {CSA}\) language whereby every machine is \(\mathrm{a}\)-unlimited, although this is also an open problem. Answering these open questions would be of interest to the automata theory community.
Notes
- 1.
We point out that, especially in the context of Turing machines, the weak measure, corresponding to the minimal cost among all accepting computations on a given input, if any, is by far the most commonly used.
References
Alur, R., Madhusudan, P.: Visibly pushdown languages. In: Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing, pp. 202–211 (2004)
Bensch, S., Björklund, J., Kutrib, M.: Deterministic stack transducers. Int. J. Found. Comput. Sci. 28(05), 583–601 (2017)
Engelfriet, J.: The power of two-way deterministic checking stack automata. Inf. Comput. 80(2), 114–120 (1989)
Greibach, S.: Checking automata and one-way stack languages. J. Comput. Syst. Sci. 3(2), 196–217 (1969)
Harrison, M.A.: Introduction to Formal Language Theory. Addison-Wesley Series in Computer Science. Addison-Wesley Pub. Co., Boston (1978)
Hartmanis, J.: Context-free languages and Turing machine computations. In: Mathematical Aspects of Computer Science. Proceedings of Symposia in Applied Mathematics, vol. 19, pp. 42–51. American Mathematical Society (1967)
Hartmanis, J.: Turing award lecture: on computational complexity and the nature of computer science. ACM Comput. Surv. 27(1), 7–16 (1995). https://doi.org/10.1145/214037.214040
Hopcroft, J., Ullman, J.: Sets accepted by one-way stack automata are context sensitive. Inf. Control 13(2), 114–133 (1968)
Hopcroft, J., Ullman, J.: Introduction to Automata Theory, Languages, and Computation Reading. Addison-Wesley, Boston (1979)
Ibarra, O.H., McQuillan, I.: Generalizations of checking stack automata: characterizations and hierarchies. In: Hoshi, M., Seki, S. (eds.) DLT 2018. LNCS, vol. 11088, pp. 416–428. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98654-8_34
Ibarra, O.H., McQuillan, I.: On store languages of languages acceptors. Theor. Comput. Sci. 745, 114–132 (2018)
King, K., Wrathall, C.: Stack languages and \(\log n\) space. J. Comput. Syst. Sci. 17(3), 281–299 (1978)
Pighizzini, G.: Nondeterministic one-tape off-line Turing machines and their time complexity. J. Autom. Lang. Comb. 14, 107–124 (2009)
Pighizzini, G., Prigioniero, L.: Pushdown automata and constant height: decidability and bounds. In: Hospodár, M., Jirásková, G., Konstantinidis, S. (eds.) DCFS 2019. LNCS, vol. 11612, pp. 260–271. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-23247-4_20
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Ibarra, O.H., Jirásek, J., McQuillan, I., Prigioniero, L. (2020). Space Complexity of Stack Automata Models. In: Jonoska, N., Savchuk, D. (eds) Developments in Language Theory. DLT 2020. Lecture Notes in Computer Science(), vol 12086. Springer, Cham. https://doi.org/10.1007/978-3-030-48516-0_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-48516-0_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-48515-3
Online ISBN: 978-3-030-48516-0
eBook Packages: Computer ScienceComputer Science (R0)





 . We use the notation
. We use the notation  ; then for
; then for  if
if 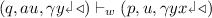 if
if 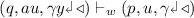 if
if  , and
, and  if
if  if
if  if
if  ; and
; and