Keywords

1 Introduction

Accurate and fast estimation of the subsurface parameters is of vital importance in the oil and gas industry. A potential candidate to handle this task is a frequency-domain full waveform inversion (FWI) (see e.g. [6]) that has been actively developing in the last decades. Due to advances in supercomputing technology, even 3D elastic inversion, that may bring the most valuable information about the subsurface, seems to be feasible. The most time consuming part of this process is the forward modeling performed several times at each iteration. The efficiency of this process is strongly dependent on how optimally the process is parallelized.

In this effort, we consider a frequency-domain elastic iterative solver proposed in [3]. It is based on a Krylov-type iteration method [5] with a special preconditioner. This method demonstrates a fast convergence at low frequencies, needed for FWI applications. In this paper, we explain an approach to parallelize it using a hybrid parallelization: MPI and OpenMP. Its quality is justified by weak and strong scaling analysis. We also illustrate, that this parallel method allows simulation in big models, including a modified 2.5D Marmousi model comprising 90 million cells, for a feasible time.

2 A Preconditioned 3D Elastic Equation

Consider an elastic equation written in the velocity-stress form, describing propagation of a monochromatic component of a wave in a 3D isotropic heterogeneous medium

$$ \left[ {i\omega \left( {\begin{array}{*{20}c} {\rho \varvec{I}_{{{\mathbf{3}} \times {\mathbf{3}}}} } & 0 \\ 0 & {\varvec{S}_{{{\mathbf{6}} \times {\mathbf{6}}}} } \\ \end{array} } \right) - \left( {\begin{array}{*{20}c} 0 & {\hat{P}} \\ {\hat{P}^{T} } & 0 \\ \end{array} } \right)\frac{\partial }{\partial x} - \left( {\begin{array}{*{20}c} 0 & {\hat{Q}} \\ {\hat{Q}^{T} } & 0 \\ \end{array} } \right)\frac{\partial }{\partial y} - \gamma \left( z \right)\left( {\begin{array}{*{20}c} 0 & {\hat{R}} \\ {\hat{R}^{T} } & 0 \\ \end{array} } \right)\frac{\partial }{\partial z}} \right]\varvec{v} = \varvec{f}, $$
(1)

where vector of unknowns \( \varvec{v} \) comprises nine components. These components include the displacement velocities and components of the stress tensor. \( \omega \) is the real time frequency, \( \rho \left( {x,y,z} \right) \) is the density, \( \varvec{I}_{{{\mathbf{3}} \times {\mathbf{3}}}} \) is 3 by 3 identity matrix, \( \hat{P} \), \( \hat{Q} \) and \( \hat{R} \) are constant matrices, \( \varvec{S}_{{{\mathbf{6}} \times {\mathbf{6}}}} \left( {x,y,z} \right) = \left( {\begin{array}{*{20}c} A & 0 \\ 0 & C \\ \end{array} } \right) \) is 6 by 6 compliance matrix, and

$$ A = \left( {\begin{array}{*{20}c} a & { - b} & { - b} \\ { - b} & a & { - b} \\ { - b} & { - b} & a \\ \end{array} } \right), C = \left( {\begin{array}{*{20}c} c & 0 & 0 \\ 0 & c & 0 \\ 0 & 0 & c \\ \end{array} } \right) . $$
(2)

Coefficients \( a\left( {x,y,z} \right) \), \( b\left( {x,y,z} \right) \) and \( c\left( {x,y,z} \right) \) are related to the Lame parameters. \( \varvec{f} \) is the right-hand side representing the seismic source. \( \gamma \left( z \right) \) is an attenuation function. Equation (1) is solved in a cuboid domain of \( N_{x} \times N_{y} \times N_{z} \) points with free surface top boundary and attenuation layers on the other boundaries.

Introducing preconditioner \( L_{0} \) (for details refer to [3]), we arrive at equation

$$ \left( {I - \delta LL_{0}^{ - 1} } \right)\tilde{\varvec{v}} = \varvec{f}, \,{\text{with}}\,\varvec{v} = L_{0}^{ - 1} \tilde{\varvec{v}},\,\delta L = L - L_{0} , $$
(3)

We solve Eq. (3) via the biconjugate gradient stabilized method (BiCGSTAB) [7]. This assumes computing several times per iteration the product of the left-hand side operator of Eq. (3) by a particular vector \( \varvec{w} \), i.e. computing \( \left[ {\varvec{w} - \delta LL_{0}^{ - 1} \varvec{w}} \right] \). Computations of \( L_{0}^{ - 1} w \) takes the most of runtime. To solve \( L_{0} q_{1} = \varvec{w} \) we assume that function \( \varvec{w}\left( {x,y,z} \right) \) is expanded into a Fourier series with respect to \( x \) and \( y \) with coefficients \( \hat{\varvec{w}}\left( {k_{x} ,k_{y} ,z} \right) \), where \( k_{x} \) and \( k_{y} \) - spatial frequencies. \( \hat{\varvec{w}} \) are solutions to equation

$$ \left[ {i\omega \left( {\begin{array}{*{20}c} {\rho_{0} \varvec{I}_{3 \times 3} } & 0 \\ 0 & {\varvec{S}_{0} } \\ \end{array} } \right) - ik_{x} \left( {\begin{array}{*{20}c} 0 & {\hat{P}} \\ {\hat{P}^{T} } & 0 \\ \end{array} } \right) - ik_{y} \left( {\begin{array}{*{20}c} 0 & {\hat{Q}} \\ {\hat{Q}^{T} } & 0 \\ \end{array} } \right) - \gamma \left( z \right)\left( {\begin{array}{*{20}c} 0 & {\hat{R}} \\ {\hat{R}^{T} } & 0 \\ \end{array} } \right)\frac{\partial }{\partial z}} \right]\hat{\varvec{v}} = \hat{\varvec{w}}, $$
(4)

with the same boundary conditions as for Eq. (1). Here \( \rho_{0} \) and \( S_{0} \) are some averaging of \( \rho \) and \( S \). We solve it numerically, applying a finite-difference approximation, resulting in a system of linear algebraic equations with a banded matrix. Computation of \( \hat{\varvec{w}} \) we perform via the 2D Fast Fourier Transform (FFT) and after \( \hat{\varvec{v}} \) are found, \( L_{0}^{ - 1} \varvec{w} \) is computed via the inverse 2D FFT.

3 Parallelization

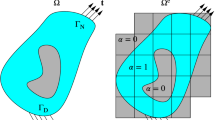
Four computational processes including BiCGSTAB, the 2D FFTs and solving (4), mainly drive the solver. We decompose the computational domain along one of the horizontal coordinates and parallelize these processes via MPI: using parallel BiCGSTAB function from PETSc [2], 2D FFT from Intel Math Kernel Library [4], and each MPI process, corresponding to a certain subdomain, solves boundary value problems (4) for its own set of spatial frequencies \( k_{x} \) and \( k_{y} \), independently of other MPI processes. The main exchanges between the MPI processes are while performing FFTs.

Following this strategy, each MPI process would independently solve its own set of \( N_{x} \cdot N_{y} /N \) (\( N \) – number of MPI processes) problems. We solve them in a loop, parallelized via OpenMP. Schematically, our parallelization strategy is presented in Fig. 1.

Fig. 1.
figure 1

Parallelization scheme.

Full size image

To investigate the properties of this parallelization we construct a 2.5D land model (left image of Fig. 2) from the open source 2D Marmousi model. It is discretized with a uniform grid of \( 551 \times 700 \times 235 \) points. In the right image of Fig. 2 we illustrate the 10 Hz monochromatic component of the computed wavefield for this model. Using 9 nodes with 7 MPI processes per node and 4 cores per process, the total computation time is 348 min.

Fig. 2.
figure 2

Left - 2.5D P-velocity model; right - 3D view of a computed wavefield.

Full size image

MPI strong scalability of the solver is defined as ratio \( t_{M} /t_{N} \), where \( t_{M} \) and \( t_{N} \) are elapsed run times to solve the problem with \( N \) and \( M > N \) MPI processes each corresponding to a different CPU. Using MPI, we parallelize two types of processes. First, those scaling ideally (solving problems (4)), for which the computational time with \( N \) processes is \( \frac{T}{N} \). Second, the FFT, that scales as \( \frac{{T_{FFT} }}{\alpha \left( N \right)} \), with coefficient \( 1 < \alpha \left( N \right) < N \). The total computational time becomes \( \frac{T}{N} + \frac{{T_{FFT} }}{\alpha \left( N \right)} \) (here we simplify, assuming no need of synchronization) with scaling coefficient \( \frac{{T + T_{FFT} }}{{\frac{T}{N} + \frac{{T_{FFT} }}{\alpha \left( N \right)}}} \), that is greater than \( \alpha \left( N \right) \). This is why, we expect very good scalability of the algorithm, somewhere between the scalability of the FFT and the ideal scalability. We did not take into account OpenMP, which can be switched on for extra speed-up. It is worth noting, that we can not use MPI instead of OpenMp here, since then the scaling would degrade. MPI may have worked well if \( T \gg T_{FFT} \), but this is not the case.

We estimate the strong scaling for modeling in two different models, both of \( 200 \times 600 \times 155 \) points: a subset of depicted in Fig. 2 and the overthrust model [1]. From the left image of Fig. 3 we conclude that our solver scales very well up to 64 MPI processes.

Fig. 3.
figure 3

Left - strong MPI scaling of the solver: blue dashed line - for the Marmousi model, red line - for the overthrust model, the dashed grey line - ideal scalability; right - weak MPI scaling measurements: the blue line - the solver and the dashed grey - ideal weak scaling. (Color figure online)

Full size image

For weak scaling estimation, we assign the computational domain to one MPI process and then extend the size of the computational domain along the y-direction, while increasing the number of MPI processes. Here, we use one MPI process per CPU. The load per CPU is fixed. For the weak scaling, we use function \( f_{weak} \left( N \right) = \frac{T\left( N \right)}{T\left( 1 \right)}, \) where \( T\left( N \right) \) is the average computational runtime per iteration with \( N \) MPI processes. The ideal weak scalability corresponds to \( f_{weak} \left( N \right) = 1 \).

To estimate it in our case, we considered a part of the model presented in Fig. 2 of size \( 200 \times 25 \times 200 \) points with a decreased 4 m step along the y-coordinate. After extending the model in the y-direction 64 times, we arrive at a model of size \( 200 \times 1600 \times 150 \) points. The right image of Fig. 3 demonstrates that for up to 64 MPI processes, weak scaling of our solver has small variations around the ideal weak scaling.

With OpenMP we parallelize the loop over spatial frequencies for solving (4). To estimate the scalability of this part of our solver, we performed simulations in a small part of the overthrust model comprising \( 660 \times 50 \times 155 \) points on a single CPU having 14 cores with hyper-threading switched off and without using MPI. Figure 4 shows that our solver scales well for all threads involved in this example. It is worth mentioning, that we use OpenMP as an extra option applied when further increasing of the number of MPI processes doesn’t improve performance any more, but the computational system is not fully loaded, i.e., there are free cores.

Fig. 4.
figure 4

Strong scalability on one CPU: blue line - ideal and red line is the solver scalability. (Color figure online)

Full size image

4 Conclusions

Further improvement of the MPI scaling may be achieved by incorporating a domain decomposition along two horizontal directions into the current MPI parallelization scheme. Moreover, the parallelization using domain decomposition along the vertical direction for solving boundary value problems 4 may be applied for accelerating the computational runtime.