Abstract
Atomistic simulations of large biomolecular systems with chemical variability such as constant pH dynamic protonation offer multiple challenges in high performance computing. One of them is the correct treatment of the involved electrostatics in an efficient and highly scalable way. Here we review and assess two of the main building blocks that will permit such simulations: (1) An electrostatics library based on the Fast Multipole Method (FMM) that treats local alternative charge distributions with minimal overhead, and (2) A λ-dynamics module working in tandem with the FMM that enables various types of chemical transitions during the simulation. Our λ-dynamics and FMM implementations do not rely on third-party libraries but are exclusively using C++ language features and they are tailored to the specific requirements of molecular dynamics simulation suites such as GROMACS. The FMM library supports fractional tree depths and allows for rigorous error control and automatic performance optimization at runtime. Near-optimal performance is achieved on various SIMD architectures and on GPUs using CUDA. For exascale systems, we expect our approach to outperform current implementations based on Particle Mesh Ewald (PME) electrostatics, because FMM avoids the communication bottlenecks caused by the parallel fast Fourier transformations needed for PME.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The majority of cellular function is carried out by biological nanomachines made of proteins. Ranging from transporters to enzymes, from motor to signalling proteins, conformational transitions are frequently at the core of protein function, which renders the detailed understanding of the involved dynamics indispensable. Experimentally, atomistic dynamics on submillisecond timescales are notoriously difficult to access, making computer simulations the method of choice. Molecular dynamics (MD) simulations of biomolecular systems are nowadays routinely used to study the mechanisms underlying biological function in atomic detail. Examples reach from membrane channels [28], microtubules [20], and whole ribosomes [4] to subcellular organelles [43]. Recently, the first MD simulation of an entire gene was reported, comprising about a billion of atoms [21].
Apart from system size, the scope of such simulations is limited by model accuracy and simulation length. Particularly the accurate treatment of electrostatic interactions is essential to properly describe a biomolecule’s functional motions. However, these interactions are numerically challenging for two reasons.
First, their long-range character (the potential drops off slowly with 1/r with distance r) renders traditional cut-off schemes prone to artifacts, such that grid-based Ewald summation methods were introduced to provide an accurate solution in 3D periodic boundaries. The current standard is the Particle Mesh Ewald (PME) method that makes use of fast Fourier transforms (FFTs) and scales as N ⋅log N with the number of charges N [11]. However, when parallelizing PME over many compute nodes, the algorithm’s communication requirements become more limiting than the scaling with respect to N. Because of the involved FFTs, parallel PME requires multiple all-to-all communication steps per time step, in which the number of messages sent between p processes scales with p 2 [29]. For the PME algorithm included in the highly efficient, open source MD package GROMACS [42], much effort has been made to reduce as much as possible the all-to-all bottleneck, e.g. by partitioning the parallel computer in long-range and short-range processors, which reduces the number of messages involved in all-to-all communication [17]. Despite these efforts, however, even for multimillion atom MD systems on modern hardware, performance levels off beyond several thousand cores due to the inherent parallelization limitations of PME [30, 42, 45].
The second challenge is the tight and non-local coupling between the electrostatic potential and the location of charges on the protein, in particular titratable/protonatable groups that adapt their total charge and potentially also their charge distribution to their current electrostatic environment. Hence, all protonation states are closely coupled, depend on pH, and therefore the protonation/deprotonation dynamics needs to be taken into account during the simulation. Whereas most MD simulations employ fixed protonation states for each titratable group, several dynamical schemes have been introduced [8, 13, 14, 23, 33, 37] that use a protonation coordinate λ to distinguish the protonated from the deprotonated state. Here, we follow and expand the λ-dynamics approach of Brooks et al. [27] and treat λ as an additional degree of freedom in the Hamiltonian with mass m λ. Each protonatable group is associated with its own λ “particle” that adopts continuous values in the interval [0, 1], where the end points around λ = 0 and λ = 1 correspond to the physical protonated or deprotonated states. A barrier potential with its maximum at λ ≈ 0.5 serves two purposes. (1) It reduces the time spent in unphysical states, and (2) it allows to tune for optimal sampling of the λ coordinate by adjusting its height [8, 9]. Current λ-dynamics simulations with GROMACS are however limited to small system sizes with a small number n λ of protonatable groups [7,8,9], as the existing, PME-based implementation (see www.mpibpc.mpg.de/grubmueller/constpH) needs an extra PME mesh evaluation per λ group and suffers from the PME parallelization problem. While these extra PME evaluations can be overcome for the case where only the charges differ between the states, for the most general case of chemical alterations this is not possible.
Without the PME parallelization limitations, a significantly higher number of compute nodes could be utilized, so that both larger and more realistic biomolecular systems would become accessible. The Fast Multipole Method [15] (FMM) is a method that by construction parallelizes much better than PME. Beyond that, the FMM can compute and communicate the additional multipole expansions that are required for the local charge alternatives of λ groups with far less overhead as compared to the PME case. This makes the communicated volume (extra multipole components) somewhat larger, but no global communication steps are involved as in PME, where the global communication volume grows linearly with n λ and quadratic with p. We also considered other methods that, like FMM, scale linearly with the number of charges, as e.g. multigrid methods. We decided in favor of FMM, because it showed better energy conservation and higher performance in a comparison study [2].
We will now introduce λ-dynamics methods and related work to motivate the special requirements they have on the electrostatics solver. Then follows an overview of our FMM-based solver and the design decisions reflecting the specific needs of MD simulation. We will describe several of the algorithmical and hardware-exploiting features of the implementation such as error control, automatic performance tuning, the lightweight tasking engine, and the CUDA-based GPU implementation.
2 Chemical Variability and Protonation Dynamics
Classical MD simulations employ a Hamiltonian \(\mathcal {H}\) that includes potential terms modeling the bonded interactions between pairs of atoms, the bond angle interactions between bonded atoms, and the van der Waals and Coulomb interactions between all pairs of atoms. For conventional, force field based MD simulations, the chemistry of molecules is fixed during a simulation because chemical changes are not described by established biomolecular force fields. Exceptions are alchemical transformations [36, 38, 46, 47], where the system is either driven from a state A described by Hamiltonian \(\mathcal {H}_{\text{A}}\) to a slightly different state B (with \(\mathcal {H}_{\text{B}}\)) via a λ parameter that increases linearly with time, or where A/B chimeric states are simulated at several fixed λ values between λ = 0 and λ = 1, as e.g. in thermodynamic integration [24]. The A → B transition is described by a combined, λ-dependent Hamiltonian
In these simulations, which usually aim at determining the free energy difference between the A and B states, the value of λ is an input parameter.
In contrast, with λ-dynamics [16, 25, 27], the λ parameter is treated as an additional degree of freedom with mass m, whose 1D coordinate λ and velocity \(\dot {\lambda }\) evolve dynamically during the simulation. Whereas in a normal MD simulation all protonation states are fixed, with λ-dynamics, the pH value is fixed instead and the protonation state of a titratable group changes back and forth during the simulation in response to its local electrostatic environment [23, 39]. If two states (or forms) A and B are involved in the chemical transition, the corresponding Hamiltonian expands to
with a bias potential V bias that is calibrated to reflect the (experimentally determined) free energy difference between the A and B states and that optionally controls other properties relating to the A \(\leftrightharpoons \) B transitions [8]. With the potential energy part V of the Hamiltonian, the force acting on the λ particle is
If coupled to the protonated and deprotonated form of an amino acid side chain, e.g., λ-dynamics enables dynamic protonation and deprotonation of this side chain in the simulation (see Fig. 1 for an example), accurately reacting to the electrostatic environment of the side chain. More generally, also alchemical transformations beyond protons are possible, as well as transformations involving more than just two forms A and B. Equation 2 shows the Hamiltonian for the simplest case of a single protonatable group with two forms A and B, but we have extended the framework to multiple protonatable groups using one λ i parameter for each chemical form [7,8,9].
Simplified sketch of a protein (right, grey) in solution (blue) with several protonatable sites (ball-and-stick representations) of which a histidine (top left) and a carboxyl group (bottom left) are highlighted. The histidine site contains four forms (two neutral, two charged), whereas the carboxyl group contains three forms (two neutral, one negatively charged). In λ-dynamics, the lambdas controls how much of each form is contributing to a site. Atom color coding: carbons-black, hydrogens/protons-white, oxygens-red, nitrogens-blue
2.1 Variants of λ-Dynamics and the Bias Potential
The key aim of λ-dynamics methods is to allow for dynamic protonation, but there are three areas in which the implementations differ from each other. These are the coordinate system used for λ, the type of the applied bias potential, and how λ is coupled to the alchemical transition. Before we discuss the different choices, let us define two terms used in the context of chemical variability and protonation. We use the term site for a part of a molecule that can interconvert between two or more chemically different states, e.g. the protonated and deprotonated forms of an aminoacid. Additionally, we call each of the chemically different states of a site a form. For instance, a protonatable group is a site with at least two forms A and B, a protonated form A and a deprotonated form B.
2.1.1 The Coordinate System for λ
Based on the coordinate system in which λ lives (or on the dynamical variables used to express λ), we consider three variants of λ-dynamics listed in Table 1. The linear variant is conceptually most straightforward, but it definitely needs a bias potential to constrain λ to the interval [0..1]. The circular coordinate system for λ used in the hypersphere variant automatically constrains the range of λ values to the desired interval, however one needs to properly correct for the associated circle entropy [8]. The Nexp variant implicitly fulfils the constraints on the N forms individual lambdas (Eq. 4) for sites that are allowed to transition between N forms different forms (N forms = 2 in the case of simple protonation), such that no additional constraint solver for the λ i is needed.
2.1.2 The Bias Potential
The bias potential V bias(λ) that acts on λ fulfils one or more of the following tasks.
-
1.
If needed, it limits the accessible values of λ to the interval [0..1], whereas slight fluctuations outside that interval may be desirable (Fig. 2a).
-
2.
It cancels out any unwanted barrier at intermediate λ values (b)
-
3.
It takes care that the resulting λ values cluster around 0 or 1, suppressing values between about 0.2 and 0.8 (c)
-
4.
It regulates the depth and width of the minima at 0 and 1, such that the resulting λ distribution fits the experimental free energy difference between protonated and deprotonated form (c + d).
-
5.
It allows to tune for optimal sampling of the λ space by adjusting the barrier height at λ = 0.5 (c)
Taken together, the various contributions to the barrier potential might look like the example given in Fig. 3 for a particular λ in a simulation.
2.1.3 How λ Controls the Transition Between States
The λ parameter can either be coupled to the transition itself between two forms (as in [8, 9]), then λ = 0 corresponds to form A and λ = 1 to form B. Alternatively, each form gets assigned its own λ α with α ∈{A, B} as weight parameter. In the latter case one needs extra constraints on the weights similar to
such that only one of the physical forms A or B is fully present at a time. For the examples mentioned so far, with just two forms, both approaches are equivalent and one would rather choose the first one, because it involves only one λ and needs no extra constraints.
If, however, a site can adopt more than two chemically different forms, the weight approach can become more convenient as it allows to treat sites with any number N forms of forms (using a number of N forms independent λ parameters). Further, it does not require that the number of forms is a power of two (\(N_{\text{forms}} = 2^{N_\lambda }\)) as in the transition approach.
2.2 Keeping the System Neutral with Buffer Sites
In periodic boundary conditions as typically used in MD simulations, the electrostatic energy is only defined for systems with a zero net charge. Therefore, if the charge of the MD system changes due to λ mediated (de)protonation events, system neutrality has to be preserved. With PME, any net charge can be artificially removed by setting the respective Fourier mode’s coefficient to zero, so that also in these cases a value for the electrostatic energy can be computed. However, it is merely the energy of a similar system with a neutralizing background charge added. Severe simulation artifacts have been reported as side effects of this approach [19].
As an alternative, a charge buffer can be used that balances the net charge of the simulation system arising from fluctuating charge of the protonatable sites [9, 48]. A reduced number of n buffer buffer sites, each with a fractional charge |q|≤ 1e (e.g. via \(\text{H}_2\text{O} \leftrightharpoons \text{H}_3\text{O}^+\)), was found to be sufficient to neutralize the N sites protonatable groups of a protein with n buffer ≪ N sites. The total charge of these buffer ions is coupled to the system’s net charge with a holonomic constraint [9]. The buffer sites should be placed sufficiently far from each other, such that their direct electrostatic interaction through the shielding solvent is negligible.
3 A Modern FMM Implementation in C++ Tailored to MD Simulation
High performance computing (HPC) biomolecular simulations differ from other scientific applications by their comparatively small particle numbers and by their extremely high iteration rates. With GROMACS, when approaching the scaling limit, the number of particles per CPU core typically lies in the order of a few hundred, whereas the wall-clock time required for computing one time step lies in the range of a millisecond or less [42]. In MD simulations with λ-dynamics, the additional challenge arises to calculate the energy and forces from a Hamiltonian similar to Eq. 2, but for N protonatable sites, in an efficient way. In addition to the Coulomb forces on the regular charged particles, the electrostatic solver has to compute the forces on the N λ particles as well [8] via
Accordingly, with λ-dynamics, for each of the λ i’s, the energies of the pure (i.e., λ i = 0 and λ i = 1) states have to be evaluated while keeping all other lambdas at their actual fractional values.
The aforementioned requirements of biomolecular electrostatics have driven several design decisions in our C++ FMM, which is a completely new C++ reimplementation of the Fortran ScaFaCoS FMM [5]. Although several other FMM implementations exist [1, 50], none of them is prepared to compute the potential terms needed for biomolecular simulations with λ-dynamics.
Although our FMM is tailored for usage with GROMACS, it can be used as an electrostatics solver for other applications as well as it comes as a separate library in a distinct Git repository. On the GROMACS side we provide the necessary modifications such that FMM instead of PME can be chosen at run time. Apart from that, GROMACS calls our FMM library via an interface that can also be used by other codes. The development of this library follows three principles. First, the building blocks (i.e., data structures) used in the FMM support each level of the hierarchical parallelism available on today’s hardware. Second, the library provides different implementations of the involved FMM operators depending on the underlying hardware. Third, the library optionally supports λ-dynamics via an additional interface.
3.1 The FMM in a Nutshell
The FMM approximates and thereby speeds up the computation of the Coulomb potential V C for a system of N charges:
For that purpose, the FMM divides the simulation box into eight smaller boxes (depth d = 1), which are subsequently subdivided into eight smaller boxes again (d = 2) and again (d = 3, 4, …). The depth d refers to the number of subdivisions. On the lowermost level, i.e. for the smallest boxes (largest d), all interactions between neighboring boxes are directly calculated (these are called the near-field interactions). Interactions with boxes further away are approximated by a multipole expansion of order p (these are called the far-field interactions). A comprehensive description of the FMM algorithm is beyond the scope of this text, however we will shortly describe the basic workflow and the different operators used in the six FMM stages as these will be referred to in the following sections. For a detailed overview of the FMM, see [22]; for an introduction in our C++ FMM implementation see [12].
3.1.1 FMM Workflow
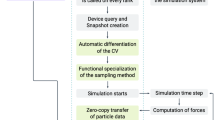
The FMM algorithm consists of six different stages, five of them required for the farfield (FF) and one for the nearfield (NF) (Fig. 4). After setting up the FMM parameters tree depth (d) and multipole order (p), the following workflow is executed.
The classical (sequential) FMM workflow consists of six stages. Only the nearfield (P2P) can be computed completely independent of all other stages. Each farfield stage (P2M, M2M, etc.) depends on the former stage and exhibits different amounts of parallelism. Especially the distribution of multipole and local moments in the tree provide limited parallelism in classical loop-based parallelization schemes
-
1.
P2M: Expand particles into spherical multipole moments ω lm up to order p on the lowest level for each box in the FMM tree. Multipole moments for particles in the same box can be summed into a multipole expansion representing the whole box.
-
2.
M2M: Translate the multipole expansion of each box to its parent box inside the tree. Again, multipole expansions with the same box center can be summed up. The translation up the tree is repeated until the root node is reached.
-
3.
M2L: Transform remote multipole moments ω lm into local moments μ lm for each box on every level. Only a limited number of interactions for each box on each level is performed to achieve linear scaling.
-
4.
L2L: Translate local moments μ lm starting from the root node down towards the leaf nodes. Local moments within the same box are summed.
-
5.
L2P: After reaching the leaf nodes, the farfield contributions for the potentials ΦFF, forces F FF, and energy E FF are computed.
-
6.
P2P: Interactions between particles within each box and its direct neighbors are computed directly, resulting in the nearfield contributions for the potentials ΦNF, forces F NF, and energy E NF.
3.1.2 Features of Our FMM Implementation
Our FMM implementation includes special algorithmical features and features that help to optimally exploit the underlying hardware. Algorithmical features are
-
Support for open and 1D, 2D and 3D periodic boundary conditions for cubic boxes.
-
Support for λ-dynamics (Sect. 2).
-
Communication-avoiding algorithms for internode communication via MPI (Fig. 9).
-
Automatic tuning of FMM parameters d and p to provide automatic error control and runtime minimization [6] based on a user-provided energy error threshold ΔE (Fig. 10).
-
Adjustable tuning to reduce or avoid energy drift (Fig. 11).
Hardware features include
-
A performance-portable SIMD layer (Sect. 3.2.1).
-
A light-weight, NUMA-aware task scheduler for CPU and GPU tasks (Sect. 3.2.2).
-
A GPU implementation based on CUDA (Sect. 3.4).
3.2 Utilizing Hierarchical Parallelism
3.2.1 Intra-Core Parallelism
A large fraction of today’s HPC peak performance stems from the increasing width of SIMD vector units. However, even modern compilers cannot generate fully vectorized code unless the data structures and dependencies are very simple. Generic algorithms like FFTs or basic linear algebra can be accelerated by using third-party libraries and tools specifically tuned and optimized for a multitude of different hardware configurations. Unfortunately, the FMM data structures are not trivially vectorizable and require careful design. Therefore, we developed a performance-portable SIMD layer for non-standard data structures and dependencies in C++.
Using only C++11 language features without third-party libraries allows to fine-tune the abstraction layer for the non-trivial data structures and achieve a better utilization. Compile-time loop-unrolling and tunable stacking are used to increase out-of-order execution and instruction-level parallelism. Such optimizations depend heavily on the targeted hardware and must not be part of the algorithmic layer of the code. Therefore, the SIMD layer serves as an abstraction layer that hides such hardware-specifics and that helps to increase code readability and maintainability. The requested SIMD width (1 ×, 2 ×, …, 16 ×) and type (float, double) is selected at compile time. The overhead costs and performance results are shown in Fig. 5. The baseline plot (blue) shows the costs of the M2L operation (float) without any vectorization enabled. All other plots show the costs of the M2L operation (float) and 16-fold vectorization (AVX-512). Since the runtime of the M2L operation is limited by the loads of the M2L operator, we try to amortize these costs by utilizing multiple (2 × … 6 ×) SIMDized multipole coefficient matrices together with a single operator via unrolling (stacking). As can be seen in Fig. 5, unrolling the multipole coefficient matrices 2 × (red), we reach the minimal computation time and the expected 16-fold speedup. Additional unroll factors (3 × … 6 ×) will not improve performance due to register spilling. To reach optimal performance, it is required to reuse (cache) the M2L operator for around 300 (or more) of these steps.
M2L operation benchmark for vectorized data structures with multipole order p = 10 on an Intel Xeon Phi 7250F CPU for a float type with 16× SIMD (AVX-512). The benchmarks shows the performance of different SIMD/unrolling combinations. E.g. the red curve (SIMD stacking 16 × 2) utilizes 16-fold vectorization together with twofold unrolling For a sufficient number (around 300) of vectorized operations, a 16-fold improvement can be measured for the re-designed data structures
The data flow of the FMM still consists of six stages. However, synchronization now happens on a fine-grained level and not only after each full stage is completed. This allows to overlap parts that exhibit poor parallelization with parts that show a high degree of parallel code. The dependencies of such a data flow graph can be evaluated and even prioritized at compile time
Intranode FMM benchmark for 1000 particles, multipole order p = 1 and tree depth d = 3 on a 2x26-core Intel Xeon Platinum 8170 CPU. When using MCS locks, simultaneous multithreading and 50 threads, the overall improvement compared to the original implementation reaches >40%, translating into a reduction in runtime from 1.93 ms down to 1.14 ms
3.2.2 Intra-Node and Inter-Node Parallelism
To overcome scaling bottlenecks of a pragma-based loop-level parallelization (see Fig. 4), our FMM employs a lightweight tasking framework purely based on C++. Being independent of other third-party tasking libraries and compiler extensions allows to utilize resources better, since algorithm-specific behavior and data-flow can be taken into account. Two distinct design features are a type-driven priority scheduler and a static dataflow dispatcher. The scheduler is capable of prioritizing tasks depending on their type at compile time. Hence, it is possible to prioritize vertical operations (like M2M and L2L) in the tree. This reduces the runtime twofold. First, it reduces the scheduling overhead at runtime by avoiding costly virtual function calls. Second, since the execution of the critical path is prioritized, the scheduler ensures that a sufficient amount of independent parallelism gets generated. The dataflow dispatcher defines the dependencies between tasks—a data flow graph—also at compile time (see Fig. 6). Together with loadbalancing and workstealing strategies, even a non-trivial FMM data flow can be executed. For compute-bound problems this design shows virtually no overhead. However, in MD we are interested in smaller particle systems with only a few hundred particles per compute node. Hence, we have to take even more hardware constraints into account. Performance penalties due to the memory hierarchy (NUMA) and costs to access memory in a shared fashion via locks introduce additional overhead. Therefore, we extended also our tasking framework with NUMA-aware memory allocations, workstealing and scalable Mellor-Crummey Scott (MCS) locks [35] to enhance the parallel scalability over many threads, as shown in Fig. 7.
Left: Intranode FMM parallelization—efficiency of different threading implementations. Near field interaction of 114,537 particles in double precision on up to 28 cores on a single node with two 14-core Intel Xeon E5-2695 v3 CPUs. Single precision computation as well as other threading schemes (std::thread, boost::thread, OpenMP) showed similar excellent scaling behavior. The plot has been normalized to the maximum turbo mode frequency which varies with the number of active cores (3.3–2.8 GHz for scalar operation, 3.0–2.6 GHz for SIMD operation). Right: Internode parallelization—strong scaling efficiency of a communication avoiding, replication-based workload distribution scheme [10]. Near field interaction of 114,537 particles on up to 65,536 Blue Gene/Q cores using replication factor c. In the initial replication phase, only c nodes within a group communicate. Afterwards, communication is restricted to all pairs of p∕c groups. For 65,536 cores, i.e. only 1–2 particles per core initially, a maximum parallel efficiency of 84% (22 ms runtime) is reached for c = 64, and the maximal replication factor c = 256 yields an efficiency of 73%, while a classical particle distribution (c = 1) would require a runtime exceeding 1 min due to communication latency
Depending on a maximum relative or absolute energy tolerance ΔE, the automatic runtime minimization provides the optimal set of FMM input parameters {d, p}. A lower requested error in energy results in an increased multipole order p (magenta). Since the computational complexity of the farfield operators M2M, M2L and L2L scales with p 3 or even p 4 (depending on the used implementation), the tree depth d is reduced accordingly to achieve a minimal runtime (green). With fractional depths [49], as used here, the runtime can be optimized even more than with integer depths
In the future, we will extend our tasking framework so that tasks can also be offloaded to local accelerators like GPUs, if available on the node.
For the node-to-node communication via MPI the aforementioned concepts do not work well (see Fig. 8), since loadbalancing or workstealing would create large overheads due to a large amount of small messages. To avoid or reduce the latency that comes with each message, we employ a communication-avoiding parallelization scheme [10]. Nodes do not communicate separately with each other, but form groups in order to reduce the total number of messages. At the same time the message size can be increased. Depending on the total number of nodes involved, the group size parameter can be tuned for performance (see Fig. 9).
Observed drift of the total energy for different electrostatics settings. Left: evolution of the total energy for PME with order 4, mesh distance 0.113 nm, ewald-rtol set to 10−5 (black line) as well as for FMM with different multipole orders p at depth d = 3 (see legend in the right panel). Test system is a double precision simulation at T ≈ 300 K in periodic boundaries of 40 Na+ and 40 Cl− ions solvated in a 4.07 nm3 box containing extended simple point charge (SPC/E) water molecules [3], comprising 6740 atoms altogether. Time step Δt = 2 fs, cutoffs at 0.9 nm, pair-list updated every ten steps. Right: Black squares show the drift with PME for different Verlet buffer sizes for the water/ions system using 4 × 4 cluster pair lists [41]. For comparison, green line shows the same for pure SPC/E water (without ions) taken from Ref. [34]. Influence of different multipole orders p on the drift is shown for a fixed buffer size of 8.3 Å. The GROMACS default Verlet buffer settings yield a drift of ≈ 8 × 10−5 kJ/mol/ps per atom for these MD systems, corresponding to the first data point on the left (black square/green circle)
3.3 Algorithmic Interface
Choosing the optimal FMM parameters in terms of accuracy and performance is difficult if not impossible to do manually as they also depend on the charge distribution itself. A naive choice of tree depth d and multipole order p might either lead to wasting FLOPs or to results that are not accurate enough. Therefore, d and p are automatically tuned depending on the underlying hardware and on a provided energy tolerance ΔE (absolute or relative acceptable error in Coulombic energy). The corresponding parameter set {d, p} is computed such that the accuracy is met at minimal computational costs (Fig. 10) [6].
Besides tuning the accuracy to achieve a certain acceptable error in the Coulombic energy for each time step, the FMM can additionally be tuned to reduce the energy drift over time.
Whereas multipole orders of about ten yield a comparable drift of the total energy over time as a typical simulation with PME, the drift with FMM can be reduced to much lower levels if desired (Fig. 11).
3.4 CUDA Implementation of the FMM for GPUs
A growing number of HPC clusters incorporate accelerators like GPUs to deliver a large part of the FLOPS. Also GROMACS evolves towards offloading more and more tasks to the GPU, for reasons of both performance and cost-efficiency [31, 32].
For system sizes that are typical for biomolecular simulations, FMM performance critically depends on the M2L and P2P operators. For multipole orders of about eight and larger their execution times dominate the overall FMM runtime (Fig. 12).
Colored bars show detailed timings for the various parts of a single FMM step on a GTX 1080Ti GPU for a 103,000 particle system using depth d = 3. For comparison, total execution time for d = 3 on an RTX 2080 GPU is shown as brown line, whereas black line shows timings for d = 4 on a GTX 1080Ti GPU. CUDA parallelization is used in each FMM stage leaving the CPU mostly idle
Hence, these operators need to be parallelized very efficiently on the GPU. At the same time, all remaining operators need to be implemented on the GPU as well to avoid memory traffic between device (GPU) and host (CPU) that would otherwise become necessary. This traffic would introduce a substantial overhead as a complete MD time step may take just a few milliseconds to execute.
Our encapsulated GPU FMM implementation takes particle positions and charges as input and returns the electrostatic forces on the particles as output. Memory transfers between host and device are performed only at these two points in the calculation step.
The particle positions and charges are split into different CUDA streams that allow for asynchronous memory transfer to the host. The memory transfer is overlapped with the computation of the spatial affiliation of the octree box.
In contrast to the CPU FMM that utilizes \(\mathcal {O}(p^3)\) far field operators (M2M, M2L, L2L), the GPU version is based on the \(\mathcal {O}(p^4)\) operator variant. The \(\mathcal {O}(p^3)\) operators require less multiplications to calculate the result, but they introduce additional highly irregular data structures to rotate the moments. Since the performance of the GPU FMM at small multipole orders is not limited by the number of floating point operations (Fig. 12) but rather by scattered memory access patterns, we use the \(\mathcal {O}(p^4)\) operators for the GPU implementation.
We will now outline our CUDA implementation of the operations needed in the various stages of the FMM (Figs. 4, 5, and 6), which starts by building the multipoles on the lowest level with the P2M operator.
3.4.1 P2M: Particle to Multipole
The P2M operation is described in detail elsewhere [44]. The large number of registers that is required and the recursive nature of this stage limits the efficient GPU parallelization. The operation is however executed independently for each particle and the requested multipole expansion is gained by summing atomically into common expansion points. The result is precomputed locally using shared memory or intra-warp communication to reduce the global memory traffic when storing the multipole moments. The multipole moments ω, local moments μ and the far field operators A, M, and C are stored as triangular shaped matrices
and \(\mathbf {M} \in \mathbb {K}^{2p\times 2p}\), where p is the multipole order.
To map the triangular matrices efficiently to contiguous memory, their elements are stored as 1D arrays of complex values and the l, m indices are calculated on the fly when accessing the data. For optimal performance, different stages of the FMM require different memory access patterns. Therefore, the data structures are stored redundantly in a Structure of Arrays (SoA) and Array of Structures (AoS) version. The P2M operator writes to AoS, whereas the far field operators use SoA. A copy kernel, negligible in runtime, does the copying from one structure to another.
3.4.2 M2M: Multipole to Multipole
The M2M operation, which shifts the multipole expansions of the child boxes to their parents, is executed on all boxes within the tree, except for the root node which has no parent box. The complexity of this operation is \(\mathcal {O}(p^4)\); one M2M operation has the form
where A is the M2M operator and a and a′ are different expansion center vectors. The operation performs \(\mathcal {O}(p^2)\) dot products between ω and a part of the operator A. These operations need to be executed in all boxes in the octree, excluding the box on level 0, i.e. the root node. The kernels are executed level wise on each depth, synchronizing between each level. Each computation of the target ω lm for a distinct (l, m) pair is performed in a different CUDA block of the kernel, with threads within a block accessing different boxes sharing the same operator. The operator can be efficiently preloaded into CUDA shared memory and is accessed for different ω lm residing in different octree boxes. Each single reduction step is performed sequentially by each thread. This has the advantage that the partial products are stored locally in registers, reducing the global memory traffic since only \(\mathcal {O}(p^2)\) elements are written to global memory. It also reduces the atomic accesses, since the results from eight distinct multipoles are written into one common target multipole.
3.4.3 M2L: Multipole to Local
The M2L operator works similarly to M2M, but it requires much more transformations as each source ω is transformed to 189 target μ boxes. The group of boxes to which a particular ω is transformed to is called the interaction set. It contains all child boxes of the direct neighbor boxes of the source’s ω parent. The M2L operation is defined as
where r and a are different expansion centers. The operation differs only slightly from M2M in the access pattern but is of the same \(\mathcal {O}(p^4)\) complexity. As the M2L runtime is crucial for the overall FMM performance, we have implemented several parallelization schemes. Which scheme is the fastest depends on tree depth and multipole order. The most efficient implementation is based on presorted lists containing interaction box pointers. The lists are presorted so that the symmetry of the operator M can be exploited. In M, the orthogonal operator elements differ only by their sign. Harnessing this minimizes the number of multiplications and global memory accesses and allows to reduce the number of spawned CUDA blocks from 189 to 54. However, it introduces additional overhead in logic to change signs and computations of additional target μ box positions, so the performance speedup is smaller than 189/54. The kernel is spawned similarly to the M2M kernel performing one dot product per CUDA block preloading the operator M into shared memory. The sign changing is done with the help of and additional bitset provided for each operator. Three different parallelization approaches are compared in Fig. 13. Considering the hardware performance bottlenecks of this stage, the limitations highly differ for particular implementations. The naive M2L kernel is clearly bandwidth limited and achieves nearly 500 GB/s for multipole orders larger than ten. This is higher than the theoretical memory throughput of the tested GPU, which is 480 GB/s, due to caching effects. The cache utilization is nearly at 100% achieving 3500 GB/s. However, the performance of this kernel can be enhanced further by moving towards more compute bound regime. With the dynamical approach the performance is mainly limited by the costs of spawning additional kernels. It can be clearly seen with the flat curve shape for multipoles smaller than 13 in Fig. 13. The hardware utilization for the symmetrical kernel is depicted in Fig. 14. The performance of this kernel depends on the multipole order p, since p 2 is a CUDA gridsize parameter [40]. The values p < 7 lead to underutilization of the underlying hardware, however they are mostly not of practical relevance. For larger values the performance is operations bound achieving about 80% of the possible compute utilization.
Comparison of three different parallelization schemes for the M2L operator, which is the most compute intensive part of the FMM algorithm. The naive implementation (red) directly maps the operator loops to CUDA blocks. It beats the other schemes only for orders p < 2. Dynamic parallelization (blue) is a CUDA specific approach that dynamically spawns thread groups from the kernels. The symmetric scheme (magenta) represents the FMM tree via presorted interaction lists. It also exploits the symmetry of the M2L operator
3.4.4 L2L: Local to Local
The L2L operation is executed for each box in the octree, shifting the local moments from the root of the tree down to the leaves, opposite in direction to M2M. Although the implementation is nearly identical, it achieves slightly better performance than M2M because the number of atomic memory accesses is reduced due to the tree traversing direction. For the L2L operator, the result is written into eight target boxes, whereas M2M gathers information from eight source boxes into one.
3.4.5 L2P: Local to Particles
The calculation of the potentials at particle positions x i requires evaluating

where  is a chargeless multipole moment of particle at position x
i and N
box the number of particles in the box. The complexity of each operation is \(\mathcal {O}(p^2)\). This stage is similar to P2M since the chargeless moments need to be evaluated for each particle using the same routine for a charge of q = 1. The performance is limited by register requirement but like in the P2M stage it runs concurrently for each particle and it is overlapped with the asynchronous memory transfer from device to host.
is a chargeless multipole moment of particle at position x
i and N
box the number of particles in the box. The complexity of each operation is \(\mathcal {O}(p^2)\). This stage is similar to P2M since the chargeless moments need to be evaluated for each particle using the same routine for a charge of q = 1. The performance is limited by register requirement but like in the P2M stage it runs concurrently for each particle and it is overlapped with the asynchronous memory transfer from device to host.
3.4.6 P2P: Particle to Particle
The FMM computes direct Coulomb interactions only for particles in the leaves of the octree and between particles in boxes that are direct neighbors. These interactions can be computed for each pair of atoms directly by starting one thread for each target particle in the box that sequentially loops over all source particles. An alternative way that better fits the GPU hardware is to compute these interactions for pairs of clusters of size M and N particles, with M × N = 32 the CUDA warp size, as laid out in [41]. The forces acting on the sources and on the targets are calculated simultaneously. The interactions are computed in parallel between all needed box-box pairs in the octree. The resulting speedup of computing all atomic interactions between pairs of clusters instead of using simpler, but longer loops over pairs of atoms is shown in Fig. 15. The P2P kernels are clearly compute bound. The exact performance evaluation of the kernel can be found in [41].
3.5 GPU FMM with λ-Dynamics Support
In addition to the regular Coulomb interactions, with λ-dynamics, extra energy terms for all forms of all λ sites need to be evaluated such that the forces on the λ particles can be derived. The resulting additional operations exhibit a very unstructured pattern that varies depending on the distribution of the particles associated with λ sites. Such a pattern can be described by multiple sparse FMM octrees that additionally interact with each other. The sparsity that emerges from a relatively small size of the λ sites necessitates a different parallelization than for a standard FMM. To support λ-dynamics efficiently, all stages of the algorithm were adapted. Especially, the most compute intense shifting (M2M, L2L) and transformation (M2L) operations need a different parallelization than that of the normal FMM to run efficiently for a sparse octree. Figure 16 shows the runtime of the CUDA parallelized λ-FMM as a function of the system size, whereas Fig. 17 shows the overhead associated with λ-dynamics. The overhead that emerges from addition of λ sites to the simulation system scales linearly with the number of additional sites with a factor of about 10−3 per site. This shows that the FMM tree structure fits particularly well the λ-dynamics requirements for flexibility to compute the highly unstructured, additional particle-particle interactions. Note that our λ-FMM kernels still have the potential for more optimizations (at the moment they achieve only about 60% of the efficiency of the regular FMM kernels) such that for the final optimized implementation we expect the costs for the additional sites to be even smaller than what is shown in Fig. 17.
As Fig. 16, but now showing relative costs of adding λ-dynamics functionality to the regular GPU FMM
4 Conclusions and Outlook
All-atom, explicit solvent biomolecular simulations with λ-dynamics are still limited to comparatively small simulation systems (<100,000 particles) and/or short timescales [7, 9, 18]. To ultimately allow for a realistic (e.g., const-pH) treatment of large biomolecular systems on long timescales, we are developing an efficient FMM that computes the long-range Coulomb interactions, including local charge alternatives for a large number of sites, with just a small overhead compared to the case without λ-dynamics.
Our FMM library is a modern C++11 based implementation tailored towards the specific requirements of biomolecular simulation, which are a comparatively small number of particles per compute core and a very short wall clock time per iteration. The presented implementation offers near-optimal performance on various SIMD architectures, an efficient CUDA version for GPUs, and it makes use of fractional tree depths for optimal performance. In addition to supporting chemical variability via λ-dynamics, it has several more unique features such as a rigorous error control, and based upon that, an automatic performance optimization at runtime. The energy drift resulting from errors in the FMM calculation can be reduced to virtually zero with a newly developed scheme that adapts the multipole expansion order p locally and on the fly in response to the requested maximum energy error. With fixed p, using multipole orders 10–14 yields drifts that are smaller than those observed for typical simulations with PME. We expect the FMM to be useful also for normal MD simulations, as a drop-in PME replacement for extreme scaling scenarios where PME reaches its scaling limit.
The GPU version of our FMM will implicitly use the same parallelization framework as the CPU version. In fact, GPUs will be treated as one of several resources a node offers (in addition to CPUs), to which tasks can be scheduled. As our GPU implementation is not a monolithic module, it can be used to calculate individual parts of the FMM, like the near-field contribution or the M2L operations of one of the local boxes only, in a fine-grained manner. How much work is offloaded to local GPUs will depend on the node specifications and on how much GPU and CPU processing power is available.
The λ-dynamics module allows to choose between three different variants of λ-dynamics. The dynamics and equilibrium distributions of the lambdas can be flexibly tuned by a barrier potential, whereas buffer sites ensure system neutrality in periodic boundary conditions. Compared to a regular FMM calculation without local charge alternatives, the GPU-FMM with λ-dynamics is only a factor of two slower even for a large (500,000 atom) simulation system with more than 100 protonatable sites.
Although some infrastructure that is needed for out-of-the-box constant-pH simulations in GROMACS still has to be implemented, with the λ-dynamics and FMM modules, the most important building blocks are in place and performing well. The next steps will be to carry out realistic tests with the new λ-dynamics implementation and to thoroughly compare to known results from older studies, before advancing to larger, more complex simulation systems that have become feasible now.
References
Agullo, E., Bramas, B., Coulaud, O., Darve, E., Messner, M., Takahashi, T.: Task-based FMM for multicore architectures. SIAM J. Sci. Comput. 36(1), C66–C93 (2014). https://doi.org/10.1137/130915662
Arnold, A., Fahrenberger, F., Holm, C., Lenz, O., Bolten, M., Dachsel, H., Halver, R., Kabadshow, I., Gähler, F., Heber, F., Iseringhausen, J., Hofmann, M., Pippig, M., Potts, D., Sutmann, G.: Comparison of scalable fast methods for long-range interactions. Phys. Rev. E 88(6), 063308 (2013)
Berendsen, H., Grigera, J., Straatsma, T.: The missing term in effective pair potentials. J. Phys. Chem. 91(24), 6269–6271 (1987)
Bock, L.V., Blau, C., Vaiana, A.C., Grubmüller, H.: Dynamic contact network between ribosomal subunits enables rapid large-scale rotation during spontaneous translocation. Nucleic Acids Res. 43(14), 6747–6760 (2015)
Bolten, M., Fahrenberger, F., Halver, R., Heber, F., Hofmann, M., Kabadshow, I., Lenz, O., Pippig, M., Sutmann, G.: ScaFaCoS, C subroutine library. http://scafacos.github.com
Dachsel, H.: An error-controlled fast multipole method. J. Chem. Phys. 132, 119901 (2010). https://doi.org/10.1063/1.3264952
Dobrev, P., Donnini, S., Groenhof, G., Grubmüller, H.: Accurate three states model for amino acids with two chemically coupled titrating sites in explicit solvent atomistic constant pH simulations and pKa calculations. J. Chem. Theory Comput. 13(1), 147–160 (2017). https://doi.org/10.1021/acs.jctc.6b00807
Donnini, S., Tegeler, F., Groenhof, G., Grubmüller, H.: Constant pH molecular dynamics in explicit solvent with λ-dynamics. J. Chem. Theory Comput. 7, 1962–1978 (2011). https://doi.org/10.1021/ct200061r
Donnini, S., Ullmann, R.T., Groenhof, G., Grubmüller, H.: Charge-neutral constant pH molecular dynamics simulations using a parsimonious proton buffer. J. Chem. Theory Comput. 12(3), 1040–1051 (2016). https://doi.org/10.1021/acs.jctc.5b01160
Driscoll, M., Georganas, E., Koanantakool, P., Solomonik, E., Yelick, K.: A communication-optimal n-body algorithm for direct interactions. In: Parallel and Distributed Processing Symposium, International, vol. 0, pp. 1075–1084 (2013). https://doi.org/10.1109/IPDPS.2013.108
Essmann, U., Perera, L., Berkowitz, M.L., Darden, T., Lee, H., Pedersen, L.G.: A smooth particle mesh Ewald method. J. Chem. Phys. 103(19), 8577–8593 (1995). https://doi.org/10.1063/1.470117
Garcia, A.G., Beckmann, A., Kabadshow, I.: Accelerating an FMM-Based Coulomb Solver with GPUs, pp. 485–504. Springer International Publishing, Cham (2016). https://doi.org/10.1007/978-3-319-40528-5_22
Goh, G.B., Knight, J.L., Brooks, C.L.: Constant pH molecular dynamics simulations of nucleic acids in explicit solvent. J. Chem. Theory Comput. 8, 36–46 (2012). https://doi.org/10.1021/ct2006314
Goh, G.B., Hulbert, B.S., Zhou, H., Brooks III, C.L.: Constant pH molecular dynamics of proteins in explicit solvent with proton tautomerism. Proteins Struct. Funct. Bioinf. 82(7), 1319–1331 (2014)
Greengard, L., Rokhlin, V.: A new version of the fast multipole method for the Laplace equation in three dimensions. Acta Numer. 6, 229–269 (1997). https://doi.org/10.1017/S0962492900002725
Guo, Z., Brooks, C., Kong, X.: Efficient and flexible algorithm for free energy calculations using the λ-dynamics approach. J. Phys. Chem. B 102(11), 2032–2036 (1998)
Hess, B., Kutzner, C., van der Spoel, D., Lindahl, E.: Gromacs 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation. J. Chem. Theory Comput. 4, 435–447 (2008). https://doi.org/10.1021/ct700301q
Huang, Y., Chen, W., Wallace, J.A., Shen, J.: All-atom continuous constant pH molecular dynamics with particle mesh Ewald and titratable water. J. Chem. Theory Comput. 12(11), 5411–5421 (2016)
Hub, J.S., de Groot, B.L., Grubmüller, H., Groenhof, G.: Quantifying artifacts in Ewald simulations of inhomogeneous systems with a net charge. J. Chem. Theory Comput. 10, 381–390 (2014). https://doi.org/10.1021/ct400626b
Igaev, M., Grubmüller, H.: Microtubule assembly governed by tubulin allosteric gain in flexibility and lattice induced fit. eLife 7, e34353 (2018)
Jung, J., Nishima, W., Daniels, M., Bascom, G., Kobayashi, C., Adedoyin, A., Wall, M., Lappala, A., Phillips, D., Fischer, W., Tung, C.S., Schlick, T., Sugita, Y., Sanbonmatsu, K.Y.: Scaling molecular dynamics beyond 100,000 processor cores for large-scale biophysical simulations. J. Comput. Chem. 40, 1919 (2019)
Kabadshow, I., Dachsel, H.: The error-controlled fast multipole method for open and periodic boundary conditions. In: Sutmann, G., Gibbon, P., Lippert, T. (eds.) Fast Methods for Long-Range Interactions in Complex Systems. IAS Series, vol. 6, pp. 85–114. FZ Jülich, Jülich (2011)
Khandogin, J., Brooks, C.L.: Constant pH molecular dynamics with proton tautomerism. Biophys. J. 89(1), 141–157 (2005)
Kirkwood, J.G.: Statistical mechanics of fluid mixtures. J. Chem. Phys. 3(5), 300–313 (1935)
Knight, J.L., Brooks III, C.L.: λ-dynamics free energy simulation methods. J. Comput. Chem. 30(11), 1692–1700 (2009)
Knight, J.L., Brooks III, C.L.: Applying efficient implicit nongeometric constraints in alchemical free energy simulations. J. Comput. Chem. 32(16), 3423–3432 (2011). https://doi.org/10.1002/jcc.21921
Kong, X., Brooks III, C.L.: λ-dynamics: a new approach to free energy calculations. J. Chem. Phys. 105, 2414–2423 (1996). https://doi.org/10.1063/1.472109
Kopec, W., Köpfer, D.A., Vickery, O.N., Bondarenko, A.S., Jansen, T.L., de Groot, B.L., Zachariae, U.: Direct knock-on of desolvated ions governs strict ion selectivity in K+ channels. Nat. Chem. 10(8), 813 (2018)
Kutzner, C., van der Spoel, D., Fechner, M., Lindahl, E., Schmitt, U.W., de Groot, B.L., Grubmüller, H.: Speeding up parallel GROMACS on high-latency networks. J. Comput. Chem. 28(12), 2075–2084 (2007). https://doi.org/10.1002/jcc.20703
Kutzner, C., Apostolov, R., Hess, B., Grubmüller, H.: Scaling of the GROMACS 4.6 molecular dynamics code on SuperMUC. In: Bader, M., Bode, A., Bungartz, H.J. (eds.) Parallel Computing: Accelerating Computational Science and Engineering (CSE), pp. 722–730. IOS Press, Amsterdam (2014). https://doi.org/10.3233/978-1-61499-381-0-722
Kutzner, C., Páll, S., Fechner, M., Esztermann, A., de Groot, B., Grubmüller, H.: Best bang for your buck: GPU nodes for GROMACS biomolecular simulations. J. Comput. Chem. 36(26), 1990–2008 (2015). https://doi.org/10.1002/jcc.24030
Kutzner, C., Páll, S., Fechner, M., Esztermann, A., de Groot, B.L., Grubmüller, H.: More bang for your buck: improved use of GPU nodes for GROMACS 2018. J. Comput. Chem. 40(27), 2418–2431 (2019). https://doi.org/10.1002/jcc.26011
Lee, M.S., Salsbury Jr, F.R., Brooks III, C.L.: Constant-pH molecular dynamics using continuous titration coordinates. Proteins Struct. Funct. Bioinf. 56(4), 738–752 (2004)
Lindahl, E., Abraham, M., Hess, B., van der Spoel, D.: GROMACS 2019.3 manual. Zenodo (2019). https://doi.org/10.5281/zenodo.3243834
Mellor-Crummey, J.M., Scott, M.L.: Algorithms for scalable synchronization on shared-memory multiprocessors. ACM Trans. Comput. Syst. (TOCS) 9(1), 21–65 (1991)
Mermelstein, D.J., Lin, C., Nelson, G., Kretsch, R., McCammon, J.A., Walker, R.C.: Fast and flexible GPU accelerated binding free energy calculations within the AMBER molecular dynamics package. J. Comput. Chem. 39(19), 1354–1358 (2018)
Mertz, J.E., Pettitt, B.M.: Molecular dynamics at a constant pH. Int. J. Supercomputer Appl. High Perform. Comput. 8(1), 47–53 (1994)
Mobley, D.L., Klimovich, P.V.: Perspective: alchemical free energy calculations for drug discovery. J. Chem. Phys. 137(23), 230901 (2012)
Mongan, J., Case, D.A.: Biomolecular simulations at constant pH. Curr. Opin. Struct. Biol. 15(2), 157–163 (2005)
NVIDIA Corporation: NVIDIA CUDA C programming guide (2019). Version 10.1.243
Páll, S., Hess, B.: A flexible algorithm for calculating pair interactions on SIMD architectures. Comput. Phys. Commun. 184, 2641–2650 (2013). https://doi.org/10.1016/j.cpc.2013.06.003
Páll, S., Abraham, M.J., Kutzner, C., Hess, B., Lindahl, E.: Tackling exascale software challenges in molecular dynamics simulations with GROMACS. In: Markidis, S., Laure. E. (eds.) Solving Software Challenges for Exascale, pp. 3–27. Springer International Publishing, Cham (2015)
Perilla, J.R., Goh, B.C., Cassidy, C.K., Liu, B., Bernardi, R.C., Rudack, T., Yu, H., Wu, Z., Schulten, K.: Molecular dynamics simulations of large macromolecular complexes. Curr. Opin. Struct. Biol. 31, 64–74 (2015)
Press, W.H., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes 3rd Edition: The Art of Scientific Computing, 3rd edn. Cambridge University Press, New York (2007)
Schulz, R., Lindner, B., Petridis, L., Smith, J.C.: Scaling of multimillion-atom biological molecular dynamics simulation on a petascale supercomputer. J. Chem. Theory Comput. 5(10), 2798–2808 (2009)
Seeliger, D., De Groot, B.L.: Protein thermostability calculations using alchemical free energy simulations. Biophys. J. 98(10), 2309–2316 (2010)
Shirts, M.R., Mobley, D.L., Chodera, J.D.: Alchemical free energy calculations: ready for prime time? Annu. Rep. Comput. Chem. 3, 41–59 (2007)
Wallace, J.A., Shen, J.K.: Charge-leveling and proper treatment of long-range electrostatics in all-atom molecular dynamics at constant pH. J. Chem. Phys. 137(18), 184105 (2012)
White, C.A., Head-Gordon, M.: Fractional tiers in fast multipole method calculations. Chem. Phys. Lett. 257(5–6), 647–650 (1996). https://doi.org/10.1016/0009-2614(96)00574-X
Yokota, R., Barba, L.A.: A tuned and scalable fast multipole method as a preeminent algorithm for exascale systems. CoRR abs/1106.2176 (2011). http://arxiv.org/abs/1106.2176
Acknowledgements
This work is supported by the German Research Foundation (DFG) Cluster of excellence Multiscale Imaging and under the DFG priority programme 1648 Software for Exascale Computing (SPPEXA).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.
The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
Copyright information
© 2020 The Author(s)
About this paper
Cite this paper
Kohnke, B. et al. (2020). GROMEX: A Scalable and Versatile Fast Multipole Method for Biomolecular Simulation. In: Bungartz, HJ., Reiz, S., Uekermann, B., Neumann, P., Nagel, W. (eds) Software for Exascale Computing - SPPEXA 2016-2019. Lecture Notes in Computational Science and Engineering, vol 136. Springer, Cham. https://doi.org/10.1007/978-3-030-47956-5_17
Download citation
DOI: https://doi.org/10.1007/978-3-030-47956-5_17
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-47955-8
Online ISBN: 978-3-030-47956-5
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)