Abstract
Threshold secret sharing allows a dealer to split a secret into n shares such that any authorized subset of cardinality at least t of those shares efficiently reveals the secret, while at the same time any unauthorized subset of cardinality less than t contains no information about the secret. Leakage-resilience additionally requires that the secret remains hidden even if one is given a bounded amount of additional leakage from every share.
In this work, we study leakage-resilient secret sharing schemes and prove a lower bound on the share size and the required amount of randomness of any information-theoretically secure scheme. We prove that for any information-theoretically secure leakage-resilient secret sharing scheme either the amount of randomness across all shares or the share size has to be linear in n. More concretely, for a secret sharing scheme with p-bit long shares, \(\ell \)-bit leakage per share, where \(\widehat{t}\) shares uniquely define the remaining \(n - \widehat{t}\) shares, it has to hold that
We use this lower bound to gain further insights into a question that was recently posed by Benhamouda et al. (CRYPTO’18), who ask to what extend existing regular secret sharing schemes already provide protection against leakage. The authors proved that Shamir’s secret sharing is 1-bit leakage-resilient for reconstruction thresholds \(t \ge 0.85n\) and conjectured that it is also 1-bit leakage-resilient for any other threshold that is a constant fraction of the total number of shares. We do not disprove their conjecture, but show that it is the best one could possibly hope for. Concretely, we show that for large enough n and any constant \(0< c < 1\) it holds that Shamir’s secret sharing scheme is not leakage-resilient for  .
.
In contrast to the setting with information-theoretic security, we show that our lower bound does not hold in the computational setting. That is, we show how to construct a leakage-resilient secret sharing scheme in the random oracle model that is secure against computationally bounded adversaries and violates the lower bound stated above.
J. B. Nielsen—Supported by the Independent Research Fund Denmark project BETHE and the Concordium Blockchain Research Center, Aarhus University, Denmark.
M. Simkin—Supported by the European Unions’s Horizon 2020 research and innovation program under grant agreement No. 669255 (MPCPRO) and No. 731583 (SODA).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Threshold secret sharing, introduced by Shamir [Sha79] and Blakley [Bla79], is a fundamental building block in modern cryptography. It allows a dealer to split a secret into n shares such that any subset of cardinality at least t of those shares efficiently reveals the secret, while at the same time any subset of cardinality less than t contains no information about the secret in the information theoretic sense. Due to its computational simplicity, its strong privacy guarantees, and its information-theoretic security, it has found applications in various areas of cryptography ranging from secure multiparty computation [BGW88, CCD88, RB89] over threshold cryptography [Des88, DF90, Sho00] to attribute-based encryption [GPSW06, Wat11]. Stronger notions, like robust [RB89] and verifiable secret sharing [CGMA85] address the lack of authenticity in the original definition and prevent the participants or the dealer from tampering with the shares. All these classical notions of secret sharing have in common that they assume that any share is either fully corrupted or completely hidden from the adversary.
In contrast to these notions, a recent line of works [DP07, BGK14, GK18a, GK18b, ADN+18, KMS18, SV18, BS18] considers secret sharing in the context of side-channel attacks, where an adversary gets some form of restricted access to all shares. Generally, these works consider two types of adversaries. Active adversaries that may tamper with all shares and passive adversaries that may leak some bounded amount of information from each share. Constructing secret sharing schemes that remain secure in the presence of such powerful adversaries is a challenging task and, unsurprisingly, existing constructions are less efficient than regular secret sharing schemes in one way or another. Understanding what price one has to pay for such strong security guarantees is a foundational theoretical question and of significant practical importance when real-world resources are limited. While the efficiency of regular threshold secret sharing is well understood [BGK16], little is known about the price of additional security against side-channel attacks.
In this work, we focus on leakage-resilient secret sharing and we measure efficiency in terms of share size and the amount of randomness needed for secret sharing a value. The share size is an important measure to optimize, since it directly affects the efficiency of cryptographic primitives, like multiparty computation protocols, that are built on top of secret sharing. The celebrated BGW protocol [BGW88] for secure multiparty computation, for instance, exhibits a one-to-one correspondence between share size of the underlying secret sharing scheme and overall communication complexity of the protocol. That is, an increase of the share size by a factor of 2 directly translates to an increase of the overall communication complexity of the protocol by the same factor. The amount of randomness that cryptographic primitives require is an important measure to optimize for real-world applications. In research, it is often assumed that randomness is simply there when needed it, yet in reality it turns out to be a precious resource with limited availability. Generating good randomness is difficult and cryptographic primitives that required more randomness than what was available have led to devastating large-scale attacks [HDWH12].
1.1 Our Contribution
We prove that for any leakage-resilient secret sharing scheme with information-theoretic security either the amount of randomness across all shares or the share size has to be large.
Theorem 1
(Informal). Let \(\mathcal{S}\) be a t-out-of-n secret sharing scheme, let p be the bit length of each share, and let \(\ell \) be the number of bits leaked from each share. If \(\mathcal{S}\) is leakage-resilient against a computationally unbounded adversary and \(\widehat{t}\) shares uniquely define the remaining \(n-\widehat{t}\) shares, then
For instance, for a  -out-of-n secret sharing scheme with 1-bit leakage, where
-out-of-n secret sharing scheme with 1-bit leakage, where  shares uniquely define the remaining shares, the theorem tells us that the share size has to be linear in the number of shares. On the other hand, if we want the share size to be o(n), then the theorem tells us that virtually all shares have to contain some independent, yet meaningful informationFootnote 1.
shares uniquely define the remaining shares, the theorem tells us that the share size has to be linear in the number of shares. On the other hand, if we want the share size to be o(n), then the theorem tells us that virtually all shares have to contain some independent, yet meaningful informationFootnote 1.
We prove our lower bound by presenting a conceptually simple generic adversary, who breaks the leakage-resilience of any secret sharing scheme that violates our bound. More concretely, the adversary is given leakage from each share and its goal is to determine the secret value. The high-level idea behind our attack is to apply one separate uniformly random leakage function to each share. By correctness of a secret sharing scheme, we know that any two vectors of secret shares corresponding to two different secrets will always differ in at least \(n-t+1\) positions. If the output of each leakage function is \(\ell \) bits long, then two different shares produce the same leakage with probability \(2^{-\ell }\). The smaller the threshold t, the larger the number of differing shares. The main observation behind our lower bound is that, with an increasing n, we quickly reach a point, where the leakage excludes all but one of the secrets that could have produced the given leakage.
We use our lower bound to gain further insights into an intriguing question that was recently posed by Benhamouda et al. [BDIR18], who ask to what extent existing regular secret sharing schemes already provide protection against leakage. Among other results, the authors show that Shamir’s secret sharing scheme over a field \(\mathbb {F}_{2^k}\) with small characteristic is not leakage-resilient. Specifically, the authors present an attack, which obtains one bit of the secret shared value from 1-bit leakage from each share. On the positive side, the authors show that t-out-of-n Shamir secret sharing over a prime order field \(\mathbb {F}_q\) is 1-bit leakage-resilient if \(t \ge 0.85n\). The authors leave it open to prove or disprove the leakage-resilience of Shamir secret sharing over \(\mathbb {F}_q\) for other parameter ranges and conjecture:
Conjecture 1
([BDIR18]). Let \(0 < c \le 1\) be a constant and let \(q \approx n\) be a prime. For large enough n, it holds that cn-out-of-n Shamir secret sharing over \(\mathbb {F}_q\) is 1-bit leakage-resilient.
We do not disprove their conjecture, but show that it is basically the best one could hope for. More concretely, we show that for a large enough n and any constant \(0< c < 1\) it holds that Shamir’s secret sharing scheme is not leakage-resilient for \(t \le cn/\log n\). Our results regarding the leakage-resilience of Shamir’s secret sharing scheme are illustrated in Fig. 1. Whereas the negative results above crucially rely on a computationally unbounded adversary, we also show that for the specific case of 2-out-of-n Shamir secret sharing there exists a computationally efficient attack.
Overview of our results on the leakage-resilience of Shamir’s secret sharing over a prime order field \(\mathbb {F}_q\) for an arbitrary number of parties n. The y-axis depicts the leakage per share in bits, the x-axis shows the reconstruction threshold. The red area indicates parameter ranges in which it is not leakage-resilient. The green area indicates parameter ranges where it is. The white area indicates parameter ranges, where we do not know anything. n is the number of parties, \(\log q\) is the number of bits per share, and \(0< c < 1\) is an arbitrary, but fixed constant. (Color figure online)
Given the lower bound for information-theoretically secure secret sharing schemes, it may be natural to hope the same bound may apply to schemes that only need to be sure against a computationally bounded adversary. We show that this is not the case by presenting a leakage-resilient secret sharing scheme in the random oracle model that has a share size of  and is secure against any computationally bounded adversary that runs in time
and is secure against any computationally bounded adversary that runs in time  . By setting, for instance, \(\ell > n\) one can see that such a scheme violates our lower bound from above for sufficiently large n.
. By setting, for instance, \(\ell > n\) one can see that such a scheme violates our lower bound from above for sufficiently large n.
2 Preliminaries
For random variables V and W we use \(V \approx _\epsilon W\) to denote that the distributions of V and W are at most \(\epsilon \) apart in \(L_1\) distance.
Our definition of threshold secret sharing follows the definition of Beimel [Bei11]. We additionally define a full reconstruction threshold \(\widehat{t}\), which defines how many shares are needed to reconstruct all shares of a particular secret sharing. In other words, the full reconstruction threshold \(\widehat{t}\) can also be seen as an upper bound on the total entropy among all shares of a secret sharing. In our definition and the remainder of the paper we assume perfectly correct secret sharing schemes. This is done for the sake of simplicity and all proofs easily extend to the case, where the reconstruction may fail with some probability.
Definition 1
(Threshold Secret Sharing Scheme). Let \(\textsc {Share}: \{0,1\}^k \rightarrow (\{0,1\}^p)^n\) be an efficient randomized algorithm mapping k bit secrets into n shares each of length p. Let \(\textsc {Rec}: (\{0,1\}^p)^n \rightarrow \{0,1\}^k\) be a deterministic algorithm that maps a collection of t shares back to a secret. The notion generalises in a straight forward manner to schemes \(\textsc {Share}: \{0,1\}^k \rightarrow \prod _{i=1}^n \{0,1\}^{p_i}\), where the shares possibly have different length. The pair \((\textsc {Share}, \textsc {Rec})\) is called a t-out-of-n secret sharing if:
-
1.
Perfect Correctness: Any t-out-of-n shares can be used to reconstruct the secret correctly. For any \(x \in \{0,1\}^k\), for any set \(T \subseteq [n]\) with \(\vert T \vert \ge t\),
$$ \Pr [\textsc {Rec}(\textsc {Share}(x)_T) = x] = 1 $$where the probability is taken over the randomness of the sharing function and \(\textsc {Share}(x)_T\) denotes the restriction of the n shares produced by \(\textsc {Share}(x)\) to the ones identified by the set T.
-
2.
Perfect Privacy: Less than t shares reveal no information about the underlying secret. More formally, for any two \(x, y \in \{0,1\}^k\), any set \(T \subseteq [n]\) with \(\vert T \vert < t\), \(\textsc {Share}(x)_T\) is identically distributed to \(\textsc {Share}(y)_T\).
-
3.
Full Reconstruction: A secret sharing scheme has \(\widehat{t}\)-full-reconstruction if \(\textsc {Share}(x)\) can be computed from any subset \(\textsc {Share}(x)_T\) with \(\vert T \vert \ge \widehat{t}\).
The notion of Full Reconstruction is non-standard, but essential to our study. Leakage-resilient secret sharing schemes like [SV18] with very high leakage resilience all seem to use some notion of non-trivial correlated randomness which makes the full reconstruction threshold larger than the reconstruction threshold. To some extend our results will explain why this is the case. If you have a scheme with low full reconstruction threshold you get poor leakage resilience. So if you have a scheme with a low reconstruction threshold and good leakage resilience, then the full reconstruction threshold must be larger than the reconstruction threshold.
To model leakage-resilient secret sharing, we use the local leakage model as defined by Goyal and Kumar [GK18a] and Benhamouda et al. [BDIR18]. Intuitively, it allows the adversary to compute arbitrary independent leakage functions on all shares, which are only restricted in the size of their leakage output. For the sake of exposition, we split the definition in weak and regular local leakage-resilience. In weak local leakage-resilience the adversary is only given the output of the leakage functions. In regular local leakage-resilience, it is additionally given \(\theta \) full shares. As such weak local leakage-resilience is a special case of regular local leakage-resilience for \(\theta = 0\).
Definition 2
(Leakage Function). We call \(\textsc {Leak}= (\textsc {Leak}_1, \dots , \textsc {Leak}_n)\) an \(\ell \)-leakage function for \((\textsc {Share}, \textsc {Rec})\) if \(\textsc {Share}: \{0,1\}^k \rightarrow \prod _{i=1}^n \{0,1\}^{p_i}\) and \(\textsc {Leak}_i: \{0,1\}^{p_i} \rightarrow \{0,1\}^\ell \). For \((\mathsf {sh}_1, \ldots , \mathsf {sh}_n) \leftarrow \textsc {Share}(s)\) we define \((b_1, \ldots , b_n) = \textsc {Leak}(\mathsf {sh}_1, \ldots , \mathsf {sh}_n)\) by \(b_i = \textsc {Leak}_i(\mathsf {sh}_i)\).
Definition 3
(Weak Local Leakage-Resilience). A secret sharing scheme \((\textsc {Share}, \textsc {Rec})\) is said to be \((\epsilon , \ell )\)-weakly-local-leakage-resilient (W-IND-LLR) if for every \(\ell \)-leakage function vector \(\textsc {Leak}\) and every pair of secrets \(x, y \in \{0,1\}^k\) it holds that
We also define leakage-resilience against a class of adversaries. Let B be a possibly randomized interactive algorithm. First the adversary outputs a pair of secrets \((x_0, x_1)\) and a leakage function \(\textsc {Leak}\). Then the game flips a uniformly random challenge bit c and inputs \(\textsc {Leak}(\textsc {Share}(x_c))\) to B. Then run B to get a guess \(g \in \{0,1\}\). Let  . We say that \((\textsc {Share}, \textsc {Rec})\) is \((\epsilon , \ell )\)-weakly-local-leakage-resilient for a class \(\mathcal{B}\) of adversaries if for all \(B \in \mathcal{B}\) it holds that
. We say that \((\textsc {Share}, \textsc {Rec})\) is \((\epsilon , \ell )\)-weakly-local-leakage-resilient for a class \(\mathcal{B}\) of adversaries if for all \(B \in \mathcal{B}\) it holds that
Definition 4
(Local Leakage-Resilience). A secret sharing scheme \((\textsc {Share},\textsc {Rec})\) is said to be \((\epsilon , \ell , \theta )\)-local-leakage-resilient (IND-LLR) if for every \(\ell \)-leakage function vector \(\textsc {Leak}\), for any set \(T \subseteq [n]\) with \(\vert T \vert < \theta \), and every pair of secrets \(x, y \in \{0,1\}^k\) it holds that
We also add a one-way notion, which we will use for proving our lower bound. We will make the notion as weak as possible while still being meaningful, which makes our lower bound as strong as possible.
Definition 5
(Weak One-Way Local Leakage-Resilience). We define what it means for a secret sharing scheme \((\textsc {Share}, \textsc {Rec})\) to be \(\ell \)-weakly one-way local-leakage-resilient (WOW-LLR). Let A be a possibly randomized interactive algorithm. Let \(x \in \{0,1\}^k\) be a secret. The game \(\textsc {WOW}_{A}(x)\) proceeds as follows. First the adversary outputs a leakage function \(\textsc {Leak}\). Then the game samples \((\mathsf {sh}_1, \ldots , \mathsf {sh}_n) \leftarrow \textsc {Share}(x)\) and we input \(\textsc {Leak}(\textsc {Share}(x))\) to A, who outputs a guess \(y \in \{0,1\}^k \cup \{ \bot \}\). The output of \(\textsc {WOW}_{A}(x)\) is 1 if and only if \(y = x\). We call A admissible if it always holds for all x that \(y = x\) or \(y = \bot \). We require that for all admissible A there exist x for which  .
.
Note that one-wayness is a very weak security notion, it only requires that all of the secret cannot be learned. Requiring that the adversary must only make guesses it knows are correct further weakens the notion, as it limits the set of adversaries, which in turn makes it easier to be WOW-LLR. We also weaken the notion by requiring only that  , as opposed to requiring that \(\Pr [\textsc {WOW}_{A}(x) = 1]\) is negligible. And finally we only require that \((\textsc {Share}, \textsc {Rec})\) hides one x from the adversary, meaning that it might in principle be possible for A to recover almost all x with certainty. It seems hard to meaningfully further weaken the notion. Not surprisingly, W-IND-LLR implies WOW-LLR, but for completeness we prove a technical lemma to this effect.
, as opposed to requiring that \(\Pr [\textsc {WOW}_{A}(x) = 1]\) is negligible. And finally we only require that \((\textsc {Share}, \textsc {Rec})\) hides one x from the adversary, meaning that it might in principle be possible for A to recover almost all x with certainty. It seems hard to meaningfully further weaken the notion. Not surprisingly, W-IND-LLR implies WOW-LLR, but for completeness we prove a technical lemma to this effect.
Lemma 1
Let \((\textsc {Share}, \textsc {Rec})\) be a secret sharing scheme. If \((\textsc {Share}, \textsc {Rec})\) is  -W-IND-LLR then \((\textsc {Share}, \textsc {Rec})\) is \(\ell \)-WOW-LLR.
-W-IND-LLR then \((\textsc {Share}, \textsc {Rec})\) is \(\ell \)-WOW-LLR.
Proof
Assume that \((\textsc {Share}, \textsc {Rec})\) is not WOW-LLR. This means that there exists an admissible A such that

for all x. Now let B be W-IND-LLR adversary which first runs as follows. First pick \(x_0\) and \(x_1\) to be any distinct secrets. Run A to get a leakage function \(\textsc {Leak}\). Output \((x_0, x_1)\) and \(\textsc {Leak}\). Get back
Input \((b_1, \ldots , b_n)\) to A and get back a guess y. If \(y = \bot \), then output a uniform random guess g. Otherwise, since A is admissible we know that \(y = x_c\) for \(c =0\) or \(c=1\). In that case, output \(g=c\). We know that the probability that A guesses \(x_c\) is larger than  . So, clearly
. So, clearly

This implies that \((\textsc {Share}, \textsc {Rec})\) is not  -W-IND-LLR.
-W-IND-LLR.
2.1 Shamir’s Secret Sharing
In t-out-of-n Shamir secret sharing [Sha79] the secrets and the shares come from a field \(\mathbb {F}_q\), where q is usually chosen to be the smallest prime larger than n. Let \(\alpha _1, \dots , \alpha _n \in \mathbb {F}_q\) be distinct non-zero elements known to all parties. To share a secret \(s \in \mathbb {F}_q\), the dealer picks a uniformly random polynomial P of degree \(t-1\) with \(p(0) = s\). The share of party i is \(\mathsf {sh}_i = P(\alpha _i)\).
To reconstruct the secret, a sufficiently large subset of parties interpolates the polynomial P from their shares and evaluates the interpolated polynomial at position 0. Correctness follows from the fact that, in a field, any t points uniquely define a polynomial of degree \(t-1\). Privacy follows from the fact that for any \(t-1\) points any secret s is still possible and all secrets are equally likely.
3 Lower Bound
In this section we prove our main result.
Theorem 2
Let \(\mathcal{S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme with \(\widehat{t}\)-full-reconstruction. If \(\mathcal {S}\) is \(\ell \)-WOW-LLR and \(\ell \ge 1\), then
Proof
We prove the theorem by exhibiting an explicit admissible adversary that breaks \(\ell \)-WOW-LLR of any secret sharing scheme with a share size  . We provide an inefficient, randomized algorithm A that exactly recovers the secret shared value from the given leakage with probability at least
. We provide an inefficient, randomized algorithm A that exactly recovers the secret shared value from the given leakage with probability at least  . Note that throughout the paper we give attacks succeeding with constant probability. It with be enough to present attacks succeeding with non-negligible probability. However, this does not seem to allow to strengthen our lower bounds.
. Note that throughout the paper we give attacks succeeding with constant probability. It with be enough to present attacks succeeding with non-negligible probability. However, this does not seem to allow to strengthen our lower bounds.
The algorithm A proceeds as follows. Pick a random \(\textsc {Leak}= (\textsc {Leak}_1, \ldots , \textsc {Leak}_n)\) where each \(\textsc {Leak}_i: \{0,1\}^p \rightarrow \{0,1\}^\ell \) is an independent, uniformly random function mapping p-bit strings to \(\ell \)-bit strings. Submit it to the leakage game and get back
where
is a secret sharing of the secret s that the algorithm should try to recover. Now iterate over all secrets \(s'\) and randomizers \(r'\) and compute
Let
This is the set of secrets \(s'\) which are consistent with the leakage \((b_1, \ldots , b_m)\). If \(\vert S \vert > 1\), then output \(\bot \). Otherwise, let \(\{ s \} = S\) and output s. Let \(\mathsf {succ}\) be the event that the output is not \(\bot \).
It is trivial to see that \(s \in S\). Hence if \(\vert S \vert = 1\), then indeed \(S = \{ s \}\). So when A does not output \(\bot \), it outputs the correct secret s. Hence A is admissible.
We now prove that  . Let \((\mathsf {sh}_1, \dots , \mathsf {sh}_n) \leftarrow \textsc {Share}(s ; r)\) be the secret sharing of the secret that A is trying to guess and denote by \(b_i \leftarrow \textsc {Leak}_i(\mathsf {sh}_i)\) the leakage from the i-th share. Let \((\mathsf {sh}'_1, \dots , \mathsf {sh}'_n) \leftarrow \textsc {Share}(s' ; r')\) be the secret sharing of some arbitrary but fixed secret \(s'\) with \(s \ne s'\) and let \(b'_i \leftarrow \textsc {Leak}_i(\mathsf {sh}'_i)\) be the corresponding leakage. By correctness of the secret sharing scheme, it is guaranteed that there exists a set \(I \subseteq [n]\) with \(\vert I \vert \ge n-t+1\) such that \(\mathsf {sh}_i \ne \mathsf {sh}'_i\) for all \(i \in I\). So it clearly holds that
. Let \((\mathsf {sh}_1, \dots , \mathsf {sh}_n) \leftarrow \textsc {Share}(s ; r)\) be the secret sharing of the secret that A is trying to guess and denote by \(b_i \leftarrow \textsc {Leak}_i(\mathsf {sh}_i)\) the leakage from the i-th share. Let \((\mathsf {sh}'_1, \dots , \mathsf {sh}'_n) \leftarrow \textsc {Share}(s' ; r')\) be the secret sharing of some arbitrary but fixed secret \(s'\) with \(s \ne s'\) and let \(b'_i \leftarrow \textsc {Leak}_i(\mathsf {sh}'_i)\) be the corresponding leakage. By correctness of the secret sharing scheme, it is guaranteed that there exists a set \(I \subseteq [n]\) with \(\vert I \vert \ge n-t+1\) such that \(\mathsf {sh}_i \ne \mathsf {sh}'_i\) for all \(i \in I\). So it clearly holds that
where the randomness is taken over a random \(\textsc {Leak}\).
Since each share is p bits long and since \(\widehat{t}\) shares uniquely define any particular secret sharing, it follows that there exists at most a total of \(2^{p\widehat{t}}\) possible secret sharings.
Let \(\mathsf {coll}\) be the event that there exists any \((s', r')\) with \(s' \ne s\) such that \((b_1, \ldots , b_n) = (\textsc {Leak}_1(\mathsf {sh}_1'), \ldots , \textsc {Leak}_n(\mathsf {sh}_n'))\) when \((\mathsf {sh}'_1, \dots , \mathsf {sh}'_n) \leftarrow \textsc {Share}(s' ; r')\). By a union bound we get that
Observe that the event \(\mathsf {succ} = \lnot \mathsf {coll}\). If all secret sharings of all values \(s' \ne s\) are inconsistent with the given leakage, then we can conclude that the secret shared value is s. For the probability of \(\lnot \mathsf {coll}\) to be larger than  , it suffices that
, it suffices that

To prevent the attack described above, we therefore need that
has to hold. Finally, we observe that when \(\ell \ge 1\), then \(\ell (n-t+1) -1 \ge \ell (n-t)\). \(\blacksquare \)
As an immediate corollary of the theorem it follows that any secret sharing scheme, which only requires a constant number of shares for full reconstruction, has to have a share size that is linear in the number of shares if it wants to be leakage-resilient.
Corollary 1
Let \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme with \(\widehat{t}\)-full-reconstruction, where t and \(\widehat{t}\) are constants. If \(\mathcal {S}\) is  -W-IND-LLR, then its share size p is in \(\varOmega (n)\).
-W-IND-LLR, then its share size p is in \(\varOmega (n)\).
When given some complete shares in addition to the leakage, then we obtain the following bound:
Theorem 3
Let \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme with \(\widehat{t}\)-full-reconstruction. If \(\mathcal {S}\) is  -IND-LLR, and \(\ell \ge 1\), then
-IND-LLR, and \(\ell \ge 1\), then
Proof
The proof here is almost identical to the proof of Theorem 2. In addition to the leakage, we are now given \(\theta \) complete shares. As before, let \((b_1, \dots , b_n)\) and \((b'_1, \dots , b'_n)\) be the leakage of some arbitrary, but fixed secret sharings \(a = \textsc {Share}(s ; r)\) and \(a' = \textsc {Share}(s' ; r')\) with \(s \ne s'\). Let \(T \subseteq [n]\) with \(\vert T \vert < \theta \) be the subset of indices of shares that we get to see in addition to the leakage. We have already established that
which implies
Let us now consider the event \(\mathsf {coll}\) that, for an arbitrary but fixed (s, r), there exists any \((s', r')\) with \(s' \ne s\) such that \((b_1, \dots , b_n, a_T) = (b'_1, \dots , b'_n, a'_T)\). There are at most \(2^{p\widehat{t}}\) possible secret sharings and at most \(2^{p(\widehat{t}-\theta )}\) possible secret sharings that match the shares \(a_T\) at the indices T. By a union bound we have
For the probability of \(\lnot \mathsf {coll}\) to be larger than  it thus suffices that
it thus suffices that
To prevent the attack described above it must therefore hold that
which for \(\ell \ge 1\) is true if
\(\blacksquare \)
3.1 A Lower Bound via Randomness Complexity
In this section we prove a lower bound via randomness complexity. To motivate it, consider the bound in Theorem 2 for the case \(t = o(n)\). In this case we have that
So, if we consider the relative leakage, then we have that
This means that to have a constant leakage rateFootnote 2, one still needs \(\widehat{t} \in \varOmega (n)\). That is, after having enough shares to reconstruct, there still needs to be randomness left in many of the other remaining shares. This explains existing constructions of leakage-resilient secret sharing schemes, where shares contain a lot more randomness than what is actually needed to get privacy against \(t-1\) parties.
However, the above theorem does not give a quantitative enough handle on this phenomenon. One could trivially get \(\widehat{t} = n\) by adding an unused uniformly random bit to each share. But intuitively, this should not help against leakage-resilience. These bits are trivial in the sense that they could just be deleted. Neither should it help if we added a little bit of non-trivial randomness to the shares, as it could just be leaked. Below we prove a theorem which gets a better quantative handle of how much randomness there must be in the shares.
The following definition will be helpful in removing trivial randomness from consideration.
Definition 6
Let \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme where share number i has length \(p_i\). We call \({{\text {comp}}}= ({{\text {comp}}}_1, \ldots , {{\text {comp}}}_n)\) a compression of \(\mathcal {S}\) if it holds for \(i = 1, \ldots , n\) that \({{\text {comp}}}_i: \{0,1\}^{p_i} \rightarrow \{0,1\}^{q_i}\) and \(q_i \le p_i\). Define \(\textsc {Share}^{{\text {comp}}}\) by
where
and
We call a compression a correct compression of \(\mathcal {S}\) if for some \(\textsc {Rec}'\) it holds that \(\mathcal {S}^{{\text {comp}}}= (\textsc {Share}^{{\text {comp}}}, \textsc {Rec}')\) is again a t-out-of-n secret sharing scheme.
We now introduce a crude measure of the randomness complexity.
Definition 7
Let \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme. Let
Let
where the minimum is taken over all correct compressions of \(\mathcal {S}\). We call a correct compression \({{\text {comp}}}\) for \(\mathcal {S}\) for which it holds that \(\log _2 {\text {size}}\ \mathcal {S}^{{\text {comp}}}= {\text {ran}}\ \mathcal {S}\) a max-compression of \({{\text {comp}}}\).
Notice that the above measure is via max-entropy. This is a very crude notion of randomness, but for illustrating the phenomenon that a lot of randomness is left in each share, it works well and allows for a significantly simpler proof.
Notice that if you secret share a random secret s using a random r, then you will hit all possible secret sharings with non-zero probability. So, the length of the random s and r must be at least \({\text {ran}}\ \mathcal {S}\). So, if we can lower bound \({\text {ran}}\ \mathcal {S}\), we also lower bounded the amount of randomness needed to sample a secret sharing.
To connect the randomness complexity to the above theorems, notice that if a secret sharing scheme \(\mathcal {S}\) has share size p, then \({\text {ran}}\ \mathcal {S}\le \widehat{t} p\).
Theorem 4
Let \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\) be a t-out-of-n secret sharing scheme with \(\widehat{t}\)-full-reconstruction. If \(\mathcal {S}\) is  -weakly-leakage-resilient and \(\ell \ge 1\), then
-weakly-leakage-resilient and \(\ell \ge 1\), then
Proof
We prove the theorem by showing a generic attack that breaks \(\ell \)-WOW-LLR of any secret sharing scheme with \({\text {ran}}\ \mathcal {S}< \ell (n -t)\). The adversary A proceeds as follows.
-
1.
Let \({{\text {comp}}}= ({{\text {comp}}}_1, \ldots , {{\text {comp}}}_n)\) be a max-compression for \(\mathcal {S} = (\textsc {Share}, \textsc {Rec})\), where \({{\text {comp}}}_i: \{0,1\}^{p_i} \rightarrow \{0,1\}^{q_i}\).
-
2.
For \(i = 1, \ldots , n\), pick a uniformly random \(\textsc {Leak}_i: \{0,1\}^{q_i} \rightarrow \{0,1\}^{\ell }\).
-
3.
For \(i = 1, \ldots , n\), let \(\textsc {Leak}_i' = \textsc {Leak}_i \circ {{\text {comp}}}_i\).
-
4.
Submit \(\textsc {Leak}' = (\textsc {Leak}'_1, \ldots , \textsc {Leak}'_n)\) to the WOW-LLR.
-
5.
Get back \((b_1, \ldots , b_n) = (\textsc {Leak}_1({{\text {comp}}}_1(\mathsf {sh}_1)), \ldots , \textsc {Leak}_n({{\text {comp}}}_n(\mathsf {sh}_n)))\) where \((\mathsf {sh}_1, \dots , \mathsf {sh}_n) \leftarrow \textsc {Share}(s ; r)\) is a secret sharing of the secret s that the algorithm should try to recover.
-
6.
Call \(s' \in \{0,1\}^k\) consistent with \((b_1, \ldots , b_n)\) if there exists \(r'\) such that
$$(b_1, \ldots , b_n) = (\textsc {Leak}_1(\mathsf {sh}_1'), \ldots , \textsc {Leak}_n(\mathsf {sh}_n'))$$when
$$(\mathsf {sh}'_1, \dots , \mathsf {sh}'_n) \leftarrow \textsc {Share}^{{\text {comp}}}(s' ; r')\ .$$Compute
$$S = \{ s' \in \{0,1\}^k \,\vert \, s' \text { is consistent with } (b_1, \ldots , b_n) \}\ .$$ -
7.
If \(\vert S \vert > 1\), then output \(\bot \). Otherwise, let \(\{ s \} = S\) and output s.
Let \(\mathsf {succ}\) be the event that the output is not \(\bot \). It is trivial to see that \(s \in S\). Hence if \(\vert S \vert = 1\), then indeed \(S = \{ s \}\). So when A does not output \(\bot \), it outputs the correct secret s and wins the WOW-LLR. We conclude the theorem by proving that  .
.
Let \((\mathsf {sh}_1, \dots , \mathsf {sh}_n) \leftarrow \textsc {Share}(s ; r)\) be the secret sharing of the secret that A is trying to guess and denote by
the leakage from the i-th share. Let
be the secret sharing of some arbitrary but fixed secret \(s'\) with \(s \ne s'\) and let \(b'_i \leftarrow \textsc {Leak}_i(\mathsf {sh}'_i)\) be the corresponding leakage. By correctness of \({{\text {comp}}}\) we have that \((\textsc {Share}^{{\text {comp}}}, \textsc {Rec})\) is correct. This guarantees that there exists a set \(I \subseteq [n]\) with \(\vert I \vert \ge n-t+1\) such that \(\mathsf {sh}_i \ne \mathsf {sh}'_i\) for all \(i \in I\). So it clearly holds that
where the randomness is taken over a the random \((\textsc {Leak}_1, \ldots , \textsc {Leak}_n)\).
Let \(\mathsf {coll}\) be the event that there exists any \((s', r')\) with \(s' \ne s\) such that \((b_1, \ldots , b_n) = (\textsc {Leak}_1(\mathsf {sh}_1'), \ldots , \textsc {Leak}_n(\mathsf {sh}_n'))\) when \((\mathsf {sh}'_1, \dots , \mathsf {sh}'_n) \leftarrow \textsc {Share}^{{\text {comp}}}(s' ; r')\). Observe that \(\mathsf {succ} = \lnot \mathsf {coll}\). By definition there are at most \(2^{{\text {ran}}\mathcal {S}}\) possible secret sharings. So, by a union bound we get that

To prevent the attack described above, we therefore need that
where we used that \(\ell \ge 1\). \(\blacksquare \)
To illustrate the theorem, consider a secret sharing scheme with constant threshold t, share size p, which tolerates leakage \(\ell = (1 - o(1))p\). The theorem tells us that it must be the case that
So on average there are p bits of randomness in each share. In particular, after learning the constant number of shares needed to reconstruct, there is still about p bits of randomness left in each share that was not used for reconstructing. This quantifies that almost all randomness goes into achieving leakage-resilient and not into privacy of the secret sharing.
As another example, consider a secret sharing scheme with \(t < c n\) for a constant  and \(\ell = d p\) for a constant d. We get that
and \(\ell = d p\) for a constant d. We get that
We have that
and thus
So after learning t shares of length p the average number of bits of randomness left per share is at least
So if
there is still randomness left in the shares.
4 Leakage-Resilience of Shamir’s Secret Sharing
Benhamouda et al. [BDIR18] investigate the local leakage-resilience of Shamir’s secret sharing. Among other results, the authors show that Shamir’s scheme is not leakage-resilient if either the number of parties is constant or the secret sharing is done over a field with small characteristic. Using Fourier analytic techniques and additive combinatorics they show that t-out-of-n Shamir secret sharing is  -W-IND-LLR in prime order fields
-W-IND-LLR in prime order fields  . In the recently published full version of the same paperFootnote 3, the authors further show that it is 1-bit leakage-resilient for \(t \approx 0.85n\). They leave it open to find other parameter ranges in which local leakage-resilience does or does not hold and postulate Conjecture 1, which was already stated in the introduction.
. In the recently published full version of the same paperFootnote 3, the authors further show that it is 1-bit leakage-resilient for \(t \approx 0.85n\). They leave it open to find other parameter ranges in which local leakage-resilience does or does not hold and postulate Conjecture 1, which was already stated in the introduction.
Our lower bound does not disprove Benhamouda et al.’s conjecture, but it does tell us how large n and thus the shares would have to be if the conjecture is indeed true. By plugging in the concrete parameters from the conjecture into Theorem 2, we get that
has to hold for the conjecture to be true. Since \(p = \log {q} = \log {n}\) it follows that the share size has to be in  and thus \(n \in \varOmega (2^{\frac{1}{c}})\).
and thus \(n \in \varOmega (2^{\frac{1}{c}})\).
Furthermore, using Theorem 2, we can show that Shamir’s secret sharing is not local leakage-resilient for a large range of parameters. Concretely, we show that two natural strengthenings of Benhamouda et al.’s conjecture are not true. In Lemma 2 we consider a mildly smaller reconstruction threshold of  . In Lemma 3 we consider a larger leakage. See Fig. 1 in the introduction for an overview of these results. A possible interpretation of these results is that the original conjecture of Benhamouda et al. is essentially the best one can hope for.
. In Lemma 3 we consider a larger leakage. See Fig. 1 in the introduction for an overview of these results. A possible interpretation of these results is that the original conjecture of Benhamouda et al. is essentially the best one can hope for.
Lemma 2
Let q be the smallest prime larger than n. Then for any constant \( 0< c < 1\) and large enough n it holds that  -out-of-n Shamir secret sharing over \(\mathbb {F}_q\) is not
-out-of-n Shamir secret sharing over \(\mathbb {F}_q\) is not  -W-IND-LLR.
-W-IND-LLR.
Proof
Via Theorem 2, we know that the adversary successfully breaks leakage-resilience, whenever
Combining this inequality with the parameters from the stated theorem, we get that
has to hold, which is true for any \(0< c < 1\) for large enough n, since \(p = \log n\). \(\blacksquare \)
Lemma 3
Let q be the smallest prime larger than n. For any constant  and any n, there exists a constant \(0< d < 1\), such that cn-out-of-n Shamir secret sharing over \(\mathbb {F}_q\) is not
and any n, there exists a constant \(0< d < 1\), such that cn-out-of-n Shamir secret sharing over \(\mathbb {F}_q\) is not  -W-IND-LLR.
-W-IND-LLR.
Proof
For the attack from Theorem 2 to work we need that
Since \(p = \log {n}\), and \((1-c) > c\), it follows that the inequality holds for any \(\ell \ge \log n\) with any  . \(\blacksquare \)
. \(\blacksquare \)
Lemma 3 provides an interesting insight into the relationship between the number of bits sufficient for reconstruction and the number of leaked bits sufficient for breaking local leakage-resilience. In general, cn-out-of-n Shamir secret sharing requires cn full shares and thus \(cn \log {n}\) bits in total for reconstructing the secretFootnote 4. Reconstruction can be seen as a form of structured leakage, where cn full shares are leaked. Lemma 3 shows that (inefficient) reconstruction is possible from unstructured leakage when the leakage is a small constant fraction larger than what is needed for reconstruction anyways, e.g. if  , then we need
, then we need  bits for regular reconstruction and
bits for regular reconstruction and  bits for reconstruction from the leakage.
bits for reconstruction from the leakage.
Illustration of our efficient attack on 2-out-of-n Shamir secret sharing. The secret shared value is \(s_1\) and the solid line represents the linear function that was used during the secret sharing. The dashed lines depict the linear functions that are interpolated from the shares under the assumption that the secret shared value is \(s_0\). Two distinct incorrect points at \(x=\alpha _1\) are extrapolated.
4.1 An Efficient Attack for 2-Out-of-n Shamir Secret Sharing
All the results described above only apply to secret sharing schemes with information-theoretic security, since the proof of Theorem 2 relies on an adversary that can enumerate all possible secret sharings and thus runs in time at least exponential in the share size p. In the following, we show that for the specific case of 2-out-of-n Shamir secret sharing, we can break weak local leakage-resilience using only a single bit of leakage per share in a highly efficient manner. Our attack only requires  field operations and does not depend on any particular properties of the underlying field.
field operations and does not depend on any particular properties of the underlying field.
Theorem 5
For any \(\delta < 1 - 2^{-n}\), 2-out-of-n Shamir secret sharing over an arbitrary field \(\mathbb {F}_q\) is not \((\delta , 1)\)-W-IND-LLR. More concretely, there exists a distinguisher B that performs  field operations and breaks weak local leakage-resilience with a success probability of \(1-2^{-n-1}\).
field operations and breaks weak local leakage-resilience with a success probability of \(1-2^{-n-1}\).
Proof
Let \(s_0\) and \(s_1\) be two arbitrary distinct secrets that are output by the adversary. Let \(f_1\) be a uniformly random leakage function. For \(2 \le i \le n\), we hardcode \(s_0\), public values \((\alpha _1, \alpha _i)\), and \(f_1\) into the leakage function \(f_i\). On input \(\mathsf {sh}_i\), the function \(f_i\) interpolates a linear function \(P_i\) between the points \((0, s_0)\) and \((\alpha _i, \mathsf {sh}_i)\). It outputs \(f_1(P_i(\alpha _1))\). The adversary receives the leaked bits \(b_1, \dots , b_n\) and has to decide whether \(s_0\) or \(s_1\) was secret shared. If \(b_1 = b_2 = \dots = b_n\), then the adversary outputs guess \(g = 0\). Otherwise it outputs \(g = 1\).
Let us consider two cases. If \(s_0\) was secret shared, then \((0,s_0)\) lies on a line with all shares and thus, for \(2\le i \le n\), each \(f_i\) interpolates the P that was initially used to compute the shares. Therefore, it holds that each \(P_i(\alpha _1) = \mathsf {sh}_1\) and it follows that all leakage functions output the same bit \(f_1(\mathsf {sh}_1)\). If \(s_1\) was secret shared, then \((s_1, 0)\) does not lie on a line with the shares. It follows that, for each \(2\le i \le n\), \(f_i\) interpolates a distinct line \(P_i\). All these lines intersect in \((s_1, 0)\) and therefore if follows that all \((P_i(\alpha _1), \alpha _1)\) are distinct. Since \(f_1\) is a uniformly random function, we can conclude that the probability that \(b_1 = b_2 = \dots = b_n\) is \(2^{-n}\). A visual illustration of the reasoning above is depicted in Fig. 2. Let \(s_c\) be the secret shared value. Based on the above observations we get

\(\blacksquare \)
Assuming a stronger definition of leakage-resilience and thus a stronger adversary, we can extent the attack described above to larger thresholds. The basic idea behind the attack is that each leakage function can interpolate a linear function using a hardcoded candidate secret and the given share. Assuming our adversary can first see \(t-2\) shares and then adaptively select the leakage-functions, then the same attack goes through in a straightforward manner for t-out-of-n Shamir secret sharing, because the adversary can hardcode \(t-2\) shares in addition to some candidate secret and let each leakage function interpolate a degree t polynomial.
Corollary 2
For any \(\delta < 1 - 2^{-n}\), t-out-of-n Shamir secret sharing over an arbitrary field \(\mathbb {F}_q\) is not \((\delta , 1)\)-W-IND-LLR against an distinguisher that sees \(t-2\) shares before choosing the leakage functions. In particular, there exists a distinguisher that performs  field operations and breaks weak local leakage-resilience with a success probability of \(1-2^{-n-1}\).
field operations and breaks weak local leakage-resilience with a success probability of \(1-2^{-n-1}\).
5 Computational Leakage-Resilient Secret Sharing
A natural question is whether our lower bound from Sect. 3 also applies to computationally secure secret sharing schemes. In this section we answer this question in the negative by presenting a leakage-resilient secret sharing scheme, which violates our lower bound, in the random oracle model that is secure against computationally bounded adversaries.Footnote 5 More concretely we show:
Theorem 6
Let  be a security parameter. In the random oracle model there exists a
be a security parameter. In the random oracle model there exists a  -W-IND-LLR 2-out-of-n secret sharing scheme \(\mathcal{S} = (\textsc {Share}, \textsc {Rec})\) for 1-bit secrets with share size \(p = \) and full reconstruction threshold \(\widehat{t} = 2\) that is secure against computationally bounded adversaries that run in time
-W-IND-LLR 2-out-of-n secret sharing scheme \(\mathcal{S} = (\textsc {Share}, \textsc {Rec})\) for 1-bit secrets with share size \(p = \) and full reconstruction threshold \(\widehat{t} = 2\) that is secure against computationally bounded adversaries that run in time  .
.
Remark 1
Note that, for instance for \(\ell > n\) for sufficiently large n, such a secret sharing scheme violates the bound for information-theoretically secure schemes. For  the share size is
the share size is  . And we have that the secret sharing scheme tolerates \(\ell \)-bits of leakage from each share. When \(\widehat{t} = 2\) and information theoretic
. And we have that the secret sharing scheme tolerates \(\ell \)-bits of leakage from each share. When \(\widehat{t} = 2\) and information theoretic  -W-IND-LLR 2-out-of-n would need to have share size \(p \ge \frac{\ell (n-t)}{\hat{t}} = \varTheta (n \ell )\). So the computational version beats the information theoretic one by a factor n in share size.
-W-IND-LLR 2-out-of-n would need to have share size \(p \ge \frac{\ell (n-t)}{\hat{t}} = \varTheta (n \ell )\). So the computational version beats the information theoretic one by a factor n in share size.
Proof
For the sake of simplicity, assume we have access to the following multiple random oracles:

We construct the secret sharing scheme for 1-bit secrets \(m \in \{0,1\}\) from the theorem statement as follows.

-
1.
Pick a seed
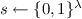 uniformly at random.
uniformly at random. -
2.
Compute \(s_1 \Vert s_2 = H_s(s)\).
-
3.
Define linear function g over
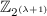 through \(g(1) = s_1\) and \(g(2) = s_2\)
through \(g(1) = s_1\) and \(g(2) = s_2\) -
4.
Extrapolate \(s_i = g(i)\) for \(i = 0, \dots , n\).
-
5.
Compute \(c = (s \Vert m) \oplus s_0\).
-
6.
Compute \(L_i = H_L(s \Vert i)\) and \(R_i = H_R(s \Vert i)\) for \(i = 1, \dots , n\).
-
7.
Compute \(R_i' = H_e(R_i)\) for \(i = 1, \dots , n\).
-
8.
Compute \(e_{i,j} = s_i \oplus \langle L_i, R_j' \rangle \) for \(i,j = 1, \dots , n\) with \(i \ne j\).
-
9.
\(P_i\)’s share \(\mathsf {sh}_i\) is defined as \((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\).
Reconstruction works as follows.

-
1.
Compute \(s_i = e_{i,j} \oplus \langle L_i, H_e(R_j) \rangle \) and \(s_j = e_{j,i} \oplus \langle L_j, H_e(R_i) \rangle \).
-
2.
Interpolate g from \(s_i\) and \(s_j\) and compute \(s_0 = g(0)\).
-
3.
Compute \((s \Vert m) = c \oplus s_0\) and return m.
It is easy to see that the proposed scheme is correct.
Note that besides learning m in reconstruction we also learn the seed s. From s we can recompute \(\textsc {Share}(m;s)\). The full reconstruction threshold \(\widehat{t}\) is 2, since given access to the random oracles, m, and s, any two parties can compute all \(L_i\), \(R_i\), \(e_{i, j}\), and thus all shares \(\mathsf {sh}_i\).
Since each party \(P_i\) holds exactly one \(L_i\), one \(R_i\), and \(n-1\) bits \(e_{i,j}\), it follows that the share size p is  .
.
It is straight forward to see that \(\textsc {Share}\) is a secret sharing scheme with threshold 2. Assume we are given one share \((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\). We have to argue that the share leaks no information on m. There are two cases, the query case and the no-query case. In the query case, at some point a query of one of the following forms were made \(H_R(s \Vert \cdot )\), \(H_L(s \Vert \cdot )\), or \(H_s(a)\). The non-query case is the complement.
If we are in the no-query case, then because we are in the random oracle model we can replace the secret sharing procedure with this one:

-
1.
Pick a seed
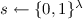 uniformly at random.
uniformly at random. -
2.
Sample uniformly random
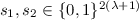 .
. -
3.
Define linear function g over
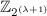 through \(g(1) = s_1\) and \(g(2) = s_2\)
through \(g(1) = s_1\) and \(g(2) = s_2\) -
4.
Extrapolate \(s_i = g(i)\) for \(i = 0, \dots , n\).
-
5.
Compute \(c = (s \Vert m) \oplus s_0\).
-
6.
Sample uniformly random
 and
and  for \(i = 1, \dots , n\).
for \(i = 1, \dots , n\). -
7.
Compute \(R_i' = H_e(R_i)\) for \(i = 1, \dots , n\).
-
8.
Compute \(e_{i,j} = s_i \oplus \langle L_i, R_j' \rangle \) for \(i,j = 1, \dots , n\) with \(i \ne j\).
-
9.
\(P_i\)’s share \(\mathsf {sh}_i\) is defined as \((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\).
It is straight forward to see that for all \(j \ne i\) we can replace \(H_e(R_j)\) by a uniformly random string, as there is not enough information in \(\mathsf {sh}_i\) to learn \(R_j\) and query \(H_e\) on this point. Namely, even if the adversary is given \(s_i\), the values \(\langle L_i, R_j' \rangle \) leaks at most one bit on \(R_j\). This gives this hybrid:

-
1.
Pick a seed
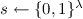 uniformly at random.
uniformly at random. -
2.
Sample uniformly random
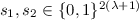 .
. -
3.
Define linear function g over
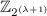 through \(g(1) = s_1\) and \(g(2) = s_2\)
through \(g(1) = s_1\) and \(g(2) = s_2\) -
4.
Extrapolate \(s_i = g(i)\) for \(i = 0, \dots , n\).
-
5.
Compute \(c = (s \Vert m) \oplus s_0\).
-
6.
Sample uniformly random
 and
and  for i and let \(R'_i = H_e(R_i)\).
for i and let \(R'_i = H_e(R_i)\). -
7.
Sample uniformly random
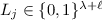 and
and 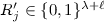 for \(j \ne i\).
for \(j \ne i\). -
8.
Compute \(e_{i,j} = s_i \oplus \langle L_i, R'_j \rangle \) for \(i,j = 1, \dots , n\) with \(i \ne j\).
-
9.
\(P_i\)’s share \(\mathsf {sh}_i\) is defined as \((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\).
Now given \(\mathsf {sh}_i\) without \(\{e_{i, j}\}_{j = 1,\dots , n}\) all the values \(\langle L_i, R'_j \rangle \) are statistically close to uniformly random and independent. Hence we can jump to this hybrid:

-
1.
Pick a seed
 uniformly at random.
uniformly at random. -
2.
Sample uniformly random
 .
. -
3.
Define linear function g over
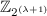 through \(g(1) = s_1\) and \(g(2) = s_2\)
through \(g(1) = s_1\) and \(g(2) = s_2\) -
4.
Extrapolate \(s_i = g(i)\) for \(i = 0, \dots , n\).
-
5.
Compute \(c = (s \Vert m) \oplus s_0\).
-
6.
Sample uniformly random
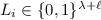 and
and 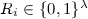 for i and let \(R'_i = H_e(R_i)\).
for i and let \(R'_i = H_e(R_i)\). -
7.
Sample uniformly random
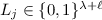 and
and 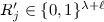 for \(j \ne i\).
for \(j \ne i\). -
8.
Sample uniformly random bits \(e_{i,j}\) for \(i,j = 1, \dots , n\) with \(i \ne j\).
-
9.
\(P_i\)’s share \(\mathsf {sh}_i\) is defined as \((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\)
Now \(\mathsf {sh}_i\) has no information on \(s_1\) and \(s_2\) and hence \(s_0\) is uniformly random given \(\mathsf {sh}_i\). Therefore we can replace \(c = (s \Vert m) \oplus s_0\) by a uniformly random value. At this point \(\mathsf {sh}_i\) contains no information on m or s.
This sequence of indistinguishable hubrids shows that when we are in the no-query case, then \(\mathsf {sh}_i\) is statistically close to independent from s and m, as desired. Note in particular that during an execution it holds until the point in time where we go into the query-case (because an oracle was queried on s for the first time) that \(\mathsf {sh}_i\) is statistically close to independent of s. This means that to query an oracle on s the adversary has to guess close to  bits of min-entropy on s. This happens with probability at most
bits of min-entropy on s. This happens with probability at most  . Therefore the query case happens with negligible probability. This concludes the proofs that \(\textsc {Share}\) is a secret sharing scheme with \(t=2\).
. Therefore the query case happens with negligible probability. This concludes the proofs that \(\textsc {Share}\) is a secret sharing scheme with \(t=2\).
We then argue that the secret sharing scheme is leakage resilient against \(\ell \) bits of leakage from each share. Here it is important that we are on the non-adaptive leakage case, where all leakage functions are picked before any leakage is seen. This ensures that when \(\textsc {Leak}_i((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\) is computed the leakage function has no information on s by the argument above that we are dealing with a secret sharing scheme with threshold \(t=2\). Hence by the sequence of hybrids above we see that \(R'_j \) is uniformly random in the view of \(\textsc {Leak}_i\) as it did not query \(H_e(R_j)\) except with negligible probability in polynomial time. Now notice that \(\textsc {Leak}_i((L_i, R_i, \{e_{i, j}\}_{j = 1,\dots , n}, c)\) will leave  bits of min-entropy in \(R_i\), as \(R_i\) has length
bits of min-entropy in \(R_i\), as \(R_i\) has length  and the leakage is at most \(\ell \) bits.
and the leakage is at most \(\ell \) bits.
In guessing the values \(\langle L_i, H_e(R_j) \rangle \) the adversary is therefore playing the following game.
Game\(^1\): Pick  uniformly at random. Ask for \(\ell \) bits of leakage on \(L_i\). Then be given \(R_j\) and try to guess \(\langle L_i, H_e(R_j) \rangle \).
uniformly at random. Ask for \(\ell \) bits of leakage on \(L_i\). Then be given \(R_j\) and try to guess \(\langle L_i, H_e(R_j) \rangle \).
An adversary winning this game, can be modified to win the following game by programming that random oracle at \(R_j\).
Game\(^2\): Pick  uniformly at random. Ask for \(\ell \) bits of leakage on \(L_i\). Then be given uniformly random
uniformly at random. Ask for \(\ell \) bits of leakage on \(L_i\). Then be given uniformly random  and try to guess \(\langle L_i, R_j' \rangle \).
and try to guess \(\langle L_i, R_j' \rangle \).
By the hard-core bit theorem, an adversary winning this game with non-negligible probability can guess \(L_i\) with non-negligible probability, a contradiction.
At this point the argument follows the one for secret sharing. We can first replace \(\{e_{i, j}\}_{j = 1,\dots , n}\) by uniformly random values and then replace c by a uniformly random value. At this point there is no more information on m in the secret sharing.
Notes
- 1.
We will precise define what we mean by meaningful information in Sect. 3.1.
- 2.
The leakage rate is defined as the ratio between the number of bits leaked per share and the share size in bits.
- 3.
- 4.
Over certain fields reconstruction can be performed with significantly fewer bits, but this approach does not work over general fields. See for example Guruswami and Wootters [GW16].
- 5.
Note that our lower bound easily extends to information-theoretically secure secret sharing schemes in the random oracle model. And unbounded distinguisher can learn the entire RO, so the RO does not help more than an exponentially long, uniformly random, common reference string (CRS). Our lower bound clearly generalises to the case with a CRS, as it goes via counting the expected number of secret sharings consistent with a given leakage. This counting argument is not affect by a public CRS.
References
Aggarwal, D., et al.: Stronger leakage-resilient and non-malleable secret-sharing schemes for general access structures. Cryptology ePrint Archive, Report 2018/1147 (2018). https://eprint.iacr.org/2018/1147
Benhamouda, F., Degwekar, A., Ishai, Y., Rabin, T.: On the local leakage resilience of linear secret sharing schemes. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 531–561. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_18
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.M., et al. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20901-7_2
Boyle, E., Goldwasser, S., Kalai, Y.T.: Leakage-resilient coin tossing. Distrib. Comput. 27(3), 147–164 (2014)
Bogdanov, A., Guo, S., Komargodski, I.: Threshold secret sharing requires a linear size alphabet. In: Hirt, M., Smith, A. (eds.) TCC 2016. LNCS, vol. 9986, pp. 471–484. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_18
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: 20th Annual ACM Symposium on Theory of Computing, pp. 1–10. ACM Press, May 1988
Blakley, G.R.: Safeguarding cryptographic keys, pp. 313–317. AFIPS Press (1979)
Badrinarayanan, S., Srinivasan, A.: Revisiting non-malleable secret sharing. Cryptology ePrint Archive, Report 2018/1144 (2018). https://eprint.iacr.org/2018/1144
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th Annual ACM Symposium on Theory of Computing, pp. 11–19. ACM Press, May 1988
Chor, B., Goldwasser, S., Micali, S., Awerbuch, B.: Verifiable secret sharing and achieving simultaneity in the presence of faults (extended abstract). In: 26th Annual Symposium on Foundations of Computer Science, pp. 383–395. IEEE Computer Society Press, October 1985
Desmedt, Y.: Society and group oriented cryptography: a new concept. In: Pomerance, C. (ed.) CRYPTO 1987. LNCS, vol. 293, pp. 120–127. Springer, Heidelberg (1988). https://doi.org/10.1007/3-540-48184-2_8
Desmedt, Y., Frankel, Y.: Threshold cryptosystems. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 307–315. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_28
Dziembowski, S., Pietrzak, K.: Intrusion-resilient secret sharing. In: 48th Annual Symposium on Foundations of Computer Science, pp. 227–237. IEEE Computer Society Press, October 2007
Goyal, V., Kumar, A.: Non-malleable secret sharing. In: Diakonikolas, I., Kempe, D., Henzinger, M. (eds.) 50th Annual ACM Symposium on Theory of Computing, pp. 685–698. ACM Press, June 2018
Goyal, V., Kumar, A.: Non-malleable secret sharing for general access structures. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10991, pp. 501–530. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96884-1_17
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006: 13th Conference on Computer and Communications Security, pp. 89–98. ACM Press, October/November 2006. Available as Cryptology ePrint Archive Report 2006/309
Guruswami, V., Wootters, M.: Repairing reed-solomon codes. In: Wichs, D., Mansour, Y. (eds.) 48th Annual ACM Symposium on Theory of Computing, pp. 216–226. ACM Press, June 2016
Heninger, N., Durumeric, Z., Wustrow, E., Alex Halderman, J.: Mining your PS and QS: detection of widespread weak keys in network devices. In: Proceedings of the 21st USENIX Security Symposium, Bellevue, WA, USA, 8–10 August 2012, pp. 205–220 (2012)
Kumar, A., Meka, R., Sahai, A.: Leakage-resilient secret sharing. Cryptology ePrint Archive, Report 2018/1138 (2018). https://eprint.iacr.org/2018/1138
Rabin, T., Ben-Or, M.: Verifiable secret sharing and multiparty protocols with honest majority (extended abstract). In: 21st Annual ACM Symposium on Theory of Computing, pp. 73–85. ACM Press, May 1989
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Shoup, V.: Practical threshold signatures. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 207–220. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_15
Srinivasan, A., Vasudevan, P.V.: Leakage resilient secret sharing and applications. Cryptology ePrint Archive, Report 2018/1154 (2018). https://eprint.iacr.org/2018/1154
Waters, B.: Ciphertext-policy attribute-based encryption: an expressive, efficient, and provably secure realization. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 53–70. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19379-8_4
Acknowledgements
We would like to thank Maciej Obremski for helpful discussions during the initial stages of this project.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Nielsen, J.B., Simkin, M. (2020). Lower Bounds for Leakage-Resilient Secret Sharing. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12105. Springer, Cham. https://doi.org/10.1007/978-3-030-45721-1_20
Download citation
DOI: https://doi.org/10.1007/978-3-030-45721-1_20
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45720-4
Online ISBN: 978-3-030-45721-1
eBook Packages: Computer ScienceComputer Science (R0)







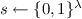 uniformly at random.
uniformly at random.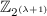 through
through 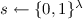 uniformly at random.
uniformly at random.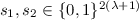 .
.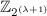 through
through  and
and  for
for 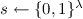 uniformly at random.
uniformly at random.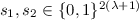 .
.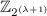 through
through  and
and  for i and let
for i and let 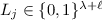 and
and 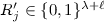 for
for  uniformly at random.
uniformly at random. .
.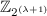 through
through 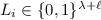 and
and 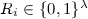 for i and let
for i and let 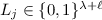 and
and 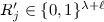 for
for 