Keywords

1 Introduction

Electroencephalography (EEG) [19, 25] and magnetoencephalography (MEG) [7] noninvasively record electric potentials and magnetic fields, respectively, due to neural currents. These methods are used as tools in clinical research, in basic neuroscience, and as diagnostic and monitoring measures in clinical practice. In addition, EEG, as well as invasive neurophysiological recordings, may be applied to enable brain-computer interfaces or BCIs (see, e.g., [1, 12, 26]) with the goal of mitigating various neurological disabilities [34].

In the most demanding clinical evaluations, EEG and/or MEG is followed by direct recordings with subdural or intraparenchymal depth electrodes. A modern high-resolution intracranial recording technique – intracranial electroencephalography or iEEG – is blossoming in various fields of human neuroscience [21]. At present, intracortical arrays with electrodes as small as 20 μm in size and with 25–100 μm electrode spacings are designed and tested (see, e.g., [37]). Local field potential (LFP) electrodes are, for example, 50-μm-diameter tungsten microwires [36]. A similar tendency toward fine resolution is observed for more accurate MEG measurement techniques [9, 24].

The ultimate goal of neurophysiological recordings of any type is an estimation of the sources generating the measured signal patterns. These sources are electric currents flowing in the micrometer-size sparse neuronal arbor; consider, for example, the arbor of pyramidal neurons in layers II and III of the neocortex shown in Fig. 1a. A large group or a cluster of such synchronously activated cortical neurons shown in Fig. 1b is the basic block in the analysis of EEG and MEG. At present, direct modeling of such extremely complicated current distributions is not possible with commonly used numerical methods, i.e., the finite element method, the boundary element method, and the finite difference method.

Fig. 1
figure 1

(a) Computer reconstruction of neuronal arbor made of clones of a realistic pyramidal neuron ID NMO_86955 from the NeuroMorpho.Org inventory Version 7.5 in layers II and III with a density of approximately 150 neurons per mm2 [2]. For this work, we did not study the field originating in layer V even though the large PNs in this layer can also produce strong electric and magnetic fields locally inside the brain. (b) A neuronal cluster with an area of approximately 16 mm2 and 2450 individual neurons reconstructed in layers II and III of the anterior central gyrus for subject #101309 of the Human Connectome Project [31]; see also the Population Head Model Repository [11, 30]. (c) Equivalent electric-current dipole model located at the “electric” gravity center of the cluster. GM stands for gray matter, WM for white matter, and CF for cerebrospinal fluid conductivity boundaries

Full size image

Therefore, a lumped macroscopic electric-current dipole model shown in Fig. 1c, which consists of a closely spaced or coinciding source and sink of electric current in a conducting medium, has traditionally been used as a source substitute for the cluster of synchronously activated cortical neurons in the analysis of EEG and MEG [7, 15, 19, 25]. Several excellent open-source software packages for the dipole-based EEG/MEG analysis are available, including Brainstorm [29], FieldTrip [20], and MNE [5].

This model is indeed a physically valid substitute for any ensemble of microscopic dipolar current sources in a homogeneous conducting medium and in the far field, i.e., at distances significantly exceeding the cluster size. However, when irregular conductivity boundaries are present in the immediate vicinity of the cluster, they may disturb the current distribution. As a result, even the integral far-field response might be different from that of the equivalent dipole.

The fast multipole method or FMM [6, 23] enables computing the response of many millions of microscopic electric sources for a comparable or even larger number of observation or target points in a short amount of time. A proper coupling of the fast multipole method and the boundary element method – the BEM-FMM approach suggested in [8, 13, 14] – further enables computing the corresponding induced charge distribution at tissue conductivity boundaries which, in turn, results in obtaining precise current, voltage, and magnetic field distributions at the boundaries and everywhere in space.

Using the BEM-FMM, one may be in position to depart from the simplified dipole model in Fig. 1c toward a more realistic computational model which follows actual microscopic electric current flow in every dendritic or axonal branch of a neuron as shown in Fig. 2a, b. Along with this, current splitting and combining according to Kirchhoff’s current law or KCL is enforced as illustrated in Fig. 2c.

Fig. 2
figure 2

(a) Morphology of neocortical pyramidal neuron ID NMO_86955 from the NeuroMorpho.Org inventory Version 7.5. (b) Realistic current paths within the microscopic arbor are schematically indicated by small circles. The circles are simultaneously the poles (9318 in the present case) or the sources and sinks of elementary current sources – microscopic electric dipoles – situated within the firing arbor. (c) Current conservation law illustrated by different sizes of the poles – microscopic current dipole strengths. We assume the same current inflow/outflow at all synaptic connections (arbor terminations) of apical dendrites with the total current accumulating toward the soma

Full size image

Moreover, one may be in position to model a large group of such tightly spaced neurons firing simultaneously, i.e., directly model the entire compact cluster of cortical neurons. Such a cluster may be located anywhere in the cerebral cortex. The realistic cluster size may be as large as 10,000 individual neurons, while the overall computation times do not exceed several minutes on a standard server.

This study is aimed to apply the developed method to answer the following question: how well does the conventional dipole model approximate a cluster of neurons with an area of 16–25 mm2 (1/7500 to 1/4800 of the total cerebral cortex area) when approaching the cortical boundaries?

2 Materials and Methods

2.1 Gyrus Cluster Construction and Analysis

Due to the geometry and electrophysiological characteristics of cortical neurons, a gyrus cluster, which is essentially parallel to the skull surface, is expected to generate a strong EEG response but a weak MEG response. Figure 3a–c shows one reconstructed gyrus cluster with an area of approximately 16 mm2 and 2450 individual pyramidal neurons (ID NMO_86955 from the NeuroMorpho.Org) located in layers II and III of the anterior central gyrus for subject #101309 of the Human Connectome Project [31]. A realistic neuronal density of approximately 150 neurons per mm2 [2] has been implemented. To do so, we cloned the individual neuron model shown in Fig. 2a for a large number of locations between the white matter (WM) and gray matter (GM) surfaces, aligned the neurons with the surface normal vectors, then moved them toward a position that was approximately 1 mm away from the WM triangular surface in the direction of its outer normal vector.

Fig. 3
figure 3

(a) Position of the gyrus cluster beneath the gray matter shell along with the coronal and sagittal observation planes. (b) Zoomed in position of the cluster between gray matter and white matter shells – the nearest macroscopic conductivity boundaries. (c) Zoomed in display of the cluster topology with a length of approximately 4 mm. Pale ivory color corresponds to apical dendrites

Full size image

The microscopic neural origin of the primary currents in EEG/MEG is thought to be the aggregate of postsynaptic longitudinal currents flowing inside the apical dendrites of the large, spatially aligned neocortical pyramidal neurons or PNs [18, 27]. We therefore assumed that the synchronized electric currents flow only in the apical dendrites of the neurons, which are shown pale ivory in Fig. 3c. The longest apical dendrite branch has a length of approximately 500 μm. We also assumed equal outflowing currents at all available synaptic connections with the total current accumulated (via accurately traversing the dendritic tree) and then terminated at the soma.

The apical dendrite branches of a single neuron have been divided into M = 2387 individual straight segments – microscopic current dipoles – each with an average length of 1.2 μm. The corresponding poles are seen in Fig. 2c. This detailed model is somewhat superfluous for EEG or iEEG purposes since all intermediate current sources along a branch will cancel out and only the end synapse sources and the soma source of opposite polarity will remain significant. However, it is meaningful for MEG purposes since the entire current path along the neuronal arbor will be reflected in the measurements. The total number of microscopic dipole sources in the present cluster is approximately 6 M.

To choose a realistic value of current dipole moment density q0 (current dipole moment per unit cross-sectional area of the active cortex) in the source region, we used the value q0 = 1 nA ∙ m/mm2 found by Murakami and Okada [17]. This value is invariant across the cerebral cortex, hippocampus, and cerebellum over a wide phylogenetic scale from reptiles to humans. This value also agrees with the dipole moment density estimated from a neural current magnetic resonance imaging (MRI) study [28]. When the microscopic dipole vector length is dm and its relative weight (equal to one at synapses and equal to 18 at the soma in the present case) is wm, an expression for the resulting current constant I0 follows from

$$ \frac{Neurons}{mm^2}\times {I}_0\sum \limits_{m=1}^M{w}_m{\boldsymbol{d}}_m={q}_0 $$
(1)

which yields I0 = 1.8 nA.

The moment of an equivalent lumped dipole shown in Fig. 1c was found as a vector sum of all individual dipole moments in the cluster. The center of an equivalent lumped dipole was found as the weighted average of all individual dipole centers in the cluster. The weights are the magnitudes of individual dipole moments.

Finally, the underlying macroscopic head model used surface meshes for seven brain compartments of the Population Head Model Repository [11, 30]. Further, the surface mesh was refined (oversampled) using a 1 × 4 barycentric triangle subdivision, and then surface-preserving Laplacian smoothing [32, 33] was applied. This resulted in the surface mesh resolution (edge length) of 0.75 mm in the cortex.

Two measurable output quantities obtained via numerical computations are the electric potential for EEG/iEEG and the magnetic field for MEG. We used a linear scale for all surface plots including inner skull or pia mater surface, skin surface, and a surface at the distance of 18 mm from the skin (a “magnetometer” surface used for MEG purposes only). For the surface plots, only the normal component of the magnetic field recorded by the flat MEG magnetometers was plotted and analyzed.

For volumetric plots corresponding to intracranial recordings close to the cluster, larger potential/field variations may be observed. In the last case, we used the log-modulus transformation [10]

$$ {\varphi}_{dB}=\mathit{\operatorname{sign}}\left(\varphi \right)\bullet 20{\log}_{10}\left(\frac{\varphi }{\varphi_0}+1\right),{\varphi}_0=0.4\ \upmu \mathrm{V} $$
(2)

A similar logarithmic transformation but without the additive constant equal to one was applied to the magnetic field magnitude with B0 = 0.4 pT.

To analyze the surface/interface data, we used two error measures to distinguish between topography and magnitude errors, respectively. These are the relative difference measure or RDM defined here as [3, 16, 22, 35]:

$$ E=\left\Vert \frac{\varphi_1}{\left\Vert {\varphi}_1\right\Vert }-\frac{\varphi_2}{\left\Vert {\varphi}_2\right\Vert}\right\Vert $$
(3)

and the magnitude (MAG) error defined as [16]:

$$ MAG=\frac{\left\Vert {\varphi}_1\right\Vert }{\left\Vert {\varphi}_2\right\Vert } $$
(4)

with φ1 being the cluster potential.

Along with this, we computed the ratio of maximum potential differences. The identical definitions were applied for the normal component of the magnetic field at the interfaces.

2.2 Sulcus Cluster Construction and Analysis

A sulcus cluster, which is essentially perpendicular to the skull surface, is expected to generate a weak EEG response but a strong MEG response. Figure 4a–c shows one reconstructed sulcus cluster with an area of approximately 25 mm2 and 3175 individual pyramidal neurons (ID NMO_86955 from the NeuroMorpho.Org) with approximately 8 M microscopic dipole sources located in layers II and III of the superior frontal sulcus for the same subject #101309 of the Human Connectome Project [31]. A slightly lower neuronal density of approximately 112 neurons per mm2 was used. However, for the current dipole moment density, we again used the value q0 = 1 nA ∙ m/mm2 found by Murakami and Okada [17] so that the total dipole moment of the cluster appears approximately 25/16 times greater than in the previous case. This was done to compensate for a larger distance from the skull surface, which is larger in the present case by a factor of approximately 5/4. Otherwise, all other parameters and the method of analysis remain the same.

Fig. 4
figure 4

(a) Position of the sulcus cluster beneath the gray matter shell along with the coronal and sagittal observation planes. (b) Zoomed in position of the cluster between gray matter and white matter shells – the nearest macroscopic conductivity boundaries. (c) Zoomed in display of the cluster topology with a length of approximately 2 mm. Pale ivory color corresponds to apical dendrites

Full size image

2.3 Modeling Algorithm

The complete mathematical algorithm of the boundary element fast multipole method, along with justification examples, will be described elsewhere. The present computations use the most recent version of the FMM library originally developed by Gimbutas and Greengard [4] and run on an Intel Xeon E5-2683 v4 CPU (2.1 GHz) server with 256 GB RAM, Windows Server 2008 R2 Enterprise, implemented on the MATLAB 2018a platform. Apart from the computations of static model-specific parameters – potential surface integrals for macroscopic boundaries – the corresponding iterative solution reaches a relative residual of 10−3 in approximately 80 sec and in ten iterations. These data are for the macroscopic head model with approximately 3 M facets and 6–8 M individual microscopic dipole sources.

3 Results

3.1 Gyrus (Nearly Horizontal) Cluster

Figure 5 shows the data for the electric potential. The left column corresponds to the cluster model, while the right column corresponds to the equivalent macroscopic current dipole. Figure 5a,b displays the volumetric potential distribution in the immediate vicinity of the cluster and the dipole, respectively. A logarithmic scale in decibels given by Eq. (2) is used. As expected, the dipole response is “sharper,” i.e., more localized in space, especially close to the pia or inner skull surface. This circumstance potentially leads to a larger RDM error given by Eq. (3), although “centers of gravity” of both responses nearly coincide, as shown by the potential distributions on the pia (Fig. 5c,d) and skin (Fig. 5e,f) surfaces, respectively. It is worth noting that the maximum values of the surface potential differ by a factor of approximately two for the pia mater.

Fig. 5
figure 5

Electric potential data for the gyrus cluster (left column) versus the equivalent-dipole data (right column). (a, b) Volumetric potential distribution in the immediate vicinity of the cluster and the dipole, respectively, using a logarithmic scale. (c, d) Surface potential distribution on the inner skull (pia) surface using a linear scale. (e, f) Surface potential distribution on the skin surface using a linear scale

Full size image

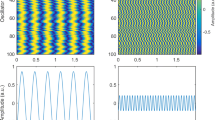
Figure 6 shows the corresponding data for the magnetic field. The left column corresponds to the cluster model, while the right column corresponds to the equivalent macroscopic current dipole. Figure 6a,b displays the volumetric distribution of the magnitude of the total magnetic field in the immediate vicinity of the cluster and the dipole, respectively. The cluster response is more inhomogeneous. A logarithmic scale in decibels given by Eq. (2) is used. Figure 6c–f shows the normal surface component (in the direction of the outer normal vector) of the magnetic field recorded by a magnetometer for the pia and skin surfaces, respectively. We observe a modest change in the field distribution pattern.

Fig. 6
figure 6

Magnetic field data for the gyrus cluster (left column) versus the equivalent-dipole data (right column). (a, b) Volumetric field magnitude distribution in the immediate vicinity of the cluster and the dipole, respectively, using a logarithmic scale. (c, d) Normal magnetic field distribution on the inner skull (pia) surface using a linear scale. (e, f) Normal magnetic field on the skin surface using a linear scale

Full size image

3.2 Sulcus (Predominantly Vertical) Cluster

Figure 7 shows the data for the electric potential. The left column corresponds to the cluster model, while the right column corresponds to the equivalent macroscopic current dipole. Figure 7a,b displays the volumetric potential distribution in the immediate vicinity of the cluster and the dipole, respectively. A logarithmic scale in decibels given by Eq. (2) is used. Again, the dipole response is somewhat “sharper,” i.e., more localized in space. A case in point is an isocurve corresponding to 38 dB in Fig. 7a,b. Potential distributions on the pia (Fig. 7c,d) and skin (Fig. 7e,f) surfaces visually look similar, at least at first sight.

Fig. 7
figure 7

Electric potential data for the sulcus cluster (left column) versus the equivalent-dipole data (right column). (a, b) Volumetric potential distribution in the immediate vicinity of the cluster and the dipole, respectively, using a logarithmic scale. (c, d) Surface potential distribution on the inner skull surface using a linear scale. (e, f) Surface potential distribution on the skin surface using a linear scale

Full size image

It is worth noting that the maximum surface potential differences appear to be higher for the cluster, which is exactly the opposite of the previous case.

Figure 8 shows the corresponding data for the magnetic field. The left column corresponds to the cluster model, while the right column corresponds to the equivalent macroscopic current dipole. Figure 8a,b displays the volumetric distribution of the magnitude of the magnetic field in the immediate vicinity of the cluster and the dipole, respectively. The cluster response is more inhomogeneous. A logarithmic scale in decibels given by Eq. (2) is used. Figure 8c–f shows the normal surface component (in the direction of the outer normal vector) of the magnetic field recorded by a magnetometer for the pia and skin surfaces, respectively. We observe a visual similarity in the field distribution patterns.

Fig. 8
figure 8

Magnetic field data for the sulcus cluster (left column) versus the equivalent-dipole data (right column). (a, b) Volumetric field magnitude distribution in the immediate vicinity of the cluster and the dipole, respectively, using a logarithmic scale. (c, d) Normal magnetic field distribution on the inner skull surface using a linear scale. (e, f) Normal magnetic field on the skin surface using a linear scale

Full size image

3.3 Quantitative Error Measures

Tables 1 and 2 summarize data for the RDM error given by Eq. (3), logarithmic magnitude (lnMAG) error given by Eq. (4), and the error in the maximum swing of the electric potential or the normal surface magnetic field, respectively, for both cases. For the normal magnetic field, we additionally include data for a magnetometer surface that was chosen to be located at a distance of 18 mm from the skin surface. Quite surprisingly, a relatively large topographic error is generated for the electric potential, despite a good visual agreement observed in Figs. 5 and 7, respectively.

Table 1 Quantitative potential/normal magnetic field deviations: gyrus cluster of 16 mm2
Full size table
Table 2 Quantitative potential/normal magnetic deviations: sulcus cluster of 25 mm2
Full size table

4 Conclusions

When the absolute response values are ignored and only the response topology or distribution in space is concerned, the representative error measure is the RDM error marked blue in Tables 1 and 2, respectively. It follows from these tables that, quantitatively, the MEG data generally indicate a better agreement between the distributed multiscale neuronal cluster model and the equivalent macroscopic lumped-dipole model. This is especially true for the magnetometer surface separated from the skin and for the most important case of the MEG sulcus cluster. The MEG RDM error also generally decreases when the distance from the cluster increases. This is in contrast to the EEG/iEEG data where the RDM error might even increase (!) when moving from the pia surface to the skin surface (Table 1).

As to the absolute response values, we observe from Figs. 5, 6, 7, and 8, from Tables 1 and 2, and from the relevant modeling data that the EEG/iEEG lumped-dipole model

  1. (i)

    Slightly overestimates the maximum iEEG/EEG response for the gyrus cluster

  2. (ii)

    Significantly underestimates the maximum iEEG/EEG response for the sulcus cluster

On the other hand, the MEG dipole model

  1. (i)

    Is in good agreement with the cluster model on the skin surface and the magnetometer surface (18 mm away from skin) for the gyrus cluster

  2. (ii)

    Significantly underestimates the maximum MEG pia/skin/magnetometer surface response for the sulcus cluster.

These observations were confirmed by running several additional relevant cases.

Since the developed BEM-FMM algorithm is quite fast, it might be possible in future to replace the entire macroscopic dipole approach by the distributed neuronal arbor modeling.