Abstract
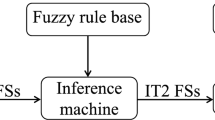
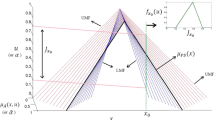
Although fuzzy control technique has been widely developed in main scientific applications and engineering system, a challenging research problem how to design the appropriate parameters of fuzzy controller in the different applications still has drawn attention of researchers in various fields. Two approximating-based methods included in this paper are summarized from our previous work. One is that the parameters of Gaussian membership function can be approximately calculated when the range and mean of the input data are given. Another is that a best crisp approximation of fuzzy set can be calculated such that an interval type-2 fuzzy set can be reduced to a type-1 fuzzy set.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
C.W. Tao, J.S. Taur, Design of fuzzy controllers with adaptive rule insertion. IEEE Trans. Syst. Man Cybern.SMC-29(3), 389–397 (1999)
L.A. Zadeh, Fuzzy sets. Inform. Control 8(3), 338–353 (1965)
D. Driankov, H. Helendoorn, M. Reinfrank, An Introduction to Fuzzy Control (Springer, New York, 1993)
H.-T. Nguyen, V. Kreinovich, How stable is a fuzzy linear system, in Proceedings od 3rd IEEE Conference on Fuzzy Systems (1994), pp. 1023–1027
H.T. Nguyen, Fuzziness in statistics, in Presented at the Speech Notes, Taiwan (2000)
C.W. Tao, J.S. Taur, Robust fuzzy control for a plant with fuzzy linear model. IEEE Trans. Fuzzy Syst. 13(1), 30–41 (2005)
C.-C. Lee, Fuzzy logic in control systems: fuzzy logic controller part I. IEEE Trans. Syst. Man Cybern. 20(2), 404–418 (1990)
K.-H. Su, S.-J. Huang, C.-Y. Yang, Development of robotic grasping gripper based on smart fuzzy controller. Int. J. Fuzzy Syst. 17(4), 595–608 (2015)
C.W. Tao, M.L. Chan, T.T. Lee, Adaptive fuzzy sliding mode controller for linear systems with mismatched time-varying uncertainties. IEEE Trans. Syst. Man Cybern. Part B Cybern. 33(2), 238–294 (2003)
K. Hirota, Industrial Application of Fuzzy Technology (Springer, New York, 2004)
P.-Z. Lin, C.-M. Lin, C.-F. Hsu, T.-T. Lee, Type-2 fuzzy controller design using a sliding-mode approach for application to dc-dc converters. IEE Proc. Electr. Power Appl. 152(6), 1482–1488 (2005)
L.A. Zadeh, The concept of a linguistic variable and its application to approximate reasoning I. Inf. Sci. 8(3), 199–249 (1975)
E. Roventa, T. Spircu, Averaging procedures in defuzzification processes. Fuzzy Sets Syst. 136, 375–385 (2003)
Y. Ogura, S. Li, D. Ralescu, Set defuzzification and choquet integral. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 9(1), 1–12 (2001)
J.M. Mendel, Uncertain Rule-based Fuzzy Logic Systems: Introduction and New Directions (Prentice-Hall, Upper Saddle River, 2001)
D. Wu, J.M. Mendel, Enhanced-karnik-mendel algorithms. IEEE Trans. Fuzzy Syst. 17(4), 923–934 (2009)
N.N. Karnik, J.M. Mendel, Q. Liang, Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 7(6), 643–658 (1999)
J.M. Mendel, Advance in type-2 fuzzy sets and systems. Inf. Sci. 177(1), 84–110 (2007)
F.J. Lin, P.H. Chou, Adaptive control of two-axis motion control system using interval type-2 fuzzy neural network. IEEE Trans. Ind. Electron. 56(1), 178–193 (2009)
H. Wu, J.M. Mendel, Uncertainty bounds and their use in the design of interval type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 10(5), 622–639 (2002)
M. Melgarejo, A fast recursive method to compute the generalized centroid of an interval type-2 fuzzy set, in 2007 Annual Meeting of the North American Fuzzy Information Processing Society (2007), pp. 190–194
H. Bernal, K. Duran, M. Melgarejo, A comparative study between two algorithms for computing the generalized centroid of an interval type-2 fuzzy set, in IEEE International Conference on Fuzzy Systems (2008), pp. 954–959
K. Duran, H. Bernal, M. Melgarejo, Improved iterative algorithm for computing the generalized centroid of an interval type-2 fuzzy set, in Fuzzy Information Processing Society (2008), pp. 1–5
C.W. Tao, C.-W. Chang, J.S. Taur, A simplify type reduction for interval type-2 fuzzy sliding controllers. Int. J. Fuzzy Syst. 15(4), 460–470 (2013)
C.W. Tao, J.S. Taur, C.-W. Chang, H.-R. Chen, An alternative type reduction approach based on information combination with interval operations for interval-valued fuzzy sliding controllers. Int. J. Intell. Syst. 32(3), 291–309 (2016)
S. Chanas, On the interval approximation of a fuzzy number. Fuzzy Sets Syst. 122, 353–356 (2001)
C.W. Tao, J. Taur, J.H. Chang, S.-F. Su, Adaptive fuzzy switched swing-up and sliding control for the double-pendulum-and-cart system. IEEE Trans. Syst. Man Cybern. Part B Cybern. 40, 241–252 (2010)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Chang, CW., Tao, CW. (2021). Applications of Type-2 Fuzzy Sets with Set Approximation Approaches: A Summary. In: Kreinovich, V. (eds) Statistical and Fuzzy Approaches to Data Processing, with Applications to Econometrics and Other Areas. Studies in Computational Intelligence, vol 892. Springer, Cham. https://doi.org/10.1007/978-3-030-45619-1_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-45619-1_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45618-4
Online ISBN: 978-3-030-45619-1
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)