Fast, Compact, and Expressive Attribute-Based Encryption

Abstract

Attribute-based encryption (ABE) is an advanced cryptographic tool and useful to build various types of access control systems. Toward the goal of making ABE more practical, we propose key-policy (KP) and ciphertext-policy (CP) ABE schemes, which first support unbounded sizes of attribute sets and policies with negation and multi-use of attributes, allow fast decryption, and are adaptively secure under a standard assumption, simultaneously. Our schemes are more expressive than previous schemes and efficient enough. To achieve the adaptive security along with the other properties, we refine the technique introduced by Kowalczyk and Wee (Eurocrypt’19) so that we can apply the technique more expressive ABE schemes. Furthermore, we also present a new proof technique that allows us to remove redundant elements used in their ABE schemes. We implement our schemes in 128-bit security level and present their benchmarks for an ordinary personal computer and smartphones. They show that all algorithms run in one second with the personal computer when they handle any policy or attribute set with one hundred attributes.

1 Introduction

Attribute-based encryption (ABE) [17] is an advanced form of public key encryption (PKE), which yields fine-grained access control over encrypted data. More concretely, ABE allows us to embed an attribute x into a ciphertext when we encrypt a message. An authority that has a master secret key can issue a secret key that is associated with a predicate y. The ciphertext can be decrypted with the secret key only if x and y satisfy some relation R.

Previously, ABE schemes have been proposed for various relations, such as equality [9], threshold [29], orthogonality of vectors [19], and so on. One of the most notable relations among them is that expressed by an access structure [7, 17]. In a key-policy ABE (KP-ABE) scheme, for instance, one can embed an access structure in a secret key such as (Year:1991–2000 AND Category:jazz). The secret key can decrypt ciphertexts that have attributes Year:1991–2000 and Category:jazz but cannot ones that only have at most one of them. Ciphertext-policy ABE (CP-ABE) is a dual of KP-ABE and allows us to embed an access structure into ciphertexts.

Recently, Agrawal and Chase proposed practical KP-ABE and CP-ABE schemes named FAME [1], which are the first schemes that simultaneously:

• 1. have no restriction on sizes of policies and attribute sets (unboundedness);

• 2. allow an arbitrary string as an attribute (large universe);

• 3. are based on the fast Type-III pairings;

• 4. need a small number of pairings for decryption;

• 5. satisfy the adaptive security under standard assumptions.

All these properties are arguably important in practice. We briefly explain the reasons. The first two properties say about scalability. It is not uncommon that we extend a system to add new attributes to a database in operation. In such cases, scalability is essential property because if the scheme does not have the scalability, we need a redeployment of the scheme. The second two properties say about efficiency. The efficiency of building blocks directly affects that of the entire system. Thus, efficient cryptographic schemes are desirable. The final property says about security. In contrast to the selective security, the adaptive security considers a model that captures a natural attack of an adversary against a scheme. Additionally, standard assumptions are based on well-studied hard problems and thus reliable. Hence, the adaptive security under standard assumptions guarantees that schemes are secure enough.

1.1 Our Contribution

Toward the goal to make ABE schemes more usable and realistic, we propose more expressive schemes. More precisely, we propose KP-ABE and CP-ABE schemes that satisfy all the above properties and additionally allow us to use

• 6. negation in a natural form (non-monotonicity);

• 7. the same attribute more than once (multi-use of attributes or compactness);

in a policy. These properties allow us to use more fine-grained policies that are commonly used in practice. Negation is essential for access control by blacklisting. Multi-use of attributes in policies is indispensable to express certain types of policies such as (A AND B) OR (A AND C) OR (B AND D), where A, B, C, D are Boolean variables.

Thanks to great works on ABE [3, 21, 27], we have several ABE schemes that can handle unbounded sizes of attribute sets and policies in prime-order groups. To our knowledge, however, there are no schemes that achieve all the properties listed above simultaneously. We summarize previous schemes and ours in Table 1.

One note is that our schemes require the random oracle model for security analysis as well as FAME. Whereas a random oracle cannot be replaced with any implemented hash function in some particular cases [11], it is still a widely accepted and standard methodology to analyze the security of cryptographic schemes. Actually, many practical schemes that are used in the real world require the random oracle model for their security analysis [5, 6, 15].

In the following, we elaborate on the last two properties.

Table 1. Comparison of unbounded KP and CP-ABE schemes based on prime-order groups.

Non-monotonicity. Previously, there are several works that consider access structures including negation (non-monotone access structures) in ABE [3, 4, 24, 26,27,28, 32]. Among them, only the negation form defined by Okamoto and Takashima (OT negation) [26, 27] is different from that by the others (non-OT negation). Considering an example is the best way to describe the difference. Let attributes consist of a pair of a label and value, e.g., Year:1991–2000, where Year is a label and 1991–2000 is a value. Suppose there are two labels Year and Category in an access control system supported by KP-ABE. Then, non-OT negation is like (NOT Year:1991–2000) whereas OT negation is like (Year:NOT 1991–2000). Semantically, the former implies that the secret key can decrypt a ciphertext if it does not have attribute Year:1991–2000. On the other hand, the latter implies that a ciphertext is decryptable if it has an attribute on label Year and its attribute is not 1991–2000.

When we consider large universe ABE, which is exactly the desirable case in practice, the natural negation form is arguably OT negation. In large universe ABE, it is unreasonable to fix all attributes used in a system at the setup phase because the most significant advantage of large universe ABE is that we can utilize an exponentially large number of attributes. Associating strings with attributes that the ABE scheme handles in an ad-hoc way by a hash function would be a better solution. However, if we use non-OT negation in the system, we have to fix all attributes that the system supports at the setup phase. This is because a secret key whose policy is negation of an attribute that the system has not supported before can decrypt all ciphertexts generated so far. More concretely, in the above example, we consider the case where we add a new label Artist in the system. Then, if an authority issues a key whose policy is (NOT Artist:The Beatles), all previous ciphertexts are decrypted by the key even if the underlying content is by The Beatles because they do not have an attribute on label Artist. On the other hand, OT negation does not cause this inconvenience because a key whose policy is (Artist:NOT The Beatles) is useless to decrypt ciphertexts without an attribute on label Artist. Thus, we refer to OT negation as a natural form.

Note that we can use monotone ABE as non-monotone ABE by preparing attributes for both positive and negative if they are small-universe constructions, in which the number of attributes are polynomially bounded. That is, non-possession of attributes can be expressed by possession of negative attributes. However, this is not the case in large-universe constructions because we cannot attach an exponentially large number of negative attributes to a ciphertext or secret key. Hence, monotone ABE and non-monotone ABE are completely different things in the context of large-universe constructions.

Multi-use of Attributes (Compactness). Many ABE schemes whose security relies on the dual system methodology [30] have a one-use restriction on access structures [12, 13, 23, 26, 27]. In an ABE scheme with the one-use restriction, one can use only policies in which all attributes appear once. That is, one cannot embed a policy into a ciphertext or secret key such as ((Year:1991–2000 AND Category:jazz) OR (Year:2001–2010 AND Category:jazz) OR (Year:2001–2010 AND Artist:The Beatles)) because attributes Category:jazz and Year:2001–2010 appear twice in the policy.

One way to circumvent this restriction is to prepare multiple nominal attributes for each single attribute in advance like Category:jazz-1, ..., Category:jazz-d for Category:jazz. However, this solution has two problems. The first is that the maximum number d of multi-use is fixed at the setup phase. Thus, the access structures that the scheme supports are still limited. The second is that, in KP-ABE, for instance, the solution increases the sizes of ciphertexts proportionally to the maximum number of multi-use, and it leads to efficiency loss. This prevents the solution to set a sufficiently large number for the limit.

On the other hand, in an ABE scheme that supports multi-use of attributes, we have no restrictions on policies and can combine any attributes in an arbitrary way to generate a policy. In KP-ABE, for instance, the sizes of ciphertexts are independent of policies and thus satisfies “compactness” [21].

1.2 Design of Our ABE Schemes

In the following, we focus on the design our KP-ABE scheme, and the CP-ABE scheme is similarly constructed. The relation R of our ABE is close to that by Okamoto and Takashima in [27]. As we mentioned, an attribute consists of a label and value. A predicate is an arbitrary Boolean formula that is a combination of variables by operations AND, OR, and NOT such as ((Year:1991–2000 AND Category:jazz) OR (Year:1991–2000 AND Artist:NOT The Beatles)). A formal definition of R is described in Definition 2.5.

Our scheme is based on the dual system encryption, which we can instantiate from either composite-order or prime-order bilinear groups [12, 25, 30, 31]. Our actual scheme is based on prime-order bilinear groups following the framework by Chen et al. [12] to utilize the dual system methodology in prime-order groups and the technique by Agrawal and Chase [1] to utilize a random oracle in asymmetric prime-order bilinear groups. For ease of exposition, we describe the composite-order variant of our scheme here. Let $N=p_{1}p_{2}$ for primes $p_{1}$ and $p_{2}$, and $(G,H,G_{T})$ be bilinear groups of order N. Let g and h be generators of G and H, and $g_{i}$ and $h_{i}$ be generators of subgroups $G_{i}$ and $H_{i}$ of order $p_{i}$ for $i=\{1,2\}$, respectively. Let $R:\{0,1\}^{*} \rightarrow G_{1} \times G_{1}$ be a hash function modeled as a random oracle, and its input is a label. We denote the output of R(i) by $(g_{1}^{u_{i}}, g_{1}^{h_{i}})$. Then, our scheme can be written as

where S is the set of labels, n is the number of variables in the formula, $\psi :[n] \rightarrow \{0,1\}^{*}$ is a function that specifies the label of each variable, $\alpha _{i}$ is a share of the secret $\alpha$, and $x_{i}$ and $y_{i}$ are the values for label i. Note that the reason $\mathsf {ct}$ and $\mathsf {sk}$ contain both elements in G and H is to utilize a hash function in asymmetric groups as FAME [1].

The high-level idea of the construction is a combination of secret sharing (SS) and two-mode identity-based encryption (TIBE) [32]. TIBE is obtained by just combining identity-based encryption (IBE) and negation of IBE (NIBE). Our scheme can instantiate an arbitrary number of TIBE on the fly by leveraging hash function R, and each instance corresponds to each label. A secret key of our scheme consists of secret keys of IBE and NIBE, and each secret key hides a share $\alpha _{i}$ of a master secret $\alpha$ generated by SS according to the formula. A ciphertext of ABE consists of ciphertexts of IBE, which have the same form as those in Boneh-Boyen IBE [8]. Note that ciphertexts of IBE and NIBE are identical, and thus we do not need to include both ciphertexts of IBE and NIBE in a ciphertext of our scheme. In decryption, one computes $\{ e(g_{1},h_{1})^{s\alpha _{i}} \}_{i}$ for labels in which the relation of (in)equality between the ciphertext and secret keys is satisfied. Note that one cannot compute $e(g_{1},h_{1})^{s\alpha _{i}}$ if the relation of (in)equality does not hold in label i, thanks to the security of underlying TIBE. If $e(g_{1},h_{1})^{s\alpha }$ is recovered via reconstruction of SS, which means that the policy in the secret key is satisfied by the attribute in the ciphertext, one can decrypt the ciphertext of ABE. By the construction, $e(g_{1},h_{1})^{s\alpha _{i}}$ cannot be computed if a ciphertext of ABE does not contain a ciphertext of TIBE for label i, and this property yields OT negation.

1.3 Our Main Technique

We can easily prove the adaptive security of our scheme from a standard assumption by the dual system methodology and the predicate encoding framework as in [31] if $\psi$ is injective, or the scheme has the one-use restriction of labels in policies. However, if it is not the case, to prove the adaptive security of the scheme from standard assumptions becomes quite difficult and had been a long-standing open problem. Very recently, Kowalczyk and Wee brought a breakthrough for this problem (KW19) [21]. More precisely, they proposed a methodology to prove the adaptive security of the most simple ABE scheme, which supports monotone $\mathsf {NC}_{1}$ circuits (or equivalently Boolean formulae) for a small attribute universe. The scheme can be written in composite-order groups as

$$\begin{aligned}&\mathsf {pk}=(g_{1}, h_{1},g_{1}^{w_{1}} , \ldots ,g_{1}^{w_{\ell }}, e(g_{1}, h_{1})^{\alpha })\\&\mathsf {ct}=(g_{1}^{s}, \{g_{1}^{sw_{i}}\}_{i \in S}, e(g_{1}, h_{1})^{s\alpha }M)\\&\mathsf {sk}= (\{h_{1}^{r_{i}} \}_{i \in [n]}, \{h^{\alpha _{i}}\cdot h_{1}^{r_{i}w_{\psi (i)}} \}_{i \in [n]} ). \end{aligned}$$

Roughly speaking, this scheme can be seen as KP-ABE whose ingredients are ElGamal-like encryption whereas the counterpart of our scheme corresponds to TIBE.

We briefly recall the framework by KW19. Their framework follows the dual system methodology, which is the standard technique to achieve the adaptive security. In the methodology, we change the challenge ciphertext and secret keys into the semi-functional form. Roughly speaking, semi-functional ciphertexts and secret keys have an additional structure in $G_{2}$ and $H_{2}$ as follows:

$$\begin{aligned}&\mathsf {ct}=(g^{s}, \{g^{sw_{i}}\}_{i \in S}, e(g, h)^{s\alpha }M)\\&\mathsf {sk}= (\{h_{1}^{r_{i}} \}_{i \in [n]}, \{h^{\alpha _{i}}\cdot h_{1}^{r_{i}w_{\psi (i)}} \cdot h_{2}^{\gamma _{i}} \}_{i \in [n]}), \end{aligned}$$

where $\gamma _{i}$ is a share of a random secret $\gamma$.

In the dual system methodology, we consider a series of hybrids where we first change the challenge ciphertext into the semi-functional form and then the secret keys into the semi-functional form one by one. In the latter part, the methodology allows us to focus on only one secret key by leveraging components in $G_{2}$ and $H_{2}$. Therefore, to show the following indistinguishability for the adaptive choice of $\mathsf {ct}$ and the one key $\mathsf {sk}$ is sufficient to change the target secret key into a semi-functional form:

where $\gamma _{0,i}$ is a share of secret 0 and $\gamma _{1,i}$ is a share of secret $\gamma$. This core component is called core 1-ABE.

The difficulty of showing the indistinguishability of core 1-ABE from a standard assumption arises from the fact that we need to embed a computational problem into $\mathsf {sk}$ depending on $\mathsf {ct}$. That is, if an adversary first asks for $\mathsf {sk}$, a simulator has no idea on how to embed the computational problem into $\mathsf {sk}$. Their framework tells us how to construct a series of hybrids to show the above indistinguishability. In each transition of hybrids, the simulator guesses a part of the adversary’s output that has sufficient information to embed the problem into $\mathsf {sk}$. Simultaneously, the part must be so small that the simulator can guess it with non-negligible probability. In our case, the part tells the correct element in $\mathsf {sk}$ where the simulator embeds the problem. Observe that each $\gamma _{i}$ is masked by ElGamal-like encryption in $H_{2}$. Thus, we can embed the DDH problem based on the guess and gradually change shares $\{\gamma _{i}\}_{i \in [n]}$.

At a glance, their framework seems applicable to our scheme directly, but actually, it does not work. The main problem is the fact that whereas their framework tells us the location and its label where we should embed the problem in $\mathsf {sk}$, it does not tell us the value of the label in $\mathsf {ct}$. In other words, the difficulty of directly applying their framework to our scheme seems essentially the same as that of proving the adaptive security of Boneh-Boyen IBE, which was proven secure only in the selective setting. This problem does not occur in the scheme by KW19 because the corresponding part is just the ElGamal-like encryption, that is, public-key encryption.

To overcome the problem, we introduce new usage of KW19 framework that allows us to utilize the dual system methodology more beneficially. As we mentioned previously, a secret key of our scheme contains many secret keys of TIBE based on the dual system encryption. Furthermore, the framework tells us which secret key should be changed in each hybrid in the core 1-ABE. Thus, we can gradually randomize the component in $H_{2}$ of each element in $\mathsf {sk}$ by the dual system methodology instead of the DDH problem in $H_{2}$.

For simplicity, we show the case where we apply our new technique to the scheme by KW19. In our technique, we consider the following indistinguishability of core 1-ABE:

The difference from the original core 1-ABE is that our core 1-ABE considers both normal space ($G_{1}$ and $H_{1}$) and semi-functional space ($G_{2}$ and $H_{2}$), whereas the original one considers only semi-functional space. We use the dual system methodology to randomize the component in $H_{2}$. Let $i^{*}$ be the location where $\gamma _{i^{*}}$ is supposed to be changed in some two hybrids, which means that $i^{*} \not \in S$. Then, from the subgroup assumption, the dual system methodology argue that $(h_{1}^{r_{i^{*}}}, h_{1}^{r_{i^{*}}w_{\psi (i^{*})}} \cdot h_{2}^{\gamma _{i^{*}} } ) \approx _{c} (h^{r_{i^{*}}}, h^{r_{i^{*}}w_{\psi (i^{*})}} \cdot h_{2}^{\gamma _{i^{*}} } ).$ Then, we can observe that $w_{\psi (i^{*})} \mod p_{2}$ in $\mathsf {sk}$ is randomly distributed in $\mathbb {Z}_{p_{2}}$ from the Chinese remainder theorem and the fact $i^{*} \not \in S$. Thus, term $\gamma _{i}$ is completely hidden by term $r_{i^{*}}w_{\psi (i^{*})}$. Unlike the framework by KW19, we can apply this technique to our scheme similarly.

1.4 Other Techniques

Furthermore, we give the following technical contributions:

• reducing the number of pairings in decryption;

• reducing the number of shares of secret sharing;

• making the proof simpler;

• presenting our CP-ABE scheme.

Number of Pairings. Our scheme described in Sect. 1.2 requires O(n) pairings in decryption. To reduce the number, we employ the construction by Agrawal and Chase in [2]. That is, we use an exponent $r_{\pi (i)}$ instead of $r_{i}$, where $\pi (i)=|\{j \mid \psi (j)=\psi (i), j \le i \}|$. In this construction, we need O(d) pairings in decryption where $d=\max \pi (i)$ is the maximum number of multi-use of labels in the policy. Because our scheme in prime-order groups follows the construction, it allows fast decryption for secret keys with a small number of multi-use of labels. We show that we can prove the security of our schemes under standard assumptions even if we use this construction. Note that the construction by Agrawal and Chase relies on a q-type assumption.

Number of Shares. In the scheme by KW19, they use a secret sharing scheme where the number of shares corresponds to the summation of the numbers of gates and input wires when we capture a Boolean formula as a circuit. On the other hand, our schemes employ a secret sharing scheme where the number of shares corresponds to only the number of input wires. Their framework derives from the technique to prove the adaptive security of secret sharing for monotone circuits by Jafargholi et al. [18], which requires the same number of shares as in KW19. We guess that this is why their construction employs such a secret sharing scheme. However, we show that we do not need shares for the gates in secret sharing schemes for Boolean formulae to utilize the framework.

Simpler Proof. Our scheme follows the technique of FAME to make our scheme unbounded by a hash function [1]. We show that we can utilize a pseudorandom function (PRF) to significantly ease the security proof. Concretely, we can skip the part that corresponds to $\mathsf {Hyb}_{0}$ to $\mathsf {Hyb}_{2,3,q}$ in their security proof [1, Appendix C]. Note that the additional computational cost by the modification is quite small compared with the whole procedure of the key generation because it requires only small numbers of PRF evaluations and multiplications in $\mathbb {Z}_p$ for each element in a secret key.

CP-ABE Scheme. We present our CP-ABE scheme and its security proof (described in the full version). Note that the security proof of our CP-ABE scheme is more complicated than that of our KP-ABE scheme, because we need two hidden spaces as in [13, 16] due to a technical reason.

1.5 Implementation and Evaluation

We implement our KP and CP-ABE schemes in 128-bit security level and measure benchmarks for an ordinary personal computer and two smartphones: iPhone XR and Pixel 3. In our schemes, a running time of each algorithm is affected by the numbers of negation and multi-use of labels in a policy as well as the number of attributes. To show the effects of these factors, we present benchmarks for four types of policies that differ in the existence of negation and multi-use.

We roughly describe the running times of our schemes when we handle a policy or attribute set with 100 attributes on a personal computer. In all cases, our KP-ABE (resp. CP-ABE) scheme takes about 0.4 to 0.7 s (resp. 0.4 to 0.9 s) for encryption and key generation. Decryption is heavily affected by a type of policy, and our schemes take only about 0.02 s (KP & CP) in the fastest case and 0.5 (KP) or 0.7 s (CP) even in the slowest case. Thus, we can conclude that our schemes take less than 1 s in any process and any cases with 100 attributes.

We also implement KP and CP-ABE schemes by Okamoto and Takashima (OT12), which are the only known ABE schemes that support OT negation and the unboundedness [27]. There are no known schemes that are as expressive as ours (see Table 1), and OT12 seems to have a closet functionality. This is why we choose OT12 to compare. The comparison between our schemes and OT12 shows that our schemes achieve significant speedups for each algorithm.

2 Preliminaries

2.1 Notation

For a natural number $n \in \mathbb {N}$, [n] denotes a set $\{ 1, \ldots ,n \}$. For a set S, $s \leftarrow S$ denotes that s is uniformly chosen from S. For matrices with the same number of rows $\varvec{\mathrm {{A}}}_{1}$ and $\varvec{\mathrm {{A}}}_{2}$, $(\varvec{\mathrm {{A}}}_{1}||\varvec{\mathrm {{A}}}_{2})$ denotes the matrix generated by their concatenation. We denote the whole space spanned by all columns of matrix $\varvec{\mathrm {{A}}}$ by $\mathsf {span}(\varvec{\mathrm {{A}}})$. For a matrix $\varvec{\mathrm {{A}}} :=(a_{j,\ell })_{j,\ell }$ over $\mathbb {Z}_p$, denotes a matrix over $G_{i}$ whose $(j,\ell )$ entry is $g_{i}^{a_{j,\ell }}$, and we apply the similar notation to vectors and scalars. We denote $([\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{A}}}]_{2})$ by $[\varvec{\mathrm {{A}}}]_{1,2}$. For matrices $\varvec{\mathrm {{A}}}$ and $\varvec{\mathrm {{B}}}$ where $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{B}}}$ is defined, we abuse the pairing notation in the following way: $e([\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{B}}}]_{2}) = [\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{B}}}]_{T}$. A function $f:\mathbb {N}\rightarrow \mathbb {R}$ is called negligible if $f(\lambda ) = \lambda ^{-\omega (1)}$ and denotes $f(\lambda ) \le \mathsf {negl}(\lambda )$. For families of distributions $X :=\{X_{\lambda }\}_{\lambda \in \mathbb {N}}$ and $Y :=\{Y_{\lambda }\}_{\lambda \in \mathbb {N}}$, $X \approx _{c} Y$ means that they are computationally indistinguishable.

2.2 Basic Tools

Boolean Formula and NC$^{1}$. A monotone Boolean formula can be represented by a Boolean circuit whose all gates have fan-in 2 and fan-out 1. We can specify a monotone Boolean formula $f:\{0,1\}^{n} \rightarrow \{0,1\}$ as $f=(n, w, v, G)$, where $n, m, v \in \mathbb {N}$ and $G:[v] \rightarrow \{\text {AND, OR}\} \times [w]^{3}$. This means the Boolean formula f has n input wires, w wires including the input wires, and v gates. We number the wires $1 , \ldots ,w$ and the gates $1 , \ldots ,v$. The function G specifies a type, incoming wires, and an outgoing wire of each gate. That is, for $G(i) = (T, a, b, c)$ such that $a< b < c$, T specifies a type of gate i, a and b specify the incoming wires, and c specifies the outgoing wire. A non-monotone Boolean formula additionally contains NOT gates, which have fan-in 1 and fan-out 1. It is well-known that we can express all non-monotone Boolean formulae by one in which all NOT gates are put on the input wires, and we only consider such formulae in this paper. Thus, we can specify a non-monotone Boolean formula $f':\{0,1\}^{n} \rightarrow \{0,1\}$ as $f'=(f, t)$, where $f=(n, w, v, G)$ is a monotone Boolean formula and $t:[n] \rightarrow \{0,1\}$ specifies input gates that connect to a NOT gate. That is, input wire i connects to a NOT gate if $t(i) = 0$ and does not if $t(i) = 1$.

Standard complexity theory tells us that circuit complexity class $\mathsf {NC}^{1}$ and Boolean formulae are equivalent. It is known also that $\mathsf {NC}^{1}$ is equivalent to the class captured by log-depth Boolean formulae (see e.g., [21]). Thus, the circuit complexity class captured by Boolean formulae is equivalent to the class captured by log-depth Boolean formulae.

Definition 2.1

(Pseudorandom Functions). A pseudorandom function (PRF) family $\mathcal {F}:=\{F_{K}\}_{K \in \mathcal {K}_\lambda }$ with a key space $\mathcal {K}_\lambda$, a domain $\mathcal {X}_\lambda$, and a range $\mathcal {Y}_\lambda$ is a function family that consists of functions $F_K :\mathcal {X}_\lambda \rightarrow \mathcal {Y}_\lambda$. Let $\mathcal {R}_\lambda$ be a set of functions consisting of all functions whose domain and range are $\mathcal {X}_\lambda$ and $\mathcal {Y}_\lambda$ respectively. For any PPT adversary $\mathcal {A}$, the following condition holds,

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {PRF}}(\lambda ) :=| \Pr [1 \leftarrow \mathcal {A}^{F_{K}(\cdot ) }] - \Pr [1 \leftarrow \mathcal {A}^{R(\cdot )}]| \le \mathsf {negl}(\lambda ), \end{aligned}$$

where $K \leftarrow \mathcal {K}_\lambda$ and $R \leftarrow \mathcal {R}_\lambda$.

Definition 2.2

(Bilinear Groups). A description of bilinear groups consist of a prime p, cyclic groups $G_{1}, G_{2}, G_{T}$ of order p, generators $g_{1}$ and $g_{2}$ of $G_{1}$ and $G_{2}$ respectively, and a bilinear map $e:G_{1} \times G_{2} \rightarrow G_{T}$, which has two properties.

• (Bilinearity): $\forall h_{1} \in G_{1}, h_{2} \in G_{2} ,a,b \in \mathbb {Z}_p, e(h^{a}_{1}, h^{b}_{2}) = e(h_{1},h_{2})^{ab}$.

• (Non-degeneracy): For $g_{1}$ and $g_{2}$, $g_{T} :=e(g_{1}, g_{2})$ is a generator of $G_{T}$.

A bilinear group generator $\mathcal {G}_{\mathsf {BG}}(1^\lambda )$ takes a security parameter $1^{\lambda }$ and outputs a description of bilinear groups $\mathbb {G}$ with $\varOmega (\lambda )$ bit prime. In this paper, we refer to Type-I groups, where efficient isomorphisms exist in both way between $G_{1}$ and $G_{2}$, as symmetric bilinear groups, and Type-III groups, where no efficient isomorphisms exist between them, as asymmetric bilinear groups.

For the proofs of our schemes, we utilize the $\mathcal {D}_{k}$-MDDH assumption [14], which is generalization of the DDH assumption. There are mainly two types of $\mathcal {D}_{k}$-MDDH assumption families for asymmetric bilinear groups. In the first one, an instance contains unilateral group elements such as the SXDH assumption. The other one consists of assumptions that are involved with bilateral group elements such as the DLIN assumption used in [1], which is sometimes called the XDLIN assumption. In our paper, we utilize the latter type.

Definition 2.3

($\mathcal {D}_{j,k}$-MDDH Assumption). For $j > k$, let $\mathcal {D}_{j,k}$ be a matrix distribution over $\mathbb {Z}_p^{j \times k}$ that outputs full rank matrix with overwhelming probability. We can assume that, wlog, the first k rows of a matrix $\varvec{\mathrm {{A}}}$ chosen from $\mathcal {D}_{j,k}$ form an invertible matrix. We consider the following distribution:

We say that the bilateral $\mathcal {D}_{j,k}$-MDDH assumption holds with respect to $\mathcal {G}_{\mathsf {BG}}$ if, for any PPT adversary $\mathcal {A}$,

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A},\mathsf {bi}}^{\mathsf {\mathcal {D}_{j,k}\text {-}MDDH}}(\lambda ) :=|\Pr [1 \leftarrow \mathcal {A}(P_{0})] - \Pr [1 \leftarrow \mathcal {A}(P_{1})]| \le \mathsf {negl}(\lambda ). \end{aligned}$$

We denote $\mathcal {D}_{k+1,k}$ by $\mathcal {D}_{k}$. Let $\mathcal {U}_{j, k}$ be a uniform distribution over full rank matrices in $\mathbb {Z}_p^{j \times k}$. Then, the following relations hold with tight reductions; ${\mathcal {D}_{{k}}\text {-}MDDH} \Rightarrow {\mathcal {U}_{{k}}\text {-}MDDH} \Rightarrow {\mathcal {U}_{{j,k}}{\text {-}}MDDH}.$

For an appropriate distribution $\mathcal {D}_{k}$, the $\mathcal {D}_{k}$-MDDH assumption generically holds in k-linear groups [14]. Thus, in asymmetric bilinear groups, we can utilize the bilateral $\mathcal {D}_{k}$-MDDH assumption for $k \ge 2$.

Matrix Notation. For a matrix $\varvec{\mathrm {{A}}} \in \mathcal {D}_{k}$, we define a matrix $\varvec{\mathrm {{A}}}^{*}$ and vectors $\varvec{\mathrm {{a}}}_{1}$ and $\varvec{\mathrm {{a}}}^{*}_{1}$ as follows. Vector $\varvec{\mathrm {{a}}}_{1}$ is a $k+1$ dimensional vector whose last entry is 1 and the others are 0. Then, it is not hard to see that $\overline{\varvec{\mathrm {{A}}}} :=(\varvec{\mathrm {{A}}}||\varvec{\mathrm {{a}}}_{1})$ forms a basis of $\mathbb {Z}_p^{k+1}$ because the first k rows of a matrix $\varvec{\mathrm {{A}}}$ chosen from $\mathcal {D}_{k}$ form an invertible matrix. $\varvec{\mathrm {{A}}}^{*}$ and $\varvec{\mathrm {{a}}}^{*}_{1}$ are the matrix that consists of the left k columns of $(\overline{\varvec{\mathrm {{A}}}}^{\top })^{-1}$ and the vector that consists of right one column of $(\overline{\varvec{\mathrm {{A}}}}^{\top })^{-1}$, respectively. Note that we have $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{A}}}^{*}=\varvec{\mathrm {{I}}}_{k}$, $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1}= \varvec{\mathrm {{0}}}$, and $\varvec{\mathrm {{A}}}^{*}\varvec{\mathrm {{A}}}^{\top } + \varvec{\mathrm {{a}}}^{*}_{1}\varvec{\mathrm {{a}}}_{1}^{\top }=\varvec{\mathrm {{I}}}_{k+1}$. We use a similar notation for a matrix $\overline{\varvec{\mathrm {{B}}}} \in \mathsf {GL}_{k+\eta }(\mathbb {Z}_p)$ where $\eta \in \mathbb {N}$. $\varvec{\mathrm {{B}}}$ and $\varvec{\mathrm {{b}}}_{i}$ denote a matrix consists of the first k columns of $\overline{\varvec{\mathrm {{B}}}}$ and a vector consists of the $k+i$-th column of $\overline{\varvec{\mathrm {{B}}}}$, respectively. Similarly, $\varvec{\mathrm {{B}}}^{*}$, $\varvec{\mathrm {{b}}}_{i}^{*}$ denote a matrix consists of the first k columns of $(\overline{\varvec{\mathrm {{B}}}}^{\top })^{-1}$ and a vector consists of the $k+i$-th column of $(\overline{\varvec{\mathrm {{B}}}}^{\top })^{-1}$, respectively. For the convenience, we denote $(\varvec{\mathrm {{b}}}_{1}||\varvec{\mathrm {{b}}}_{2})$ by $\varvec{\mathrm {{B}}}_{12}$, and this notation is applied to other cases similarly.

2.3 Attribute-Based Encryption

Definition 2.4

(Attribute-Based Encryption). An attribute-based encryption (ABE) scheme for relation $R:\mathcal {X}_{} \times \mathcal {Y}\rightarrow \{0,1\}$ consists of four algorithms, where $\mathcal {X}$ and $\mathcal {Y}$ are an attribute universe and predicate universe, respectively.

• $\mathsf {Setup}(1^{\lambda })$: It takes a security parameter $1^{\lambda }$ and outputs a public key $\mathsf {pk}$ and a master secret key $\mathsf {msk}$. $\mathsf {pk}$ specifies a message space $\mathcal {M}$.

• $\mathsf {Enc}(\mathsf {pk}, x, m)$: It takes $\mathsf {pk}$, an attribute $x \in \mathcal {X}$ and a message $m \in \mathcal {M}$ and outputs a ciphertext $\mathsf {ct}_{x}$.

• $\mathsf {KeyGen}(\mathsf {pk}, \mathsf {msk}, y)$: It takes $\mathsf {pk}, \mathsf {msk}$, and a predicate $y \in \mathcal {Y}$ and outputs a secret key $\mathsf {sk}_{y}$.

• $\mathsf {Dec}(\mathsf {pk}, \mathsf {ct}_{x}, \mathsf {sk}_{y})$: It takes $\mathsf {pk}, \mathsf {ct}_{x}$ and $\mathsf {sk}_{y}$ and outputs a message $m'$ or $\bot$.

Correctness. An ABE scheme is correct if it satisfies the following condition. For all $\lambda \in \mathbb {N}$, $x \in \mathcal {X}$, $y \in \mathcal {Y}$ such that $R(x,y)=1$, and $m \in \mathcal {M}$, we have

$$\begin{aligned} \mathsf{Pr}\left[ m=m'\; \begin{array}{|l} (\mathsf {pk},\mathsf {msk}) \leftarrow \mathsf {Setup}(1^{\lambda })\\ \mathsf {ct}_{x} \leftarrow \mathsf {Enc}(\mathsf {pk}, x, m)\\ \mathsf {sk}_{y} \leftarrow \mathsf {KeyGen}(\mathsf {pk}, \mathsf {msk}, y)\\ m' :=\mathsf {Dec}(\mathsf {pk}, \mathsf {ct}_{x}, \mathsf {sk}_{y}) \end{array} \right] = 1. \end{aligned}$$

Security. An ABE scheme is adaptively secure if it satisfies the following condition. That is, the advantage of $\mathcal {A}$ defined as follows is negligible in $\lambda$ for all stateful PPT adversary $\mathcal {A}$:

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {ABE}}(\lambda ) :=\left| \mathsf {Pr} \left[ \beta =\beta '\; \begin{array}{|l} \beta \leftarrow \{0,1\}\\ (\mathsf {pk}, \mathsf {msk}) \leftarrow \mathsf {Setup}(1^{\lambda })\\ (x^{*}, m_{0}, m_{1}) \leftarrow \mathcal {A}^{\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},\cdot )}(\mathsf {pk})\\ \mathsf {ct}_{x^{*}} \leftarrow \mathsf {Enc}(\mathsf {pk}, x^{*}, m_{\beta })\\ \beta ' \leftarrow \mathcal {A}^{\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},\cdot )}(\mathsf {ct}_{x^{*}})\\ \end{array} \right] -\frac{1}{2} \right| , \end{aligned}$$

where $\{y_{i}\}_{i \in [q_{\mathsf {sk}}]}$ on which $\mathcal {A}$ queries $\mathsf {KeyGen}$ must satisfy $R(x^{*},y_{i})=0$.

A relation for ABE that we consider in our paper is expressed by a non-monotone Boolean formula over the equivalence relation in $\mathbb {Z}_p$. More specifically, each input of the Boolean formula is decided by whether certain components in an attribute and predicate are equal. Then, the relation is decided by the output of the formula. Our relation is very close to that formulated by Okamoto and Takashima in [27], though their scheme has one-use restriction on labels in policies. One caveat is that we can use only a non-monotone Boolean formula for a predicate in our scheme, whereas the relation by Okamoto and Takashima allows us to use a more powerful non-monotone span program for a predicate. In the following, we consider only non-monotone Boolean formulae where NOT gates exist only on input wires.

Definition 2.5

(Relation R). Relations $R_{\mathsf {KP}}$ and $R_{\mathsf {CP}}$ for our KP and CP-ABE schemes, respectively, are defined as follows. Let $R:\mathcal {X}\times \mathcal {Y}\rightarrow \{0,1\}$ be a relation defined as follows:

• $\mathcal {X}= \bigcup _{i \in \mathbb {N}}\mathbb {Z}_p^{i} \times \varPhi _{i}$, where $\varPhi _{i}$ consists of all injective functions such that $\phi :[i] \rightarrow \{0,1\}^{*}$.

• $\mathcal {Y}= \bigcup _{i \in \mathbb {N}} \mathbb {Z}_p^{i} \times \mathcal {F}_{i} \times \varPsi _{i} \times \mathcal {T}_{i}$, where $\mathcal {F}_{i}$ consists of all monotone Boolean formulae whose input lengths are i, and $\varPsi _{i}$ and $\mathcal {T}_{i}$ consist of all functions such that $\psi :[i] \rightarrow \{0,1\}^{*}$ and $t:[i] \rightarrow \{0,1\}$, respectively.

• For $x = (\varvec{\mathrm {{x}}} \in \mathbb {Z}_p^{m}, \phi )$ and $y = (\varvec{\mathrm {{y}}} \in \mathbb {Z}_p^{n}, f, \psi , t)$, we define $b = (b_{1} , \ldots ,b_{n}) \in \{0,1\}^{n}$ as $b_{i} :={\left\{ \begin{array}{ll} t(i) \odot \mathrm {true}(x_{\phi ^{-1}(\psi (i))} =y_{i}) &{} \psi (i) \subseteq \mathrm {Im}(\phi )\\ 0 &{}\psi (i) \not \subseteq \mathrm {Im}(\phi ) \end{array}\right. },$ where $\odot$ denotes xnor. Then, $R(x,y) =1 \Leftrightarrow f(b)=1$.

Then, $R_{\mathsf {KP}}: \mathcal {X}_{\mathsf {KP}} \times \mathcal {Y}_{\mathsf {KP}} \rightarrow \{0,1\}$ is defined as $\mathcal {X}_{\mathsf {KP}} :=\mathcal {X}$, $\mathcal {Y}_{\mathsf {KP}} :=\mathcal {Y}$, and $R_{\mathsf {KP}}(x,y) = R(x,y)$, whereas $R_{\mathsf {CP}}: \mathcal {X}_{\mathsf {CP}} \times \mathcal {Y}_{\mathsf {CP}} \rightarrow \{0,1\}$ is defined as $\mathcal {X}_{\mathsf {CP}} :=\mathcal {Y}$, $\mathcal {Y}_{\mathsf {CP}} :=\mathcal {X}$, and $R_{\mathsf {CP}}(x,y) = R(y,x)$.

For $\mathcal {X}$, each element of $\varvec{\mathrm {{x}}} \in \mathbb {Z}_p^{m}$ corresponds to a value for some label, and $\phi$ specifies which label each element of $\varvec{\mathrm {{x}}}$ is associated with. For instance, when we consider an attribute (Age:22, Hobby:tennis), $x=(\varvec{\mathrm {{x}}}, \phi )$ can be set as $\varvec{\mathrm {{x}}}:=(22, H_{1}(\text {tennis}))$, $\phi (1):=$ Age, and $\phi (2):=$ Hobby where $H_{1}:\{0,1\}^{*} \rightarrow \mathbb {Z}_p$ is a collision resistant hash function.

For $\mathcal {Y}$, each element of $\varvec{\mathrm {{y}}} \in \mathbb {Z}_p^{n}$ corresponds to the value for each input wire of f, and $\psi$ specifies which label each input wire of f is associated with. Additionally, t specifies whether each input wire connects to a NOT gate. For instance, let us consider a predicate (Age:25 AND Hobby:NOT baseball). Then, $y = (\varvec{\mathrm {{y}}}, f, \psi , t)$ can be set as $\varvec{\mathrm {{y}}} :=(25, H_{1}(\text {baseball}))$, f is a formula with a single AND gate, $\psi (1):=$ Age and $\psi (2):=$ Hobby, and $t(1)=1$ and $t(2)=0$.

Definition 2.6

(Linear Secret Sharing Scheme). A linear secret sharing scheme (LSSS) for a function class $\mathcal {F}$ consists of two algorithms $\mathsf {Share}$ and $\mathsf {Rec}$.

• $\mathsf {Share}(f, \varvec{\mathrm {{k}}})$: It takes a function $f \in \mathcal {F}$ where $f:\{0,1\}^{n} \rightarrow \{0,1\}$ and a vector $\varvec{\mathrm {{k}}} \in \mathbb {Z}_p^{\ell }$. Then, outputs shares $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n} \in \mathbb {Z}_p^{\ell }$.

• $\mathsf {Rec}(f, x, \{\varvec{\mathrm {{k}}}_{i}\}_{x_{i} = 1} )$: It takes $f:\{0,1\}^{n} \rightarrow \{0,1\}$, a bit string $x :=(x_{1} , \ldots ,x_{n}) \in \{0,1\}^{n}$ and shares $\{\varvec{\mathrm {{k}}}_{i}\}_{x_{i} = 1}$. Then, outputs a vector $\varvec{\mathrm {{k}}}'$ or $\bot$.

In particular, $\mathsf {Rec}$ computes a linear function on shares to reconstruct a secret; $\varvec{\mathrm {{k}}} = \sum _{x_{i}=1}a_{i}\varvec{\mathrm {{k}}}_{i}$ where each $a_{i}$ is determined by f. A LSSS has two properties.

• Correctness: For any $f \in F$, $x \in \{0,1\}^{n}$ such that $f(x)=1$,

  $$\begin{aligned} \Pr [\mathsf {Rec}(f,x,\{\varvec{\mathrm {{k}}}_{i}\}_{x_{i} = 1}) = \varvec{\mathrm {{k}}} \mid \varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n} \leftarrow \mathsf {Share}(f, \varvec{\mathrm {{k}}}) ]=1. \end{aligned}$$

• Security: For any $f \in F$, $x \in \{0,1\}^{n}$ such that $f(x)=0$, and $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n} \leftarrow \mathsf {Share}(f, \varvec{\mathrm {{k}}})$, shares $\{\varvec{\mathrm {{k}}}_{i} \}_{x_{i} =1}$ have no information about $\varvec{\mathrm {{k}}}$.

2.4 Piecewise Guessing Framework

Here, we briefly recall the piecewise guessing framework by Kowalczyk and Wee [21], which is based on the framework by Jafargholi et al. [18]. The framework helps us to prove adaptive security of cryptographic schemes that are selectively secure.

Definition 2.7

(Interactive Game). An interactive game $\mathsf {G}$ is a game between an adversary $\mathcal {A}$ and a challenger $\mathcal {C}$. In the game, $\mathcal {A}$ and $\mathcal {C}$ send messages interactively, and the messages sent by $\mathcal {C}$ depend on the game $\mathsf {G}$. After the interaction, $\mathcal {A}$ outputs $\beta \in \{0,1\}$. We denotes the output of $\mathcal {A}$ in $\mathsf {G}$ by $\langle \mathcal {A}, \mathsf {G} \rangle$. Let $z \in \{0,1\}^{R}$ be a part of messages supposed to be sent by $\mathcal {A}$ in the game. In the adaptive game $\mathsf {G}$, $\mathcal {A}$ can send z at arbitrary points as long as it follows a rule of the game. We define the selective variant of $\mathsf {G}$, denoted by $\widehat{\mathsf {G}}$, to be the same as $\mathsf {G}$ except that $\mathcal {A}$ has to declare z that will be sent in the game, at the beginning of the interaction.

Suppose we want to show that adaptive games $\mathsf {G}_{0}$ and $\mathsf {G}_{1}$ are computationally indistinguishable, i.e.,

$$\begin{aligned} |\Pr [ \langle \mathcal {A}, \mathsf {G}_{0} \rangle =1] - \Pr [ \langle \mathcal {A}, \mathsf {G}_{1} \rangle =1] | \le \mathsf {negl}(\lambda ). \end{aligned}$$

Then, we consider a series of selective hybrids $\widehat{\mathsf {H}}^{h_{0}} , \ldots ,\widehat{\mathsf {H}}^{h_{L}}$ such that

$$\begin{aligned} \widehat{\mathsf {G}}_{0} = \widehat{\mathsf {H}}^{h_{0}} \approx _{c} \widehat{\mathsf {H}}^{h_{1}} \approx _{c} , \ldots ,\approx _{c} \widehat{\mathsf {H}}^{h_{L}} = \widehat{\mathsf {G}}_{1}, \end{aligned}$$

where $h_{0} , \ldots ,h_{L}:\{0,1\}^{R} \rightarrow \{0,1\}^{R'}$ for some $R' \ll R$, and $\widehat{\mathsf {H}}^{h_{\iota }}$ is an interactive game in which $\mathcal {C}$’s messages depend on $u :=h_{\iota }(z)$. Additionally, $h_{0}$ and $h_{L}$ need to be constant functions. Note that $\mathcal {C}$ can generate messages depending on u because z is declared at the beginning of the interaction. Next, we define variants of $\widehat{\mathsf {H}}^{h_{\iota }}$, namely, $\widehat{\mathsf {H}}^{h_{\iota }}_{0}$ and $\widehat{\mathsf {H}}^{h_{\iota }}_{1}$ as follows. In $\widehat{\mathsf {H}}^{h_{\iota }}_{\beta }$ for $\beta \in \{0,1\}$, $\mathcal {A}$ has to declare $h_{\iota -1+\beta }(z)$ and $h_{\iota +\beta }(z)$ instead of z at the beginning of the game. Then, $\mathcal {C}$ interacts with $\mathcal {A}$ setting $u :=h_{\iota }(z)$ in both $\widehat{\mathsf {H}}^{h_{\iota }}_{0}$ and $\widehat{\mathsf {H}}^{h_{\iota }}_{1}$. In other words, $\widehat{\mathsf {H}}^{h_{\iota }}_{\beta }$ is the same as $\widehat{\mathsf {H}}^{h_{\iota }}$ except that only partial information of z is declared by $\mathcal {A}$. Now we are ready to state the adaptive security lemma.

Lemma 2.1

(Adaptive Security Lemma [21]). Let $\mathsf {G}_{0}$ and $\mathsf {G}_{1}$ be adaptive interactive games and $\{\widehat{\mathsf {H}}^{h_{i}}\}_{0 \le i \le L}$ be selective hybrids defined above. Suppose they satisfy the two properties:

• $\mathsf {G}_{0} = \mathsf {H}^{h_{0}}$ and $\mathsf {G}_{1} = \mathsf {H}^{h_{L}}$, where $\mathsf {H}^{h_{0}}$ and $\mathsf {H}^{h_{L}}$ are the same as $\widehat{\mathsf {H}}^{h_{0}}$ and $\widehat{\mathsf {H}}^{h_{L}}$, respectively, except that $\mathcal {A}$ does not declare z at the beginning. Note that $\mathcal {C}$’s messages can be correctly defined because $h_{0}$ and $h_{L}$ are constant functions.

• For all PPT adversary $\mathcal {A}$ and all $\iota \in {L}$, we have

  $$\begin{aligned} |\Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1}^{h_{\iota -1}} \rangle =1 ]- \Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{0}^{h_{\iota }} \rangle =1]| \le \epsilon .\end{aligned}$$

Then, we have

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {G}_{0} \rangle =1 ]- \Pr [\langle \mathcal {A}, \mathsf {G}_{1} \rangle =1]| \le 2^{2R'}L\epsilon . \end{aligned}$$

2.5 Pebbling Strategy for Boolean Formula

A pebbling strategy is used for a guide of how to construct a series of hybrids in the piecewise guessing framework.

Definition 2.8

(Pebbling Game). A player of the pebbling game is given a monotone Boolean formula $f:\{0,1\}^{n} \rightarrow \{0,1\}$ and input $b = (b_{1} , \ldots ,b_{n}) \in \{0,1\}^{n}$ such that $f(b)=0$. The goal of the game is to reach the state where a pebble is placed on only the output gate (the gate with the output wire), starting from the state with no pebbles on the Boolean formula f, following a pebbling rule. The rule is defined as follows.

• 1. We can place or remove a pebble on input wire i whose input corresponds to 0, i.e., $b_{i}=0$.

• 2. We can place or remove a pebble on an AND gate if at least one of its incoming wires comes from a gate or input wire with a pebble on it.

• 3. We can place or remove a pebble on an OR gate if both of its incoming wires come from a gate or input wire with a pebble on it, respectively.

• 4. We can pass the turn, which allows us to increase the total number of steps in the game without changing the pebbling strategy.

Definition 2.9

(Pebbling Record). A pebbling record $\mathcal {R}:=(r_{0} , \ldots ,r_{L}) \in (\{0,1\}^{R'})^{L}$ is a list of all pebbling configuration that a player took from the start to the goal in the pebbling game. $R'$-bit string $r_{\iota }$ specifies the configuration at the $\iota$-th step in the play. Thus, $r_{0}$ specifies the state with no pebbles and $r_{L}$ specifies the state with one pebble on the output gate. It also means that the player takes L steps to reach the goal, and all pebbling configurations that the player took can be specified by an $R'$-bit string.

The following lemma says that, for any monotone Boolean formula and input, there exists a pebbling strategy where all pebbling configurations can be specified with a “short” bit string.

Lemma 2.2

(Pebbling Lemma [21]). Let $f:\{0,1\}^{n} \rightarrow \{0,1\}$ be any monotone Boolean formula with a depth $d \le B$, and $b \in \{0,1\}^{n}$ be any bit string such that $f(b)=0$. Then, there exists a deterministic algorithm $\mathsf {PebRec}(f,b)$ that takes f and b and outputs a record $\mathcal {R}$ consisting of $8^{B}$ strings whose lengths are 3B bits.

3 Our KP-ABE Scheme

First, we describe a linear secret sharing scheme that we use in our schemes as a building block.

3.1 Linear Secret Sharing for Boolean Formulae

Our secret sharing scheme for monotone Boolean formulae is described in Fig. 1, which is essentially the same as the scheme in [22, Appendix G]. Note that it works similarly if all vectors in Fig. 1 are group elements. Let f be a formula and $b=(b_{1}, \ldots ,b_{n})$ be a bit string such that $f(b)=1$. Then, for reconstruction, it is not difficult to see that there exists a set $S \subseteq \{i \mid b_{i}=1 \}$ such that $\sum _{i \in S} \varvec{\mathrm {{\sigma }}}_{i} = \varvec{\mathrm {{k}}}$.

Clearly, the number of shares for formula f corresponds to the number of its input wires. The secret sharing scheme employed by Kowalczyk and Wee is different from ours [20], where the number of shares corresponds to the summation of the numbers of input wires and gates in f. We show that we can utilize their framework even if we replace the secret sharing scheme to ours.

Fig. 1.

Our linear secret sharing scheme for Boolean formulae.

We use the following lemma on the secret sharing scheme in the security proof of our scheme.

Lemma 3.1

Let $\mathsf {Share}$ be the algorithm defined in Fig. 1. For all $\ell ,n \in \mathbb {N}$, monotone Boolean formulae $f=(n,w,v,G)$, $\varvec{\mathrm {{k}}}, \varvec{\mathrm {{a}}} \in \mathbb {Z}_p^{\ell }$, and $\mu \in \mathbb {Z}_p$, we define the following distribution.

Then, the two distributions are identical:

$$\begin{aligned} \{ \varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n}\}\; and \; \{\varvec{\mathrm {{k}}}'_{1}+\sigma _{1}\varvec{\mathrm {{a}}} , \ldots ,\varvec{\mathrm {{k}}}'_{n}+\sigma _{n}\varvec{\mathrm {{a}}}\}. \end{aligned}$$

The proof of Lemma 3.1 is presented in the full version.

3.2 Construction

For generality, we describe our scheme using a matrix distribution $\mathcal {D}_{k}$. When we instantiate our scheme from asymmetric pairings, we typically choose the k-Lin family $\mathcal {L}_{k}$ with $k=2$. In this case, we can set matrices as

where $a_{1},a_{2}\leftarrow \mathbb {Z}_p$. Let $H:\{0,1\}^{*} \rightarrow G_{1}^{(k+1)\times k} \times G_{1}^{(k+1)\times k}$ be a hash function modeled as a random oracle. Let $F_{K}: \{0,1\}^{*} \rightarrow \mathbb {Z}_p^{k+1} \times \mathbb {Z}_p^{k+1}$ be a PRF with a secret key K. Let $\mathcal {K}_{\lambda }$ be a key space of the PRF. Let $\mathsf {Share}$ be the LSSS described in Fig. 1. Note that we can instantiate H from a hash function $H':\{0,1\}^{*} \rightarrow G_{1}$ by generating each output group element of H with $H'$. More precisely, each output group element of H(i) is defined by $H'(i||\$|| j)$, where $ is a special symbol and $j \in [2k(k+1)]$ specifies the location of the matrices. The symbol $ can be expressed by encoding, e.g., $0 \rightarrow 00$, $1 \rightarrow 11$, and $\$ \rightarrow 01$. Our scheme for $R_{\mathsf {KP}}$ is described as follows.

• $\mathsf {Setup}(1^{\lambda })$: It takes a security parameter $1^{\lambda }$ and outputs $\mathsf {pk}$ and $\mathsf {msk}$ as follows.

  

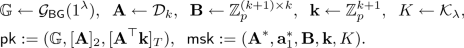
• $\mathsf {Enc}(\mathsf {pk}, x, M)$: It takes $\mathsf {pk}$, an attribute $x=(\varvec{\mathrm {{x}}} \in \mathbb {Z}_p^{m}, \phi )$, and a message $M \in G_{T}$ and outputs $\mathsf {ct}_{x}$ as follows.

  

• $\mathsf {KeyGen}(\mathsf {pk}, \mathsf {msk}, y)$: It takes $\mathsf {pk}$, $\mathsf {msk}$, and a predicate $y = (\varvec{\mathrm {{y}}} \in \mathbb {Z}_p^{n}, f, \psi , t)$ and outputs $\mathsf {sk}_{y}$ as follows. Let $\pi :[n] \rightarrow \mathbb {N}$ be a function such that $\pi (i) :=|\{j \mid \psi (j) = \psi (i), j \le i\}|$. Let d be the maximum number of multi-use of labels in f, i.e., $d :=\max _{i \in [n]} \pi (i)$.

  

• $\mathsf {Dec}(\mathsf {pk}, \mathsf {ct}_{x}, \mathsf {sk}_{y})$: It takes $\mathsf {pk}$, $\mathsf {ct}_{x}$, and $\mathsf {sk}_{y}$. It computes $b \in \{0,1\}^{n}$ from x and y as in Definition 2.5. If $f(b)=0$, it outputs $\bot$. Otherwise, computes a set $S \subseteq \{i \mid b_{i}=1\}$ such that $\varvec{\mathrm {{k}}} = \sum _{i \in S} \varvec{\mathrm {{k}}}_{i}$. Let $S_{1} :=S \cap \{i \mid t(i)=1 \}$ and $S_{0} :=S \cap \{i \mid t(i)=0 \}$. Then outputs $M'$ as follows.

  $$\begin{aligned}&D_{1,j} :=e\left( \sum _{\begin{array}{c} \pi (i)=j\\ i\in S_{1} \end{array}}k_{2,i}+\sum _{\begin{array}{c} \pi (i)=j\\ i \in S_{0} \end{array}} \frac{1}{y_{i}-x_{\phi ^{-1}(\psi (i))}}(x_{\phi ^{-1}(\psi (i))}k_{2,i,1}+k_{2,i,2}),c_{1} \right) ^{\top }\\&D_{2,j} :=e\left( \sum _{\begin{array}{c} \pi (i)=j\\ i\in S_{1} \end{array}}c_{2,\phi ^{-1}(\psi (i))} + \sum _{\begin{array}{c} \pi (i)=j\\ i \in S_{0} \end{array}} \frac{1}{y_{i}-x_{\phi ^{-1}(\psi (i))}}c_{2,\phi ^{-1}(\psi (i))}, k_{1,j} \right) \\&M' :=c_{3}/\prod _{j \in [d]}(D_{1,j}/D_{2,j}). \end{aligned}$$

• Correctness: For honestly generated $\mathsf {ct}_{x}$ and $\mathsf {sk}_{y}$ such that $R(x,y)=1$,

  

  In the above, we use the relations $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{A}}}^{*}=\varvec{\mathrm {{I}}}_{k}$ and $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1}= \varvec{\mathrm {{0}}}$. Because $x_{\phi ^{-1}(\psi (i))} = y_{i}$ for $i \in S_{1}$, we have $\prod _{j \in [d]}(D_{1,j}/D_{2,j})= [\varvec{\mathrm {{s}}}^{\top }\varvec{\mathrm {{A}}}^{\top }\sum _{j \in [d]} \sum _{\begin{array}{c} i \in S \\ \pi (i) =j \end{array}}$ $\varvec{\mathrm {{k}}}_{i}]_{T} = [\varvec{\mathrm {{s}}}^{\top }\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{k}}}]_{T}$. Thus, $M'=M$.

3.3 Security

Theorem 3.1

Let B be the maximum depth of formulae on which $\mathcal {A}$ queries $\mathsf {KeyGen}$. Let $q_{\mathsf {sk}}$ be the maximum number of $\mathcal {A}$’s queries to $\mathsf {KeyGen}$. Then, our scheme is adaptively secure as long as $B = O(\log {\lambda })$. More precisely, for any PPT adversary $\mathcal {A}$, there exist PPT algorithms $\mathcal {B}_{1}$ and $\mathcal {B}_{2}$ such that

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}}^{\mathsf {ABE}}(\lambda ) \!\le \! \mathsf {Adv}_{\mathcal {B}_{1}}^{\mathsf {PRF}}(\lambda )\!+\! (2^{9B+2}q_{\mathsf {sk}}\!+\!1)(\mathsf {Adv}_{\mathcal {B}_{2},\mathsf {bi}}^{\mathsf {\mathcal {D}_{k}\text {-}MDDH}}(\lambda )\!+\!2^{-\varOmega (\lambda )}). \end{aligned}$$

Proof Overview. We prove Theorem 3.1 following the standard dual system methodology. To do so, we first replace the PRF with a random function. Then, our scheme basically follows the construction on the dual system group from prime-order groups in [12]. Concretely, we can rewrite $c_{2,i}$ and $k_{2,i}$ in the challenge ciphertext and secret keys as

where $\varvec{\mathrm {{W}}}_{i,b} \in \mathbb {Z}_p^{(k+1)\times (k+1)}$. Next, we change the challenge ciphertext into a semi-functional form, where $\varvec{\mathrm {{A}}}\varvec{\mathrm {{s}}}$ is replaced with a vector $\varvec{\mathrm {{c}}} \leftarrow \mathbb {Z}_p^{k+1}$. That is, the elements in a ciphertext are

$$\begin{aligned} c_{1}=[\varvec{\mathrm {{c}}}]_{2},\; c_{2,i}=[(x_{i}\varvec{\mathrm {{W}}}^{\top }_{\phi (i),0}+\varvec{\mathrm {{W}}}^{\top }_{\phi (i),1})\varvec{\mathrm {{c}}}]_{1},\; c_{3}=[\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{k}}}]_{T} M. \end{aligned}$$

The indistinguishability directly follows from the $\mathcal {D}_{k}$-MDDH assumption. After that, we gradually change the secret keys into a semi-functional form, where $\varvec{\mathrm {{k}}}_{i}$ is a share of secret $\varvec{\mathrm {{k}}}+\mu \varvec{\mathrm {{a}}}^{*}_{1}$ instead of $\varvec{\mathrm {{k}}}$ for $\mu \leftarrow \mathbb {Z}_p$. To prove each indistinguishability, we utilize the KW technique [21]. In the final hybrid, we can argue that $\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{k}}}$ in the challenge ciphertext is statistically close to a uniform randomness.

Proof

We consider a series of hybrids $\mathsf {H}_{0}$, $\mathsf {H}_{1}$, $\mathsf {H}_{2}$, and $\mathsf {H}_{3,\iota }$ for $i \in \{0, \ldots ,q_{\mathsf {sk}}\}$, where $\mathsf {H}_{0}$ is the real game and $\mathsf {H}_{3, q_{\mathsf {sk}}}$ is the final game. In the following, we denote the event $\beta = \beta '$ in hybrid $\mathsf {H}$ by $\langle \mathcal {A}, \mathsf {H} \rangle _{\mathsf {win}}$, where $\beta$ is a random bit chosen by the challenger, and $\beta '$ is the output of $\mathcal {A}$. Note that we have

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {H}_{0} \rangle _{\mathsf {win}}]-1/2| = \mathsf {Adv}_{\mathcal {A}}^{\mathsf {ABE}}(\lambda ). \end{aligned}$$

(1)

$\underline{\mathsf {H}_{1}}$. We define $\mathsf {H}_{1}$ as the same as $\mathsf {H}_{0}$ except replacing PRF $F_{K}$ in $\mathsf {KeyGen}$ with a random function $R:\{0,1\}^{*} \rightarrow \mathbb {Z}_p^{k+1} \times \mathbb {Z}_p^{k+1}$. From the definition of PRFs, we have

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {H}_{0} \rangle _{\mathsf {win}}]- \Pr [\langle \mathcal {A}, \mathsf {H}_{1} \rangle _{\mathsf {win}}] | \le \mathsf {Adv}_{\mathcal {B}}^{\mathsf {PRF}}(\lambda ). \end{aligned}$$

(2)

$\underline{\mathsf {H}_{2}}$. Next, we define $\mathsf {H}_{2}$. We change the behavior of random oracle H and random function R. Consider another random oracle $H':\{0,1\}^{*} \rightarrow \mathbb {Z}_p^{(k+1)\times (k+1)} \times \mathbb {Z}_p^{(k+1)\times (k+1)}$ that only the challenger can access. We denote the first and second elements of $H'(i)$ by $\varvec{\mathrm {{W}}}_{i,0}$ and $\varvec{\mathrm {{W}}}_{i,1}$, respectively. In $\mathsf {H}_{2}$, H(i) outputs $([\varvec{\mathrm {{W}}}^{\top }_{i,0}\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{W}}}^{\top }_{i,1}\varvec{\mathrm {{A}}}]_{1})$, and R(i) outputs $(\varvec{\mathrm {{W}}}^{\top }_{i,0}\varvec{\mathrm {{a}}}_{1}, \varvec{\mathrm {{W}}}^{\top }_{i,1}\varvec{\mathrm {{a}}}_{1})$. Then, we have

$$\begin{aligned} \Pr [\langle \mathcal {A}, \mathsf {H}_{1} \rangle _{\mathsf {win}}] = \Pr [\langle \mathcal {A}, \mathsf {H}_{2} \rangle _{\mathsf {win}}]. \end{aligned}$$

(3)

It is not difficult to confirm that the above equality holds because $\overline{\varvec{\mathrm {{A}}}} = (\varvec{\mathrm {{A}}}||\varvec{\mathrm {{a}}}_{1})$ is a regular matrix, and thus $\varvec{\mathrm {{W}}}^{\top }_{i,b}\overline{\varvec{\mathrm {{A}}}}$ is randomly distributed in $\mathbb {Z}_p^{(k+1)\times (k+1)}$ for $\mathcal {A}$. By this conceptual change, we can rewrite $c_{2,i}$ and $k_{2,i}$ in the challenge ciphertext and secret keys as follows:

In the above, we use the relations $\varvec{\mathrm {{A}}}^{*}\varvec{\mathrm {{A}}}^{\top } + \varvec{\mathrm {{a}}}^{*}_{1}\varvec{\mathrm {{a}}}_{1}^{\top }=\varvec{\mathrm {{I}}}_{k+1}$.

$\underline{\mathsf {H}_{3,\iota }}$. To describe $\mathsf {H}_{3,\iota }$, we define some distributions on ciphertexts and secret keys as follows. Concretely, we define two types of ciphertexts and secret keys, namely, normal and semi-functional. A normal ciphertext is one generated as in $\mathsf {H}_{2}$. That is,

A semi-functional ciphertext is the same as the normal one except that $\varvec{\mathrm {{A}}}\varvec{\mathrm {{s}}}$ is replaced with $\varvec{\mathrm {{c}}} \leftarrow \mathbb {Z}_p^{k+1}$. That is,

Similarly, a normal secret key is one generated as in $\mathsf {H}_{2}$. That is,

(4)

Especially, $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n}$ in $k_{2,i}$ is outputs of $\mathsf {Share}(f, \varvec{\mathrm {{k}}})$. On the other hand, in a semi-functional secret key, $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n}$ in $k_{2,i}$ is outputs of $\mathsf {Share}(f, \varvec{\mathrm {{k}}} + \mu \varvec{\mathrm {{a}}}^{*}_{1})$ where $\mu \leftarrow \mathbb {Z}_p$. Then, $\mathsf {H}_{3,\iota }$ is the same as $\mathsf {H}_{2}$ except that the challenge ciphertext and the first $\iota$ keys that $\mathcal {A}$ is given are semi-functional.

Lemma 3.2

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {H}_{2} \rangle _{\mathsf {win}}]- \Pr [\langle \mathcal {A}, \mathsf {H}_{3,0} \rangle _{\mathsf {win}}] | \le \mathsf {Adv}_{\mathcal {B},\mathsf {bi}}^{\mathsf {\mathcal {D}_{k}\text {-}MDDH}}(\lambda ). \end{aligned}$$

(5)

Proof

To show this, we describe $\mathcal {B}$, which is given an instance of the $\mathcal {D}_{k}$-MDDH problem $(\mathbb {G}, [\varvec{\mathrm {{A}}}]_{1,2}, [\varvec{\mathrm {{t}}}_{\beta }]_{1,2})$. Let $H':\{0,1\}^{*} \rightarrow \mathbb {Z}_p^{(k+1)\times (k+1)} \times \mathbb {Z}_p^{(k+1)\times (k+1)}$ be a random oracle simulated by $\mathcal {B}$ that $\mathcal {A}$ cannot access.

• 1. $\mathcal {B}$ generates $\varvec{\mathrm {{B}}}$ and $\varvec{\mathrm {{k}}}$ by itself.

• 2. $\mathcal {B}$ computes $\mathsf {pk}= (\mathbb {G}, [\varvec{\mathrm {{A}}}]_{2}, e([\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{k}}}]_{2}))$ and gives it to $\mathcal {A}$.

• 3. For query H(i), $\mathcal {B}$ answers with $([\varvec{\mathrm {{W}}}^{\top }_{i,0}\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{W}}}^{\top }_{i,1}\varvec{\mathrm {{A}}}]_{1})$, where $(\varvec{\mathrm {{W}}}_{i,0}, \varvec{\mathrm {{W}}}_{i,1})$ is an output of $H'(i)$.

• 4. For query $\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},y)$, $\mathcal {B}$ computes $\mathsf {sk}_{y}$ as in Eq. (4). Note that $\mathcal {B}$ can generate $\mathsf {sk}$ without the random function R because it does not contain terms related to $\varvec{\mathrm {{A}}}$ any more.

• 5. For the challenge query with the attribute $x^{*}=(\varvec{\mathrm {{x}}}, \phi )$, $\mathcal {B}$ flip the coin $\delta \leftarrow \{0,1\}$ and generates $\mathsf {ct}_{x^{*}}$ as

  

• 6. $\mathcal {B}$ outputs $\mathrm {true}(\delta = \delta ')$, where $\delta '$ is an output of $\mathcal {A}$.

The case $\beta =0$ corresponds to $\mathsf {H}_{2}$ and the case $\beta =1$ corresponds to $\mathsf {H}_{3,0}$.   $\square$

In the next lemma, we prove the indistinguishability between $\mathsf {H}_{3,\iota -1}$ and $\mathsf {H}_{3,\iota }$. That is, all PPT adversaries cannot distinguish whether the $\iota$-th secret key is normal or semi-functional. To prove this one-secret-key indistinguishability, we introduce core 1-ABE game $\mathsf {G}_{\beta }^{\text {1-ABE}}$ where $\beta \in \{0,1\}$ such that $\mathsf {G}_{0}^{\text {1-ABE}}$ and $\mathsf {G}_{1}^{\text {1-ABE}}$ are computationally indistinguishable. Roughly speaking, the core 1-ABE game is designed so that we can construct a distinguisher between $\mathsf {G}_{0}^{\text {1-ABE}}$ and $\mathsf {G}_{1}^{\text {1-ABE}}$ if there exists an adversary that can distinguish $\mathsf {H}_{3,\iota -1}$ and $\mathsf {H}_{3,\iota }$.

It is convenient for us to parametrize the core 1-ABE game by $\eta \in \{1,2\}$ because we also use it in the security proof of our CP-ABE scheme. We use the game with $\eta = 1$ in the security proof of our KP-ABE scheme, and that with $\eta = 2$ in the security proof of our CP-ABE scheme.

Definition 3.1

(Core 1-ABE). For $\eta \in \{1,2\}$ and $\beta \in \{0,1\}$, we define $\mathsf {G}_{\eta , \beta }^{\text {1-ABE}}$ as Fig. 2. In $\mathsf {G}_{\eta ,\beta }^{\text {1-ABE}}$, $\mathcal {A}$ can query $\mathcal {O}_{X}$ and $\mathcal {O}_{F}$ only once whereas $\mathcal {A}$ can query $\mathcal {O}_{R}$ polynomially many times. All queries can be done adaptively. Furthermore, $x \in \mathcal {X}$ and $y \in \mathcal {Y}$ on which $\mathcal {A}$ queries $\mathcal {O}_{X}$ and $\mathcal {O}_{F}$ must satisfy $R(x,y)=0$. $\mathcal {X}$ and $\mathcal {Y}$ are defined in Definition 2.5. Note that the difference between $\mathsf {G}_{\eta , 0}^{\text {1-ABE}}$ and $\mathsf {G}_{\eta , 1}^{\text {1-ABE}}$ lies in the input of $\mathsf {Share}$ in $\mathcal {O}_{F}$. We define the advantage of $\mathcal {A}$ against $\mathsf {G}_{\eta , \beta }^{\text {1-ABE}}$ as follows:

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}, \eta }^{\mathsf {1\text {-}ABE}}(\lambda )&:=|\Pr [\langle \mathcal {A}, \mathsf {G}_{\eta ,0}^{\text {1-ABE }} \rangle =1]- \Pr [\langle \mathcal {A}, \mathsf {G}_{\eta ,1}^{\text {1-ABE }} \rangle = 1]|. \end{aligned}$$

We defer the proof of the indistinguishability between the two games to Sect. 4.

Lemma 3.3

For $\iota \in [q_{\mathsf {sk}}]$, we have

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {H}_{3,\iota -1} \rangle _{\mathsf {win}}]- \Pr [\langle \mathcal {A}, \mathsf {H}_{3,\iota } \rangle _{\mathsf {win}}] | \le \mathsf {Adv}_{\mathcal {B},1}^{\mathsf {1\text {-}ABE}}(\lambda ). \end{aligned}$$

(6)

Fig. 2.

Core 1-ABE game.

Proof

We consider an adversary $\mathcal {B}$ against $\mathsf {G}^{\text {1-ABE}}_{1,\beta }$ where $\eta = 1$. We describe $\mathcal {B}$’s behavior.

• 1. $\mathcal {B}$ is given $(\mathbb {G}, \varvec{\mathrm {{A}}}, [\varvec{\mathrm {{B}}}]_{1,2}, \textsf {d}, \varvec{\mathrm {{W}}})$ from the 1-ABE game.

• 2. $\mathcal {B}$ sets $\textsf {k}:=\varvec{\mathrm {{W}}}\textsf {d}$ and gives $\mathsf {pk}= (\mathbb {G}, [\varvec{\mathrm {{A}}}]_{2}, [\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{k}}}]_{T})$ to $\mathcal {A}$.

• 3. For query H(i), $\mathcal {B}$ makes a query $\mathcal {O}_{R}(i)$ and answers with $([\varvec{\mathrm {{W}}}^{\top }_{i,0}\varvec{\mathrm {{A}}}]_{1}, [\varvec{\mathrm {{W}}}^{\top }_{i,1}\varvec{\mathrm {{A}}}]_{1})$.

• 4. For the challenge query with an attribute $x^{*}$, $\mathcal {B}$ flips the coin $\delta \leftarrow \{0,1\}$. Then, $\mathcal {B}$ obtains $(A_{0}, \{A_{i}\}_{i \in [m]})$ as the reply of $\mathcal {O}_{X}(x^{*})$. $\mathcal {B}$ returns $\mathsf {ct}_{x^{*}}$ as

  $$\begin{aligned} \mathsf {ct}_{x^{*}} :=\left( [A_{0}]_{2}, \{[A_{i}]_{1}\}_{i \in [m]}, [A^{\top }_{0}\varvec{\mathrm {{k}}}]_{T}M_{\delta }\right) . \end{aligned}$$

• 5. For the $\ell$-th query $\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},y)$, where $\ell < \iota$ and $y=(\varvec{\mathrm {{y}}},f,\psi ,t)$, $\mathcal {B}$ computes $\mathsf {sk}_{y}$ as in Eq. (4) by setting $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n} \leftarrow \mathsf {Share}(f,\varvec{\mathrm {{k}}}+\mu \varvec{\mathrm {{a}}}^{*}_{1})$ with a fresh randomness $\mu \leftarrow \mathbb {Z}_p$.

• 6. For the $\ell$-th query $\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},y)$, where $\ell = \iota$ and $y=(\varvec{\mathrm {{y}}},f,\psi ,t)$, $\mathcal {B}$ obtains $(P_{0}, \{P_{i}\}_{i \in [n]})$ as the reply of $\mathcal {O}_{F}(y)$. Then, $\mathcal {B}$ returns $\mathsf {sk}_{y}$ as

  $$\begin{aligned} \mathsf {sk}_{y} :=(P_{0}, \{P_{i}\}_{i \in [n]}). \end{aligned}$$

• 7. For the $\ell$-th query $\mathsf {KeyGen}(\mathsf {pk},\mathsf {msk},y)$, where $\ell > \iota$ and $y=(\varvec{\mathrm {{y}}},f,\psi ,t)$, $\mathcal {B}$ computes $\mathsf {sk}_{y}$ as in Eq. (4) by setting $\varvec{\mathrm {{k}}}_{1} , \ldots ,\varvec{\mathrm {{k}}}_{n} \leftarrow \mathsf {Share}(f,\varvec{\mathrm {{k}}})$.

• 8. $\mathcal {B}$ outputs $\mathrm {true}(\delta = \delta ')$, where $\delta '$ is an output of $\mathcal {A}$.

From Lemma 3.1, the term $\varvec{\mathrm {{k}}}_{i}+\sigma _{i}\varvec{\mathrm {{a}}}^{*}_{1}$ in the reply of $\mathcal {O}_{F}$ is identically distributed with the i-th output of $\mathsf {Share}(\varvec{\mathrm {{k}}}+\beta \mu \varvec{\mathrm {{a}}}^{*}_{1})$. Thus, if the oracles are those in $\mathsf {G}_{1,0}^{\text {1-ABE}}$, $\mathcal {A}$’s view corresponds to $\mathsf {H}_{3,\iota -1}$, and otherwise, it corresponds to $\mathsf {H}_{3,\iota }$.   $\square$

Lemma 3.4

$$\begin{aligned} |\Pr [\langle \mathcal {A}, \mathsf {H}_{3,q_{\mathsf {sk}}} \rangle _{\mathsf {win}}] -1/2| \le 2^{-\varOmega (\lambda )}. \end{aligned}$$

(7)

Proof

Because $(\varvec{\mathrm {{A}}}^{*}||\varvec{\mathrm {{a}}}^{*}_{1})$ forms a basis, redefining $\varvec{\mathrm {{k}}}$ as $\varvec{\mathrm {{k}}} :=\varvec{\mathrm {{A}}}^{*}\varvec{\mathrm {{z}}}+z\varvec{\mathrm {{a}}}^{*}_{1}$ where $\varvec{\mathrm {{z}}} \leftarrow \mathbb {Z}_p^{k}$ and $z \leftarrow \mathbb {Z}_p$ does not change its distribution. Recall that the information on $\varvec{\mathrm {{k}}}$ that $\mathcal {A}$ obtains throughout the game is $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{k}}}$ in $\mathsf {pk}$, $\mathsf {Share}(f,\varvec{\mathrm {{k}}}+\mu \varvec{\mathrm {{a}}}^{*}_{1})$ in $\mathsf {sk}_{y}$, and $\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{k}}}$ in $\mathsf {ct}_{x^{*}}$. However, $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{k}}}$ does not contain the information on z because $\varvec{\mathrm {{A}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1}=\varvec{\mathrm {{0}}}$. Similarly, each $\varvec{\mathrm {{k}}}+\mu \varvec{\mathrm {{a}}}^{*}_{1}$ also does not contain the information on z because it is masked by fresh randomness $\mu$. Thus, $z\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1}$ is randomly distributed in $\mathbb {Z}_p$ for $\mathcal {A}$, and so is $\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{k}}}$, unless $\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1}=0$. Since $\varvec{\mathrm {{c}}}$ is randomly chosen from $\mathbb {Z}_p^{k+1}$, $\varvec{\mathrm {{c}}}^{\top }\varvec{\mathrm {{a}}}^{*}_{1} = 0$ with a probability $2^{-\varOmega (\lambda )}$. If it is not the case, $\mathsf {ct}_{x^{*}}$ does not have information on $\beta$, and the lemma holds.   $\square$

Thanks to Eqs. (1) to (3) and (5) to (7) and Lemma 4.1, Theorem 3.1 holds.   $\square$

4 Adaptive Security for Core Component

In this section, we prove the indistinguishability between $\mathsf {G}_{\eta , 0}^{\text {1-ABE}}$ and $\mathsf {G}_{\eta , 1}^{\text {1-ABE}}$ defined in Definition 3.1. This is formally stated in the following lemma.

Lemma 4.1

(Core 1-ABE Security). Let B be the maximum depth of formula f for all choice of f by $\mathcal {A}$. For any PPT adversary $\mathcal {A}$ and $\eta \in \{1,2\}$, there exists a PPT algorithm $\mathcal {B}$ such that

$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}, \eta }^{\mathsf {1\text {-}ABE}}(\lambda ) \le 2^{9B+2}(\mathsf {Adv}_{\mathcal {B},\mathsf {bi}}^{\mathsf {\mathcal {D}_{k}\text {-}MDDH}}(\lambda )+2^{-\varOmega (\lambda )}). \end{aligned}$$

Proof

We prove Lemma 4.1 by extending the KW technique [21]. We omit the variable $\eta$ from the notation of hybrid games for conciseness, but all hybrids are parametrized by $\eta$. Following the piecewise guessing framework, we define a series of selective hybrids $\widehat{\mathsf {H}}^{h_{0}}$ to $\widehat{\mathsf {H}}^{h_{L}}$, where $L = 8^{B}$, and two intermediate games $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$ and $\mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }}$, which satisfy

• $\widehat{\mathsf {G}}_{0}^{\text {1-ABE }} = \widehat{\mathsf {H}}^{h_{0}} \approx _{c} , \ldots ,\approx _{c} \widehat{\mathsf {H}}^{h_{L}} = \widehat{\mathsf {G}}_{\mathsf {M}0}^{\text {1-ABE }}$

• $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }} = \mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }}$.

Let $z :=(x,y) \in \{0,1\}^{R}$ on which $\mathcal {A}$ queries $\mathcal {O}_{X}$ and $\mathcal {O}_{F}$, respectively. Let $b \in \{0,1\}^{n}$ be a string computed from z following Definition 2.5. Note that $f(b) = 0$ because the game imposes the condition $R(x,y)=0$ on $\mathcal {A}$. Let $\mathcal {R}$ be the pebbling record generated as $\mathcal {R}= (r_{1} , \ldots ,r_{L}) = \mathsf {PebRec}(f,b)$ as defined in Lemma 2.2. Then, we define $h_{\iota }:\{0,1\}^{R} \rightarrow \{0,1\}^{3B}$ as $h_{\iota }(z) :=r_{\iota }$. Note that $h_{0}$ and $h_{L}$ are constant functions because they specify the pebbling configurations where no pebbles on it and a pebble is placed on only the output gate, respectively.

The hybrids and intermediate games only differ in the $\mathsf {Share}$ algorithm in $\mathcal {O}_{F}$ as follows. That is, $\widehat{\mathsf {H}}^{h_{\iota }}$ is the same as $\widehat{\mathsf {G}}_{0}^{\text {1-ABE }}$ except that $\mathsf {Share}(f,0)$ is replaced with $\widetilde{\mathsf {Share}}(f,0,h_{\iota }(z))$, which is described in Fig. 3. $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$ is the same as $\mathsf {H}^{h_{L}}$, and $\mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }}$ is the same as $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$ except that $\widetilde{\mathsf {Share}}(f,0,h_{L}(z))$ is replaced with $\widetilde{\mathsf {Share}}(f,\mu ,h_{L}(z))$.

We prove that

• $\mathsf {G}_{0}^{\text {1-ABE }} \approx _{c} \mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$,

• $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }} = \mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }}$,

• $\mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }} \approx _{c} \mathsf {G}_{1}^{\text {1-ABE }}$.

First, we prove item 2, then prove item 1. We omit the proof of item 3 because it is almost the same as that of item 1. Then, we are done.

Fig. 3.

Description of $\widetilde{\mathsf {Share}}$.

$\underline{\mathsf {G}_{\mathsf {M}0}^{1-ABE } = \mathsf {G}_{\mathsf {M}1}^{\text {1-ABE }}}$. Recall that the difference between the two games lies in the input of $\widetilde{\mathsf {Share}}$, namely, $(f,0,h_{L}(z))$ or $(f,\mu ,h_{L}(z))$. First, we note that $u = h_{L}(z)$ is a constant that specifies the pebbling configuration on f where a pebble is placed on only the output gate. In this case, it is not difficult to see that the output of $\widetilde{\mathsf {Share}}$ is independent of the second argument of the input. This is because the values set on the two incoming wires of the output gate are chosen independently of $\sigma _{\mathsf {out}}$ when a pebble is placed on the output gate (see item 3 in Fig. 3). Then, the values to be set on the rest of wires are computed based on these values set on the incoming wires of the output gate. Thus, the output of $\widetilde{\mathsf {Share}}$ is identically distributed in both games, and the claim holds.

$\underline{\mathsf {G}_{0}^{\text {1-ABE }} \approx _{c} \mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}}$. Following Lemma 2.1, we prove the two properties:

• 1. $\mathsf {G}_{0}^{\text {1-ABE }} = \mathsf {H}^{h_{0}}$ and $\mathsf {H}^{h_{L}} = \mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$,

• 2. $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}} \approx _{c} \widehat{\mathsf {H}}_{0}^{h_{\iota }}$ for $\iota \in [L]$.

where $\widehat{\mathsf {H}}_{\beta }^{h_{i}}$ for $\beta \in \{0,1\}$ is defined in Sect. 2.4. For item 1, the latter holds because we defined $\mathsf {G}_{\mathsf {M}0}^{\text {1-ABE }}$ in such a way. To show the former, we need to confirm that the output of $\mathsf {Share}(f, 0)$ and $\widetilde{\mathsf {Share}}(f,0,h_{0}(z))$ is identically distributed. Recall that $h_{0}$ is a constant function that specifies the pebbling configuration where no pebbles on it. In this case, no gates correspond to item 3 or 6 in Fig. 3, and the remaining procedures are exactly the same as $\mathsf {Share}(f, 0)$. Thus, the former also holds.

The remaining thing is to prove $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}} \approx _{c} \widehat{\mathsf {H}}_{0}^{h_{\iota }}$. Formally, we show that, for any PPT adversary $\mathcal {A}$, there exists a PPT adversary $\mathcal {B}$ such that

To show this, we additionally consider three intermediate selective hybrids $\widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}}$ to $\widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}}$.

In the following, we denote the pebbling configuration on f that is specified by a bit string u by C(f, u). Let $u_{0}$ and $u_{1}$ be the committed values by $\mathcal {A}$, which correspond to $h_{\iota -1}(z)$ and $h_{\iota }(z)$ for z chosen by $\mathcal {A}$. Then, $C(f,u_{0})$ and $C(f,u_{1})$ are adjacent pebbling configurations for some input $b \in \{0,1\}^{n}$ for f. In other words, there exists b such that $u_{0}$ and $u_{1}$ correspond to $r_{\iota -1}$ and $r_{\iota }$ where $(r_{0} , \ldots ,r_{L}) = \mathsf {PebRec}(f,b)$. Thus, $C(f,u_{0})$ can be changed to $C(f,u_{1})$ in one step following the rule defined in Definition 2.8. Recall that the difference between $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$ and $\widehat{\mathsf {H}}_{0}^{h_{\iota }}$ is the input of $\widetilde{\mathsf {Share}}$. That is, the input is $(f, 0, u_{0})$ in $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$ and $(f, 0, u_{1})$ in $\widehat{\mathsf {H}}_{0}^{h_{\iota }}$. Thus, in case of $u_{0} = u_{1}$, $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$ and $\widehat{\mathsf {H}}_{0}^{h_{\iota }}$ are clearly identical. In the following, we consider the case of $u_{0} \ne u_{1}$.

Let an object O be either a gate g or an input wire $i^{*}$, in which the difference between $C(f,u_{0})$ and $C(f,u_{1})$ lies. We consider only the case where a pebble is placed on g or $i^{*}$, since the case where a pebble is removed is just the reverse of the former case. Intermediate hybrids $\widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}}$ to $\widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}}$ are different from $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$ only in $\mathcal {O}_{F}$ as shown in Fig. 4. That is, when O is a gate, $\widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}}$ to $\widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}}$ are the same as $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$. When O is an input wire, these hybrids are defined as follows:

• $\widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}}$ is the same as $\widehat{\mathsf {H}}_{1}^{h_{\iota -1}}$ except that $\varvec{\mathrm {{v}}}_{\pi (i^{*})} \leftarrow \mathsf {span}(\textsf {B}, \textsf {b}_{1})$,

• $\widehat{\mathsf {H}}_{1,2}^{h_{\iota -1}}$ is the same as $\widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}}$ except that random value u is added to $\sigma _{i^{*}}$,

• $\widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}}$ is the same as $\widehat{\mathsf {H}}_{1,2}^{h_{\iota -1}}$ except that $\varvec{\mathrm {{v}}}_{\pi (i^{*})} :=\varvec{\mathrm {{B}}}\varvec{\mathrm {{r}}}_{\pi (i^{*})}$ for $\varvec{\mathrm {{r}}}_{\pi (i^{*})} \leftarrow \mathbb {Z}_p^{k}$.

Thanks to Lemmas 4.2 to 4.5 and observations so far, Lemma 4.1 holds.   $\square$

Lemma 4.2

$|\Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1}^{h_{\iota -1}} \rangle =1]- \Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}} \rangle = 1]| \le \mathsf {Adv}_{\mathcal {B},\mathsf {bi}}^{\mathsf {\mathcal {D}_{k}\text {-}MDDH}}(\lambda ).$

Lemma 4.3

$|\Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,1}^{h_{\iota -1}} \rangle =1]- \Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,2}^{h_{\iota -1}} \rangle = 1] \le 2^{-\varOmega (\lambda )}.$

Lemma 4.4

$|\Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,2}^{h_{\iota -1}} \rangle =1]- \Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}} \rangle = 1]| \le \mathsf {Adv}_{\mathcal {B},\mathsf {bi}}^{\mathsf {\mathcal {D}_{k}\text {-}MDDH}}(\lambda ).$

Fig. 4.

Description of $O_{F}$ in hybrids.

Lemma 4.5

$\Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{1,3}^{h_{\iota -1}} \rangle = 1] = \Pr [\langle \mathcal {A}, \widehat{\mathsf {H}}_{0}^{h_{\iota }} \rangle =1].$

We present the proof of Lemmas 4.2, 4.3 and 4.5 in the full version. We omit the proof of Lemma 4.4 because the proof of this lemma is almost the same as that of Lemma 4.2.

Fig. 5.

Benchmarks of our KP-ABE on PC.

Fig. 6.

Benchmarks of our CP-ABE on PC.

Fig. 7.

Comparison of KP-ABE between ours and OT12 on PC.

Fig. 8.

Comparison of CP-ABE between ours and OT12 on PC.

5 Implementation and Evaluation

We implement our KP-ABE and CP-ABE schemes and measure the benchmarks of our schemes on an ordinary personal computer (PC) and two smartphones, Apple iPhone XR and Google Pixel 3. The details of our implementation are described in the full version.

The efficiency of $\mathsf {KeyGen}$ and $\mathsf {Dec}$ in KP-ABE (resp. $\mathsf {Enc}$ and $\mathsf {Dec}$ in CP-ABE) is affected by formula f used in a secret key (resp. a ciphertext). More concretely, in $\mathsf {KeyGen}$ of our KP-ABE and $\mathsf {Enc}$ of our CP-ABE, the numbers of exponentiation in $G_{1}$ and $G_{2}$ increase proportionally to those of negation and multi-use, respectively. On the other hand, the number of hashing decreases proportionally to that of multi-use. In $\mathsf {Dec}$, the numbers of exponentiation and pairings increase proportionally to the numbers of negation and multi-use, respectively.

To clarify the effects of these factors, we consider the four types of formulae.

• 1. no negations and multi-uses (no neg. & no mult.):

  i.e., (Label-1:$v_{1}$ AND Label-2:$v_{2}$ AND ...),

• 2. all negations and no multi-uses (all neg. & no mult.):

  i.e., (Label-1:NOT $v_{1}$ AND Label-2:NOT $v_{2}$ AND ...),

• 3. no negations and all multi-uses (no neg. & all mult.):

  i.e., (Label-1:$v_{1}$ AND Label-1:$v_{1}$ AND ...),

• 4. all negations and multi-uses (all neg. & all mult.):

  i.e., (Label-1:NOT $v_{1}$ AND Label-1:NOT $v_{2}$ AND ...).

We present the benchmarks on the PC in Figs. 5 and 6 and smartphones in the full version. The figures show the benchmarks with respect to a formula or attribute set with $1,10, 20 , \ldots ,100$ attributes for each case listed above. $\mathsf {Enc}$ in KP-ABE and $\mathsf {KeyGen}$ in CP-ABE are not affected by the types of formula, and we measure the benchmark for encryption/key generation with attributes Label-1:$v_{1} , \ldots ,$ Label-n:$v_{n}$.

In all cases, our KP-ABE (resp. CP-ABE) scheme takes about 0.4 to 0.7s (resp. 0.4 to 0.9s) for encryption and key generation on the PC to handle 100 attributes. Our schemes allow very fast decryption for a monotone formula without multi-use (item 1), and they take only about 0.02s (KP & CP) for a formula with 100 attributes. We can assume that our schemes allow similarly fast decryption also for a formula in which the ratio of negation and multi-use is small. Even in the slowest case (item 4), it takes about 0.5 (KP) or 0.7s (CP) for decryption.

Because of small computational resource compared with the PC, the smartphones take more time for each algorithm. The benchmarks show that running times on iPhone XR are relatively close to those on the PC, and they are approximately 1.5 times slower. Google Pixel 3 takes further more time and its running times are 3 to 3.5 times as slow as those on the PC.

Effects of Negation and Multi-use. The benchmarks for $\mathsf {KeyGen}$ in KP-ABE and $\mathsf {Enc}$ in CP-ABE show that both negation and multi-use slow the running time down. It is reasonable that negation slows the running time down because it increases the number of exponentiation in $G_{1}$. In contrast, multi-use decreases the number of hashing to $G_{1}$ whereas it increases that of exponentiation in $G_{2}$. The benchmarks show that the former effect is smaller than the latter in our implementation. However, multi-use can shorten the running time in a platform where exponentiation in $G_{2}$ is more efficient or hashing to $G_{1}$ is less efficient.

In $\mathsf {Dec}$, both negation and multi-use extend the running time, and the effect of multi-use is larger. This is since the number of negation affects that of exponentiation in $G_{1}$ while the number of multi-use affects that of heavier pairings.

Comparison with OT12. We also implement KP and CP schemes by Okamoto and Takashima in [27] (OT12), which are the only schemes that support OT negation and unboundedness, and thus whose functionalities are the closest to our schemes among known ABE schemes. The comparison between our schemes and OT12 on PC is presented in Figs. 7 and 8, which shows that our schemes achieve significant speedups in every algorithm. We compare them in the one-use restriction of labels (no multi-use), which corresponds to item 1 and item 2 in the four cases, since OT12 does not support multi-use of labels. Hence, the blue and gray lines in Fig. 5 are the same as those in Fig. 7 up to scale (similarly in Figs. 6 and 8). In contrast to our schemes, negation hardly affects the efficiency in OT12. Note that although we can utilize a bounded number of multi-use of labels by preparing multiple nominal labels for each single label in OT12, this significantly affects the efficiency. For example, when we set the bound as 10, this slows down $\mathsf {Enc}$ in KP-ABE or $\mathsf {KeyGen}$ in CP-ABE by 10 times.

CCA Security. In practice, the chosen ciphertext attack (CCA) security is a de facto standard and desirable security requirement. The Fujisaki-Okamoto conversion [15] is not suitable for our case because it requires the decryption algorithm to run the encryption algorithm, which causes a significant efficiency loss. However, our schemes can be efficiently converted to CCA secure ones via Boneh-Katz conversion [10] in a similar manner to [26].