Skip to main content
SpringerLink
Log in

Models of Cell Motion and Tissue Growth

  • Chapter
  • First Online:
The Mathematics of Mechanobiology

Part of the book series: Lecture Notes in Mathematics ((LNMCIME,volume 2260))

  • 747 Accesses

Abstract

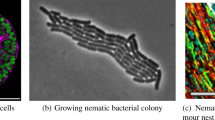
The mathematical description of cell movement, from the individual scale to the collective motion, is a rich and complex domain of biomathematics which leads to several types of questions and partial differential equations. For instance, bacteria move by run-and-tumble movement, which is well described, at the cell scale, by a kinetic equation in the phase coordinates. At the population scale, chemotactic effects lead to the famous parabolic Keller–Segel system, and the many improvements of it that have been addressed recently.

When considering living tissues, concepts issued from mechanics arise. Notions of pressure, phases, incompressibility are used in systems which carry the typical parabolic and hyperbolic characters of fluid mechanics. Their complexity is directly related to the details in the biological description and opens numerous mathematical questions which are poorly understood.

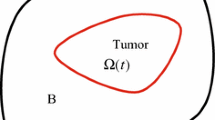
The various process involved in cell movements can be considered at the cell scale, at the population scale and, for tissues, at the organ scale. This leads to study singular perturbation problems of various types. For tumor growth, the tumor boundary can appear as a free boundary or as an internal layer.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 49.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 64.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. J. Adler, Chemotaxis in bacteria. Science 153, 708–716 (1966)

    Google Scholar 

  2. A. Agosti, P.F. Antonietti, P. Ciarletta, M. Grasselli, M. Verani, A Cahn-Hilliard type equation with application to tumor growth dynamics. Math. Methods Appl. Sci. 40(18), 7598–7626 (2017)

    MathSciNet  MATH  Google Scholar 

  3. W. Alt, Biased random walk models for chemotaxis and related diffusion approximations. J. Math. Biol. 9, 147–177 (1980)

    MathSciNet  MATH  Google Scholar 

  4. H.W. Alt, E. DiBenedetto, Nonsteady flow of water and oil through inhomogeneous porous media. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 12(3), 335–392 (1985)

    Google Scholar 

  5. H.W. Alt, S. Luckhaus, A. Visintin, On nonstationary flow through porous media. Ann. Mat. Pura Appl. (4) 136, 303–316 (1984)

    Google Scholar 

  6. D.G. Aronson, P. Bénilan, Régularité des solutions de l’équation des milieux poreux dans R N. C. R. Acad. Sci. Paris Sér. A-B 288(2), A103–A105 (1979)

    MATH  Google Scholar 

  7. C. Bardos, R. Santos, R. Sentis, Diffusion approximation and computation of the critical size. Trans. Amer. Math. Soc. 284(2), 617–649 (1984)

    MathSciNet  MATH  Google Scholar 

  8. N. Bellomo, M. Winkler, A degenerate chemotaxis system with flux limitation: maximally extended solutions and absence of gradient blow-up. Commun. Part. Diff. Equ. 42, 436–473 (2017)

    MathSciNet  MATH  Google Scholar 

  9. N. Bellomo, N.K. Li., P.K. Maini, On the foundations of cancer modelling: selected topics, speculations, and perspectives. Math. Models Methods Appl. Sci. 4, 593–646 (2008)

    Google Scholar 

  10. H.C. Berg, E. coli in Motion (Springer, Berlin, 2004)

    Google Scholar 

  11. M. Bertsch, D. Hilhorst, H. Izuhara, M. Mimura, A nonlinear parabolic-hyperbolic system for contact inhibition of cell-growth. Diff. Eqs. Appl. 4, 137–157 (2012)

    MathSciNet  MATH  Google Scholar 

  12. P. Biler, L. Corrias, J. Dolbeault, Large mass self-similar solutions of the parabolic-parabolic Keller-Segel model of chemotaxis. J. Math. Biol. 63(1), 1–32 (2011)

    MathSciNet  MATH  Google Scholar 

  13. A. Blanchet, J. Dolbeault, B. Perthame, Two-dimensional Keller-Segel model: optimal critical mass and qualitative properties of the solutions. Electron. J. Diff. Equ. 2006(44), 1–32 (2006)

    MathSciNet  MATH  Google Scholar 

  14. A. Blanchet, J.A. Carrillo, P. Laurençot, Critical mass for a Patlak-Keller-Segel model with degenerate diffusion in higher dimensions. Calc. Var. Partial Differential Equations 35(2), 133–168 (2009)

    MathSciNet  MATH  Google Scholar 

  15. E. Bouin, V. Calvez, G. Nadin, Propagation in a kinetic reaction-transport equation: travelling waves and accelerating fronts. Arch. Ration. Mech. Anal. 217(2), 571–617 (2015)

    MathSciNet  MATH  Google Scholar 

  16. N. Bournaveas, V. Calvez, Critical mass phenomenon for a chemotaxis kinetic model with spherically symmetric initial data. Ann. Inst. H. Poincaré Anal. Non Linéaire 26(5), 1871–1895 (2009)

    MathSciNet  MATH  Google Scholar 

  17. N. Bournaveas, V. Calvez, S. Gutièrrez, B. Perthame, Comm. Partial Diff. Equ. 33, 79–95 (2008)

    Google Scholar 

  18. M.P. Brenner, L.S. Levitov, E.O. Budrene, Physical mechanisms for chemotactic pattern formation by bacteria. Biophys J. 74, 1677–1693 (1998)

    Google Scholar 

  19. F. Bubba, C. Pouchol, B. Perthame, M. Schmidtchen, Incompressible limit for a two species model of tissue growth in one space dimension. Arch. Ration. Mech. Anal. 236(2), 735–766 (2020)

    MathSciNet  MATH  Google Scholar 

  20. E.O. Budrene, H.C. Berg, Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature 376, 49–53 (1995)

    Google Scholar 

  21. H.M. Byrne, M. Chaplain, Growth of necrotic tumors in the presence and absence of inhibitors. Math. Biosci. 135(2),187–216 (1996)

    MATH  Google Scholar 

  22. H. Byrne, D. Drasdo, Individual-based and continuum models of growing cell populations: a comparison. J. Math. Biol. 58, 657–687 (2009)

    MathSciNet  MATH  Google Scholar 

  23. H. Byrne, L. Preziosi, Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 20, 341–66 (2004)

    MATH  Google Scholar 

  24. H.M. Byrne, J.R. King, D.L.S. McElwain, L. Preziosi, A two-phase model of solid tumor growth. Appl. Math. Lett. 16, 567–573 (2003)

    MathSciNet  MATH  Google Scholar 

  25. H. Byrne, L. Preziosi, Modelling solid tumour growth using the theory of mixtures. Math. Med. Biol. 20(4), 341–366 (2003)

    MATH  Google Scholar 

  26. V. Calvez, Chemotactic waves of bacteria at the mesoscale. arXiv:1607.00429 (2016)

    Google Scholar 

  27. V. Calvez, J.A. Carrillo, Refined asymptotics for the subcritical Keller-Segel system and related functional inequalities. Proc. Amer. Math. Soc. 140(10), 3515–3530 (2012)

    MathSciNet  MATH  Google Scholar 

  28. V. Calvez, G. Raoul, C. Schmeiser, Confinement by biased velocity jumps: aggregation of Escherichia coli. Kinet. Relat. Models 8(4), 651–666 (2015)

    MathSciNet  MATH  Google Scholar 

  29. V. Calvez, B. Perthame, S. Yasuda, Traveling wave and aggregation in a flux-limited Keller-Segel model. Kinet. Relat. Models 11(4), 891–909 (2018)

    MathSciNet  MATH  Google Scholar 

  30. C. Cancès, T.O. Gallouët, L. Monsaingeon, Incompressible immiscible multiphase flows in porous media: a variational approach. Anal. PDE 10(8), 1845–1876 (2017)

    MathSciNet  MATH  Google Scholar 

  31. J.A. Carrillo, S. Fagioli, F. Santambrogio, M. Schmidtchen, Splitting schemes and segregation in reaction cross-diffusion systems. SIAM J. Math. Anal. 50(5), 5695–5718 (2018)

    MathSciNet  MATH  Google Scholar 

  32. C. Cercignani, R. Illner, M. Pulvirenti, The mathematical theory of dilute gases. In: Applied Mathematical Sciences, vol. 106 (Springer, New York, 1994), viii+347 pp.

    Google Scholar 

  33. F. Chalub, P.A. Markowich, B. Perthame, C. Schmeiser, Kinetic models for chemotaxis and their drift-diffusion limits. Monatsh. Math. 142, 123–141 (2004)

    MathSciNet  MATH  Google Scholar 

  34. C. Chatelain, T. Balois, P. Ciarletta, M. Ben Amar, Emergence of microstructural patterns in skin cancer: a phase separation analysis in a binary mixture. New J. Phys. 13(11), 115013 (2011)

    Google Scholar 

  35. A. Chertock, A. Kurganov, X. Wang, Y. Wu, On a chemotaxis model with saturated chemotactic flux. Kinetic Related Models 5, 51–95 (2012)

    MathSciNet  MATH  Google Scholar 

  36. P. Ciarletta, L. Foret, M. Ben Amar, The radial growth phase of malignant melanoma: multi-phase modelling, numerical simulations and linear stability analysis. J. R. Soc. Interface 8(56), 345–368 (2011)

    Google Scholar 

  37. T. Colin, D. Bresch, E. Grenier, B. Ribba, O. Saut, Computational modeling of solid tumor growth: the avascular stage. SIAM J. Sci. Comput. 32(4), 2321–2344 (2010)

    MathSciNet  MATH  Google Scholar 

  38. T. Colin, A. Iollo, D. Lombardi, O. Saut, System identification in tumor growth modeling using semi-empirical eigenfunctions. Math. Models Methods Appl. Sci. 22(6), 1250003 (30 pp) (2012)

    Google Scholar 

  39. F. Cornelis, O. Saut, P. Cumsille, D. Lombardi, A. Iollo, J. Palussière, T. Colin, In vivo mathematical modeling of tumor growth from imaging date: Soon to come in the future? Diagn. Interv. Imaging 94(6), 593–600 (2013)

    Google Scholar 

  40. M.G. Crandall, M. Pierre, Regularizing effects for u t =  Δϕ(u). Trans. Am. Math. Soc. 274(1), 159–168 (1982)

    MATH  Google Scholar 

  41. Y. Dolak, C. Schmeiser, Kinetic models for chemotaxis: hydrodynamic limits and spatio-temporal mechanisms. J. Math. Biol. 51, 595–615 (2005)

    MathSciNet  MATH  Google Scholar 

  42. R. Eftimie, Hyperbolic and kinetic models for self-organized biological aggregations and movement: a brief review. J. Math. Biol. 65, 35–75 (2012)

    MathSciNet  MATH  Google Scholar 

  43. R. Erban, H. Othmer, From individual to collective behaviour in bacterial chemotaxis. SIAM J. Appl. Math. 65(2), 361–391 (2004)

    MathSciNet  MATH  Google Scholar 

  44. R. Erban, H. Othmer, Taxis equations for amoeboid cells. J. Math. Biol. 54, 847–885 (2007)

    MathSciNet  MATH  Google Scholar 

  45. J. Escher, G. Simonett, Classical solutions for Hele-Shaw models with surface tension. Adv. Diff. Equ. 2(4), 619–642 (1997)

    MathSciNet  MATH  Google Scholar 

  46. A. Friedman, A hierarchy of cancer models and their mathematical challenges. Discrete Contin. Dynam. Systems Ser. B 4(1), 147–159 (2004)

    MathSciNet  MATH  Google Scholar 

  47. S. Frigeri, M. Grasselli, E. Rocca, On a diffuse interface model of tumor growth. European J. Appl. Math. 26, 215–243 (2015)

    MathSciNet  MATH  Google Scholar 

  48. H. Garcke, K.F. Lam, R. Nürnberg, E. Sitka, A multiphase Cahn-Hilliard-Darcy model for tumour growth with necrosis. Math. Models Methods Appl. Sci. 28(3), 525–577 (2018)

    MathSciNet  MATH  Google Scholar 

  49. R. Glassey, The Cauchy Problem in Kinetic Theory (SIAM, Philadelphia, 1996)

    MATH  Google Scholar 

  50. I. Golding, Y. Kozlovsky, I. Cohen, E. Ben Jacob, Studies of bacterial branching growth using reaction–diffusion models for colonial development. Physica A 260, 510–554 (1998)

    Google Scholar 

  51. A. Goriely, The mathematics and mechanics of biological growth. In: Interdisciplinary Applied Mathematics, vol. 45 (Springer, New York, 2017)

    Google Scholar 

  52. P. Gwiazda, B. Perthame, A. Świerczewska-Gwiazda, A two species hyperbolic-parabolic model of tissue growth. Comm. Partial Diff. Equ. 44(12), 1605–1618 (2019)

    MathSciNet  MATH  Google Scholar 

  53. T. Hillen, H.G. Othmer, The diffusion limit of transport equations derived from velocity-jump processes. SIAM J. Appl. Math. 61, 751–775 (2000)

    MathSciNet  MATH  Google Scholar 

  54. T. Hillen, K.J. Painter. A user’s guide to PDE models for chemotaxis. J. Math. Biol. 58, 183–217 (2009)

    MathSciNet  MATH  Google Scholar 

  55. T. Hillen, A. Swan, The diffusion limit of transport equations in biology. In: Mathematical Models and Methods for Living Systems. Lecture Notes in Mathematics, vol. 2167, pp. 73–129. Fond. CIME/CIME Found. Subser (Springer, Cham, 2016)

    Google Scholar 

  56. S. Hoehme, D. Drasdo, A cell-based simulation software for multi-cellular systems. Bioinformatics 26(20), 2641–2642 (2010)

    MATH  Google Scholar 

  57. H.J. Hwang, K. Kang, A. Stevens, Global solutions of nonlinear transport equations for chemosensitive movement. SIAM. J. Math. Anal. 36, 1177–1199 (2005)

    MathSciNet  MATH  Google Scholar 

  58. F. James, N. Vauchelet, Chemotaxis: from kinetic equations to aggregate dynamics. Nonlinear Diff. Eq. Appl. 20(1), 101–127 (2013)

    MathSciNet  MATH  Google Scholar 

  59. T. Kawakami, Y. Sugiyama, Uniqueness theorem on weak solutions to the Keller-Segel system of degenerate and singular types. J. Diff. Equ. 260(5), 4683–4716 (2016)

    MathSciNet  MATH  Google Scholar 

  60. E.F. Keller, L.A. Segel, Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 30, 235–248 (1971)

    MATH  Google Scholar 

  61. I. Kim, N. Požár, Porous medium equation to Hele-Shaw flow with general initial density. Trans. Amer. Math. Soc. 370(2), 873–909 (2018)

    MathSciNet  MATH  Google Scholar 

  62. J.-G. Liu, A. Lorz, A coupled chemotaxis-fluid model: global existence. Ann. Inst. H. Poincaré Anal. Non Linéaire 28(5), 643–652 (2011)

    MathSciNet  MATH  Google Scholar 

  63. T. Lorenzi, A. Lorz, B. Perthame, On interfaces between cell populations with different mobilities. Kinetic and Related Models 10(1), 299–311 (2016)

    MathSciNet  MATH  Google Scholar 

  64. J.S. Lowengrub, H.B. Frieboes, F. Jin, Y.-L. Chuang, X. Li, P. Macklin, S.M. Wise, V. Cristini, Nonlinear modelling of cancer: bridging the gap between cells and tumours. Nonlinearity 23, R1–R91 (2010)

    MathSciNet  MATH  Google Scholar 

  65. B. Mazzag, I. Zhulin, A. Mogilner, Model of bacterial band formation in aerotaxis. Biophys. J. 85, 3558–3574 (2003)

    Google Scholar 

  66. A. Mellet, B. Perthame, F. Quiros, A Hele-Shaw problem for tumor growth. J. Funct. Anal. 273, 306–3093 (2017)

    MathSciNet  MATH  Google Scholar 

  67. N. Mittal, E.O. Budrene, M.P. Brenner, A. Van Oudenaarden, Motility of Escherichia coli cells in clusters formed by chemotactic aggregation. Proc. Natl. Acad. Sci. USA 100, 13259–13263 (2003)

    Google Scholar 

  68. M. Mizoguchi, M. Winkler, Blow-up in the two-dimensional parabolic Keller-Segel system. Per. Commun.

    Google Scholar 

  69. J.D. Murray, Mathematical Biology, vol. 2, 2nd edn. (Springer, Berlin, 2002)

    Google Scholar 

  70. G. Nadin, B. Perthame, L. Ryzhik, Traveling waves for the Keller-Segel system with Fisher birth terms. Interface Free Bound 10, 517–538 (2008)

    MathSciNet  MATH  Google Scholar 

  71. H. Othmer, S. Dunbar, W. Alt, Models of dispersal in biological systems. J. Math. Biol. 26, 263–298 (1988)

    MathSciNet  MATH  Google Scholar 

  72. H.G. Othmer, T. Hillen, The diffusion limit of transport equations II: Chemotaxis equations. SIAM J. Appl. Math. 62, 122–1250 (2002)

    MathSciNet  MATH  Google Scholar 

  73. B. Perthame, Math. Tools for Kinetic Equations. Bull. Am. Math. Soc. 41(2) (2004)

    Google Scholar 

  74. B. Perthame, Transport equations in biology. In: Frontiers in Mathematics (Birkhäuser Verlag, Basel, 2007), x+198 pp.

    Google Scholar 

  75. B. Perthame, N. Vauchelet, Z. Wang, The flux limited Keller-Segel system; properties and derivation from kinetic equations. Rev. Mat. Iberoam. 36(2), 357–386 (2020)

    MathSciNet  MATH  Google Scholar 

  76. B. Perthame, S. Yasuda, Stiff-response-induced instability for chemotactic bacteria and flux-limited Keller-Segel equation. Nonlinearity 31, 4065–4089 (2018)

    MathSciNet  MATH  Google Scholar 

  77. B. Perthame, F. Quiròs, J.-L. Vàzquez, The Hele-Shaw asymptotics for mechanical models of tumor growth. Arch. Ration. Mech. Anal. 212(1), 93–127 (2014)

    MathSciNet  MATH  Google Scholar 

  78. B. Perthame, M. Tang, N. Vauchelet, Traveling wave solution of the Hele–Shaw model of tumor growth with nutrient. Math. Models Methods Appl. Sci. 24(13), 2601–2626 (2014)

    MathSciNet  MATH  Google Scholar 

  79. B. Perthame, M. Tang, N. Vauchelet, Derivation of the bacterial run-and-tumble kinetic equation from a model with biochemical pathway. J. Math. Biol. 73(5), 1161–1178 (2016)

    MathSciNet  MATH  Google Scholar 

  80. A.B. Potapov, T. Hillen, Metastability in chemotaxis model. J. Dyn. Diff. Equat. 17(2), 293–330 (2005)

    MathSciNet  MATH  Google Scholar 

  81. L. Preziosi, A. Tosin, Multiphase modeling of tumor growth and extracellular matrix interaction: mathematical tools and applications. J. Math. Biol. 58, 625–656 (2009)

    MathSciNet  MATH  Google Scholar 

  82. L. Preziosi, G. Vitale, A multiphase model of tumor and tissue growth including cell adhesion and plastic reorganization. Math. Models Methods Appl. Sci. 21(9), 1901–1932 (2011)

    MathSciNet  MATH  Google Scholar 

  83. J. Ranft, M. Basan, J. Elgeti, J.-F. Joanny, J. Prost, F. Jülicher, Fluidization of tissues by cell division and apoptosis. Proc. Natl. Acad. Sci. U. S. A. 107(49), 20863–20868 (2010)

    Google Scholar 

  84. B. Ribba, O. Saut, T. Colin, D. Bresch, E. Grenier, J. P. Boissel, A multiscale mathematical model of avascular tumor growth to investigate the therapeutic benefit of anti-invasive agents. J. Theoret. Biol. 243(4), 532–541 (2006)

    MathSciNet  Google Scholar 

  85. T. Roose, S. Chapman, P. Maini, Mathematical models of avascular tumour growth: a review. SIAM Rev. 49(2), 179–208 (2007)

    MathSciNet  MATH  Google Scholar 

  86. J. Saragosti, V. Calvez, N. Bournaveas, A. Buguin, P. Silberzan, B. Perthame, Mathematical description of bacterial traveling pulses. PLoS Comput. Biol. 6(8), e1000890 (2010)

    Google Scholar 

  87. J. Saragosti, V. Calvez, N. Bournaveas, B. Perthame, A. Buguin, P. Silberzan, Directional persistence of chemotactic bacteria in a traveling concentration wave. Proc. Natl. Acad. Sci. 108(39), 16235–16240 (2011)

    Google Scholar 

  88. J.A. Sherratt, M.A.J. Chaplain, A new mathematical model for avascular tumour growth. J. Math. Biol. 43(4), 291–312 (2001)

    MathSciNet  MATH  Google Scholar 

  89. G. Si, M. Tang, X. Yang, A pathway-based mean-field model for E. coli chemo-taxis: mathematical derivation and keller-segel limit. Multiscale Model Simul. 12(2), 907–926 (2014)

    Google Scholar 

  90. M.J. Tindall, P.K. Maini, S.L. Porter, J.P. Armitage, Overview of mathematical approaches used to model bacterial chemotaxis II: bacterial populations. Bull Math Biol. 70, 1570–1607 (2008)

    MathSciNet  MATH  Google Scholar 

  91. J.-L. Vázquez, The porous medium equation. Mathematical theory. Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, Oxford, 2007). ISBN:978-0-19-856903-9

    Google Scholar 

  92. M. Winkler, Emergence of large population densities despite logistic growth restrictions in fully parabolic chemotaxis systems. Discrete Contin. Dyn. Syst. Ser. B 22(7), 2777–2793 (2017)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author has received partial funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 740623) and partial funding from the ANR blanche project Kibord ANR-13-BS01-0004 funded by the French Ministry of Research.

Author information

Authors and Affiliations

  1. Sorbonne Université, CNRS, Université de Paris, Inria, Laboratoire Jacques-Louis Lions, Paris, France

    Benoît Perthame

Authors
  1. Benoît Perthame
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Benoît Perthame .

Editor information

Editors and Affiliations

  1. Department of Mathematical Sciences, Polytechnic University of Turin, Torino, Italy

    Davide Ambrosi

  2. MOX, Dipartimento Di Matematica, Polytechnic University of Milan, Milano, Italy

    Pasquale Ciarletta

Rights and permissions

Reprints and permissions

Copyright information

© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG

About this chapter

Check for updates. Verify currency and authenticity via CrossMark

Cite this chapter

Perthame, B. (2020). Models of Cell Motion and Tissue Growth. In: Ambrosi, D., Ciarletta, P. (eds) The Mathematics of Mechanobiology. Lecture Notes in Mathematics(), vol 2260. Springer, Cham. https://doi.org/10.1007/978-3-030-45197-4_2

Download citation

Publish with us

Policies and ethics

Search

Navigation